Presión osmótica

 Regresar a [Propiedades de las disoluciones]

 Este fenómeno, también denominado depresión del volumen de un solvente puro o aumento en el volumen de un solvente impuro, se alinea más directamente con los nombres de otras propiedades coligativas y describe de forma más precisa su funcionamiento mecánico.

Figura 1. [Jean-Antoine Nollet] fue un físico, químico y sacerdote francés, pionero de la electricidad experimental. Investigó la electricidad estática, empleó la botella de Leyden y realizó célebres demostraciones públicas sobre conducción eléctrica. Sus experimentos y escritos impulsaron el desarrollo de la electrostática y la divulgación científica en el siglo XVIII.

Figura 2. [Dorothy Jordan Lloyd] fue una bioquímica británica pionera en el estudio de proteínas, coloides, geles y membranas semipermeables. Investigó cómo el agua y los solutos atraviesan estructuras gelatinosas, aportando bases para comprender la ósmosis, la hidratación proteica y el desarrollo posterior de membranas artificiales.

En los modelos, en lugar de presiones, observamos cambios de volumen. Se refiere a la tendencia de flujo de agua (o solvente) a través de una membrana semipermeable que permite el paso del solvente, pero no del soluto, hacia el lado con mayor cantidad de impurezas. Al igual que sucede con el cambio en la temperatura crítica, las impurezas son indiferentes a la identidad del soluto o incluso a su tamaño; todas cuentan por igual, ya que se comportan como entidades ideales en este contexto.

Figura 1. La presión osmótica en un tubo en U se define por la diferencia de alturas causada por concentraciones iniciales de soluto. El flujo de solvente va al lado de mayor concentración. Modelamos esto con fuerzas opuestas, donde el lado con más soluto ejerce una presión osmótica neta positiva, atrayendo agua hasta el equilibrio.

La noción de presión osmótica surge debido a que este cambio de volumen puede generar una diferencia de alturas en un manómetro de doble salida abierta, donde normalmente se esperaría una alineación de los niveles de líquido. Esta diferencia indica un cambio en la presión interna que altera el equilibrio hidrostático. El lado con más impurezas, al absorber líquido, aumenta su presión interna, elevándose en contra de la presión de la atmósfera hasta alcanzar el equilibrio. Así, la presión osmótica es la presión que se debe aplicar para evitar el flujo neto de solvente a través de la membrana semipermeable, lo que demuestra la resistencia de la disolución impura a diluirse más allá de cierto punto.

El tono y las células

En una mezcla isotónica, las concentraciones de soluto en ambos lados de la membrana son iguales, y no hay flujo neto de solvente entre las dos soluciones, ya que las concentraciones de soluto son las mismas. Esto es lo que ocurre, por ejemplo, en los fluidos corporales, como la solución salina fisiológica, que tiene la misma concentración de soluto que el plasma sanguíneo, por lo que no provoca movimiento de agua hacia dentro o fuera de las células.

Por otro lado, la ósmosis inversa es el proceso en el que el flujo de solvente ocurre en dirección contraria, desde la región más concentrada (hipertónica) hacia la menos concentrada (hipotónica), pero solo cuando se aplica una presión externa mayor a la presión osmótica. Este proceso es utilizado en sistemas de filtración de agua, como en el purificador de agua doméstico, donde se obliga al agua a pasar a través de una membrana semipermeable, eliminando impurezas y contaminantes. Por ejemplo, si se aplica presión a un lado de un sistema de ósmosis inversa, el agua pasará a través de la membrana dejando atrás las impurezas que no pueden atravesarla.

Cuando se tiene una mezcla hipertónica, el punto analizado (el interior de una célula, por ejemplo) está más concentrado en soluto que el punto externo. En este caso, el agua del entorno fluye hacia el interior de la célula para equilibrar las concentraciones, lo que provoca que la célula se hinche y aumente su volumen. Este proceso puede ser dañino si el volumen celular se incrementa demasiado, lo que puede llevar a la ruptura celular. Un ejemplo claro de esto es el caso de la deshidratación celular cuando una célula se encuentra en un medio hipertónico, como una disolución salina muy concentrada.

Figura 2. Las células mantienen su volumen en soluciones isotónicas. En hipotónicas, el agua entra y pueden estallar; en hipertónicas, sale y se arrugan. Han desarrollado mecanismos como paredes celulares, osmorregulación activa o vacuolas contráctiles para resistir estas tensiones tónicas. Células especializadas en ambientes extremos acumulan solutos compatibles para sobrevivir.

En una mezcla hipotónica, el punto analizado está menos concentrado que el punto externo, lo que provoca que el agua fluya desde el exterior de la célula hacia su interior. Este flujo de agua puede hacer que la célula aumente de volumen hasta el punto de romperse, en un proceso conocido como lisis celular. Un ejemplo de esto sería una célula animal colocada en agua pura (hipotónica), donde el agua ingresará a la célula debido a la diferencia de concentración y presión, lo que podría resultar en la ruptura de la célula si no se regula adecuadamente.

Escenarios comparativos

Como con todas las propiedades coligativas, los escenarios comparativos no se resuelven utilizando su fórmula específica, sino a través del teorema de cantidad de sustancia efectiva. Esto se debe a que es la cantidad de sustancia efectiva es la que realmente impulsa y modifica estas propiedades. Esta cantidad representa la suma real de todas las entidades (partículas) presentes en el equilibrio de la disolución.

[Teoremas de la presión osmótica] Factor marcado [1] Presión osmótica neta [2] Presión osmótica en función de la molaridad efectiva [3] Presión osmótica en función de la molaridad de sustancia [4] Presión osmótica en función de la masa de sustancia Álgebra simbólica [1] Presión osmótica neta [2] Presión osmótica en función de la molaridad efectiva [3] Presión osmótica en función de la molaridad de sustancia [4] Presión osmótica en función de la molaridad de sustancia Demostraciones [Demostración de los teoremas de la presión osmótica] Parámetros y unidades comunes \(\Delta \Pi\) Presión osmótica neta; \(\Pi\) Presión osmótica interna o del lado derecho; \(\Pi_{rev}\) Presión osmótica externa o del lado izquierdo; \(R\) constante del gas ideal (0.08206 atm L / mol K); \(T\) Temperatura absoluta (K); \(c_{ef}\) concentración molar efectiva, \(i_{i}\) factor de van´t Hoff (adimensional); \(c_{i}\) concentración molar de sustancia (mol/L; M); \(m_{i}\) masa de sustancia (g); \(M_{i}\) masa molar de sustancia (g/mol; u); \(V}\) volumen de disolución (L);

Miremos un ejemplo.

Ejemplo 1.  El agua de mar contiene 3,4 g de sales por cada litro de solución. Suponiendo que el soluto consiste enteramente en NaCl (58.44 u) (de hecho, más del 90% de la sal es de hecho NaCl), calcule la presión osmótica del agua de mar a 20 °C. Etapa analítica. Usaremos la forma [4] de [Teoremas de la presión osmótica]. La temperatura absoluta es 293.15 K. Asumiremos un factor de ionización teórico de 2. Etapa numérica por factor marcado. Etapa numérica por álgebra simbólica.

Oposición de fuerzas

Normalmente, modelamos la presión osmótica en un tubo en U, lo que nos genera un escenario de oposición de fuerzas semejante al de una máquina de Atwood con una polea. Es decir, tendremos dos fuerzas opuestas. Esto se debe a que a ambos lados de la membrana semipermeable podemos tener solvente con soluto, por ende, dos presiones osmóticas en oposición [1] [Teoremas de la presión osmótica] que generarán una presión osmótica neta.

Este escenario de oposición no se observa en otras situaciones semejantes, como la depresión de la presión de vapor. En el caso de la presión de vapor, el solvente en la fase gaseosa actúa como si siempre fuera puro por definición, simplificando el análisis a una única presión de vapor ejercida por la disolución. Sin embargo, en la ósmosis, esta suposición de pureza en uno de los lados bien puede no ser cierta. La presencia de solutos en ambos compartimentos del tubo en U crea una competencia por el flujo de solvente, resultando en una diferencia de presiones osmóticas que impulsa el movimiento neto hasta alcanzar el equilibrio. 

Simplificación estándar

A pesar de la complejidad que la presencia de solutos en ambos compartimentos introduce, en la mayoría de los ejercicios de lápiz y papel, se ejecuta una simplificación estándar: asumiremos que uno de los lados, usualmente el externo o izquierdo, está puro. Esta convención, aunque arbitraria en cuanto a qué lado es "puro" (podría ser el derecho o izquierdo, da igual), simplifica drásticamente el cálculo. El punto clave es que siempre tendremos un lado puro y otro impuro.

El lado impuro siempre será nuestro marco de referencia positivo. Esto significa que, al calcular la presión osmótica, siempre esperaremos y buscaremos valores positivos. Esto se debe a que el flujo neto de solvente ocurrirá siempre hacia el lado con mayor concentración de soluto (el lado impuro), generando una presión que se considera positiva en este contexto. Por ende, siempre calcularemos presiones osmóticas positivas, a menos que el enunciado del problema presente variantes complejas que explícitamente sugieran una situación de equilibrio o flujos netos en la dirección opuesta, lo cual es raro en ejercicios introductorios. Esta simplificación permite a los estudiantes centrarse en el concepto fundamental de la ósmosis sin sobrecargar los cálculos iniciales. 

En la mayoría de los casos donde se incluye la ósmosis inversa, esta siempre está ajustada para recuperar los niveles y concentraciones originales de la disolución pura o deseada. Por esta razón, su valor absoluto es igual al de la presión osmótica directa. Esto significa que, aunque conceptualmente la ósmosis inversa se opone al flujo osmótico natural (requiriendo una presión externa para forzar el solvente hacia el lado de menor concentración), en la práctica podremos resolverla utilizando la misma magnitud que la presión osmótica interna del lado de referencia positivo. Es decir, calculamos la presión osmótica como si fuera el proceso directo, y simplemente interpretamos ese valor como la presión que necesitamos aplicar (o que se opone al flujo) para revertir la ósmosis, aunque su sentido físico sea opuesto

Dirección del flujo osmótico a R y T constantes

En condiciones constantes de temperatura (T) y considerando la constante universal de los gases (R), como ocurre en la interfaz de una membrana semipermeable, la dirección del flujo osmótico está determinada exclusivamente por la diferencia de concentración efectiva neta entre ambos lados. Específicamente, el lado con la mayor cantidad de partículas de soluto total (o mayor concentración efectiva) es el que genera una presión osmótica a su favor, atrayendo el solvente y, por ende, impulsando el flujo osmótico hacia sí mismo. Esto significa que para determinar la dirección del flujo, solo es necesario calcular y comparar las concentraciones efectivas netas de cada lado. Ni siquiera necesitas realizar una resta explícita; la mera inspección de cuál lado posee la mayor concentración efectiva ya te indicará la dirección del flujo.

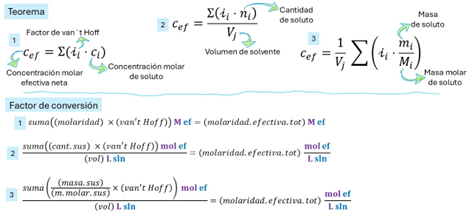
[Teoremas de la concentración molar efectiva] Factor marcado [1] En función de las concentraciones de sustancia [2] En función de las cantidades de sustancia [3] En función de las masas de sustancia Álgebra simbólica [1] En función de las concentraciones de sustancia [2] En función de las cantidades de sustancia [3] En función de las masas de sustancia Demostraciones [Teoremas de la concentración molar efectiva] Parámetros y unidades comunes \(c_{ef}\) concentración molar efectiva neta (mol/L o M); \(i_{i}\) factor de van´t Hoff (adimensional); \(c_i\) concentración molar de la sustancia (mol/L o M); \(n_i\) cantidad de la sustancia (mol o adimensional);  \(m_i\) masa de la sustancia (g);  \(M_i\) masa molar de la sustancia (g/mol o u).

 

Referencias

Baeza Baeza, J. J., & García Álvarez-Coque, M. C. (2014). Extent of reaction balances. A convenient tool to study chemical equilibria.

Brown, T. L., LeMay, H. E. Jr., Bursten, B. E., Murphy, C. J., & Woodward, P. M. (2022). Chemistry: The Central Science (15th ed., AP Edition). Pearson Savvas Higher Education.

Chang, R., & Overby, J. (2022). Chemistry (14th ed., AP Edition). McGraw Hill.

da Silva, D. J. (2017). The basis of the limiting reagent concept, its identification and applications. World Journal of Chemical Education, 5(1), 1-8.

DeToma, R. P. (1994). Symbolic algebra and stoichiometry. Journal of chemical education, 71(7), 568.

García García, J. L. (2020). El álgebra de la estequiometría. Educación química, 31(1), 138-150.

García García, J. L. (2021). Deduciendo las relaciones entre las unidades de concentración en disoluciones líquidas. Educación química, 32(3), 38-51.

García García, J. L. (2021b). Hacia un equilibrio químico verdaderamente analítico. Educación química, 32(1), 133-146.

García, J. L. G. (2025). Dimensional Analysis in Chemistry Textbooks 1900-2020 and an Algebraic Alternative. Educación Química, 36(1), 82-108.

Garst, J. F. (1974). The extent of reaction as a unifying basis for stoichiometry in elementary chemistry. Journal of Chemical Education, 51(3), 194.

IUPAC. (2019). Compendium of chemical terminology (2nd ed.). IUPAC. https://doi.org/10.1351/goldbook

Moretti, G. (2015). The “extent of reaction”: a powerful concept to study chemical transformations at the first-year general chemistry courses. Foundations of Chemistry, 17(2), 107-115.

Mousavi, A. (2019). Stoichiometry of equations through the Inverse de Donder relation. Chemistry Teacher International, 1(1), 20180006.

Schmitz, G. (2005). What is a reaction rate?. Journal of chemical education, 82(7), 1091.

Smith, W. R., & Missen, R. W. (1979). What is chemical stoichiometry?. Chemical Engineering Education, 13(1), 26-32.

SOLAZ, J. J., & Quilez, J. (2001). Changes of extent of reaction in open chemical equilibria. Chemistry Education Research and Practice, 2(3), 303-312.

Timberlake, K. C. (2024). An Introduction to General, Organic, and Biological Chemistry (14th ed.). Pearson.

Vandezande, J. E., Vander Griend, D. A., & DeKock, R. L. (2013). Reaction extrema: Extent of reaction in general chemistry. Journal of Chemical Education, 90(9), 1177-1179.

Zumdahl, S. S., & Zumdahl, S. A. (2018). Chemistry (10th ed.). Cengage Learning.