Estequiometría de gases

[Estequiometría] Sección 8. Conceptos clave. [Estequiometría de gases] [Tabla de presiones de vapor] Otros conceptos. [Pastillas efervescentes] [Horneando pan]

La estequiometría de gases es la parte de la estequiometría química que estudia las relaciones cuantitativas entre sustancias en una reacción química cuando al menos uno de los componentes del cálculo —ya sea un dato o una incógnita— corresponde a un gas. Este tipo de análisis permite determinar cantidades como el volumen, la masa o el número de moles de un gas involucrado en una reacción, a partir de relaciones molares y leyes físicas que rigen el comportamiento gaseoso.

Existen tres enfoques principales para abordar la estequiometría de gases, dependiendo de las condiciones en las que se encuentra el gas:

1. Estequiometría en condiciones estándar de un gas ideal: Se basa en el supuesto de que el gas se comporta idealmente y se encuentra a condiciones estándar de presión y temperatura (0 °C o 273,15 K y 1 atm). En este caso, se usa el volumen molar estándar de un gas ideal: 1 mol = 22.41 L. Esta aproximación permite simplificar los cálculos, ya que la proporción molar entre gases se puede interpretar directamente como proporción de volúmenes.
2. Estequiometría en condiciones no estándar de un gas ideal: Aquí también se asume que el gas se comporta idealmente, pero se encuentra a condiciones distintas a las estándar. En este caso, se utiliza la ecuación del gas ideal: PV = nRT, donde P es la presión, V el volumen, n el número de moles, R la constante de los gases ideales, y T la temperatura en kelvin. Este enfoque es más general y permite calcular la cantidad de sustancia o volumen bajo cualquier condición.
3. Estequiometría de gases reales: Considera las desviaciones del comportamiento ideal que presentan los gases en condiciones extremas (altas presiones o bajas temperaturas). Se utilizan ecuaciones más complejas como la ecuación de van der Waals. Sin embargo, omitiremos en esta discusión el caso de los gases reales, ya que nuestro enfoque estará centrado únicamente en gases ideales, tanto en condiciones estándar como en condiciones variables.

Así, el estudio de la estequiometría de gases en este contexto se limita a analizar cómo los gases ideales se relacionan con otras sustancias en una reacción química, aprovechando las leyes de los gases y las proporciones molares para resolver problemas cuantitativos con precisión.

Cantidad de reacción y gas en exceso

Observa que, para este punto, ya hemos definido la cantidad de sustancia de múltiples formas: a partir de la masa (moles = masa / masa molar), de la concentración molar (moles = M·V), del volumen molar en condiciones normales (CN) y de la ley de los gases ideales en condiciones generales. Todas estas expresiones pueden integrarse en el teorema mol a mol, permitiendo convertir una cantidad química en otra según convenga.

Figura 1. Cantidad de reacción en condiciones normales. Demostración.

Figura 2. Cantidad de reacción para cualquier condición. Demostración.

Sin embargo, esta versatilidad tiene un costo: nos enfrentamos a una proliferación de rutas, fórmulas y teoremas posibles. A este fenómeno lo llamamos el problema de la proliferación estequiométrica. Lo mismo ocurre con los factores de conversión: surgen tantos caminos posibles para resolver un mismo problema que el sistema se vuelve una red intrincada. Aunque todos los caminos convergen en el ratio estequiométrico —la relación entre moles en la ecuación balanceada—, el exceso de opciones puede confundir al estudiante y fragmentar el aprendizaje.

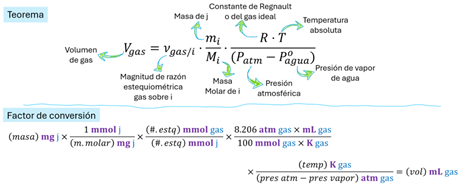
Figura 3. Volumen remanente del gas reactante en exceso. Demostración.

Figura 4. Volumen remanente del gas reactante en exceso en cualquier condición. Demostración

Figura 5. Presión remanente del gas reactante en exceso en cualquier condición. Demostración

Por esta razón, proponemos una estrategia más simple y unificadora: calcular siempre la cantidad de reacción, es decir, los moles de la propia reacción “la cantidad de veces que ocurre la reacción en moles”, y desde ahí usar únicamente las expresiones específicas según el tipo de dato. En el caso de los gases, esto nos deja solo dos expresiones clave, ambas basadas en la ley de los gases ideales:

Estas dos ecuaciones son suficientes y pueden despejarse según sea necesario. Así, reducimos la complejidad del sistema sin perder capacidad de análisis.

Estequiometría de masas y gases

Plantearemos la estequiometría gas-masa exclusivamente porque resulta especialmente relevante en el contexto de un diseño experimental clásico: el desplazamiento de gases. Este procedimiento permite medir indirectamente la cantidad de sustancia generada o consumida en una reacción química mediante el volumen de gas desplazado, lo que lo convierte en una técnica fundamental en laboratorios educativos y profesionales.

Figura 6. Estequiometría gas a masa. Demostración.

Figura 7. Estequiometría gas a masa. Demostración.

Además, esta ruta es la más comúnmente utilizada en los libros de texto al abordar ejercicios de estequiometría de gases, ya que conecta de forma clara y directa conceptos como masa, moles y volumen gaseoso, facilitando así el aprendizaje y la resolución de problemas prácticos. Su uso sistemático responde tanto a su utilidad experimental como a su valor pedagógico.

Desplazamiento de gases

El experimento de desplazamiento de gases es un diseño experimental clásico en química que permite recolectar un gas producido durante una reacción mediante su desplazamiento de un líquido, generalmente agua. Este gas se acumula en un recipiente invertido, como una probeta o bureta, sumergido en agua. El volumen desplazado proporciona una medida indirecta de la cantidad de gas generado.

La diferencia clave entre este experimento y un ejercicio típico de estequiometría masa-gas radica en la naturaleza del gas recolectado. En los problemas teóricos, se asume que el gas es puro y corresponde únicamente al producto gaseoso de la reacción. Sin embargo, en el experimento real, la burbuja de gas recogida no está compuesta exclusivamente por el gas de interés, sino que también contiene vapor de agua, debido a la evaporación del líquido desplazado. Esta contribución del vapor de agua se manifiesta como una presión parcial adicional, conocida como la presión de vapor del agua.

Figura 8. Estequiometría de desplazamiento de gases para la masa. Demostración.

Figura 9. Estequiometría de desplazamiento de gases para la burbuja. Demostración.

Por esta razón, el gas recolectado en este experimento representa una mezcla de gases, lo que exige aplicar tanto el principio de Dalton de presiones parciales como las ecuaciones del gas ideal para aislar la cantidad real del gas deseado. Así, el análisis experimental del desplazamiento de gases se convierte en una intersección entre la estequiometría, la física de gases y las propiedades del agua, exigiendo una mayor atención a las condiciones del sistema, como la temperatura y la presión ambiental.

Figura 10. Diseño experimental del desplazamiento de gases.

Referencias

Baeza Baeza, J. J., & García Álvarez-Coque, M. C. (2014). Extent of reaction balances. A convenient tool to study chemical equilibria.

da Silva, D. J. (2017). The basis of the limiting reagent concept, its identification and applications. World Journal of Chemical Education, 5(1), 1-8.

García García, J. L. (2020). El álgebra de la estequiometría. Educación química, 31(1), 138-150.

García García, J. L. (2021). Deduciendo las relaciones entre las unidades de concentración en disoluciones líquidas. Educación química, 32(3), 38-51.

García García, J. L. (2021b). Hacia un equilibrio químico verdaderamente analítico. Educación química, 32(1), 133-146.

Garst, J. F. (1974). The extent of reaction as a unifying basis for stoichiometry in elementary chemistry. Journal of Chemical Education, 51(3), 194.

IUPAC. (2019). Compendium of chemical terminology (2nd ed.). IUPAC. https://doi.org/10.1351/goldbook

Moretti, G. (2015). The “extent of reaction”: a powerful concept to study chemical transformations at the first-year general chemistry courses. Foundations of Chemistry, 17(2), 107-115.

Mousavi, A. (2019). Stoichiometry of equations through the Inverse de Donder relation. Chemistry Teacher International, 1(1), 20180006.

Schmitz, G. (2005). What is a reaction rate?. Journal of chemical education, 82(7), 1091.

Smith, W. R., & Missen, R. W. (1979). What is chemical stoichiometry?. Chemical Engineering Education, 13(1), 26-32.

SOLAZ, J. J., & Quilez, J. (2001). Changes of extent of reaction in open chemical equilibria. Chemistry Education Research and Practice, 2(3), 303-312.

Vandezande, J. E., Vander Griend, D. A., & DeKock, R. L. (2013). Reaction extrema: Extent of reaction in general chemistry. Journal of Chemical Education, 90(9), 1177-1179.