Calorimetría a presión constante

[Termoquímica] Sección 5. Conceptos clave. [Calorimetría a presión constante] [Calorimetría a volumen constante] Otros conceptos. [Termos comerciales]

La calorimetría es la rama de la termodinámica que se encarga de la medición del calor transferido durante un proceso físico, químico o biológico. Su objetivo principal es determinar los cambios de energía que acompañan a estas transformaciones, cuantificando el calor absorbido o liberado. Para ello, utiliza un instrumento especializado conocido como calorímetro, diseñado para aislar el sistema y permitir una medición precisa de los intercambios de calor.

La calorimetría a presión constante es un tipo específico de calorimetría donde las mediciones se realizan manteniendo la presión del sistema constante durante todo el proceso. Esto es particularmente relevante porque en muchos procesos químicos y biológicos, las reacciones ocurren a presión atmosférica constante. Las mediciones de calor bajo estas condiciones se relacionan directamente con el cambio de entalpía (ΔH) del sistema. Un ejemplo común de calorímetro a presión constante es el calorímetro de taza de café, utilizado para reacciones en solución acuosa.

Figura 1. El calorímetro de taza de café mide cambios de temperatura en reacciones a presión constante, usando vasos de icopor, tapa de corcho, termómetro y agitador. Para resultados precisos, la tapa debe ajustarse bien. No se recomienda usar aluminio, ya que aumenta la conductividad térmica, lo que compromete el aislamiento y la exactitud del experimento.

En calorimetría, abordaremos dos escenarios principales: la calorimetría de cuerpo inerte y la calorimetría de cuerpo reactivo. Cada uno de estos tipos de calorimetría posee su propia serie de fórmulas y metodologías específicas para cuantificar los intercambios de calor involucrados.

Calorimetría de cuerpo inerte

En la calorimetría de cuerpo inerte, interactúan dos cuerpos o sustancias con temperaturas iniciales diferentes. Estos intercambian calor hasta alcanzar una temperatura de equilibrio común. Dentro del calorímetro, que actúa como un sistema aislado, se busca que este punto de equilibrio sea independiente del entorno externo. Por ello, la capacidad calorífica del propio calorímetro debe ser nula o significativamente despreciable, lo que implica que el instrumento no absorbe ni emite calor de forma apreciable.

La calorimetría para un cuerpo inerte se basa en el flujo de calor entre dos sustancias: una de propiedades incógnita o variable, y otra, generalmente agua, cuyas propiedades son conocidas. El principio fundamental es que el cuerpo inerte NO reacciona químicamente con el agua; su interacción se limita a un intercambio puramente físico de calor.

Dado que el teorema general puede ser complejo de despejar en casos triviales, propondremos fórmulas concretas. Estas se adaptarán a dos situaciones principales: (a) donde sea sencillo despejar parámetros como el calor específico, la masa o la diferencia de temperaturas de la sustancia incógnita y (b) el cálculo de las temperaturas inicial o final de la sustancia incógnita.

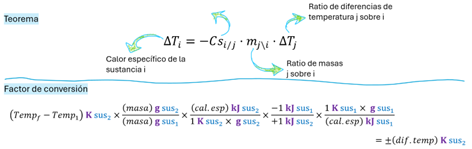
Figura 2. Calor específico de un cuerpo incógnita (i) típicamente un metal, usando el calor específico de un solvente (j), típicamente agua, por factores de conversión y teoremas algebraicos. Se expresa con ratios inversos de masas y diferencias de temperatura (parámetros de j en el numerador, i en el denominador).

Figura 3. Masa de un cuerpo incógnita (i), como un metal, se usa un solvente conocido (j), usualmente agua. El cálculo se logra con factores de conversión o teoremas algebraicos, empleando ratios inversos de calores específicos y diferencias de temperatura (j en numerador, i en denominador). Ambas herramientas facilitan la precisa caracterización térmica.

Figura 4. Diferencia de temperatura de la sustancia incógnita (i), como un metal, usando propiedades de i y un solvente (j). Permite, además, hallar trivialmente la temperatura inicial de i si se conoce la temperatura de equilibrio. Su versatilidad facilita diversas resoluciones en calorimetría.

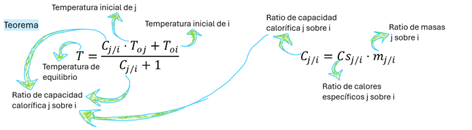
Figura 5. Calcular la temperatura de equilibrio en calorimetría inerte es complejo. Su demostración, con factores comunes y repetición de cuatro términos, es tediosa. Se simplifica usando una razón de calores específicos. No se ofrece factor de conversión porque sumas/restas dificultan el seguimiento dimensional, revelando una debilidad en este método para leyes de conservación.

Con estos teoremas podremos resolver ejercicios sobre calorimetría de cuerpo inerte a presión constante.

Calorimetría de cuerpo reactivo

Por otro lado, en la calorimetría de cuerpo reactivo, se estudia una reacción química que libera o absorbe energía. A medida que la reacción avanza, esta energía calórica provoca un cambio en la temperatura del sistema. Normalmente, estas son reacciones sencillas en las que un metal muy reactivo o alguna otra sustancia se expone a un solvente reactante, como agua o algún ácido. A este respecto, es muy importante saber elegir el material del calorímetro, ya que algunos materiales pueden verse atacados por ciertos reactivos. Por lo tanto, es conveniente seleccionar materiales inertes y resistentes a la corrosión o disolución por parte de los reactivos empleados, como el vidrio de borosilicato o plásticos específicos.

Por ejemplo, el ácido clorhídrico permite reacciones rápidas y exotérmicas, pero su alta reactividad puede atacar y disolver ciertos materiales del calorímetro, comprometiendo la integridad del experimento y la precisión de las mediciones. Es por esto que la mayoría de las experiencias con este fenómeno se realizan con calorímetros con recubrimientos internos resistentes para reacciones en solución que generen calor, asegurando que el calorímetro no participe en la reacción ni altere los resultados.

Un problema adicional en este escenario surge al trabajar con disoluciones molares, donde el parámetro de concentración molar (denotado con 'c' "minúscula" según la IUPAC) puede coincidir visualmente con los símbolos utilizados para la capacidad calorífica (C "mayúscula") y los calores específicos (Cs). Esta similitud en la notación es una fuente potencial de confusión. Por lo tanto, es imperativo que, al aplicar los teoremas pertinentes, se preste una atención rigurosa al contexto de cada símbolo y a las unidades asociadas para asegurar una correcta interpretación y evitar errores en los cálculos.

Continuando, la mayoría de los ejercicios que hemos abordado sobre este escenario versan precisamente sobre disoluciones reactivas en agua. Por ello, vale la pena tener en cuenta las siguientes consideraciones: normalmente, las temperaturas iniciales de las disoluciones son las mismas, y el calor específico de las disoluciones es semejante al del agua. Esto es una extensión de los presupuestos que vimos en las propiedades coligativas concernientes a la disolución ideal.

Si bien la disolución ideal tiene impurezas que marcan su identidad reactiva, para el calor específico, y para todas las consideraciones significativas, asumiremos que este será igual al del agua, sin importar si la disolución es ácida o básica. Por ende, a priori, para los ejercicios de lápiz y papel, supondremos que el calor específico de las disoluciones es el mismo que el del agua. Lo mismo sucede con las densidades, a menos que el ejercicio las proporcione explícitamente. Esto nos permitiría convertir de un plumazo los volúmenes en masas, utilizando la densidad del agua de 1 g/mL o 1 kg/L.

Figura 6. El teorema del calorímetro de taza de café aplica a reacciones en disoluciones líquidas ideales, donde una es limitante y el agua actúa como solvente. Se iguala el calor absorbido por el solvente con la entalpía de reacción. Asumiendo densidades y calores específicos iguales, se puede calcular la entalpía estándar a partir de temperaturas y volúmenes medidos.

Figura 7. En un calorímetro de taza de café con sólido reactivo, la cantidad de reacción se calcula con masa y masa molar, asumiendo que el sólido es el reactivo limitante. El solvente, usualmente agua, debe estar en exceso. Aunque algunas reacciones liberan gas, se considera despreciable su efecto en la presión constante del sistema.

Figura 8. La entalpía de la reacción de un reactivo disuelto adapta el modelo tradicional usando concentración molar y volumen en lugar de moles directos. Esto permite trabajar con disoluciones en el laboratorio. El factor de conversión relaciona volumen, molaridad, estequiometría y entalpía estándar para obtener la entalpía experimental en kilojulios, útil en prácticas escolares y análisis termodinámico

Con estos teoremas podremos resolver ejercicios sobre calorimetría de cuerpo reactivo a presión constante.

Referencias

Baeza Baeza, J. J., & García Álvarez-Coque, M. C. (2014). Extent of reaction balances. A convenient tool to study chemical equilibria.

Brown, T. L., LeMay, H. E. Jr., Bursten, B. E., Murphy, C. J., & Woodward, P. M. (2022). Chemistry: The Central Science (15th ed., AP Edition). Pearson Savvas Higher Education.

Chang, R., & Overby, J. (2022). Chemistry (14th ed., AP Edition). McGraw Hill.

da Silva, D. J. (2017). The basis of the limiting reagent concept, its identification and applications. World Journal of Chemical Education, 5(1), 1-8.

DeToma, R. P. (1994). Symbolic algebra and stoichiometry. Journal of chemical education, 71(7), 568.

García García, J. L. (2020). El álgebra de la estequiometría. Educación química, 31(1), 138-150.

García García, J. L. (2021). Deduciendo las relaciones entre las unidades de concentración en disoluciones líquidas. Educación química, 32(3), 38-51.

García García, J. L. (2021b). Hacia un equilibrio químico verdaderamente analítico. Educación química, 32(1), 133-146.

García, J. L. G. (2025). Dimensional Analysis in Chemistry Textbooks 1900-2020 and an Algebraic Alternative. Educación Química, 36(1), 82-108.

Garst, J. F. (1974). The extent of reaction as a unifying basis for stoichiometry in elementary chemistry. Journal of Chemical Education, 51(3), 194.

IUPAC. (2019). Compendium of chemical terminology (2nd ed.). IUPAC. https://doi.org/10.1351/goldbook

Moretti, G. (2015). The “extent of reaction”: a powerful concept to study chemical transformations at the first-year general chemistry courses. Foundations of Chemistry, 17(2), 107-115.

Mousavi, A. (2019). Stoichiometry of equations through the Inverse de Donder relation. Chemistry Teacher International, 1(1), 20180006.

Schmitz, G. (2005). What is a reaction rate?. Journal of chemical education, 82(7), 1091.

Seager, S. L., Slabaugh, M. M., & Hansen, M. M. (2022). Chemistry for Today (10th ed.). Cengage Learning.

Serway, R. A., & Jewett, J. W. J. (2014). Physics for Scientists and Engineers with Modern Physics, Ninth Edition (9th ed.). Boston: Brooks/Cole.

Smith, W. R., & Missen, R. W. (1979). What is chemical stoichiometry?. Chemical Engineering Education, 13(1), 26-32.

SOLAZ, J. J., & Quilez, J. (2001). Changes of extent of reaction in open chemical equilibria. Chemistry Education Research and Practice, 2(3), 303-312.

Timberlake, K. C. (2024). An Introduction to General, Organic, and Biological Chemistry (14th ed.). Pearson.

Tipler, P. A., & Llewellyn, R. A. (2012). Modern Physics (6th ed.). New York: Freeman.

Vandezande, J. E., Vander Griend, D. A., & DeKock, R. L. (2013). Reaction extrema: Extent of reaction in general chemistry. Journal of Chemical Education, 90(9), 1177-1179.

Zumdahl, S. S., & Zumdahl, S. A. (2018). Chemistry (10th ed.). Cengage Learning.