A finales del siglo XVIII, los científicos lograron un
avance crucial al descubrir relaciones consistentes entre presión, volumen
y temperatura en los gases, lo que dio origen a las leyes de
los gases. Estas leyes surgieron de una observación rigurosa y
experimentación meticulosa. Aunque los resultados experimentales no eran
idénticos debido a la variabilidad natural y a las limitaciones de los
instrumentos, fue posible establecer relaciones matemáticas simples mediante el
redondeo de los datos, lo que permitió formular principios generales con
notable precisión para la época.
Las leyes empíricas de los gases se desarrollaron a
lo largo de varios siglos, siendo consolidadas durante la Revolución
Francesa y el Imperio Napoleónico, una época de profundos avances
científicos impulsados por la necesidad de entender fenómenos naturales en un
contexto de agitación política y social. Sin embargo, la formulación de la ecuación
de estado para los gases, que unifica y generaliza estas leyes, se planteó
en un entorno de mayor estabilidad política tras la Paz de Viena
(1815), cuando Europa comenzó a reorganizarse después de las guerras
napoleónicas. Esta estabilidad permitió un desarrollo más sistemático de la
ciencia, facilitando la colaboración internacional y la consolidación de
teorías fundamentales en la termodinámica y la química.
Rectas
Las relaciones entre presión, volumen y temperatura
se convirtieron en la base de las leyes de los gases, aplicables a una
amplia variedad de sustancias y fundamentales para entender su comportamiento
en distintas condiciones. El estudio de estas leyes ha evolucionado con el
tiempo, sentando las bases de la termodinámica y teniendo un impacto
clave en la ciencia y la tecnología modernas.
Figura 1.
La mayoría de estas leyes se basan en un modelo matemático
simple: la recta. Este puede adoptar dos formas principales: una recta
ascendente, que representa una relación directamente proporcional, y
una curva asintótica, que refleja una relación inversamente
proporcional. La primera se observa en la ley de Charles y la ley
de Gay-Lussac, donde el aumento de una variable implica el aumento
proporcional de otra, lo que se representa con una pendiente positiva en un
gráfico.
La segunda forma aparece en la ley de Boyle-Mariotte,
que establece una relación inversa entre presión y volumen: al
aumentar una, la otra disminuye. En un gráfico, esto se muestra como una curva
que se aproxima a los ejes sin tocarlos. Esta ley es única entre las leyes de
los gases por adoptar esta representación inversa.
Figura 2. La inversa de la recta, representada como 1/x, describe una relación donde, al aumentar una variable, la otra disminuye proporcionalmente. En química, esta relación es clave en fenómenos como la ley de Boyle, donde la presión y el volumen de un gas son inversamente proporcionales. Este modelo es fundamental para entender el comportamiento de gases en condiciones de presión variable.
Dado que la mayoría de estas relaciones son lineales,
siempre intervienen dos variables: una dependiente y una independiente,
unidas por una constante de proporcionalidad. Esta constante permite
expresar las ecuaciones en una forma más dinámica, útil para describir cambios
de estado en los sistemas gaseosos.
Principales autores
La ecuación de estado de los gases ideales es un
modelo matemático que describe el comportamiento de los gases reales,
basándose en un concepto idealizado conocido como gas ideal, cuya
naturaleza es puramente conceptual. Aunque el gas ideal no tiene existencia
física, su utilidad radica en que, bajo ciertas condiciones de presión y
temperatura, los gases reales muestran un comportamiento similar
al gas ideal debido a la baja interacción entre sus partículas y la
insignificancia de su volumen.
Figura
3. Benoît Paul Émile Clapeyron (26 de
enero, 1799 - 28 de enero, 1864) fue un ingeniero y físico francés, padre
(entre otros) de la teoría termodinámica
Cuando los gases reales alcanzan temperaturas extremadamente
bajas o presiones muy altas, pueden transformarse en líquidos. Si la
temperatura es excesivamente alta, los gases reales pueden descomponerse o
ionizarse. En cambio, el gas ideal permanece en estado gaseoso en todas las
condiciones, ya que es solo una construcción teórica.
La formulación de la ecuación de los gases ideales se
basó en observaciones empíricas y en las contribuciones de científicos como Benoît
Paul Émile Clapeyron, Rudolf Julius Emmanuel Clausius y Henri
Victor Regnault, cuyas investigaciones fueron fundamentales para el
desarrollo de las leyes empíricas que describen el comportamiento de los gases
en condiciones específicas.
Figura
4. Rudolf Julius Emmanuel Clausius,
físico alemán del siglo XIX, es conocido por sus contribuciones a la
termodinámica, especialmente por su formulación del segundo principio y el
concepto de entropía.
Conversiones de temperatura
Benoît Paul Émile Clapeyron jugó un papel fundamental al
establecer una relación entre presión y volumen de los gases,
aunque su ecuación original no describía directamente el volumen, sino el volumen
específico. Este último, que es la inversa de la densidad del gas,
fue un concepto clave en su formulación. Además, la ecuación de Clapeyron
incorporaba la temperatura en grados Kelvin, pero con un valor de cero
absoluto ligeramente distinto, usando 267 en lugar de 273.15.
Más tarde, Henri Victor Regnault corrigió esta
conversión, adoptando el valor de 273 para el cero absoluto, lo que ajustó la
ecuación a la temperatura absoluta correcta. Así, la ecuación de estado
de los gases ideales quedó expresada como P u = R (273 + t), donde P
es la presión, u el volumen específico (la inversa de la
densidad), t la temperatura, y R la constante de
proporcionalidad.
La elección de la letra R para la constante en la
ecuación no tiene un origen claro históricamente. Sin embargo, es ampliamente
aceptado que podría ser un homenaje a Henri Victor Regnault, cuyas
valiosas contribuciones experimentales permitieron corregir la ecuación para
adaptarla a la escala de temperatura. Por ello, la constante R a menudo
se conoce como la constante de Regnault en reconocimiento a su impacto
en la formulación correcta de la ecuación.
Figura
5. Henri Victor Regnault, científico
francés del siglo XIX, destacó en la física y la química, investigando
propiedades de los gases y contribuyendo al estudio de la termodinámica y la
calorimetría.
Originalmente, la ecuación era conocida como la ley de
Mariotte-Gay-Lussac, ya que los científicos franceses tendían a asociar la
ley de Boyle con el nombre de Mariotte. De esta forma, la ley de Mariotte-Gay-Lussac
describe la relación entre presión, volumen específico y temperatura
de un gas, y su nombre rinde homenaje a Edme Mariotte y Joseph Louis
Gay-Lussac, quienes fueron clave en su desarrollo.
El concepto de gas ideal
La ecuación de estado de los gases ideales es eficaz
en condiciones prácticas, siempre que las mediciones no requieran una precisión
extrema y que no se superen las temperaturas y presiones críticas.
Bajo estas condiciones, la mayoría de los gases reales tienden a
ajustarse a los resultados teóricos de la ecuación. Aunque la ecuación puede
generar valores ligeramente diferentes en los valores críticos, en 1864, Rudolf
Clausius introdujo el concepto de gas ideal, un gas que siempre se
ajusta a la ecuación, sin importar la temperatura o presión. Sin
embargo, es importante señalar que el gas ideal es una entidad puramente
conceptual, similar a un ideal platónico.
Este concepto ha ganado gran relevancia en química, ya que
sirve como base para modelos más avanzados, que se exploran en áreas como la termodinámica,
la termoquímica y la ingeniería. Aunque el gas ideal es un
concepto abstracto, resulta ser una herramienta clave para comprender y modelar
fenómenos gaseosos en la práctica científica y en aplicaciones tecnológicas.
La diferencia entre los gases ideales y los gases
reales es significativa. Mientras que los gases reales, al calentarse en
exceso, pueden ionizarse, y al enfriarse demasiado, se condensan en líquidos,
los gases ideales no presentan tales comportamientos. Además, los gases reales
muestran ligeras diferencias en volúmenes y presiones ideales debido
a las interacciones entre partículas, mientras que los ideales son
conceptualmente perfectos, aunque no existen físicamente.
Una forma imperfecta
Sin embargo, existe un considerable trayecto desde la simple
expresión:
\[P \cdot u = R (273 + t)\]
hasta la moderna ecuación de estado.
Empecemos con el término (273 + t), que representa la
fórmula básica para convertir la temperatura a la escala absoluta en kelvin.
Esto simplifica la ecuación a
\[P \cdot u = R \cdot T\]
No obstante, aún faltan dos componentes esenciales: el volumen
simple V y la cantidad de sustancia n. Este último
parámetro no fue definido hasta casi 100 años después. Por lo tanto, durante la
primera mitad del siglo XX, la ecuación del gas ideal tal como la
conocemos hoy no existía en su forma completa.
Referencias
Brown, T.
L., LeMay, H. E. J., Bursten, B. E., Murphy, C. J., Woodward, P., &
Stoltzfus, M. W. (2015). Chemistry the Central Science.
Brown, T.
L., LeMay, H. E. J., Bursten, B. E., Murphy, C. J., Woodward, P., Stoltzfus, M.
W., & Lufaso, M. W. (2022). Chemistry, the central science (15th ed.).
Pearson.
Chang, R.
(2010). Chemistry (10th ed.). McGraw-Hill New York.
Chang, R.,
& Overby, J. (2021). Chemistry (14th ed.). McGraw-Hill.
Jensen, W.
B. (2003). The universal gas constant R. Journal of Chemical Education, 80(7),
731.
Matamala, M., & González Tejerina, P. (1975). Química
(1ª ed.). Bogotá: Ediciones Cultural.
Seager, S.
L., Slabaugh, M. M., & Hansen, M. M. (2022). Chemistry for Today (10th
ed.). Cengage Learning.
Zumdahl, S.
S., Zumdahl, S. A., DeCoste, D. J., & Adams, G. (2018). Chemistry
(10th ed.). Cengage Learning.




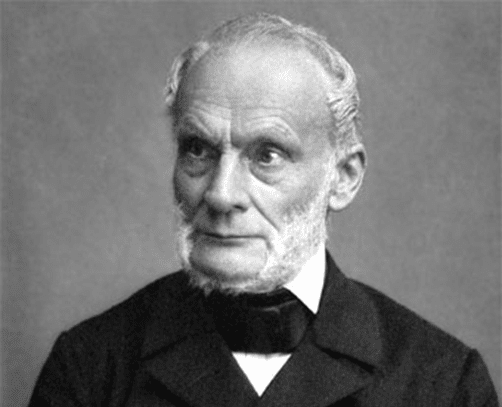

No hay comentarios:
Publicar un comentario