Índice
Portada
Reglamento
|| REGRESAR AL INDICE ||
IED Venecia. José Luís García García, salón 312
Correo: jlgarciag@educacionbogota.edu.co
Mecanismo de evaluación
Actividades de cuaderno de aula y de tareas 35%.
👉 Evaluación uno 25 %
👉 Evaluación dos 25 %
👉 Cuaderno 25%
👉 Proyecto Ambiental Escolar 10%
👉 Coevaluación 10%
👉 Asistencia 5%
Adicionalmente se manejará un sistema de puntos positivos por:
👉 Apoyar en el aseo del salón.
👉 Participación.
👉 Resolución de ejercicios de lápiz y papel
👉 Resolución de ejercicios en tablero.
👉 Y puntos negativos por Indisciplina
El cuaderno de química/biología debe ser un cuaderno cuadriculado, GRANDE de cualquier marca. Necesitará 6 colores de cualquier marca, lápiz, borrador y dos esferos de colores diferentes.
Puntualidad con respecto a la entrega de actividades
Las actividades solo se evalúan dentro de la semana de plazo asignada, después de lo cual no serán evaluadas. La única excepción es que no tengamos sesiones en la semana asignada y la evaluación deberá posponerse a la siguiente semana, o que presente una excusa justificada.
Las fallas justificadas serán única y exclusivamente las que expida el coordinador de disciplina Hector Rojas en forma de un documento con sello y firma, las cuales deberán presentarse de manera simultánea con las actividades evaluadas el día que no asistió.
El rango de espera para poder presentar la actividad no deberá superar nunca las dos semanas posteriores al reingreso, después de las cuales, las actividades no serán evaluadas aun con la justificación.
Evaluación de la asistencia y disciplina
La asistencia se evaluará con un máximo de tres llamados, ante los cuales deberá prestar atención pues:
👉 Si contesta al primer llamado su nota será 50.
👉 Si contesta al segundo llamado su nota será 40.
👉 Si contesta al segundo llamado su nota será 30.
👉 Después del tercer llamado se define un retardo o inasistencia, discriminados de la siguiente manera:
👉 Retardo leve: reportar su asistencia después del tercer llamado, pero antes de que el profesor inicie la clase. Nota de 25.
👉 Retardo fuerte no justificado: es aquel que interrumpe la clase. Nota de 20.
👉 Evasión: No presentarse al aula y/o no reportarse en caso de haber llegado muy tarde. Nota de cero.
👉 Falla justificada nota de 49.9
👉 Falla injustificada nota de 10
Retardos justificados 49.8.
👉 Al llegar tarde, recuerde siempre acercarse para retirarle la falla 10 por un retardo 20, de lo contrario la falla permanece, y para clases de dos bloques, cuenta por doble falla y por ende, por doble nota.
Plataforma
Una vez que se consignan sus nombres en la planilla se les asignará un código para la realización de las tareas en línea. Para ello deberá acceder a la plataforma:
https://cienciasdejoseleg.blogspot.com/2023/01/2023-indice.html
Reglamento de tareas
Las tareas se basan fundamentalmente en la consulta de principios teóricos. Los criterios para evaluar las tareas son:
👉 Presencia de contenidos.
👉 Habilidad artística en texto: tipo de letra, majeo del color, presentación de las figuras.
👉 Habilidad artística en ilustraciones, tablas y gráficas: Las figuras solo contarán si son dibujadas a MANO, no se aceptan recortes.
👉 Densidad: se acepta renglón de por medio a letra pequeña, si usa letra grande solo para consumir espacio, será tenido en cuenta negativamente.
👉 Extensión: Cada página cuenta como un punto a la tarea. La extensión mínima será de 3 páginas.
👉 Sustentación: Al evaluar la tarea se realizarán preguntas, aquellos que no las respondan tendrán una penalización del 20% sobre la nota básica de su tarea.
Tareas período 1
|| REGRESAR AL INDICE ||
Semana 1
Semana 2
Semana 3
Semana 4
Semana 5
Semana 6
El nuevo sistema internacional
Lenguaje del sistema internacional
Semana 7
Semana 8
(2) Historia de las ecuaciones del movimiento
El cálculo en física el inicio hasta el punto 5.3, del 5.4 en adelante lo vemos en clase
Semana 9
Dibujos PRAE del período.
Realizar la ilustración del personaje en la portada y consultar su biografía.
Tareas período 2
|| REGRESAR AL INDICE ||
Semana 10
Fechas del 10 abril al 14 abril.
Semana 11
Fechas del 17 abril al 21 abril.
Conversiones de unidades. Teoría y los ejemplos, pero no los ejercicios finales.
Semana 12
Fechas del 24 abril al 28 abril.
Prefijos decimales (deben estar las tablas de equivalencias de prefijo a potencia)
Conversiones de unidades. Copiar la resolución de los ejercicios de Química la ciencia central 13 desde Muestra 1.10 hasta el último, debe anotar las suficientes instrucciones como para que usted puesa usar dichos procedimientos para resolver ejercicios diferentes.
PRAE II, abril. (Dibuijarlo en el cuaderno y resolver las preguntas).
Semana 13
Fechas del 01 mayo al 05 mayo.
Parámetros fundamentales del movimiento rectilíneo
Semana 14
Fechas del 08 mayo al 12 mayo.
Movimiento rectilíneo uniforme MUR: Conceptos teóricos y ecuaciones clave claras, resaltadas y elegantes.
Semana 15
Fechas del 15 mayo al 19 mayo.
Movimiento rectilíneo uniformemente acelerado MRUA: Conceptos teóricos y ecuaciones clave claras, resaltadas y elegantes.
Semana 16
Fechas del 22 mayo al 26 mayo.
Semana 17
Fechas del 29 mayo al 02 junio.
Componentes de un vector euclidiano
Semana 18
Fechas del 05 junio al 09 junio. Realizar un resumen de las siguientes presentaciones y resolver las preguntas (si ya se que el primero lo vimos en clase, pero tengo mis dudas sobre si recuerdan esa parte del procedimiento)
||18.1|| Si la velocidad instantánea de la tortuga es la derivada del cambio infinitesimal de posición con respecto al tiempo, y que la posición está dada por:
Donde rx es la posición final en el eje x, vx es la velocidad con la que se mueve en el eje x y t es el tiempo como variable independiente. Plantee la fórmula de derivación.
||18.2|| Si la velocidad instantánea de Aquiles es la derivada del cambio infinitesimal de posición con respecto al tiempo, y que la posición está dada por:
Donde rx es la posición final en el eje x, ax es la aceleración con la que se mueve en el eje x y t es el tiempo. Plantee la fórmula de derivación.
||18.3|| ¿Es posible derivar un polinomio completo?
||18.4|| ¿Qué debemos hacer con un polinomio para poder derivarlo?
||18.5|| ¿Cuál es el único símbolo que debe derivarse?
||18.6|| ¿Qué pasa con los valores o los símbolos que no sean la variable de derivación?
||18.7|| ¿Cuál es la derivada de una constante, sea esta símbolo o valor?
||18.8|| ¿Cuál es la regla de derivación de una variable de derivación elevada a una constante?
||18.9|| ¿Se deben hacer otras operaciones al reemplazar las derivadas parciales?
||18.10|| ¿Cuál es la derivada de la variable de derivación cuando esta tiene exponente uno?
||18.11|| ¿Cómo se lee g en el segundo ejemplo?
||18.12|| ¿Cómo se lee vo en el segundo ejemplo?
||18.13|| ¿Cómo se lee ro,y en el segundo ejemplo?
||18.14|| ¿Qué pasa con una constante que no esté acompañando a la variable de derivación?
||18.15|| ¿Qué implicación física tiene asumir que vo,y = 0?
||18.16|| ¿Por qué razón una operación de derivación aparenta ser tan compleja?
Anote los siguientes procedimientos pulsando en el enlace para ver la explicación.
Resuelva los siguientes ejercicios.
||18.20|| Un automóvil se desplaza en línea recta y su posición en función del tiempo está dada por la ecuación r = -(1/2)kt2 + 10zt + 2, donde r representa la posición en metros y t el tiempo en segundos. Encuentra la velocidad instantánea del automóvil en el instante t = 5 segundos.
R = v = 5 m/s.
||18.21|| Una partícula se mueve a lo largo de una trayectoria recta, y su posición en función del tiempo está dada por la ecuación r = (1/2)t2 + 8t, donde r representa la posición en metros y t el tiempo en segundos. Determina la velocidad de la partícula en el instante t = 4 segundos. Plantee las constantes de proporcionalidad necesarias para el análisis dimensional.
R: v = 12 m/s. k1 = m/s2. k1 = m/s.
||18.22|| Un objeto se desplaza en línea recta y su posición en función del tiempo está dada por la ecuación r= (1/3)t3 - (1/2)t2 + 8t, donde r representa la posición en metros y t el tiempo en segundos. Halla la aceleración del objeto en el instante t = 10 segundos. Corrija las unidades para obtener una aceleración de m/s2.
R: v = 9 m/s2.
Que tengan suerte
Semana 19
Fechas del 12 junio al 16 junio.
|
Tareas período 3
|| REGRESAR AL INDICE ||
Semana 20
Fechas del 10 julio al 14 julio.
|20.1|| Copie el siguiente ejercicio con las suficientes instrucciones como para resolver uno de estructura semejante:
|20.2|| Copie la siguiente lección sobre integrales:
||20.3|| Transcriba el siguiente ejercicio con las instrucciones necesarias para resolver uno semejante.
||20.4|| Transcriba el siguiente ejercicio con las instrucciones necesarias para resolver uno semejante.
||20.5|| Transcriba el siguiente ejercicio con las instrucciones necesarias para resolver uno semejante.
||20.6|| Transcriba el siguiente ejercicio con las instrucciones necesarias para resolver uno semejante.
Semana 21
Fechas del 17 julio al 21 julio.
Transcriba los siguientes ejemplos con las suficientes indicaciones para resolver ejercicios semejantes.
Ejemplo. Un móvil se desplaza a velocidad constante de 90 km/h. ¿Qué distancia recorre en 3 s?
Semana 22
Fechas del 24 julio al 28 julio.
Transcriba los siguientes ejemplos con las suficientes indicaciones para resolver ejercicios semejantes.
Ejemplo. Desde el reposo, un automóvil aceleró a 8 m/s2 durante 10 segundos. a) ¿Cuál es la posición del automóvil al final de los 10 segundos? b) ¿Cuál es la velocidad del automóvil al final de los 10 segundos?
Semana 23
Fechas del 31 julio al 04 agosto.
Semana 24
Fechas del 07 agosto al 11 agosto.
Semana 25
Fechas del 14 agosto al 18 agosto.
Copie las indicaciones de la lección teórica sobre vectores y las ecuaciones clave.
Transcriba los siguientes ejemplos con las suficientes indicaciones para resolver ejercicios semejantes.
Ejemplo. Dibuje el vector que inicia en el punto (3, 4) y termina en el punto (5, 6).
Ejemplo. Dibuje el vector que inicia en el punto (-3.5, 1) y termina en el punto (0, 4).
Ejemplo. Un objeto se desplaza con una velocidad de (5.0; 330°) m/s en coordenadas polares. Convierte esta velocidad a coordenadas cartesianas.
Ejemplo. Sume los siguientes vectores y determine la resultante. 3.0 m/s, 45 grados y 5.0 m/s, 135 grados
Semana 26
Fechas del 21 agosto al 25 agosto.
Semana 27
Fechas del 28 agosto al 01 septiembre.
Transcriba los siguientes ejemplos con las suficientes indicaciones para resolver ejercicios semejantes.
1. Vectores 2.
4. Lección teórica, el tiro parabólico.
5. Como resolver un ejercicio de tiro parabólico.
Semana 28
Fechas del 04 septiembre al 08 septiembre.
6. Un cañón que forma un ángulo de 45° con la horizontal lanza un proyectil a 20.0 m/s, a 20.0 m de este se encuentra un muro de 21.0 m de altura, asuma de la aceleración gravitacional es 10 m/s2. Determinar: a. a que altura del muro hace impacto el proyectil b. que altura máxima lograra el proyectil c. que alcance tendrá d. cuanto tiempo transcurrirá entre el disparo y el impacto en el muro.
Semana 29
Fechas del 11 septiembre al 15 septiembre.
1. Lección. Dinámica 1, Leyes de Newton
2. Lección. Dinámica 2, Analítica de las leyes de Newton.
3. Convierta 5.0 libras-fuerza a newtons.
4. Convierta 40.0 newtons a dinas
Solución de la evaluación tema A.
Tareas período 4
|| REGRESAR AL INDICE ||
Semana 30
Fechas del 18 septiembre al 22 septiembre.
1. Lección. Dinámica 3. Peso, Normal y elástica
5. Demostración. Determine la constante de un resorte, cuando a este le cuelga una masa y se deforma al estirarse
Semana 31
Fechas del 25 septiembre al 29 septiembre.
1. Lección. Dinámica 4: externas, contacto y tensiones.
2. Demostración. Demuestre una fórmula para calcular la fuerza de contacto resultante al comprimir dos cajas con fuerzas opuestas.
9. Calcule las tensiones entre las cuerdas A y B si se sabe que sostienen un cuerpo de 200 N.
10. Calcule las tensiones entre las cuerdas A a 50° y B a 0° si se sabe que sostienen un cuerpo de 800 N.
Semana 32
Fechas del 02 octubre al 06 octubre.
Semana 33
Fechas del 16 octubre al 20 octubre.
1a- Demostración del formulario para planos inclinados de uno o dos cuerpos.
1b- Optimización del formulario para planos inclinados de uno o dos cuerpos.
2 Calcule la aceleración de dos masas unidas por una polea en un plano inclinado doble, donde las masas son 40 y 300 kg, los ángulos 53 y 37 y los coeficientes de rozamiento 0.3 a ambos lados versión 1.
2a- (Método clásico)- Solución por algoritmo clásico.
2b- (Método alternativo)- Solución por algoritmo de 4 ecuaciones.
3 Dos masas están conectadas por una cuerda que corre sobre una polea sin fricción. La masa m1 = 16 kg está sobre un plano inclinado de 30° y la masa m2 = 4 kg está suspendida libremente el coeficiente de fricción cinético entre el bloque y el plano es de 0.2 ¿cuál es la aceleración de las masas?
3a- (Método clásico)- Solución por algoritmo clásico.
3b- (Método alternativo)- Solución por algoritmo de 4 ecuaciones.
4 Dos bloques de 3.50 kg y 8 kg de masa se conectan por medio de una cuerda de masa despreciable que pasa por una polea sin fricción. El coeficiente de fricción cinético en todas las superficies es de 0.25. Nos piden calcular la aceleración del sistema y la tensión del sistema.
4a- (Método clásico)- Solución por algoritmo clásico.
4b- (Método alternativo)- Solución por algoritmo de 4 ecuaciones.
5- Resuelva el siguiente cuestionario con la información presentada.
Semana 34
Fechas del 23 octubre al 27 octubre.
Sin tareas
Semana 35
Fechas del 30 octubre al 03 Noviembre.
Realizar un resumen del texto desde la introducción hasta completar la sección 4
https://cienciasdejoseleg.blogspot.com/2023/09/energia.html
Semana 36 en adelante
Sin tareas
1. Las matemáticas y las ciencias de la naturaleza.
|| REGRESAR AL INDICE ||
"Sin las matemáticas no se puede hacer nada. Todo lo que nos rodea es matemático. Todo lo que nos rodea son números". – Shakuntala Devi, escritora y calculista mental india, conocida como la "mujer computadora" por su capacidad para los cálculos mentales.
Objetivo: reconocer la importancia de las matemáticas puras o abstractas con los fenómenos naturales.
Nota: no se altere con las soluciones numéricas presentadas, lo que nos interesa de momento son las ideas que fundamentan dichas soluciones, por ejemplo, que una ecuación lineal permite describir una línea recta, que un cuadrado describe una ecuación cuadrática, o que un cubo describe una ecuación cúbica.
Preguntas introductorias
||1.1|| ¿Está usted de acuerdo con la de Shakuntala Devi? Explique su respuesta en un párrafo con una frase que contenga su idea, dos frases que argumenten o soporten su idea, y una frase que concluya todo.
||1.2|| ¿Cómo cree usted que surgieron las matemáticas originalmente?
Vea el siguiente video Cómo se Inventaron los Números Imaginarios (Enlace →) y responda las siguientes preguntas.
https://www.youtube.com/watch?v=VN7nipynE0c
||1.3|| ¿Cuál era el problema de los matemáticos puros con la ecuación cúbica ax3+bx2+cx+d=0? Explique su respuesta en un párrafo con una frase que contenga su idea, dos frases que argumenten o soporten su idea, y una frase que concluya todo.
||1.4|| ¿Cómo se resuelve la ecuación cuadrática general ax2+bx+c=0 actualmente y como se resolvía antes de la invención de la notación algebraica moderna?
||1.5|| Explique la razón por la cual los matemáticos de la edad media no publicaban sus descubrimientos inmediatamente, y cuál era la consecuencia de esto en el avance de la ciencia y las matemáticas.
||1.6|| ¿Con que objeto geométrico de resolvieron los problemas del tipo ax3+bx+c=0?
||1.7|| ¿Qué es un algoritmo matemático y como se escribían en la edad media?
||1.8|| ¿Cuál es el problema con la raíz cuadrada en un número negativo y como se llaman este tipo de números?
||1.9|| ¿Cuál fue el impacto de los números imaginarios en la química-física moderna?
2. Unidades, medidas y propiedades de la materia 1.
|| REGRESAR AL INDICE ||
Objetivo: Aprender a leer los símbolos en química y física para las unidades fundamentales del sistema internacional.
La química básica tradicionalmente se modela mediante algoritmos aritméticos instructivos, que funcionan como recetas culinarias. Sin embargo, otra parte del curso de química se modela mediante algoritmos algebraicos, los cuales usan la notación algebraica inventada por François Viète “Francisco Vieta” en 1591.
2.1 Siguiendo un algoritmo
Siendo las variables a, b y c:
||2.1|| Si el primer objeto tiene valor de 1, y sabemos que el segundo objeto tiene el mismo valor del primero, determine el valor del segundo objeto.
||2.2|| El primer objeto tiene un valor de 3, sume este valor con otro 3.
||2.3|| Multiplique el valor del primer objeto que es 3, con el valor de un segundo objeto que también es 3.
2.2 Principio de identidad
En matemáticas, una identidad es la constatación de que dos objetos que matemáticamente se escriben diferente, son de hecho el mismo objeto.
||2.4|| Siendo a = 1, si a = b, ¿Cuánto vale b?
||2.5|| Siendo a = 5, si b = a +5, ¿Cuánto vale b?
||2.6|| Siendo a = 5 y b = 5, si c = a x b, ¿Cuánto vale c?
||2.7||¿Cuál es la relación entre los ejercicios anteriores?
||2.8||¿Cuál algoritmo le parece más eficiente, más general y/o más sencillo? Argumente su respuesta con una afirmación, dos argumentos y una conclusión.
2.3 Términos compuestos
Los términos empleados en física y química difieren de los que se usan en algebra pura debido a que hacen referencia a ideas más complejas como mediciones o constantes físicas. Por ejemplo, si deseas expresar la masa de Juanito, lo haces con el símbolo de la magnitud llamada masa (m) seguido con un subíndice o entre paréntesis del objeto medido: mjuanito; m(juanito).
Para generalizar el objeto medido se emplean notaciones algebraicas más cortas, siendo normalmente las letras i, j, k, x, a, b. De esta forma la masa de cualquier objeto representada como mj o m(j).
Existen símbolos especiales como:
👉 Δ: Diferencia o cambio, representa la resta entre un parámetro inicial menos uno final. Por ejemplo, Δt = t – t0
👉 (º): Estándar, ubicado a la derecha y como superíndice indica que un parámetro ha sido estandarizado en una tabla.
👉 (o): Inicial, ubicado a la derecha y como subíndice indica que un parámetro ha sido medido en el estado inicial del sistema.
Nota: aunque la notación subíndice es mas elegante, si usted es malo escribiéndolos, use la notación paréntesis.
||2.9|| Sean los parámetros: volumen V, densidad ρ, presión P, temperatura T, tiempo t, número estequiométrico ν, rapidez v, cantidad de sustancia n, masa m, masa molar M, número de entidades “átomos, moléculas, iones, ruedas, personas, páginas etc” N. Indique cuales símbolos se pueden llegar a confundir, y que va a hacer para evitarlo.
||2.10|| Exprese simbólicamente
El volumen de la mesa k.
La densidad del bloque de madera i.
La presión en la válvula z.
El tiempo transcurrido en la reacción x.
El número estequiométrico del dióxido de carbono CO2.
La rapidez del proyectil número 4 p4.
La masa molar del agua H2O.
El número de átomos de carbono C.
||2.11|| Exprese textualmente
Vj, si j = tanque 1.
ρi, si i = oro metálico.
P0, si 0 = estado inicial del sistema.
T°, si ° = estado estándar o de referencia.
Δn
mi, si i = CO2.
Mi, si i = CO2.
ni, si i = CO2.
Ni, si i = CO2. Nota, CO2 es una molécula.
En ocasiones existen variables complejas en las cuales tenemos más de un símbolo de modificación, por ejemplo, el parámetro avance de reacción ξ, puede presentarse como la diferencia de avance de la reacción r1 estándar:
O la masa inicial del agua.
||2.12|| Exprese simbólicamente
- La diferencia de entalpía (H) estándar de la reacción r1.
- La carga estándar de la reacción r2.
- La cantidad de sustancia estándar de H2O.
- La presión inicial de gas nitrógeno N2.
- La temperatura inicial de gas cloro Cl2.
2.4 Cantidades físicas fundamentales y sus unidades
Los símbolos anteriormente descritos se emplean para representar cantidades o parámetros físicos (Physical Quantities). La gran mayoría de los parámetros físicos poseen unidades asociadas, que permiten su comparación y medición con instrumentos estandarizados.
||2.13|| Con que instrumento de mide:
- La masa.
- La temperatura.
- El tiempo.
Los instrumentos se calibran por medio de encarnaciones físicas de las unidades de medición. Hasta el año 2019 las encarnaciones físicas eran objetos concretos almacenados en la ciudad de Sevres en Francia, por ejemplo, un cilindro único de platino e iridio encarnaba a la propia idea del kilogramo patrón estándar. Sin embargo, a partir del año 2019 las manifestaciones o encarnaciones físicas de las unidades más fundamentales pasan a ser entidades derivadas de constantes físicas fundamentales:
👉 La masa (m) se mide con el kilogramo (kg) definido con la constante de Planck.
👉 La distancia (x entre otros símbolos) se mide con el metro (m) definido con la velocidad de la luz en el vacío.
👉 El tiempo (t) se mide con el segundo (s) definido las vibraciones del átomo de cesio-133.
👉 La intensidad eléctrica (I) se mide con el amperio (A) definido con la constante de carga elemental “el valor absoluto de la carga de un único protón o de un único electrón”.
👉 La temperatura (T) se mide con el kelvin (K) definido con la constante de Boltzman o con la constante de gases ideales y la constante de Avogadro.
👉 La cantidad de sustancia (n) se mide con el mol (mol) definido con el número de Avogadro.
👉 La intensidad luminosa (J) se mide con la candela (cd) definida con la luz del color definido a 5.4x1014 hertz a una potencia de 1/683 watts.
Es importante no confundir un símbolo de cantidad física (masa m) con un símbolo de unidad (metro m), por ende, se aconseja escribir las cantidades físicas un poco más grande y en cursiva, y los símbolos de las unidades, un poco más pequeño y en letra normal. Por ejemplo, la masa de Felipe es igual a 47 kilogramos.
En procesadores de texto la diferencia se basa en cursivas para cantidades físicas y texto normal para las unidades.
Algunas cantidades físicas como el número de entidades son ambiguas. Según el sistema internacional de unidades que es la recomendación de la Unión Internacional de Química Pura y Aplicada IUPAC, dicho parámetro es adimensional, no lleva unidades. Sin embargo, por tradición los escritores de libro de texto indican que la unidad de número de entidades debe ser igual a la entidad contada.
Por comodidad simbólica, seguiremos las recomendaciones de la IUPAC, pero teniendo en cuenta que, si usted busca en un libro de texto, número de entidades estará asociado a la entidad medida como su unidad.
||2.14|| Exprese simbólicamente
- La masa estándar de la unidad patrón del sistema internacional es equivalente a 1000 gramos.
- El desplazamiento, definido como a diferencia entre dos distancias, recorrido por el proyectil p1 fue de unos 500 metros.
- El tiempo que tardó Sandra en recorrer el patio fue de 30 segundos.
- La intensidad eléctrica necesaria para matar a un ser humano es mayor o igual a 0.1 amperios. El símbolo mayor o igual es “menor ≤ mayor”.
- La temperatura estándar en gases “que equivale a 0 °C” es de 273.15 kelvin.
- La cantidad de sustancia inicial del amoníaco fue de 4 moles.
- La intensidad luminosa de un videobeam nuevo es de 3000 candelas para el color blanco.
||2.15|| Exprese textualmente
- m(José) = 70.1 kg.
- Δx(Firulais)cuadra = 70 m.
- t0 = 0 s.
- I(electrólisis) = 4 A.
- T°(disoluciones líquidas) = 298.15 K.
- n(CO2) = 7 mol .
- J(Videobeam)viejo= 1000 cd.
3. Unidades, medidas y propiedades de la materia 2.
|| REGRESAR AL INDICE ||
Objetivo: Vincular varias magnitudes físicas mediante ecuaciones y asociar las ecuaciones a las leyes de la naturaleza que describen las propiedades de la materia, sean estas intensivas o extensivas, químicas o físicas.
||3.1|| Ofrecer un resumen de los temas principales de la lección anterior en 3 frases.
||3.2|| Plantear alguna pregunta sobre lo visto en la lección anterior.
3.1 Propiedades de la materia
En física clásica y química general, la materia es cualquier sustancia que tiene masa y ocupa espacio al tener volumen (Multhauf, 1962), aunque cada tipo de materia puede presentar muchísimas otras propiedades, las cuales son medibles por medio de cantidades físicas. La materia no debe confundirse con la masa, pues esta es solo propiedad de algunos tipos de materia. Por ejemplo, las partículas que forman a la luz, llamadas fotones o cuantos no poseen masa.
3.2 Cualitativas vs cuantitativas
Las propiedades cualitativas se basan en comparaciones relativas de una cantidad física. Sin embargo, la misma cantidad física puede ser también cuantitativa, pero para eso, necesitamos un instrumento que nos traduzca la cualidad en una cantidad numérica.
||3.3|| Defina las siguientes propiedades como cualitativas o cuantitativas.
a-El objeto 1 tiene un color de 535 nanómetros (Enlace) y el objeto 2 de 680 nanometros (Enlace).
b-La dureza se define como la resistencia al rayado, se sabe que ningún objeto natural puede rayar un diamante más que otro diamante de estructura más organizada.
c-La dureza del diamante es de 10 mohs, mientras que la del cuarzo es de 7 mohs.
d-El objeto 1 tiene un color verde y el objeto 2 rojo.
3.3 Intensivas y extensivas
Las propiedades extensivas son las que dependen de la cantidad de materia presentes. Estas normalmente siguen patrones de líneas rectas ascendentes con intercepto en el origen. Adicionalmente, tendremos la presencia de intercepto, y ecuaciones no lineales, cosa que no ocurre con sus equivalentes en química, cuyos interceptos en (y) son casi siempre cero.
||3.4|| Dibujar la gráfica de una hipotética propiedad extensiva que sigue la regla y = x2 + y0.
||3.5|| Si multiplicamos la ecuación anterior por una constante k, ¿Cómo cambiaría la gráfica?
3.4 Químicas y físicas
A diferencia de la química, en física las propiedades de los objetos no dependen de su identidad química, sino que están asociados al objeto debido a su masa, y cantidad de movimiento. Por ejemplo, la ley del movimiento cinético en el eje x, lo que nos importa es que el cuerpo se mueve linealmente en el eje x, no su identidad, por lo que lo mismo da que sea 1 gramo de oro, un electrón o un automóvil:
La cual se interpreta como la velocidad de un cuerpo cualquiera en el eje x es igual a la aceleración constante en el eje x por el tiempo, más la velocidad inicial en x.
||3.6|| Con la Ecuación 3.1:
(a) Despejar el cambio de velocidad Δvx.
(b) Despejar la aceleración en el eje x.
(c) Despejar el tiempo.
(d) Despejar la velocidad inicial en el eje x.
3.5 Homogeneidad dimensional
El símbolo de = en una ecuación química-física no solo implica que los símbolos numéricos son iguales, también implica que las unidades deben ser las mismas. En caso de aparentar no serlo se debe aplicar las reglas del análisis dimensional. La regla fundamental implica que el brazo operativo de la ecuación debe cancelarse de forma tal que las unidades resultantes pertenezcan dimensionalmente al término despejado.
👉 Las unidades de una suma o una resta son iguales a la unidad factor común, como en este calculo de calor estándar del sistema.
👉 Si dos o más unidades homogéneas se multiplican, se deja como base y el exponente indica cuantas se han multiplicado
👉 Las raíces equivalen a potencias fraccionarias. Cuando elevas una potencia a otra potencia, los exponentes se multiplican.
👉 Si una unidad se encuentra en un cociente que multiplica, el numerador multiplicará en la solución, pero el denominador también será denominador en la solución.
👉 Si la misma unidad está multiplicando y dividiendo, se pueden cancelar.
👉 Si una unidad está dividiendo a una división, en realidad está multiplicando.
👉 Si dos modificadores decimales están multiplicando y dividiendo, se pueden cancelar con independencia a las unidades base que estén modificando. Si quedan unidades sin cancelarse, estas pasan a la respuesta.
👉 Los modificadores decimales están sometidos a la ley distributiva de la multiplicación, el orden de los factores no altera el producto, por ende, podemos transferir un modificador decimal de una unidad a otra, sin tener que hacer un paso intermedio de convertir a la potencia base 10.
👉 Si se tiene un cociente de variable semejante con unidad semejantes, las unidades se pueden cancelar analíticamente, es decir, cancelarse mentalmente.
👉 Si se tienen varias opciones para despejar una ecuación y todas son algebraicamente válidas, exprese la forma más elegante. La forma más elegante es aquella que permite hacer el análisis dimensional más sencillo, por ejemplo, en las siguientes opciones, la más elegante es la que permite ver el cociente de presiones.
|
||3.7|| Compruebe la homogeneidad dimensional de los siguientes ejercicios, tendiendo en cuenta el parámetro despejado.
(a) Las unidades del SI para la velocidad y la rapidez son metro sobre segundo (m/s).
(b) Las unidades del SI para la velocidad y la rapidez son metro sobre segundo (m/s).
(c) Las unidades del SI para la aceleración son metro sobre segundo al cuadrado (m/s2).
(d) Despeje la presión final de forma tal que la fórmula esté en su forma más elegante posible.
(e) Calcular la presión final del sistema, empleando la respuesta anterior, si sabemos que la temperatura inicial era de 295 K (unidad de temperatura absoluta kelvin), la presión inicial 202 kPa (unidad de presión kilopascal), y la temperatura final 468 K.
4. Incertidumbre y cifras significativas
|| REGRESAR AL INDICE ||
Objetivo: Reconocer la incertidumbre en una medición, y algunos instrumentos simples para simbolizarla y compararla
||4.1|| Ofrecer un resumen de los temas principales de la lección anterior en 3 frases.
||4.2|| Plantear alguna pregunta sobre lo visto en la lección anterior.
El acto de medir
Medir es comparar una propiedad con un estándar de esa propiedad. El problema radica en que definir el estándar de una propiedad es problemático ya que involucran aspectos más allá de la ciencia, como la tradición cultural, o la importancia política.
||4.3|| El Sistema Imperial de unidades actualmente solo es oficial en los Estados Unidos de América, ¿explique por qué es un sistema de medición que sigue siendo importante en países como Colombia?
A la hora de medir, existen dos tipos de instrumentos, análogos o digitales. Un instrumento análogo es aquel que simple la analogía de la distancia medida con una regla, esto se logra mediante una aguja y una escala móviles acopladas a un instrumento. El mecanismo permite traducir la señal de la propiedad a la aguja o la escala móviles. Los instrumentos digitales emiten el valor en un panel numérico sin hacer la analogía de la regla
||4.4|| Indique si es un instrumento análogo o digital:
Muchas veces la propiedad medida no cabe de manera perfecta en el estándar, por lo que tenemos un valor medido y un residuo que no podemos cuantificar fácilmente. Este valor residual lo llamamos incertidumbre. Todos los instrumentos poseen incertidumbres asociadas a su última cifra medible o significativa, y el modo de leer la incertidumbre cambia si tenemos un instrumento análogo o digital.
👉 La última cifra significativa de un instrumento análogo es la mitad de su graduación más pequeña. Así, por ejemplo:
Deberá reportar 5.35 ± 0.05 cm, donde la última cifra significativa es aquella en la que tenemos dudas por lo ambiguo.
🔎 La expresión xavg ± z, donde xavg es el valor medido promedio y z la incertidumbre lo llamaremos intervalo de confianza.
🔎 Una forma alternativa de expresar un intervalo de confianza es como el rango superior e inferior (xo; x). donde x0 es la frontera más pequeña y x la frontera más grande del intervalo.
||Ejemplo|| Convertir el intervalo de confianza 3.35 ± 0.05 cm a su rango superior e inferior.
||4.5|| Convertir el intervalo de confianza a un rango: 4.5 ± 0.5 L; 750.3 ± 0.5 mL; 300 ± 0.1 s
👉 La última cifra significativa de un instrumento digital es su último dígito medido (el mas pequeño), siendo calibrara a un rango de ± una décima, por ejemplo, en un reloj digital 35.4 s la incertidumbre digital es ±0.1 s.
||4.6|| Reporte los valores de las siguientes mediciones, teniendo en cuenta la incertidumbre.
A-
B-
C-
4.1 Error aleatorio y error sistemático
La incertidumbre vista en la sección anterior es un ejemplo de error sistemático o incertidumbre sistemática, ya que está se debe a los límites tecnológicos de los instrumentos, y siempre son de un mismo tipo. Otro tipo de incertidumbre llamada aleatoria ocurre debido a errores del operario al manipular un instrumento.
||4.7|| Tres estudiantes con el cronómetro de su celular deberán salir, deberán activar y desactivar el cronómetro lo más rápido posible tres veces cuando el profesor de la señal. Anote los resultados y etiquete las medidas para los estudiantes A, B y C. ¿Son los resultados iguales? De no serlo, de una razón de las diferencias.
Los estadísticos han desarrollado múltiples formas, algoritmos y modelos para medir la incertidumbre aleatoria como la desviación estándar, la t de student o la prueba de Z. Por el momento, nos conformaremos nuevamente con un intervalo de confianza, donde (x) es la medida más grande y (xo) la más pequeña.
||4.8|| Estime la incertidumbre sistemática de las medidas de los celulares de los estudiantes A, B y C.
Una vez estimado el error sistemático de un instrumento, expresaremos el resultado como xavg ± z, donde xavg es el valor medido promedio y z la incertidumbre. En este caso, dado que tenemos varias medidas, diferentes, el valor de xavg será igual al promedio aritmético.
||4.9|| Calcule el promedio aritmético para cada uno de los estudiantes.
||4.10|| Exprese cada promedio aritmético con la incertidumbre sistemática en el formato xavg ± z.
||4.11|| Exprese los intervalos de confianza anteriores en el formato de rango (xo; x).
Para calcular la incertidumbre debida a error aleatorio, usaremos una fórmula muy primitiva pero fácil de memorizar.
Donde x es la medición más grande y xo la medición más pequeña.
||4.12|| Calcule la incertidumbre aleatoria z de cada estudiante.
||4.13|| Exprese cada promedio aritmético con la incertidumbre sistemática en el formato xavg ± z.
||4.14|| Marque las incertidumbres sistemáticas debido a los instrumentos como incertidumbres estpandar z°.
||4.15|| Compare la incertidumbre sistemática debido al instrumento z° con la incertidumbre aleatoria debido al operario z. ¿Cuál es la mayor fuente de incertidumbre en una medida?
4.2 Precisión y exactitud
Podemos comparar dos intervalos de confianza de manera muy sencilla, empleando el concepto de error absoluto ε del promedio y de la incertidumbre.
donde μ es el valor verdadero. Para poder tener un intervalo de confianza, podemos emplear la ecuación anterior para la frontera superior e inferior del intervalo de confianza. Así por ejemplo si el sujeto de pruebas tiene los reflejos medidos como (0.44; 0.85; 0.50) generando un intervalo de confianza 0.60 ± 0.21. Si el tiempo de reacción del ser humano es de 0.20 s podemos calcular el error absoluto para el punto medio y el error absoluto de la incertidumbre 200 ± 5 %.
||4.16|| Calcule el error absoluto debido a la incertidumbre sistemática de los estudiantes ABC tanto para los promedios aritméticos como para las incertidumbres.
Los resultados anteriores nos permiten estimar la precisión y la exactitud.
👉 Exactitud
Es la tendencia de una medición o conjunto de mediciones a acercarse al valor verdadero μ. Para aproximarnos a la exactitud emplearemos εavg, la exactitud aumenta a medida que εavg se acerca a cero.
👉 Precisión
Es la tendencia de que varias mediciones se acerquen al punto medio. Para aproximarnos a la presición emplearemos εz, la exactitud aumenta a medida que εz se acerca a cero.
||4.17|| Indique cual es el estudiante que posee la mayor exactitud.
||4.18|| Indique cual es el estudiante que posee la mayor precisión.
4.3 Operaciones con cifras significativas
Es muy común que los resultados de una medición se combinan con otras para obtener un resultado, como sumar dos distancias para obtener un total, o multiplicar largo y ancho para obtener un área, ¿Cómo se determinan las cifras significativas y la incertidumbre?
👉 La regla de redondeo
Dicta que si la primera cifra NO-significativa es 5 o mayor se redondea hacia arriba.
👉 Cifras significativas en sumas y restas
Son iguales al menor número de decimales de confianza de uno de los miembros en una suma. Los decimales no significativos deben operarse para ver que regla de redondeo debe aplicarse.
👉 Cifras significativas en multiplicaciones y divisiones
Son iguales a las cifras que tiene el término con menos cifras significativas.
👉 Notación científica
Si las cifras significativas deben obtenerse de un número muy grande o de uno muy pequeño, se debe aplicar la notación científica.
👉 Disponibilidad de la calculadora
Si cuenta con calculadora, opere con todos los decimales y redondee a las cifras significativas hasta el final.
Si NO cuenta con calculadora, y la respuesta es abierta, redondee al principio con la regla de redondeo normal.
Si NO cuenta con calculadora, y la respuesta es cerrada “selección múltiple”, aplique redondeo de Fermi.
||4.19|| Determine el número de cifras significativas en las siguientes medidas:
(a) 478 cm, (b) 6.01 g, (c) 0.825 m,
(d) 0.043 kg, (e) 1.310 × 1022 átomos, (f) 7000 mL.
||4.20|| Determine el número de decimales de confianza
(a) 0.006 L, (b) 0.0605 dm, (c) 60.5 mg,
||4.21|| ¿Qué diferencia existe entre los valores medidos 4.0 y 4.00 g?
||4.22|| Asuma que el volumen de un cubo de lados x, y, z está mediado por la fórmula:
(a) Calcular el volumen para x = 1.0, y = 2.00, z = 3.000
(b) Calcular el volumen para x = 2.0, y = 2.00, z = 2.000
(c) Calcular el volumen para x = 6.0, y = 3.01, z = 4.001
P1. PRAE I el Chulo.
|| REGRESAR AL INDICE ||
Objetivo: Dar cumplimiento a las actividades PRAE 2023
Con la información contenida en el siguiente enlace.
||P1.30|| Realice una ilustración en el cuaderno siguiendo las instrucciones del tutorial.
||P1.31|| Cual es la importancia de los buitres para el mantenimiento del equilibrio de un ecosistema, argumente su respuesta con un párrafo estándar.||P1.32|| En biología evolutiva tenemos el concepto de evolución convergente, y evolución paralela. La evolución convergente implica la evolución de adaptaciones semejantes a partir de linajes evolutivos independientes. La evolución paralela es un caso de la evolución convergente, donde los dos linajes de los que se generan las especies con apariencia semejante están muy cercanamente emparentados, lo que hace difícil distinguir que son grupos que descienden de ancestros diferentes. Explique porque los buitres son un ejemplo clásico de evolución convergente y de evolución paralela con un párrafo estándar.
||P1.3|| Normalmente se acusa al Condor de los Andes (Vultur gryphus) de tener comportamientos predatorios facultativos frente al ganado, cuando en realidad es el buitre común (Coragyps atratus), lo cual ha llevado a su persecución y casi extinción. Plantee su opinión sobre el comportamiento de los ganaderos, a la luz de los argumentado en el tutorial, empleando un párrafo estándar.
||NOTA|| La estructura de un párrafo estándar es:
(a) Frase número 1, tesis, o afirmación central.
(b) Frases 2 y 3, argumentos obtenidos de la experimentación, el análisis matemático o la observación.
(c) Frase 4, síntesis, una frase que concluye la afirmación a la luz de los datos.
(d) Cada frase debe contener a su vez una estructura mínima de sujeto, verbo y predicado coherentes.
5. El problema de la velocidad instantánea
|| REGRESAR AL INDICE ||
Objetivo: Comprender el concepto de pendiente, pendiente promedio y pendiente instantánea.
||5.1|| Ofrecer un resumen de los temas principales de la lección anterior en 3 frases.
||5.2|| Plantear alguna pregunta sobre lo visto en la lección anterior.
5.1 Coordenadas cartesianas
Algunos enunciados no ofrecen directamente la ecuación, sino que darán un punto inicial po y un punto final p, que cumplen con la notación p(x, y). Esta notación se conoce como el sistema de coordenadas cartesianas. Para dibujar la recta solo debemos trazar una línea entre esos dos puntos. A esta técnica se la conoce como dibujar una cuerda entre dos puntos.
||5.3|| Dibuje la recta que pasa por (-1, 3) y (1, 4)
||5.4|| Dibuje la recta que pasa por (1.5, 1) y (3, 5)
5.2 Dibujando una recta con la técnica de la cuerda
Para dibujar una recta, debemos tener acceso a dos puntos o a la ecuación de la recta. Si tenemos acceso a los dos puntos, simplemente se plasman y se dibuja la recta entre esos dos puntos. Manualmente la recta se obtiene calculando el valor de y para un punto final y un punto inicial de valores arbitrarios de x. Lo más sencillo siempre es reemplaza xo = 0, y x = 1, con lo que obtienes yo y y respectivamente. La recta se traza entre ambos puntos. A esto se lo conoce como la técnica de la cuerda.
||5.5|| Empleando la técnica de la cuerda, dibuje la recta de las siguientes ecuaciones.
(a) y = 1.5 x + 2
(b) v = 1.6 t + 4
5.3 La pendiente de una recta
El cambio en una variable se calcula como a diferencia Δ que hay entre su posición final y su posición inicial. Por ejemplo, para la variable x, será Δx = x – x0.
||5.6|| Plantee el cambio de posición en términos de la posición inicial y final (r).
||5.7|| Plantee el cambio de tiempo en términos de la tiempo inicial y final (t).
Una tasa de cambio es un parámetro relativo que surge del cociente entre dos cambios. Por ejemplo, la velocidad promedio es la pendiente, cociente o tasa de cambio entre el cambio de posición con respecto al cambio en el tiempo:
||5.8|| Plantee las siguientes tasas de cambio en términos de la variable que multiplica sobre la que divide y despliegue la diferencia.
(a) pendiente m en términos del cambio de y con respecto al cambio en x.
(b) aceleración promedio aavg en términos de del cambio en la velocidad promedio con respecto a cambio en el tiempo.
(c) el tirón, sacudida, golpeteo o sobreaceleración promedio javg se define como el cambio de aceleración promedio con respecto al cambio en el tiempo.
(d) La potencia promedio Pavg se define como el cambio en el trabajo mecánico W con respecto al cambio en el tiempo.
5.4 Ecuación de la recta con la gráfica
Para encontrar la ecuación de una recta con los datos de la gráfica o de una tabla de datos, debe hallar la pendiente, y el intercepto en el eje vertical cuando la variable independiente u horizontal vale cero.
||5.9|| Calcule la pendiente y la ecuación de la siguiente recta.
5.5 La cuerda de una curva
No todos los modelos matemáticos empleados para describir un fenómeno físico son rectas, y el primero en darse cuenta de eso fue Galileo. Cuando Galileo medió el tiempo necesario para que un objeto cubra una determinada distancia en una caída libre, se dio cuenta que, a mayor cantidad de tiempo, la distancia recorrida superaba por mucho la esperada de un modelo de líneas rectas.
||5.10|| Ingrese al siguiente simulador de caída libre, enfóquese a la grafica de distancia contra tiempo y determine cual es la función matemática que mas se ajusta a los datos. http://sahyun.net/physics/html5/NGPET_freefall/
El hecho de que la caída libre genere una curva exponencial genera que el concepto de velocidad instantánea sea diferente de la velocidad promedio. La velocidad instantánea es la velocidad de la partícula en un punto único de tiempo, lo cual es complicado:
Resuelva las siguientes preguntas con el video.
||5.11|| ¿Cómo se modifica la posición para que siempre genere valores positivos?
||5.12|| ¿Cuál es el símbolo empleado para representar el parámetro de posición?
||5.13|| ¿Qué fenómeno físico es representado por la gráfica de posición contra tiempo?
||5.14|| Al comparar la distancia que recorre la partícula entre t = 0 y t = 2s con la que recorre entre t = 4 s y t = 6 s podemos afirmar que
(a) es igual (b) es mayor entre t = 0 y t = 2s (c) es mayor entre t = 4s y t = 6s
||5.15|| ¿Cuál es el problema de usar la técnica de la cuerda para intentar modelar la velocidad instantánea en una caída libre?
||5.16|| Analizando la gráfica, si calculáramos la velocidad promedio con la pendiente de la cuerda, su valor sería _________ al de la velocidad instantánea.
(a) igual (b) mayor (c) menor
||5.17|| ¿Instintivamente cuál es la estrategia para intentar que la cuerda arroje una aproximación cada vez más y más cercana a la velocidad instantánea?
||5.18|| ¿Que sucede en la resta límite infinitesimalmente pequeña cuando el cambio de tiempo es cero?
||5.19|| ¿Que podemos afirmar sobre la velocidad promedio y la velocidad instantánea de un cuerpo en caída libre?
||5.20|| ¿Cuál es el argumento para indicar la existencia de una velocidad instantánea?
||5.21|| ¿Cuáles son los símbolos para representar las diferencias o restas normales y cual para las restas infinitamente pequeñas o infinitesimales?
||5.22|| ¿Qué letra se usa usualmente en lugar del símbolo apropiado del cambio infinitesimal?
||5.23|| ¿Qué tipo de matemáticas se usa para enfrentar los problemas de tasas de cambio infinitesimales en curvas?
||5.24|| ¿Qué es lo que permite obtener las herramientas del cálculo?
6. La derivada de una función
|| REGRESAR AL INDICE ||
Objetivo: Derivar funciones sencillas para calcular la pendiente o tasa de cambio instantánea de curvas y rectas.
||6.1|| Ofrecer un resumen de los temas principales de la lección anterior en 3 frases.
||6.2|| Plantear alguna pregunta sobre lo visto en la lección anterior.
6.1 La paradoja de Aquiles y la tortuga
||6.3||¿Cómo usa Zenón la paradoja para negar la existencia del movimiento?
||6.4||¿Como sabemos que en verdad Aquiles sobrepasará a la tortuga?
||6.5||¿Cuál es el parámetro físico que Zenón ralentiza maliciosamente (hace tender a infinitamente pequeño) para que su paradoja tenga sentido?
||6.6|| Como podemos plantear matemáticamente la paradoja de Aquiles y la tortuga empleando los parámetros de cambio de posición con respecto al cambio en el tiempo?
||6.7|| ¿Qué relación podemos plantear entre el problema de la pendiente instantánea de una curva con la paradoja de Aquiles y la tortuga?
6.2 Planteando la derivada
||6.8|| Un objeto se desplaza en línea recta y su posición en función del tiempo está dada por la ecuación r = 2t^2 - 5t + 3, donde r representa la posición en metros y t el tiempo en segundos. Encuentra la velocidad instantánea del objeto en el instante t = 2 segundos.
||6.9|| Un automóvil se desplaza en línea recta y su posición en función del tiempo está dada por la ecuación r = 4t^3 + 2t^2 - 6t, donde r representa la posición en metros y t el tiempo en segundos. Encuentra la velocidad instantánea del automóvil en el instante t = 3 segundos.
||6.10|| Una partícula se mueve a lo largo de una trayectoria recta, y su posición en función del tiempo está dada por la ecuación r = 3t - 2t^2 + 5, donde r representa la posición en metros y t el tiempo en segundos. Determina la velocidad de la partícula en el instante t = 1 segundo. Plantee las constantes de proporcionalidad necesarias para el análisis dimensional.
||6.11|| Un objeto se desplaza en línea recta y su posición en función del tiempo está dada por la ecuación r = -5t^3 + 2t^2 - 3t, donde r representa la posición en metros y t el tiempo en segundos. Encuentra la velocidad instantánea del objeto en el instante t = 4 segundos.
||6.12|| Una partícula se mueve a lo largo de una trayectoria recta, y su posición en función del tiempo está dada por la ecuación r = t^2 + 3t + 1, donde r representa la posición en metros y t el tiempo en segundos. Determina la velocidad y la aceleración de la partícula en el instante t = 2 segundos. Plantee las constantes de proporcionalidad necesarias para el análisis dimensional.
||6.13|| Un objeto se desplaza en línea recta y su posición en función del tiempo está dada por la ecuación r = -2t^3 + 4t^2 - 6t, donde r representa la posición en metros y t el tiempo en segundos. Halla la velocidad y la aceleración del objeto en el instante t = 3 segundos. Corrija las unidades para obtener una aceleración de m/s^2.
PRAE II, abril
|| Regresar al índice ||
Con la información contenida en el siguiente enlace.
||P2.1|| Realice una ilustración en el cuaderno siguiendo las instrucciones del tutorial.
||P2.2|| Mencione los cuatro tipos de especies del ave de la familia Trochilidae.
||P2.3|| ¿Cuales son las diferencias entre el barbudito cascocrestado macho y hembra?.
||P2.4|| ¿A qué se debe la disminución de la población del barbudito cascocrestado?
||P2.5|| ¿A qué se debe la disminución de la población del barbudito cascocrestado?
||P2.5|| Cual es la alimentación del barbudito cascocrestado?
||P2.7|| Cual es la época de reproducción del barbudito cascocrestado y cuál es su tamaño de nidada?
PRAE III, mayo
|| Regresar al índice ||
Objetivo: Dar cumplimiento a las actividades PRAE 2023
Con la información contenida en el siguiente enlace.
||P2.1|| Realice una ilustración en el cuaderno siguiendo las instrucciones del tutorial.
||P3.2|| Crea una línea de tiempo que muestre los hitos importantes en la historia del género Espeletia desde la expedición de Von Humboldt y Bonpland hasta la actualidad. Incluye eventos como el descubrimiento de la especie, su nombramiento, estudios científicos, reconocimiento como símbolo de biodiversidad, y su estado actual de conservación.
||P3.3|| Cual importancia ecológica, económica, cultural y estética de la Espeletia grandiflora en los páramos de. Proporciona argumentos a favor y en contra de la protección de esta especie y concluye con tu opinión sobre el tema. Organiza la información en un cuadro.
||P3.4|| Compara la estructura floral de la Espeletia grandiflora con la de una flor simple ideal, como una margarita. Destaca las diferencias en la organización de las partes florales y explica cómo estas adaptaciones permiten a la Espeletia grandiflora atraer polinizadores y reproducirse eficazmente en su hábitat de los páramos. Organiza la información en un cuadro comparativo.
7. Derivadas e integrales
|| Regresar al índice ||
Objetivo: Aplicar derivadas e integrales a escenarios elementales de física general.
||7.1|| Calcular la velocidad promedio entre 2 y 6 segundos de una partícula cuya trayectoria está determinada por la función rx= 3 t 2. donde rx es la posición en x dada en metros y t el tiempo en segundos. Luego, calcular la velocidad instantánea de la partícula en los instantes 2 segundos, 4 segundos y 6 segundos. Respuestas:
Velocidad promedio entre 2 y 6 segundos: 24 metros/segundo.
Velocidad instantánea en 2 segundos: 12 metros/segundo.
Velocidad instantánea en 4 segundos: 48 metros/segundo.
Velocidad instantánea en 6 segundos: 108 metros/segundo.
||7.2|| Integre la ecuación de desplazamiento asumiendo que la aceleración es constante, y luego calcule la posición final después de 3 segundos, asumiendo que el objeto se mueve con una aceleración de 1.5 m/s2 desde el reposo y desde el origen. Respuestas:
La posición final después de 3 segundos es 6.75 metros.
||7.3|| Integre la ecuación de desplazamiento asumiendo que la aceleración es dada por la expresión (5 - 2t), y luego calcule la posición final para 5 segundos, asumiendo que el objeto se mueve desde el reposo y desde el origen. Respuestas:
La posición final después de 5 segundos es [respuesta].
Nivelación del semestre 1
|| Regresar al índice ||
Transcriba los ejercicios presentados en los siguientes enlaces, y en caso de ser lecciones teóricas, consígnelas como si fuera una clase. Cada video o lección debe estar perfectamente separad de las demás con una marca de color.
Problema-1.33ad. Determine el número de cifras significativas en los siguientes valores: (a) 4867 mi (b) 56 mL (c) 60,104 ton (d) 2900 g.
Ejemplo. Redondee el peso atómico del carbono, el hidrógeno y el oxígeno a sin decimales.
Ejemplo. Redondee el peso atómico del sodio, el litio y el potasio a dos decimales de confianza.
Ejemplo. Realizar la siguiente operación teniendo en cuenta las cifras significativas A = 6.221 x 5.2
Ejemplo. Realizar la siguiente operación teniendo en cuenta las cifras significativas n = 60 / 12.01
Ejemplo. Exprese el siguiente número como una notación científica a dos cifras significativas 4898
Ejemplo. Exprese el siguiente número como una notación científica a una cifras significativa 354
Ejemplo. Exprese el siguiente número como una notación científica a dos cifras significativas 0.000488
Ejemplo. Exprese el siguiente número como una notación científica a dos cifras significativas 0.000052
Ejemplo. Realizar la operación teniendo en cuenta las cifras significativas 5.2 x 10-2 + 4.8 x10-2.
Ejemplo. Realizar la operación teniendo en cuenta las cifras significativas 3.52 x 10-3 + 7.402 x10-2.
Ejemplo. Realizar la operación teniendo en cuenta las cifras significativas (4.1x10-3) x (2.35x10-2).
Ejemplo. Realizar la operación teniendo en cuenta las cifras significativas (2.5 x 10-3) / ( 1.53 x10-2 ).
Ejemplo. Convertir 1250 mL a L por factor de conversión, regla de tres y reemplazo algebraico.
Ejemplo. Convertir 300 kg a mg por regla de tres.
Ejemplo. Convertir 300 kg a mg por factor de conversión.
Ejemplo. Convertir 300 kg a mg por reemplazo algebraico.
Ejemplo. Convertir los siguientes datos de temperatura a Kelvin o a centígrados: 280 K, 10 °C, 315 K, 100 °C.
Lección: El problema de la pendiente.
Lección: La paradoja de Aquiles y la tortuga.
Lección: Derivación 1, planteando la derivada.
Lección: Derivación 2, resolviendo la derivada.
Ejemplo. Una partícula se mueve a lo largo de una trayectoria recta, y su posición en función del tiempo está dada por la ecuación r = 3t3 + 2t2 - t, donde r representa la posición en metros y t el tiempo en segundos. Determina la velocidad de la partícula en el instante t = 3 segundos. Plantee las constantes de proporcionalidad necesarias para el análisis dimensional.
Ejemplo. Un objeto se desplaza en línea recta y su posición en función del tiempo está dada por la ecuación r= t3 - 4t2 + 2t, donde r representa la posición en metros y t el tiempo en segundos. Halla la aceleración del objeto en el instante t = 10 segundos.
Ejemplo. Una partícula se mueve de acuerdo con la ecuación x=10t2, donde ``x´´ está en metros y ``t´´ en segundos: (a) encuentre la velocidad promedio en el intervalo de 2 a 3 segundos; (b) determine la velocidad promedio de 2 a 2.1 segundos.
8 Cinemática en una dimensión
|| Regresar al índice ||
Objetivo: Realizar cálculos analíticos y numéricos de cinemática en una dimensión.
||8.1|| Escriba las ecuaciones de mostradas en la lección anterior en limpio y titúlelas como:
a Velocidad final en términos de la velocidad inicial y el tiempo.
b Desplazamiento en términos de las velocidades y la aceleración.
c Posición final en términos de la velocidad inicial, el tiempo y la posición inicial.
d Solución general o solución cuadrática del tiempo.
||8.2|| Defina desplazamiento en términos de una resta ¿Cuáles son los parámetros involucrados en dicha resta?
||8.3|| Modifique las ecuaciones del punto 7.1 asumiendo posición inicial igual a cero.
||8.4|| Modifique las ecuaciones del punto 7.1 asumiendo aceleración cero.
||8.5|| Un corredor de atletismo corre los 100 metros en 10.2 segundos. ¿Cuál es la velocidad promedio del corredor en metros por segundo?
||8.6|| Un ciclista sale de su casa y se dirige al parque. En su camino, pedalea a una velocidad constante de 15 km/h durante 40 minutos. Luego se detiene en una tienda durante 20 minutos antes de continuar su trayecto hacia el parque, donde pedalea a una velocidad constante de 20 km/h durante 1.5 horas. a) ¿Cuál es el desplazamiento total del ciclista desde su casa hasta el parque? b) ¿Cuál es la velocidad promedio del ciclista durante todo el recorrido?
||8.7|| Un automóvil comienza a acelerar desde el reposo a una tasa constante de 2 m/s² durante 10 segundos. Luego, mantiene una velocidad constante de 30 m/s durante 40 segundos. Finalmente, el automóvil desacelera uniformemente a una tasa de -3 m/s² hasta detenerse.
||8.8|| Un motociclista parte pasa por un punto de inicio con una velocidad de 150 m/s y acelera uniformemente a razón de -3 m/s² durante un tiempo hasta llegar a un punto de retorno. Luego, el ciclista se detiene en ese punto, invierte su dirección y regresa a su casa siguiendo la misma aceleración. Después de un tiempo adicional, el ciclista alcanza su casa nuevamente. Calcule el tiempo necesario para que el motociclista pase por el punto 20 metros en las trayectorias de ida y retorno.
9. Vectores
|| Regresar al índice ||
9.1. Dibuja el vector que inicia en el punto (1, 2) y termina en el punto (7, 9).
9.2. Dibuja el vector que inicia en el punto (-2, -2) y termina en el punto (3, -5).
9.3. (a) Dibuja el vector que inicia en el origen, tiene una magnitud de 7 y un ángulo theta de 60°. (b) Dibuja el vector que inicia en (-1, 3), tiene una magnitud de 7 y un ángulo theta de 60°. Compara los vectores.
9.4. Un objeto se encuentra en la posición (-6.0, 8.0) m en coordenadas cartesianas. Convierte esta posición a coordenadas polares.
9.5. Un objeto se encuentra en la posición (4.0, -4.0) m en coordenadas cartesianas. Convierte esta posición a coordenadas polares.
9.6. Un objeto se desplaza con una velocidad de (10.0, 120°) m/s en coordenadas polares. Convierte esta velocidad a coordenadas cartesianas.
9.7. Un automóvil se desplaza con una velocidad de 12 km/h con una dirección de 30° con respecto a su punto inicial. Convierte esta velocidad a coordenadas cartesianas.
9.8. Imagina que un objeto está experimentando una aceleración de 15 m/s² a 30° con respecto a su posición actual. Convierte esta aceleración a coordenadas cartesianas.
9.9. Un objeto está sometido a dos fuerzas alineadas con los ejes de coordenadas en la siguiente coordenada cartesiana (-3.0, 6.0) N. Calcula la fuerza resultante en términos de coordenadas polares.
9.10. Sume los siguientes vectores y determina la resultante: 4.0 m/s, 30 grados y 6.0 m/s, 150 grados.



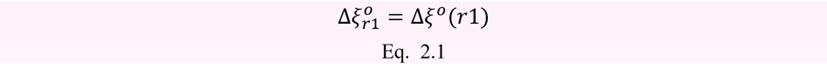









































No hay comentarios:
Publicar un comentario