Índice
||1|| Introducción ||2|| El vector euclidiano ||3|| Componentes de un vector euclidiano ||4|| El plano de coordenadas | ||7|| Vector unitario ||8|| Ángulos notables ||9|| Cambio en el marco de referencia ||R|| Referencias bibliográficas ||E|| Ejercicios resueltos |
Portada
1. Introducción
|| REGRESAR AL INDICE ||
En matemáticas y física, vector es un término que se refiere coloquialmente a algunas cantidades que no se pueden expresar con un solo número (un escalar), o a elementos de algunos espacios vectoriales. Históricamente, los vectores se introdujeron en la geometría y la física (típicamente en la mecánica) para cantidades que tienen tanto una magnitud como una dirección, como desplazamientos, fuerzas y velocidad. Tales cantidades se representan mediante vectores geométricos de la misma manera que las distancias, las masas y el tiempo se representan mediante números reales.
1.1 Euclides
Euclides fue un antiguo matemático griego activo como geómetra y lógico. Considerado el "padre de la geometría", es conocido principalmente por el tratado Elementos, que estableció las bases de la geometría que dominó en gran medida el campo hasta principios del siglo XIX. Su sistema, ahora conocido como geometría euclidiana, involucró nuevas innovaciones en combinación con una síntesis de teorías de matemáticos griegos anteriores, incluidos Eudoxo de Cnido, Hipócrates de Quíos, Tales y Teeteto. Con Arquímedes y Apolonio de Perge, Euclides es generalmente considerado uno de los más grandes matemáticos de la antigüedad y uno de los más influyentes en la historia de las matemáticas.
Se sabe muy poco de la vida de Euclides, y la mayor parte de la información proviene de los filósofos Proclo y Pappus de Alejandría muchos siglos después. Hasta principios del Renacimiento, a menudo se lo confundía con el filósofo anterior Euclides de Megara, lo que provocó que su biografía se revisara sustancialmente. En general, se acepta que pasó su carrera bajo Ptolomeo I en Alejandría y vivió alrededor del 300 a. C., después de Platón y antes de Arquímedes. Existe cierta especulación de que Euclides fue estudiante de la Academia Platónica y luego enseñó en el Musaeum. A menudo se considera que Euclides une la tradición platónica anterior en Atenas con la tradición posterior de Alejandría.
En los Elementos, Euclides dedujo los teoremas a partir de un pequeño conjunto de axiomas. También escribió obras sobre perspectiva, secciones cónicas, geometría esférica, teoría de números y rigor matemático. Además de los Elementos, Euclides escribió un texto inicial central en el campo de la óptica, Óptica, y obras menos conocidas, como Datos y Fenómenos. Se ha cuestionado la autoría de Euclides de otros dos textos, Sobre divisiones de figuras, Catoptrics. Se cree que escribió muchas obras ahora perdidas.
2. El vector euclidiano
|| REGRESAR AL INDICE ||
En matemáticas, física e ingeniería, un vector euclidiano o simplemente un vector (a veces llamado vector geométrico o vector espacial) es un objeto geométrico que tiene magnitud (o longitud) y dirección. Los vectores se pueden sumar a otros vectores según el álgebra vectorial. Un vector euclidiano se representa con frecuencia mediante un segmento de línea dirigido, o gráficamente como una flecha que conecta un punto inicial po con un punto terminal p.
Un vector es lo que se necesita para "llevar" el punto A al punto B; la palabra latina vector significa "portador" o “transportador”. Fue utilizado por primera vez por astrónomos del siglo XVIII que investigaban órbita planetaria alrededor del Sol. La magnitud del vector es la distancia entre los dos puntos, y la dirección se refiere a la dirección del desplazamiento de desde po hasta p. Muchas operaciones algebraicas con números reales, como la suma, la resta, la multiplicación y la negación, tienen analogías cercanas con los vectores, operaciones que obedecen a las conocidas leyes algebraicas de conmutatividad, asociatividad y distributividad. Estas operaciones y leyes asociadas califican a los vectores euclidianos como un ejemplo del concepto más generalizado de vectores definidos simplemente como elementos de un espacio vectorial.
2.2 Importancia de los vectores
Los vectores juegan un papel importante en la física: la velocidad y la aceleración de un objeto en movimiento y las fuerzas que actúan sobre él pueden describirse con vectores. Muchas otras cantidades físicas pueden considerarse útiles como vectores. Aunque la mayoría de ellos no representan distancias (excepto, por ejemplo, posición o desplazamiento), su magnitud y dirección aún pueden representarse mediante la longitud y la dirección de una flecha. La representación matemática de un vector físico depende del sistema de coordenadas utilizado para describirlo. Otros objetos similares a vectores que describen cantidades físicas y se transforman de manera similar bajo cambios en el sistema de coordenadas incluyen pseudovectores y tensores.
2.2 Origen del concepto
A pesar de que asociamos casi toda la física clásica a la figura de Isaac Newton, la verdad es que el vector a pesar de que es un concepto muy empleado en física básica es un concepto muy posterior a su trabajo. El concepto de vector, tal como lo conocemos hoy, es el resultado de un desarrollo gradual durante un período de más de 200 años.
Alrededor de una docena de personas contribuyeron significativamente a su desarrollo (Vince, 2021). En 1835, Giusto Bellavitis abstrajo la idea básica cuando estableció el concepto de equipolencia.
Figura 2.1. Giusto Bellavitis (22 de noviembre de 1803 - 6 de noviembre de 1880) fue un matemático, senador y concejal municipal italiano. Nacido en Bassano del Grappa en 1803 de Ernesto Bellavitis y Giovanna Navarini, Giusto estudió principalmente solo. En 1840 ingresó en el Institut Venitian y en 1842 comenzó a dar clases en el Lycee de Vicence. En 1845 se convirtió en profesor de geometría descriptiva en la Universidad de Padua. Con la unificación de Italia, aprovechó la oportunidad para revisar el plan de estudios para incluir álgebra y geometría analítica complementarias. Bellavitis se casó en 1842 y tuvo un hijo que también enseñó geometría en la Universidad de Padua.
El término vector fue introducido por William Rowan Hamilton como parte de un cuaternión, que es una suma q = s + v de un número real s (también llamado escalar) y un vector tridimensional.
2.2 Parte de la matemática del siglo XIX
Varios otros matemáticos desarrollaron sistemas de tipo vectorial a mediados del siglo XIX, incluidos Augustin Cauchy, Hermann Grassmann, August Möbius, Comte de Saint-Venant y Matthew O'Brien. El trabajo de Grassmann de 1840 Theorie der Ebbe und Flut (Teoría del reflujo y el flujo) fue el primer sistema de análisis espacial similar al sistema actual y tenía ideas correspondientes al producto cruzado, el producto escalar y la diferenciación vectorial. El trabajo de Grassmann se descuidó en gran medida hasta la década de 1870 (Vince, 2021). Peter Guthrie Tait llevó el estandarte del cuaternión después de Hamilton. Su Tratado elemental de cuaterniones de 1867 incluyó un tratamiento extenso del operador nabla o del ∇. En 1878, William Kingdon Clifford publicó Elements of Dynamic. Clifford simplificó el estudio de cuaterniones al aislar el producto escalar y el producto vectorial de dos vectores del producto de cuaterniones completo. Este enfoque hizo que los cálculos vectoriales estuvieran disponibles para los ingenieros y otros que trabajaban en tres dimensiones y eran escépticos con respecto a la cuarta.
Josiah Willard Gibbs, que estuvo expuesto a los cuaterniones a través del Tratado sobre electricidad y magnetismo de James Clerk Maxwell, separó su parte vectorial para un tratamiento independiente. La primera mitad de Elements of Vector Analysis de Gibbs, publicada en 1881, presenta lo que es esencialmente el sistema moderno de análisis vectorial (Vince, 2021). En 1901, Edwin Bidwell Wilson publicó Vector Analysis, adaptado de las conferencias de Gibb, que eliminó cualquier mención de cuaterniones en el desarrollo del cálculo vectorial.
3. Componentes de un vector euclidiano
|| REGRESAR AL INDICE ||
En física e ingeniería, un vector se considera típicamente como una entidad geométrica caracterizada por una magnitud y una dirección. Se define formalmente como un segmento de línea dirigida, o flecha, en un espacio euclidiano.
2.2 El espacio euclidiano
El espacio euclidiano es el espacio fundamental de la geometría, destinado a representar el espacio físico. Originalmente, es decir, en los Elementos de Euclides, era el espacio tridimensional de la geometría euclidiana, pero en las matemáticas modernas existen espacios euclidianos de cualquier dimensión entera positiva n, que se denominan n-espacios euclidianos cuando se quiere especificar su dimensión.
La recta y el plano
Aunque lo anterior suena un poco complejo, usted ya ha sido expuesto a espacios euclidianos y al menos domina n = 1 y n = 2. El espacio euclidiano n = 1, también es conocido como la recta que posee un origen en cero y dos direcciones a las que arbitrariamente asignamos positivo/derecha y negativo/izquierda. el espacio euclidiano n = 2, también es conocido como el plano cartesiano, el cual está compuesto por la intersección de dos rectas, a las cuales denominamos ejes, y arbitrariamente les asignamos el nombre de eje x eje y.
Restricción del concepto de vector
Dado que en este curso de física vamos a manejar principalmente el plano cartesiano (como espacio euclidiano principal) podemos definir que un vector es una flecha que existe en el plano cartesiano. de lo anterior el lector deberá tener en cuenta que la definición matemática de vector moderna es mucho más amplia y mucho más compleja, pero para los objetivos de este curso en particular los vectores estarán estrictamente definidos como flechas en el espacio euclidiano.
Origen del concepto
El espacio euclidiano fue introducido por los antiguos griegos como una abstracción de nuestro espacio físico tridimencional. Su gran innovación, que apareció en los Elementos de Euclides, fue construir y probar toda la geometría a partir de unas pocas propiedades muy básicas, que se abstraen/transforman el mundo físico en un sistema simbólico de letras/números. Estas propiedades se denominan postulados o axiomas en lenguaje moderno. Esta forma de definir el espacio euclidiano todavía se usa bajo el nombre de geometría sintética.
Reducción al álgebra
En 1637, René Descartes introdujo las coordenadas cartesianas y demostró que esto permite reducir problemas geométricos a cálculos algebraicos con números. Esta reducción de la geometría al álgebra supuso un gran cambio de punto de vista, ya que, hasta entonces, los números reales se definían en términos de longitudes y distancias.
Generalización a espaciones no-euclidianos
La geometría euclidiana no se aplicó en espacios de más de tres dimensiones hasta el siglo XIX. Ludwig Schläfli generalizó la geometría euclidiana a espacios de dimensión n superiores a al espacio tridimensional n = 3, utilizando métodos sintéticos y algebraicos, y descubrió todos los politopos regulares (análogos de dimensiones superiores de los sólidos platónicos) que existen en espacios euclidianos de cualquier dimensión, de los cuales el más famoso en la cultura popular es el tesseracto (Polo-Blanco & Gonzalez-Sanchez, 2010).
Figura 3.1. Dado que el teseracto es una figura geométrica superdimencional, es imposible representarla en el espacio tridimensional, por lo que debemos emplear una dimensión más (el tiempo) para poder visualizarla, en este caso como un objeto que aparenta moverse.
A pesar del amplio uso del enfoque de Descartes, que se denominó geometría analítica, la definición del espacio euclidiano se mantuvo sin cambios hasta finales del siglo XIX. La introducción de espacios vectoriales abstractos permitió su uso en la definición de espacios euclidianos con una definición puramente algebraica, y por ende, desconectada de tener que dibujarlos en papel. Se ha demostrado que esta nueva definición es equivalente a la definición clásica en términos de axiomas geométricos aunque no puedan plasmarse visualmente sin tener que hacer reducciones, simplificaciones y concesiones de la complejidad de los conceptos a representaciones que nuestra mente espacial pueda “ver”. Es esta definición algebraica la que ahora se usa más a menudo para introducir espacios euclidianos.
2.2 Tipos de vectores por su punto de inicio
Al ser una flecha, un vector euclidiano posee un punto inicial po y un punto terminal p definidos. Un vector con punto inicial y terminal fijos se llama vector ligado. Cuando solo importan la magnitud y la dirección del vector, entonces el punto inicial particular no tiene importancia, y el vector se llama vector libre.
2.2 Dirección o sentido
La dirección de un vector es muy importante para poderlo definir, hoy ya existen varias maneras de representarla. la primera y la más sencilla es conocer los: que definen a la fecha y saber cuál de los: el inicial y cuál el final. hoy sin embargo conocer los: no es estrictamente necesario para reconocer la dirección de un vector. por ejemplo en un espacio euclidiano de dimensión uno es decir la línea recta, podemos representar al vector conociendo su punto inicial y el signo positivo o negativo, hoy el cual indicará de manera inequívoca la dirección del vector ya sea hacia la derecha o hacia la izquierda.
en el plano cartesiano o en el espacio tridimensional determinar la dirección de un vector es una cosa un poco más complicada. nuevamente será muy sencillo si conocemos los puntos. pero en caso de que solo conozcamos el punto inicial y la magnitud del vector, la dirección de este podrá ser determinada empleando los ángulos de ese vector con respecto a los ejes de coordenadas, lo cual invariablemente va a generar un sistema de triángulos y por lo tanto deberemos introducir el álgebra de los triángulos y los ángulos, es decir la trigonometría.
2.2 Magnitud
La magnitud de un vector es la longitud de este comparada con respecto a las unidades del marco de referencia. El marco de referencia no es otra cosa que el espacio euclidiano y por eso dicho espacio es tan importante para definir un vector. existen espacios euclidianos que son adimensionales como los que dibujamos en matemáticas puras. Sin embargo, en física vamos a tener espacios euclidianos definidos para unidades de medida como la distancia (m), la velocidad (m/s), la aceleración (m/s2), la fuerza (kg m/s2) entre otras magnitudes vectoriales.
La magnitud de un vector no tiene en cuenta su dirección, por ende, si estamos trabajando con vectores que se mueven en un espacio euclidiano unidimensional, no tendremos en cuenta signos positivos o negativos. y si estamos trabajando con vectores en espacios euclidianos bi o tridimensionales, no nos importarán los ángulos que forman las flechas con respecto a los ejes de coordenadas.
De lo anterior podemos definir que la magnitud del vector es igual al valor absoluto de éste cuando se mueve en un espacio unidimensional, de allí que la representación estándar de la magnitud de un vector esté mediada por el concepto de valor absoluto; mientras que en el espacio euclidiano bidimensional la magnitud del vector va a estar mediada por el cálculo de una hipotenusa ignorando su ángulo con respecto a alguno de los ejes de coordenadas.
4. El plano de coordenadas
|| REGRESAR AL INDICE ||
Hay una leyenda que afirma que el sistema de coordenadas cartesianas se descubrió cuando René Descartes estaba enfermo en cama. Mientras miraba hacia el techo cuadriculado con fiebre, vio una mosca. Se preguntó cómo podría describir la posición de la mosca en el techo. Si se toma una esquina de la habitación como punto de referencia u origen, la posición de la mosca podría describirse como el número de fichas horizontales desde el origen seguido por el número de fichas verticales desde el origen. Estos dos números son las coordenadas de la posición de la mosca. René Descartes publicó por primera vez el sistema de coordenadas que lleva su nombre en 1637. A veces se le llama sistema de coordenadas rectangulares porque la cuadrícula está formada por cuadrados (Kuhn, 2003).
Fue descubierto de forma independiente por Pierre de Fermat, quien también trabajó en tres dimensiones, aunque Fermat no publicó el descubrimiento. Nicolas Oresme utilizó construcciones similares a las coordenadas cartesianas mucho antes de la época de Descartes y Fermat (Vásquez, 2017).
Tanto Descartes como Fermat utilizan un solo eje en sus tratamientos y tienen una longitud variable medida en referencia a este eje. El concepto de utilizar un par de hachas se introdujo más tarde, después de que La Géométrie de Descartes fuera traducida al latín en 1649 por Frans van Schooten y sus alumnos. Estos comentaristas introdujeron varios conceptos al tratar de aclarar las ideas contenidas en la obra de Descartes.
El desarrollo del sistema de coordenadas cartesianas jugaría un papel fundamental en el desarrollo del cálculo de Isaac Newton y Gottfried Wilhelm Leibniz. La descripción de dos coordenadas del plano se generalizó más tarde en el concepto de espacios vectoriales. Se han desarrollado muchos otros sistemas de coordenadas desde Descartes, como las coordenadas polares para el plano y las coordenadas esféricas y cilíndricas para el espacio tridimensional.
2.1 El sistema de coordenadas cartesianas
Un sistema de coordenadas cartesianas en dos dimensiones (también llamado sistema de coordenadas rectangulares o sistema de coordenadas ortogonales) se define por un par ordenado de líneas perpendiculares (ejes), una sola unidad de longitud para ambos ejes y una orientación para cada uno. El punto donde se encuentran los ejes se toma como origen de ambos, convirtiendo así cada eje en una recta numérica.
En consecuencia, para describir completamente a un punto en el plano debemos posee información correspondiente a su reflejo en cada eje de coordenadas. El reflejo del punto p se interpreta como un número. Los dos números, en ese orden elegido, son las coordenadas cartesianas de p (x, y). La construcción inversa permite determinar el punto p dadas sus coordenadas, siendo p igual al punto en que las proyecciones de (x, y) se interceptan.
Figura 4.1. El diagrama cartesiano. A la izquierda tenemos una versión simplificada en la que se muestra un solo cuadrante, mientras que a la derecha tenemos su versión completa con los cuatro cuadrantes.
En nomenclatura matemática, los reflejos de los dos ejes (x, y) reciben nombres, siendo la absica igual al reflejo del eje x, mientras que la ordenada es el reflejo del eje y; y el punto donde se encuentran los ejes se llama origen del sistema de coordenadas. Las coordenadas generalmente se escriben como dos números entre paréntesis, en ese orden, separados por una coma, como en (3, −4). Así, el origen tiene coordenadas (0, 0), y los puntos en los semiejes positivos, a una unidad del origen, tienen coordenadas (1, 0) y (0, 1).
Figura 4.2. Ubicación del punto (3,-4) en un diagrama de cuatro cuadrantes.
En matemáticas, física e ingeniería, el primer eje suele definirse o representarse como horizontal y orientado hacia la derecha, y el segundo eje es vertical y orientado hacia arriba. (Sin embargo, en algunos contextos de gráficos por computadora, el eje de ordenadas puede estar orientado hacia abajo). El origen a menudo se denomina o, y las dos coordenadas a menudo se indican con las letras X e Y, o x e y. Entonces, los ejes pueden denominarse eje x y eje y. Las elecciones de letras provienen de la convención original, que consiste en utilizar la última parte del alfabeto para indicar valores desconocidos. La primera parte del alfabeto se utilizó para designar valores conocidos.
2.2 La ecuación de la recta
La ecuación de la recta o modelo lineal es la ecuación más común que nos encontraremos a lo largo del curso de física general, siendo esta la base para realizar argumentaciones deductivas, o la base para hacer modificaciones empleando las técnicas del cálculo lineal. Esta ecuación ya la trabajamos en la sección de movimiento en una dimensión, donde el tiempo siempre ejercía como variable independiente.
Los vectores, al ser entidades lineales se describen por medio de líneas rectas, pero no infinitas, estos tienen una magnitud que denominaremos r (que puede reemplazarse con el símbolo del parámetro físico como velocidad v, aceleración a o fuerza F) y una dirección, cuando ambos se tienen en cuenta simultáneamente se representan como r (a veces con una flecha encima si el procesador de texto lo permite, de lo contrario se usa fuente en negrita como en el caso de los vectores velocidad v, aceleración a o fuerza F).
Podemos describir un vector en un plano cartesiano si contamos con dos puntos, y la dirección. Para indicar la dirección nos basta con asignar un estado inicial a uno de los puntos (po), el cual marca el punto de inicio del vector, y a la punta del vector, donde este finaliza simplemente le asignamos (p), por lo tanto, podemos definir un vector como la diferencia entre dos puntos en el plano.
Propios
Ejemplo. Dibuje el vector que inicia en el punto (3, 4) y termina en el punto (5, 6).
Ejemplo. Dibuje el vector que inicia en el punto (-3.5, 1) y termina en el punto (0, 4).
4.3 El sistema de coordenadas polares
El sistema de puntos inicial y final para especificar a un vector en el plano cartesiano no es la única forma para determinar la magnitud y dirección de un vector. Una alternativa es el sistema de coordenadas polares. A diferencia del sistema de puntos, en el sistema de coordenadas polares se específica la magnitud del vector, y su dirección con dos parámetros separados (r, θ).
👉 Donde r es la magnitud del vector r o, dicho de otro modo:
el valor absoluto del vector, despojado de su dirección (r = |r|) si este se mueve en un solo eje de coordenadas.
La hipotenusa de los vectores unitarios del vector, siendo los vectores unitarios, las sombras que proyecta el vector en cada eje de coordenadas.
👉 Donde θ es el ángulo medido desde el eje x (flecha dirección →) en contra de las manecillas del reloj, la razón para esta aparentemente arbitraria elección radica en el hecho de que esto nos permite aplicar el modelo matemático del teorema de Pitágoras.
Figura 4.3. Las coordenadas polares permiten describir la ubicación del punto. Tenga en cuenta que en ángulo teta se cuenta desde el eje x positivo en contra de las manecillas del reloj.
A pesar de lo anterior, el sistema (r, θ) o de coordenada polar requiere del punto po para su completa especificación, puesto que, aunque normalmente po = (0, 0) o el origen, esto no es necesariamente cierto en todas las ocasiones.
Propios
4.4 Trigonometría de las coordenadas polares
El teorema de Pitágoras establece que “En un triángulo rectángulo, el cuadrado del lado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados”. Los lados de este triángulo se han denominado Perpendicular, Base e Hipotenusa, pero en nuestro contexto será compuesto por la abscisa, la ordenada y el radio del vector (r), sin embargo, para describir completamente al vector, no podremos eliminar por completo el sistema de coordenadas cartesianas, pues aún necesitaremos el punto inicial (po).
Aquí, el vector (r) es el lado más largo, ya que es opuesto al ángulo de 90°. Los lados de un triángulo rectángulo (digamos rx, ry, r) que tienen valores enteros positivos, cuando se elevan al cuadrado, se ponen en una ecuación, también llamada terna pitagórica.
A parte de la terna pitagórica, también podemos invocar otras tres fórmulas fundamentales desde la trigonometría, siendo estas las leyes del seno, coseno y tangente definidas para triángulos rectángulos.
Sin embargo, para que los axiomas anteriores nos sirvan para convertir coordenadas cartesianas a polares y viceversa, es conveniente hacer unas modificaciones.
Propios
La razón por la cual se mide el ángulo desde el eje positivo de x en sentido contrario a las manecillas del reloj es una convención ampliamente aceptada en matemáticas y física. Esta convención se conoce como el sistema de coordenadas polares estándar. En este sistema, el ángulo se mide en sentido contrario a las manecillas del reloj desde el eje positivo de x, que generalmente se toma como referencia para el ángulo cero. Esta elección se debe a que coincide con la dirección positiva del ángulo en trigonometría. Medir los ángulos en sentido contrario a las manecillas del reloj desde el eje positivo de x ayuda a establecer una consistencia en los cálculos y en la interpretación geométrica de las coordenadas polares. Además, facilita la conexión entre las coordenadas polares y las funciones trigonométricas, como el seno y el coseno.
En caso de tener un ángulo negativo con respecto al eje positivo x, opere sin problemas, aunque puede corregirlo a un ángulo positivo sumándole 360, el resultado que obtenga en la calculadora será el mismo.
Propios
Ejemplo. Un objeto se desplaza con una velocidad de (5.0; 330°) m/s en coordenadas polares. Convierte esta velocidad a coordenadas cartesianas.
Serway novena edición
5. Parámetros escalares y vectoriales
|| REGRESAR AL INDICE ||
Ahora describimos formalmente la diferencia entre cantidades escalares y cantidades vectoriales. Cuando desee saber la temperatura exterior para saber cómo vestirse, la única información que necesita es un número “con su signo” y la unidad "grados C" o "grados F". La temperatura es, por lo tanto, un ejemplo de una cantidad escalar.
5.1 Cantidades escalares
Una cantidad escalar está completamente especificada por un solo valor con una unidad apropiada y no tiene dirección. Otros ejemplos de cantidades escalares son el volumen, la masa, la rapidez “speed”, el tiempo y los intervalos de tiempo. En las traducciones se debe tener mucho cuidado, los traductores automáticos pueden traducir speed como velocidad, pero en física, la velocidad si es un vector como veremos más tarde.
Algunos escalares son siempre positivos, como la masa y la rapidez. Otros, como la temperatura, pueden tener valores positivos o negativos debido a que están definidos con escalas arbitrarias, aunque la escala absoluta definida con el cero absoluto o escala de Kelvin, si cumple con ser un escalar siempre positivo. Las reglas de la aritmética ordinaria se utilizan para manipular cantidades escalares.
3.2 Cantidades vectoriales
Si te estás preparando para pilotar un avión pequeño y necesitas saber la velocidad del viento, debes saber tanto la rapidez del viento como su dirección tridimensional. Debido a que la dirección es importante para su especificación completa, la velocidad “velocity” es una cantidad vectorial: una cantidad vectorial se especifica completamente mediante un número con una unidad apropiada (la magnitud del vector) más una dirección. Otro ejemplo de cantidad vectorial es el desplazamiento.
Figura 5.1. Cuando una partícula se mueve de A a B a lo largo de una trayectoria arbitraria representada por la línea discontinua, su desplazamiento es una cantidad vectorial que se muestra mediante la flecha dibujada de A → B.
Suponga que una partícula se mueve desde algún punto A hasta algún punto B a lo largo de una trayectoria recta como se muestra en la Figura 3.1. Representamos este desplazamiento dibujando una flecha de A a B, con la punta de la flecha apuntando hacia afuera del punto de partida. La dirección de la punta de la flecha representa la dirección del desplazamiento y la longitud de la flecha representa la magnitud del desplazamiento. Si la partícula viaja a lo largo de algún otro camino de A a B, como lo muestra la línea discontinua en la Figura 3.1, su desplazamiento sigue siendo la flecha dibujada de A a B.
El desplazamiento depende solo de las posiciones inicial (xA) y final (xB), por lo que el vector de desplazamiento es independiente del camino tomado por la partícula entre estos dos puntos. Cuando esto se cumple decimos que el parámetro es una variable de estado.
3.3 Representación simbólica de los parámetros vectoriales
En el capítulo de unidades y medidas determinamos que los símbolos de las unidades se representan en texto normal, mientras que los parámetros para las cantidades físicas sean estas constantes o variables se escribían en cursivas.
Los parámetros vectoriales poseen su propia simbología, siendo la más común: texto normal a negrita con una flecha sobre ella: como por ejemplo para los símbolos vectoriales de velocidad v, aceleración a o fuerza F. Algunas formas de procesadores de texto son complejas para colocar la flecha vectorial, como ocurre con el texto normal de Word o el texto en blogger, pues para este ejemplo tuve que usar un editor de ecuaciones llamado Mathtype configurado para que sus imágenes tuvieran el tamaño de las letras en este texto. Otro editor de ecuaciones útil es https://editor.codecogs.com/ ya que es gratuito y no requiere de instalar, aunque usa lenguaje de LaTex para ecuaciones.
Por lo anterior, también se aceptarán los símbolos a texto normal y negrita, pero sin la flecha. La magnitud de un vector tendrá el mismo símbolo, pero irá a cursiva. La magnitud de un vector tiene unidades físicas, como metros para el desplazamiento; o metros por segundo para la velocidad. La magnitud de un vector es siempre un número positivo.
6. Propiedades de los vectores
|| REGRESAR AL INDICE ||
En esta sección, investigaremos las propiedades generales de los vectores que representan cantidades físicas. También discutimos cómo sumar y restar vectores usando métodos algebraicos y geométricos.
4.1 Igualdad de dos vectores
Para muchos propósitos, dos vectores A y B pueden definirse como iguales si tienen la misma magnitud y si apuntan en la misma dirección, aunque sus puntos iniciales po sean diferentes. Esta propiedad nos permite mover un vector a una posición paralela a sí mismo en un diagrama sin afectar el vector, con tan solo cambiar el valor de po.
Figura 6.1. Estos cuatro vectores son iguales porque tienen la misma longitud y apuntan en la misma dirección, aunque la diferencia radica en que sus puntos iniciales po son diferentes.
4.2 Suma de vectores
El vector resultante r de la suma de dos o más vectores (j), es igual a la suma de todos los componentes en los ejes independientes para recalcular el vector respuesta. Para un vector descrito por el sistema de coordenadas cartesianas, podemos argumentar que cada componente del vector r es una cantidad conservada, por lo que cada componente de r será la suma de las componentes individuales de los vectores que se suman.
DEMOSTRACION. Encuentre una fórmula para sumar vectores empleando coordenadas polares.
Las ecuaciones 6.1 y 6.2 las denominaremos como descomposición de vectores individuales y recomposición del vector resultante. Una vez que tengamos las dos componentes resultantes, solo es cuestión de reciclar las ecuaciones: 4.9 para hallar el ángulo aparente o de calculadora, 4.7 para hallar el ángulo verdadero, y 4.8 para hallar la magnitud del vector resultante en la suma.
Ejemplos
Ejemplo. Sume los siguientes vectores y determine la resultante. 3.0 m/s, 45 grados y 5.0 m/s, 135 grados.
Física de Sarwey
La resta de vectores funciona igual, ya que recuerde que una resta aritmética también sigue modelándose dentro de las ecuaciones de sumas algebraicas, solo que son signos negativos. Si tenemos un vector negativo, todos sus componentes serán multiplicados por negativo.
6.3 Producto vector por escalar
Al multiplicar un vector por un escalar, el vector se extiende o contrae tantas veces como indique el escalar en ambos componentes, por lo que podemos definir que el escalar es factor común de los componentes del vector, pero el ángulo θ resultante no se verá afectado.
El signo del escalar también funcionará como factor común, lo cual cambiará la dirección del vector y su ángulo, el cual pasará a estar definido para su marco de referencia opuesto, por lo que en tal caso habrá de modificar para el cuadrante. Un ejemplo de este tipo de situaciones involucra a las ecuaciones de cinemática en dos dimensiones, donde el tiempo es el escalar, que multiplicará a velocidad o aceleración vectoriales, y se mantendrá constante cuando estas se descomponen.
En cinemática básica, algunas de las magnitudes escalares más comunes que se utilizan son:
(a) Tiempo (t): Representa la duración de un evento o el intervalo entre dos sucesos.
(b) Longitud o distancia (|d|): Mide la extensión física entre dos puntos.
(c) Rapidez o velocidad escalar (|v|): Indica la cantidad de distancia recorrida por unidad de tiempo, sin tener en cuenta la dirección.
(d) Masa (m): Es la cantidad de materia de un objeto.
(e) Temperatura (T): Indica el nivel de calor de un cuerpo.
(f) Energía (E): Representa la capacidad de un sistema para realizar trabajo o transferir calor.
Estas magnitudes se consideran escalares porque solo tienen una magnitud numérica y no una dirección asociada. En la cinemática básica, se utilizan principalmente para describir el movimiento y las propiedades físicas de los objetos sin tener en cuenta la dirección o el sentido del movimiento.
Ejemplos
Sin embargo obviamos algo en el ejemplo anterior, y es que si bien el escalar afecta a la descomposición vectorial, la propiedad implica que no es necesario hacer la descomposición vectorial, podemos obtener el mismo resultado multiplicando la magnitud del vector original, pero manteniendo el mismo ángulo. Aun cuando un vector cambia a otro al ser multiplicado por un escalar, su dirección no cambia, lo cual facilita los ejercicios en dos dimensiones al tener que administrar menos términos trigonométricos.
Ejemplos
6.4 Producto punto
Una operación que toma dos vectores y devuelve una cantidad escalar. El producto escalar de dos vectores se puede definir como el producto de las magnitudes de los dos vectores y el coseno del ángulo entre los dos vectores. Alternativamente, se define como el producto de la proyección del primer vector sobre el segundo vector y la magnitud del segundo vector. Así,
(a) Trabajo (W): El trabajo realizado por una fuerza F sobre un objeto es el producto punto entre la fuerza y el desplazamiento del objeto. El trabajo se calcula como W = F·d, donde F es el vector fuerza y d es el vector desplazamiento.
(b) Potencia (P): La potencia representa la tasa a la cual se realiza trabajo. Se calcula como el producto punto entre la fuerza aplicada sobre un objeto y la velocidad con la que se realiza el trabajo. P = F·v.
Ejemplos
7. Vector unitario
|| REGRESAR AL INDICE ||
Las cantidades vectoriales a menudo se expresan en términos de vectores unitarios. Un vector unitario es un vector adimensional que tiene una magnitud de exactamente 1. Los vectores unitarios se usan para especificar una dirección dada y no tienen otro significado físico. Se utilizan únicamente como conveniencia contable para describir una dirección en el espacio. Usaremos los símbolos i, j y k (en notación vectorial en texto cuando no es posible colocarles es acento circunflejo), o en ecuaciones:
Para representar vectores unitarios que apuntan en las direcciones positivas x, y y z, respectivamente. (Los "sombreros" o acentos circunflejos en los símbolos son una notación estándar para los vectores unitarios). La magnitud de cada vector unitario es igual a 1 adimensional. En consecuencia, podemos afirmar de momento que la función del vector unitario es la de ser un sinónimo de las coordenadas cartesianas, y ayudarnos a ver cuáles la dirección de las componentes.
Donde k representa un valor numérico y el signo, mientras que el vector unitario contiene la dirección, los vectores unitarios se expresan como sumas cuyo factor común es la unidad de la magnitud física, así por ejemplo si tenemos una posición r esta puede expresarse como r = (2.0 i + 2.0 j)m o r = 2.0 m a 45° o como rx = 2.0 m más ry = 2.0 m.
8. Ángulos notables
|| REGRESAR AL INDICE ||
La trigonometría es una rama de las matemáticas que estudia las relaciones entre los ángulos y las longitudes de los lados de los triángulos. Los ángulos notables son aquellos que tienen medidas específicas y cuyas funciones trigonométricas (seno, coseno y tangente) tienen valores que pueden expresarse de manera exacta. Estos ángulos desempeñan un papel fundamental en diversos campos, como la física, la ingeniería y la navegación. En este artículo, exploraremos los ángulos notables más importantes y sus funciones trigonométricas asociadas.
Los ángulos de los cuatro cuadrantes
En el sistema de coordenadas, los cuatro ejes, correspondientes a los ángulos de 0°, 90°, 180° y 270°, desempeñan un papel esencial en la trigonometría al representar los puntos cardinales y sus propiedades trigonométricas asociadas.
(a) En el eje positivo de las abscisas (x) (0°), el seno es 0, el coseno es 1 y la tangente es 0, ya que el lado opuesto es nulo y el lado adyacente es igual a la hipotenusa.
(b) En el eje positivo de las ordenadas (y) (90°), el seno es 1, el coseno es 0 y la tangente es indefinida, ya que el lado opuesto es igual a la hipotenusa y el lado adyacente es nulo.
(c) En el eje negativo de las abscisas (x) (180°), el seno es 0, el coseno es -1 y la tangente es 0, dado que el lado opuesto es nulo y el lado adyacente es igual a la hipotenusa, pero con signo negativo.
(d) Finalmente, en el eje negativo de las ordenadas (y) (270°), el seno es -1, el coseno es 0 y la tangente es indefinida, ya que el lado opuesto es igual a la hipotenusa, pero con signo negativo, y el lado adyacente es nulo.
Estas propiedades trigonométricas en los ejes de coordenadas son fundamentales para comprender cómo las funciones seno, coseno y tangente varían en diferentes direcciones del plano cartesiano.
La influencia de los ángulos notables se extiende más allá de la pura trigonometría y tiene un impacto significativo en el análisis de fuerzas en contextos físicos. En numerosas ocasiones, al realizar la suma de fuerzas en aplicaciones de la segunda ley de Newton, es común introducir inadvertidamente signos negativos en los cálculos. Este error a menudo surge de una interpretación apresurada o implícita de las funciones trigonométricas resultantes en -1. Uno de los desaciertos más frecuentes en este escenario es añadir un signo negativo junto con la función trigonométrica, lo que resulta en la anulación errónea del signo correcto.
Figura 8.1. Si intuitivamente reemplaza un vector como negativo, es por que ya está tomando en cuenta su componente trigonométrico.
Es fundamental reconocer que los ángulos notables y las funciones trigonométricas asociadas, como el seno, el coseno y la tangente, se entrelazan con la manera en que analizamos las fuerzas en un sistema. Cuando se descomponen fuerzas en componentes según los ejes de coordenadas, es imprescindible tener en mente los signos particulares de cada cuadrante. En esta situación, el segundo cuadrante se destaca, ya que el seno es positivo, pero el coseno es negativo. Sin embargo, una interpretación precipitada podría llevar a colocar un signo negativo junto a la función trigonométrica, lo que resultaría en un error al cancelar el signo correcto.
La comprensión detallada de las propiedades trigonométricas en distintos cuadrantes es esencial para evitar errores al aplicar las leyes físicas en problemas prácticos. Asegurar que los signos y las funciones trigonométricas se utilicen correctamente al descomponer fuerzas contribuirá a un análisis más preciso y sólido en diversas situaciones físicas y de ingeniería.
Signos generales de las identidades trigonométricas
De lo anterior se desprende que:
(a) el seno positivo se genera cuando el vector apunta hacia arriba en cualquier dirección diagonal entre los ángulos del 0 al 180°.
(b) el seno negativo se genera cuando el vector apunta hacia abajo en cualquier dirección diagonal entre los ángulos del 180° al 360°.
(c) el coseno positivo se genera cuando el vector apunta hacia la derecha entre los ángulos de 90° y 270 °.
(d) el coseno negativo se genera cuando el vector apunta hacia la izquierda entre los ángulos de 90° y 270°.
Si tomamos la información de los signos de las identidades trigonométricas, con la información anterior, podemos decir que solo tenemos que memorizar las identidades trigonométricas en el primer cuadrante, puesto que las identidades de los otros tres son solo cambios de signo.
Las diagonales
El ángulo notable de 45°, también conocido como π/4 radianes, desempeña un papel clave en la trigonometría debido a sus propiedades especiales y su relación con los ángulos notables a 90°. Este ángulo se encuentra en el segundo cuadrante y se forma en un triángulo rectángulo isósceles, donde ambos catetos son de igual longitud. La relación fundamental entre el ángulo de 45° y el ángulo de 90° es que, al dividir el triángulo en dos partes iguales, el ángulo de 45° crea dos triángulos rectángulos idénticos.
La magnitud del seno y el coseno del ángulo de 45° y sus otros tres ángulos hermanos (135°, 225°, y 315°) tienen la misma magnitud, |1/√2| o |√2/2| pero los signos varían dependiendo de la dirección del vector y la función trigonométrica. Por ejemplo, los ángulos de 225° y 315° que apuntan hacia abajo siempre tendrán un seno negativo por lo que su seno es -1/√2 = √2/2.
Las tercias
Los ángulos notables que son tercias del ángulo recto de 90 grados, también conocidos como ángulos de 30°, 60°, desempeñan un papel significativo en la trigonometría debido a sus propiedades geométricas y a su relación con los triángulos equiláteros.
Figura 8.1. Los ángulos notables de la circunferencia unitaria y sus funciones trigonométricas
Estos ángulos son parte de lo que se llama "ángulos notables en la circunferencia unitaria", y su medida se basa en múltiplos de la fracción (pi)/3 radianes.
La relación entre las funciones trigonométricas de los ángulos de 30° y 60°, así como los otros seis ángulos a 90° de cada uno, en los cuatro cuadrantes, es de carácter intuitivo. Al visualizar los triángulos correspondientes en un plano, se revela que uno es esencialmente el reflejo del otro a lo largo del eje de 45°. Esto implica que si conocemos las funciones seno y coseno del ángulo de 30°, podemos obtener las del ángulo de 60° simplemente intercambiando los valores. Además, al sumar 90° a cada uno de estos ángulos, observamos que las funciones mantienen los mismos valores absolutos, pero adquieren signos opuestos. Este patrón es fundamental en la comprensión de cómo se relacionan y transforman las funciones trigonométricas en diferentes puntos de la circunferencia unitaria, resultando en una herramienta esencial para resolver problemas que involucran ángulos y funciones trigonométricas en diversos contextos.
En consecuencia, si sabemos que el seno de 30° es √3/2 y su coseno es 1/2 entonces en 60° se intercambia y el seno de 60° es 1/2 y el coseno es √3/2. Ahora, si sumamos por ejemplo 90° a 60° el resultado es 150° un ángulo de vector que apunta hacia arriba, por lo que su seno es positivo 1/2, pero si coseno es negativo -√3/2 como se muestra en la figura.
Conclusiones
Aunque los ángulos de la circunferencia unitaria parecen difíciles de memorizar, ya que se plantean 16 ángulos cada uno con su seno y coseno, ¡en realidad solo debemos memorizar la ley de signos y los ángulos 45° y 30°! El de 60° es igual al de 30° pero trocando los resultados de seno y coseno, lo cual afecta a la tangente invirtiéndola, y todos los demás ángulos no son más que alteraciones de signo.
Tabla 8.1. Tabla de ángulos notables resumida. Los demás ángulos notables son siempre adiciones de 90° cuyos valores serán iguales al ángulo base, pero con cambio de signos según la función trigonométrica, o para 30°→60° y para 0°→90° se intercambia la solución de seno → coseno y coseno → seno.
9. Cambio en el arco de referencia
|| REGRESAR AL INDICE ||
Cambiar el marco de referencia o punto de vista es una técnica poderosa y versátil en la resolución de problemas físicos, especialmente cuando se trata de situaciones más complejas como planos inclinados. Al modificar el sistema de coordenadas según la geometría de la situación, podemos simplificar los cálculos y abordar problemas con mayor eficacia.
Supongamos que tenemos un objeto deslizándose sobre un plano inclinado. En muchos casos, el sistema de coordenadas estándar puede no ser la elección más conveniente, ya que los ejes x e y pueden estar alineados de manera poco favorable con la dirección del movimiento. Sin embargo, podemos rotar o inclinar el sistema de coordenadas para que uno de los ejes esté alineado con la dirección del plano inclinado. Esto no solo simplifica la descripción de los vectores que actúan sobre el objeto, sino que también puede eliminar componentes no deseados en una dirección no relevante para el problema.
Figura 9.1. Suponga que un cuerpo se mueve por un plano inclinado en dirección determinada por el ángulo ϕ. Intuitivamente sabemos que si no estuviera el plano, el ejercicio sería un trivial escenario de movimiento en una sola dimensión, pero el ángulo del plano complica todo.
Figura 9.2. Con solo alterar el marco de referencia, se consigue simplificar el escenario.
Al realizar este cambio de perspectiva, algunos vectores como el peso del objeto y la normal del plano inclinado pueden descomponerse directamente a lo largo de los nuevos ejes. Esto facilita enormemente el cálculo de las componentes relevantes en la dirección del plano inclinado y perpendicular a él. Al aplicar las funciones trigonométricas adecuadas, como el seno y el coseno, para descomponer y sumar estas fuerzas, podemos obtener una solución más clara y eficiente para el problema.
Un ejemplo de esto es la relación peso contra normal. En un plano inclinado normal el peso apunta hacia abajo, pero la normal apunta en una dirección de plano inclinado mas 90° por definición, el peso se puede calcular fácil, pero la normal no. Al hacer el giro del plano inclinado es posible descomponer el peso y a través de el obtener la normal en pasos que se hacen triviales.
Lo que debe tener en cuenta es que al cambiar la dirección del plano todos los vectores cambian sus ángulos respectivos a razón de θ + ϕ. Por lo que si un vector apuntaba a 270° ahora lo hará a 270° + ϕ que es la dirección del plano inclinado.
Tenga en cuenta que en muchas ocasiones no nos interesa si el plano está dirigido la derecha o a la izquierda, pero por convención diremos que el plano inclinado fundamental es el que hemos dibujado anteriormente, y su reflejo tendrá las mismas soluciones, pero con signos negativos.
Lo anterior tiene un efecto especialmente significativo en cualquier vector que originalmente hubiera estado asociado a un ángulo notable como (0°, 90°, 180° o 270°).
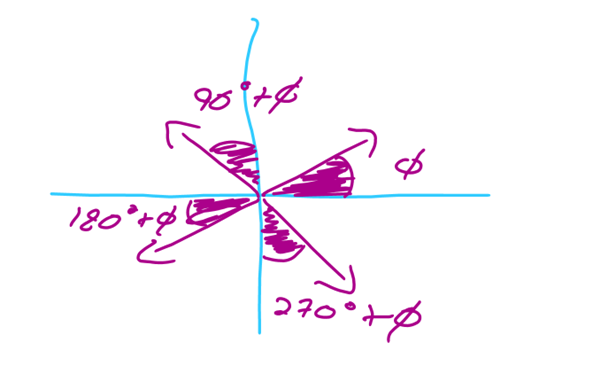
Figura 9.3. Los vectores que originalmente estaban alineados con los ejes de coordenadas originales pasarán a estar definidos en términos de un ángulo notable más el ángulo del plano inclinado.
Dado que el ángulo verdadero o θ pasa a estar definido por una suma estándar, y que esa suma estándar tiene un componente de ángulo estándar, eso implica un impacto trigonométrico estándar que permite expresar las ecuaciones en términos del ángulo del plano inclinado de manera directa. En un plano inclinado, el vector que mas nos interesa es el peso, y por ende será el único que analicemos.
El peso siempre se encuentra a 270°, por lo que al cambiar el marco de referencia obtendremos que el nuevo ángulo verdadero θ es de 270° + ϕ, donde ϕ es la pendiente de inclinación. Cuando esto pasa, el término 270° siempre tiene el mismo efecto en las funciones trigonométricas y es alterar las funciones trigonométricas trocándolas, por lo que para ese caso en particular el vector peso Fg tendrá unas definiciones trigonométricos especiales:
En caso de que debamos identificar otros vectores al cambiar el plano de inclinación siempre convendrá encontrar cual es la relación entre el ángulo teta el ángulo del plano de inclinación, y la modificación estándar, de forma tal que la ecuación final pueda expresarse siempre en términos del ángulo del plano inclinado.
Este enfoque de cambio de marco de referencia también se aplica en otras situaciones, como el análisis de movimiento en curvas o en sistemas rotatorios. Al adaptar el sistema de coordenadas al problema específico, simplificamos la descripción de los vectores y las variables involucradas, lo que facilita el razonamiento y la resolución de problemas más complejos de manera más efectiva.
Referencias bibliográficas
|| REGRESAR AL INDICE ||
Kuhn, W. (2003). Semantic reference systems. International Journal of Geographical Information Science, 17(5), 405–409.
Polo-Blanco, I., & Gonzalez-Sanchez, J. (2010). Four-dimensional polytopes: Alicia Boole Stott’s algorithm. The Mathematical Intelligencer, 32(3), 1–6.
Serway, R. A., & Jewett, J. W. J. (2014). Physics for Scientists and Engineers with Modern Physics, Ninth Edition (9th ed.). Boston: Brooks/Cole.
Tipler, P. A., & Mosca, G. (2008). Physics for scientists and engineers, with modern physics (6th ed.). New York: W. H. Freeman and Company.
Vásquez, C. M. (2017). Pierre de Fermat, René Descartes y el surgimiento de la Geometría analítica. Revista Vinculando.
Vince, J. (2021). History of Vector Analysis. In Vector Analysis for Computer Graphics (pp. 1–7). Springer.
Ejercicios resueltos
|| REGRESAR AL INDICE ||
Propios
Ejemplo. Un objeto se desplaza con una velocidad de (5.0; 330°) m/s en coordenadas polares. Convierte esta velocidad a coordenadas cartesianas.
Ejemplo. Sume los siguientes vectores y determine la resultante. 3.0 m/s, 45 grados y 5.0 m/s, 135 grados
Física de Sarwey


























No hay comentarios:
Publicar un comentario