Índice
Portada
1. Introducción al movimiento en una dimensión
|| REGRESAR AL INDICE ||
La física es una rama de la ciencia cuyos principales objetos de estudio son la materia y la energía. Los descubrimientos de la física encuentran aplicaciones en las ciencias naturales y en la tecnología, ya que la materia y la energía son los componentes básicos del mundo natural. Algunos otros dominios de estudio, más limitados en su alcance, pueden considerarse ramas que se han separado de la física para convertirse en ciencias por derecho propio. La física de hoy puede dividirse libremente en física clásica y física moderna.
1.1 Galileo di Vincenzo Bonaiuti de 'Galilei
(Italiano: 15 de febrero de 1564 - 8 de enero de 1642), comúnmente conocido como Galileo, fue un astrónomo, físico e ingeniero, a veces descrito como un erudito, de Pisa, en la actual Italia. Galileo ha sido llamado el "padre" de la astronomía observacional, la física moderna, el método científico, y la ciencia moderna.
Galileo estudió la rapidez, velocidad, gravedad y caída libre, el principio de relatividad, inercia, movimiento de proyectiles y también trabajó en ciencia y tecnología aplicadas, describiendo las propiedades de péndulos y "balances hidrostáticos". Inventó el termoscopio y varias brújulas militares, y usó el telescopio para observaciones científicas de objetos celestes. Sus contribuciones a la astronomía observacional incluyen la confirmación telescópica de las fases de Venus, la observación de los cuatro satélites más grandes de Júpiter, la observación de los anillos de Saturno y el análisis de las manchas solares.
La defensa de Galileo del heliocentrismo copernicano (la Tierra gira diariamente y gira alrededor del sol) se encontró con la oposición dentro de la Iglesia Católica y de algunos astrónomos. El asunto fue investigado por la Inquisición Romana en 1615, que concluyó que el heliocentrismo era tonto, absurdo y herético ya que contradecía las Sagradas Escrituras.
Más tarde, Galileo defendió sus puntos de vista en Diálogo sobre los dos sistemas mundiales principales (1632), que pareció atacar al Papa Urbano VIII y, por lo tanto, alejó tanto al Papa como a los jesuitas, que habían apoyado a Galileo hasta ese momento. Fue juzgado por la Inquisición, encontrado "vehementemente sospechoso de herejía" y obligado a retractarse. Pasó el resto de su vida bajo arresto domiciliario. Durante este tiempo, escribió Two New Sciences (1638), principalmente sobre la cinemática y la resistencia de los materiales, resumiendo el trabajo que había realizado unos cuarenta años antes.
2. La física del mundo antiguo
|| REGRESAR AL INDICE ||
Los elementos de lo que se convirtió en física se extrajeron principalmente de los campos de la astronomía, la óptica y la mecánica, que se unieron metodológicamente mediante el estudio de la geometría. Estas disciplinas matemáticas comenzaron en la antigüedad con los babilonios y con escritores helenísticos como Arquímedes y Ptolomeo. Mientras tanto, la filosofía antigua, incluida la llamada "física", se centró en explicar la naturaleza a través de ideas como los cuatro tipos de "causa" de Aristóteles.
2.1 Grecia
El movimiento hacia una comprensión racional de la naturaleza comenzó al menos desde el período arcaico en Grecia (650-480 aC) con los filósofos presocráticos. El filósofo Tales de Mileto (siglos VII y VI AEC), denominado "el Padre de la Ciencia" por negarse a aceptar varias explicaciones sobrenaturales, religiosas o mitológicas de los fenómenos naturales, proclamó que cada evento tenía una causa natural (Singer, 1949).
Figura 2.1. Tales de Mileto (Mileto, c. 624 a. C.-ibid., c. 546 a. C.) fue un filósofo, matemático, geómetra, físico y legislador griego. Se suele aceptar que Tales comenzó a usar el pensamiento deductivo aplicado a la geometría, y se le atribuye la enunciación de dos teoremas geométricos que llevan su nombre. También se lo reconoce como el padre del método naturalistas-materialista, en el cual las explicaciones para los fenómenos naturales deben obtenerse del mundo natural.
Tales sugirió que el agua es el elemento básico, experimentando con la atracción entre imanes y ámbar frotado y formulando las primeras cosmologías registradas. Anaximandro, famoso por su teoría protoevolucionaria, disputó las ideas de Tales y propuso que, en lugar de agua, una sustancia llamada apeiron era la piedra angular de toda la materia. Alrededor del año 500 a. C., Heráclito propuso que la única ley básica que rige el Universo era el principio del cambio y que nada permanece en el mismo estado indefinidamente. Esta observación lo convirtió en uno de los primeros eruditos en física antigua en abordar el papel del tiempo en el universo, un concepto clave y a veces polémico en la física moderna y actual. El físico temprano Leucipo (primera mitad del siglo V a. C.) se opuso rotundamente a la idea de la intervención divina directa en el universo, proponiendo en cambio que los fenómenos naturales tenían una causa natural. Leucipo y su alumno Demócrito fueron los primeros en desarrollar la teoría del atomismo, la idea de que todo está compuesto enteramente de varios elementos imperecederos e indivisibles llamados átomos.
Durante el período clásico en Grecia (siglos VI, V y IV a. C.) y en la época helenística (de los reinos de los generales de Alejandro Magno), la filosofía natural se convirtió lentamente en un campo de estudio emocionante y polémico. Aristóteles ( (384 - 322 a. C.), un estudiante de Platón, promovió el concepto de que la observación de los fenómenos físicos podría conducir al descubrimiento de las leyes naturales que los rigen. Los escritos de Aristóteles cubren la física, metafísica, poesía, teatro, música, lógica, retórica, lingüística, política, gobierno, ética, biología y zoología.
Figura 2.2. Aristóteles (Estagira, 384 a. C.-Calcis, 322 a. C.) fue un filósofo, polímata y científico nacido en la ciudad de Estagira, al norte de Antigua Grecia. Es considerado junto a Platón, el padre de la filosofía occidental. Sus ideas han ejercido una enorme influencia sobre la historia intelectual de Occidente por más de dos milenios.
Escribió el primer trabajo que se refiere a esa línea de estudio como "Física": en el siglo IV a. C., Aristóteles fundó el sistema conocido como física aristotélica. Intentó explicar ideas como el movimiento (y la gravedad) con la teoría de cuatro elementos. Aristóteles creía que toda la materia estaba compuesta de éter, o alguna combinación de cuatro elementos: tierra, agua, aire y fuego. Según Aristóteles, estos cuatro elementos terrestres son capaces de transformarse y moverse hacia su lugar natural, por lo que una piedra cae hacia el centro del cosmos, pero las llamas se elevan hacia la circunferencia “cabe anotar que esta física predecía una forma esférica para la Tierra, pero nadie sabía su tamaño hasta la estimación de Eratóstenes”. Finalmente, la física aristotélica se hizo enormemente popular durante muchos siglos en Europa, informando los desarrollos científicos y académicos de la Edad Media. Siguió siendo el paradigma científico principal en Europa hasta la época de Galileo Galilei e Isaac Newton.
Al principio de la Grecia clásica, el conocimiento de que la Tierra es esférica ("redonda") era común. Alrededor de 240 a. C., como resultado de un experimento seminal, Eratóstenes (276–194 a. C.) estimó con precisión su circunferencia. En contraste con las vistas geocéntricas de Aristóteles, Aristarco de Samos (griego: Ἀρίσταρχος; c.310 - c.230 aC) presentó un argumento explícito para un modelo heliocéntrico del sistema solar, es decir, para colocar el Sol, no la Tierra, en su centro. Seleuco de Seleucia, un seguidor de la teoría heliocéntrica de Aristarco, declaró que la Tierra giraba alrededor de su propio eje, que, a su vez, giraba alrededor del Sol. Aunque los argumentos que utilizó se perdieron, Plutarco declaró que Seleuco fue el primero en probar el sistema heliocéntrico a través del razonamiento.
Figura 2.3. Arquímedes de Siracusa (Siracusa (Sicilia), ca. 287 a. C.-ibidem, ca. 212 a. C.) fue un físico, ingeniero, inventor, astrónomo y matemático griego. Aunque se conocen pocos detalles de su vida “aunque los que, si son casi legendarios”, es considerado uno de los científicos más importantes de la Antigüedad clásica. Entre sus avances en física se encuentran sus fundamentos en hidrostática, estática y la explicación del principio de la palanca. Es reconocido por haber diseñado innovadoras máquinas, incluyendo armas de asedio y el tornillo de Arquímedes, que lleva su nombre. Experimentos modernos han probado las afirmaciones de que Arquímedes llegó a diseñar máquinas capaces de sacar barcos enemigos del agua o prenderles fuego utilizando una serie de espejos.
En el siglo III a. C., el matemático griego Arquímedes de Siracusa (287–212 a. C.), generalmente considerado como el mayor matemático de la antigüedad y uno de los más grandes de todos los tiempos, sentó las bases de la hidrostática, la estática y calculó Las matemáticas subyacentes de la palanca. Un destacado científico de la antigüedad clásica, Arquímedes también desarrolló sistemas elaborados de poleas para mover objetos grandes con un mínimo de esfuerzo. El tornillo de Arquímedes apuntala la hidroingeniería moderna, y sus máquinas de guerra ayudaron a contener a los ejércitos de Roma en la Primera Guerra Púnica. Arquímedes incluso desgarró los argumentos de Aristóteles y su metafísica, señalando que era imposible separar las matemáticas y la naturaleza y lo demostró al convertir las teorías matemáticas en invenciones prácticas. Además, en su trabajo On Floating Bodies, alrededor del año 250 a. C., Arquímedes desarrolló la ley de flotabilidad, también conocida como el principio de Arquímedes. En matemáticas, Arquímedes utilizó el método de agotamiento para calcular el área bajo el arco de una parábola con la suma de una serie infinita, y dio una aproximación notablemente precisa de pi. También definió la espiral con su nombre, fórmulas para los volúmenes de superficies de revolución y un ingenioso sistema para expresar números muy grandes. También desarrolló los principios de los estados de equilibrio y los centros de gravedad, ideas que influirían en los conocidos eruditos, Galileo y Newton.
Hiparco (190–120 a. C.), centrándose en la astronomía y las matemáticas, utilizó técnicas geométricas sofisticadas para mapear el movimiento de las estrellas y los planetas, incluso prediciendo los tiempos en que ocurrirían los eclipses solares. Además, agregó cálculos de la distancia del Sol y la Luna desde la Tierra, en función de sus mejoras en los instrumentos de observación utilizados en ese momento. Otro de los más famosos de los primeros físicos fue Ptolomeo (90–168 CE), una de las mentes más destacadas durante la época del Imperio Romano. Ptolomeo fue el autor de varios tratados científicos, al menos tres de los cuales fueron de importancia continua para la ciencia islámica y europea posterior. El primero es el tratado astronómico ahora conocido como el Almagesto. El segundo es la Geografía, que es una discusión exhaustiva del conocimiento geográfico del mundo grecorromano.
Gran parte del conocimiento acumulado del mundo antiguo se perdió. Incluso de las obras de los pensadores más conocidos, sobrevivieron pocos fragmentos. Aunque escribió al menos catorce libros, casi nada del trabajo directo de Hiparco sobrevivió. De las 150 obras aristotélicas de renombre, solo existen 30, y algunas de ellas son "poco más que apuntes".
2.2 India y China
También existieron importantes tradiciones físicas y matemáticas en las antiguas ciencias chinas e indias.
En la filosofía india, Maharishi Kanada fue el primero en desarrollar sistemáticamente una teoría del atomismo alrededor del año 200 a. C (Quinn, 2000). aunque algunos autores le asignaron una era anterior en el siglo VI a. C. Fue elaborado por los atomistas budistas Dharmakirti y Dignāga durante el primer milenio CE. Pakudha Kaccayana, filósofo indio del siglo VI a. C. y contemporáneo del Buda Gautama, también había propuesto ideas sobre la constitución atómica del mundo material. Estos filósofos creían que otros elementos (excepto el éter) eran físicamente palpables y, por lo tanto, comprendían partículas minúsculas de materia. La última partícula minúscula de materia que no pudo subdividirse se denominó Parmanu. Estos filósofos consideraban que el átomo era indestructible y, por lo tanto, eterno. Los budistas pensaban que los átomos eran objetos diminutos que no se podían ver a simple vista y que aparecían y desaparecían en un instante. La escuela de filósofos de Vaisheshika creía que un átomo era un mero punto en el espacio. También fue el primero en representar las relaciones entre movimiento y fuerza aplicadas. Las teorías indias sobre el átomo son muy abstractas y están enredadas en la filosofía, ya que se basan en la lógica y no en la experiencia personal o la experimentación. En astronomía india, Aryabhatiya de Aryabhata (499 CE) propuso la rotación de la Tierra, mientras que Nilakantha Somayaji (1444-1544) de la escuela de astronomía y matemáticas de Kerala propuso un modelo semi-heliocéntrico que se asemeja al sistema Tycho Brahe (Hagens, 2009; Riepe, 1996).
El estudio del magnetismo en la antigua China se remonta al siglo IV a. C. (en el Libro del Maestro del Valle del Diablo) (Lyubina & Gutfleisch, n.d.), Uno de los principales contribuyentes a este campo fue Shen Kuo (1031–1095), un polímata y estadista que fue el primero en describir la brújula de aguja magnética utilizada para la navegación, también como establecer el concepto del verdadero norte. En óptica, Shen Kuo desarrolló independientemente una cámara oscura (Belbachir & Göbel, 2009).
2.3 El mundo islámico
En los siglos VII al XV, se produjo un progreso científico en el mundo musulmán. Muchas obras clásicas en indio, asirio, sasánida (persa) y griego, incluidas las obras de Aristóteles, fueron traducidas al árabe (Lapidus, 1996). Contribuciones importantes fueron hechas por Ibn al-Haytham (965-1040), un científico árabe, considerado como uno de los fundadores de la óptica moderna. Ptolomeo y Aristóteles teorizaron que la luz brillaba desde el ojo para iluminar objetos o que "formas" emanaban de los objetos mismos, mientras que al-Haytham (conocido por el nombre en latín "Alhazen") sugirió que la luz viaja al ojo en rayos desde diferentes puntos en un objeto. Las obras de Ibn al-Haytham y Abū Rayhān Bīrūnī (973-1050), un científico persa, finalmente pasaron a Europa occidental, donde fueron estudiados por académicos como Roger Bacon (Piniés, 2016).
Figura 2.4. Ibn al-Haytham (llamado en Occidente Alhazen o Alhacén) fue un matemático, físico y astrónomo árabe musulmán. Está considerado el creador del método científico, realizó importantes contribuciones a los principios de la óptica y a la concepción de los experimentos científicos.
Ibn al-Haytham y Biruni fueron los primeros defensores del método científico. Ibn al-Haytham es considerado el "padre del método científico moderno" debido a su énfasis en los datos experimentales y la reproducibilidad de sus resultados (Heinen, 1974). El primer enfoque metódico para los experimentos en el sentido moderno es visible en los trabajos de Ibn al-Haytham, quien introdujo un método inductivo-experimental para lograr resultados. Bīrūnī introdujo los primeros métodos científicos para varios campos de investigación diferentes durante los años 1020 y 1030, incluyendo un método experimental temprano para la mecánica. La metodología de Biruni se parecía al método científico moderno, particularmente en su énfasis en la experimentación repetida.
Ibn Sīnā (980–1037), conocido como "Avicena", fue un polímato de Bukhara (en la actual Uzbekistán) responsable de importantes contribuciones a la física, la óptica, la filosofía y la medicina. Publicó su teoría del movimiento en el Libro de Sanación (1020), donde argumentó que el lanzador imparte un impulso a un proyectil y creía que era una virtud temporal que disminuiría incluso en el vacío. Lo veía como persistente, requiriendo fuerzas externas como la resistencia del aire para disiparlo (Nasr, 2003). Ibn Sina hizo una distinción entre 'fuerza' e 'inclinación' (llamada "mayl"), y argumentó que un objeto ganó mayl cuando el objeto está en oposición a su movimiento natural. Concluyó que la continuación del movimiento se atribuye a la inclinación que se transfiere al objeto, y ese objeto estará en movimiento hasta que se gaste el mayl. También afirmó que el proyectil en el vacío no se detendría a menos que se actúe sobre él. Esta concepción del movimiento es consistente con la primera ley del movimiento de Newton, la inercia, que establece que un objeto en movimiento permanecerá en movimiento a menos que una fuerza externa actúe sobre él. Esta idea que disintió de la visión aristotélica fue descrita más tarde como "ímpetu" por John Buridan, quien fue influenciado por el Libro de Sanación de Ibn Sina.
Omar Khayyám (1048-1131), un científico persa, calculó la duración de un año solar y solo estuvo fuera por una fracción de segundo en comparación con nuestros cálculos modernos. Usó esto para componer un calendario considerado más preciso que el calendario gregoriano que apareció 500 años después. Está clasificado como uno de los primeros grandes comunicadores científicos del mundo, dijo, por ejemplo, haber convencido a un teólogo sufí de que el El Mundo gira sobre un eje (Wilson, 2001).
Hibat Allah Abu'l-Barakat al-Baghdaadi (c. 1080-1165) adoptó y modificó la teoría de Ibn Sina sobre el movimiento de proyectiles. En su Kitab al-Mu'tabar, Abu'l-Barakat declaró que el motor imparte una inclinación violenta (mayl qasri) sobre el movimiento y que esto disminuye a medida que el objeto en movimiento se distancia del motor (Gutman, 2003). También propuso una explicación de la aceleración de los cuerpos que caen por la acumulación de incrementos sucesivos de potencia con incrementos sucesivos de velocidad. Según Shlomo Pines, la teoría del movimiento de al-Baghdaadi fue "la negación más antigua de la ley dinámica fundamental de Aristóteles [es decir, que una fuerza constante produce un movimiento uniforme], [y es así] una anticipación vaga de la ley fundamental de mecánica clásica [es decir, que una fuerza aplicada continuamente produce aceleración]" (Franco, 2003). Jean Buridan y Alberto de Sajonia más tarde se refirieron a Abu'l-Barakat al explicar que la aceleración de un cuerpo que cae es el resultado de su ímpetu creciente.
Ibn Bajjah (c. 1085-1138), conocido como "Avempace" en Europa, propuso que para cada fuerza siempre hay una fuerza de reacción. Si bien no especificó que estas fuerzas sean iguales, fue un precursor de la tercera ley de movimiento de Newton que establece que para cada acción hay una reacción igual y opuesta (Franco, 2003). Ibn Bajjah fue un crítico de Ptolomeo y trabajó en la creación de una nueva teoría de la velocidad para reemplazar la teoría de Aristóteles. Dos futuros filósofos apoyaron las teorías que Avempace creó, conocidas como dinámicas Avempaceanas. Estos filósofos fueron Tomás de Aquino, un sacerdote católico, y John Duns Scotus (Gracia, 2002). Galileo adoptó la fórmula de Avempace "que la velocidad de un objeto dado es la diferencia del poder motriz de ese objeto y la resistencia del medio de movimiento" (Gracia, 2002).
2.4 La edad media
La conciencia de las obras antiguas volvió a entrar en Occidente a través de traducciones del árabe al latín. Su reintroducción, combinada con comentarios teológicos judeoislámicos, tuvo una gran influencia en filósofos medievales como Tomás de Aquino. Los eruditos europeos escolásticos, que buscaban conciliar la filosofía de los antiguos filósofos clásicos con la teología cristiana, proclamaron a Aristóteles como el pensador más grande del mundo antiguo. En los casos en que no contradicen directamente la Biblia, la física aristotélica se convirtió en la base de las explicaciones físicas de las Iglesias europeas. La cuantificación se convirtió en un elemento central de la física medieval (Crombie, 1961).
Basada en la física aristotélica, la física escolástica describió las cosas como moviéndose de acuerdo con su naturaleza esencial. Los objetos celestes se describían como moviéndose en círculos, porque el movimiento circular perfecto se consideraba una propiedad innata de los objetos que existían en el reino incorrupto de las esferas celestes. La teoría del ímpetu, el antepasado de los conceptos de inercia e impulso fue desarrollada en líneas similares por filósofos medievales como John Philoponus y Jean Buridan. Los movimientos debajo de la esfera lunar se consideraban imperfectos y, por lo tanto, no se podía esperar que exhibieran movimientos consistentes. Un movimiento más idealizado en el reino "sublunar" solo se podía lograr a través del artificio, y antes del siglo XVII, muchos no veían los experimentos artificiales como un medio válido para aprender sobre el mundo natural. Las explicaciones físicas en el reino sublunar giraron en torno a las tendencias. Las piedras contenían el elemento tierra, y los objetos terrenales tendían a moverse en línea recta hacia el centro de la tierra (y el universo en la vista geocéntrica aristotélica) a menos que se les impida lo contrario (McVaugh, 1995).
3. La revolución científica
|| REGRESAR AL INDICE ||
Durante los siglos 16 y 17, un gran avance del progreso científico conocido como la revolución científica tuvo lugar en Europa. La insatisfacción con los enfoques filosóficos más antiguos había comenzado antes y había producido otros cambios en la sociedad, como la Reforma Protestante, pero la revolución en la ciencia comenzó cuando los filósofos naturales comenzaron a lanzar un ataque sostenido al programa filosófico escolástico y supusieron que los esquemas descriptivos matemáticos adoptados a partir de campos como la mecánica y la astronomía en realidad podrían dar caracterizaciones universalmente válidas del movimiento y otros conceptos.
3.1 Nicolás Copérnico
El astrónomo polaco Nicolaus Copérnico (1473-1543) hizo un gran avance en astronomía cuando, en 1543, dio argumentos sólidos para el modelo heliocéntrico del sistema solar, aparentemente como un medio para hacer que las tablas que grafican el movimiento planetario sean más precisas y simplificar su producción. En los modelos heliocéntricos del sistema solar, la Tierra orbita alrededor del Sol junto con otros cuerpos en la galaxia de la Tierra, una contradicción según el astrónomo griego-egipcio Ptolomeo (siglo II EC; ver arriba), cuyo sistema colocó a la Tierra en el centro del Universo que había sido aceptado por más de 1.400 años.
Figura 3.1. Nicolás Copérnico (nacido como Niklas Koppernigk; en latín, Nicolaus Copernicus; en polaco, Mikołaj Kopernik; en alemán, Nikolaus Kopernikus; Thorn, Prusia Real, 19 de febrero de 1473-Frauenburg, Prusia Real, 24 de mayo de 1543) fue un monje astrónomo prusiano12 del Renacimiento que formuló la teoría heliocéntrica del sistema solar, concebida en primera instancia por Aristarco de Samos. Su libro De revolutionibus orbium coelestium (Sobre las revoluciones de las esferas celestes) suele ser considerado como el punto inicial o fundador de la astronomía moderna, además de ser una pieza clave en lo que se llamó la Revolución científica en la época del Renacimiento. Copérnico pasó cerca de veinticinco años trabajando en el desarrollo de su modelo heliocéntrico del universo. En aquella época resultó difícil que los científicos lo aceptaran, ya que suponía una auténtica revolución. Copérnico fue matemático, astrónomo, jurista, físico, clérigo católico, gobernador, diplomático y economista. Junto con sus extensas responsabilidades, la astronomía figuraba como poco más que una distracción. Por su enorme contribución a la astronomía, en 1935 se dio el nombre «Copernicus» a uno de los mayores cráteres lunares, ubicado en el Mare Insularum.
El astrónomo griego Aristarco de Samos (c.310 - c.230 aC) había sugerido que la Tierra gira alrededor del Sol, pero el razonamiento de Copérnico condujo a una aceptación general duradera de esta idea "revolucionaria". El libro de Copérnico que presenta la teoría (De revolutionibus orbium coelestium, "Sobre las revoluciones de las esferas celestes") se publicó justo antes de su muerte en 1543 y, como ahora se considera generalmente que marca el comienzo de la astronomía moderna, también se considera marca el comienzo de la revolución científica. La nueva perspectiva de Copérnico, junto con las precisas observaciones hechas por Tycho Brahe, permitió al astrónomo alemán Johannes Kepler (1571–1630) formular sus leyes sobre el movimiento planetario que siguen en uso hoy en día.
3.2 Galileo Galilei
El matemático, astrónomo y físico italiano Galileo Galilei (1564–1642) fue la figura central de la revolución científica y famoso por su apoyo al copernicanismo, sus descubrimientos astronómicos, experimentos empíricos y su mejora del telescopio. Como matemático, el papel de Galileo en la cultura universitaria de su época estaba subordinado a los tres temas principales de estudio: derecho, medicina y teología (que estaba estrechamente relacionado con la filosofía).
Figura 3.2. Galileo Galilei (Pisa, Toscana; 15 de febrero de 15644-Arcetri, Toscana; 8 de enero de 1642) fue un astrónomo, filósofo, ingeniero, matemático y físico italiano, relacionado estrechamente con la revolución científica. Eminente hombre del Renacimiento, mostró interés por casi todas las ciencias y artes (música, literatura, pintura). Sus logros incluyen la mejora del telescopio, gran variedad de observaciones astronómicas, la primera ley del movimiento y un apoyo determinante a la «Revolución de Copérnico». Ha sido considerado como el «padre de la astronomía moderna», el «padre de la física moderna» y el «padre de la ciencia».
Sin embargo, Galileo sintió que el contenido descriptivo de las disciplinas técnicas justificaba el interés filosófico, particularmente porque el análisis matemático de las observaciones astronómicas, en particular, el análisis de Copérnico de los movimientos relativos del Sol, la Tierra, la Luna y los planetas, indicaba que las declaraciones de los filósofos sobre la naturaleza del universo, se podría demostrar que estaba en error. Galileo también realizó experimentos mecánicos, insistiendo en que el movimiento en sí mismo, independientemente de si se produjo "naturalmente" o "artificialmente" (es decir, deliberadamente), tenía características universalmente consistentes que podrían describirse matemáticamente.
Los primeros estudios de Galileo en la Universidad de Pisa fueron en medicina, pero pronto se sintió atraído por las matemáticas y la física. A los 19 años, descubrió (y, posteriormente, verificó) la naturaleza isocrónica del péndulo cuando, usando su pulso, cronometró las oscilaciones de una lámpara oscilante en la catedral de Pisa y descubrió que permanecía igual para cada oscilación, independientemente de la amplitud del mismo. Pronto se hizo conocido por su invención de un equilibrio hidrostático y por su tratado sobre el centro de gravedad de cuerpos sólidos. Mientras enseñaba en la Universidad de Pisa (1589-1592), inició sus experimentos sobre las leyes de los cuerpos en movimiento que arrojaron resultados tan contradictorios a las enseñanzas aceptadas de Aristóteles que despertó un fuerte antagonismo. Descubrió que los cuerpos no caen con velocidades proporcionales a sus pesos. La famosa historia en la que se dice que Galileo dejó caer pesas desde la Torre Inclinada de Pisa es apócrifa, pero descubrió que el camino de un proyectil es una parábola y se le atribuyen conclusiones que anticiparon las leyes de movimiento de Newton (por ejemplo, la noción de inercia). Entre estos se encuentra lo que ahora se llama relatividad galileana, la primera declaración formulada con precisión sobre las propiedades del espacio y el tiempo fuera de la geometría tridimensional.
Galileo ha sido llamado el "padre de la astronomía observacional moderna" (Singer, 2013), el "padre de la física moderna" (Weidhorn, 2005), el "padre de la ciencia", (Weidhorn, 2005) y "el padre de la ciencia moderna". Según Stephen Hawking, "Galileo, tal vez más que cualquier otra persona, fue responsable del nacimiento de la ciencia moderna" (Hawking, 2009). A medida que la ortodoxia religiosa decretaba una comprensión geocéntrica o ticónica del sistema solar, el apoyo de Galileo al heliocentrismo provocó controversia y Fue juzgado por la Inquisición. Encontrado "vehementemente sospechoso de herejía", se vio obligado a retractarse y pasó el resto de su vida bajo arresto domiciliario (Gingerich, 1982).
Las contribuciones que hizo Galileo a la astronomía observacional incluyen la confirmación telescópica de las fases de Venus; su descubrimiento, en 1609, de las cuatro lunas más grandes de Júpiter (posteriormente se le dio el nombre colectivo de "lunas galileanas"); y la observación y análisis de manchas solares. Galileo también persiguió la ciencia y la tecnología aplicadas, inventando, entre otros instrumentos, una brújula militar. Su descubrimiento de las lunas jovianas se publicó en 1610 y le permitió obtener el puesto de matemático y filósofo en la corte de los Medici. Como tal, se esperaba que entablara debates con filósofos de la tradición aristotélica y recibió una gran audiencia por sus propias publicaciones, como Discursos y demostraciones matemáticas sobre dos nuevas ciencias (publicado en el extranjero después de su arresto por la publicación de Diálogo sobre los Dos Máximos Sistemas del Mundo). El interés de Galileo en experimentar y formular descripciones matemáticas del movimiento estableció la experimentación como parte integral de la filosofía natural. Esta tradición, combinada con el énfasis no matemático en la recopilación de "historias experimentales" por reformistas filosóficos como William Gilbert y Francis Bacon, atrajo a seguidores significativos en los años previos y posteriores a la muerte de Galileo, incluidos Evangelista Torricelli y los participantes en la Accademia del Cimento en Italia; Marin Mersenne y Blaise Pascal en Francia; Christiaan Huygens en los Países Bajos; y Robert Hooke y Robert Boyle en Inglaterra.
3.3 René Descartes
El filósofo francés René Descartes (1596-1650) estaba bien conectado y era bastante influyente dentro de las redes de filosofía experimental de la época. Sin embargo, Descartes tenía una agenda más ambiciosa, orientada a reemplazar por completo la tradición filosófica escolástica.
Figura 3.3. René Descartes, también llamado Renatus Cartesius (en escritura latina) (La Haye en Touraine, 31 de marzo de 1596-Estocolmo, Suecia, 11 de febrero de 1650), fue un filósofo, matemático y físico francés, considerado como el padre de la filosofía moderna, así como uno de los protagonistas con luz propia en el umbral de la revolución científica.
Al cuestionar la realidad interpretada a través de los sentidos, Descartes buscó restablecer esquemas explicativos filosóficos al reducir todos los fenómenos percibidos como atribuibles al movimiento de un mar invisible de "corpúsculos". (Notablemente, reservó el pensamiento humano y a Dios de su esquema, manteniéndolos separados del universo físico). Al proponer este marco filosófico, Descartes supuso que los diferentes tipos de movimiento, como el de los planetas versus el de los objetos terrestres, no eran fundamentalmente diferentes, sino simplemente manifestaciones diferentes de una cadena interminable de movimientos corpusculares que obedecen a principios universales. Particularmente influyentes fueron sus explicaciones para los movimientos astronómicos circulares en términos del movimiento vórtice de los corpúsculos en el espacio (Descartes argumentó, de acuerdo con las creencias, si no los métodos, de los escolásticos, que un vacío no podría existir), y su explicación de gravedad en términos de corpúsculos que empujan objetos hacia abajo (Descartes, 1999).
Descartes, como Galileo, estaba convencido de la importancia de la explicación matemática, y él y sus seguidores fueron figuras clave en el desarrollo de las matemáticas y la geometría en el siglo XVII. Las descripciones matemáticas cartesianas del movimiento sostenían que todas las formulaciones matemáticas debían ser justificables en términos de acción física directa, una posición mantenida por Huygens y el filósofo alemán Gottfried Leibniz, quien, siguiendo la tradición cartesiana, desarrolló su propia alternativa filosófica al escolasticismo, que describió en su obra de 1714, The Monadology. Descartes ha sido denominado el "Padre de la filosofía moderna", y gran parte de la filosofía occidental posterior es una respuesta a sus escritos, que se estudian de cerca hasta el día de hoy. En particular, sus Meditaciones Sobre la Primera Filosofía continúa siendo un texto estándar en la mayoría de los departamentos de filosofía universitarios. La influencia de Descartes en las matemáticas es igualmente evidente; el sistema de coordenadas cartesianas, que permite que las ecuaciones algebraicas se expresen como formas geométricas en un sistema de coordenadas bidimensional, recibió su nombre. Se le acredita como el padre de la geometría analítica, el puente entre el álgebra y la geometría, importante para el descubrimiento del cálculo analítico.
3.4 Johannes Kepler
Kepler era profesor de matemáticas en una escuela de seminario en Graz, donde se convirtió en asociado del príncipe Hans Ulrich von Eggenberg. Más tarde se convirtió en asistente del astrónomo Tycho Brahe en Praga, y finalmente en el matemático imperial del emperador Rodolfo II y sus dos sucesores, Matías y Fernando II. También enseñó matemáticas en Linz y fue asesor del general Wallenstein. Además, realizó un trabajo fundamental en el campo de la óptica, inventó una versión mejorada del telescopio refractor (o kepleriano) y fue mencionado en los descubrimientos telescópicos de su contemporáneo Galileo Galilei. Fue miembro correspondiente de la Accademia dei Lincei en Roma (Abetti, 1975).
Kepler vivió en una época en la que no había una distinción clara entre astronomía y astrología, pero había una fuerte división entre astronomía (una rama de las matemáticas dentro de las artes liberales) y física (una rama de la filosofía natural). Kepler también incorporó argumentos y razonamientos religiosos en su trabajo, motivado por la convicción religiosa y la creencia de que Dios había creado el mundo de acuerdo con un plan inteligible al que se puede acceder a través de la luz natural de la razón (Barker & Goldstein, 2001). Kepler describió su nueva astronomía como "física celestial" (Donahue, 1994), como "una excursión a la metafísica de Aristóteles", y como "un suplemento de los cielos de Aristóteles", transformando la antigua tradición de la cosmología física al tratar astronomía como parte de una física matemática universal.
Figura 3.4. Johannes Kepler (Weil der Stadt, 27 de diciembre de 1571-Ratisbona, 15 de noviembre de 1630), figura clave en la revolución científica, fue un astrónomo y matemático alemán; conocido fundamentalmente por sus leyes sobre el movimiento de los planetas en su órbita alrededor del Sol. Fue colaborador de Tycho Brahe, a quien sustituyó como matemático imperial de Rodolfo II.
Más allá de su papel en el desarrollo histórico de la astronomía y la filosofía natural, Kepler se ha destacado en la filosofía e historiografía de la ciencia. Kepler y sus leyes del movimiento fueron centrales en las primeras historias de la astronomía, como Histoire des mathématiques de Jean-Étienne Montucla de 1758 y Histoire de l'astronomie moderne de 1821 de Jean-Baptiste Delambre. Estas y otras historias escritas desde una perspectiva de la Ilustración trataron los argumentos metafísicos y religiosos de Kepler con escepticismo y desaprobación, pero más tarde los filósofos naturales de la era romántica vieron estos elementos como centrales para su éxito. William Whewell, en su influyente Historia de las Ciencias Inductivas de 1837, descubrió que Kepler era el arquetipo del genio científico inductivo; en su Filosofía de las Ciencias Inductivas de 1840, Whewell sostuvo a Kepler como la encarnación de las formas más avanzadas de método científico. Del mismo modo, Ernst Friedrich Apelt, el primero en estudiar extensamente los manuscritos de Kepler, después de su compra por Catalina la Grande, identificó a Kepler como la clave de la "Revolución de las ciencias". Apelt, quien vio las matemáticas, la sensibilidad estética, las ideas físicas y la teología de Kepler como parte de un sistema unificado de pensamiento, produjo el primer análisis extendido de la vida y el trabajo de Kepler.
Los filósofos de la ciencia, como Charles Sanders Peirce, Norwood Russell Hanson, Stephen Toulmin y Karl Popper, recurrieron repetidamente a Kepler: se han encontrado ejemplos de inconmensurabilidad, razonamiento analógico, falsificación y muchos otros conceptos filosóficos en el trabajo de Kepler. El físico Wolfgang Pauli incluso utilizó la disputa de prioridad de Kepler con Robert Fludd para explorar las implicaciones de la psicología analítica en la investigación científica.
3.5 Isaac Newton
A fines del siglo XVII y principios del siglo XVIII, se vieron los logros de la figura más grande de la revolución científica: el físico y matemático de la Universidad de Cambridge, Sir Isaac Newton (1642-1727), considerado por muchos como el científico más grande e influyente que jamás haya existido. Newton, miembro de la Royal Society of England, combinó sus propios descubrimientos en mecánica y astronomía con los anteriores para crear un sistema único para describir el funcionamiento del universo. Newton formuló tres leyes del movimiento que modelaron la relación entre el movimiento y los objetos, y también la ley de la gravitación universal, la última de las cuales podría usarse para explicar el comportamiento no solo de los cuerpos que caen sobre la Tierra sino también de los planetas y otros cuerpos celestes. Para llegar a sus resultados, Newton inventó una forma de una rama matemática completamente nueva: el cálculo (también inventado independientemente por Gottfried Leibniz), que se convertiría en una herramienta esencial en gran parte del desarrollo posterior en la mayoría de las ramas de la física. Los hallazgos de Newton se exponen en su Philosophiæ Naturalis Principia Mathematica ("Principios matemáticos de la filosofía natural"), cuya publicación en 1687 marcó el comienzo del período moderno de la mecánica y la astronomía.
Newton pudo refutar la tradición mecánica cartesiana de que todos los movimientos deberían explicarse con respecto a la fuerza inmediata ejercida por los corpúsculos. Utilizando sus tres leyes del movimiento y la ley de la gravitación universal, Newton eliminó la idea de que los objetos seguían caminos determinados por formas naturales y, en cambio, demostró que no solo los caminos observados regularmente, sino que todos los movimientos futuros de cualquier cuerpo podrían deducirse matemáticamente basándose en el conocimiento de su movimiento existente, su masa y las fuerzas que actúan sobre ellos. Sin embargo, los movimientos celestes observados no se ajustaban con precisión a un tratamiento newtoniano, y Newton, que también estaba profundamente interesado en la teología, imaginó que Dios intervino para garantizar la estabilidad continua del sistema solar.
Figura 3.5. Isaac Newton (Woolsthorpe, Lincolnshire; 25 de diciembre de 1642jul./ 4 de enero de 1643 greg.-Kensington, Londres; 20 de marzojul./ 31 de marzo de 1727 greg.) fue un físico, teólogo, inventor, alquimista y matemático inglés. Es autor de los Philosophiæ naturalis principia mathematica, más conocidos como los Principia, donde describe la ley de la gravitación universal y estableció las bases de la mecánica clásica mediante las leyes que llevan su nombre. Entre sus otros descubrimientos científicos destacan los trabajos sobre la naturaleza de la luz y la óptica (que se presentan principalmente en su obra Opticks), y en matemáticas, el desarrollo del cálculo infinitesimal.
Los principios de Newton (pero no sus tratamientos matemáticos) resultaron controvertidos con los filósofos continentales, quienes encontraron su falta de explicación metafísica para el movimiento y la gravitación filosóficamente inaceptable. A partir de alrededor de 1700, se abrió una grieta amarga entre las tradiciones filosóficas continentales y británicas, que fueron avivadas por disputas acaloradas, continuas y viciosamente personales entre los seguidores de Newton y Leibniz sobre la prioridad sobre las técnicas analíticas de cálculo, que cada una se había desarrollado de forma independiente. Inicialmente, las tradiciones cartesianas y leibnizianas prevalecieron en el continente (lo que condujo al dominio de la notación de cálculo leibniziano en todas partes, excepto Gran Bretaña). El propio Newton permaneció en privado perturbado por la falta de una comprensión filosófica de la gravitación mientras insistía en sus escritos que no era necesario inferir su realidad. A medida que avanzaba el siglo XVIII, los filósofos naturales continentales aceptaron cada vez más la voluntad de los newtonianos de renunciar a las explicaciones metafísicas ontológicas de los movimientos matemáticamente descritos (Schofield, 2015).
Newton construyó el primer telescopio reflector funcional y desarrolló una teoría del color, publicada en Opticks, basada en la observación de que un prisma descompone la luz blanca en los muchos colores que forman el espectro visible. Mientras Newton explicaba que la luz estaba compuesta de pequeñas partículas, Christiaan Huygens presentó una teoría rival de la luz que explicaba su comportamiento en términos de ondas en 1690. Sin embargo, la creencia en la filosofía mecanicista junto con la reputación de Newton significaba que la teoría de las ondas tuvo relativamente poco apoyo hasta el siglo XIX. Newton también formuló una ley empírica de enfriamiento, estudió la velocidad del sonido, investigó series de potencia, demostró el teorema binomial generalizado y desarrolló un método para aproximar las raíces de una función. Su trabajo en series infinitas se inspiró en los decimales de Simon Stevin. Lo más importante, Newton demostró que los movimientos de los objetos en la Tierra y de los cuerpos celestes se rigen por el mismo conjunto de leyes naturales, que no eran caprichosas ni malévolas. Al demostrar la coherencia entre las leyes del movimiento planetario de Kepler y su propia teoría de la gravitación, Newton también eliminó las últimas dudas sobre el heliocentrismo. Al reunir todas las ideas expuestas durante la revolución científica, Newton estableció efectivamente las bases de la sociedad moderna en matemáticas y ciencias (Gleick, 2004).
Y con Sir Isaac iniciaremos nuestra aventura matemática para describir la naturaleza.
4. Historia de las ecuaciones del movimiento en una dimensión
|| REGRESAR AL INDICE ||
Hay dos descripciones principales del movimiento en física clásica: dinámica y cinemática. La dinámica es general, ya que se tienen en cuenta los momentos, las fuerzas y la energía de las partículas. En este caso, a veces el término dinámica se refiere a las ecuaciones diferenciales que satisface el sistema (por ejemplo, la segunda ley de Newton o las ecuaciones de Euler-Lagrange) y, a veces, a las soluciones de esas ecuaciones. Sin embargo, la cinemática es más simple. Se trata sólo de variables derivadas de las posiciones de los objetos y el tiempo. En circunstancias de aceleración constante, estas ecuaciones de movimiento más simples generalmente se denominan ecuaciones SUVAT, que surgen de las definiciones de cantidades cinemáticas: desplazamiento (Δx), rapidez inicial (vo), rapidez final (v), aceleración (a), tiempo inicial (t0) y tiempo final (t). Es común que el tiempo inicial sea el punto de referencia del sistema, por lo que (t0 = 0), lo cual permitirá usar integrales indefinidas.
4.1 La antigüedad, física aristotélica
La cinemática, la dinámica y los modelos matemáticos del universo se desarrollaron gradualmente durante tres milenios, gracias a muchos pensadores, de los cuales solo conocemos algunos nombres. En la antigüedad, sacerdotes, astrólogos y astrónomos predijeron los eclipses solares y lunares, los solsticios y los equinoccios del Sol y el período de la Luna. Pero no tenían nada más que un conjunto de algoritmos desconectados e inducidos para guiarlos. Las ecuaciones de movimiento no se escribieron hasta otros mil años.
👉 el método científico de ruta inductiva es el que parte con muchos datos aparentemente desconectados y confusos, los filtra buscando patrones, para generar leyes empíricas.
👉 Los elementos
En este contexto, el autor más importante por casi dos milenios fue Aristóteles, que, aunque siendo un gran filósofo, llegó a conclusiones erróneas que mantendrían a los filósofos naturales posteriores dando vueltas sin resultados concretos. Aristóteles dividió el universo en una región terrestre o sublunar, que abarca la Tierra y se extiende hasta la esfera de la Luna, y una región celeste o supralunar, que se extiende desde la esfera de la Luna hasta las estrellas fijas. Se pensaba que toda la materia de la región terrestre estaba compuesta por cuatro elementos: tierra, agua, aire y fuego, mientras que se suponía que la región celestial estaba llena del quinto elemento o elemento divino, el éter. Se creía que el éter era inmune a todos los cambios excepto al movimiento local. La materia ordinaria estaba sujeta no solo al movimiento local sino también a otros tipos de cambios.
👉 Tipos de movimiento
Aristóteles distinguió entre dos tipos de movimiento local: natural y violento.
Los movimientos naturales son aquellos que exhibe un cuerpo cuando no se ve obstaculizado. Los movimientos violentos ocurren cuando un cuerpo es desplazado de su lugar de descanso natural.
Movimientos celestes, Según Aristóteles, los cuerpos celestes se mueven naturalmente en círculos o combinaciones de estos. Como se pensaba que el éter no impedía en modo alguno este movimiento, se concluyó que estos cuerpos celestiales no presentan movimientos violentos. Los cuerpos compuestos de materia ordinaria se comportan de manera bastante diferente y de una manera íntimamente ligada a la estructura del mundo sublunar.
Figura 4.1. La cosmología planteada por Aristóteles se tomó como cierta por casi dos mil años, sincretizándose con la religión cristiana, a tal punto que cuando Galileo se atrevió a cuestionarla se metió en problemas con las autoridades civiles y religiosas de su tiempo.
Movimiento de los elementos mundanos, la región terrestre del universo de Aristóteles estaba compuesta por cuatro áreas concéntricas, cada una de las cuales era el lugar natural de uno de los cuatro elementos. Cuando se desplaza, se creía que cada elemento se mueve naturalmente en forma rectilínea hacia su anillo concéntrico (si no se ve obstaculizado). El anillo exterior era el lugar natural del fuego, debajo el anillo de aire, debajo el anillo de agua y debajo el anillo de tierra. Aristóteles atribuyó distintos grados de pesadez o ligereza a los elementos básicos para explicar su tendencia a buscar su lugar natural. El elemento tierra se consideró absolutamente pesado. Como tal, se movió naturalmente hacia el centro de la Tierra desde las regiones superiores, lo cual, aunque erróneo, sí que predecía una forma esférica para el mundo terrestre, por lo que la idea de que los filósofos antiguos y de la edad media pensaban que el mundo era plano no es más que un mito. De manera similar, la absoluta ligereza del fuego hizo que se elevara desde abajo a su lugar natural sobre el anillo de aire.
👉 Los movimientos violentos y la fuerza de impulso
Explicar el movimiento violento requería un mecanismo diferente. Aristóteles creía que la fuerza responsable del movimiento debía estar en constante contacto físico con el cuerpo en movimiento. Cuando se iniciaba un movimiento violento, se identificaba fácilmente el impulso del motivo que lo originaba: la cuerda del arco para disparar una flecha, la mano para lanzar una piedra, etc. Aristóteles sostenía que el motor original no sólo pone en movimiento la flecha o la piedra, sino también activa el medio circundante, en este caso el aire. El aire se parte antes de la flecha o la roca y regresa en círculos para mantener una fuerza motriz continua detrás del objeto. Esta fuerza disminuye gradualmente debido a la resistencia del medio. Cuando se disipa por completo, la flecha o piedra cae hacia abajo de acuerdo con su movimiento natural. Por consecuencia, en Aristóteles no tenemos una ley de inercia, sino una ley de impulso, un cuerpo requiere de una fuerza que lo impulsa en todo momento para moverse, lo cual parece intuitivamente correcto, y fue aceptado hasta los trabajos de Galileo y Newton.
Aristóteles formuló reglas específicas para describir las consecuencias de esta doctrina del impulso. Afirmó que la velocidad de un cuerpo en movimiento violento es directamente proporcional a la fuerza motriz e inversamente proporcional a la resistencia. Este último incluía el poder resistivo del cuerpo en movimiento (un concepto que no se definió) y la resistencia ofrecida por el medio externo. En consecuencia, la velocidad de un cuerpo podría duplicarse duplicando la fuerza aplicada o reduciendo a la mitad la resistencia.
👉 El vacío
Esta doctrina del movimiento también llevó a Aristóteles a negar la existencia del vacío. Dado que la velocidad era proporcional a la densidad del medio, una rarefacción indefinida del medio produciría un aumento indefinido correspondiente en la velocidad. Pero si el medio desapareciera por completo, entonces la velocidad de un cuerpo sería infinita. Esto era claramente absurdo. Aún más serio, el movimiento en el vacío violó la afirmación de Aristóteles de que el movimiento violento necesariamente ocurría en un medio, y que el medio era quien generaba el impulso. Además, Aristóteles tomó como axiomático que los cuerpos de diferentes pesos necesariamente caen a diferentes velocidades, siendo sus velocidades directamente proporcionales a su peso. Sin embargo, se dio cuenta de que, sin un medio material, los cuerpos más livianos se moverían tan rápido como los cuerpos más pesados. Para evitar estas conclusiones, Aristóteles rechazó el vacío y postuló un universo lleno por todas partes de materia.
4.2 La edad media
Los eruditos medievales del siglo XIII —por ejemplo, en las relativamente nuevas universidades de Oxford y París— recurrieron a los antiguos matemáticos (Euclides y Arquímedes) y filósofos (Aristóteles) para desarrollar un nuevo cuerpo de conocimiento, ahora llamado física. En Oxford, el Merton College acogió a un grupo de estudiosos dedicados a las ciencias naturales, principalmente a la física, la astronomía y las matemáticas, de talla similar a los intelectuales de la Universidad de París. Thomas Bradwardine extendió cantidades aristotélicas como la distancia y la velocidad, y les asignó intensidad y extensión. Bradwardine sugirió una ley exponencial que involucra fuerza, resistencia, distancia, velocidad y tiempo. Nicholas Oresme amplió aún más los argumentos de Bradwardine. La escuela de Merton demostró que la cantidad de movimiento de un cuerpo que experimenta un movimiento uniformemente acelerado es igual a la cantidad de un movimiento uniforme a la velocidad alcanzada a la mitad del movimiento acelerado.
Figura 4.2. El Merton College es uno de los colleges (facultades) que constituyen la Universidad de Oxford en el Reino Unido. Su fundación puede datarse en la década de 1260, cuando Walter de Merton, secretario de Enrique III de Inglaterra y posteriormente de Eduardo I de Inglaterra, estableció los primeros estatutos para una nueva institución académica independiente y estableció presupuestos que la apoyaran. Una de las características fundamentales de la fundación de De Merton fue que este college se iba a autogobernar y que los presupuestos iban a ser directamente creados por el director y los profesores y miembros del college. Su existencia permitió crear una de las primeras comunidades académicas.
4.3 Galileo
Para los escritores de cinemática anteriores a Galileo, dado que no se podían medir los intervalos de tiempo pequeños, pues no existían cronómetros precisos, la afinidad entre el tiempo y el movimiento era oscura e intuitiva. Usaron el tiempo en función de la distancia, y en caída libre, mayor velocidad como resultado de una mayor elevación. Solo Domingo de Soto, teólogo español, en su comentario a la Física de Aristóteles publicado en 1545, después de definir el movimiento "uniforme deforme" (que es un movimiento uniformemente acelerado) -no se usó la palabra velocidad- como proporcional al tiempo, declaró correctamente que este tipo de movimiento era identificable con cuerpos y proyectiles que caían libremente, sin que probara estas proposiciones ni sugiriera una fórmula que relacionara el tiempo, la velocidad y la distancia. Los comentarios de De Soto son notablemente correctos con respecto a las definiciones de aceleración y la observación de que la aceleración sería negativa durante el ascenso, pues el cuerpo pierde movimiento en el proceso.
Discursos como estos se extendieron por toda Europa, dando forma al trabajo de Galileo Galilei y otros, y ayudaron a sentar las bases de la cinemática en términos de una comunidad científica crítica, con problemas de investigación comunes. Galileo indujo la ecuación de la caída libre (Humphreys, 1967), usando la regla de Merton, ahora conocida como un caso especial de una de las ecuaciones de la cinemática.
Galileo fue el primero en demostrar que la trayectoria de un proyectil es una parábola. Galileo comprendió la fuerza centrífuga y dio una definición correcta de momento cinético (cantidad de movimiento). Este énfasis en la cantidad de movimiento como una cantidad fundamental en la dinámica es de suma importancia. Midió el impulso por el producto de la velocidad y el peso; la masa es un concepto posterior, desarrollado por Huygens y Newton. En el balanceo de un péndulo simple, Galileo dice en Discursos que "cada impulso adquirido en el descenso a lo largo de un arco es igual al que hace que el mismo móvil ascienda a través del mismo arco". Su análisis sobre proyectiles indica que Galileo había captado la primera ley y la segunda ley del movimiento, pero no las formalizó matemáticamente. No generalizó ni los hizo aplicables a cuerpos no sujetos a la gravitación terrestre. Ese paso fue la contribución de Newton.
El término "inercia" fue utilizado por Kepler quien lo aplicó a los cuerpos en reposo. Galileo no comprendió del todo la tercera ley del movimiento, la ley de la igualdad de acción y reacción, aunque corrigió algunos errores de Aristóteles. Con Stevin y otros, Galileo también escribió sobre estática. Formuló el principio del paralelogramo de fuerzas, pero no reconoció completamente su alcance.
Galileo también se interesó por las leyes del péndulo, cuyas primeras observaciones fueron cuando era joven. En 1583, mientras rezaba en la catedral de Pisa, su atención fue atraída por el movimiento de la gran lámpara encendida y girando, tomando como referencia su propio pulso para medir el tiempo, se percató que el período era semejante, incluso después de que el movimiento había disminuido mucho, descubriendo el isocronismo del péndulo (Gamow, 1988). Experimentos más cuidadosos realizados por él más tarde, y descritos en sus Discursos, revelaron que el período de oscilación varía con la raíz cuadrada de la longitud, pero es independiente de la masa del péndulo.
4.4 La revolución científica
Así llegamos a René Descartes, Isaac Newton, Gottfried Leibniz, y el resto de la primera comunidad científica verdaderamente moderna; y las formas evolucionadas de las ecuaciones de movimiento que empiezan a ser reconocidas como las modernas. Y que son el enfoque de nuestro curso de física clásica. Pero antes de trabajar las ecuaciones del movimiento y sus conceptos, debemos tener ciertas nociones de las matemáticas creadas para ellas por Isaac Newton, el cálculo.
5. El cálculo de la física
|| REGRESAR AL INDICE ||
“Physics without calculus sucks”. Vincent Bian A part-time student and a full-time nerd
El cálculo, originalmente llamado cálculo infinitesimal o "el cálculo de los infinitesimales", es el estudio matemático del cambio continuo, de la misma manera que la geometría es el estudio de la forma y el álgebra es el estudio de las generalizaciones de las operaciones aritméticas. Tiene dos ramas principales, cálculo diferencial y cálculo integral; el primero se refiere a las tasas de cambio instantáneo y las pendientes de las curvas, mientras que el último se refiere a la acumulación de cantidades y áreas debajo o entre las curvas. Estas dos ramas están relacionadas entre sí por el teorema fundamental del cálculo y hacen uso de las nociones fundamentales de convergencia de secuencias infinitas y series infinitas hasta un límite bien definido.
El cálculo infinitesimal fue desarrollado de forma independiente a finales del siglo XVII por Isaac Newton y Gottfried Wilhelm Leibniz. El trabajo posterior, incluida la codificación de la idea de los límites, colocó estos desarrollos sobre una base conceptual más sólida. Hoy en día, el cálculo tiene usos generalizados en la ciencia, la ingeniería y las ciencias sociales.
5.1 Cuál es la relación entre el cálculo y la física clásica
Una respuesta básica sería que la física es el estudio de la materia y los fenómenos en el espacio y el tiempo, mientras que el cálculo es el aspecto de las matemáticas que estudia cómo un objeto cambia con respecto a cómo otro objeto cambia simultáneamente en un cociente, por ejemplo, el cambio de posición con respecto al cambio de tiempo. Dado que la mayor parte de la física se ocupa de sistemas que cambian con respecto al espacio y el tiempo, el cálculo es en realidad el marco matemático empleado para el 90% de todos los sistemas físicos. Sin embargo, la respuesta completa vas más allá de que las dos cosas están unidas cuando los científicos las usan, pues ambos han estado relacionados desde su nacimiento como ciencia moderna.
Evidentemente, existió física antes del cálculo, después de todo la mecánica de las máquinas, y ciertos conceptos sobre el funcionamiento del mundo han ido desarrollándose desde los tiempos de Arquímedes, pero solo hasta la llegada de Isaac Newton tenemos que la física, y de hecho, toda la ciencia se hacen más parecidas a lo que hacemos actualmente.
Isaac Newton cambió el mundo cuando inventó el cálculo en 1665 y lo inventó para poder entender su nueva física. Hoy damos esto tan por sentado actualmente, que intentamos enseñar y aprender las dos cosas por separado, pero lo que Newton logró a la edad de 24 años es simplemente asombroso, pues lo que el diseñó para la física no se quedó solo en la física. El cálculo tiene usos en química, biología, economía, matemáticas puras, todas las ramas de la ingeniería y más. No es una exageración decir que la visión de Newton en el desarrollo del cálculo realmente ha revolucionado nuestra capacidad para buscar nuevas ramas de la ciencia y la ingeniería. Se usa en problemas cuando una cantidad cambia en función de otra, que es cómo se comportan la mayoría de los problemas en la realidad.
En primer lugar, deberás saber quién fue Isaac Newton y por qué fue y sigue siendo tan importante para todas las ciencias modernas. Newton un físico, matemático y cosmólogo que se destacó en el siglo XVII. Probablemente sea mejor conocido por formular las leyes del movimiento y la gravitación universal. Su influencia no puede ser exagerada. Uno de sus muchos logros fue la invención del cálculo. Sin duda, su propio trabajo en física lo llevó a este problema y sintió la necesidad de resolverlo con un nuevo marco matemático que simplemente no había existido hasta ese momento. Su enfoque en la gravedad y las leyes del movimiento están vinculados a su gran avance en el cálculo.
Newton comenzó tratando de describir la velocidad de un objeto que cae. Cuando hizo esto, descubrió que la velocidad de un objeto que cae aumenta cada segundo, pero que no existía una explicación matemática para esto. El tema del movimiento y la tasa de cambio aún no se había explorado de manera significativa en el campo de las matemáticas, por lo que Newton vio un vacío que debía llenarse. Empezó a trabajar de esta manera correcta, incorporando también a su teoría las elipses planetarias para tratar de explicar la órbita de los planetas. Descubrió que mediante el uso del cálculo podía explicar cómo se movían los planetas y por qué las órbitas de los planetas están en una elipse. Este es uno de los avances de Newton: que la fuerza gravitatoria que nos mantiene en el suelo es la misma fuerza que hace que los planetas giren alrededor del Sol y que la Luna gire alrededor de la Tierra.
Todo esto muestra que cuando Newton llegó a desarrollar la idea del cálculo y su enfoque en la tasa de cambio, alimentó su trabajo anterior en física. Fue ayudado por su ya sólida comprensión conceptual de la física y el movimiento. No fue una desviación completa de su otro trabajo. Y esto quizás demuestra mejor que todo el vínculo directo entre el campo de las matemáticas y el campo de la física. Al menos para Newton, los dos iban de la mano, y ¿quiénes somos nosotros para cuestionarlo? Newton usó tasas de cambios para formar la base del Cálculo, y su teoría revisada se publicó en 1676.
Nuestro problema académico radica en que nuestro sistema de estudios cuestiona las raíces históricas y conceptuales que dan nacimiento a la física como una ciencia moderna, y separan las dos materias en años académicos diferentes, física clásica para décimo y cálculo para once, sin embargo, tratar de trabajar la física sin el cálculo es algo que es muy complejo al pasar a fundamentarse en la intuición del descubrimiento de los conceptos, pero sin una manera de formalizarlo.
En palabras de Ivan Savov “El cálculo y la mecánica a menudo se enseñan como materias separadas. No debería ser así. Si aprendes cálculo sin mecánica, será aburrido. Si aprendes física sin cálculo, no entenderás realmente.” (Savov, 2014)
5.2 La función matemática
En matemáticas, una función es una relación entre dos o más parámetros matemáticos. Normalmente relacionados dos parámetros variables y otras constantes. En una función entre dos variables, que podemos llamar (x) y (y), definimos como una dependiente de la otra mediante una función, de forma tal que con cada valor arbitrario de la variable independiente se obtiene un valor en la dependiente. Las funciones son básicamente ecuaciones que opera a (x) para obtener a (y). Las funciones fueron originalmente la idealización de cómo una cantidad variable depende de otra cantidad. Por ejemplo, la posición de un planeta es una función del tiempo x(t) o xt. Históricamente, el concepto se elaboró con el cálculo infinitesimal a finales del siglo XVII y, hasta el siglo XIX, las funciones que se consideraban eran derivables (es decir, tenían un alto grado de regularidad). El concepto de función se formalizó a finales del siglo XIX en términos de la teoría de conjuntos, y esto amplió enormemente los dominios de aplicación del concepto.
Para nuestro curso de física las funciones más comunes son las lineales directas, lineales inversas y cuadráticas.
Figura 5.1. representaciones gráficas de tres funciones comunes: (A) la función lineal positiva directa, (B) la función lineal positiva inversa y (C) brazo positivo de la función cuadrática.
5.3 La pendiente de una recta
El concepto de derivada se desprende de el concepto de diferencia o cambio de estado de una cantidad física. El cambio de estado en una cantidad física se calcula como a diferencia Δ que hay entre su posición final y su posición inicial. Por ejemplo, para la variable x, será Δx = x – xo.
Una tasa de cambio o pendiente es un parámetro relativo que surge del cociente entre dos cambios de estado relacionados. Por ejemplo, la velocidad promedio es la pendiente, cociente o tasa de cambio entre el cambio de posición con respecto al cambio en el tiempo.
En matemáticas, la pendiente, tasa, radio, ratio, razón o gradiente (slope) de una línea es un número que describe la proporción de cambio entre el eje x y el eje y de una línea recta, siendo esta proporción representada como un cociente o división entre las diferencias de ambos parámetros.
Por tradición el parámetro que simboliza la pendiente en matemáticas puras es la m, sin embargo, en química y física sumaos k por una razón, y es que para una línea recta la pendiente es siempre constante, sin importar que tan grande o que tan pequeño sea el intervalo de la resta usada para calcularla. No hay una respuesta clara a la pregunta de por qué la letra m se usa para la pendiente en lugar de k que denota constante indeterminada o desconocida, pero su primer uso en inglés aparece en O'Brien (1844), quien escribió la ecuación de una línea recta como "y = m x + b", donde b representa el punto que la recta atraviesa el eje (y). Sin embargo, estos símbolos no son obligatorios, especialmente cuando usamos la función lineal para representar leyes físicas. En química el problema del intercepto en el eje y no es problemático, ya que la gran mayoría de sus leyes lineales tienen un intercepto en el origen. En física esto no ocurre. De esta forma podemos definir al intercepto como el punto y cuando x vale cero, o simplemente y inicial yo.
DEMOSTRACION. Hallar la ecuación de la recta con la definición de la pendiente.
5.4 La pendiente de una curva
Encontrar la pendiente en una recta es simplemente plantear una resta simple, sin embargo, cuando queremos calcular la pendiente en una curva, como la que genera la función cuadrática la cuestión se hace más difícil, pues la resta simple genera una pendiente promedio, pero una pendiente promedio es solo el ratio para una recta, y no el ratio en la curva para un punto verdaderamente instantáneo.
Figura 5.2. El problema con la pendiente instantánea en una curva radica en que al hacer la resta para cualquier conjunto de puntos, esta dará un valor diferente, por lo que la idea es que la distancia entre los dos puntos sea cada vez más y más pequeña, hasta ser casi cero, pero sin ser cero, a esto lo llamaremos un cambio o diferencia infinitesimal.
¿Cómo podemos calcular la pendiente instantánea en un punto cualquiera de una curva? Aquí es donde entra el concepto de límite, si asumimos mentalmente que cada vez hacemos restas más y más pequeñas, de forma tal que la resta en el eje independiente tienda a cero “es casi infinitesimalmente cero, pero no cero”, la pendiente promedio se hará más cercana a la pendiente instantánea:
Para evitarnos tener que escribir la notación límite a cada rato, empleamos la notación cambio infinitesimal con la letra delta minúscula.
Aunque hemos generado una de las definiciones más importantes del cálculo, en realidad no nos sirve de nada, pues esto nos traslada a la pregunta ¿Cómo podemos hacer la resta infinitesimalmente pequeña? Aquí es donde va a pasar unos cuantos meses mientras su instructor le da un paseo por la definición fundamental del cálculo, definición que evadiremos aquí, ya que esto no es un curso de cálculo. El punto es que los matemáticos han creado algoritmos para evadir el problema de la resta infinitesimalmente pequeña, y al mismo tiempo generar su resultado. El resultado de esta resta infinitesimalmente pequeña la llamaremos derivada, y a su algoritmo para ser generada la llamaremos técnica de derivación.
La palabra Algoritmo significa “Un conjunto de reglas a seguir en los cálculos u otras operaciones de resolución de problemas” o “Un procedimiento para resolver un problema matemático en un número finito de pasos que frecuentemente mediante operaciones recursivas”. Las técnicas de derivación son algoritmos que permiten generar la derivada de una función, conociendo la ecuación de la función original. Las técnicas de derivación están consignadas en tablas de derivación que usted deberá consignar en su cuaderno, y al menos memorizarse las más sencillas. En las tablas de derivación, la derivada (δy/δx) se representa de una manera más compacta denominada f prima (f´), siendo esta un sinónimo de derivada, y esta a su vez un sinónimo de la pendiente instantánea. La letra (f) sin el símbolo prima se usa para representar la función original.
👉 Las técnicas de derivación permiten obtener la derivada o pendiente instantánea si conocemos la función original,
sin embargo, en el curso de física nos encontraremos notablemente con el problema opuesto, que se resuelve con
👉 las técnicas de integración o antiderivada, dada la pendiente instantánea que no es constante, obtener la función original.
Esta función original realmente recibe el nombre de la antiderivada o integral. El teorema fundamental del cálculo establece básicamente de la derivación y la integración son operaciones opuestas, como la suma y la resta, por lo que la integral de una derivada recupera la función original. Al igual que con la derivación, la integración ha sido reducida por el arduo esfuerzo de los matemáticos a algoritmos resumidos en la tabla de técnicas de integración.
5.5 La derivada
La derivada es un concepto fundamental en cálculo que permite calcular la tasa de cambio instantánea de una función en relación a su variable independiente. Matemáticamente, la derivada de una función ecuación se denota como dy/dx donde y representa la variable dependiente y la ecuación a derivar y x la variable independiente o variable de derivación y se define como el límite de la razón incremental de la función cuando el incremento en la variable independiente tiende a cero.
En términos más intuitivos, la derivada representa la pendiente de la recta tangente a la curva de la función en un punto dado. Indica cómo está cambiando el valor de la función en ese punto y la dirección de ese cambio. Si la derivada es positiva, la función está aumentando en ese punto, mientras que si la derivada es negativa, la función está disminuyendo. Una derivada nula indica un punto crítico o una posible extremidad.
La derivada tiene múltiples aplicaciones en matemáticas y física. Se utiliza para resolver problemas de optimización, determinar la velocidad y aceleración de objetos en movimiento, analizar el crecimiento de poblaciones, estudiar el comportamiento de sistemas dinámicos y modelar fenómenos naturales, entre otros. Además, es la base para el estudio de la integración, la cual permite calcular áreas bajo curvas y resolver problemas inversos a los que se resuelven con la derivada. A continuación introducimos algunas reglas de derivación.
Para plantear una derivada es necesario identificar cual es son las dos variables o cantidades físicas que cambian de estado, y cual de ellas representa a la variable independiente. Algunas tasas de cambio famosas representan a su vez otras cantidades físicas de importancia, por ejemplo la aceleración es el cambio de estado infinitesimal de la velocidad con respecto al tiempo. En este caso, tiempo es la variable independiente o de derivación.
👉 La derivada de una constante (k) es cero. Esto tiene sentido dado que, al graficar una constante, esta no tiene pendiente, pues y no cambia con respecto a x, lo cual implica que si y = k entonces Δy = 0.
👉 La derivada de una variable elevada a la n potencia. La regla de derivación establece:
Por ejemplo, si deseamos derivar la función y = x2 + yo, donde (yo) es una constante. En este caso la derivada de la función completa es igual a la derivada de cada uno de los términos por separado.
Ejemplos
Ejemplo. Una partícula se mueve a lo largo de una trayectoria recta, y su posición en función del tiempo está dada por la ecuación r = 3t3 + 2t2 - t, donde r representa la posición en metros y t el tiempo en segundos. Determina la velocidad de la partícula en el instante t = 3 segundos. Plantee las constantes de proporcionalidad necesarias para el análisis dimensional.
Ejemplo. Un objeto se desplaza en línea recta y su posición en función del tiempo está dada por la ecuación r= t3 - 4t2 + 2t, donde r representa la posición en metros y t el tiempo en segundos. Halla la aceleración del objeto en el instante t = 10 segundos.
Ejemplo. Una partícula se mueve de acuerdo con la ecuación x=10t2, donde ``x´´ está en metros y ``t´´ en segundos: (a) encuentre la velocidad promedio en el intervalo de 2 a 3 segundos; (b) determine la velocidad promedio de 2 a 2.1 segundos.
5.6 La integral
La integral es un concepto fundamental en cálculo que permite calcular la función opuesta a la derivada así como otras aplicaciones como la de calcular áreas debajo de curvas suaves.
Existen dos tipos principales de integrales: la integral definida y la integral indefinida. La integral definida se utiliza para calcular el área exacta bajo una curva en un intervalo específico.
Por otro lado, la integral indefinida es una función primitiva o antiderivada de una función dada. La integral indefinida es una familia de funciones, donde se agrega una constante arbitraria conocida como constante de integración.
La integral tiene numerosas aplicaciones en matemáticas y física. Se utiliza para calcular áreas, volúmenes, longitudes de curvas, calcular el trabajo realizado por una fuerza, encontrar el centro de masa de un objeto, resolver ecuaciones diferenciales y modelar fenómenos físicos y naturales. También es una herramienta esencial en el campo de la estadística, donde se utiliza para calcular probabilidades y distribuciones de probabilidad.
El símbolo
El símbolo ∫ se conoce como el símbolo de la integral y se utiliza para representar una operación de integración en matemáticas. Fue introducido por el matemático alemán Gottfried Wilhelm Leibniz en el siglo XVII. Leibniz desarrolló el cálculo diferencial e integral de forma independiente junto con Sir Isaac Newton.
Leibniz buscaba una notación compacta y elegante para representar la operación de integración. Se inspiró en la letra "S" mayúscula, que representa la palabra latina "summa" o "suma", y le dio una forma estilizada con una línea curva en la parte superior. Este símbolo se convirtió en la representación estándar de la integral y ha perdurado a lo largo de los siglos. El símbolo ∑, conocido como sigma mayúscula, se utiliza para representar una operación de suma en matemáticas. A diferencia del símbolo de la integral (∫), que representa una suma continua o acumulativa de infinitos términos, el símbolo sigma (∑) se utiliza para denotar una suma discreta o finita de términos. Es algo semejante a la relación de resta finita Δ y resta infinitesimal δ.
El desarrollo del cálculo y la notación integral fue un avance importante en las matemáticas, ya que permitió el estudio y la resolución de problemas complejos relacionados con el cálculo de áreas, volúmenes, velocidades, aceleraciones, entre otros conceptos fundamentales en física, ingeniería y muchas otras disciplinas.
Desde su introducción, el símbolo de la integral se ha utilizado ampliamente en textos matemáticos y ha sido adoptado en todo el mundo como una herramienta fundamental en el cálculo y el análisis matemático.
👉 La integral de una constante (k) con respecto a la variable independiente infinitesimal (δx). La integral no afecta a la constante, esto se debe a que la integral funciona como una gran suma, y la constante en una suma puede ser expulsada de la suma al aplicar factor común. Luego, la integral de un cambio infinitesimal es el cambio simple. Por ejemplo, si sabemos que la pendiente instantánea (δy/δx) es 4, ¿Cuál será su función antiderivada? Para hacer esto, despejas el cambio infinitesimal en la variable dependiente (δy), y aplicas la integral entre los estados final e inicial. La constante no se afecta por la integral. El efecto de la integral es convertir el cambio infinitesimal en la resta simple.
👉 La integral de una variable elevada a la n potencia. La regla de integración establece:
Al igual que con las derivadas, si tenemos que integrar una función de suma o resta varios términos, la integral de la función completa es igual a la integral de cada uno de los términos por separado. Por ejemplo, sabemos que la pendiente instantánea de cierta función no constante es 2x + 5, y deseamos conocer la forma de la función original y entre el punto inicial y el punto final de medición.
Ejemplos
6. Modelos de análisis
|| REGRESAR AL INDICE ||
Un modelo de análisis es una situación común que ocurre una y otra vez al resolver problemas de física química o biología, y cuyos patrones pueden resolverse mediante un algoritmo fijo, que solo debe demostrarse una vez, y luego aplicarse a todos los escenarios semejantes. Dependiendo de la presencia o no de un algoritmo conocido, clasificaremos a los escenarios de lápiz y papel en dos categorías:
👉 problemas verdaderos: son escenarios cuyo algoritmo es desconocido, por lo que debe buscarse en la literatura o demostrar una solución empleando los conceptos fundamentales de la física, la química, la biología, el algebra y el cálculo.
👉 ejercicios triviales: son escenarios cuyo algoritmo es conocido, ya sea porque hay un ejemplo resuelto semejante, o se cuenta con la ecuaciòn que lo resuelve “y se sabe cómo usarla”.
6.1 Modelado
Los modelos de análisis nos ayudan a reconocer esas situaciones comunes y nos guían hacia una solución al problema. La forma que adopta un modelo de análisis es una descripción de
👉 el comportamiento de alguna entidad física o
👉 la interacción entre esa entidad y el entorno.
Cuando encuentre un nuevo problema, debe identificar los detalles fundamentales del problema e intentar reconocer cuáles de las situaciones que ya ha visto podrían usarse como modelo para el nuevo problema. Por ejemplo, suponga que un automóvil se mueve a lo largo de una autopista sin peaje a una velocidad constante. ¿Es importante que sea un automóvil? ¿Es importante que sea una autopista? Si las respuestas a ambas preguntas son no, pero el automóvil se mueve en línea recta a velocidad constante, modelamos el automóvil como una partícula a velocidad constante, que discutiremos en esta sección. Una vez que se ha modelado el problema, ya no se trata de un automóvil. Se trata de una partícula que experimenta un cierto tipo de movimiento, un movimiento que hemos estudiado antes.
Este método es algo similar a la práctica común en la profesión jurídica de encontrar "precedentes legales". Si se puede encontrar un caso previamente resuelto que es muy similar legalmente al actual, se usa como modelo y se presenta un argumento en la corte para vincularlos lógicamente. El hallazgo en el caso anterior se puede utilizar para influir en el hallazgo en el caso actual. Haremos algo similar en física, química y biología. Para un problema dado, buscamos un "precedente", un modelo con el que ya estamos familiarizados y que pueda aplicarse al problema actual.
Todos los modelos de análisis que desarrollaremos en física se basan en cuatro modelos de simplificación fundamentales. El primero de los cuatro es el modelo de partículas discutido en la introducción de este capítulo. Observaremos una partícula bajo diversos comportamientos e interacciones ambientales. Se introducen modelos de análisis adicionales en capítulos posteriores basados en modelos de simplificación de un sistema, un objeto rígido y una onda. Una vez que hayamos introducido estos modelos de análisis, veremos que aparecen una y otra vez en diferentes situaciones problemáticas.
6.2 Respuestas analíticas vs numéricas
Al resolver un problema, debe evitar navegar por el capítulo buscando una ecuación que contenga la variable desconocida que se solicita en el problema. En muchos casos, la ecuación que encuentre puede no tener nada que ver con el problema que está tratando de resolver. Es mucho mejor dar este primer paso:
👉 identificar el modelo de análisis apropiado para el problema. Para hacerlo, piense detenidamente sobre lo que está sucediendo en el problema y acóplelo a una situación que haya visto antes.
👉 Una vez que se identifica el modelo de análisis, hay un pequeño número de ecuaciones para elegir que son apropiadas para ese modelo, a veces solo una ecuación. Por lo tanto, el modelo le dice qué ecuación (es) usar para la representación matemática.
👉 Posteriormente, debe evitar la tentación de reemplazar primero y despejar después, pues esto aumenta la cantidad de símbolos en la línea, y por ende la dificultad real del problema.
👉 Dado lo anterior, es mejor jugar algebraicamente con los términos, despejando aquel relacionado con la pregunta, y solo ese.
👉La ecuación expresada como una respuesta universal para toda situación homóloga se denominará la respuesta analítica, mientras que su magnitud después de reemplazar y operar será la respuesta numérica.
7. Parámetros fundamentales del movimiento rectilíneo
|| REGRESAR AL INDICE ||
El movimiento lineal (también llamado movimiento rectilíneo) es un movimiento unidimensional a lo largo de una línea recta y, por lo tanto, puede describirse matemáticamente utilizando solo una dimensión espacial. El movimiento lineal puede ser de dos tipos: movimiento lineal uniforme con velocidad constante o aceleración cero; Movimiento lineal no uniforme con velocidad variable o aceleración distinta de cero. El movimiento de una partícula (un objeto similar a un punto) a lo largo de una línea se puede describir por su posición, que varía con respecto al tiempo. Un ejemplo de movimiento lineal es un atleta corriendo 100 metros a lo largo de una pista recta.
7.1 El modelo de la partícula
En nuestro estudio del movimiento, usamos lo que se llama modelo de partículas y describimos el objeto en movimiento como una partícula independientemente de su tamaño o forma, incluso ignoramos la masa en estas primeras discusiones. En general, una partícula es un objeto similar a un punto, es decir, un objeto que tiene masa, pero es de tamaño infinitesimal. Por ejemplo, si deseamos describir el movimiento de la Tierra alrededor del Sol, podemos tratar la Tierra como una partícula y obtener datos razonablemente precisos sobre su órbita. Esta aproximación se justifica porque el radio de la órbita de la Tierra es grande en comparación con las dimensiones de la Tierra y el Sol. Como ejemplo a una escala mucho más pequeña, es posible explicar la presión ejercida por un gas en las paredes de un recipiente tratando las moléculas de gas como partículas, sin tener en cuenta la estructura interna de las moléculas.
Debes desarrollar un proceso de construcción de modelos a medida que estudias todas las ciencias naturales. En este estudio, tendrás que resolver muchos problemas matemáticos. Una de las técnicas de resolución de problemas más importantes es construir un modelo para el problema: identificar un sistema de componentes físicos para el problema y hacer predicciones del comportamiento del sistema en función de las interacciones entre sus componentes o la interacción entre el sistema y su entorno.
7.2 Marco de referencia
En física, un marco de referencia consiste en un sistema de coordenadas abstractas y el conjunto de puntos de referencia físicos que fijan (localizan y orientan) de manera única el sistema de coordenadas y estandarizan las mediciones dentro de ese marco. Para el caso del movimiento en una dimensión, el marco de referencia consta de una línea recta que se proyecta en sentidos opuestos desde un punto central u origen, y con respecto al cual se van cuantizando los valores de medida de distancia con respecto a dicho origen.
7.3 Tiempo y el cambio
El tiempo es el progreso indefinido y continuo de la existencia y los eventos que ocurren en una sucesión aparentemente irreversible del pasado, a través del presente, hacia el futuro. Es una cantidad componente de varias mediciones utilizadas para secuenciar eventos, para comparar la duración de los eventos o los intervalos entre ellos, y para cuantificar las tasas de cambio de cantidades en la realidad material o en la experiencia consciente. El tiempo a menudo se conoce como una cuarta dimensión, junto con tres dimensiones espaciales.
El tiempo en física se define por su medición: el tiempo es lo que lee un reloj. En la física clásica, no relativista, es una cantidad escalar y, como la longitud, la masa y la carga, generalmente se describe como una cantidad fundamental. El tiempo se puede combinar matemáticamente con otras cantidades físicas para derivar otros conceptos como movimiento, energía cinética y campos dependientes del tiempo. El cronometraje es un complejo de cuestiones tecnológicas y científicas, y parte de la base del mantenimiento de registros.
El tiempo está asociado al cambio, y en las ciencias naturales tendremos tres tipos, el cambio cualitativo, que nos permite señalar que la variable medida para un mismo objeto puede arrojar magnitudes diferentes debido a que ha ocurrido un cambio en el tiempo. Cuando medimos el tiempo cuantitativamente lo podemos diferenciar en dos aspectos, uno finito o macro, y otro infinitesimal o micro. En general iniciaremos con cambios macro de tiempo, definidos por la resta.
El cambio en el tiempo ∆t será la diferencia entre el tiempo inicial to y el tiempo final t.
7.4 Posición y el desplazamiento
La posición de una partícula es la ubicación de la partícula con respecto a un punto de referencia elegido que podemos considerar como el origen de un sistema de coordenadas. El movimiento de una partícula es completamente conocido si la posición de la partícula en el espacio se conoce en todo momento. La distancia es una medida numérica de la distancia entre objetos o puntos, siendo esta relativa entre los dos puntos o absoluta en la cual se tiene en cuenta un marco de referencia. En física o uso diario, la distancia puede referirse a una longitud física o una estimación basada en otros criterios (por ejemplo, "dos condados más"). En la mayoría de los casos, "distancia de A a B" es intercambiable con "distancia de B a A". En matemáticas, una función de distancia o métrica es una generalización del concepto de distancia física, una forma de describir lo que significa que los elementos de algún espacio estén "cerca" o "lejos" el uno del otro.
Figura 7.1. Distancia d a lo largo de un camino en comparación con el desplazamiento ∆x.
El desplazamiento tiene varios símbolos, siendo estos: d por displacement, s por spatium, Δr por cambio en el vector de posición, Δrj por el vector de posición en un eje j cualquiera de {x, y, z} posibles, o su versión más vulgar siendo Δx para el cambio de posición en x. Tan conveniente y común como Δx pueda ser, su uso provoca que confundamos la posición con el desplazamiento, de lo anterior plantearemos que para este curso de física general:
👉 el valor de la magnitud del vector posición será r, y sus vectores unitarios rn en caso de no conocer el eje dimensión del movimiento, o rx, ry, rz en caso de si conocerlo. El vector posición hace referencia a un punto estático con respecto a un punto de referencia arbitrario.
👉 el valor de la magnitud del vector desplazamiento será d tal como lo define la IUPAP “Unión Internacional de Física Pura y Aplicada” (IUPAP, 2007), y sus vectores unitarios dn en caso de no conocer el eje dimensión del movimiento, o dx, dy, dz en caso de si conocerlo. El vector desplazamiento hace referencia al movimiento de una partícula entre dos puntos, con respecto a un punto de referencia.
Las dos cantidades anteriores estarán vinculadas por la función diferencia.
Que deberá leerse como el desplazamiento en un eje dimensional n-cualquiera es igual a la diferencia entre la posición final en dicho eje, menos la posición inicial en ese mismo eje.
El desplazamiento es una variable de estado, por lo que no nos importa que sucede entre los puntos inicial y final de posición, solo dichas posiciones finales e iniciales. Dado que nos enfocaremos en el movimiento en una dimensión, podremos evadir ciertos problemas de álgebra de vectores de momento, los cuales involucran trigonometría de triángulos rectángulos.
7.5 Distancia realmente recorrida
Dado que el desplazamiento es una variable de estado cabe la pregunta ¿Qué magnitud toma en cuenta la trayectoria verdadera de una partícula entre los estados inicial y final? Por ejemplo, en un desplazamiento entre los puntos A y B puedo hacer un recorrido directo, pero en otro desplazamiento puedo hacer recorridos intermedios que avanzan y retroceden. Es evidente que la partícula se mueve más en el segundo caso, pero al aplicar la fórmula de desplazamiento, solo nos seguirían interesando las posiciones inicial y final.
El problema que tenemos aquí no obedece a la dificultad del concepto, sino al lenguaje limitado para simbolizar matemáticamente estos conceptos. El símbolo utilizado para representar la distancia real recorrida en física es "d". La distancia real recorrida por un objeto es la longitud total del camino que ha seguido desde su punto inicial hasta su punto final, y se mide en unidades de longitud, como metros o kilómetros. Es importante no confundir este concepto con el desplazamiento, que se refiere a la distancia en línea recta entre el punto inicial y el punto final de un objeto en movimiento, y se representa también con el símbolo "d". Ambos conceptos son importantes en la descripción del movimiento de un objeto y en la resolución de problemas de cinemática en la física.
Es el mismo problema que tendríamos si tuviéramos que plantear los conceptos de zorro, lobo y perro; y sólo contamos con una sola palabra para los tres conceptos “perro”, dado que el lenguaje limita el concepto, muchas personas terminarían por creer que el lobo el zorro y el perro son la misma cosa.
Para evitar este problema es indispensable por lo tanto discriminar algebraicamente los parámetros de distancia real recorrida y desplazamiento con letras diferentes. Para poder parametrizar algebraicamente, denominaremos a la distancia real recorrida dr, siendo esta igual a la suma de los valores absolutos de cada desplazamiento m entre los puntos inicial y final.
Que deberá leerse como la distancia realmente recorrida en el eje n-cualquiera es igual a la suma de los valores absolutos de cada desplazamiento m, iniciando por el primer desplazamiento, hasta el último desplazamiento.
Propios
7.6 Velocidad y rapidez promedio en un eje del espacio
Con los conceptos de desplazamiento y distancia real podemos distinguir dos conceptos que de otro modo parecen iguales, la velocidad y la rapidez. Iniciaremos mencionando que ambos tienen casi los mismos símbolos, pero para evitar ambigüedades nos aprovecharemos que la propia Unión Internacional de Física Pura y Aplicada aprueba varios símbolos posibles para velocidad y rapidez, por lo que tomaremos dos, y les daremos usos específicos.
👉 sea vn,avg la velocidad promedio de un cuerpo en un eje n-cualquiera el cociente entre el desplazamiento y el cambio en el tiempo:
👉 sea un,avg la rapidez promedio de un cuerpo en un eje n-cualquiera el cociente entre el la distancia realmente recorrida y el cambio en el tiempo:
Podemos afirmar que la velocidad promedio es una propiedad de estado, es decir, una en la que solo nos importa el valor inicial y final, pero no lo que sucede en medio. Por el contrario, la rapidez no es una propiedad de estado, pues en esta sí que nos interesa lo que sucede entre los dos puntos iniciales.
La unidad SI de velocidad promedio es la misma que la unidad de rapidez promedio: metros sobre segundo (m/s). Sin embargo, a diferencia de la velocidad promedio, la rapidez promedio no tiene dirección y siempre se expresa como un número positivo.
7.7 Diagramas de movimiento
Un diagrama de movimiento representa el movimiento de un objeto al mostrar su ubicación en varios momentos igualmente espaciados en el mismo diagrama. Los diagramas de movimiento son una descripción pictórica del movimiento de un objeto. Muestran inicialmente la posición y la velocidad de un objeto y presentan varios puntos en el centro del diagrama. Estos puntos revelan si el objeto ha acelerado o desacelerado o no (Etkina, Wenning, Vesenka, & Bryan, 2008). Para simplificar, el objeto se representa con una forma simple, como un círculo relleno, pero en ocasiones se muestran representaciones de personas, carros entre otros. Contiene información sobre las posiciones de los objetos en instancias de tiempo particulares.
Los conceptos de velocidad (rapidez) y aceleración (aceleración lineal) a menudo se confunden entre sí, pero en realidad son cantidades bastante diferentes. Al formar una representación mental de un objeto en movimiento, una representación pictórica llamada diagrama de movimiento a veces es útil para describir la velocidad y la aceleración mientras un objeto está en movimiento. Se puede formar un diagrama de movimiento imaginando una fotografía estroboscópica (imágenes en secuencia ligeramente diferentes que dan la ilusión de continuidad) de un objeto en movimiento, que muestra varias imágenes del objeto tomadas mientras la luz estroboscópica parpadea a una velocidad constante.
Figura 7.2. Diagramas de movimiento de un automóvil que se mueve a lo largo de una carretera recta en una sola dirección. La velocidad en cada instante se indica con una flecha roja y la aceleración constante se indica con una flecha morada. (Arriba) Este carro se mueve a rapidez constante con aceleración cero, (Centro) este carro se ha movido con aceleración constante en la misma dirección que la rapidez, (Abajo) este carro se ha movido con una aceleración opuesta a la de la rapidez.
Física de Serway 9
8. Movimiento rectilíneo uniforme MUR
|| REGRESAR AL INDICE ||
El Movimiento Rectilíneo Uniforme (MRU) es un tipo de movimiento en el cual un objeto se mueve en línea recta con velocidad constante. En otras palabras, la velocidad del objeto no cambia con el tiempo y se mueve en una trayectoria recta a una velocidad constante.
En un MRU, la velocidad promedio del objeto en un intervalo de tiempo dado es igual a su velocidad instantánea. Además, la velocidad se mide en unidades de distancia por unidad de tiempo (por ejemplo, metros por segundo o kilómetros por hora).
Un ejemplo común de un MRU es un automóvil que viaja en una carretera recta y nivelada a una velocidad constante de 100 kilómetros por hora. En este caso, la velocidad del automóvil no cambia y se mueve en línea recta a una velocidad constante de 100 kilómetros por hora.
8.1 Importancia del movimiento rectilíneo uniforme
El Movimiento Rectilíneo Uniforme (MRU) tiene varias aplicaciones importantes en la física y en otras áreas de la ciencia y la tecnología. Algunas de las importancias del MRU son:
👉 Permite la descripción matemática simple de un movimiento: El MRU es uno de los movimientos más simples que existen y su estudio permite introducir conceptos básicos como velocidad, aceleración, distancia y tiempo de manera sencilla.
👉 Facilita el análisis de otros movimientos más complejos: El MRU se utiliza como base para describir otros movimientos más complejos, ya que permite descomponer un movimiento en diferentes componentes rectilíneas.
👉 Ayuda a entender la relación entre la velocidad y el tiempo: Al estudiar el MRU, se puede entender mejor cómo varía la velocidad de un objeto con respecto al tiempo, lo cual es fundamental para la comprensión de otros movimientos.
👉 Es utilizado en la industria: El MRU es utilizado en la industria para el diseño y funcionamiento de maquinarias y dispositivos que requieren un movimiento rectilíneo constante, como en la producción de materiales, máquinas herramientas, etc.
👉 Se aplica en la navegación y la geolocalización: El MRU es utilizado en la navegación marítima y aérea para calcular la posición y la trayectoria de los vehículos. También se utiliza en la geolocalización de dispositivos móviles.
En resumen, el estudio del MRU es fundamental para la comprensión de otros movimientos más complejos y tiene diversas aplicaciones en la ciencia, la tecnología y la industria.
8.2 Axiomas del MUR
El modelo de análisis del movimiento rectilíneo se basa en axiomas o presupuestos que no se cuestionan, y que forman la base de la elaboración posterior. A estos presupuestos que asumimos inicialmente sin contar con la experiencia, los denominaremos axiomas.
👉 Una partícula sin estructura interna o masa: por ende, no se usa el parámetro masa.
👉 que se mueve en el vacío de forma rectilínea: por lo que solo analizamos una dimensión por vez, sea esta el eje x, el eje y o en eje z.
👉 sin interactuar con ninguna otra partícula: Lo cual trae dos consecuencias importantes:
👉 La ecuación principal deberá tener la forma de una línea recta. Lo cual implica que la velocidad promedio será igual a la velocidad instantánea, pues esta es una propiedad de las pendientes en una línea recta, pues allí cualquier cuerda que dibujemos entre dos puntos será igual a la propia recta.d
👉 No hay cambios en su velocidad. Esto se conoce como el principio de inercia, e implica que la velocidad inicial y final son iguales.
Este es el axioma más complicado. Aristóteles opinaba que un cuerpo en tales condiciones disminuiría su rapidez con el tiempo, ya que necesitaría de algo que lo impulsara constantemente. Sin embargo, como revemos más adelante, un cuerpo no necesita que lo impulsen para mantener su movimiento, lo que necesita es que no interactúen con él, de esta forma, su desplazamiento no cambia para cualquier intervalo de tiempo.
👉 en un intervalo de tiempo: (Δt) que representa la variable independiente con respecto a la cual se deriva o se integra. Tenga en cuenta que dependiendo del marco de referencia to “tiempo inicial” puede ser igual a cero o dejarse como desconocido.
8.3 Modelo matemático
DEMOSTRACIÓN. Encuentre una ecuación que modele a una partícula que cumpla con los axiomas del movimiento rectilíneo uniforme.
El cual debe leerse de la siguiente manera, la posición final en un eje de coordenadas n (que puede ser x, y, z) es igual al producto de la velocidad en dicho eje de coordenadas multiplicado por el tiempo más la posición inicial en ese eje de coordenadas.
8.4 Analizando la ecuación
Una vez en posesión del modelo, en este caso, la ecuación (8.3), debemos analizarla y ver en qué casos puede servir. La ecuación consta de tres parámetros, las posiciones iniciales ro,n y finales rn en algún eje de coordenadas, que al restarse forman el desplazamiento d = rn - ro,n, así como la velocidad en el eje vn y el tiempo final t, por lo tanto, permitirá:
👉 calcular la posición final: si el enunciado proporciona la posición inicial ro,n, la velocidad vn y el tiempo final t.
Siendo esta la forma predeterminada Eq. 8.3, sin embargo, esta es mucho más poderosa, pues al aplicar manipulación algebraica simple, podremos:
👉 calcular la posición inicial: si el enunciado proporciona la posición final rn, la velocidad vn y el tiempo final t.
👉 calcular la velocidad: si el enunciado proporciona el desplazamiento Δx = d y el tiempo final t.
👉 calcular el tiempo final: si el enunciado proporciona el desplazamiento Δx = d y la velocidad vn.
👉 calcular el desplazamiento: si el enunciado proporciona la velocidad vn y el tiempo final t.
Podríamos plantear el formulario de ecuaciones para estos otros cuatro casos, sin embargo aconsejamos al estudiante mecanizar las técnicas de despeje del álgebra elemental, pues esto le permitirá memorizar menos ecuaciones, o en el caso de que se le permita usar una hoja de formularios, desperdiciar menos espacio.
Observe adicionalmente que el tiempo es el único parámetro independiente al eje del movimiento, lo cual lo delata como un parámetro escalar, mientras que todos los demás deberán estar atados a un eje de movimiento n, donde n puede ser el eje x, el eje y o en eje z.
Ejemplo. Un móvil se desplaza a velocidad constante de 90 km/h. ¿Qué distancia recorre en 3 s?
Hipertexto
Física de Serway 9
8.5 Introducción al movimiento circular
No siempre vamos a aplicar directamente la ecuación x, pues algunos enunciados, aunque cane bajo los axiomas del MUR, tienen ciertas variaciones que deben tenerse en cuenta desde una perspectiva analítica.
El desplazamiento s (o d) en una función del radio R (Eq. 8.4), por lo que podemos modificar el modelo (Eq. 8.3).
|
8.6 Dos partículas de masa despreciable que se mueven en una recta
Otra serie de problemas que pueden llegar a ser retadores debido a su naturaleza analítica, y por ende, los libros de texto no explicitarán, son aquellos derivados de la interacción de las dos partículas sin masa o cuya masa es despreciable. Esta serie de problemas puede descomponerse en:
👉 Las persecuciones
Las cuales se dividen en aquellas en las que se da alcance a una rapidez relativa, aquellas en las que se mantiene una distancia de separación constante en todo tiempo t, y aquellas en la que una partícula se aleja de la otra a una rapidez relativa.
👉 Alejamientos
debido a que las dos partículas se mueven en direcciones opuestas.
👉 Colisiones de masa despreciable
Que son los movimientos de dos partículas que inician en posiciones diferentes de una recta, y se mueven en sentidos opuestos hasta encontrarse.
Tenga en cuenta que, al cumplir con el axioma de masa despreciable, podremos ignorar otros parámetros más avanzados como la energía del impacto, y la elasticidad, por el momento solo nos interesan los parámetros básicos del tiempo en que chocan, y el punto en la recta donde se encuentran.
Podríamos deducir una serie de ecuaciones independientes para cada sub-caso en ejercicios triviales, pero ese no es el espíritu de la física teórica, el objetivo es obtener una serie de ecuaciones generales, que puedan ser aplicadas a casos triviales posteriores con pocas modificaciones, o cuyas modificaciones se convierta en la aplicación de un algoritmo estandarizado.
De lo anterior obtenemos una serie de teoremas, iniciando por lo evidente, ambas partículas siguen la ley del movimiento rectilíneo uniforme:
👉 j o partícula 1: que será la que inicie su movimiento en t = 0.
👉 i o partícula 2: que será la que inicie su movimiento en algún momento t ≥ 0.
Hemos decidido ignorar el indicador del eje dimensional, ya que el movimiento en una dimensión implica implícitamente que todo ocurre en un eje dimensional, y ya para estos casos, agrega información innecesaria. De lo anterior definimos los conceptos de distancia de separación inicial dro (Eq. 8.8), la distancia de separación final dr (Eq. 8.9), la velocidad relativa de separación o acercamiento u (Eq. 8.10), y la diferencia de tiempo para el inicio del movimiento de la segunda partícula Δto,i (Eq. 8.11).
El modelo anterior presenta dos presupuestos clave:
👉 que j es quien inicia el movimiento, lo cual debe tomarse en cuenta en algunos enunciados.
👉 que t es común para ambas partículas, como si todo estuviera en una grabación y detuviéramos en un tiempo t ambas simultáneamente.
9. Movimiento rectilíneo uniformemente acelerado MRUA
|| REGRESAR AL INDICE ||
El Movimiento Uniformemente Acelerado (MUA) es un tipo de movimiento en el cual un objeto se mueve en línea recta con una aceleración constante. En otras palabras, la velocidad del objeto cambia uniformemente con el tiempo y se mueve en una trayectoria recta con una aceleración constante.
En un MUA, la aceleración es la misma en todo momento y se mide en unidades de distancia por unidad de tiempo al cuadrado (por ejemplo, metros por segundo al cuadrado). Además, la velocidad del objeto cambia a una tasa constante, lo que significa que la velocidad promedio del objeto en un intervalo de tiempo dado NO es igual a su velocidad instantánea en ese momento.
Un ejemplo común de un MUA es un objeto que cae libremente debido a la gravedad. En este caso, la aceleración debido a la gravedad es constante y la velocidad del objeto aumenta uniformemente a medida que cae.
El estudio del MUA es importante porque muchos fenómenos en la naturaleza y la tecnología involucran movimientos con aceleración constante. La descripción matemática del MUA permite predecir la posición y la velocidad del objeto en cualquier momento durante el movimiento y es fundamental para entender la dinámica de los objetos en movimiento.
9.1 Importancia del movimiento uniformemente acelerado
El Movimiento Uniformemente Acelerado (MUA) es importante en la física y otras áreas de la ciencia y la tecnología por las siguientes razones:
👉 Permite entender la relación entre la velocidad, el tiempo y la aceleración: El estudio del MUA permite entender cómo la velocidad de un objeto cambia a medida que transcurre el tiempo en un movimiento con aceleración constante.
👉 Se utiliza para describir muchos fenómenos naturales y tecnológicos: El MUA se presenta en muchos fenómenos naturales y tecnológicos, como la caída libre de objetos, el movimiento de los cuerpos celestes, la aceleración de vehículos, entre otros.
👉 Es útil en la ingeniería y la tecnología: El conocimiento del MUA es fundamental en la ingeniería y la tecnología, ya que permite diseñar dispositivos y maquinarias que requieren un movimiento acelerado, como los cohetes espaciales, los automóviles, los trenes, etc.
👉 Permite calcular trayectorias y posiciones: El estudio del MUA permite calcular la trayectoria y la posición de un objeto en cualquier momento del movimiento con aceleración constante.
👉 Facilita el análisis de otros movimientos más complejos: El estudio del MUA se utiliza como base para describir otros movimientos más complejos, como el movimiento parabólico o el movimiento circular uniformemente acelerado.
En resumen, el estudio del MUA es fundamental en la física y otras áreas de la ciencia y la tecnología, ya que permite entender y describir muchos fenómenos naturales y tecnológicos, así como diseñar dispositivos y maquinarias que requieren un movimiento acelerado. Además, el MUA es útil en el cálculo de trayectorias y posiciones de objetos en movimiento.
9.2 Axiomas del MUR
👉 Una partícula sin estructura interna o masa: por ende, no se usa el parámetro masa.
👉 que se mueve en el vacío de forma rectilínea: la ecuación principal deberá tener la forma de una línea recta.
👉 interactuando con una fuerza que aumenta/disminuye su rapidez constantemente: lo cual nos intriduce un nuevo parámetro, el cambio de rapidez, que definiremos como la aceleración lineal.
👉 en un intervalo de tiempo: (Δt) que representa la variable independiente con respecto a la cual se deriva o se integra. Tenga en cuenta que dependiendo del marco de referencia to “tiempo inicial” puede ser igual a cero o dejarse como desconocido.
9.3 Definición de aceleración y sus consecuencias
Dado lo anterior, podemos definir la aceleración lineal como el cambio en la rapidez con respecto al tiempo, y dado que es un modelo lineal, la aceleración promedio será igual a la aceleración instantánea, por lo que no necesitaremos aplicar las técnicas del cálculo, en este paso inicial.
Rapidez aceleración de un cuerpo como el desplazamiento con respecto al cambio de tiempo en una dimensión.
Demostración. Obtener una función de rapidez en función del tiempo con aceleración constante, asumiendo que se aplica un modelo lineal simple.
Por lo que si bien la resta de restas no afectará la unidad en el denominador, que seguirán siendo unidades de desplazamiento (metros), la unidad en el denominador estará elevada al cuadrado (segundo cuadrado s2). Ahora, dado que la rapidez cambia, significa que la función para calcular la posición también debe haber cambiado, el problema es que esta vez no podremos saltarnos el cálculo debido a que la ecuación resultante no es lineal, como lo muestran las unidades de la aceleración.
Demostración. Deducir las ecuaciones del movimiento rectilíneo uniformemente acelerado para calcular el desplazamiento.
Dos partículas de masa despreciable
Es aconsejable que el objeto que parte la referencia del tiempo cero sea quien se encuentra en MUR, para simplificar el álgebra. En tal caso, debe usarse el tiempo refractario para calcular su posición inicial al momento en que el objeto en MRUA inicia a su desplazamiento, al hacer esto, la fórmula de posición final se convierte en:
Lo mismo puede aplicarse para un escenario en que los dos objetos estén en MRUA.
Propios
Ejemplo. Desde el reposo, un automóvil aceleró a 8 m/s2 durante 10 segundos. a) ¿Cuál es la posición del automóvil al final de los 10 segundos? b) ¿Cuál es la velocidad del automóvil al final de los 10 segundos?
Física de Serway 9
10. Caída libre
|| REGRESAR AL INDICE ||
Es bien sabido que, en ausencia de resistencia al aire, todos los objetos que caen cerca de la superficie de la Tierra caen hacia la Tierra con la misma aceleración constante bajo la influencia de la gravedad de la Tierra. No fue sino hasta alrededor de 1600 que se aceptó esta conclusión. Antes de ese tiempo, las enseñanzas del filósofo griego Aristóteles (384–322 a. C.) habían sostenido que los objetos más pesados caen más rápido que los más livianos.
10.1 La importancia de Galileo
El italiano Galileo Galilei (1564-1642) originó nuestras ideas actuales sobre los objetos que caen. Existe la leyenda de que demostró el comportamiento de los objetos que caen al observar que dos pesos diferentes caídos simultáneamente desde la Torre Inclinada de Pisa golpearon el suelo aproximadamente al mismo tiempo. Aunque hay algunas dudas de que realizó este experimento en particular, está bien establecido que Galileo realizó muchos experimentos en objetos que se mueven en planos inclinados. En sus experimentos, hizo rodar las bolas por una ligera pendiente y midió las distancias que cubrían en intervalos de tiempo sucesivos. El propósito de la inclinación era reducir la aceleración, lo que le permitió hacer mediciones precisas de los intervalos de tiempo. Al aumentar gradualmente la pendiente de la pendiente, finalmente fue capaz de sacar conclusiones sobre objetos que caen libremente porque una bola que cae libremente es equivalente a una bola que se mueve por una pendiente vertical.
10.2 Un experimento de gedanken
Un experimento de Gedanken es un experimento mental, también conocido como experimento de pensamiento, que se utiliza en la física teórica y otras áreas de la ciencia. En un experimento de Gedanken, se plantea una situación hipotética o un escenario imaginario que se utiliza para explorar las implicaciones de una teoría o concepto sin la necesidad de realizar el experimento en la realidad (Clement, 2009; Dahlbom, 2013; Forró, 2000; Stephens & Clement, 2011).
La idea detrás de los experimentos de Gedanken es que a veces es imposible realizar ciertos experimentos en la realidad debido a limitaciones técnicas, éticas o económicas. Por lo tanto, los experimentos mentales permiten a los científicos explorar ideas y conceptos que no pueden ser investigados de otra manera. Además, los experimentos mentales a menudo se utilizan para probar la validez de una teoría o modelo (Clement, 2009; Dahlbom, 2013; Forró, 2000; Stephens & Clement, 2011).
Einstein es conocido por utilizar los experimentos de Gedanken en su desarrollo de la teoría de la relatividad especial. Un ejemplo famoso de un experimento de Gedanken es el "paradoja de los gemelos", en el que se imagina a dos gemelos, uno de los cuales viaja a velocidades cercanas a la velocidad de la luz, mientras que el otro se queda en la Tierra. Este experimento mental se utiliza para ilustrar los efectos de la relatividad del tiempo y ha sido fundamental en la comprensión de la física moderna(Clement, 2009; Dahlbom, 2013; Forró, 2000; Stephens & Clement, 2011).
10.3 La paradoja del martillo y la pluma
La paradoja del martillo y pluma de Galileo se refiere a una contradicción aparente en la física clásica que fue descubierta por el famoso científico italiano Galileo Galilei. La paradoja se refiere a la idea de que si se suelta un martillo y una pluma desde una cierta altura, según la física clásica, deberían golpear el suelo al mismo tiempo debido a que tienen la misma aceleración de gravedad. Sin embargo, la realidad es que el martillo, al tener una mayor resistencia al aire que la pluma, llegará al suelo ligeramente después que el pluma.
Este fenómeno fue observado por Galileo mientras realizaba experimentos en la torre inclinada de Pisa en el siglo XVII. Al observar que los objetos más pesados y los más livianos caían a la misma velocidad, Galileo llegó a la conclusión de que la fuerza de la gravedad actuaba de manera igual en todos los objetos, independientemente de su masa.
Sin embargo, la observación de la caída del martillo y la pluma parecía contradecir esta idea. Esto llevó a Galileo a darse cuenta de que la resistencia del aire era un factor importante para tener en cuenta en la caída de los objetos y que esta resistencia podía afectar el tiempo que tardaba un objeto en caer al suelo.
En resumen, la paradoja del martillo y la pluma de Galileo es una aparente contradicción entre la física clásica y la observación empírica que fue fundamental en el desarrollo de la comprensión de la caída libre de los objetos.
Figura 10.1. El 2 de agosto de 1971, el astronauta David Scott realizó tal demostración en la Luna. Simultáneamente lanzó un martillo y una pluma, y los dos objetos cayeron juntos a la superficie lunar. ¡Esta simple demostración seguramente habría complacido a Galileo!
10.4 Un experimento más simple
Quizás quieras probar el siguiente experimento. Simultáneamente, deje caer una moneda y un trozo de papel arrugado desde la misma altura. Si los efectos de la resistencia del aire son insignificantes, ambos tendrán el mismo movimiento y tocarán el suelo al mismo tiempo. En el caso idealizado, en el que la resistencia del aire está ausente, dicho movimiento se denomina movimiento de caída libre. Si este mismo experimento pudiera llevarse a cabo en el vacío, en el cual la resistencia al aire es realmente insignificante, el papel y la moneda caerían con la misma aceleración incluso cuando el papel no se arruga.
10.5 La caída libra también involucra los lanzamientos
Cuando usamos la expresión objeto que cae libremente, no necesariamente nos referimos a un objeto que cae del reposo. Un objeto que cae libremente es cualquier objeto que se mueve libremente bajo la influencia de la gravedad sola, independientemente de su movimiento inicial. Los objetos arrojados hacia arriba o hacia abajo y los liberados del reposo caen libremente una vez que se liberan. Cualquier objeto que cae libremente experimenta una aceleración dirigida hacia abajo, independientemente de su movimiento inicial.
10.6 La aceleración gravitacional
La aceleración gravitacional es la aceleración que experimenta un objeto debido a la atracción gravitatoria de otro objeto. La aceleración gravitacional es una constante que depende de la masa del objeto que genera el campo gravitatorio y la distancia entre los dos objetos.
La aceleración gravitacional es la razón por la cual los objetos caen hacia la Tierra cuando se sueltan en el aire. También es la aceleración que mantiene a los planetas en órbita alrededor del Sol y a las lunas en órbita alrededor de los planetas. La aceleración gravitacional es una de las fuerzas fundamentales de la naturaleza y es una parte fundamental de la física y la astronomía.
Denotaremos la magnitud de la aceleración de caída libre, también llamada aceleración gravitacional, por el símbolo g. El valor de g disminuye al aumentar la altitud sobre la superficie de la Tierra. Además, se producen ligeras variaciones en g con los cambios en la latitud.
10.7 Valores de la aceleración gravitacional
En la superficie de la Tierra, es decir, a nivel del mar, el valor de g es de aproximadamente 9.80665 m/s2.
En la superficie de la Tierra, es decir, a nivel del mar, el valor de g es de aproximadamente 9.764 m/s2. Es importante tener en cuenta que este valor es solo una aproximación, ya que la aceleración gravitacional puede variar en diferentes partes de la Tierra debido a factores como la altitud, la densidad de la Tierra y la rotación terrestre (Rezzolla, 2023).
A menos que se indique lo contrario, utilizaremos este valor para cuando realicemos cálculos. Para hacer estimaciones rápidas, use 10 m/s2. El signo negativo del valor de la aceleración hace parte de su naturaleza vectorial, pues esta tiene una dirección que apunta en todo momento al centro de masas del objeto mas grande, en este caso, el núcleo del planeta Tierra.
10.8 Presupuestos para evitar que el modelo se haga muy complejo
Si descuidamos la resistencia del aire y asumimos que la aceleración de caída libre no varía con la altitud en distancias verticales cortas, el movimiento de un objeto que cae libremente moviéndose verticalmente es equivalente al movimiento de una partícula bajo aceleración constante en una dimensión.
10.9 Modelo matemático de la caída libre
Por lo tanto, se pueden aplicar las ecuaciones desarrolladas en la Sección anterior para la partícula bajo el modelo de aceleración constante. La única modificación para los objetos que caen libremente que necesitamos hacer en estas ecuaciones es notar que el movimiento está en la dirección vertical (la dirección y) en lugar de en la dirección horizontal (x) y que la aceleración es hacia abajo y tiene una magnitud de 9.80 m/s2.
Demostración. Plantee ecuaciones modificadas para la caída libre asumiendo que la aceleración en el eje y es la aceleración gravitacional.
La altura en los modelos de caída libre se denota comúnmente con la letra "h" en lugar de la letra "d" porque "h" representa la altura vertical medida desde un punto de referencia, mientras que "d" representa la distancia medida en cualquier dirección con un sentido vectorial, el desplazamiento, incluyendo la horizontal, por lo que podríamos decir de | ∆rmax | = | dmax |= h.
En la caída libre, la altura vertical desde la que cae un objeto es importante porque determina el tiempo que tardará en caer y la velocidad que alcanzará. Además, la altura se mantiene constante a lo largo de la caída libre, mientras que la distancia recorrida horizontalmente puede variar dependiendo de la trayectoria de la caída.
Es por esta razón que en la mayoría de los modelos y ecuaciones de caída libre se utiliza "h" para representar la altura vertical positiva, mientras que "d" se utiliza para medir la distancia recorrida en cualquier dirección horizontal.
De acuerdo con la ecuación 10.5, es imposible calcular la velocidad real con su signo vectorial, debido a que al despejar siempre terminamos con la raíz cuadrada de un número elevado al cuadrado, eso se sabe por que el análisis dimensional siempre arroja (m2/s2), y la raíz cuadrada de un número elevado al cuadrado siempre arrojará positivo.
Sin embargo, en el caso de la caída libre, cuando el objeto se mueve hacia abajo, debemos considerar la velocidad final como negativa en relación con una referencia de dirección positiva hacia arriba. Esto se debe a que hemos establecido una convención de signos para representar el movimiento hacia arriba como positivo y el movimiento hacia abajo como negativo. Por lo tanto, aunque la velocidad final al cuadrado puede ser positiva según la ecuación, deberemos asignarle un valor negativo arbitrariamente a la respuesta para respetar la convención. Este problema solo ocurre con la ecuación 10.5, pues si hacemos el cálculo a dos pasos empleando las ecuaciones 10.3 y 10.4 obtendremos los signos correctos.
Es importante tener en cuenta que el uso de signos positivos y negativos en las ecuaciones es una convención y una herramienta matemática para representar y analizar fenómenos físicos. Los físicos y matemáticos consideran el contexto y la interpretación física adecuada al aplicar estas convenciones en sus cálculos y análisis, es por esto que parte del análisis dimensional involucra aplicar la inteligencia humana para evaluar el sentido de un valor numérico.
Ejemplos
Física de Serway 9
10.10 El tiempo de vuelo y la altura máxima
La caída libre es un caso simple de movimiento en el que un objeto cae libremente bajo la influencia exclusiva de la gravedad, sin resistencia del aire u otras fuerzas externas significativas. Sin embargo, existen subcasos interesantes que pueden presentar complicaciones analíticas y plantear preguntas específicas.
Uno de estos subcasos es el tiempo de vuelo y la altura máxima de una partícula que se eleva y luego cae. Este escenario implica lanzar un objeto hacia arriba, alcanzar una altura máxima y luego caer de nuevo hacia abajo. La pregunta clave es cuánto tiempo permanece en el aire y qué altura alcanza antes de volver al suelo.
Este problema tiene diversas aplicaciones prácticas en campos como la física, la ingeniería y la mecánica. Algunos ejemplos son:
(a) Proyectiles: El estudio del tiempo de vuelo y la altura máxima es esencial en el diseño de proyectiles, como cohetes, misiles y proyectiles balísticos. Comprender estos parámetros es crucial para determinar la trayectoria y el alcance de los proyectiles.
(b) Deportes: En deportes como el salto en altura, el salto con pértiga o el salto de esquí, es importante conocer el tiempo de vuelo y la altura máxima que un atleta puede alcanzar. Estos datos ayudan a evaluar el rendimiento y mejorar las técnicas.
(c) Diseño de parques de atracciones: En la planificación y construcción de atracciones de caída libre, como montañas rusas o caídas libres controladas, es fundamental calcular el tiempo de vuelo y la altura máxima para garantizar una experiencia segura y emocionante para los visitantes.
Fue Newton quien desarrolló ecuaciones que permitían calcular tanto el tiempo de vuelo como la altura máxima en un movimiento de caída libre, cosa que no habían abordado sus predecesores como Tartaglia o Galileo. El estudio del tiempo de vuelo y la altura máxima también es relevante en el contexto de la exploración espacial. Durante el desarrollo de la tecnología de cohetes y la planificación de misiones espaciales, es esencial comprender y calcular con precisión estos parámetros. Desde los primeros cohetes hasta los viajes a la Luna y más allá, el análisis de la caída libre ha sido fundamental para el éxito de las misiones espaciales.
Recuerda que estas ecuaciones son válidas bajo las suposiciones de que el efecto del rozamiento del aire es despreciable y que solo estamos considerando el componente vertical del movimiento.
Es importante tener en cuenta que la velocidad inicial de ascenso debe tener un signo positivo y la aceleración debido a la gravedad debe tener un signo positivo, ya que la partícula está subiendo en la dirección positiva y la gravedad actúa hacia abajo en la dirección negativa, pero este negativo ya se ha tenido en cuenta en las ecuaciones base para la demostración.
Estas ecuaciones son aplicables en diversos contextos, como el lanzamiento de proyectiles, cohetes y cuerpos en caída libre vertical. Sin embargo, es importante recordar que son simplificaciones y no tienen en cuenta otros factores como la resistencia del aire, la variación de la gravedad con la altura o la curvatura terrestre, que pueden influir en los resultados en situaciones más complejas.
Ejemplos
10.11 El marco de referencia inercial
Como siempre sucede, la cosa es mas o menos sencilla hasta que tenemos que modelar un escenario en el que dos partículas caen al mismo tiempo. Aunque conceptualmente parece que la cosa se complica, matemáticamente la cosa puede hacerse mas fácil si cuentas con las ecuaciones inerciales.
Una ecuación de marco de referencia inercial es una expresión matemática que describe el movimiento de un objeto o sistema en relación con un marco de referencia que se considera inercial. Un marco de referencia inercial es aquel en el que se cumple la primera ley del movimiento de Newton (ley de inercia), es decir, un marco en el que un objeto en reposo permanece en reposo y un objeto en movimiento continúa moviéndose con velocidad constante en línea recta a menos que actúe sobre él una fuerza externa.
La utilidad de las ecuaciones de marco de referencia inercial radica en que permiten describir el movimiento de un objeto sin la necesidad de considerar las fuerzas externas que actúan sobre él. Al enfocarse únicamente en la aceleración inherente del objeto y la inercia del marco de referencia, estas ecuaciones simplifican el análisis del movimiento y permiten obtener resultados precisos y coherentes.
Las ecuaciones de marco de referencia inercial se utilizan en muchos campos científicos y tecnológicos, como la física, la ingeniería y la navegación espacial, para estudiar y predecir el movimiento de objetos y sistemas en ausencia de fuerzas externas significativas. Estas ecuaciones forman la base de muchas teorías y modelos científicos que nos permiten comprender y controlar el comportamiento de los objetos en movimiento.
Para crear una ecuación o ecuaciones inerciales para dos partículas cayendo consideraremos que cuando ambas caen, lo hacen acelerando con la misma magnitud gravitacional, por lo que si elegimos a una de las partículas como el marco de referencia, el movimiento de la otra pasa de ser acelerado a rectilíneo o de plano, estático.
Figura 10.2. El ejemplo de los dos paracaidistas en caída libre ilustra el concepto de marco de referencia inercial. Desde el marco de referencia inercial, los paracaidistas parecen no moverse uno con respecto al otro, mientras que, desde un marco de referencia no inercial, se puede apreciar un cambio en la distancia entre ellos con respecto al suelo a medida que caen.
Supongamos que tenemos dos paracaidistas, A y B, que se encuentran en caída libre. Inicialmente, ambos paracaidistas están en reposo con respecto al suelo, es decir, no tienen velocidad inicial en relación con un observador en tierra. Ambos paracaidistas están sometidos únicamente a la fuerza de gravedad y caen verticalmente.
Si consideramos el marco de referencia inercial de un observador en tierra, que se considera en reposo o en movimiento rectilíneo uniforme, podemos analizar el movimiento relativo de los paracaidistas.
Dado que ambos paracaidistas están cayendo debido a la misma fuerza de gravedad y no hay fuerzas externas actuando sobre ellos, en el marco de referencia inercial, parecerá que los paracaidistas no se mueven uno con respecto al otro. Esto se debe a que su movimiento relativo es rectilíneo y uniforme. La distancia entre ellos se mantendrá constante a medida que caen, siempre y cuando ambos inicien su caída mas o menos al mismo tiempo y a la misma altura, y asuman configuraciones corporales aerodinámicamente semejantes que eviten que la resistencia del aire afecte su velocidad decaída.
Figura 10.3. Los miembros de un equipo internacional de paracaidistas se han unido en el aire en un total de 164 paracaidistas, construyendo la mayor formación de paracaidismo vertical, viajando a velocidades de hasta 240 mph. Después de un total de 13 intentos, el equipo logró batir la marca de 2012 fijada en 138 paracaidistas.
Desde el punto de vista de un observador externo, los cambios en la configuración corporal no afectarán significativamente la velocidad de la caída, pero desde el punto de vista del otro paracaidista, estos cambios le permiten al otro paracaidista moverse y "nadar en el aire".
Demostración: Generalizar las ecuaciones anteriores.
R. Referencias bibliográficas
|| REGRESAR AL INDICE ||
Abetti, G. (1975). 9.5. Harmonies of the world. Vistas in Astronomy, 18, 537–539.
Barker, P., & Goldstein, B. R. (2001). Theological foundations of Kepler’s astronomy. Osiris, 16, 88–113.
Belbachir, A. N., & Göbel, P. M. (2009). Smart cameras: a historical evolution. In Smart cameras (pp. 3–17). Springer.
Clement, J. J. (2009). The role of imagistic simulation in scientific thought experiments. Topics in Cognitive Science, 1(4), 686–710.
Crombie, A. C. (1961). Quantification in medieval physics. Isis, 52(2), 143–160.
Dahlbom, B. (2013). Gedankenexperiment: Entertaining and thought-provoking scenarios. Springer.
Descartes, R. (1999). Descartes: vida e obra. São Paulo: Nova Cultural.
Donahue, W. H. (1994). Kepler’s invention of the second planetary law. The British Journal for the History of Science, 27(1), 89–102.
Etkina, E., Wenning, C. J., Vesenka, J., & Bryan, J. (2008). JPTEO. JOURNAL OF PHYSICS TEACHER EDUCATION Online, 4(4). Retrieved from http://physicsed.buffalostate.edu/pubs/phy690/Tatto2007NCSUrev/jpteo4(4)spr08.pdf
Forró, L. (2000). Beyond gedanken experiments. Science, 289(5479), 560–561.
Franco, A. B. (2003). Avempace, projectile motion, and impetus theory. Journal of the History of Ideas, 64(4), 521–546.
Gamow, G. (1988). The great physicists from Galileo to Einstein. Courier Corporation.
Gingerich, O. (1982). The Galileo Affair. Scientific American, 247(2), 132–143.
Gleick, J. (2004). Isaac Newton. Vintage.
Gracia, J. J. E. (2002). Philosophy in the middle ages: An introduction. A Companion to Philosophy in the Middle Ages, 1.
Gutman, O. (2003). Pseudo-Avicenna. Liber celi et mundi: A critical edition with introduction. Brill.
Hagens, G. (2009). Syncretism and Ancient Chronology: Can Democritus Date the Buddha? Mouseion: Journal of the Classical Association of Canada, 9(1), 29–55.
Halliday, D., Resnick, R., & Walker, J. (2014). Fundamentals of Physics (10th ed.). John Wiley & Sons.
Hawking, S. (2009). Galileo and the birth of modern science. American Heritage’s Invention & Technology, 24(1), 36.
Heinen, A. M. (1974). Al-Biruni and Ibn Al-Haytham: A Comparative Study of Scientific Method.
Humphreys, W. C. (1967). Galileo, falling bodies and inclined planes: An attempt at reconstructing Galileo’s discovery of the law of squares. The British Journal for the History of Science, 3(3), 225–244.
IUPAP. (2007). Symbols, Units, Nomenclature and Fundamental Constants in Physics. Retrieved July 7, 2023, from https://archive2.iupap.org/wp-content/uploads/2014/05/A4.pdf
Lapidus, I. M. (1996). The Cambridge illustrated history of the Islamic world. Cambridge University Press.
Lyubina, J., & Gutfleisch, O. (n.d.). Nanostructured hard magnets.
McVaugh, M. R. (1995). The Beginnings of Western Science: The European Scientific Tradition in Philosophical, Religious, and Institutional Context, 600 BC to AD 1450. The Journal of Interdisciplinary History, 25(4), 665–667.
Nasr, S. H. (2003). The achievements of Ibn Sina in the field of science and his contributions to its philosophy. Islam & Science, 1(2), 235.
O’Brien, M. (1844). A Treatise on Plane Co-Ordinate Geometry or the Application of the Method of Co-Ordinates in the Solution of Problems in Plane Geometry. England: Deightons: Cambridge Univ Press.
OpenStax. (2017). College Physics. Retrieved from https://openstax.org/details/college-physics
Piniés, M. R. (2016). On Science and the construction of identities: Remembering Ibn al-Haytham (965-1039). Contributions to Science, 95–102.
Quinn, P. (2000). Oliver Leaman, Key Concepts in Eastern Philosophy Reviewed by.
Rezzolla, L. (2023). The Irresistible Attraction of Gravity: A Journey to Discover Black Holes. Cambridge University Press.
Riepe, D. M. (1996). Naturalistic Tradition in Indian Thought. Motilal Banarsidass Publ.
Savov, I. (2014). No bullshit guide to math and physics. Minireference Co.
Schofield, R. E. (2015). Mechanism and materialism: British natural philosophy in the age of reason. Princeton University Press.
Sears, F. W., Zemansky, M. W., Young, H. D., & Freedman, R. A. (2017). University physics with modern physics. (Addison Wesley, Ed.) (14th ed.).
Serway, R. A., & Jewett, J. W. J. (2014). Physics for Scientists and Engineers with Modern Physics, Ninth Edition (9th ed.). Boston: Brooks/Cole.
Singer, C. (1949). A Short History of Science to the 19th century. Oxford.
Singer, C. (2013). A short history of science to the nineteenth century. Courier Corporation.
Stephens, A. L., & Clement, J. J. (2011). The role of thought experiments in science and science learning. In Second international handbook of science education (pp. 157–175). Springer.
Tipler, P. A., & Mosca, G. (2008). Physics for scientists and engineers, with modern physics (6th ed.). New York: W. H. Freeman and Company.
Weidhorn, M. (2005). The person of the millennium: the unique impact of Galileo on world history. Iuniverse.
Wilson, R. J. (2001). Calendars. Stamping Through Mathematics, 48–49.

























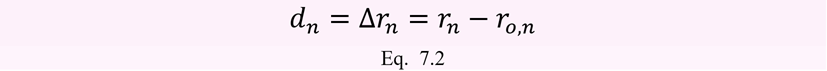


















No hay comentarios:
Publicar un comentario