En matemáticas, todo número posee una precisión infinita,
ya que idealmente está definido por una cantidad ilimitada de cifras
decimales. Un ejemplo emblemático es el número π (pi): aunque
comúnmente usamos 3,14 o 22/7, su valor real se extiende infinitamente sin
repetición. Esta naturaleza infinita no suele ser evidente porque muchas
veces los números decimales “terminan en ceros”, lo que nos da una falsa
sensación de exactitud. Sin embargo, incluso los números aparentemente
sencillos —como 2,5— en realidad encierran una infinitud de posibles dígitos
que nuestra mente y nuestros instrumentos deciden ignorar.
Aquí surge la cuestión de la medición. Un instrumento
científico transforma una propiedad cualitativa —como la temperatura o
la masa— en un valor numérico cuantitativo mediante una escala de
referencia. Pero todo instrumento tiene un límite de sensibilidad:
por debajo de ese umbral, el instrumento ya no distingue entre valores
cercanos. Filosóficamente, la propiedad medida posee un valor exacto con
infinitas cifras decimales, pero físicamente, ese valor es incognoscible
con medios finitos. Por eso adoptamos prácticas como el uso de cifras
significativas y el redondeo controlado, que nos permiten comunicar
resultados con una precisión compatible con los instrumentos utilizados, como
ya hemos trabajado en secciones anteriores.
Pero, ¿qué ocurre cuando no contamos con instrumentos
de medición? ¿O cuando el tiempo es limitado y aún así necesitamos una
respuesta útil? Es en estos escenarios donde emergen las aproximaciones de
Fermi. Este tipo de razonamiento estimativo, popularizado por el físico Enrico
Fermi, se basa en fragmentar un problema complejo en elementos
simples, haciendo supuestos razonables y multiplicando factores
conocidos o estimables. Las soluciones obtenidas pueden no ser exactas, pero
son sorprendentemente cercanas al valor real, lo suficiente para tomar decisiones
rápidas o evaluar la viabilidad de un proyecto científico. Estas
aproximaciones se apoyan en la intuición cuantitativa, el criterio
lógico y la experiencia práctica, convirtiéndose en herramientas
esenciales cuando los datos son escasos y el contexto exige eficiencia sin
sacrificar sentido físico.
Figura
1. El acceso
a carreras científicas suele depender de pruebas estandarizadas que
priorizan la rapidez en cálculos, dejando de lado habilidades como el razonamiento,
la creatividad y la comunicación científica. Esto puede excluir
perfiles valiosos para la ciencia real, limitando la diversidad
cognitiva. Una evaluación integral permitiría incluir talentos con pensamiento
crítico, curiosidad e intuición científica.
Uno de los contextos más comunes donde las aproximaciones
de Fermi se convierten en una herramienta decisiva es en las evaluaciones
estandarizadas que deben resolverse con lápiz, papel y bajo presión de
tiempo. Estas pruebas —como el Gaokao en China, el SAT en
Estados Unidos o el Saber 11 en Colombia— no solo miden conocimientos
académicos, sino que también funcionan como filtros sociales y económicos.
Son el umbral simbólico entre la infancia protegida y una adultez donde
se espera productividad, autonomía y responsabilidad.
El Gaokao (高考), o "examen nacional de
ingreso a la universidad", es considerado el examen más exigente del
mundo. Se realiza anualmente durante dos días en junio y evalúa matemáticas,
literatura china, inglés y una asignatura adicional según el área elegida. Solo
el 2% de los más de 11 millones de estudiantes que lo presentan accede a las
universidades más prestigiosas. En este contexto, incluso diferencias mínimas
en el puntaje pueden definir el futuro económico y social de una
persona. El SAT, por su parte, mide lectura crítica, escritura y
matemáticas. Es utilizado por las universidades estadounidenses como parte del
proceso de admisión, y aunque existen múltiples intentos para reformarlo, aún
refleja sesgos de clase y raza. El Saber 11, en Colombia, evalúa
áreas como matemáticas, lectura crítica, ciencias y competencias ciudadanas, y
sus resultados inciden en becas y acceso a la educación pública universitaria.
Fallar estas pruebas puede tener consecuencias
estructurales profundas. En sociedades con alta desigualdad, el resultado
de un examen se convierte en una sentencia: define si alguien podrá estudiar
medicina o si tendrá que conformarse con un empleo precario. La lógica
meritocrática esconde que muchos estudiantes enfrentan condiciones desiguales:
escasez de recursos, deficiente calidad educativa, hambre, estrés o falta de
acompañamiento familiar. Así, las pruebas no solo filtran por talento o
esfuerzo, sino también por capital cultural y económico, reproduciendo
formas de elitismo educativo.
Además del impacto académico, estas pruebas generan presión
emocional y estrés familiar. En China, no es raro que padres renuncien a
sus trabajos para apoyar a sus hijos en el año previo al Gaokao. En Colombia,
muchas familias concentran todas sus esperanzas en que el joven acceda a una
universidad pública por medio de un puntaje alto. El fracaso en estas pruebas
puede desencadenar crisis familiares, rupturas de expectativas y
deterioro de la salud mental. Aunque el sistema puede parecer injusto
o excluyente, es una realidad institucionalizada que miles de jóvenes deben
afrontar.
Figura
2. Las pruebas
estandarizadas como el Gaokao, el SAT o
el Saber 11 buscan medir el dominio conceptual en
áreas clave como matemáticas, física, química y biología.
A través de ejercicios numéricos y teóricos, estas evaluaciones valoran la
capacidad del estudiante para aplicar el método científico,
resolver problemas concretos y demostrar habilidades de cálculo y razonamiento
lógico. Su diseño responde a la necesidad de establecer un criterio objetivo
y comparable para evaluar el conocimiento adquirido en la educación
media, lo cual es especialmente útil en sistemas educativos con alta demanda de
ingreso a la educación superior.
Es precisamente en ese contexto que las estimaciones tipo
Fermi se revelan como una herramienta intelectual poderosa. Frente a
problemas complejos o datos ausentes, el estudiante puede usar el método Fermi
para dividir el problema en partes, asignar valores plausibles y
hacer cálculos rápidos con base en lógica, no en exactitud. En lugar de
memorizar resultados o fórmulas, se entrena la capacidad de pensar
estructuradamente bajo presión, lo cual resulta crucial en pruebas donde el
tiempo es limitado y el acceso a instrumentos como calculadoras está
restringido.
Lejos de ser atajos burdos, las aproximaciones de Fermi
representan una forma de eficiencia cognitiva. Enseñan a pensar con
flexibilidad, a dudar de las cifras redondas y a confiar en la lógica cuando no
hay recursos. Este tipo de razonamiento permite no solo sobrevivir
académicamente, sino también cultivar una forma de pensamiento crítico y
adaptativo que sirve tanto en un examen como en la vida cotidiana. En un mundo
injusto donde la educación formal aún está atravesada por barreras
estructurales, pensar como Fermi puede ser un acto de resistencia, una forma de
inteligencia al servicio de la supervivencia.
Figura
3. Enrico
Fermi fue un físico italoestadounidense clave en la creación del primer reactor
nuclear y en el avance de la física moderna. Ganador del Premio
Nobel en 1938, destacó también por sus problemas de Fermi,
estimaciones lógicas con datos mínimos. Su enfoque combinó ciencia rigurosa
y pensamiento práctico, dejando un legado duradero en la física y en el
arte de razonar con ingenio.
Las aproximaciones de Fermi se basan en una idea
fundamental: usar la estimación como aliada de la aritmética, no como un
sustituto de la exactitud. En contextos como las evaluaciones estandarizadas,
donde las respuestas suelen estar en formato de selección múltiple, no
necesitas dar con el valor exacto, sino acercarte lo suficiente para
reconocer la opción correcta. Esa es la clave: aproximar con astucia, no con
descuido.
La estrategia comienza por segmentar el problema en
factores manejables y luego redondear los valores numéricos buscando
un balance compensatorio. ¿Recuerdas cuando Thanos hablaba del
equilibrio del universo? Aquí sucede algo similar: si redondeas un número hacia
arriba, puedes redondear el otro hacia abajo, de modo que los errores se compensen
mutuamente y el resultado global se mantenga cerca del real. Así, el
producto final será más fácil de calcular mentalmente, sin desviarse
drásticamente del valor correcto.
Cuando se trata de razones o proporciones —por
ejemplo, velocidad, densidad o rendimiento—, la clave está en redondear
ambos términos en la misma dirección y de forma proporcional. Si
aumentas el numerador, haz lo mismo con el denominador en una proporción
razonable. Esto asegura que la fracción resultante mantenga su valor
aproximado, pero se simplifique a una división aritmética accesible, como
20/5 o 150/30, que puedes resolver mentalmente en segundos.
Otra técnica efectiva es la de operar solo con las cifras
significativas relevantes. En lugar de perder tiempo con decimales
interminables o múltiples dígitos poco relevantes, puedes redondear los valores
a dos o tres cifras significativas antes de realizar la operación. Así, la
carga cognitiva se reduce y la probabilidad de errores disminuye
drásticamente, algo fundamental bajo presión de tiempo.
La combinación inteligente de todas estas estrategias
convierte las aproximaciones de Fermi en un filtro cognitivo de eficiencia
matemática. No solo ayudan a responder preguntas rápidamente, sino que
también permiten verificar resultados obtenidos con calculadora,
contrastando el orden de magnitud con un cálculo estimado. Esto es útil incluso
cuando se tiene acceso a herramientas tecnológicas: la estimación sigue siendo
la forma más rápida de detectar errores de digitación o incoherencias
numéricas.
Aprender a estimar como lo hacía Enrico Fermi no solo es
útil para resolver acertijos científicos o calcular la cantidad de afinadores
de piano en Nueva York. Es una habilidad crítica en entornos de alta presión,
como los exámenes estandarizados que determinan oportunidades académicas y
laborales. Más que un simple cálculo, es una estrategia de supervivencia
intelectual en un mundo que exige resultados rápidos y precisos, pero que
rara vez concede el lujo de hacerlo sin presión.
Referencias
Ärlebäck, J. B., & Albarracín, L. (2019). The use and potential of Fermi
problems in the STEM disciplines to support the development of twenty first
century competencies. ZDM – Mathematics Education, 51(6), 979–990.
https://doi.org/10.1007/s11858-019-01075-3
Au, W.
(2009). Unequal by design: High stakes testing and the standardization
of inequality. Routledge.
Beiser, A.
(2003). Concepts of Modern Physics (6. ed.). McGraw Hill.
Bevington,
P. R., & Robinson, D. K. (2003). Data Reduction and Error Analysis
for the Physical Sciences (3. ed.). McGraw Hill.
BIPM –
Bureau International des Poids et Mesures. (2019). The International
System of Units (SI) (9. ed.). Recuperado de
https://www.bipm.org/en/publications/si-brochure
Gibson, D. E. (2008). Fermi estimation and its pedagogical applications in physics
education. Physics Education, 43(4), 364–370.
https://doi.org/10.1088/0031-9120/43/4/008
Harte, J.
(1988). Consider a spherical cow: A course in environmental problem
solving. University Science Books.
Herman, J.,
& Golan, S. (1991). Effects of standardized tests on teachers and
learning—Another look. CSE Technical Report No. 334. Center
for the Study of Evaluation, UCLA.
International
Organization for Standardization. (1995). Guide to the Expression of
Uncertainty in Measurement (ISO GUM). ISO.
Knoll, G.
F. (2010). Radiation Detection and Measurement (4. ed.).
Wiley.
Kohn, A.
(2000). The case against standardized testing: Raising the scores,
ruining the schools. Heinemann.
Mahajan, S.
(2010). Street fighting mathematics: The art of educated guessing and
opportunistic problem solving. MIT Press.
Milligan,
J. R., & Zoltowski, M. D. (2002). Measurement uncertainty and the teaching
of significant figures. Journal of Chemical Education, 79(5),
595–597. https://doi.org/10.1021/ed079p595
Mohr, P.
J., Newell, D. B., & Taylor, B. N. (2016). CODATA recommended values of the
fundamental physical constants: 2014. Reviews of Modern Physics, 88(3),
035009. https://doi.org/10.1103/RevModPhys.88.035009
Robinson,
A. W. (2007). Don’t just stand there—teach Fermi problems! Physics
Education, 43(1), 83–87.
Swartz, C.
(2003). Back of the envelope physics. Johns Hopkins University
Press.
Taylor, J.
R. (1997). An Introduction to Error Analysis: The Study of
Uncertainties in Physical Measurements (2. ed.). University Science
Books.
Taylor, J.
R., & Kuyatt, C. E. (1994). Guidelines for Evaluating and
Expressing the Uncertainty of NIST Measurement Results. NIST Technical
Note 1297. Recuperado de
https://nvlpubs.nist.gov/nistpubs/Legacy/TechnicalNotes/NIST.TN.1297.pdf
Young, H. D., & Freedman, R. A. (2019). University Physics with Modern Physics (15. ed.). Pearson.



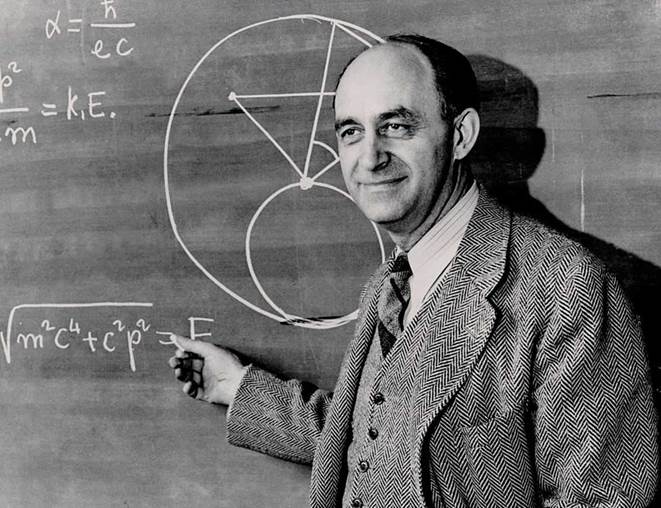
No hay comentarios:
Publicar un comentario