La teoría cuántica

[Átomo moderno] Sección 4. [Mecánica cuántica] [La luz] [La teoría cuántica] [Aplicaciones de la teoría cuántica] [Configuración electrónica]

En el desarrollo histórico de la química se justificaron las fórmulas estequiométricas basándose en el concepto del átomo clásico y en la constante de Avogadro, lo que permitió cuantificar la materia de manera precisa. Sin embargo, este enfoque resultó insuficiente para explicar ciertas propiedades intrínsecas del átomo que se evidenciaron mediante experimentos y observaciones, evidenciando la necesidad de vincular la química con los avances de la física moderna.

El modelo de Rutherford surgió para explicar los resultados del experimento de la lámina de oro, revelando la existencia de un núcleo central denso y rodeado de electrones. No obstante, la aplicación de las leyes de la mecánica clásica, en particular la formulación de la ley de Larmor, mostraba que un electrón en movimiento acelerado debía emitir radiación electromagnética, lo que implicaría una pérdida continua de energía, un hecho que contradecía la estabilidad observada en los átomos.

Figura 1. La rotación y el color. (Izquierda) Una partícula que rota a una velocidad constante alrededor de un punto, aunque su rapidez es constante y por lo tanto genera periodos de rotación iguales, la partícula acelera todo el tiempo, ya que en cada punto su dirección cambia. (Derecha)  El electrón debería emitir radiación de forma continua en todo el espectro electromagnético que le permita su alejamiento del núcleo, a medida que emite energía s velocidad disminuye acercándose en una espiral continua hasta el núcleo atómico.

Al aplicar conceptos clásicos al movimiento orbital se puede establecer una analogía con el sistema Tierra-Luna. En este contexto, la Luna, si no alcanza la velocidad de escape adecuada, tendería a caer hacia la Tierra o, si se moviera con una velocidad ideal (teóricamente imposible según Newton), se mantendría en una órbita perpetua. De forma similar, un electrón que se moviera conforme a las leyes newtonianas debería, al perder energía, colapsar en una espiral hacia el núcleo, lo que evidencia la incompatibilidad entre la mecánica clásica y la estabilidad atómica.

Un concepto clave en este análisis es el de aceleración, entendido no solo como el incremento de la rapidez, sino también como el cambio en la dirección del movimiento. Incluso si un electrón mantiene una velocidad constante, el hecho de cambiar de dirección implica una aceleración constante, lo que, según la física clásica, forzaría la emisión de energía continua. Esta perspectiva resulta crucial para comprender por qué el modelo clásico predice una ineludible pérdida de energía en sistemas orbitales.

Figura 2. La luz emitida en un tubo de descarga que contiene un gas puro al atravesar un prisma se comporta de manera notablemente diferente a la luz del sol. Mientras que la radiación solar produce un espectro continuo que genera un arcoíris, la luz de un tubo de descarga presenta un patrón de líneas específicas, similar a un código de barras. Esto ocurre porque los átomos del gas absorben y emiten energía en longitudes de onda particulares, lo que resulta en un espectro de emisión discontinuo. Este fenómeno es fundamental para la espectroscopía, ya que permite identificar la composición química del gas y comprender mejor las propiedades de la materia en diversas condiciones. Este conocimiento impulsa importantes avances en ciencia moderna.

El problema central se presenta en la aparente emisión ininterrumpida de radiación electromagnética por parte de los electrones. De acuerdo con la fórmula de Larmor, un electrón en órbita debería irradiar energía en todas las longitudes de onda posibles, provocando que, a medida que su energía cinética disminuye, se acerque progresivamente al núcleo en una espiral descendente, fenómeno conocido como el colapso electrónico. Este escenario paradójico indicaba que, bajo la óptica de la física clásica, la existencia misma de los átomos sería inviable.

La solución a esta paradoja comenzó a vislumbrarse gracias a estudios en espectroscopía, los cuales revelaron que los átomos emiten o absorben luz en longitudes de onda discretas y no en un espectro continuo. Las observaciones de las líneas de Fraunhofer en el espectro solar demostraron que los electrones sólo pueden ocupar niveles de energía determinados, ya que al realizar transiciones entre ellos se produce la emisión o absorción de fotones en longitudes de onda específicas. Estos hallazgos resultaron decisivos para cuestionar la validez del modelo clásico y plantear la necesidad de una nueva teoría.

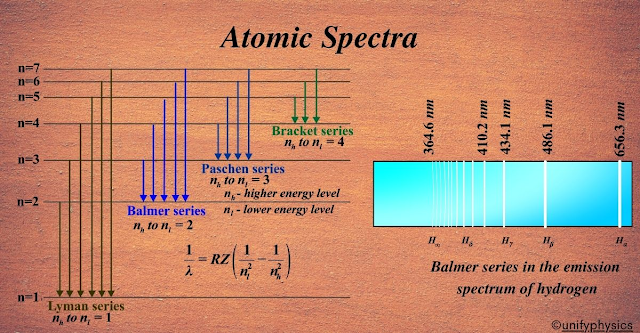
Figura 3. Las series y fórmulas de Rydberg y Balmer son desarrollos empíricos que se fundamentan en observaciones experimentales de los espectros de emisión de los átomos. Estas fórmulas permiten predecir con exactitud las posiciones en las que se deben medir las líneas o barras espectrales tanto en el rango visible como en el infrarrojo o ultravioleta, identificando patrones repetitivos en la distribución de la energía. Sin embargo, aunque proporcionan una herramienta útil para ubicar las bandas de emisión, no ofrecen una explicación teórica acerca de las razones fundamentales por las cuales se producen estas transiciones discretas. Es decir, si bien determinan dónde se manifiestan las barras, no explican el mecanismo subyacente que origina la cuantización de los niveles energéticos de los electrones. Estas fórmulas empíricas abrieron camino hacia la teoría cuántica.

La consolidación de la cuantización energética se materializó a través de la formulación empírica de la serie de Balmer, que describió las longitudes de onda correspondientes a las transiciones en el hidrógeno, y que fue posteriormente generalizada por Rydberg. La serie de Balmer-Rydberg evidenció que las emisiones de luz se daban en forma de saltos cuánticos entre niveles discretos de energía, en lugar de transitar de forma continua. Este descubrimiento no solo explicó la estabilidad atómica, sino que también marcó el advenimiento de una nueva física, la mecánica cuántica, que fundamenta la comprensión actual de la materia a escalas subatómicas.

Las explicaciones de los fenómenos de dispersión y difracción fueron uno de los grandes éxitos de la teoría ondulatoria de la luz de Maxwell, que gozaba del mismo prestigio que la mecánica newtoniana en la transición del siglo XIX al XX. Durante ese periodo muchos científicos afirmaban que el universo podía reducirse a las teorías de Newton y Maxwell, aunque la luz no encajaba en este marco. A finales del siglo XIX se evidenciaron discrepancias entre los resultados experimentales y las predicciones ondulatorias, revelando que ciertos fenómenos lumínicos escapaban al dominio de la física clásica y abriendo la necesidad de replantear su estudio para futuros análisis científicos rigurosos.

Figura 4. Picos de espectro de cuerpo negro. Fue Wilhelm Wien 1864-1928 quien describió que el pico de un espectro de cuerpo negro en la gráfica de R por λ se encuentra relacionado a una tercera variable, la temperatura T describiendo todo en una fórmula que lleva su nombre, la ley de Wien. La ley de Wien permite predecir que los objetos fríos como nosotros emitimos luz en el espectro infrarrojo, que los objetos muy fríos emiten en radio y que los objetos muy calientes tienden a tener un brillo azulado.

Entre las primeras evidencias que apuntaban a la naturaleza cuántica de la radiación se encuentran los estudios sobre las propiedades de la superficie de los cuerpos opacos. Cuando la radiación incide sobre un objeto, parte de ella se refleja y el resto es absorbido, comportándose según la textura y el color del material. Un espejo refleja casi toda la energía radiante, mientras que las superficies oscuras absorben dicha energía. Este fenómeno se aprovecha en dispositivos como los termos, donde se emplean recubrimientos reflectantes para minimizar la pérdida térmica. Así, la interacción entre la radiación y la superficie se convierte en una clave para comprender el comportamiento lumínico real.

Figura 5. Para aproximarse al comportamiento ideal de un cuerpo negro, se ha desarrollado un modelo experimental que utiliza una botella con forma de poporo. Esta botella resulta ser el objeto más cercano a la entidad teórica denominada cuerpo negro, ya que está diseñada para absorber casi toda la radiación que incide sobre ella, imitando la capacidad perfecta de absorción sin reflejar luz. Gracias a su estructura y materiales seleccionados, el dispositivo reduce significativamente las reflexiones internas, permitiendo que la radiación se disperse uniformemente y se convierta en una herramienta valiosa para experimentos en radiación térmica y estudios espectroscópicos. Este modelo es fundamental para validar conceptos teóricos en física, y avances modernos.

La radiación térmica emitida por objetos densos, como líquidos y sólidos, presenta un espectro continuo que abarca todas las longitudes de onda, en contraste con los gases en baja densidad que muestran espectros discretos. Estudios pioneros de Kirchhoff y la ley de Wien demostraron que la forma del espectro de un cuerpo negro depende únicamente de su temperatura. Esto explica por qué los objetos fríos emiten luz en el infrarrojo, mientras que los más calientes despliegan picos en el azul y ultravioleta. La relación entre temperatura y emisión radiante se erige en un pilar fundamental para interpretar la energía según la longitud de onda, clave para la física.

No obstante, pese al éxito en describir ciertos aspectos de la radiación, la física clásica enfrentó serias limitaciones al intentar explicar la distribución de energía en función de la longitud de onda. La ley de Rayleigh-Jeans, basada en los principios de Maxwell y la mecánica newtoniana, predecía un aumento ilimitado de la intensidad en el ultravioleta, fenómeno denominado la catástrofe ultravioleta. Esta predicción contrastaba con los resultados experimentales, que mostraban una marcada disminución en esa región. Tal discrepancia evidenció que las teorías clásicas eran insuficientes para describir el comportamiento de la radiación, revelando la necesidad de un nuevo enfoque que incorporara la idea de discreción en la transferencia.

Figura 6. En la representación gráfica de la radiación emitida por un cuerpo negro al calentarse, se aprecian dos curvas de modelos en competencia que reflejan los resultados de las ecuaciones de Rayleigh y Planck. La ley de Rayleigh-Jeans, fundamentada en la física clásica, anticipa una emisión infinita en el rango ultravioleta, lo cual se conoce como la catástrofe ultravioleta. En contraste, la ecuación de Planck, introduciendo la cuantización de la energía, ajusta perfectamente la curva experimental, mostrando un pico en la región visible y una caída en longitudes de onda menores. Estos modelos evidencian la transición de la física clásica a la cuántica, resaltando la importancia de la hipótesis de Planck para explicar de manera coherente y concluyente la radiación térmica.

Ante esta problemática, Planck propuso una solución revolucionaria basada en la suposición de que la energía se intercambia en paquetes discretos o cuantos, en lugar de variar de manera continua. Con la formulación de la hipótesis cuántica, expresada en la ecuación $E = n \cdot h \cdot f$, se logró derivar una fórmula que se ajustaba a las observaciones y evitaba la catástrofe del ultravioleta. Aunque su propuesta fue inicialmente considerada una mera conjetura matemática sin respaldo experimental directo, la innovadora idea de Planck permitió explicar la distribución de la intensidad radiante y sentó las bases para el desarrollo de la física cuántica, que realmente transformó para siempre nuestra comprensión del universo.

El caso de la hipótesis de Planck evidencia que la física clásica resulta inadecuada para describir los fenómenos lumínicos y que los avances científicos pueden surgir de conjeturas teóricas audaces. Esta situación desafía la visión experimentalista tradicional que asume que el descubrimiento depende exclusivamente de los experimentos en laboratorio, como si el científico “cocinara” un hallazgo de la nada. En realidad, la formulación matemática de Planck, inicialmente especulativa, abrió la puerta a la revolución cuántica, demostrando que la creatividad y el razonamiento abstracto son tan fundamentales como la experimentación en el progreso del conocimiento científico, lo que confirma la importancia de la teoría en la ciencia muy fundamental con rigor.

La solución de Max Planck en 1900 para explicar la radiación de cuerpo negro representó un hito que abrió el camino hacia una nueva visión de la energía y la radiación, ya que postuló que la energía se emitía en paquetes discretos denominados cuantos. Inspirado por este planteamiento, Albert Einstein aplicó la hipótesis de cuantización energética al fenómeno del efecto fotoeléctrico, proponiendo que la luz, en lugar de comportarse como una onda continua, estaba compuesta por unidades elementales de energía, conocidas como fotones, cuya energía está dada por el producto de la constante de Planck ($h$) por la frecuencia de la luz ($f$). Esta idea surgió en un contexto en el que la teoría atómica comenzaba a ser aceptada por la comunidad científica, y aunque modelos como el de Thomson habían sido formulados, la idea de que las leyes newtonianas regían a nivel atómico se estaba poniendo en tela de juicio. Experimentos tempranos, como los realizados por Heinrich Hertz en 1887, demostraron la existencia de ondas electromagnéticas y, de manera simultánea, revelaron el enigmático efecto fotoeléctrico, en el que la emisión de electrones al incidir la luz sobre un material no podía explicarse adecuadamente con los postulados de la física clásica. Estos hechos forzaron a los científicos a replantear la naturaleza de la luz y a considerar la posibilidad de que su comportamiento discontinuo ofreciera una mejor descripción de los procesos a escala microscópica.

Figura 7. Max Karl Ernst Ludwig Planck fue un destacado físico y matemático alemán, nacido el 23 de abril de 1858 en Kiel y fallecido el 4 de octubre de 1947 en Göttingen. Es reconocido como el padre de la teoría cuántica, debido a su revolucionaria propuesta de que la energía se emite en paquetes discretos denominados cuantos. Esta idea transformó radicalmente la comprensión de la radiación y la materia, abriendo el camino a desarrollos posteriores en la física moderna. Planck introdujo la constante que lleva su nombre, fundamental en la mecánica cuántica, y fue galardonado con el Premio Nobel de Física en 1918. Su legado sigue siendo crucial para el avance de la ciencia y la tecnología contemporáneas. Su influencia perdura..

El efecto fotoeléctrico se define como la emisión de electrones de un material cuando éste es iluminado con radiación electromagnética de suficiente frecuencia, de manera que cada fotón aporta una cantidad de energía determinada, proporcional a su frecuencia, a un electrón. En contraste con las predicciones de la teoría clásica, que asumía que una onda continua transferiría energía de forma gradual y acumulativa, los experimentos demostraron que los electrones son expulsados únicamente cuando la frecuencia de la luz supera un umbral crítico, independientemente de la intensidad de la radiación. Es decir, aumentar la intensidad de una luz de baja frecuencia no produce fotoemisión, ya que ningún fotón individual alcanza la energía necesaria para superar la función de trabajo del material. Esta observación se sintetiza en la relación fundamental $E = h \cdot f$, donde la energía de cada fotón debe ser mayor o igual a la energía requerida para liberar al electrón, parte de la cual se utiliza para vencer la atracción del núcleo y el resto se traduce en la energía cinética del electrón liberado. Así, mientras que la cantidad de electrones emitidos puede variar con la intensidad de la luz, la energía cinética de cada uno depende exclusivamente de la frecuencia de la radiación, una conclusión que fue decisiva para la aceptación del modelo cuántico de la luz y que proporcionó a Einstein el fundamento teórico para explicar la anomalía observada en los experimentos.

La aplicación de la constante de Planck en el contexto del efecto fotoeléctrico validó la hipótesis de la cuantización de la energía y marcó el inicio de una revolución en la física y la química, ya que permitió comprender fenómenos que la mecánica clásica no podía explicar. Einstein, al interpretar la luz como un conjunto de fotones, ofreció una solución elegante a la aparente contradicción entre la teoría ondulatoria y los resultados experimentales, explicando por qué la emisión de electrones no dependía de la intensidad luminosa sino de la frecuencia de la radiación incidente. Esta perspectiva no solo resolvió el enigma del efecto fotoeléctrico, sino que también sentó las bases para el desarrollo del concepto de dualidad onda-partícula, que es fundamental en la mecánica cuántica moderna. La confirmación experimental de la ley de Einstein, a través de estudios meticulosos como los de Robert Millikan, consolidó la idea de que la naturaleza de la luz es intrínsecamente cuántica, y demostró que los procesos a nivel atómico y subatómico no pueden ser entendidos completamente bajo los principios de la física clásica. De esta forma, la integración de la constante de Planck en la formulación teórica del efecto fotoeléctrico se convirtió en uno de los pilares sobre los cuales se edificó la física cuántica, transformando nuestra comprensión de la interacción entre la radiación y la materia y abriendo el camino para el desarrollo de tecnologías basadas en esta revolucionaria concepción de la naturaleza.

Figura 8. Efecto fotoeléctrico. Semejante a un tubo de descarga, lo que completa el circuito son los electrones emitidos por la placa del ánodo al ser estimulada por un haz de luz de frecuencia alta “ultravioleta”. En 1914 Robert Millikan confirmó la ley de Einstein sobre el efecto fotoeléctrico, Einstein fue galardonado con el premio Nobel de física en 1921 por su descubrimiento de la ley que rige al efecto fotoeléctrico y Millikan fue galardonado con el permio nobel de física en 1923 por su trabajo experimental sobre el efecto fotoeléctrico.