Índice
||1|| Introducción ||2|| Historia ||3|| Descomponiendo los vectores de movimiento | ||6|| Aceleración tangencial y radial ||7|| Velocidad relativa y aceleración relativa ||R|| Referencias bibliográficas ||E|| Ejercicios resueltos |
Portada
1. Introducción
|| REGRESAR AL INDICE ||
En este capítulo, exploramos la cinemática de una partícula que se mueve en dos dimensiones. Conocer los conceptos básicos del movimiento bidimensional nos permitirá, en capítulos futuros, examinar una variedad de situaciones, que van desde el movimiento de satélites en órbita hasta el movimiento de electrones en un campo eléctrico uniforme. Comenzaremos estudiando con mayor detalle la naturaleza vectorial de la posición, la velocidad y la aceleración. Luego tratamos el movimiento de proyectil y el movimiento circular uniforme como casos especiales de movimiento en dos dimensiones. También discutimos el concepto de movimiento relativo, que muestra por qué los observadores en diferentes marcos de referencia pueden medir diferentes posiciones y velocidades para una partícula dada.
A pesar de lo anterior, la principal aplicación de este campo de la física fue por mucho tiempo la aplicación a la balística y el tiro parabólico, cuando los proyectiles no llegaban muy lejos, y no se debía tener en cuenta la circunferencia de la Tierra para darle al blanco. Los humanos llevamos arrojándonos cosas a la cabeza con mala actitud desde antes de ser humanos, y después de milenios de desarrollo empírico, la disciplina de la balística fue inicialmente estudiada y desarrollada por el matemático italiano Niccolò Tartaglia en 1531 (Groetsch, 2004; Menegat & Saito, 2016; Pisano, Capecchi, Pisano, & Capecchi, 2016)
Tartaglia continuó utilizando segmentos de movimiento rectilíneo, convenciones establecidas por el filósofo griego Aristóteles y Alberto de Sajonia, pero con la novedad de que conectó las líneas rectas mediante un arco circular. Galileo estableció el principio del movimiento compuesto en 1638, utilizando el principio para derivar la forma parabólica de la trayectoria balística (Groetsch, 2004). Isaac Newton sentó la balística sobre una sólida base científica y matemática con la publicación de Philosophiæ Naturalis Principia Mathematica en 1687 (Newton, 2013). Esto proporcionó leyes matemáticas del movimiento y la gravedad que, por primera vez, hicieron posible predecir trayectorias con éxito, no solo de una roca a la cabeza de tu enemigo, sino de la trayectoria de la Luna alrededor de la Tierra, o de asteroides alrededor del Sol que pasan cada cuantas décadas.
1.1 Niccolò Fontana Tartaglia (1499-1557)
Fue un matemático, ingeniero (diseñador de fortificaciones), agrimensor (de topografía, búsqueda de los mejores medios de defensa o ataque) y contador italiano de la entonces República de Venecia. Publicó muchos libros, incluidas las primeras traducciones italianas de Arquímedes y Euclides, y una aclamada compilación de matemáticas. Tartaglia fue el primero en aplicar las matemáticas a la investigación de las trayectorias de las balas de cañón, conocida como balística, en su Nova Scientia (Una nueva ciencia, 1537); su trabajo fue posteriormente validado y reemplazado por los estudios de Galileo sobre la caída de cuerpos y de Newton que dio un argumento analítico. También publicó un tratado sobre la recuperación de barcos hundidos y desarrolló un método para resolver el término x en una ecuación cúbica reducida (sin el término elevado al cuadrado).
Niccolò Fontana Tartaglia fue un matemático y científico italiano del siglo XVI que hizo importantes contribuciones al estudio del movimiento en dos dimensiones y al movimiento de proyectiles. En particular, Tartaglia fue el primero en proponer una solución matemática para el problema de la trayectoria de un proyectil en vuelo.
Tartaglia demostró que la trayectoria de un proyectil en vuelo seguía una curva parabólica, y desarrolló fórmulas para calcular la altura, la distancia horizontal y el tiempo de vuelo de un proyectil en movimiento. También descubrió que el alcance máximo se obtiene cuando el ángulo de lanzamiento es de 45 grados.
Las contribuciones de Tartaglia fueron fundamentales para el desarrollo posterior de la física y la balística, y sentaron las bases para el estudio moderno del movimiento en dos dimensiones y el movimiento de proyectiles. Sus descubrimientos también ayudaron a los ingenieros y científicos a comprender mejor la trayectoria de los proyectiles y a diseñar armas y proyectiles más eficaces y precisos.
En resumen, Niccolò Fontana Tartaglia fue un pionero en el estudio del movimiento en dos dimensiones y el movimiento de proyectiles, y sus contribuciones fueron fundamentales para el desarrollo posterior de la física y la balística.
Niccolò Fontana Tartaglia fue un precursor en el estudio del movimiento de proyectiles, y sus aportes fueron significativos para el desarrollo de la física y la balística en su época. Sin embargo, Galileo Galilei y, especialmente, Isaac Newton son considerados como los principales exponentes de la física clásica y el estudio del movimiento en dos dimensiones y el movimiento de proyectiles.
Galileo fue uno de los primeros en hacer experimentos para estudiar el movimiento, y demostró que todos los objetos caen al mismo ritmo, independientemente de su peso. También desarrolló la ley de la inercia, que establece que un objeto en movimiento continuará en movimiento a menos que se aplique una fuerza externa sobre él.
Newton, por su parte, estableció las leyes del movimiento que todavía se utilizan hoy en día en la física clásica. En particular, su segunda ley del movimiento establece que la fuerza aplicada sobre un objeto es igual a su masa multiplicada por su aceleración. Además, desarrolló la ley de la gravitación universal, que describe cómo los objetos se atraen entre sí en función de su masa y la distancia entre ellos.
Si bien Niccolò Fontana Tartaglia hizo importantes aportes al estudio del movimiento en dos dimensiones y el movimiento de proyectiles, Galileo y Newton son generalmente considerados como los principales exponentes de la física clásica y su legado es más amplio y profundo en la historia de la ciencia.
2. Historia
|| REGRESAR AL INDICE ||
Como mencionamos en la introducción, la historia del movimiento en dos dimensiones es básicamente la historia del tiro parabólico.
2.1 Balística
Los primeros proyectiles balísticos conocidos fueron piedras, palos y lanzas ligeras llamadas jabalinas (Nandi, Sen, & Mahanti, 2021). La evidencia más antigua de proyectiles con punta de piedra, que pueden o no haber sido propulsados por un arco (cf. atlatl), que data de 64 000 años, fueron encontrados en la cueva de Sibudu, actual Sudáfrica (d’Errico et al., 2017). La evidencia más antigua del uso de arcos para disparar flechas data de hace unos 10 000 años; se basa en flechas de madera de pino que se encuentran en el valle de Ahrensburg al norte de Hamburgo. Tenían ranuras poco profundas en la base, lo que indica que se dispararon con un arco (McEwen, Miller, & Bergman, 1991). El arco más antiguo recuperado hasta ahora tiene unos 8 000 años y se encuentra en el pantano de Holmegård en Dinamarca.
Figura 2.1. Debemos tener en cuenta que la balística en realidad es un problema de movimiento en tres dimensiones pues no solo se trata de la elevación y el alcance del proyectil sino de la posibilidad que tiene este de ser desviado por fuerzas como el viento o el rozamiento con el aire.
El tiro con arco parece haber llegado a las Américas con la tradición de las herramientas pequeñas del Ártico, hace unos 4500 años. Los griegos darían el siguiente paso, el ingeniero Dionisio el Viejo de Siracusa, que buscaba desarrollar un nuevo tipo de arma, inventó la catapulta alrededor del año 400 aC y partir de entonces, se convirtió en un arma clave en la guerra y permaneció así hasta la época medieval, cuando fue reemplazada por el trabuquete o fundíbulo (Nandi et al., 2021).
Figura 2.2. El fundíbulo es una máquina compuesta que hace uso de la ventaja mecánica de una palanca para lanzar un proyectil. Por lo general, son construcciones grandes, con una longitud de viga de hasta 15 metros, y algunas supuestamente son incluso más grandes
Un trabuquete/fundúbulo consta principalmente de una viga larga unida por un eje suspendido a gran altura sobre el suelo por un marco y una base robustos, de modo que la viga puede girar verticalmente a través de un arco amplio (generalmente más de 180 °). Una honda está unida a un extremo de la viga para sostener el proyectil. El proyectil se lanza cuando la viga gira rápidamente aplicando fuerza al extremo opuesto de la viga. La ventaja mecánica se obtiene principalmente al tener la sección del proyectil de la viga mucho más larga que la sección opuesta donde se aplica la fuerza, generalmente de cuatro a seis veces más larga (Chevedden, Eigenbrod, Foley, & Soedel, 1995).
Los primeros dispositivos identificados como armas con proyectiles de pólvora aparecieron en China alrededor del año 1000 d. C., y en el siglo XII la tecnología se estaba extendiendo por el resto de Asia y en Europa en el siglo XIII, las cuales rápidamente crecieron en tamaño y en precisión, reemplazando simultáneamente a otras armas de proyectiles como arcos, ballestas, catapultas y fundíbulos (Andrade, 2017; Streusand, 2018).
2.2 La física de Aristóteles
Fue en la época de transición y mejoramiento de las primeras armas de pólvora, que el estudio de la balística se hizo matemático, gracias a la labor de Tartaglia. En ese entonces, la física aristotélica dominante usaba categorías como "pesado", "natural" y "violento" para describir el movimiento, evitando generalmente las explicaciones matemáticas.
Aunque bajo el marco de referencia de la física clásica escolarizada estas categorías parecen extrañas, en realidad son categorías intuitivas sobre el movimiento de los objetos. Para los aristotélicos el estado natural es el reposo, y solo un acto violento hace que una partícula deje el reposo para iniciar un movimiento. Y el movimiento solo se mantendrá si y solo sí esa fuerza violenta se mantiene de manera permanente en el tiempo, pues en el momento en que la fuerza ejercida sobre el móvil desaparece, el objeto paulatinamente regresará a su estado natural de reposo.
La expresión de peso implica que los objetos más pesados van a ser aquellos que tiendan más naturalmente el reposo, por lo que se necesita mucha más violencia para poder hacer que se muevan. En cierto sentido esos fundamentos de la física aristotélica son intuitivos.
2.3 Avances de Tartaglia dentro del marco de referencia aristotélico
Uno de los objetivos de Nicolo Tartaglia fue el de convertir las afirmaciones y conceptos de la física de Aristóteles en afirmaciones y conceptos matemáticos, específicamente enfocados en el movimiento de los proyectiles (Henninger-Voss, 2002). Uno de sus descubrimientos fue que el alcance máximo de un proyectil se lograba dirigiendo el cañón en un ángulo de 45° con respecto al horizonte.
El modelo de Tartaglia para el vuelo de una bala de cañón era que procedía del cañón en línea recta, luego, después de un tiempo, comenzaba a arquearse hacia la tierra a lo largo de un camino circular, y finalmente caía en otra línea recta directamente hacia la tierra (Stitik, 1996). Al final del Libro 2 de Nova Scientia, Tartaglia propone encontrar la longitud de esa trayectoria rectilínea inicial para un proyectil disparado a una altura de 45°, participando en un argumento de estilo euclidiano, pero uno con números adjuntos a segmentos de línea y áreas, y eventualmente procede algebraicamente para encontrar la cantidad deseada (Valleriani, 2013).
Figura 2.3. Modelo gráfico de Tartaglia que describe su comprensión del movimiento de proyectiles. En ese podemos darnos cuenta que, aunque se acerca a la descripción de un movimiento circular parcial, no describe realmente una parábola que es como entendemos nosotros comprendemos este tipo de movimiento de proyectiles sobre el planeta Tierra.
Mary J. Henninger-Voss señala que "el trabajo de Tartaglia sobre ciencia militar tuvo una enorme circulación en toda Europa", siendo una referencia para los artilleros comunes hasta el siglo XVIII, a veces a través de traducciones no atribuidas.
2.4 Galileo y la descomposición del movimiento en dos dimensiones
El trabajo de Tartaglia también influyó en Galileo, quien poseía copias "ricamente anotadas" de sus trabajos sobre balística cuando se dispuso a resolver el problema de los proyectiles de una vez por todas (Henninger-Voss, 2002). Una de las características más importantes de las técnicas de análisis del movimiento en dos dimensiones es precisamente que este se puede descomponer en dos movimientos de una sola dimensión, este enfoque se lo debemos a Galileo.
Comenzando en la página 244 de Two New Sciences, Galileo da su análisis clásico del movimiento de un proyectil como un movimiento compuesto, formado por un movimiento horizontal que tiene una velocidad constante en una dirección fija, y un movimiento vertical que es su "aceleración natural", adquiriendo velocidad en la dirección hacia abajo a un ritmo constante (Henninger-Voss, 2002).
Sin embargo, los instrumentos de análisis serán los que derivo Newton en sus Principia, empleando simbología moderna. A la postre se basa en aplicar las ecuaciones del movimiento en una dimensión, a dos dimensiones que se comportaran como las componentes de un vector, de allí que tuviéramos que analizar un poco de algebra de vectores antes de este capítulo (Henninger-Voss, 2002).
3. Descomponiendo los vectores posición, velocidad y aceleración
|| REGRESAR AL INDICE ||
En esta sección estandarizaremos los símbolos para los vectores dados, y sus componentes en dos dimensiones.
3.1 Vector posición
Sea r el vector posición, estará compuesto por las componentes rxi + ryj. Nos indica la posición de una partícula en el plano. El vector posición es un concepto fundamental en la física y se utiliza para describir la posición de un objeto en un sistema de coordenadas. Se define como un vector que va desde el origen del sistema de coordenadas hasta el objeto en cuestión.
El vector posición se expresa matemáticamente como una flecha con una magnitud y una dirección. La magnitud del vector posición es la distancia desde el origen del sistema de coordenadas hasta el objeto, y la dirección del vector posición es la dirección desde el origen hacia el objeto.
Por ejemplo, si un objeto se encuentra a una distancia de 5 metros al este y 3 metros al norte del origen de un sistema de coordenadas, entonces el vector posición del objeto será un vector que apunta hacia el noreste, con una magnitud de 52 + 32 = 25 + 9 = 34 metros.
El vector posición es importante en la física porque permite describir la posición de los objetos en un espacio tridimensional y también se utiliza para describir el movimiento de los objetos. De cierta manera podemos describir el vector posición como una variable de estado, pues la posición es una propiedad de un objeto que se encuentra estático, hoy o cuando artificialmente paralizamos el tiempo para ver en qué posición se encuentra el objeto.
3.2 Vector desplazamiento
Definiremos el desplazamiento s = Δr como el cambio de posición inicial ro a una posición final r, y a su vez estará determinado por las componentes dxi + dyj = Δrxi + Δryj. Es importante tener en cuenta que la elección de la letra depende del contexto y puede variar según la convención utilizada. Además, la magnitud y la dirección del vector desplazamiento se representan mediante la longitud y la orientación de la flecha.
Se utiliza para describir el cambio de posición de un objeto en un determinado intervalo de tiempo. Se define como un vector que va desde la posición inicial del objeto hasta su posición final, es decir, conectando las puntas de dos vectores de posición, y formando un triángulo de vectores.
El vector desplazamiento se representa por un vector que tiene una magnitud y una dirección. La magnitud del vector desplazamiento es la distancia entre la posición inicial y la posición final del objeto, y su dirección apunta desde la posición inicial hacia la posición final.
Por ejemplo, si un objeto se mueve desde una posición inicial de 3 metros al este y 2 metros al norte hasta una posición final de 5 metros al oeste y 6 metros al norte, el vector desplazamiento del objeto será un vector que apunta hacia el oeste y tiene una magnitud de 5 metros - 3 metros = 2 metros en la dirección horizontal, y una magnitud de 6 metros - 2 metros = 4 metros en la dirección vertical.
El vector desplazamiento es importante en la física porque permite describir el movimiento de los objetos y se utiliza para calcular la velocidad, la aceleración y otras magnitudes que describen el movimiento.
3.3 Vector velocidad promedio
Definiremos la velocidad promedio vavg como el cambio de posición con respecto al tiempo, o como el desplazamiento con respecto al tiempo, siendo el resultado una cuerda que pasa por los puntos inicial y final de posición y tiempo.
El vector velocidad promedio es un concepto utilizado en física para describir el movimiento de un objeto durante un intervalo de tiempo. Se define como el desplazamiento del objeto dividido por el tiempo que tarda en recorrer ese desplazamiento.
El vector velocidad promedio es un vector que tiene una magnitud y una dirección. La magnitud de la velocidad promedio es igual al cociente entre la distancia recorrida por el objeto (es decir, el desplazamiento) y el tiempo que tardó en recorrer esa distancia. La dirección del vector velocidad promedio es la dirección del desplazamiento del objeto.
El vector velocidad promedio es importante en la física porque permite describir el movimiento de los objetos y se utiliza para calcular la aceleración y otras magnitudes que describen el movimiento.
3.4 Velocidad instantánea
La velocidad instantánea es el límite de la velocidad promedio cuando la diferencia de tiempo tiende a cero.
A su vez estará determinado por las componentes vxi + vyj. El vector velocidad instantánea es un concepto utilizado en física para describir la velocidad de un objeto en un instante de tiempo específico. Se define como el límite al que se aproxima el vector desplazamiento dividido por el tiempo transcurrido, cuando el intervalo de tiempo considerado se hace cada vez más pequeño, tendiendo a cero.
En otras palabras, la velocidad instantánea de un objeto es la velocidad en un momento preciso en su trayectoria, y se determina calculando la magnitud y dirección del vector desplazamiento en un intervalo de tiempo muy corto, hoy y para lo cual debemos emplear las técnicas del cálculo infinitesimal como la derivada o la integral, es decir no es tan fácil como hacer una resta muy muy pequeñita porque se le va a encontrar una indefinición.
El vector velocidad instantánea es un vector que tiene una magnitud y una dirección. La magnitud del vector velocidad instantánea es la tasa de cambio instantánea de la posición del objeto, mientras que la dirección es la dirección del vector desplazamiento en ese instante específico.
Por ejemplo, si un objeto se mueve en una trayectoria curva, su velocidad instantánea en un punto específico de la trayectoria será el vector tangente a la curva en ese punto. Este vector tangente indica la dirección en la que se mueve el objeto en ese momento preciso y su magnitud es la velocidad instantánea del objeto.
El vector velocidad instantánea es importante en la física porque permite describir el movimiento de los objetos con mayor precisión que la velocidad promedio, ya que considera la velocidad del objeto en un momento específico en su trayectoria. Se utiliza para calcular la aceleración, la fuerza y otras magnitudes que describen el movimiento.
3.5 Aceleración
La aceleración será definida como el cambio de la velocidad instantánea sobre el cambio instantáneo en el tiempo, y por lo tanto tendrá componentes axi + ayj.
El vector aceleración instantánea es un concepto utilizado en física para describir cómo la velocidad de un objeto cambia en un instante específico de tiempo. Se define como el límite al que se aproxima el cambio en el vector velocidad dividido por el tiempo transcurrido, cuando el intervalo de tiempo considerado se hace cada vez más pequeño, tendiendo a cero. En otras palabras, la aceleración instantánea de un objeto es la aceleración en un momento preciso en su trayectoria, y se determina calculando la magnitud y dirección del cambio en la velocidad del objeto en un intervalo de tiempo muy corto, tan corto que debe usarse cálculo infinitesimal.
El vector aceleración instantánea es un vector que tiene una magnitud y una dirección. La magnitud del vector aceleración instantánea es la tasa de cambio instantánea de la velocidad del objeto, mientras que la dirección es la dirección del cambio en la velocidad en ese instante específico.
Por ejemplo, si un objeto se mueve en una trayectoria curva, su aceleración instantánea en un punto específico de la trayectoria será el vector que apunta hacia el centro de la curva en ese punto. Este vector indica la dirección en la que cambia la velocidad del objeto en ese momento preciso y su magnitud es la aceleración instantánea del objeto.
El vector aceleración instantánea es importante en la física porque permite describir cómo la velocidad de los objetos cambia a lo largo del tiempo. Se utiliza para calcular la fuerza y otras magnitudes que describen el movimiento.
3.6 Combinaciones
Las formas específicas de las ecuaciones dependerán de si la aceleración es o no constante. Aunque, dado que ya hicimos las demostraciones para el movimiento en una dimensión, solo se trata de transliterar en los casos posibles, que pueden ser:
a- Ambos componentes con movimiento rectilíneo uniforme.
b- Ambos componentes con movimiento rectilíneo uniformemente acelerado.
c- Movimiento de proyectiles, con movimiento rectilíneo uniforme en x y movimiento uniformemente acelerado en y con aceleración igual a la aceleración gravitacional.
Física de Serway
Lo anterior implica que los ángulos entre dos vectores relacionados por un escalar varían, y por ende, no siempre podremos aplicar el producto vector escalar para solucionar un ejercicio, pero vale preguntarse entonces, ¿en que condiciones si? la respuesta a esto es que el ángulo se mantendrá constante únicamente en caso de que ambos movimientos sean rectilíneos o ambos acelerados, y deben cumplir adicionalmente que sus parámetros iniciales sean cero.
4. Tiro parabólico o movimiento de proyectiles
|| REGRESAR AL INDICE ||
El movimiento parabólico o de proyectiles es un tipo de movimiento en dos dimensiones en el que un objeto es lanzado o proyectado en el aire y sigue una trayectoria curva conocida como una parábola. Este movimiento se produce cuando un objeto se mueve en el aire bajo la influencia de la gravedad y la resistencia del aire, aunque esta última es normalmente ignorada en los capítulos introductorios.
4.1 Componentes del movimiento
El movimiento parabólico se puede describir utilizando dos componentes vectoriales: una horizontal y otra vertical.
👉 La componente horizontal de la velocidad del objeto es constante y no se ve afectada por la gravedad.
👉 La componente vertical de la velocidad, por otro lado, cambia debido a la influencia de la gravedad y se puede describir utilizando las leyes del movimiento de Newton.
En el movimiento parabólico, el objeto se mueve en un arco parabólico hacia arriba y hacia abajo hasta que finalmente alcanza el suelo o el objetivo deseado. La altura y la distancia alcanzada por el objeto dependen de varios factores, como la velocidad y el ángulo de lanzamiento, la masa y la forma del objeto, la gravedad y la resistencia del aire.
4.2 Importancia e historia
El movimiento parabólico es importante en la física y en la ingeniería, ya que se utiliza en el diseño de proyectiles y en la predicción de trayectorias de vuelo de objetos lanzados. También se aplica en deportes como el lanzamiento de bala y el salto largo, donde los atletas deben calcular la trayectoria parabólica de sus lanzamientos para lograr una distancia y precisión óptimas.
Aunque la información anterior hace que este movimiento aparente tener una gran complejidad en realidad es muy simple, simplemente debemos aplicar la estrategia de Galileo Galilei y es descomponer el movimiento completo en 2 componentes, para los cuales ya hemos demostrado ecuaciones en el capítulo de movimiento en una dimensión, y ya sabemos cómo descomponer y recomponer el vector completo en sus componentes en el capítulo de vectores. Dado que la aceleración es constante, la aceleración inicial es igual a la final, por lo que aplicamos las ecuaciones del movimiento uniformemente rectilíneo. Para el eje y aplicaremos las ecuaciones de caída libre.
4.3 Concepto de trayectoria
La trayectoria de un proyectil en el tiro parabólico se refiere a la forma en la que se desplaza el proyectil en el aire desde su punto de lanzamiento hasta su punto de impacto. Es la curva trazada por el proyectil en el espacio durante su vuelo.
En el tiro parabólico, la trayectoria del proyectil sigue una forma característica de una parábola debido a la influencia de la gravedad y la ausencia de fuerzas externas significativas. La trayectoria es simétrica y se compone de una subida inicial seguida de una caída hasta el punto de impacto.
Es importante destacar que la trayectoria del proyectil no se refiere directamente al vector posición final o la función de dicha posición con respecto al tiempo. Estos conceptos están relacionados con la posición específica del proyectil en un momento dado o cómo varía dicha posición a lo largo del tiempo. La trayectoria, por otro lado, describe el camino general que sigue el proyectil desde el inicio hasta el final de su vuelo.
Figura 4.1. Representación clásica de un movimiento de proyectiles el cual dependerá del ángulo de disparo con respecto al eje horizontal. Como ya mencionamos anteriormente fue Niccolo Fontana Tartaglia quien identificó correctamente que el ángulo ideal para que el alcance sea máximo es 45°.
La trayectoria de un proyectil en el tiro parabólico se puede representar mediante una gráfica que muestra todas las posiciones que el proyectil ocupa en el espacio durante un intervalo de tiempo desde to (momento inicial) hasta t (momento final). En esta gráfica, el eje x representa la posición horizontal del proyectil y el eje y representa la posición vertical.
La trayectoria en el tiro parabólico forma una curva suave y simétrica que se asemeja a una parábola. La forma de la curva depende de varios factores, como la velocidad inicial del proyectil, el ángulo de lanzamiento y la fuerza gravitacional. La gráfica de la trayectoria es útil para visualizar y analizar el movimiento del proyectil en el plano xy. Permite determinar la altura máxima alcanzada por el proyectil, el alcance horizontal, el tiempo de vuelo y otros parámetros relacionados con su movimiento.
En resumen, la trayectoria en el tiro parabólico se representa mediante una gráfica que muestra todas las posiciones del proyectil en el plano xy durante un intervalo de tiempo. Esta gráfica nos permite visualizar y analizar el movimiento del proyectil en el espacio.
4.4 La parábola y la solución cuadrática
La parábola y la solución cuadrática son conceptos fundamentales en el estudio de las matemáticas y tienen una estrecha relación entre sí. La parábola, una curva simétrica que se encuentra en muchas áreas de la ciencia y la naturaleza, tiene propiedades únicas que la hacen fascinante y versátil. Por otro lado, la solución cuadrática es una poderosa herramienta algebraica utilizada para resolver ecuaciones de segundo grado, las cuales están estrechamente vinculadas con las propiedades de la parábola.
En el tiro parabólico la parábola es simétrica en condiciones ideales donde la posición final ry es la misma que la posición inicial roy. Sin embargo, existen situaciones no ideales en las que esta simetría no se cumple y pueden surgir excepciones.
Figura 4.2. Tiro parabólico con una parábola incompleta de brazo derecho mas corto que el izquierdo debido a que la posición final en (y) es mayor que la inicial.
Una excepción común ocurre cuando hay una diferencia significativa en la altura entre el punto de lanzamiento y el punto de aterrizaje (ry es diferente de roy). En tales casos, la parábola ya no es simétrica y la trayectoria puede desviarse considerablemente de una forma parabólica ideal. Esto se debe a que o bien la parábola no se completa hasta su vértice, o a que la parábola real del proyectil no alcanza a generar dos brazos simétricos, sea porque el brazo derecho al vértice queda incompleto (ry es mayor que roy) o porque el brazo derecho se extiende mas largo que el izquierdo cuando ry es menor de roy.
Figura 4.3. Tiro parabólico con una parábola extendida de brazo derecho debido a que la posición final en (y) es menor que la inicial.
Además, otros factores como la resistencia del aire, la presencia de vientos o la irregularidad del terreno pueden afectar la trayectoria del objeto y provocar desviaciones de la forma parabólica esperada.
Las ecuaciones que se presentan en muchos textos generalmente proporcionan soluciones para situaciones ideales, donde no se consideran estos factores adicionales, siendo la mas relevante, asumir que ry es igual de roy. Estas ecuaciones simplificadas son útiles para comprender los conceptos básicos del tiro parabólico pero deben tomarse coin pinzas cuando se trasladan a situaciones especiales donde ry es diferente de roy.
Una de las principales consecuencias de asumir que ry es igual a roy es que nos evitamos toparnos con una respuesta con dos soluciones, que requiere de la ecuación cuadrática, y eso es lo que veremos en la siguiente sección.
4.5 Ecuaciones del tiro parabólico
Antes de continuar tenga en cuenta que el signo de la aceleración gravitacional debe ser positivo al reemplazar con respecto al marco de referencia, g = 9.80665 m/s² para el planeta Tierra, esto porque la convención negativa se estrae de la constante a la ecuación de caída libre. Teniendo esto en cuenta, normalmente en el tiro parabólico lo que en verdad nos interesa es el alcance máximo vertical o altura y el alcance máximo horizontal o rango. Antes de continuar, se supone que ya deberíamos ser capaces de demostrar uno de los descubrimientos de Tartaglia sobre el tiro parabólico, y es el hecho de que el alcance máximo del proyectil se alcanza con un ángulo de 45° sobre un plano.
En el contexto del movimiento parabólico, existe un subcaso en el cual la altura final del proyectil es diferente de su altura inicial. Esto implica que el proyectil se eleva o desciende con respecto a su punto de partida. En este escenario, hay varios parámetros que se ven afectados, como el tiempo de vuelo y el rango máximo, pero la altura máxima se mantiene constante.
Cuando la altura final difiere de la altura inicial, el tiempo de vuelo del proyectil se ve modificado. El tiempo de vuelo es el intervalo de tiempo total en el cual el proyectil está en movimiento antes de volver al suelo, pero en este caso el tiempo de vuelo es aquel en el que el proyectil alcanza la altura deseada. En este caso, si la altura final es mayor que la altura inicial, el tiempo de vuelo se reduce con respecto al tiempo de vuelo dado por la ecuación 4.4 y 4.6, a demás de ser dos posibles respuestas. Esto se debe a que como el tiro parabólico es una parábola inversa, la trayectoria toca un punto superior al inicial dos veces excepto cuando alcanza la altura máxima que corresponde al vértice de la parábola. De lo anterior se desprende que una solución completa y a falta de mas contexto involucra dos soluciones posibles a menos que sea la altura máxima.
Por el contrario, si la altura final es menor que la altura inicial, el tiempo de vuelo es mucho mayor que el dado por las ecuaciones normales, a demás de ser una respuesta única. Esto se debe a que la parábola solo es simétrica para toda solución en y que cumpla la condición de que la posición inicial sea mayor o igual a la inicial. Después de eso, la posición inicial se convierte en el marco de referencia absoluto, por lo que la parábola no puede seguir extendiendo su brazo izquierdo ya que esa trayectoria jamás existió. De lo anterior se desprende que, si la posición final es mas baja que la inicial, tendremos una respuesta única en el tiempo.
Técnicamente, la ecuación clave a obtener es la que corresponde al tiempo de vuelo para altura deseada, una vez demostrado podemos emplear la mayoría de las ecuaciones demostradas para el movimiento parabólico ideal como rango máximo.
Lección matematizada.
Ejemplo. Un cañón que forma un ángulo de 45° con la horizontal lanza un proyectil a 20.0 m/s, a 20.0 m de este se encuentra un muro de 21.0 m de altura, asuma de la aceleración gravitacional es 10 m/s2. Determinar: a. a que altura del muro hace impacto el proyectil b. que altura máxima lograra el proyectil c. que alcance tendrá d. cuanto tiempo transcurrirá entre el disparo y el impacto en el muro.
Hipertexto
Física de Serway
4.6 Tiro al blanco móvil
Nuevamente, la cosa parece ser relativamente fácil, hasta que pasa a ser relativamente compleja cuando adicionas una partícula extra la cual posee su propio tipo de movimiento. En este caso tenemos una partícula j con movimiento parabólico que debe impactar con partícula que cae, en pleno vuelo.
Propios
4.7 Plano inclinado
El escenario de tiro parabólico sobre un plano inclinado que asciende y desciende es un caso interesante que presenta ciertas características únicas y desafíos matemáticos adicionales. En este escenario, el proyectil es lanzado desde una posición elevada en un ángulo determinado con respecto a la horizontal, y su trayectoria se ve afectada por la inclinación del plano.
Una de las características distintivas de este escenario es que el plano inclinado puede influir tanto en la altura máxima alcanzada por el proyectil como en el rango total de su movimiento. A diferencia de un tiro parabólico convencional en un plano horizontal, aquí la trayectoria puede variar considerablemente debido a la pendiente.
Los retos matemáticos asociados con este escenario incluyen el cálculo de la altura máxima alcanzada por el proyectil, el tiempo de vuelo y el rango total. Además, es necesario considerar la componente de la gravedad que actúa tanto en la dirección vertical como en la dirección paralela al plano inclinado.
Este escenario de tiro parabólico sobre un plano inclinado puede tener diversas aplicaciones prácticas. Por ejemplo, en el ámbito deportivo, podría ser relevante para el estudio del lanzamiento de objetos en terrenos inclinados, como en el caso de saltos de esquí o lanzamientos en rampas. Además, en el campo de la ingeniería, comprender las trayectorias y alcances de proyectiles en superficies inclinadas puede ser fundamental para el diseño y la seguridad en la construcción de rampas, toboganes o pendientes en carreteras.
Explorar este escenario de tiro parabólico sobre un plano inclinado nos permitirá profundizar en los conceptos de la física y las matemáticas, y comprender mejor las complejidades de los movimientos proyectiles en condiciones no ideales. A lo largo de este video, desglosaremos los cálculos necesarios y exploraremos las aplicaciones prácticas de este fascinante escenario. ¡Acompáñanos en esta emocionante aventura de aprendizaje!
La clave para resolver este escenario radica en entender que las ecuaciones calcularán dos tipos de posiciones finales en y, una para el movimiento puro y otra para la altura de contacto con el plano inclinado.
El ángulo final para el vector de posición final es el mismo ángulo de la pendiente ϕ.
Propios
Física de Serway
5. Movimiento circular uniforme
|| REGRESAR AL INDICE ||
En física, el movimiento circular es el movimiento de un objeto a lo largo de la circunferencia de un círculo o la rotación a lo largo de una trayectoria circular. Puede ser uniforme, con velocidad angular de rotación y velocidad constantes, o no uniforme con una velocidad de rotación variable. La rotación alrededor de un eje fijo de un cuerpo tridimensional implica el movimiento circular de sus partes. Las ecuaciones de movimiento describen el movimiento del centro de masa de un cuerpo. En el movimiento circular, la distancia entre el cuerpo y un punto fijo en la superficie permanece igual.
Los ejemplos de movimiento circular incluyen: un satélite artificial que orbita la Tierra a una altura constante, las aspas de un ventilador de techo que giran alrededor de un eje, una piedra que está atada a una cuerda y se balancea en círculos, un automóvil que toma una curva en una carrera pista, un electrón que se mueve perpendicularmente a un campo magnético uniforme y un engranaje que gira dentro de un mecanismo.
Dado que el vector de velocidad del objeto cambia constantemente de dirección, el objeto en movimiento experimenta una aceleración por una fuerza centrípeta en la dirección del centro de rotación. Sin esta aceleración, el objeto se movería en línea recta, de acuerdo con las leyes de movimiento de Newton.
5.1 Parámetros angulares y parámetros de la partícula
A parte de la posición, velocidad y aceleración que sufra la partícula en movimiento circular, existen otros parámetros que conciernen al propio ángulo teta, los cuales son
Cuantas veces completa un círculo completo, parámetro que llamaremos el periodo T.
Que tanto cambia un ángulo en unidades de medida angular con respecto al tiempo, parámetro que denominaremos, velocidad angular.
5.2 Velocidad angular
En física, la velocidad angular o velocidad de rotación (ω, omega minúscula), también conocida como vector de frecuencia angular, es una representación pseudovectorial de qué tan rápido cambia la posición angular δθ o la orientación de un objeto con el tiempo δt (es decir, qué tan rápido un objeto gira con respecto a un punto o eje).
La magnitud ω indica la velocidad a la que el objeto gira, y su dirección es normal al plano instantáneo de rotación o desplazamiento angular. La unidad SI de velocidad angular es radianes por segundo, siendo el radián una cantidad adimensional, por lo tanto, las unidades SI de velocidad angular pueden enumerarse como s−1 o herzios. La velocidad angular generalmente se representa con el símbolo omega (ω, a veces Ω). Por convención, la velocidad angular positiva indica una rotación en el sentido contrario a las agujas del reloj, mientras que la negativa es en el sentido de las agujas del reloj. Dado que los ángulos pueden medirse en grados o en radianes, resulta conveniente conocer cómo se realiza la conversión.
Por ejemplo, un satélite geoestacionario completa una órbita por día sobre el ecuador, o 360 grados cada 24 horas, y tiene una velocidad angular ω = (360°)/(24 h) = 15°/h, o (2π rad)/( 24 h) ≈ 0.26 rad/h.
Figura 5.1. Tabla de homologación de los ángulos más comunes a radianes.
Ejemplos
Ejemplo 4.1. Convertir 270° a radianes.
Ejemplo 4.1. Convertir 150 radianes a grados.
5.3 Velocidad angular y velocidad tangencial
Si imaginamos que una partícula gira alrededor de un eje, es evidente que la velocidad con la que la partícula se desplaza que llamaremos como la velocidad tangencial, es una función de la velocidad angular y del vector de posición r, cuya magnitud equivale al radio del propio circulo. Dado que r está medido en unidades de distancia y la velocidad angular en inverso del tiempo, su producto arroja las unidades correspondientes, por lo que o la constante de proporcionalidad es adimensional o es inexistente.
DEMOSTRACIÓN. Expresar la velocidad tangencial en términos de la velocidad angular.
Velocidad tangencial vtan como una función de la velocidad angular ω y el radio r o valor de un vector posición.
5.4 Una aceleración permanente
A pesar de que podríamos argumentar que, dado que estamos ante un movimiento uniforme, la aceleración es inexistente, esto solo es cierto para la aceleración angular, sin embargo, si analizamos los vectores de posición, es evidente la existencia de una aceleración para los ejes x y y que cambia infinitesimalmente siempre en dirección del eje de rotación. A esta aceleración la denominaremos la aceleración centrípeta. Ahora, dado que la aceleración centrípeta siempre apunta hacia el centro en un instante dado, esta tiene propiedades, como estar alineada al vector posición, pero con un origen siempre cambiante e igual al punto en que finaliza el vector posición.
Figura 5.2. Representación del vector aceleración centrípeta.
Si pensamos en la rotación de un planeta, por ejemplo, si la aceleración centrípeta es mas grande, el radio o valor del vector posición será más pequeño, por lo que, la aceleración centrípera es inversamente proporcional al vector posición.
DEMOSTRACIÓN. Expresar la magnitud de la aceleración centrípeta en términos de la velocidad tangencial.
5.5 El período
Con la figura Fig 5.1 podemos definir al periodo como el tiempo necesario para completar 360° o 2 pi radianes.
DEMOSTRACIÓN. Expresar el periodo en términos de la velocidad tangencial.
Física de Serway
Ejemplo 4.6A. ¿Cuál es la aceleración centrípeta de la Tierra cuando se mueve en su órbita alrededor del Sol?
Ejemplo 4.6B. ¿Cuál es la velocidad angular de la Tierra en su órbita alrededor del Sol?
6. Aceleración tangencial y radial
|| REGRESAR AL INDICE ||
Consideremos ahora un escenario donde la aceleración no es constante, pero eso no significa un cambio arbitrario, sino más bien que la aceleración es una función de otras magnitudes. Por ejemplo, si un vehículo se mueve por pendientes suaves con una aceleración neta a esta tendrá dos componentes, una aceleración tangencial a la curva atan y una aceleración radial arad que es perpendicular a la tangente en un punto dado instantáneo, por lo que las dos aceleraciones siempre forman un ángulo de 90°.
6.1 Aceleración tangencial
El vector velocidad es paralelo a la aceleración tangencial, y sea que estén en el mismo sentido aumentando su valor, u oponiéndose a este, causando una reducción en la velocidad. Por ende, sin importar el eje de movimiento, las magnitudes de la aceleración tangencial y la velocidad estarán dadas por.
6.2 Aceleración radial
La aceleración radial se deriva de la aceleración centrípeta, sin embargo, uno se pregunta, ¿centrípeta en cual circulo? Recuerde que iniciamos esta discusión asumiendo a priori que el móvil se mueve por pendientes suave, y cada pendiente se puede asumir como el fragmento de un círculo completo, por ende, podemos asumir que, en un punto cualquiera del movimiento, la aceleración radial estará dada por los parámetros de un círculo diferente como se muestra en la siguiente figura.
Figura 6.1. Modelo de una partícula que se mueve entre 3 puntos A, B y C. Siendo el punto a la representación de la parte más baja de un valle, B la representación hoy de casi la cima de una colina de pendiente suave, y C una región de descenso de dicha colina.
En consecuencia, podemos emplear el modelo de la aceleración centrípeta, que es la que siempre apunta hacia el centro del círculo, como equivalente de la aceleración radial.
El signo negativo indica que la dirección de la aceleración centrípeta es hacia el centro del círculo que representa el radio de curvatura. La dirección es opuesta a la del vector unitario radial rc, que siempre se aleja del origen en el centro del círculo. Sin embargo, el dilema del signo es irrelevante ya que, como ambas aceleraciones son perpendiculares entre sí, se sigue que sus valores forman una hipotenusa igual al valor de la aceleración total, por lo que los cuadrados en el teorema de Pitágoras anulan los signos negativos.
6.3 Dirección del movimiento
Donde los signos si juegan un papel fundamental es en la dirección de movimiento. Para entender la dirección en que se desplaza el móvil, deberemos distinguir entre tres ángulos,
👉 el ángulo teta θ que es absoluto, y es formado por el marco de referencia donde se mueve la partícula. Cada una de las aceleraciones tendrá su propio ángulo θ instantáneo,
👉 el ángulo psi ϕ que es el ángulo opuesto a la aceleración radial, siendo el ángulo relativo formado por las dos aceleraciones,
👉 y el ángulo teta mayúscula que es el ángulo de la dirección del vector aceleración total.
DEMOSTRACIÓN. Encuentre una relación entre los ángulos teta y psi con la aceleración radial y tangencial, de forma tal que podamos indicar la dirección de movimiento. Asumiremos que conocemos el ángulo teta de la aceleración o velocidad tangencial con respecto al origen.
Ejemplo 4.67. Un automóvil sale de una señal de alto y exhibe una aceleración constante de 0.300 m/s2 paralela a la calzada. El automóvil pasa sobre una elevación en la calzada tal que la parte superior de la elevación tiene la forma de un arco de círculo de 500 m de radio. En el momento en que el automóvil está en la cima de la elevación, su vector de velocidad es horizontal y tiene una magnitud de 6.00 m/s. ¿Cuáles son la magnitud y la dirección del vector de aceleración total del automóvil en este instante?
7. Velocidad relativa y aceleración relativa
|| REGRESAR AL INDICE ||
Hasta ahora hemos descrito los parámetros básicos del movimiento como si nosotros, el observador estuviéramos siempre abstraídos en un punto de referencia fijo, en tales casos decimos que podemos describir posiciones, velocidades y aceleraciones absolutas.
Sin embargo, en la realidad existen situaciones donde no es posible plantear un marco de referencia absoluto. Una de las situaciones más sencillas es evaluar cómo se relacionan dichos parámetros para dos partículas en movimiento, y dicha relación es la que se describe con la palabra relativa.
👉 La posición relativa es la relación entre la posición de A y B.
👉 La velocidad relativa es la relación entre las velocidades de A y B.
👉 La aceleración relativa es la relación entre las aceleraciones de A y B
En este escenario seguiremos describiendo al tiempo como absoluto para las dos partículas.
7.1 Definiciones arbitrarias
Definiremos arbitrariamente A como el observador relativo y B como el móvil.
7.2 Posición relativa
La posición relativa la evaluaremos como la distancia del observador móvil al blanco móvil.
Y con base a estas ecuaciones, podemos trasladar a los parámetros de velocidad y aceleración.
7.3 Transformación galileana
En física, se usa una transformación galileana para transformar entre las coordenadas de dos marcos de referencia que difieren solo por un movimiento relativo constante dentro de las construcciones de la física newtoniana. Galileo formuló estos conceptos en su descripción del movimiento uniforme (Timon, 2020). El tema fue motivado por su descripción del movimiento de una pelota rodando por una rampa, mediante la cual midió el valor numérico de la aceleración de la gravedad cerca de la superficie de la Tierra. Aunque las transformaciones llevan el nombre de Galileo, es el tiempo y el espacio absolutos tal como los concibió Isaac Newton lo que proporciona su dominio de definición. En esencia, las transformaciones galileanas incorporan la noción intuitiva de suma y resta de velocidades como vectores.
Imaginemos una partícula p que se mueve en un marco de referencia que a su vez se mueve de un marco de referencia absoluto. Dicho marco de referencia relativo recibe el nombre de q, ya que q puede ser un objeto que mueve a p, como, por ejemplo, una cinta transportadora, o un rio; mientras que p es un objeto que se mueve dentro de q, como una persona caminando por la cinta o un barco.
La idea es que q se mueve con respecto al marco de referencia absoluto, y p con respecto a q en un movimiento aparente; sin embargo, p también tendrá un movimiento absoluto o real, que será representado por la suma de los vectores de movimiento de q y de qp “siendo qp el movimiento aparente”.
DEMOSTRACIÓN. Encuentre las ecuaciones del movimiento de un objeto p se que es movido por un objeto q, siendo que q también posee un movimiento con respecto al origen. Asuma que p y q poseen sus propias velocidades en dos dimensiones, pero constantes.
Ejemplo 4.8a. Un bote que cruza un río ancho se mueve con una velocidad de 10.0 km/h con respecto al agua. El agua en el río tiene una velocidad uniforme de 5.00 km/h hacia el este en relación con la Tierra. (A) Si el bote se dirige hacia el norte, determine la velocidad del bote en relación con un observador que se encuentra en cualquiera de las orillas.
Ejemplo 4.8b. Un bote que cruza un río ancho se mueve con una velocidad de 10.0 km/h con respecto al agua. El agua en el río tiene una velocidad uniforme de 5.00 km/h hacia el este en relación con la Tierra. Si el bote viaja con la misma velocidad de 10.0 km/h en relación con el río y debe viajar hacia el norte como se muestra en la figura 4.21b, ¿cuál debería ser su rumbo aparente?
Referencias bibliográficas
|| REGRESAR AL INDICE ||
Andrade, T. (2017). The gunpowder age: China, military innovation, and the rise of the West in world history. Princeton University Press.
Chevedden, P. E., Eigenbrod, L., Foley, V., & Soedel, W. (1995). The trebuchet. Scientific American, 273(1), 66–71.
d’Errico, F., Banks, W. E., Warren, D. L., Sgubin, G., van Niekerk, K., Henshilwood, C., … Sánchez Goñi, M. F. (2017). Identifying early modern human ecological niche expansions and associated cultural dynamics in the South African Middle Stone Age. Proceedings of the National Academy of Sciences, 114(30), 7869–7876.
Groetsch, C. W. (2004). Nascent function concepts in Nova Scientia. International Journal of Mathematical Education in Science and Technology, 35(6), 867–875.
Halliday, D., Resnick, R., & Walker, J. (2014). Fundamentals of Physics (10th ed.). John Wiley & Sons.
Henninger-Voss, M. J. (2002). How the" New Science" of Cannons Shook up the Aristotelian Cosmos. Journal of the History of Ideas, 63(3), 371–397.
McEwen, E., Miller, R. L., & Bergman, C. A. (1991). Early bow design and construction. Scientific American, 264(6), 76–83.
Menegat, A., & Saito, F. (2016). Niccolò Tartaglia e a trajetória dos projéteis. História Da Ciência e Ensino: Construindo Interfaces, 14, 56–68.
Nandi, K., Sen, D. J., & Mahanti, B. (2021). BALLISTICS: THE MODERN DAY FORENSIC WEAPON.
Newton, I. (2013). Philosophie naturalis principia Mathematica.
OpenStax. (2017). College Physics. Retrieved from https://openstax.org/details/college-physics
Pisano, R., Capecchi, D., Pisano, R., & Capecchi, D. (2016). Niccolò Tartaglia and the Renaissance Society Between Science and Technique. Tartaglia’s Science of Weights and Mechanics in the Sixteenth Century: Selections from Quesiti et Inventioni Diverse: Books VII–VIII, 3–111.
Sears, F. W., Zemansky, M. W., Young, H. D., & Freedman, R. A. (2017). University physics with modern physics. (Addison Wesley, Ed.) (14th ed.).
Serway, R. A., & Jewett, J. W. J. (2014). Physics for Scientists and Engineers with Modern Physics, Ninth Edition (9th ed.). Boston: Brooks/Cole.
Stitik, T. P. (1996). Pharmacology in Rehabilitation. American Journal of Physical Medicine & Rehabilitation. https://doi.org/10.1097/00002060-199609000-00006
Streusand, D. E. (2018). Islamic Gunpowder Empires: Ottomans, Safavids, and Mughals. Routledge.
Timon, I. (2020). Galilean Transformations. Retrieved April 6, 2023, from https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_Mechanics_and_Relativity_(Idema)/11%3A_Lorentz_Transformations/11.01%3A_Classical_Case-_Galilean_Transformations
Tipler, P. A., & Mosca, G. (2008). Physics for scientists and engineers, with modern physics (6th ed.). New York: W. H. Freeman and Company.
Valleriani, M. (2013). Metallurgy, Ballistics and Epistemic Instruments. The Nova scientia of Nicolò Tartaglia–A New Edition. Edition Open Access.





























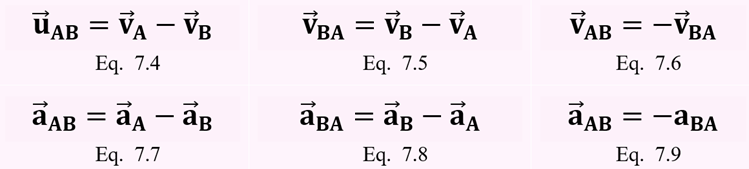

No hay comentarios:
Publicar un comentario