Química de gases
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Introducción a la química][Propiedades de la materia][Gases][El átomo químico][El átomo físico clásico][El átomo físico cuántico][Química nuclear]
Índice
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
Portada
(1) Introducción
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
Los gases representan uno de los cuatro estados fundamentales de la materia, junto con el sólido, el líquido y el plasma. Un gas puro puede estar compuesto por átomos individuales, como en el caso de un gas noble como el neón \(\textrm{Ne}\), moléculas elementales formadas por un solo tipo de átomo, como el oxígeno \(\textrm{O}_2\), o moléculas compuestas que consisten en una variedad de átomos, como el dióxido de carbono \(\textrm{CO}_2\). Por otro lado, una mezcla de gases, como el aire, contiene una diversidad de gases puros. La característica distintiva de los gases en comparación con los líquidos y sólidos es la considerable separación entre las partículas individuales de gas, lo que generalmente resulta en que un gas sea incoloro e invisible para el observador humano (Brown, LeMay, Bursten, Murphy, & Woodward, 2009; Brown et al., 2017; Chang, 2010; Matamála & Gonzalez, 1976).
(1.1) Louis Joseph Gay-Lussac
Louis Joseph Gay-Lussac, nacido en 1778 en Saint-Léonard-de-Noblat, Francia, fue un destacado químico y físico. Su legado perdura en la historia de la ciencia gracias a sus contribuciones pioneras en la investigación de las propiedades de los gases y la formulación de la Ley de Gay-Lussac, que establece la relación entre la temperatura y la presión de un gas. Su trabajo revolucionó la comprensión de la termodinámica y la química.
(1.1.1) Contexto social
Creció en Francia, en medio de un periodo de agitación política marcado por la Revolución Francesa. Creció en un país que experimentaba una transformación radical en su estructura política y social, con la caída de la monarquía y el ascenso de la República y, posteriormente, el Imperio de Napoleón Bonaparte.
En términos económicos, la Revolución y el posterior imperio estaban marcados por la guerra constante, lo que influyó en la vida cotidiana de las personas. Sin embargo, también se implementaron reformas económicas importantes, como la creación del Banco de Francia y la estabilización de la moneda.
La Revolución Francesa no solo alteró la política y la economía, sino que también transformó la sociedad. Se promovieron principios de igualdad y justicia social, desafiando las jerarquías tradicionales y las diferencias de clase. Esto moldeó la mentalidad de la época y las aspiraciones de la sociedad.
En el ámbito religioso, la Revolución Francesa provocó una drástica separación entre la Iglesia católica y el Estado. Las leyes restrictivas limitaron el poder e influencia de la Iglesia en la vida pública.
Culturalmente, el legado de la Ilustración seguía influyendo en la sociedad francesa. La promoción de la razón, la ciencia y la educación era evidente en la mentalidad de la época, lo que posiblemente influenció la inclinación de Gay-Lussac hacia la investigación científica y el conocimiento.
(1.1.2) Infancia
Desde temprana edad, mostró un interés natural por la ciencia y las matemáticas. Su padre, Anthony Gay, hijo de un médico, era abogado y fiscal, y trabajó como juez en el Puente de Noblat. Padre de dos hijos y tres hijas, era propietario de gran parte del pueblo de Lussac y comenzó a agregar el nombre de este caserío a su propio nombre, siguiendo una costumbre del Antiguo Régimen (los nobles condes, duques y príncipes adicionaban el nombre de su feudo a su propio apellido). Hacia el año 1803, padre e hijo adoptaron formalmente el nombre de Gay-Lussac. Durante la Revolución, bajo la Ley de los Sospechosos, su padre, antiguo fiscal del rey, fue encarcelado en Saint Léonard desde 1793 hasta 1794. Gay-Lussac recibió su educación temprana a cargo del Abad Católico de Bourdeix. Bajo la tutela del Abad de Dumonteil, comenzó su educación en París y finalmente ingresó a la École Polytechnique en 1798.
(1.1.3) Logros
Louis Joseph Gay-Lussac, un destacado químico y físico francés, recibió su educación temprana a manos del Abad Católico de Bourdeix. Sin embargo, su verdadera formación académica comenzó cuando ingresó en 1798 a la prestigiosa École Polytechnique en París.
La École Polytechnique, comúnmente conocida como "X" o "Polytechnique", es una de las instituciones educativas más prestigiosas de Francia y del mundo. Fundada en 1794 durante la Revolución Francesa, esta escuela desempeñó un papel fundamental en la transformación de la educación científica y técnica en Francia y tuvo un impacto significativo en la ciencia y la ingeniería a nivel global. La Polytechnique se estableció con el propósito de formar una élite de ingenieros y científicos capaces de abordar los desafíos técnicos y científicos de la nación. Ha mantenido su estatus como una institución de élite a lo largo de los años y ha sido la cuna de muchas mentes brillantes que han contribuido a la ciencia, la tecnología y la industria.
Este modelo educativo desarrollado en la Polytechnique enfatizaba las matemáticas y las ciencias aplicadas, lo que influyó en la educación técnica y científica en Francia y en otros lugares. Su énfasis en la formación científica rigurosa ha servido de inspiración para la creación de instituciones similares en todo el mundo. La École Polytechnique ha producido numerosos científicos y matemáticos de renombre cuyas investigaciones y descubrimientos han tenido un impacto duradero en la ciencia. Científicos notables como Augustin-Louis Cauchy, Sadi Carnot, y Henri Poincaré se graduaron de esta institución.
Además de su contribución a la formación científica, la Polytechnique ha desempeñado un papel esencial en el desarrollo de la ingeniería y la tecnología en Francia. Ha proporcionado a la industria y al gobierno expertos técnicos y científicos que han contribuido a avances significativos en campos como la construcción de puentes, el desarrollo de infraestructuras, la tecnología militar y la energía. A lo largo de los años, la École Polytechnique ha acogido a estudiantes y profesores de todo el mundo, lo que ha contribuido a la diversidad y la colaboración internacional en el ámbito de la ciencia y la ingeniería. Su influencia se ha extendido mucho más allá de sus fronteras, contribuyendo al progreso científico y tecnológico a nivel global. En resumen, la École Polytechnique ha sido una fuerza motriz en la educación científica y técnica, así como un importante centro de investigación y desarrollo en Francia, con un impacto significativo en el mundo de la ciencia y la ingeniería.
Allí, bajo la influencia de científicos notables como Claude-Louis Berthollet y Joseph Louis Lagrange, Gay-Lussac profundizó sus conocimientos en matemáticas y ciencias, allanando el camino para sus futuros logros científicos. Entre sus logros mas importantes podemos contar:
(a) Primera Ley de Gay-Lussac: En 1802, Gay-Lussac formuló la Primera Ley de Gay-Lussac, su famosa ley de los gases que establece la relación entre la presión y la temperatura de un gas a volumen constante. Esta ley fue pionera en la comprensión del comportamiento de los gases y sentó las bases para el estudio de la termodinámica de los gases.
(b) Segunda Ley de Gay-Lussac o Ley de Volúmenes de Combinación: fue una contribución igualmente significativa. Esta ley describe la relación cuantitativa entre los volúmenes de los reactivos y productos en una reacción química. Fue críticamente importante en la química, ya que desencadenó conexiones con la teoría atómica y la estequiometría. Esta ley estableció una base fundamental para la comprensión de la composición y la relación de masas en las reacciones químicas.
Si bien Gay-Lussac hizo contribuciones sustanciales a la química y la física, también tuvo sus desaciertos. Uno de sus errores notables fue su negación inicial de la teoría atómica de John Dalton. Aunque finalmente aceptó la teoría, inicialmente la rechazó debido a sus propias observaciones sobre la combinación de gases. Esta controversia temporal con Dalton fue superada con el tiempo.
(1.1.4) Comunidad científica
Gay-Lussac fue una figura destacada en la comunidad científica de su época. A lo largo de su carrera, colaboró con varios científicos destacados, estableció amistades notables, y se encontró en medio de algunas controversias y oposiciones. Aquí, se describen algunos de los aspectos más notables de su vida en la comunidad científica:
(a) Alexander von Humboldt: Gay-Lussac tuvo una colaboración científica notable con el explorador y naturalista alemán Alexander von Humboldt. Juntos realizaron una expedición en globo aerostático en 1804 para estudiar la atmósfera a diferentes altitudes, lo que contribuyó a importantes hallazgos sobre la composición del aire y la presencia de gases en la alta atmósfera.
(b) André-Marie Ampère: Gay-Lussac mantuvo una estrecha amistad y colaboración con el físico André-Marie Ampère. Juntos trabajaron en proyectos de electrólisis y también compartieron intereses en la electroquímica.
(c) Joseph Louis Gay-Lussac: El propio hermano de Louis Joseph, Joseph Louis Gay-Lussac, fue un médico y científico. Aunque no era tan prominente como su hermano, compartió intereses científicos y colaboró en algunas investigaciones.
(d) John Dalton: A pesar de ser contemporáneos y trabajar en campos similares, Gay-Lussac y el químico británico John Dalton tuvieron diferencias científicas. En particular, Gay-Lussac inicialmente rechazó la teoría atómica de Dalton debido a sus propias observaciones sobre la combinación de gases. Sin embargo, posteriormente, Gay-Lussac reconoció la validez de la teoría atómica de Dalton.
(e) Otto von Guericke: El físico alemán Otto von Guericke fue un crítico de algunas de las teorías de Gay-Lussac relacionadas con la expansión de los gases. Guericke sostenía que la adhesión de las partículas en un gas afectaba la expansión, una idea con la que Gay-Lussac estaba en desacuerdo.
Louis Joseph Gay-Lussac vivió en una época de agitación política en Francia debido a la Revolución Francesa y el ascenso de Napoleón Bonaparte al poder. Aunque no se destacó por tener enemigos declarados en el sentido tradicional, su vida estuvo influenciada por el contexto político de la época.
(1.1.5) Reconocimientos
Louis Joseph Gay-Lussac fue un científico cuyos notables logros le valieron numerosos reconocimientos en vida y póstumos, lo que atestigua su significativa contribución a la comunidad científica. A continuación, se detallan algunos de los principales honores que recibió:
(a) Caballero de la Legión de Honor: En 1804, a la temprana edad de 26 años, Gay-Lussac fue nombrado Caballero de la Legión de Honor por Napoleón Bonaparte en reconocimiento a sus destacados logros científicos y su participación en la histórica expedición en globo aerostático con Alexander von Humboldt.
(b) Miembro de la Académie des Sciences: En 1806, fue elegido como miembro de la Académie des Sciences, lo que marcó un importante hito en su carrera y una señal de respeto y reconocimiento dentro de la comunidad científica.
(c) Medalla Copley de la Royal Society (postuma): En 1855, la Royal Society de Londres otorgó a Louis Joseph Gay-Lussac la prestigiosa Medalla Copley de forma póstuma. Este reconocimiento es uno de los más altos honores en el ámbito científico y se concede a individuos que han realizado contribuciones sobresalientes a la ciencia.
(d) Nomenclatura química: El trabajo de Gay-Lussac en la formulación de las leyes de los gases y su relación con la estequiometría y la química le ha valido un lugar destacado en la historia de la química. Su contribución a la nomenclatura química y la comprensión de los gases es ampliamente reconocida en la comunidad científica y se enseña en todo el mundo.
(e) Monumentos conmemorativos: En su ciudad natal, Saint-Léonard-de-Noblat, se han erigido monumentos conmemorativos en honor a Louis Joseph Gay-Lussac para destacar su legado científico.
(f) Instituciones y calles con su nombre: En Francia y otros lugares, instituciones educativas, calles y avenidas llevan el nombre de Gay-Lussac como un tributo a sus contribuciones científicas.
(g) Eventos conmemorativos y celebraciones: Se han organizado eventos conmemorativos y celebraciones en honor a Gay-Lussac en ocasiones especiales, subrayando su influencia perdurable en la comunidad científica y su legado científico.
(1.1.6) ¿Por qué él es importante?
El trabajo pionero de Louis Joseph Gay-Lussac en los campos de la química y la física ha dejado una huella profunda en nuestra vida cotidiana. A pesar de que realizó sus investigaciones en el siglo XIX, sus descubrimientos siguen teniendo un impacto duradero en nuestra comprensión de la ciencia y su aplicación en el mundo moderno.
Una de las contribuciones más notables de Gay-Lussac fue la formulación de las leyes de los gases, incluida la Ley de los Volúmenes de Combinación. Estas leyes, que describen cómo los gases se comportan en diferentes condiciones de temperatura y presión, son fundamentales en la ingeniería, la meteorología y la industria química. Nos permiten diseñar sistemas de calefacción y refrigeración eficientes, entender el clima y desarrollar productos químicos y materiales esenciales.
Además de sus contribuciones a la comprensión de los gases, Gay-Lussac desempeñó un papel crucial en la nomenclatura química, influenciando la forma en que nombramos y clasificamos elementos y compuestos. Esto es esencial para la comunicación en la química y tiene un impacto directo en la producción de medicamentos, productos químicos y materiales que utilizamos en nuestra vida diaria.
Sus investigaciones sobre la estequiometría, que se centra en la relación cuantitativa entre las sustancias en una reacción química, son fundamentales en la formulación de medicamentos, la producción de alimentos y la gestión de residuos, lo que influye directamente en nuestra calidad de vida.
Además, los experimentos y observaciones de Gay-Lussac sobre los gases sentaron las bases para la termodinámica y nuestra comprensión de cómo funcionan los procesos de transferencia de calor y energía. Esto es esencial para el diseño de sistemas de calefacción y refrigeración, la generación de energía y la producción de alimentos.
Por último, el trabajo de Gay-Lussac es una parte integral de la educación científica moderna. Sus leyes de los gases y otros logros son enseñados en escuelas y universidades de todo el mundo, contribuyendo a la formación de científicos, ingenieros y profesionales en diversas disciplinas.
(1.1.7) ¿Qué debemos aprender de él?
La vida de Louis Joseph Gay-Lussac nos brinda una serie de inspiraciones y lecciones valiosas que van más allá de sus notables contribuciones científicas. Su trayectoria en un contexto de cambio político y social en Francia ofrece una perspectiva única sobre cómo abordar desafíos y aprovechar oportunidades:
Louis Joseph Gay-Lussac, nacido en una familia acaudalada en el Antiguo Régimen, enfrentó la pérdida de derechos y privilegios durante la Revolución Francesa. Sin embargo, en lugar de oponerse al cambio, utilizó su patrimonio cultural y sus conocimientos científicos para mejorar la ciencia en Francia. Su historia nos enseña la importancia de aplicar el conocimiento y la experiencia para contribuir al bienestar de la sociedad en tiempos de transformación. Gay-Lussac encarnó la idea de que la educación y la ciencia pueden ser motores para el progreso, sin importar el contexto político.
Su compromiso con el avance científico es evidente en su dedicación a la química y la física. Su determinación y curiosidad lo llevaron a realizar investigaciones revolucionarias que han tenido un impacto duradero en la ciencia. Su vida nos inspira a perseguir nuestros intereses y pasiones con fervor y a contribuir al avance del conocimiento en nuestros respectivos campos. Además, Gay-Lussac demostró resiliencia ante la adversidad. A pesar de los desafíos que enfrentó, no se rindió, sino que adaptó su enfoque y se convirtió en un científico exitoso y respetado. Su historia nos enseña la importancia de adaptarnos a las circunstancias y superar los obstáculos con determinación.
No solo se destacó en la ciencia, sino que también participó en la política y el servicio público, sirviendo como inspector de fábricas. Su compromiso cívico nos recuerda la importancia de involucrarnos en nuestra comunidad y contribuir al bienestar público. La colaboración internacional fue otro aspecto clave de su vida. La expedición en globo aerostático que realizó junto al científico alemán Alexander von Humboldt es un ejemplo de cómo trabajar en conjunto a nivel global puede llevar a avances significativos en la ciencia.
(2) Generalidades de los gases
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
La química de gases, a pesar de parecer inicialmente menos intrigante en comparación con los estados sólido y líquido, desempeña un papel fundamental en nuestra comprensión de la ciencia y la naturaleza. Los gases a menudo se perciben como entidades etéreas e intangibles, lo que podría llevar a la idea de que son el estado de la materia menos interesante. Sin embargo, esto está lejos de ser cierto.
Desde una perspectiva puramente matemática, los gases son el estado de la materia más sencillo de describir. Esto se debe a que siguen leyes y comportamientos predecibles. A medida que estudiamos los gases, se vuelven evidentes una serie de supuestos que desembocan en la teoría atómica, uno de los pilares fundamentales de la química moderna.
Por lo tanto, el estudio de la química de gases es esencial, ya que proporciona una base sólida para comprender conceptos químicos más avanzados y contribuye a la formación de la teoría atómica. Además, los gases desempeñan un papel crítico en una amplia gama de aplicaciones prácticas, desde la producción de energía hasta la fabricación de productos químicos y la gestión del medio ambiente. En última instancia, la química de gases es un campo de estudio intrigante que nos ayuda a desentrañar los misterios de la materia y sus interacciones en el mundo que nos rodea.
(2.1) ¿Qué es un gas?
La palabra gas fue utilizada por primera vez por el químico flamenco Jan Baptist van Helmont de principios del siglo XVII. Identificó el dióxido de carbono, el primer gas conocido además del aire. La palabra de Van Helmont parece haber sido simplemente una transcripción fonética de la palabra griega antigua Chaos. Una historia alternativa es que el término de Van Helmont se derivó de "gahst (o geist), que significa un fantasma o espíritu". Los editores del Oxford English Dictionary no dan crédito a esa historia. En contraste, el historiador franco-estadounidense Jacques Barzun especuló que Van Helmont había tomado prestada la palabra del alemán Gäscht, es decir, la espuma resultante de la fermentación.
En muchos sentidos, los gases son la forma más fácil de entender la materia. A pesar de que diferentes sustancias gaseosas pueden tener propiedades químicas muy diferentes, se comportan de manera similar en lo que respecta a sus propiedades físicas. Por ejemplo, el N2 y el O2 que representan aproximadamente el 99% de nuestra atmósfera tienen propiedades químicas muy diferentes: el O2 es necesario para la respiración aeróbica, pero no, por nombrar solo una diferencia, pero estos dos componentes del aire se comportan físicamente como un material gaseoso incoloro, inodoro y poco denso porque sus propiedades físicas en dicho estado son esencialmente idénticas.
De los pocos elementos que existen como gases a temperaturas y presiones ordinarias, He, Ne, Ar, Kr y Xe son monoatómicos y H2, O2, F2, Cl2 son diatómicos. Muchos compuestos moleculares son gases o existen en una dualidad gas-líquido a temperatura ambiente como el H2O, CH4, o el HCl. En general para los compuestos moleculares es más fácil existir como gas si sus moléculas no son polares “por lo que no se atraen entre sí”, por ello es más fácil tener metano que vapor de agua a temperatura ambiente. Las sustancias que son líquidas o sólidas en condiciones normales también pueden existir en estado gaseoso, donde a menudo se las denomina vapores. La sustancia H2O, por ejemplo, puede existir como agua líquida, hielo sólido o vapor de agua.
Los gases difieren significativamente de los sólidos y líquidos en varios aspectos. Por ejemplo, un gas se expande espontáneamente para llenar su contenedor. En consecuencia, el volumen de un gas es igual al volumen de su contenedor. Los gases también son altamente compresibles: cuando se aplica presión a un gas, su volumen disminuye rápidamente. Los sólidos y líquidos, por otro lado, no se expanden para llenar sus contenedores y no son fácilmente compresibles. Dos o más gases forman una mezcla homogénea independientemente de las identidades o proporciones relativas de los gases. Dos o más líquidos o dos o más sólidos pueden o no formar mezclas homogéneas, dependiendo de su naturaleza química. Por ejemplo, cuando se mezclan agua y gasolina, los dos líquidos permanecen como capas separadas. Por el contrario, el vapor de agua y los vapores de gasolina forman una mezcla de gases homogénea.
Las propiedades características de los gases que se expanden para llenar un recipiente, siendo altamente compresibles, formando mezclas homogéneas, surgen porque las moléculas están relativamente separadas. En cualquier volumen de aire dado, por ejemplo, las moléculas ocupan solo alrededor de 0.1% del volumen total y el resto es espacio vacío. Por lo tanto, cada molécula se comporta en gran medida como si las otras no estuvieran presentes: no chocarán, se atraerán o repelerán. Como resultado, diferentes gases pueden comportarse de manera similar a pesar de que están compuestos de diferentes moléculas. Esta tendencia conllevó a la formulación de una entidad teórica generalizante conocida como el gas ideal. Un gas ideal es en esencia una entidad teórico-matemática empleada para poder entender el comportamiento general de los gases, como norma todos los gases tienen un comportamiento semejante que se acerca al gas ideal, pero que difiere levemente en base a sus propias propiedades químicas reales. Dependiendo del nivel de exactitud que se requiera en un contexto dado, el gas ideal puede ser suficiente para entenderlos, pero de lo contrario se requieren entidades teórico-matemáticas más realistas.
(3) Propiedades de los gases
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
Los gases tienen tres propiedades características: (1) son fáciles de comprimir, (2) se expanden para llenar sus recipientes y (3) ocupan mucho más espacio que los líquidos o sólidos a partir de los cuales se forman.
(3.1) Compresibilidad
Un motor de combustión interna proporciona un buen ejemplo de la facilidad con la que se pueden comprimir los gases. En un motor típico de cuatro tiempos, primero se extrae el pistón del cilindro para crear un vacío parcial, que atrae una mezcla de vapor de gasolina y aire hacia el interior del cilindro (vea la figura a continuación). Luego, el pistón se empuja hacia el interior del cilindro, comprimiendo la mezcla de gasolina y aire a una fracción de su volumen original.
La relación entre el volumen del gas en el cilindro después del primer golpe y su volumen después del segundo golpe es la relación de compresión del motor. Los automóviles modernos funcionan con relaciones de compresión de alrededor de 9:1, lo que significa que la mezcla de gasolina y aire en el cilindro se comprime por un factor de nueve en el segundo golpe. Después de comprimir 9 veces el volumen inicial la mezcla de gasolina y aire gaseosos, la bujía en la parte superior del cilindro se enciende y la explosión resultante empuja el pistón fuera del cilindro en el tercer golpe. Finalmente, el pistón es empujado hacia atrás dentro del cilindro en el cuarto golpe, limpiando los gases de escape.
Los líquidos son mucho más difíciles de comprimir que los gases. Son tan difíciles de comprimir que los sistemas de frenos hidráulicos que se utilizan en la mayoría de los automóviles funcionan según el principio de que esencialmente no hay cambios en el volumen del líquido de frenos cuando se aplica presión a este líquido. La mayoría de los sólidos son aún más difíciles de comprimir. Las únicas excepciones pertenecen a una clase rara de compuestos que incluye caucho natural y sintético. La mayoría de las pelotas de goma que parecen fáciles de comprimir, como una pelota de ráquetbol, están llenas de aire, que se comprime cuando se aprieta la pelota.
(3.2) Expansibilidad
Cualquiera que haya entrado en una cocina donde se estaba horneando pan ha experimentado el hecho de que los gases se expanden para llenar sus recipientes, a medida que el aire de la cocina se llena de olores maravillosos. Desafortunadamente, sucede lo mismo cuando alguien rompe un huevo podrido y el olor característico del sulfuro de hidrógeno (H2S) se difunde rápidamente por la habitación. Debido a que los gases se expanden para llenar sus recipientes, es seguro asumir que el volumen de un gas es igual al volumen de su recipiente. De lo anterior también se concluye que los gases son capaces de ejercer y recibir fuerzas newtonianas, por lo que son susceptibles de ser modelados empleando las técnicas de la mecánica clásica.
(3.3) Volumen de un gas
La diferencia entre el volumen de un gas y el volumen del líquido o sólido del que se forma se puede ilustrar con los siguientes ejemplos. Un gramo de oxígeno líquido en su punto de ebullición (-183°C) tiene un volumen de 0.894 mL. La misma cantidad de gas O2 a 0°C y presión atmosférica tiene un volumen de 700 mL, que es casi 800 veces mayor. Se obtienen resultados similares cuando se comparan los volúmenes de sólidos y gases. Un gramo de CO2 sólido tiene un volumen de 0.641 mL. A 0°C y presión atmosférica, la misma cantidad de gas CO2 tiene un volumen de 556 mL, que es más de 850 veces mayor. Como regla general, el volumen de un líquido o sólido aumenta en un factor de aproximadamente 800 cuando se forma un gas.
Las consecuencias de este enorme cambio de volumen y la posibilidad de recibir/ejercer fuerzas newtonianas se aprovechan con frecuencia para realizar trabajos. La máquina de vapor, que provocó la revolución industrial, se basa en el hecho de que el agua hierve para formar un gas (vapor) que tiene un volumen mucho mayor. Por lo tanto, el gas se escapa del recipiente en el que se generó y el vapor que se escapa se puede hacer trabajar. El mismo principio se aplica cuando se usa dinamita para hacer estallar rocas. En 1867, el químico sueco Alfred Nobel descubrió que el explosivo líquido altamente peligroso conocido como nitroglicerina podía absorberse en arcilla o aserrín para producir un sólido que era mucho más estable y, por lo tanto, más seguro de usar. Cuando se detona la dinamita, la nitroglicerina se descompone para producir una mezcla de gases CO2, H2O, N2 y O2: nitroglicerina+oxígeno+chispa→gases a presión más calor.
Los gases salen a presión debido a que la descomposición de su fuente también libera enormes cantidades de energía, que calientan los gases, generando una expansión y por ende, la posibilidad de ejercer fuerza en sus alrededores. El mismo fenómeno ocurre en una escala mucho más pequeña cuando hacemos palomitas de maíz. Cuando los granos de palomitas de maíz se calientan en aceite, los líquidos dentro del grano se convierten en gases. La presión que se acumula dentro del núcleo es enorme y eventualmente explota.
(4) Temperatura
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
La temperatura es una cantidad física que expresa calor y frío o una medida de la energía cinética promedio de los átomos o moléculas en el sistema. Es la manifestación de la energía térmica, presente en toda la materia, que es la fuente de la aparición del calor, un flujo de energía, cuando un cuerpo está en contacto con otro más frío o caliente. La temperatura no debe confundirse con el calor.
La temperatura se mide con un termómetro. Los termómetros están calibrados en varias escalas de temperatura que históricamente han utilizado varios puntos de referencia y sustancias termométricas para su definición. Las escalas más comunes son la escala Celsius (anteriormente llamada centígrada, denotada como °C), la escala Fahrenheit (denotada como °F) y la escala Kelvin (denotada como K), la última de las cuales se usa predominantemente con fines científicos por convenciones del Sistema Internacional de Unidades (SI).
La temperatura teórica más baja es el cero absoluto, a la que no se puede extraer más energía térmica de un cuerpo. Experimentalmente, solo puede acercarse muy de cerca (100 pK, picokelvin), pero no alcanzarse, lo que se reconoce en la tercera ley de la termodinámica.
La temperatura es importante en todos los campos de las ciencias naturales, incluidas la física, la química, las ciencias de la Tierra, la astronomía, la medicina, la biología, la ecología, la ciencia de los materiales, la metalurgia, la ingeniería mecánica y la geografía, así como en la mayoría de los aspectos de la vida cotidiana.
(4.1) Efecto de la temperatura en un gas
La capacidad que tienen los gases de ejercer una fuerza en sus alrededores es un concepto tecnológico que ya estaba muy presente en la cultura griega, un ejemplo de esto es la eolipila. Un eolipila, del griego "αιολουπυλη", también conocido como motor de un Heron, es una turbina de vapor radial simple sin aspas que gira cuando se calienta el recipiente central de agua. El par es producido por chorros de vapor que salen de la turbina. El matemático e ingeniero griego-egipcio Heron de Alejandría describió el dispositivo en el siglo I d. C., y muchas fuentes le atribuyen el mérito de su invención (Boas, 1949; Sparavigna, 2011). Sin embargo, Vitruvio fue el primero en describir este aparato en su De architectura (ca. 30-20 a. C.) (Kirk, 1953).
Este es solo otro ejemplo de la expansibilidad de los gases como una función que depende de la temperatura, cosa que mas tarde sería identificada como la ley de Charles. Sin embargo, para poder definir la ley de Charles o cualquier ley de los gases debemos entender que primero debemos poseer instrumentos que permiten la medición precisa de los parámetros que controlan a las propiedades de los gases.
(4.2) Un reto de ingeniería
El calor es una medida de la energía en un cuerpo o material: cuanta más energía, más caliente está. Pero a diferencia de las propiedades físicas de masa y longitud, ha sido difícil de medir durante la mayor parte de la historia humana. La mayoría de los métodos han sido indirectos, observando el efecto que tiene el calor sobre algo y deduciendo la temperatura a partir de esto; y relativos, es decir, refiriéndose a algo como más caliente o más frío con respecto a algún punto de referencia.
Crear una escala de medición también ha sido un desafío. En 1664, Robert Hooke propuso que el punto de congelación del agua se usara como un punto cero, y las temperaturas se midieran a partir de este. Casi al mismo tiempo, Ole Roemer vio la necesidad de dos puntos fijos, permitiendo la interpolación entre ellos. Los puntos que eligió fueron el punto de congelación de Hooke y también el punto de ebullición del agua. Esto, por supuesto, deja abierta la pregunta de qué tan calientes o frías pueden llegar a ser las cosas.
Eso fue respondido por Gay-Lussac y otros científicos que trabajan en las leyes de los gases. Durante el siglo XIX, mientras investigaban el efecto de la temperatura en el gas a presión constante, observaron que el volumen aumenta en una fracción de 1/267 por grado Celsius (más tarde revisado a 1/273,15). Esto condujo al concepto de cero absoluto a menos 273.15 °C.
(4.3) Observando la Expansión
Se informa que Galileo construyó un dispositivo que mostraba cambios de temperatura en algún momento alrededor de 1592. Esto parece haber usado la contracción del aire en un recipiente para dibujar una columna de agua, la altura de la columna indica la extensión de enfriamiento. Sin embargo, esto estuvo fuertemente influenciado por la presión del aire y fue poco más que una novedad.
El termómetro tal como lo conocemos fue inventado en 1612 en lo que ahora es Italia por Santorio Santorii. Selló un líquido dilatable dentro de un tubo de vidrio, observando cómo subía por el tubo a medida que se expandía. Una escala en el tubo facilitaba ver los cambios, pero el sistema carecía de unidades precisas.
(4.4) Escalas de temperatura
Una escala de temperatura es una manera de medir y comparar la temperatura de un objeto o sustancia. La escala de temperatura absoluta, también conocida como escala termodinámica, es una escala que comienza en el cero absoluto, la temperatura más baja posible en la que las partículas de una sustancia dejan de moverse. En esta escala, la temperatura se mide en kelvins (K), y el cero absoluto corresponde a 0 K.
A lo largo de los siglos, han surgido varias escalas de temperatura para medir el calor y el frío, como la escala Celsius y la escala Fahrenheit. Cada una de estas escalas tiene sus propios puntos de referencia y unidades de medición. Sin embargo, la escala de temperatura absoluta, basada en el cero absoluto, es fundamental en la ciencia y la termodinámica, ya que proporciona una base objetiva y universal para medir la temperatura:
(4.4.1) Escala de Rømer
La primera escala de temperatura calibrada documentada fue ideada en 1701 por el astrónomo danés Ole Christensen Rømer (1644-1710), quien es más famoso por demostrar que la velocidad de la luz es finita. Inicialmente, definió la temperatura de congelación de la salmuera en 0 grados; esta sería la temperatura más baja que se puede esperar medir con la tecnología de la época, evitando así valores negativos. Su segundo punto de calibración fue el agua hirviendo; usando un sistema hexagesimal definió su temperatura como 60 grados. Sin embargo, pronto descubrió que la salmuera era difícil de estandarizar, por lo que también decidió usar agua pura para la calibración, definiendo su punto de congelación en 7.5 grados, por lo que su escala original solo tuvo que modificarse ligeramente (Matthiesen, 2022).
(4.4.2) Escala de Newton
En el mismo año (1701), Isaac Newton (1642-1727) publicó su escala que usaba “el calor del aire en invierno donde el agua comienza a congelarse” como “0 grados de calor” (“zero gradus caloris”) y un rango de otros puntos de referencia, algunos bastante ambiguos y difíciles de estandarizar (“el calor del mediodía de julio”), otros basados en el punto de fusión de materiales misceláneos como la cera, el bismuto y el plomo. Su escala es particularmente impresionante ya que cubre temperaturas de hasta 600°C. Uno de sus puntos de referencia fue el agua hirviendo a 33 grados, y la escala de Newton se interpretó más tarde como una escala lineal entre el punto de congelación y el de ebullición, utilizando aceite de linaza como líquido termómetro (Grigull, 1984).
(4.4.3) Escala Fahrenheit
La primera escala de temperatura que encontró una aplicación generalizada fue introducida en 1724 por el físico alemán Daniel Gabriel Fahrenheit (1686-1736). Después de visitar a Ole Rømer en Copenhague, quiso refinar la idea de utilizar salmuera congelada como punto de calibración. Encontró que una mezcla de partes iguales de agua, hielo y cloruro de amonio es una “mezcla frigorífica”, es decir, una mezcla que alcanza una temperatura de equilibrio independiente de la temperatura ambiente, en este caso -17.8 °C; esta temperatura reproducible la usó como punto cero para su escala (Matthiesen, 2022).
Él definió otros dos puntos de calibración: 32 grados para una mezcla 1 a 1 de hielo y agua (es decir, el punto de congelación nuevamente) y 96 grados para la temperatura más alta del cuerpo humano. Nuevamente, estos puntos de calibración fueron menos reproducibles de lo esperado, por lo que la escala Fahrenheit pronto se redefinió para usar el punto de congelación fácilmente reproducible (=32 °F) y el punto de ebullición (=212 °F) del agua pura (Matthiesen, 2022).
La escala Fahrenheit se convirtió en la principal escala de temperatura en los países de habla inglesa en el siglo XVIII hasta bien entrada la segunda mitad del siglo XX. Hoy en día, todavía se usa en la vida cotidiana (informes meteorológicos de televisión, recetas de cocina, etc.) en un puñado de países (Bahamas, Belice, las Islas Caimán, Palau y EE. UU.), pero en la ciencia ha sido reemplazado por el grado Celsius, o escala Kelvin en todo el mundo (Matthiesen, 2022).
(4.4.4) Escala Ferchault
Contemporáneo de Fahrenheit, en 1730, el científico francés René Antoine Ferchault de Réaumur (1683-1757) introdujo otra escala que sería ampliamente utilizada. Volvió a establecer el punto de congelación del agua como el punto cero de su escala de temperatura. El segundo punto de calibración volvió a ser esencialmente el punto de ebullición, aunque de forma indirecta: usó alcohol diluido para el termómetro y dividió el tubo en intervalos de modo que un grado equivalía a 1/1000 del volumen del bulbo hasta el cero (Matthiesen, 2022).
El alcohol debía diluirse de tal manera que se expandiera un 8% cuando se pasara de un baño de agua helada a agua hirviendo. Esto definió esencialmente una escala de 80 grados entre el punto de congelación y el de ebullición. Sin embargo, el alcohol era un inconveniente, requería diseños de termómetros grandes y voluminosos y podía evaporarse o hervir, por lo que los fabricantes de instrumentos preferían el mercurio (Matthiesen, 2022).
Pero entonces la gradación en el termómetro ya no sería lineal, ya que el mercurio tenía una característica de expansión diferente, lo que generaba cierta confusión y estándares diferentes. No obstante, las variaciones de la escala Réaumur se utilizaron ampliamente en Europa, particularmente en Francia, Rusia y muchos estados alemanes, en el siglo XVIII y en algunas regiones hasta el siglo XIX. Hoy en día, es principalmente de interés histórico, y sus principales aplicaciones se encuentran ahora en la fabricación de queso y confitería (Matthiesen, 2022).
(4.4.5) Escala de l'Isle
Aproximadamente al mismo tiempo, en 1732, el astrónomo francés Joseph Nicolas de l'Isle (1688-1768) desarrolló un termómetro de mercurio, usando el punto de ebullición del agua como el cero de su escala. La gradación estaba definida por la contracción del mercurio: un grado era una reducción de volumen de 1/100000 de un invierno ruso --- Zar Peter the Great invitó a Delisle a San Petersburgo en 1725 - entonces tenía alrededor de 2500 grados (Matthiesen, 2022).
(4.4.6) Escala Weitbrecht
El profesor de anatomía alemán Josias Weitbrecht (1702-1747), quien también trabajó en San Petersburgo, notó que el punto de congelación del agua estaba cerca de los 1500 grados en el termómetro de Delisle, por lo que en 1738 recalibró el termómetro utilizando el punto de congelación como punto de calibración. , definido como 150 °De; esta escala redefinida se conoció como la escala de Delisle y fue la escala de temperatura predominante en uso en Rusia durante más de un siglo. Para los físicos modernos, es contrario a la intuición que la escala de Delisle esté "al revés" y tenga valores altos para temperaturas bajas. Sin embargo, sin nuestra comprensión de la temperatura como medida de la energía termodinámica, no hay una razón clara para preferir una dirección; desde un punto de vista fenomenológico no importa si el "frío" se mide en valores altos o bajos (Matthiesen, 2022).
(4.4.7) Escala Celsius
Delisle envió su termómetro a colegas de toda Europa, entre ellos el astrónomo, físico y matemático sueco Anders Celsius (1701-1744) en Uppsala. Al igual que Weitbrecht, pero aparentemente de forma independiente, le resultó difícil calibrar los termómetros en función de la contracción fraccionaria del mercurio y, en cambio, decidió en 1742 utilizar el punto de congelación del agua como segundo punto de calibración, dividiendo la escala del termómetro en 100 "centígrados" ( del latín centum=cien y gradus=paso). Al igual que la escala Delisle (o Weitbrecht), fue "hacia atrás" con valores crecientes a medida que las temperaturas se enfrían (Matthiesen, 2022).
(4.4.8) Escala de Lineo, nuevo Celsius, Celcius moderno o Centígrada
En 1745, el botánico sueco Carl von Linné (Carolus Linnaeus/Carlos Lineo), que, como Celsius, vivía y trabajaba en Uppsala, recibió su propio termómetro, fabricado por el fabricante de instrumentos Daniel Ekstrøm en Estocolmo (un instrumento anterior, encargado en 1743 y que debía ser entregado en 1744, fue dañado durante el transporte) (Matthiesen, 2022).
Linné había decidido invertir la escala de temperatura, introduciendo la ahora familiar escala Celsius con 100 grados centígrados entre 0 °C para agua congelada y 100 °C para agua hirviendo, que se consideró más apropiada para mediciones botánicas. Se conoció como la escala sueca, Celsius novum ("nuevo Celsius") o más tarde simplemente la escala Celsius. La primera medición de temperatura documentada en grados centígrados "modernos" se registró el 16 de diciembre de 1745 en el invernadero de naranjos del Jardín Botánico de la Universidad de Uppsala. Linné fue uno de los primeros académicos en investigar sistemáticamente el efecto de la temperatura en las plantas (Matthiesen, 2022).
(4.4.9) Escala Kelvin o de cero absoluto
Todas estas escalas son escalas fenomenológicas, basadas en la expansión y contracción de un determinado material (mercurio o alcohol), pero el concepto de temperatura no estaba ligado a otros conceptos físicos fundamentales. Esto cambió en el siglo XIX con el desarrollo de la teoría termodinámica. La clave para comprender el significado físico de la temperatura provino de la investigación del comportamiento de los gases. En 1802, el científico francés Joseph Louis Gay-Lussac (1778-1850) publicó lo que ahora se conoce como la Ley de Charles, reconociendo el trabajo inédito de Jacques Alexandre César Charles (1746-1823) aunque una década antes; Guillaume Amontons (1663-1705) había publicado ideas similares en 1702 (Matthiesen, 2022).
Esta ley de los gases establece que el volumen de un gas a presión constante es proporcional a la temperatura de manera lineal, al proyectar varias líneas de gases diferentes, todas convergía en un mismo punto de intersección de alrededor de -273 °C (Matthiesen, 2022).
El físico británico William Thomson (1824-1907) “Lord Kelvin para la mayoría” desarrolló más este concepto en su artículo "On an Absolute Thermometric Scale" (Kelvin, 1848) y propuso una escala con un punto cero en el "frío infinito" como el "punto correspondiente al volumen de aire reducido a nada, lo que se marcaría como -273° de la escala''. William Thomson fue ennoblecido en 1892 por su trabajo en termodinámica y se convirtió en el primer barón Kelvin (después del río Kelvin que fluye cerca de su laboratorio en Glasgow), y su escala de temperatura, en consecuencia, se conoció como la escala Kelvin (Matthiesen, 2022).
(4.4.10) Escala Rankine
Una escala similar es la escala de Rankine (unidad °R o °Ra cuando existe la posibilidad de confusión con Réaumur). Es, como la escala Kelvin, una escala termodinámica, con un punto cero en el cero absoluto, pero su intervalo está basado en la escala Fahrenheit. El punto de congelación del agua es entonces 491.688 °Ra. Esta escala fue propuesta en 1859, una década después de Kelvin, por el ingeniero escocés William John Macquorn Rankine (1820-1872). Se usó en algunas aplicaciones de ingeniería en países de habla inglesa donde dominaba la escala Fahrenheit.
La pieza final para comprender la temperatura fue proporcionada por el físico austriaco Ludwig Eduard Boltzmann (1844-1906). Desarrolló la mecánica estadística, vinculando el comportamiento colectivo de átomos o moléculas con propiedades físicas macroscópicas como la capacidad calorífica o la viscosidad; la temperatura ahora podría entenderse como una medida de la energía cinética media de partículas vibratorias en el vacío, un punto de vista que vincula los parámetros de estado de un gas con la teoría atómica (Matthiesen, 2022).
(4.5) Interpretación moderna
La temperatura de un gas está relacionada con la energía cinética de sus partículas. Por ejemplo, si tenemos un gas a 200 K en un contenedor rígido y lo calentamos a una temperatura de 400 K, las partículas de gas tendrán el doble de energía cinética que lo que hicieron a 200 K. Esto también significa que el gas a 400 K ejerce dos veces la presión del gas a 200 K. Aunque se mide la temperatura del gas con un termómetro en Celsius, todas las comparaciones del comportamiento del gas y todos los cálculos relacionados con la temperatura en ejercicios de lápiz y papel deben usar la escala de temperatura de Kelvin. Las conversiones entre Kelvin y Celsius son las más frecuentes en nuestro contexto, por lo tanto, describiremos el algoritmo de conversión en texto.
Para convertir de grados Celsius a Kelvin, simplemente sumamos 273.15 al valor en grados Celsius, y el resultado se expresa en Kelvin.
Por otro lado, para convertir de Kelvin a grados Celsius, restamos 273.15 del valor en Kelvin, y el resultado se expresa en grados Celsius.
En general, solemos recurrir a ecuaciones para describir estas conversiones, y técnicamente, este es uno de los pocos casos en los que una solución algorítmica resulta más práctica que la ecuación general. Para convertir a Fahrenheit si requieres una fórmula más compleja. \[ T_F= (T_K - 273.15) \cdot \frac{9}{5} + 32\]Eq 4.1. Grados Fahrenheit como una función de temperatura en kelvin donde \(T_K\) se reemplaza sin unidades.
Ejemplo. Convertir los siguientes datos de temperatura a Kelvin o a centígrados: 280 K, 10 °C, 315 K, 100 °C. Química la ciencia central 13 Muestra 1.3. Un meteorólogo predice que la temperatura alcanzará los 31 °C. ¿Cuál es esta temperatura (a) en K, (b) en °F?
(5) Volumen de un gas
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
El volumen es una cantidad escalar que expresa la cantidad de espacio tridimensional encerrado por una superficie cerrada. Por ejemplo, el espacio que ocupa o contiene una sustancia (sólido, líquido, gas o plasma) o una forma tridimensional, por ejemplo formas cúbicas como las que modelan las siguientes ecuaciones.
|
\[V=x^3\] |
Eq 5.1. Volumen de un cubo. |
|
\[V=A\cdot h\] |
Eq 5.2. Volumen de un prisma rectangular |
|
\[V=x_1 \cdot x_1 \cdot x_3 \] |
Eq 5.3. Volumen de un prisma rectangular irregular |
|
\[V=\frac{4}{3} \cdot \pi \cdot r^3\] |
Eq 5.4. Volumen de una esfera de radio conocido |
|
\[V=\frac{1}{3} \cdot A \cdot h\] |
Eq 5.5. Volumen de una pirámide |
|
\[V=\frac{1}{3} \cdot \pi \cdot h \cdot r^2\] |
Eq 5.6. Volumen de un cono |
|
\[V= \pi \cdot h \cdot r^2\] |
Eq 5.7. Volumen de un cilindro. |
El volumen a menudo se cuantifica numéricamente utilizando la unidad derivada del SI, el metro cúbico. El volumen de un contenedor se entiende generalmente como la capacidad del contenedor; es decir, la cantidad de fluido (gas o líquido) que podría contener el contenedor, en lugar de la cantidad de espacio que desplaza el contenedor en sí. A las formas matemáticas tridimensionales también se les asignan volúmenes. Los volúmenes de algunas formas simples, como las formas regulares, de bordes rectos y circulares, se pueden calcular fácilmente usando fórmulas aritméticas.
Los volúmenes de formas complicadas se pueden calcular con cálculo integral si existe una fórmula para el límite de la forma. A las figuras unidimensionales (como las líneas) y las formas bidimensionales (como los cuadrados) se les asigna un volumen cero en el espacio tridimensional.
El volumen de un sólido (ya sea de forma regular o irregular) se puede determinar mediante el desplazamiento de un fluido. El desplazamiento de líquido también se puede utilizar para determinar el volumen de un gas. El volumen combinado de dos sustancias suele ser mayor que el volumen de una sola de las sustancias. Sin embargo, a veces una sustancia se disuelve en la otra y en tales casos el volumen combinado no es aditivo.
(5.1) Diseños experimentales
Hasta este punto es evidente que medir el volumen de un gas es importante para poder determinar su presión como lo hizo Torricelli, sin embargo, vale la pena evaluar otros diseños experimentales para su evaluación. La medición del volumen de gas contribuye a los estudios sobre las velocidades de reacción y la viabilidad comercial de los procesos químicos y bioquímicos en los que un gas es un subproducto. Además, también se requiere la medición de volúmenes de vapores para la determinación de pesos moleculares de líquidos volátiles mediante el método Victor-Meyer.
En comparación, la medición de volúmenes de líquidos es más simple, ya que un líquido se puede medir con un cilindro graduado, un matraz volumétrico, un balón aforado, una bureta, una pipeta o un vial graduado. Esto es posible porque los líquidos adquieren la forma del recipiente de medición y el nivel del menisco se puede observar con precisión y sin dificultad, pues, aunque muchos son volátiles, la pérdida de volumen solo se aprecia después de que ha pasado mucho tiempo, de horas a días. Los volúmenes de líquido se ven influidos de manera insignificante por los cambios de presión, pero los cambios de temperatura tienen un efecto significativo, por lo que es esencial especificar la temperatura de medición.
Las mediciones de volumen de gases, por otro lado, no son tan simples ya que la mayoría de los gases son invisibles y sus volúmenes dependen significativamente tanto de la temperatura como de la presión, el problema más grave es que los gases se escapan, por lo que es fundamental diseñar un cierre hermético que impida el escape. El volumen de gas informado sin especificar estos dos parámetros no tiene significado.
(5.2) Desplazamiento
Imagina que necesitas hacer un experimento de laboratorio donde se genera gas hidrógeno y necesitas medir su volumen, pero dado que es un gas, no lo puedes medir con un instrumento volumétrico a menos que resuelvas inconvenientes como:
(a) Sellar herméticamente el hidrógeno,
(b) pero de una manera que permita medir su expansión,
(c) y con una manera de trasladar el hidrógeno desde el reactor hasta el instrumento de medición
La técnica de desplazamiento usa agua como medio sellante, y su afore con respecto a una burbuja de gas formada en su interior a medida que transcurre la reacción como medio de medición, y una manguera de volumen despreciable que permite transferir el gas formado desde el reactor hasta la burbuja en formación.
La burbuja puede formarse dentro de un instrumento volumétrico graduado como una probeta invertida. Debe tenerse en cuenta que el gas acumulado en la probeta estará contaminado por una fracción de vapor de agua, la cual debe medirse en experimentos de estandarización. En la sección de gases húmedos veremos cómo se efectúan esos cálculos.
Sabemos que este diseño experimental estaba disponible para los filósofos naturales y alquimistas, como mínimo, para el siglo XVII debido a que una variación de él fue empleada para determinar la producción de gas por parte de las plantas como producto natural del proceso de fotosíntesis y que recibe el nombre de experimento de Senebier (Farmer, 2010).
Tratar de comprender qué obtenían las hojas del agua en la que estaban sumergidas requería más que observación: se necesitaban experimentos. Aquí iba a ser el interés de Senebier por la química y su voluntad de experimentar con productos químicos lo que proporcionó la clave de su éxito. Así queda patente en sus Mémoires Physico-chimiques (1782), más aún en sus Recherches (1783), y también en un tercer libro publicado cinco años después.
Más interesante aún, la lectura de este libro ilustra que la propia forma de Senebier de hacer experimentos ayudó a abrir una nueva forma de investigar un sistema vivo (la hoja) al someterlo a tratamientos químicos. El enfoque de Senebier equivalía a algo que uno podría denominar "fisiología química" (Farmer, 2010).
Con el tiempo, y para medir la cantidad de gas que despedían las hojas, Senebier empleó recipientes de vidrio de varios tipos. Quizás el más útil de estos vasos se parecía a un embudo invertido con un cuello cerrado y graduado (Figura 5.2 Izquierda). Para cada experimento, hojas sanas recién cortadas en la base de sus pecíolos se colocaron en el recipiente lleno de agua que luego se sumergió en un baño de agua más grande para eliminar todas las burbujas de aire. Luego, se podría colocar una base similar a un platillo sobre el embudo. Entonces, el aparato habría sido sacado del baño de agua e invertido como se muestra en la (Figura 5.2 Izquierda). Finalmente, el platillo se llenó con agua y luego se expuso el recipiente a la luz solar. A medida que pasaba el tiempo, la hoja liberaba gas y la cantidad producida podía leerse en las graduaciones del cuello del aparato. El gas obtenido era de hecho, una mezcla de oxígeno gaseoso y agua (Farmer, 2010).
El agua no es el único líquido desplazable, otros montajes emplean mercurio o instrumentos mecánicos como émbolos en pistones móviles, pero la idea es la misma, a medida que aumenta la cantidad de gas, la burbuja se expande ejerciendo una fuerza que da movimiento al objeto de medición.
(5.3) Interpretación moderna
El volumen de gas es igual al tamaño del contenedor en el que se coloca el gas. Cuando infla un neumático o una pelota de baloncesto, está agregando más partículas de gas. El aumento en el número de partículas que golpean las paredes del neumático o el baloncesto aumenta el volumen. A veces, en una mañana fría, una llanta se ve plana. El volumen del neumático ha disminuido porque una temperatura más baja disminuye la velocidad de las moléculas, lo que a su vez reduce la fuerza de sus impactos sobre las paredes del neumático. Las unidades más comunes para la medición de volumen son litros L y mililitros mL.
(5.4) Unidades de volumen
Sin embargo, las unidades de volumen tienen varios trucos, el primera el símbolo del volumen litro puede ser L cuando está solo o l cuando está acompañado de un prefijo como en mililitros ml. El otro problemilla concierna a las equivalencias con el metro cúbico, aunque 1 ml = cm3 que llamaremos igualdad de medidas largas, 1 L ≠ 1 m3, de denominaremos como la desigualdad de las medidas largas.
Ejemplo. Demuestre la relación entre litros y metros cúbicos por factor de conversión y reemplazo algebraico.
Lo que hace que un metro cúbico sea una medida masiva de volumen cuando la comparas con el humilde litro:1 ml = 1 cm3; 1 m3 = 103 L. Una vez eres consciente de la igualdad de litro y metro cúbico, puedes usarla como igualdad de conversión directa:
Ejemplo. Convertir 4.5 m3 a litros Ejemplo. Convertir 750 ml a L
(6) La presión de un gas
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
La presión \(P\) es la fuerza \(F\) aplicada perpendicularmente a la superficie \(A\) de un objeto por unidad de área sobre la cual se distribuye esa fuerza.
|
\[P=\frac{F}{A}\] |
Eq 6.1. Definición de presión en términos de una fuerza. |
El desarrollo del concepto de presión estuvo vinculado a la discusión sobre la existencia del aire como sustancia que ocupa un lugar en el espacio. Normalmente no podemos calcular la presión directamente ya que no medimos todas las fuerzas con dinamómetros, en su lugar empleamos la masa. DEMOSTRACION. Demuestre una función que permita calcular la presión en función de la masa de un objeto, la gravedad del planeta y el área.
|
\[P=a_g \cdot \frac{m}{A}\] |
Eq 6.2. Definición de presión en términos una masa y una aceleración. |
Ejercicio 10.15. Suponga que una mujer que pesa 130 lb y usa zapatos de tacón alto momentáneamente coloca todo su peso sobre el talón de un pie. Si el área del talón es de 0.50 pulg2, calcule la presión ejercida sobre la superficie subyacente en (a) kilopascales, (b) atmósferas y (c) libras por pulgada cuadrada. Ejercicio 10.16. Un conjunto de estantes para libros descansa sobre una superficie de piso duro sobre cuatro patas, cada una con una dimensión de sección transversal de 3.0 x 4.1 cm en contacto con el piso. La masa total de los estantes más los libros apilados en ellos es de 262 kg. Calcule la presión en pascales que ejercen las zapatas sobre la superficie.
(6.1) La existencia del aire
¿Cómo sabemos que el aire existe y pesa? La existencia del aire es algo evidente cuando este fluye de un lugar a otro formando el viento, pero lo que es menos evidente es que esa cosa, sea lo que fuere, tiene un peso asociado y ocupa un lugar en el espacio. Existe una sutil diferencia entre darse cuenta de que el aire es una sustancia (en oposición a un vacío), establecer que tiene peso y luego intentar medir dicho valor.
Como en muchas preguntas básicas como esta, los griegos ya habían arrojado una respuesta, fue Empédocles (c. 490-430 aC) utilizando quizás uno de los primeros aparatos experimentales de la historia, una clepsidra. Una clepsidra es un contendor de agua con dos tipos de orificio, en un extremo una serie de orificios semejantes al de las duchas modernas con forma de pera, y del otro extremo un tubo abierto a la atmósfera (Georgakellos, 2019).
Si se sumerge una clepsidra, el agua ingresará, y si esta se retira, el agua saldrá por los múltiples orificios formando muchos chorros individuales, semejantes a las cabezas de un dragón de muchas cabezas, de allí que el aparato comparta el nombre la raíz de su nombre con la Hidra de Lerna. Lo interesante es que, si se pone el dedo en el tubo opuesto a la cabeza de la clepsidra, y se retira esta del pozo, no perderá agua de manera significativa, aunque los orificios pequeños estén abiertos, pero al momento de retirar el dedo, los orificios de la cabeza comenzarán a emitir sus chorros de agua.
Sin embargo, si el extremo está cubierto con su dedo mientras se sumerge la cabeza en el pozo no entra agua por los huecos, ni sale aire tampoco, esto demostró que el aire y el agua son sustancias que pueden llenar un mismo espacio, pero no de manera simultánea, si una ingresa, la otra sale, por lo tanto, no puede entrar agua hasta que sale el aire, ergo el aire es una sustancia y no un espacio vacío.
Figura 6.3. Si se tapa el orificio superior antes de sumergirlo, este quedará saturado de aire que ocupa espacio, y por ende, no puede ser desplazado por el agua, siempre y cuando la columna de agua no genere una presión superior a la de la atmósfera (Video).
(6.2) Pesando globos inflados y la fuerza boyante
Ingenuamente se podría pensar que para demostrar que el aire pesa, un observador moderno solo tiene que tomar dos globos, uno colapsado, y otro inflado con el aire de sus pulmones, y luego pesarlos usando una balanza analítica. Pero la cosa es un poco más complicada que eso debido a la fuerza boyante. Para medir la masa debemos medir su peso, que es una fuerza resultante de la gravitación de la tierra sobre esa masa y hacer la conversión apropiada, pero eso solo funciona si la densidad del fluido que rodea al objeto a medir es despreciable con respecto al objeto medido, y si bien es evidente que los cuerpos sólidos son mucho más densos que el aire, un globo de aire tiene una densidad semejante, y por ende la fuerza boyante desviará los cálculos que se hagan de manera significativa.
En el contexto griego la cosa era más difícil ya que un simple globo es una pieza de tecnología moderna, pero ellos ya intuían la posibilidad de medir la masa del aire ¿Cómo lo hicieron ellos? Aristóteles describe otro experimento, con una vejiga inflada, en el que se basó su creencia en el peso del aire en De Caelo [Sobre los cielos] Libro IV.4:
“La tierra, entonces, y los cuerpos en los que predomina la tierra, deben tener peso en todas partes, mientras que el agua es pesada en cualquier lugar menos en la tierra, y el aire es pesado cuando no está en el agua o en la tierra. En su propio lugar, cada uno de estos cuerpos tiene peso excepto el fuego. , incluso aire. De esto tenemos evidencia en el hecho de que una vejiga cuando está inflada pesa más que cuando está vacía.”
El punto de vista de Aristóteles fue más o menos aceptado durante la Edad Media. Pero este podría haber sido un caso de creer lo correcto por las razones equivocadas, un ejemplo histórico de lo que ahora se llama el problema del conocimiento de Gettier. Galileo se mostró escéptico:
"Me inclino a creer que el aumento de peso observado en la botella de cuero o en la vejiga no se debe a la gravedad del aire, sino a los muchos vapores espesos mezclados con él en estas regiones inferiores. A esto atribuiría el aumento de peso en la botella de cuero ".
Como veremos más adelante el aire posee un contenido de agua llamado humedad, por lo que Galileo distingue la humedad que puede condensarse en un líquido del aire en si mismo que no se condensa. Esto aplica a nuestros pulmones, ya que el aire de los pulmones humanos se mezcla con agua en nuestro interior a través del moco y la sangre, por ende, el experimento con los globos tendría el mismo problema mencionado por Galileo, si lo inflamos con nuestros pulmones, lo que estaríamos introduciendo es aire húmedo desoxigenado. Adicionalmente existe otro problema con el experimento de los globos y es la boyancia o fuerza boyante.
Algunos de nosotros hemos tratado de sumergir una bola de playa en el agua y sentimos como el agua la empuja nuevamente hacia arriba. A esta fuerza se le llama Fuerza Boyante y todos los líquidos aplican esta fuerza a todo objeto que es sumergido en estos. La Fuerza Boyante existe porque la presión del fluido es más alta a mayor profundidad. El problema es que el aire también ejerce fuerza boyante sobre el globo inflado y por ende una balanza analítica es incapaz de registrar la ganancia en masa de aire real, más allá del vapor de agua que ingrese y se condense.
La solución a estos problemas escapó a los intentos de Galileo, posiblemente debido a que mucho de su tiempo estuvo enfrascado con su conflicto con la iglesia católica y las autoridades civiles sobre la posición de la Tierra y el Sol, por lo que la solución del peso del aire quedó en manos de su alumno, Evangelista Torricelli.
(6.3) El barómetro de Torricelli
En el siglo XVII, muchos científicos y filósofos creían que la atmósfera no tenía peso. Evangelista Torricelli (1608-1647), estudiante de Galileo, demostró que esto era falso. Inventó el barómetro, que está hecho de un tubo de vidrio de más de 760 mm de largo que está cerrado en un extremo, completamente lleno de mercurio e invertido en un plato de mercurio. (Se debe tener cuidado de que no entre aire en el tubo, ni entrar en contacto con el mercurio porque es altamente tóxico).
Figura 6.5. El barómetro de mercurio.
Cuando el tubo se invierte en el plato, parte del mercurio sale del tubo, pero queda una columna de mercurio en el tubo. Torricelli argumentó que la superficie de mercurio en el plato experimenta toda la fuerza de la atmósfera terrestre, que empuja el mercurio hacia arriba por el tubo hasta que la presión ejercida por la columna de mercurio hacia abajo, debido a la gravedad, es igual a la presión atmosférica en la base del tubo. Por lo tanto, la altura, h, de la columna de mercurio es una medida de la presión atmosférica y cambia a medida que cambia la presión atmosférica.
Aunque la explicación de Torricelli encontró una feroz oposición, también tuvo partidarios. Blaise Pascal, por ejemplo, hizo que llevaran uno de los barómetros de Torricelli a la cima de una montaña y comparó su lectura allí con la lectura de un barómetro duplicado en la base de la montaña. A medida que se elevaba el barómetro, la altura de la columna de mercurio disminuía, como se esperaba, porque la cantidad de atmósfera que presionaba el mercurio en el plato disminuía a medida que el instrumento se elevaba. Estos y otros experimentos finalmente prevalecieron, y se aceptó la idea de que la atmósfera tiene peso, por ende, una masa, es decir el aire es un algo que existe una entidad física medible, aunque no podamos verla.
En la siguiente demostración veremos como el concepto de presión se deriva directamente de mediciones físicas empleando conceptos Newtonianos como fuerza y aceleración: DEMOSTRACION Demuestre el funcionamiento de un Barómetro de Torricelli a partir de la ley de la conservación de la masa.
|
\[ P_{\mathrm{Hg}}= P_{\mathrm{atm}}\] |
Eq 6.3. Igualdad fundamental de un barómetro de Torricelli. Tenga en cuenta que se usa mercurio debido a que es el único líquido lo bastante masivo como para generar una presión que contrarreste a la de la atmósfera. |
|
\[P_{\mathrm{atm}}=h_i \cdot \rho_i \cdot a_g\] |
Eq 6.4. Presión atmosférica en términos de la altura y densidad de una columna de un líquido (i) y la aceleración gravitacional. |
Con las que podemos resolver problemas inversos. Química la ciencia central 13. Muestra 10.01. Torricelli usó mercurio en su barómetro porque tiene una densidad muy alta, lo que permite hacer un barómetro más compacto que uno basado en un fluido menos denso. Calcule la densidad del mercurio, utilizando la observación de que la columna de mercurio tiene 760 mm de altura cuando la presión atmosférica es 1.01 x 105 Pa. Suponga que el tubo que contiene el mercurio es un cilindro con un área de sección transversal constante. Química la ciencia central 13. Muestra 10.01.1. ¿Cuál sería la altura de la columna si la presión externa fuera de 101 kPa y se usara agua (densidad = 1.00 g/cm3) en lugar de mercurio? (a) 0.0558 m, (b) 0.760 m, (c) 1.03 x 104 m, (d) 10.3 m, (e) 0.103 m. Química la ciencia central 13. Muestra 10.01.2. El galio se funde justo por encima de la temperatura ambiente y es líquido en un rango de temperatura muy amplio (30–2204 °C), lo que significa que sería un fluido adecuado para un barómetro de alta temperatura. Dada su densidad, (6.0 g/cm3), ¿cuál sería la altura de la columna si se usa galio como fluido barómetro y la presión externa es 9.5 x 104 Pa? Química la ciencia central 13. Ejercicio 10.17b. ¿Cuál es la presión, en atmósferas, sobre el cuerpo de un buzo si él o ella está a 39 pies por debajo de la superficie del agua cuando la presión atmosférica en la superficie es de 0.97 atm? Química la ciencia central 13. Ejercicio 10.18. El compuesto 1-yodododecano es un líquido no volátil con una densidad de 1.20 g/mL. La densidad del mercurio es 13.6 g/mL. ¿Qué predice para la altura de la columna de un barómetro basado en 1-yodododecano, cuando la presión atmosférica es de 749 torr?
(6.4) El peso del aire
Aunque las ecuaciones anteriores aparentemente sólo nos permiten hallar la presión de mercurio y la presión de la atmósfera, como vimos en su proceso de demostración, estas presiones están vinculadas a las masas, lo anterior implica que la masa de la columna de mercurio debe ser necesariamente igual a la masa de la columna de aire que se encuentra enfrentándola en el punto de equilibrio, por ende, el peso del aire será igual al peso de esa columna de mercurio, pero a diferencia del aire, sí podemos pesar la columna de mercurio, siempre y cuando contemos con una medida del volumen que se encuentra al interior de la columna, empleando la definición de densidad.
(6.5) El manómetro
El barómetro permite determinar el peso por unidad de área de toda la columna atmosférica sobre la que se encuentra el plato de mercurio, pero aún nos queda el problema de pesar una muestra de gas, como el aire, sin que la boyancia del resto de la atmosfera anule su peso. Para resolver esto se emplea un instrumento semejante al barómetro, denominado el manómetro.
Un manómetro es un dispositivo para medir presiones. Un manómetro simple común consiste en un tubo de vidrio en forma de U lleno de un poco de líquido. Normalmente, el líquido es mercurio debido a su alta densidad. Si ambos extremos del tubo están abiertos entonces la altura de ambas columnas es la misma, eso se debe a que la presión atmosférica está ejerciendo un impacto igual en ambos lados. Sin embargo, si la presión del gas en el tubo cerrado aumenta este puede empujar la columna opuesta, lo cual demostraría que la presión interna es superior a la presión atmosférica.
Figura 6.6. Modelos generales de manómetros simples.
Figura 6.7. Modelos generales de un manómetro ideal.
En 1661, el físico y astrónomo holandés Christian Huygens inventó el manómetro de tubo en U, que era una modificación del barómetro de Torricelli para determinar las diferencias de presión de gas. La idea se fundamenta en el hecho de que, si conocemos la presión de la atmosfera en un punto de equilibrio con la ayuda de dos columnas de mercurio, es posible determinar la presión del gas incógnita para que el punto de equilibrio se mantenga, en esencia es como si estuviéramos modelando una balanza, pero en lugar de que se conserve la masa, lo que se conserva es la presión. Idealmente una vez que se convierte la presión a peso empleando la mecánica newtoniana, es posible obtener una medida del peso de un gas que no esté afectada por la boyancia atmosférica como si sucede con el intento ingenuo de pesar dos globos de aire. El problema es que una vez que se tuvo este instrumento, se dieron cuenta que la altura de la columna podía variar en función de la temperatura, por lo que hallar la masa del gas sin que fuera afectado por la boyancia, seguía siendo un problema. DEMOSTRACION. Como calcular la altura del brazo abierto de un manómetro con la suma de alturas y la diferencia de alturas.
|
\[\Delta h = h_{\mathrm{atm}}-h_{\mathrm{gas}}\] |
Eq 6.5. Definición de la diferencia de alturas en los dos brazos del manómetro. |
DEMOSTRACION. Demuestre el funcionamiento de un manómetro a partir del modelo matemático del barómetro de Torricelli.
|
\[ P_{\mathrm{gas}}= P_{\mathrm{atm}}-\Delta h \cdot \rho \cdot a_g \] |
Eq 6.6. Ecuación que modela el funcionamiento del barómetro de Torricelli. |
Química la ciencia central 13. Muestra 10.02. Cierto día, un barómetro de laboratorio indica que la presión atmosférica es de 764.7 torr. Se coloca una muestra de gas en un matraz unido a un manómetro de mercurio de extremo abierto y se usa una varilla de medición para medir la altura del mercurio en los dos brazos del tubo en U. La altura del mercurio en el brazo del extremo abierto es de 136.4 mm y la altura del brazo en contacto con el gas en el matraz es de 103.8 mm. ¿Cuál es la presión del gas en el matraz (a) en atmósferas, (b) en kilopascales? Química la ciencia central 13. Práctica 10.02.1. Si el gas dentro del matraz en el ejercicio anterior se enfría de modo que su presión se reduzca a un valor de 715.7 torr, ¿cuál será la altura del mercurio en el brazo abierto? (Sugerencia: la suma de las alturas en ambos brazos debe permanecer constante independientemente del cambio de presión). (a) 49.0 mm, (b) 95.6 mm, (c) 144.6 mm, (d) 120.1 mm. Química la ciencia central 13. Práctica 10.02.2. Si se aumentara la presión del gas dentro del matraz y la altura de la columna en el brazo de extremo abierto aumentara 5.0 mm, ¿cuál sería la nueva presión del gas en el matraz, en torr? Química la ciencia central 13. Ejercicio 10.17a. ¿Qué altura en metros debe tener una columna de agua para ejercer una presión igual a la de una columna de mercurio de 760 mm? La densidad del agua es de 1.0 g/mL, mientras que la del mercurio es de 13.6 g/mL. Química la ciencia central 13. Ejercicio 10.23a. Si la presión atmosférica es de 0.995 atm, ¿cuál es la presión del gas encerrado si la diferencia de niveles de mer curio (h) es de 52 cm? Química la ciencia central 13. Ejercicio 10.23b. Si la presión atmosférica es de 0.995 atm, ¿cuál es la presión del gas encerrado si la diferencia de niveles de mer curio (h) es de 67 cm? Química la ciencia central 13. Ejercicio 10.23c. Si la presión atmosférica es de 0.995 atm, ¿cuál es la presión del gas encerrado si la diferencia de niveles de mer curio (h) es de 10.3 cm? Química la ciencia central 13. Ejercicio 10.24a. Un manómetro de extremo abierto que contiene mercurio está conectado a un recipiente de gas, como se muestra en el ejercicio de muestra 10.2. ¿Cuál es la presión del gas encerrado en torr en cada una de las siguientes situaciones? El mercurio en el brazo unido al gas es 15.4 mm más alto que en el abierto a la atmósfera; la presión atmosférica es de 0.985 atm.
Química la ciencia central 13. Ejercicio 10.24b. Un manómetro de extremo abierto que contiene mercurio está conectado a un recipiente de gas, como se muestra en el ejercicio de muestra 10.2. ¿Cuál es la presión del gas encerrado en torr en cada una de las siguientes situaciones? El mercurio en el brazo unido al gas es 12.3 mm más bajo que en el abierto a la atmósfera; la presión atmosférica es de 0.99 atm.
Hallar el peso del gas es un poco más complicado, ya que, a diferencia del barómetro, la medida de un manómetro no solo está condicionada por la presión de la atmósfera y la presión del gas en el contenedor, los científicos se dieron cuenta rápidamente que los cambios en la temperatura afectaban la dilatación del gas en el interior del recipiente, por lo que hallar el peso de un gas, sin que este se encuentre afectado por la fuerza boyante es algo un poco más complejo.
(7) Calculando la presión de una atmósfera
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
(7.1) La presión de la atmósfera
La fórmula que usamos para modelar el barómetro de Torricelli nos permitiría, en el papel, calcular la densidad de la columna de aire, empleando la densidad conocida del mercurio, el problema es que esa densidad de aire sería en realidad la densidad promedio del aire en la columna sobre el barómetro, desde donde se mide hasta el final de la atmósfera.
Sin embargo, como cualquier montañista sabe, la densidad del aire y su contenido de oxígeno disminuyen rápidamente a medida que aumentamos la altitud. De hecho, en una gráfica de altitud contra presión atmosférica obtendremos que:
Figura 7.1. Altitud en función de la presión atmosférica.
La altitud se relaciona con la presión de la atmósfera por medio de una curva inversa, de forma tal que, a menor altitud, la presión de la atmósfera es mayor, y viceversa, en términos de un valor acumulativo que es superior a una línea recta, en otras palabras, la mayor parte de la atmósfera de la Tierra se encuentra cerca del nivel del mar, y esta disminuye rápidamente con solo elevarnos a una distancia relativamente baja, aunque la atmosfera como tal sea comparativamente más alta.
Figura 7.2. Aunque normalmente se nos dice que los gases se expanden homogéneamente en un contenedor, esto no es cierto para contenedores de alturas elevadas frente a una fuente de gravedad que atrae las partículas, la atmosfera por lo tanto es heterogénea en su distribución, siendo más densa en el nivel del mar.
Las personas, los cocos y las moléculas del aire experimentan una fuerza gravitacional atractiva que los empuja hacia el centro de la Tierra. Cuando un coco se suelta de un árbol, por ejemplo, esta fuerza hace que el coco se acelere hacia la Tierra, aumentando su velocidad a medida que su energía potencial se convierte en energía cinética.
Los átomos y moléculas de gas de la atmósfera también experimentan una aceleración gravitacional. Sin embargo, debido a que estas partículas tienen masas tan pequeñas, sus energías térmicas de movimiento (sus energías cinéticas) anulan las fuerzas gravitacionales parcialmente. Algunas partículas, las que acumulan más energía pueden vibrar a gran altitud sin que la aceleración gravitacional las afecte significativamente, pero aquellas moléculas que pierden calor o no se calientan caen hasta la superficie del mar.
Los datos que emergen de un barómetro nos permiten concluir que la mayoría de las moléculas de aire vibran con baja energía a nivel del mar, hasta que logran calentarse y elevarse, pero muy pocas lograran elevarse hasta llegar al límite superior de la atmósfera.
(7.2) Definición moderna
Actualmente definimos la presión de un gas como la suma promedio de los choques de las partículas del gas contra las paredes de su contenedor. Cuando golpean las paredes de un contenedor, ejercen presión. Si calentamos el contenedor, las moléculas se mueven más rápido y se estrellan contra las paredes más a menudo y con mayor fuerza, lo que aumenta la presión. Las partículas de gas en el aire, principalmente oxígeno y nitrógeno, ejercen una presión sobre nosotros llamada presión atmosférica. A medida que vas a altitudes mayores, la presión atmosférica es menor porque hay menos partículas en el aire, lo cual incluye menos oxígeno, por lo que se hace más difícil respirar.
(7.3) Unidades
Las unidades de la variable presión son problemáticas debido a su gran diversidad, las unidades más comunes utilizadas para la medición de la presión del gas son la atmósfera (atm) y milímetros de mercurio (mmHg) al ser las primeras que empleó Torricelli. En el informe meteorológico de TV, es posible que escuches o veas la presión atmosférica en pulgadas de mercurio o kilopascales (kPa) en países distintos de los Estados Unidos. En un hospital, se puede usar la unidad torricelli (torr) o libras por pulgada cuadrada (psi).
Tabla 7.1. Algunas equivalencias de unidades de presión.
| Atm | Bar | Psi | Pa | Torr | mmHg |
|---|---|---|---|---|---|
| 1 | 1.01325 | 14.6959 | 101325 | 760 | 760 |
Ejemplo. Convertir los siguientes datos de presión a atmósferas: 2.026 bar; 303 955 Pa; 1140 mmHg
Química de Chang 10. Ejemplo 5.1. La presión fuera de un avión a reacción que vuela a gran altura cae considerablemente por debajo de la presión atmosférica estándar. Por lo tanto, el aire dentro de la cabina debe estar presurizado para proteger a los pasajeros. ¿Cuál es la presión en atmósferas en la cabina si la lectura del barómetro es 688 mmHg? Química de Chang 10. Práctica 5.1. Convertir 749 mmHg a atmósferas Química de Chang 10. Ejemplo 5.2. La presión atmosférica en San Francisco en un día determinado fue de 732 mmHg. ¿Cuál fue la presión en kPa? Química de Chang 10. Práctica 5.2. Convertir 295 mmHg a kilopascales Química de Chang 10. Problema-5.13. Convierta 562 mmHg en atm Química de Chang 10. Problema-5.14. La presión atmosférica en la cima del monte McKinley es de 606 mmHg en un día determinado. ¿Cuál es la presión en atm y en kPa?
Química La ciencia Central 11. 10.1.a. Convertir 0.357 atm a torr. Química La ciencia Central 11. 10.1.b. Convertir 6.6 x 10-2 torr en atm. Química La ciencia Central 11. 10.1.c. Convertir 147.2 kPa a Torr. Química La ciencia Central 11. Práctica 10.01. En países que utilizan el sistema métrico, como Canadá, la presión atmosférica en los informes meteorológicos se da en unidades de kPa. Convierta una presión de 745 Torr en kPa. Química La ciencia Central 11. Práctica 10.01b. Una unidad inglesa de presión que a veces se usa en ingeniería es libras por pulgada cuadrada (lb/in2), o psi: 1 atm = 14.7 lb/in2. Si una presión se informa como 91.5 psi, exprese la medida en atmósfera.
Química La ciencia Central 13. Ejercicio 10.19a. La presión atmosférica típica en la cima del monte Everest (29 028 pies) es de aproximadamente 265 torr. Convierta esta presión a atm. Química La ciencia Central 13. Ejercicio 10.19bc. La presión atmosférica típica en la cima del monte Everest (29 028 pies) es de aproximadamente 265 torr. Convierta esta presión a mmHg y pascales Química La ciencia Central 13. Ejercicio 10.19d. La presión atmosférica típica en la cima del monte Everest (29 028 pies) es de aproximadamente 265 torr. Convierta esta presión a bars Química La ciencia Central 13. Ejercicio 10.19e. La presión atmosférica típica en la cima del monte Everest (29 028 pies) es de aproximadamente 265 torr. Convierta esta presión a psi Química La ciencia Central 13. Ejercicio 10.20a. Convertir 0.912 atm a torr, Química La ciencia Central 13. Ejercicio 10.20b. Convertir 0.685 bar a kilopascales Química La ciencia Central 13. Ejercicio 10.20c. Convertir 655 mm Hg a atmósferas Química La ciencia Central 13. Ejercicio 10.20d. Convertir 1.323 x 105 Pa a atmósfera Química La ciencia Central 13. Ejercicio 10.21a. En los Estados Unidos, las presiones barométricas generalmente se expresan en pulgadas de mercurio (in. Hg). En un hermoso día de verano en Chicago, la presión barométrica es de 30.45 pulgadas Hg. Convierta esta presión a torr. Química La ciencia Central 13. Ejercicio 10.21b. En los Estados Unidos, las presiones barométricas generalmente se expresan en pulgadas de mercurio (in. Hg). En un hermoso día de verano en Chicago, la presión barométrica es de 30.45 pulgadas Hg. Convierta esta presión a atm. Química La ciencia Central 13. Ejercicio 10.22a. El huracán Wilma de 2005 es el huracán más intenso registrado en la cuenca del Atlántico, con una lectura de baja presión de 882 mbar (milibares). Convierta esta lectura en atmósferas. Química La ciencia Central 13. Ejercicio 10.22b. El huracán Wilma de 2005 es el huracán más intenso registrado en la cuenca del Atlántico, con una lectura de baja presión de 882 mbar (milibares). Convierta esta lectura en torr. Química La ciencia Central 13. Ejercicio 10.22c. El huracán Wilma de 2005 es el huracán más intenso registrado en la cuenca del Atlántico, con una lectura de baja presión de 882 mbar (milibares). Convierta esta lectura en pulgadas de Hg.
(7.4) La presión sanguínea
La presión arterial se mide con un dispositivo llamado esfigmomanómetro (del griego sphygmos = “pulso”). Consiste en un manguito inflable para restringir el flujo sanguíneo, un manómetro para medir la presión y un método para determinar cuándo comienza el flujo sanguíneo y cuándo se impide. Desde su invención en 1881, ha sido un dispositivo médico esencial. Hay muchos tipos de esfigmomanómetros: manuales que requieren un estetoscopio y son utilizados por profesionales médicos; los de mercurio, usados cuando se requiere la mayor precisión; mecánicos menos precisos; y digitales que se pueden utilizar con poca formación pero que tienen limitaciones. Cuando se usa un esfigmomanómetro, el manguito se coloca alrededor de la parte superior del brazo y se infla hasta que el flujo de sangre se bloquea por completo, luego se suelta lentamente. A medida que late el corazón, la sangre forzada a través de las arterias provoca un aumento de la presión. Este aumento de presión en el que comienza el flujo sanguíneo es la presión sistólica, la presión máxima en el ciclo cardíaco. Cuando la presión del manguito es igual a la presión sistólica arterial, la sangre fluye más allá del manguito, creando sonidos audibles que se pueden escuchar con un estetoscopio. A esto le sigue una disminución de la presión a medida que los ventrículos del corazón se preparan para otro latido. A medida que la presión del manguito continúa disminuyendo, eventualmente ya no se escucha el sonido; esta es la presión diastólica, la presión más baja (fase de reposo) en el ciclo cardíaco. Las unidades de presión arterial de un esfigmomanómetro están expresadas en milímetros de mercurio (mmHg).
(7.5) La presión atmosférica a gran escala
A lo largo de los siglos, la gente ha observado las nubes, los vientos y las precipitaciones, tratando de discernir patrones y hacer predicciones: cuándo es mejor plantar y cosechar; si es seguro emprender un viaje por mar; y mucho más. Ahora enfrentamos desafíos complejos relacionados con el clima y la atmósfera que tendrán un gran impacto en nuestra civilización y el ecosistema. Varias disciplinas científicas diferentes utilizan principios químicos para ayudarnos a comprender mejor el tiempo, la atmósfera y el clima. Estos son la meteorología, la climatología y la ciencia atmosférica. La meteorología es el estudio de la atmósfera, los fenómenos atmosféricos y los efectos atmosféricos en el clima de la Tierra. Los meteorólogos buscan comprender y predecir el clima a corto plazo, lo que puede salvar vidas y beneficiar la economía. Los pronósticos meteorológicos son el resultado de miles de mediciones de presión atmosférica, temperatura y similares, que se compilan, modelan y analizan en centros meteorológicos de todo el mundo.
En cuanto al clima, los sistemas de baja presión ocurren cuando la presión atmosférica en la superficie de la tierra es más baja que la del entorno circundante: el aire húmedo se eleva y se condensa, produciendo nubes. El movimiento de la humedad y el aire dentro de varios frentes meteorológicos provoca la mayoría de los fenómenos meteorológicos.
Un frente de baja presión de humedad sobre el océano genera un efecto de esponja o jeringa sobre el agua, formando nubes a gran velocidad en un sistema cíclico que puede terminar en trombas marinas, tormentas o huracanes/tifones con un poder energético comparable únicamente al de las bombas nucleares.
(8) Masa de un gas
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
Como se mencionó, para medir la presión, la fuerza boyante desviará nuestra medición de la masa de aire, por lo que, para determinar la masa de un gas, primero es importante saber cómo se mide la fuerza boyante, y la clave para esto reside en la bomba de vacío.
Para pesar un gas con una balanza primero debes pesar una masa de calibración en aire y luego en vacío, el cual se ha generado con una bomba de vacío. La diferencia entre las mediciones de masa nos permite calcular la fuerza boyante, que es constante para una sustancia como el aire, por lo que ahora podremos usar la lectura de masa en aire, y corregirla con la medición de la fuerza boyante.
De lo anterior se deduce que la bomba de vacío fue importante para el desarrollo de la química.
(8.1) La bomba de vacío
El predecesor de la bomba de vacío fue la bomba de succión. Se encontraron bombas de succión de doble acción en la ciudad de Pompeya. El ingeniero árabe Al-Jazari describió más tarde las bombas de succión de doble acción como parte de las máquinas elevadoras de agua en el siglo XIII (Safley, 2018). La bomba de succión apareció más tarde en la Europa medieval a partir del siglo XV (Shapiro, 1964).
En el siglo XVII, los diseños de bombas de agua habían mejorado hasta el punto de que producían vacíos medibles, pero esto no se entendió de inmediato. Lo que se sabía era que las bombas de succión no podían sacar agua más allá de cierta altura: 18 yardas florentinas según una medida tomada alrededor de 1635, o unos 34 pies (10 m) (Coulston, 1960). Este límite fue motivo de preocupación en los proyectos de riego, drenaje de minas y fuentes de agua decorativas planificadas por el duque de Toscana, por lo que el duque encargó a Galileo Galilei que investigara el problema. Galileo sugiere incorrectamente en sus Dos nuevas ciencias (1638) que la columna de una bomba de agua se romperá por su propio peso cuando el agua se haya elevado a 34 pies (Coulston, 1960). Otros científicos aceptaron el desafío, incluido Gasparo Berti, quien lo replicó al construir el primer barómetro de agua en Roma en 1639 (Solari, 2019). El barómetro de Berti produjo un vacío sobre la columna de agua, pero no pudo explicarlo.
El estudiante de Galileo, Evangelista Torricelli, hizo un gran avance en 1643. Sobre la base de las notas de Galileo, construyó el primer barómetro de mercurio y escribió un argumento convincente de que el espacio en la parte superior era un vacío. La altura de la columna se limitó entonces al peso máximo que la presión atmosférica podía soportar; esta es la altura límite de una bomba de succión.
En 1650, Otto von Guericke inventó la primera bomba de vacío (Solari, 2019). Cuatro años más tarde, llevó a cabo su famoso experimento de los hemisferios de Magdeburg, demostrando que las yuntas de caballos no podían separar dos hemisferios de los que se había evacuado el aire. Robert Boyle mejoró el diseño de Guericke y realizó experimentos sobre las propiedades del vacío. Robert Hooke también ayudó a Boyle a producir una bomba de aire que ayudó a producir el vacío, por lo que ya desde la época de Boyle era posible determinar la masa de un gas sin el inconveniente de la fuerza boyante.
(8.2) Aislamiento de elementos gaseosos
Ahora que se cuenta con la tecnología para determinar la masa de un gas, el problema recaía en identificar los tipos de gases, siendo estos puros o mezclas, y medir sus masas. Probablemente los primeros gases con los que contaban los científicos eran el aire y los vapores de líquidos volátiles en el vacío, pero para poder avanzar en la historia de la química debemos pasar de propiedades físicas, a propiedades químicas, y eso implica tener a nuestra disposición sustancias puras, sean estos elementos como el oxígeno o compuestos como el dióxido de carbono.
(8.2.1) Oxígeno 1604
El oxígeno fue aislado por Michael Sendivogius antes de 1604, pero comúnmente se cree que el elemento fue descubierto de forma independiente por Carl Wilhelm Scheele, en Uppsala, en 1773 o antes, y Joseph Priestley en Wiltshire, en 1774. A menudo se da prioridad a Priestley porque su el trabajo fue publicado primero. Priestley, sin embargo, llamó al oxígeno "aire desflogistizado" y no lo reconoció como un elemento químico. El nombre oxígeno fue acuñado en 1777 por Antoine Lavoisier, quien fue el primero en reconocer el oxígeno como elemento químico y caracterizó correctamente el papel que desempeña en la combustión (Singh, 2021).
(8.2.2) Hidrógeno 1766
El hidrógeno fue descubierto por el físico inglés Henry Cavendish en 1766. Los científicos habían estado produciendo hidrógeno durante años antes de que fuera reconocido como un elemento. Los registros escritos indican que Robert Boyle produjo gas hidrógeno ya en 1671 mientras experimentaba con hierro y ácidos (West, 2014).
(8.2.3) Dióxido de carbono
Los primeros científicos pudieron observar los efectos del dióxido de carbono mucho antes de saber exactamente qué era. Alrededor de 1630, el científico flamenco Jan van Helmont descubrió que ciertos vapores diferían del aire, que entonces se pensaba que era una sola sustancia o elemento.
Joseph Black, un químico y médico escocés, identificó por primera vez el dióxido de carbono en la década de 1750. Descubrió que la piedra caliza (carbonato de calcio) podía calentarse o tratarse con ácidos para producir un gas que llamó "aire fijo". Observó que el aire fijo era más denso que el aire y no apoyaba al fuego ni a la vida animal. Black también descubrió que cuando se burbujeaba a través de agua de cal (una solución acuosa saturada de hidróxido de calcio), precipitaba carbonato de calcio. Usó este fenómeno para ilustrar que el dióxido de carbono es producido por la respiración animal y la fermentación microbiana. En 1772, el químico inglés Joseph Priestley publicó un artículo titulado Impregnating Water with Fixed Air en el que describía un proceso de goteo de ácido sulfúrico (o aceite de vitriolo, como Priestley lo conocía) sobre tiza para producir dióxido de carbono y obligar al gas a evaporarse (Priestley, 1772; Soentgen, 2010).
(8.2.4) Gases elementales conocidos en la época de Avogadro
Para la época de Avogadro ya se contaba con elementos gaseosos puros como cloro, nitrógeno, hidrógeno, oxígeno, así como una variedad de gases compuestos, con los cuales se podían hacer mediciones.
(8.3) La masa específica y el mol
Con el termómetro, el manómetro y la bomba de vacío, los químicos pronto se dieron cuenta que un determinado gas tendría una relación masa-volumen constante si se mantenía la presión y la temperatura bajo parámetros estables, a este parámetro se lo conoció como la masa específica de un gas, aunque nosotros la llamamos actualmente la densidad.
|
\[\rho_i=\frac{m_i}{V_i}\] |
Eq 8.1. Definición de densidad. |
Ejemplo. Tienes un gas con un volumen de 15 cm3 y una masa de 45 g. ¿Cuál es su densidad en g/cm3? Ejemplo. Una muestra de CO2 tiene una densidad de 2.0 g/cm3. Determine el volumen que ocuparía si su masa es de 60 g.
De todos los parámetros de volumen-presión-temperatura posibles, Stanislao Cannizzaro propuso como valores estándar 22.4 L 0°C y 1 atm de presión, lo cual permitió definir pesos estándar para los elementos y compuestos gaseosos, lo cual permitió la aparición de los conceptos de pesos atómicos y moleculares, nombres incorrectos porque las masas medidas no eran ni de átomos o moléculas, sino de cantidades visibles de sustancia, por lo que más tarde se lo definió simplemente como el peso de una mol de sustancia, siendo el mol igual a los 22.4 L a 0°C y 1 atm (Furio, Azcona, & Guisasola, 2002; Furio, Azcona, Guisasola, & Ratcliffe, 2000; Jensen, 2004).
(8.4) Cantidad de sustancia y número de entidades
Posteriormente se abandonó la conexión entre el mol y las condiciones de gas, y pasó a convertirse en la unidad del parámetro cantidad de sustancia. La cantidad de sustancia igual a 1 mol contiene siempre un numero de partículas fijo que actualmente se denomina como el número de Avogadro (Deslattes, 1980; Güttler, Rienitz, & Pramann, 2019; Perrin, 1911, 1913). De lo anterior podemos análoga el número de Avogadro como semejante al número par o al número docena, es decir, como un conjunto de partículas para contar con comodidad. Contar la cantidad de sustancia es útil ya que permite hacer cálculos sencillos sobre reacciones químicas con información teórica de proporciones, en lugar de emplear proporciones experimentales.
(8.5) Relación masa y cantidad de sustancia
El hecho de que las partículas de gas se expandan no implica que no posean una masa y pesen. Una pipeta de gas propano llena es bastante masiva, esto se debe precisamente a que el gas posee masa, y por lo tanto cuando es afectado por la aceleración gravitacional del planeta también posee un peso asociado. Las unidades de medida de la masa de un gas pueden ser específicas, en cuyo caso empleamos el mol, o inespecíficas, en cuyo caso empleamos gramos u otras unidades no específicas que ya trabajamos en la unidad de estequiometria y disoluciones.
La variable cantidad de sustancia \(n_i\) tiene como unidad el mol y sus modificaciones.
La variable masa de sustancia: \(m_i\) tiene como unidad el kilogramo y sus modificaciones.
Las masas de los gases están vinculadas a reacciones químicas, por lo que una reacción que consuma una sustancia gaseosa disminuirá la masa del gas, mientras que una reacción que produce una sustancia gaseosa aumentará la masa del gas y por consiguiente todas las variables vinculadas a la masa del gas.
|
\[M_i=\frac{m_i}{n_i}\] |
Eq 8.2. Definición fundamental de la masa molar. |
El problema con la masa molar “también llamado peso fórmula o peso de la fórmula, peso molecular o masa de la fórmula molecular” \(M_i\) es que al estar definida en moles de sustancia si es específica para el tipo de sustancia, para los átomos individuales los valores se sacan de la tabla periódica dado que el peso atómico y la masa molar tienen los mismos valores aunque diferentes unidades \(M_i\), y para moléculas hay que hacer una suma ponderada. \[M_j = M_u \cdot \sum_{J}^{} (Ar_J \cdot s_{J})\]Eq 8.3. Definición de la masa molar en términos de los pesos atómicos (masas relativas) de cada elemento J-ésimo \(Ar_J\), el subíndice de cada elemento \(si_J\) y la constante de masa molar \(M_u\) que se asume como 1 g/mol por definición.
El término de ponderación es el subíndice \(si_I\) que representa la cantidad de veces que se repite un elemento en una molécula. La unidad de la masa molar es gramos en cada mol de sustancia “g / mol” y dependerá de la cantidad de veces que se repite un átomo en la formula molecular y del peso atómico expresado en la tabla periódica.
Ejemplo. Como calcular la masa molar de Cl2, S8, P4 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de He, H2, N2 y O2 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de Cl2, S8, P4 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de H2O a cuatro cifras significativas Ejemplo. Como calcular la masa molar de CO2 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de H3PO4 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de NaOH y Ca(OH)2 a cuatro cifras significativas
Ejemplo. Como calcular la masa molar de NO2 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de C6H12O6 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de Na3PO4 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de C3H8 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de MnCl2 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de KClO3 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de (NH4)2SO4 a cuatro cifras significativas
Ejemplo. Como calcular la masa molar de CaCO3 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de NH3 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de CuSO4 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de C2H5OH a cuatro cifras significativas Ejemplo. Como calcular la masa molar de CuSO4·5H2O a cuatro cifras significativas Ejemplo. Como calcular la masa molar de NH4NO2 a cuatro cifras significativas
Ejemplo. Como calcular la masa molar de Al(OH)3 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de Li2CO3 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de K2Cr2O7 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de KMnO4 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de metanol CH3OH a cuatro cifras significativas Ejemplo. Como calcular la masa molar de HNO2 a cuatro cifras significativas
Ejemplo. Como calcular la masa molar de Na2O a cuatro cifras significativas Ejemplo. Como calcular la masa molar de Ca(NO3)2 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de Fe2O3 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de NaI y NaCl a cuatro cifras significativas Ejemplo. Como calcular la masa molar de NaClO y KOH a cuatro cifras ignificativas Ejemplo. Como calcular la masa molar de Al2(SO4)3 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de C9H10O a cuatro cifras significativas Ejemplo. Como calcular la masa molar de Na2CO3 a cuatro cifras significativas
Ejemplo. Como calcular la masa molar de Mg3N2 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de C6H8O6 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de (NH4)2HPO4 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de H2SO4 a cuatro cifras significativas Ejemplo. Como calcular la masa molar de HNO3 a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de NaNO3 a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de KNO3 a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de ZnCl2 a cuatro cifras significativas.
Ejemplo. Como calcular la masa molar de Na2HPO4 a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de HgCl2 a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de (NH4)2Fe(SO4)2 a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de NH4Cl a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de HCN a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de MgCl2*6H2O a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de AgNO3 a cuatro cifras significativas.
Ejemplo. Como calcular la masa molar de KHCO3 a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de Na2B4O7 a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de ZnSO4 a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de AlCl3 a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de Fe(SO4)3*9H2O a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de Cu(NO3)2*6H2O a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de CH3COOH a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de NiCl2 a cuatro cifras significativas.
Ejemplo. Como calcular la masa molar de KAl(SO4)2*12H2O a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de C6H6O a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de C4H10O3 a cuatro cifras significativas. Ejemplo. Como calcular la masa molar de Fe2(SO4)3 a cuatro cifras significativas.
Una vez que tienes la masa molar puedes calcular los moles o los gramos de una sustancia manipulando adecuadamente la definición de masa molar \(M = m / n\).
Ejemplo. ¿Cuantos moles hay en 90 g de H2? Ejemplo. ¿Cuantos moles hay en 4.0 g de N2?
(9) Historia de las leyes de los gases
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
A finales del siglo XVIII, los científicos comenzaron a forjar un entendimiento más profundo de los gases al descubrir que existían relaciones consistentes entre la presión, el volumen y la temperatura de las muestras gaseosas. Este descubrimiento marcó el surgimiento de las leyes de los gases, un hito fundamental en la historia de la ciencia.
Estas leyes no surgieron por casualidad, sino como resultado de una cuidadosa observación y experimentación. A pesar de que en la ciencia real es raro que los resultados de experimentos idénticos sean exactamente iguales debido a la variabilidad inherente, los científicos de la época pudieron establecer relaciones matemáticas simples al redondear los valores experimentales, teniendo en cuenta la precisión de los instrumentos disponibles en ese momento.
Estas relaciones entre presión, volumen y temperatura de los gases se convirtieron en los pilares de las leyes de los gases, que se aplican a una amplia variedad de sustancias gaseosas y proporcionan una base fundamental para comprender el comportamiento de los gases en diversas situaciones. El estudio de las leyes de los gases ha continuado evolucionando con el tiempo, contribuyendo al desarrollo de la termodinámica y teniendo un impacto significativo en la ciencia y la tecnología modernas.
El modelo matemático fundamental que subyace a la mayoría de las leyes de los gases es el de la línea recta. Este modelo se presenta en dos formas principales: la recta simple ascendente y la inversa de la recta, que forma una curva asintótica. Estas representaciones matemáticas son esenciales para comprender cómo las variables de presión, volumen y temperatura se relacionan entre sí en el comportamiento de los gases. La representación de una línea recta ascendente se encuentra en leyes como la Ley de Charles y la Ley de Gay-Lussac. En estas relaciones, a medida que una variable aumenta, la otra también lo hace de manera directamente proporcional, lo que se refleja en una línea recta con una pendiente positiva en un gráfico.
Figura 9.1. La línea recta.
Por otro lado, la inversa de la recta, que forma una curva asintótica, se encuentra en la Ley de Boyle-Mariotte. Esta ley establece que la presión y el volumen de un gas son inversamente proporcionales, lo que significa que a medida que uno aumenta, el otro disminuye y viceversa. En un gráfico, esta relación se representa como una curva que se acerca asintóticamente al eje de las coordenadas. Es interesante destacar que, de todas las leyes de los gases, solo la Ley de Boyle-Mariotte se modela con la inversa de la recta, lo que la distingue de las otras leyes. Este enfoque matemático proporciona una base sólida para comprender las propiedades fundamentales de los gases y es crucial en la descripción de su comportamiento en diversas condiciones de presión y temperatura.
Figura 9.2. La línea inversa a la recta 1/x.
(9.1) La ley de Boyle 1662
Las leyes de los gases fueron desarrolladas a lo largo del siglo XVII, XVIII y XIX cuando los científicos determinaron las relaciones entre presión, volumen, temperatura, cantidad de materia y energía de los gases, y mucho más importante, se desarrollaron por técnicas experimentales y matemáticas para formular las primeras leyes científicas expresadas como fórmulas matemáticas simples, aunque no necesariamente en su forma algebraica moderna, ya que nuestro lenguaje moderno es bastante reciente cuando lo comparamos con las propias leyes. Históricamente las leyes individuales de los gases fueron propuestas antes de la ley de los gases ideales, siendo empíricas, pero a través de esta última podemos recordar las demás a un nivel práctico cuando vamos a resolver los ejercicios de lápiz y papel. Esto se debe a que los ejercicios, y por extensión en los experimentos, lo que nos interesa es crear un modelo que nos permita identificar cuales términos son constantes, cuales son variables y cuales son datos medibles, un proceso semejante al que se hizo con la geometría analítica y el álgebra durante la edad media.
Figura 9.3. Robert Boyle. (Waterford, 25 de enero de 1627-Londres, 31 de diciembre de 1691)1 fue un filósofo natural, químico, físico e inventor. Es conocido principalmente por la formulación de la ley de Boyle. además de que es generalmente considerado hoy como el primer químico moderno y por lo tanto uno de los fundadores de la química moderna. Su obra The Sceptical Chymist (El químico escéptico) es considerada una obra fundamental en la historia de la química.
Robert Boyle, también conocido como "el padre de la química", nació el 25 de enero de 1625 en el castillo de Lismore, Munster, Irlanda, y era el decimocuarto hijo de su padre, Sir Richard Boyle. Boyle era anglicano / episcopal en religión y de niño; Boyle había aprendido a hablar los idiomas latin y francés. El primer libro publicado por Boyle (New Experiments Physico-Mechanicall, Touching the Spring of the Air and Its Effects (1660) explicó las propiedades físicas del aire. Fue en este libro que mostró una serie de experimentos usando una bomba de aire para crear un vacío. La segunda parte de este libro fue el primer documento que muestra lo que ahora conocemos como 'Ley de Boyle' (Reville, 2001) donde: “el volumen de una cantidad dada de gas mantenida a temperatura constante varía inversamente con la presión aplicada cuando la temperatura y la masa es constante”.
Esto dio una comprensión hacia la ciencia sobre la naturaleza de los gases al mostrar que, si una cierta cantidad de gas tiene un gran volumen, tendrá una presión baja, pero si el volumen de ese mismo gas es pequeño, la presión será mayor. Boyle escribió otro libro titulado El químico escéptico en 1661 donde 'atacó' la teoría de Aristóteles de que todo estaba compuesto de cuatro elementos (fuego, agua, aire y tierra), pero en cambio describe elementos como: "cierto principio simple, o cuerpos perfectos no mezclados”.
Figura 9.4. El químico escéptico: o las dudas y paradojas quimio-físicas (en inglés, The sceptical chymist: or chymico-physical doubts & paradoxes, touching the spagyrist's principles commonly call'd hypostatical; as they are wont to be propos'd and defended by the generality of alchymists) es el título de la principal obra científica de Robert Boyle, publicada en Londres en 1661, y por la que ha sido llamado «fundador de la química moderna». (Boyle, 1911)
Durante sus estudios en Oxford, Boyle pudo explicar que los gases pueden comprimirse ya que hay espacio entre cada uno de los átomos o moléculas, por lo que cada molécula del gas podría presionarse más y más. Boyle también dijo que no debe haber mucho espacio entre las moléculas en líquidos y sólidos, ya que son mucho más difíciles de comprimir. Otras partes de la ciencia a las que contribuyó Boyle fueron que mostró cómo se necesitaba aire para que se produzca la combustión, para que los animales respiren y para la transmisión del sonido.
La ley de Boyle es una expresión matemática entre la presión y el volumen que fue inicialmente notada por Richard Towneley y Henry Power, Robert Boyle la confirmó mediante experimentos y un procesamiento matemático y publicó los resultados en 1662 obteniendo la prioridad del descubrimiento (Pickover, 2008). De acuerdo con Robert Gunther, fue el asistente de Boyle llamado Robert Hooke quien construyó el diseño experimental. Esta ley tiene una enorme importancia en la historia de las ciencias, y posiblemente podría ser catalogada como la primera ley de la ciencia moderna ya que es la primera relación entre dos variables simples en ser expresada matemáticamente de manera reconocida (Schofield, 2015), además de corresponder a un modelo matemático muy usado actualmente, el modelo lineal que relaciona dos variables con una constante de proporcionalidad.
En ese momento, el aire todavía era visto como uno de los cuatro elementos, pero Boyle no estaba de acuerdo. El interés de Boyle probablemente fue entender el aire como un elemento esencial de la vida; por ejemplo, publicó trabajos sobre el crecimiento de plantas sin aire. Boyle usó un tubo cerrado en forma de J y después de verter mercurio, por un lado, obligó al aire del otro lado a contraerse bajo la presión del mercurio.
Después de repetir el experimento varias veces y usar diferentes cantidades de mercurio, descubrió que, bajo condiciones controladas, la presión de un gas es inversamente proporcional al volumen ocupado por él. El físico francés Edme Mariotte (1620–1684) descubrió la misma ley independientemente de Boyle en 1679, pero Boyle ya la había publicado en 1662. Sin embargo, Mariotte descubrió que el volumen de aire cambia con la temperatura. Por lo tanto, esta ley a veces se conoce como la ley de Mariotte, especialmente en Francia, o la ley de Boyle-Mariotte. Más tarde, en 1687 en Philosophiæ Naturalis Principia Mathematica, Newton demostró matemáticamente que en un fluido elástico que consiste en partículas en reposo, entre las cuales hay fuerzas repulsivas inversamente proporcionales a su distancia, la densidad sería directamente proporcional a la presión, pero este tratado matemático no es la explicación física de la relación observada. En lugar de una teoría estática, se necesita una teoría cinética, que fue proporcionada dos siglos después por Maxwell y Boltzmann, y ambas a su vez descansando en la teoría atómica, la idea de que los gases no son realmente fluidos continuos, sino conjuntos de partículas discretas y contables individualmente.
(9.2) Hacia las leyes térmicas
Guillaume Amontons (1663–1705) investigó hacia 1702 la relación entre presión y temperatura en los gases, aunque carecía de termómetros precisos. Aunque sus resultados fueron, en el mejor de los casos, semicuantitativos, estableció que la presión de un gas aumenta aproximadamente un tercio entre las temperaturas de frío y el punto de ebullición del agua. Este fue un paso sustancial hacia las leyes de gas posteriores y, en particular, la ley de Gay-Lussac. Su trabajo lo llevó a especular que una reducción suficiente de la temperatura conduciría a la desaparición de la presión. Aunque estuvo cerca de encontrar el cero absoluto: la temperatura teórica por la cual el volumen de aire en su termómetro de aire se reducirá a cero (estimado por él como en la escala Celsius), el descubrimiento no estaría completo hasta al menos un siglo después.
Daniel Gabriel Fahrenheit (1686–1736) diseñó un termómetro de mercurio en vidrio en 1714 y desarrolló una escala de temperatura que ahora lleva su nombre. Los tres puntos de calibración utilizados son una mezcla congelante de hielo / sal (0 ° F), una mezcla de agua / hielo (32 ° F) y la temperatura del cuerpo humano (96 ° F). Anders Celsius (1701–1744) desarrolló en 1742 una nueva escala de temperatura basada en los puntos de congelación y ebullición del agua. Celsius asignó un valor de 100° para el punto de congelación y 0° para el punto de ebullición. Un año después de su muerte, la escala se invierte para hacerla más práctica. James Six (1731–1793) inventó en 1780 un termómetro que permitió medir temperaturas máximas y mínimas durante un período de tiempo determinado. Demostró ser de gran utilidad para los meteorólogos, y el diseño básico sigue en uso hoy en día.
(9.3) La ley de la conservación de la masa 1789
La Ley de la Conservación de la Masa, formulada por el químico francés Antoine Lavoisier a finales del siglo XVIII, es un principio fundamental en la química que establece que, en una reacción química cerrada, la masa total de las sustancias antes de la reacción es igual a la masa total de las sustancias después de la reacción. En otras palabras, la masa no se crea ni se destruye en una reacción química, simplemente se reorganiza.
La Ley de la Conservación de la Masa se publicó en 1789 en el libro "Traité Élémentaire de Chimie" (Tratado Elemental de Química) de Lavoisier. Esta ley revolucionó la química al refutar la antigua idea de la transmutación de las sustancias, que sostenía que los elementos podían convertirse en otros elementos. Lavoisier demostró que los átomos se reorganizan en las reacciones químicas, pero la cantidad total de masa se mantiene constante.
Esta ley sentó las bases para la estequiometría, que es la medición de las proporciones de masa en las reacciones químicas, y es un principio fundamental en la química moderna. La Ley de la Conservación de la Masa es esencial en la comprensión de las reacciones químicas y en la formulación de ecuaciones químicas balanceadas. Además, contribuyó a la transformación de la química en una ciencia precisa y rigurosa.
(9.4) Ley de las proporciones recíprocas 1792
La Ley de las Proporciones Recíprocas, propuesta en 1792 por Jeremias Richter, es un principio fundamental en la química que a menudo se pasa por alto en la enseñanza moderna debido a su complejidad matemática. Esta ley establece que, si dos elementos diferentes se combinan por separado con el mismo peso de un tercer elemento, la relación de las masas en las que lo hacen es la misma o un simple múltiplo de la relación de masa en la que se combinan.
En términos más simples, la Ley de las Proporciones Recíprocas nos dice que, si conocemos las proporciones de elementos en dos compuestos distintos, por ejemplo, AB y BC, podemos utilizar esta información para determinar la proporción de elementos en un tercer compuesto, AC. Estas proporciones se expresan generalmente en forma de cocientes de masas, lo que nos proporciona una valiosa herramienta para comprender cómo los elementos se combinan en compuestos químicos.
A pesar de su importancia histórica y su contribución a la comprensión de la estequiometría y la formación de compuestos, la Ley de las Proporciones Recíprocas tiende a recibir menos atención en la educación química moderna. Esto podría deberse, en parte, a la complejidad matemática asociada con su resolución. A pesar de esto, es un principio esencial en la química que arroja luz sobre las relaciones de masas en las reacciones químicas y merece ser reconocido por su influencia en la evolución de la química como ciencia.
(9.5) La ley de las proporciones definidas 1799
La Ley de las Proporciones Definidas, también conocida como Ley de las Proporciones Fijas, es un principio fundamental en química que establece que un compuesto químico dado siempre contiene los mismos elementos en las mismas proporciones en masa, independientemente de su origen o método de preparación. Esta ley fue propuesta por el químico francés Joseph Proust a finales del siglo XVIII.
En otras palabras, cuando dos o más elementos se combinan para formar un compuesto químico, lo hacen en proporciones específicas y constantes en términos de masa. Esta ley implica que la relación de masas entre los elementos en un compuesto es constante y se puede expresar en forma de una relación estequiométrica.
La Ley de las Proporciones Definidas se publicó por primera vez en la obra "Recherches sur les proportions des principes constitutifs des sels et les lois des proportions chimiques" (Investigaciones sobre las proporciones de los principios constitutivos de las sales y las leyes de las proporciones químicas) de Joseph Proust, publicada en 1799. Esta ley fue un avance significativo en la química, ya que refutó la idea anterior de que las sustancias podían combinarse en proporciones variables y abrió el camino para la formulación precisa de compuestos químicos.
La Ley de las Proporciones Definidas es un pilar fundamental en la estequiometría y es esencial para comprender y predecir las reacciones químicas. Además, desempeñó un papel importante en la consolidación de la química como una ciencia exacta y cuantitativa.
(9.6) Las ley de Dalton de presiones parciales 1801
La Ley de las Presiones Parciales, a menudo llamada Ley de Dalton, es un principio fundamental en la química y la física que describe cómo se comportan las mezclas de gases. Esta ley fue formulada por el químico británico John Dalton a principios del siglo XIX. John Dalton fue un científico pionero en el estudio de la naturaleza de la materia y las propiedades de los gases. Su investigación lo llevó a desarrollar la teoría atómica, que postulaba que la materia estaba compuesta por partículas indivisibles llamadas átomos. A raíz de esta teoría, Dalton también se interesó en el comportamiento de los gases y las mezclas gaseosas. La Ley de Dalton, formulada por primera vez en 1801, establece que, en una mezcla de gases, la presión total ejercida por la mezcla es igual a la suma de las presiones parciales de los gases individuales.
Para llegar a esta ley, John Dalton llevó a cabo experimentos en los que estudió el comportamiento de las mezclas gaseosas a diferentes presiones y temperaturas. Utilizó instrumentos como barómetros para medir la presión y termómetros para medir la temperatura. Observó que la presión ejercida por un gas en una mezcla no dependía de la presencia de otros gases y que la suma de las presiones parciales era igual a la presión total de la mezcla.
La Ley de Dalton fue un avance significativo en la comprensión del comportamiento de los gases y sentó las bases para la teoría cinética de los gases. Esta ley es esencial en química y física, y su formulación sigue siendo válida en la actualidad para describir el comportamiento de mezclas de gases.
(9.7) La ley de Charles 1802
El nombre de la ley rinde homenaje al pionero del globo Jacques Charles, quien en 1787 hizo experimentos sobre cómo el volumen de gases dependía de la temperatura. La ironía es que Charles nunca publicó el trabajo por el cual es recordado, ni fue el primero o el último en hacer este descubrimiento. En dos de una serie de cuatro ensayos presentados entre el 2 y el 30 de octubre de 1801, John Dalton demostró por experimento que todos los gases y vapores que estudió se expandieron en la misma cantidad entre dos puntos fijos de temperatura. El filósofo natural francés Joseph Louis Gay-Lussac confirmó el descubrimiento en una presentación al Instituto Nacional Francés el 31 de enero de 1802 (Gay-Lussac, 1802), aunque atribuyó el descubrimiento al trabajo inédito de la década de 1780 por Jacques Charles. Los principios básicos ya habían sido descritos por Guillaume Amontons y Francis Hauksbee un siglo antes (Adcock, 1998; Gay-Lussac, 1802; Hauksbee, 2017).
Figura 9.6. Jacques Charles (12 de noviembre de 1746 - 7 de abril de 1823), inventor, científico y matemático francés. Rompió el récord de globo aerostático, el 27 de agosto de 1783. El 1 de diciembre de ese año, junto con Ainé Roberts, logró elevarse hasta una altura de 1000 metros. Inventó varios dispositivos, entre ellos un densímetro (también llamado hidrómetro), aparato que mide la gravedad específica de los líquidos.
Es bastante sorprendente que docenas de sustancias diferentes se comporten exactamente igual. La explicación aceptada, que James Clerk Maxwell propuso alrededor de 1860, es que la cantidad de espacio que ocupa un gas depende únicamente del movimiento de las moléculas de gas. En condiciones típicas, las moléculas de gas están muy lejos de sus vecinas, y son tan pequeñas que su propio volumen es insignificante. Empujan hacia afuera en frascos, pistones o globos simplemente rebotando en esas superficies a alta velocidad. Dentro de un globo de helio, alrededor de átomos de helio golpean cada centímetro cuadrado de goma cada segundo, ¡a velocidades de aproximadamente dos kilómetros por cada segundo!
(9.8) La primera ley de Gay-Lussac 1802
Joseph Louis Gay-Lussac (1778-1850) creció durante las revoluciones francesa y la revolución de la química. Su cómoda existencia como el hijo con tutoría privada de un abogado acomodado fue interrumpida por trastornos políticos y sociales de la Revolución Francesa: su tutor huyó y su padre fue encarcelado. Joseph, sin embargo, se benefició del nuevo orden cuando fue seleccionado para asistir a la École Polytechnique, una institución de la Revolución Francesa diseñada para crear liderazgo científico y técnico, especialmente para el ejército. Allí sus mentores incluyeron a Pierre Simon de Laplace y Claude Louis Berthollet, entre otros científicos convertidos por Antoine-Laurent Lavoisier a la química del oxígeno. La propia carrera de Gay-Lussac como profesor de física y química comenzó en la École Polytechnique.
Figura 9.7. Joseph-Louis Gay-Lussac. (Saint-Léonard-de-Noblat, 6 de diciembre de 1778-París, 9 de mayo de 1850) fue un químico y físico francés. Es conocido en la actualidad por su contribución a las leyes de los gases. En 1802, Gay-Lussac fue el primero en formular la ley según la cual un gas se expande proporcionalmente a su temperatura (absoluta) si se mantiene constante la presión (Ley de Charles) y que aumenta proporcionalmente su presión si el volumen se mantiene constante (Ley de Gay-Lussac). También se le cita como Louis Joseph en algunas fuentes de información.
Compartió el interés de Lavoisier y otros en el estudio cuantitativo de las propiedades de los gases. De su primer gran programa de investigación en 1801–1802, concluyó que volúmenes iguales de todos los gases se expanden igualmente con el mismo aumento de temperatura: esta conclusión generalmente se llama "ley de Charles" debido a que el propio Gay-Lussac lo reconoció a él y no a Guillaume Amontons y Francis Hauksbee que realmente la habían descubierto un siglo antes (Adcock, 1998; Gay-Lussac, 1802; Hauksbee, 2017).
En 1804, Gay-Lussac realizó varias audaces ascensiones de más de 7 000 metros sobre el nivel del mar en globos llenos de hidrógeno, una hazaña que no fue igualada por otros 50 años, y que le permitieron investigar otros aspectos de los gases. No solo reunió mediciones magnéticas a varias altitudes, sino que también tomó mediciones de presión, temperatura y humedad; además tomó muestras de aire, que luego analizó químicamente.
La segunda gran ley de los gases propuesta por Gay-Lussac es la que relaciona presión a temperatura fue generada entre 1800-1802, y es la que nos convoca en esta sección. Sin embargo, esta no fue la ley más importante, pues aún faltaba su tercera y más importante ley, los volúmenes de combinación.
Con su compañero profesor en la École Polytechnique, Louis Jacques Thénard, Gay-Lussac también participó en la investigación electroquímica temprana, investigando los elementos descubiertos por sus medios. Entre otros logros, descompusieron el ácido bórico mediante el uso de potasio fundido, descubriendo así el elemento boro. Los dos también participaron en debates contemporáneos que modificaron la definición de ácidos de Lavoisier y promovieron su programa de análisis de compuestos orgánicos para determinar su contenido de oxígeno e hidrógeno
(9.9) La ley de Henry 1803
La Ley de Henry, formulada por el químico británico William Henry en el siglo XIX, describe cómo la cantidad de un gas que se disuelve en un líquido a una temperatura dada es directamente proporcional a la presión parcial de ese gas en la fase gaseosa. Esta ley es fundamental en el estudio de la solubilidad de los gases en líquidos y es ampliamente aplicada en campos como la química, la biología y la industria.
William Henry llegó a esta ley a través de una serie de experimentos en los que estudió la solubilidad de varios gases en agua a diferentes temperaturas y presiones. Utilizó instrumentos como tubos cerrados y agua en contacto con el gas para determinar la cantidad de gas disuelto en función de la presión del gas. Observó que, a temperaturas constantes, la cantidad de gas disuelto era directamente proporcional a la presión del gas. Este comportamiento se convirtió en la base de la Ley de Henry.
La Ley de Henry es especialmente relevante en aplicaciones que involucran la disolución de gases en líquidos, como la carbonatación de bebidas gaseosas, la oxigenación de aguas para acuicultura y la transferencia de oxígeno en la sangre en biología y medicina. Además, esta ley es fundamental en la teoría de la respiración y en la comprensión de cómo los gases se disuelven en los fluidos biológicos del cuerpo humano.
(9.10) La segunda ley de Gay-Lussac 1808
En 1808, Gay-Lussac publicó su "Ley de las Proporciones de Volúmenes en la Combinación de Gases". En sus experimentos, descubrió que cuando diferentes gases reaccionaban entre sí, lo hacían en proporciones de volúmenes pequeños y enteros (por ejemplo, dos volúmenes de hidrógeno reaccionaban con un volumen de oxígeno para formar H2O, el agua). Este hallazgo representó uno de los avances más significativos de su época y sentó las bases para la teoría atómica posterior y la comprensión de cómo ocurren las reacciones químicas.
En sus experimentos, Gay-Lussac utilizó una variedad de gases y sustancias. Uno de sus experimentos más notables involucró la reacción de hidrógeno y oxígeno para formar agua, como se mencionó en el ejemplo. También estudió la reacción de gases como el hidrógeno, el oxígeno, el nitrógeno y otros. Sus observaciones indicaron que las relaciones de volumen entre los gases en las reacciones químicas seguían patrones específicos, lo que llevó a la formulación de la Ley de Gay-Lussac sobre las proporciones de volúmenes en la combinación de gases.
El trabajo de Gay-Lussac, junto con los descubrimientos de otros científicos de la época, contribuyó en gran medida al desarrollo de la química moderna y la teoría atómica. Sus experimentos proporcionaron evidencia sólida de que las sustancias reaccionaban en proporciones fijas y reproducibles, lo que impulsó la idea de que la materia estaba formada por átomos y que las reacciones químicas obedecían a leyes fundamentales. Este avance revolucionó nuestra comprensión de la química y allanó el camino para futuros descubrimientos en el campo de la química.
(9.11) La teoría atómica de Dalton 1808
La Teoría Atómica de Dalton se publicó en 1808. John Dalton presentó sus ideas en su obra "A New System of Chemical Philosophy" (Un nuevo sistema de filosofía química), la cual se publicó en dos volúmenes en 1808 y 1810. Esta obra estableció las bases de la teoría atómica y su impacto en la química y la ciencia en general ha sido trascendental. La Teoría Atómica de Dalton, propuesta por el científico británico John Dalton a principios del siglo XIX, revolucionó nuestra comprensión de la materia y las reacciones químicas. Dalton postuló que
a- Los átomos son las unidades fundamentales de la materia y son indivisibles (Composición).
b- Los átomos de un elemento son idénticos en masa y propiedades, pero son diferentes de los átomos de otros elementos (identidad).
c- Los compuestos se forman mediante la combinación de átomos en relaciones fijas y enteras (molecularidad).
d- En una reacción química, los átomos no se crean ni se destruyen, solo se reorganizan (cambio químico).
La Teoría Atómica de Dalton proporcionó una explicación coherente para los patrones de combinación química observados y estableció la base para la estequiometría y la teoría moderna de la química. Esta teoría cambió la forma en que percibimos la materia y allanó el camino para futuros descubrimientos en la química, incluyendo la Ley de las Proporciones Definidas y la Ley de las Proporciones Múltiples, que respaldaron y ampliaron sus ideas.
(9.12) La primera ley de Avogadro 1811
El Conde Lorenzo Romano Amedeo Carlo Avogadro Señor de Quaregna y Cerreto, nació en una familia de abogados italianos distinguidos en 1776. Siguiendo los pasos de su familia, estudió derecho canónico y comenzó a practicar por su cuenta antes de finalmente volver su atención a las ciencias naturales. En 1800, comenzó estudios en la física y las matemáticas. Sus primeros experimentos se llevaron a cabo con su hermano sobre el tema de la electricidad.
Figura 9.8. Lorenzo Romano Amedeo Carlo Avogadro, Conde de Quaregna y Cerreto (Turín, 9 de agosto de 1776 - 9 de julio de 1856), fue un físico y químico italiano, profesor de física de la Universidad de Turín desde 1820 hasta su muerte. Formuló la llamada ley de Avogadro, que dice que «volúmenes iguales de gases distintos bajo las mismas condiciones de presión y temperatura, contienen el mismo número de moléculas». Avanzó en el estudio y desarrollo de la teoría atómica, y en su honor se le dio el nombre al número de Avogadro.
En 1809, Avogadro comenzó a enseñar ciencias naturales en un liceo (escuela secundaria) en Vericelli. Fue en Vericelli, mientras que la experimentaba con densidades de gas, que Avogadro notó algo sorprendente: la combinación de dos volúmenes de gas hidrógeno con un volumen de gas oxígeno producido dos volúmenes de vapor de agua (Ley de volúmenes de combinación previamente reportada por Gay-Lussac). Avogadro había esperado que la reacción para produciría sólo un volumen de vapor de agua, pues la teoría atómica de Dalton planteaba que el agua estaba formada por un peso equivalente de hidrógeno y otro de oxígeno HO. Esto le hizo conjeturar que las partículas de oxígeno se componían de dos entidades elementales, que hoy llamamos átomos. En sus escritos, Avogadro se refirió a tres diferentes tipos de entidades elementales que llamaba “moléculas:” moléculas integrales (más similares a lo que los científicos llaman moléculas de hoy en día), moléculas constituyentes (los que son parte de un elemento), y moléculas elementales (similar a lo que los científicos llaman ahora átomos). A parte de la hipótesis de gases diatómicos, Avogadro sostenía que las sustancias estaban hechas de moléculas, por lo que el volumen de un gas estaba regido por la cantidad de moléculas, esta fue la hipótesis de Avogadro, aunque hay que destacar que esta no es la ley que usamos para resolver ejercicios de lápiz y papel, de hecho, en la actualidad existen tres relaciones matemáticas que podemos llamar ley de Avogadro.
Hablamos de las leyes de Avogadro en el plural debido a que realmente son dos afirmaciones matematizables, que, aunque relacionadas entre sí, involucran variables diferentes, que son rastreables al propio Avogadro. Para distinguirlas las denominaremos, la ley molecular de Avogadro (históricamente la hipótesis de Avogadro), y la ley molar de Avogadro (que es la que explican los libros de texto, ambas hacia 1811 (Pickover, 2008). A parte de estas dos leyes, existe una tercera que es la fusión de las dos anteriores, la cual es la definición de la cantidad de sustancia, una de las unidades fundamentales del sistema internacional de unidades.
El término "molar" (del latín "una gran masa") fue introducido por primera vez en la química por el químico alemán August Wilhelm von Hofmann 1818-1892, alrededor de 1865. Originalmente se pensó para indicar cualquier gran masa macroscópica, en contraste con una masa submicroscópica o "molecular" (también derivada del sufijo latino -cular, que significa "pequeño o diminutivo"). En otras palabras, en lugar de hablar de macroscópicas versus microscópicas, se habla de molar versus molecular. Este uso particular del término molar también ganó vigencia en la literatura de física, donde fue de uso común al menos hasta la década de 1940.
En términos matemáticos, diremos que la ley molecular va a requerir una variable que describa la cantidad de moléculas, y esa será Ni que se leerá como el número de partículas de la sustancia i; mientras que la ley molar empleará la variable cantidad de sustancia macro ni que se lee como cantidad de sustancia en moles de la sustancia i.
La hipótesis de Avogadro (como se la conocía originalmente) se formuló con el mismo espíritu de las leyes de gases empíricas anteriores, como la ley de Boyle (1662), la ley de Charles (1787) y la ley de Gay-Lussac (1808). La hipótesis fue publicada por primera vez por Amadeo Avogadro en 1811, y concilió la teoría atómica de Dalton con la idea "incompatible" de Joseph Louis Gay-Lussac de que algunos gases estaban compuestos de diferentes sustancias fundamentales (moléculas) en proporciones enteras. En 1814, independientemente de Avogadro, André-Marie Ampère publicó la misma ley con conclusiones similares. Como Ampère era más conocido en Francia, la hipótesis generalmente se refería allí como la hipótesis de Ampère, y más tarde también como la hipótesis de Avogadro-Ampère o incluso la hipótesis de Ampère-Avogadro.
Los estudios experimentales realizados por Charles Frédéric Gerhardt y Auguste Laurent en la forma molar demostraron que la ley de Avogadro explicaba por qué las mismas cantidades de moléculas en un gas tienen el mismo volumen. Sin embargo, los experimentos relacionados con algunas sustancias inorgánicas mostraron aparentes excepciones a la ley. Esta aparente contradicción finalmente fue resuelta por Stanislao Cannizzaro, como se anunció en el Congreso de Karlsruhe en 1860, cuatro años después de la muerte de Avogadro. Explicó que estas excepciones se debieron a disociaciones moleculares a ciertas temperaturas, y que la ley de Avogadro determinó no solo las masas moleculares, sino también las masas atómicas.
(9.13) La hipótesis de los gases diatómicos 1811
La Hipótesis de los Gases Diatómicos, también conocida como Hipótesis de Avogadro, fue propuesta por el científico italiano Amedeo Avogadro en 1811 y se publicó en su artículo "Essai d'une manière de déterminer les masses relatives des molécules élémentaires des corps, et les proportions selon lesquelles elles entrent dans ces combinaisons" (Ensayo sobre una manera de determinar las masas relativas de las moléculas elementales de las sustancias y las proporciones en las que entran en estas combinaciones). Esta hipótesis desempeñó un papel esencial al intentar armonizar dos conceptos en apariencia contradictorios en la química de la época.
Por un lado, el modelo atómico propuesto por John Dalton sostenía que los elementos eran monoatómicos, lo que implicaba que los gases debían consistir en átomos individuales. Por otro lado, las observaciones experimentales de Joseph Louis Gay-Lussac sobre los volúmenes de combinación de los gases parecían contradecir los números estequiométricos en la síntesis del agua, ya que sugerían relaciones de volumen distintas a las relaciones predichas por Dalton. Dalton, por su parte, se oponía tanto a la hipótesis de los gases diatómicos como a las mediciones de Gay-Lussac, argumentando que este último había medido incorrectamente los volúmenes.
A la postre, la hipótesis de Avogadro ofreció una solución a esta aparente contradicción al postular que los gases consistían en moléculas en lugar de átomos individuales. Esto permitió la reconciliación de los resultados de Gay-Lussac con la teoría atómica de Dalton (a pesar de la oposición de este último a modelar los elementos como moléculas diatómicas) y resolvió la aparente inconsistencia en las relaciones de volumen en las reacciones químicas. Esta reconciliación fue un paso crucial en el camino hacia la comprensión moderna de la química y la estequiometría, ya que unificó dos teorías aparentemente divergentes y allanó el camino para futuros desarrollos en la teoría cinética de los gases y la química en general.
(9.14) La ley de pesos atómicos de Cannizzaro
La Ley de los Pesos Atómicos representa un hito en la historia de la química que se desarrolló a lo largo del siglo XIX. Inicialmente, los primeros pesos atómicos fueron propuestos por John Dalton, quien formuló su teoría atómica y asignó un valor de 1 al peso atómico del hidrógeno, considerándolo un átomo indivisible. Sin embargo, esta elección dio como resultado una escala de pesos atómicos que presentaba deficiencias, ya que no tenía en cuenta que el hidrógeno, en realidad, existía en forma de moléculas diatómicas compuestas por dos átomos de hidrógeno.
Fue Stanislao Cannizzaro quien, al recopilar y combinar las leyes de Amedeo Avogadro y Joseph Louis Gay-Lussac con la teoría atómica de Dalton, logró desarrollar un método para calcular los pesos atómicos más precisos. Cannizzaro se basó en la hipótesis de Avogadro, que sostenía que volúmenes iguales de gases a la misma temperatura y presión contenían el mismo número de moléculas. Utilizando esta idea, Cannizzaro unificó y estandarizó la escala de pesos atómicos en relación con el hidrógeno, tomando el valor de 1 para el peso atómico del hidrógeno monoatómico. Esto permitió establecer una referencia común y precisa para la determinación de los pesos atómicos de otros elementos y compuestos.
Con la ayuda de nuestro modelo matemático moderno, podemos rastrear la técnica de Cannizzaro hasta una ecuación simple y análoga a las leyes de los gases. Según esta ecuación, la masa molar de un gas es el producto de su densidad por una constante de proporcionalidad llamada volumen molar. Cannizzaro eligió la densidad como el parámetro relevante, ya que este se puede estandarizar a condiciones específicas, es decir, a 1 atmósfera de presión y 0°C de temperatura (STP). Además, seleccionó el volumen molar, ya que al considerar que el hidrógeno gaseoso era diatómico, permitía que la masa del hidrógeno fuera aproximadamente de 2 gramos, siguiendo la hipótesis de gases diatómicos. Esta elección de 2 gramos para el hidrógeno se basa en la idea de que la masa relativa de un solo átomo de hidrógeno se vinculaba a un gramo estándar.
Es importante destacar que la elección de vincular el peso de un solo átomo de hidrógeno a un gramo estándar es una decisión arbitraria y convencional. La selección de un gramo como unidad base en la escala de pesos atómicos de Cannizzaro se basó en una convención histórica, aunque también podría haberse relacionado con otras unidades de masa, como la libra avoirdupois, como se mencionó.
La escala de pesos atómicos relativos, que se emplea en la tabla periódica y toma al hidrógeno como referencia con un valor de 1, se denomina de esta manera porque los pesos atómicos de los demás elementos se expresan en relación con el hidrógeno monoatómico asumido como 1 gramo estándar. Esta convención facilita la comparación de los pesos atómicos de diferentes elementos y compuestos, permitiendo que los químicos trabajen con una referencia común.
Cabe resaltar que la cantidad de átomos monoatómicos de hidrógeno en un gramo estándar no se calculó hasta el siglo XX, gracias al trabajo de científicos como Jean Perrin. Esta determinación más precisa contribuyó significativamente a la comprensión de la masa atómica y a la consolidación de la escala de pesos atómicos relativos tal como la conocemos en la actualidad.
A partir de este punto en la historia, se presentan tres direcciones claves. La primera conduce a la creación de la tabla periódica moderna, ya que es gracias a la escala de pesos atómicos relativos de Cannizzaro que la tabla periódica de Mendeleev se vuelve posible. La segunda ruta se enfoca en la teoría atómica estándar, que a su vez desemboca en el desarrollo de la física cuántica. La tercera vía nos lleva hacia los estudios en gases y estequiometría. Aunque en este contexto seguiremos la tercera ruta, es importante destacar que estas historias se desarrollan simultáneamente y se entrelazan en múltiples puntos de manera compleja. Por lo tanto, la elección de explorar un capítulo sobre otro puede ser subjetiva y dependerá de la perspectiva de cada profesor al abordar este tema.
(10) La ecuación de estado de los gases ideales
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
La ecuación de estado de los gases ideales constituye un modelo matemático que facilita la descripción del comportamiento de diversos gases reales, utilizando como referencia una concepción idealizada conocida como gas ideal, de naturaleza platónica. Aunque es importante destacar que el gas ideal en sí no tiene una existencia física real, la utilidad de esta ecuación radica en que, debido a la escasa interacción entre las partículas de los gases reales y el hecho de que sus volúmenes son despreciables en ciertas condiciones de presión y temperatura, los gases reales tienden a comportarse de manera muy similar al gas ideal.
Cuando los gases reales alcanzan una temperatura críticamente baja o superan una presión críticamente alta, experimentan una transición hacia el estado líquido. Por otro lado, si la temperatura es superior a un nivel críticamente alto, los gases reales pueden descomponerse y o ionizarse. En contraste, el gas ideal mantiene su estado gaseoso en todas las condiciones, ya que, vale la pena recordar, es una entidad conceptual que solo existe en la mente de los químicos.
La ecuación de los gases ideales se formuló a partir de datos empíricos y contribuciones significativas de científicos como Benoît Paul Émile Clapeyron, Rudolf Julius Emmanuel Clausius y Henri Victor Regnault. Estos investigadores fueron fundamentales en el desarrollo de leyes empíricas que sentaron las bases para comprender el comportamiento de los gases en condiciones específicas.
Benoît Paul Émile Clapeyron desempeñó un papel crucial al ser el primero en vislumbrar una relación entre las presiones y los volúmenes de los gases. Su ecuación original, sin embargo, no describía directamente el volumen del gas, sino que presentaba una versión modificada llamada volumen específico. Es importante señalar que el volumen específico es, de hecho, la inversa de la densidad de un gas.
Además, la ecuación de Clapeyron introducía una conversión a la temperatura en grados Kelvin, pero con un valor de cero absoluto ligeramente diferente, utilizando 267 en lugar de 273.15. Posteriormente, Henri Victor Regnault corrigió esta conversión a la temperatura absoluta, estableciendo un valor de 273. Así, la forma original de la ecuación de estado se expresaba como P u = R (273 + t), donde P es la presión, u es el volumen específico (la inversa de la densidad del gas), t es la temperatura, y R representa una constante de proporcionalidad (Jensen, 2003).
La elección de la letra R para representar la constante en la ecuación de estado de los gases ideales no tiene una causa históricamente clara. No obstante, en la actualidad, existe un consenso que sugiere que la letra R podría ser un homenaje a Henri Victor Regnault. Sin sus valiosos datos experimentales, la ecuación no habría sido corregida para adaptarse a la escala de temperatura, y por lo tanto, la constante R es a menudo referida como la constante de Regnault en reconocimiento a su contribución crucial en la corrección de la ecuación de estado de los gases ideales.
La ecuación mencionada anteriormente fue originalmente conocida como la ley de Mariotte-Gay-Lussac. Esta denominación se debe al hecho de que, siendo franceses, los científicos atribuían el nombre de Mariotte a lo que comúnmente se conoce como la ley de Boyle. Así, la ley de Mariotte-Gay-Lussac describe la relación entre la presión, el volumen específico y la temperatura de un gas, y su nombre rinde homenaje a los científicos franceses Edme Mariotte y Joseph Louis Gay-Lussac, quienes contribuyeron significativamente a su desarrollo.
Dada la eficacia de la ecuación de estado de los gases ideales en condiciones prácticas, siempre y cuando las mediciones no sean extremadamente precisas y no se superen las temperaturas y presiones críticas, la mayoría de los gases reales demostraron conformarse a los resultados teóricos de la ecuación. Aunque esta podía arrojar datos ligeramente diferentes a los valores críticos, en 1864, Rudolf Clausius introdujo el concepto de gas ideal para referirse al gas que siempre se ajusta a la ecuación bajo cualquier condición. Sin embargo, es importante destacar que este gas ideal solo existe en nuestra conceptualización, algo similar a un amor platónico.
De hecho, los químicos han desarrollado una afinidad por el gas ideal, ya que sirve como base para numerosos modelos más avanzados que se exploran en capítulos de termodinámica, termoquímica e ingeniería. Este concepto, aunque abstracto, ha demostrado ser una herramienta invaluable en la comprensión y modelado de diversos fenómenos gaseosos en la práctica científica y la ingeniería.
Sin embargo, existe un trayecto considerable desde la simple expresión \(P \cdot u = R \cdot (273 + T)\) hasta la moderna ecuación de estado. Comencemos con el término \(273 + T\), que representa la fórmula elemental para convertir la temperatura a la escala absoluta en kelvin, denotada como \(T\). Por lo tanto, la ecuación se simplifica a \(P \cdot u = R \cdot T\). No obstante, aún nos faltan dos componentes esenciales: el volumen simple y la cantidad de sustancia. Los químicos del siglo XIX, a pesar de contar con acceso a los pesos atómicos gracias a la técnica de Cannizzaro, aún se encontraban perplejos en cuanto al concepto de molécula-gramo y volumen molar.
La relación entre el volumen estándar de un gas puro a 0°C y 1 atm de presión, que completaba 22.41 L con la masa registrada en esas condiciones, fue conocida como molécula-gramo. El término "molécula-gramo" fue acuñado por Wilhelm Ostwald en su publicación "Zeitschrift für Physikalische Chemie" en 1893. Este concepto resultó útil ya que simplificaba la explicación de la relación entre la masa y el volumen de 22.41 L en condiciones de 0°C y 1 atm de presión. A pesar de que Ostwald no creía en la existencia de moléculas, la terminología "molécula-gramo" daba a entender que, de alguna manera, las moléculas eran una realidad.
Con el tiempo, la expresión "molécula-gramo" se consideró demasiado extensa y teóricamente tendenciosa. Como solución, la idea se simplificó a "mol", un diminutivo de "molécula-gramo". Esta palabra, además de ser más concisa, eliminaba la referencia directa a las moléculas, lo que permitía realizar cálculos químicos sin necesidad de involucrarse en el mundo molecular en el cual Ostwald no creía.
A principios del siglo XIX, los científicos observaron el movimiento de partículas de polen en el agua, un fenómeno que podía explicarse asumiendo la existencia de moléculas. Albert Einstein fue pionero al realizar los primeros cálculos teóricos, los cuales luego fueron confirmados experimentalmente por Jean Perrin. Así, hacia 1911, se había establecido la existencia de los átomos.
Los experimentos de Perrin también llevaron a otra conclusión importante: la cantidad de entidades en una mol de sustancia era una constante mensurable. Esta constante se conoce como el número de Avogadro, y su valor aproximado es de 6.022 x 10^23 entidades en cada mol de una sustancia, independientemente de las condiciones.
El dilema radicaba en que, a pesar de conocer la cantidad específica de entidades en un mol, lo que generaba un cierto volumen en un gas, este concepto carecía de una correspondencia física como la masa o los litros. Esta carencia fue subsanada de manera ingeniosa en 1961 por Edward Guggenheim, quien inventó la "cantidad de sustancia". Esta medida cuantifica la cantidad de partículas en un sistema, contándolas en paquetes de Avogadro que denominamos moles.
Guggenheim también definió la relación entre la masa en gramos y la cantidad de sustancia en moles, a la que denominó "masa molar". Este parámetro tenía la intención de reemplazar conceptos como el átomo-gramo y el molécula-gramo, la masa atómica y la masa molecular, así como la masa relativa atómica y la masa relativa molecular. Sin embargo, es relevante mencionar que estos conceptos aún persisten en el uso cotidiano, aunque ahora se empleen para designar conceptos ligeramente diferentes.
Volviendo a la ecuación de estado \(P \cdot u = R \cdot T\), es importante destacar que en su forma original, la constante \(R\) no era universal; variaba de un gas a otro. Esto se debía a que \(R\) era, en realidad, una relación entre la verdadera constante \(R\) y la masa molar \(M\) del gas específico. Mientras tanto, \(u\), el inverso de la densidad, podía expresarse como \(V/m\). Si multiplicamos ambos lados de la ecuación por \(m\), obtenemos en el denominador el cociente \(m/M\), que es equivalente a la cantidad de sustancia \(n\). De esta manera, se llega a la forma moderna de la ecuación de estado: \(P \cdot V = n \cdot R \cdot T\).
Lo anterior nos permite reconocer que el propio lenguaje de la química ha experimentado significativos cambios a lo largo de las décadas. Por lo tanto, no es de esperar encontrar ecuaciones como \(P \cdot V = n \cdot R \cdot T\) en libros de texto de principios del siglo XX. El inconveniente radica en que algunos químicos muestran resistencia a adoptar estos cambios lingüísticos. Como resultado, incluso hoy en día, hay quienes siguen solicitando cálculos en términos de átomo-gramo o molécula-gramo. Si no tienes conocimientos de este antiguo lenguaje, podrías sentirte confundido, ya que en esencia, se trata de cálculos de masas molares, como los que hemos revisado en lecciones anteriores.
Por otro lado, la ecuación de estado puede recuperarse fácilmente al multiplicar dos ecuaciones: la ley de Gay-Lussac (\(P = k \cdot T\)) y la segunda ley de Avogadro (\(V = V_m \cdot n\)). Al multiplicar estas dos ecuaciones, es importante recordar que al multiplicar dos constantes se obtiene una nueva constante. DEMOSTRACION. Obtener la ley de los gases ideales a partir de las leyes de los gases
En lo que respecta al valor de la constante \(R\), esta es igual al producto de dos de las siete constantes fundamentales del universo, específicamente la constante de Avogadro por la constante de Boltzmann. Esto convierte a \(R\) en una constante extremadamente fundamental que aparece en numerosos modelos físico-químicos. Su valor puede variar según las unidades utilizadas para medir los otros cuatro parámetros, pero la unidad más comúnmente empleada es \(0.08206 \, \text{atm} \, \text{L} / (\text{mol} \, \text{K})\).
La ecuación de estado no solo incorpora las leyes de Avogadro y Gay-Lussac, sino que también sirve como la base teórica para deducir varias otras leyes empíricas fundamentales. En este contexto, utilizaremos la ecuación de estado como un teorema fundamental, del cual derivaremos ecuaciones para leyes empíricas de los gases, así como otros modelos, incluyendo las leyes de propiedades coligativas como la ley de Henry, e incluso el modelo matemático de estequiometría conocido como el avance de la reacción. Este enfoque implica que, al ser una fórmula maestra, la ecuación de estado es la única que realmente vale la pena memorizar. En las próximas lecciones, utilizaremos la ecuación de estado para derivar las leyes específicas con las que trabajaremos detalladamente.
(11) La ley de Boyle, T constante
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
La ley de Boyle es una ley de los gases que describe la relación entre la presión y el volumen de un gas a temperatura constante. Esta ley fue formulada por el físico británico Robert Boyle en el siglo XVII. La ley de Boyle establece que, a temperatura constante, el volumen de una cantidad fija de gas es inversamente proporcional a su presión. En otras palabras, si la presión de un gas aumenta, su volumen disminuirá, y viceversa, siempre y cuando la temperatura se mantenga constante. Definiremos matemáticamente la Ley de Boyle como la consecuencia que se deriva de mantener la cantidad de sustancia y la temperatura constantes en la ecuación de estado. DEMOSTRACIÓN. Deducir la ley de Boyle a partir de P V = n R T
|
\[P_i \cdot V_i = k\] |
Eq 11.1. Forma estática de la ley de Boyle. |
|
\[P_i \cdot V_i = P_{oi} \cdot V_{oi} \] |
Eq 11.2. Forma dinámica de la ley de Boyle. |
(11.1) Aplicaciones de la ley de Boyle
La Ley de Boyle se utiliza para explicar el funcionamiento del sistema respiratorio en el cuerpo humano, específicamente en la modificación del volumen pulmonar. Este proceso, guiado por la Ley de Boyle, conlleva cambios en la presión del aire dentro de los pulmones, generando una diferencia de presión entre el aire pulmonar y el entorno circundante. Esta variación de presión desencadena los procesos de inhalación y exhalación, ya que el aire fluye desde áreas de alta presión a bajas presiones.
Durante la inhalación, los pulmones se expanden, disminuyendo la presión interna y permitiendo que el aire fluya hacia ellos por difusión, llenándolos de aire. En la exhalación, los pulmones se contraen, aumentando la presión interna y expulsando el aire al entorno externo.
La Ley de Boyle no solo tiene relevancia en el sistema respiratorio, sino que también desempeña un papel fundamental en diversas aplicaciones médicas e industriales. En la ventilación mecánica, es esencial para controlar la presión y el volumen del aire en el tratamiento de pacientes con problemas respiratorios. En la anestesia, se aplica para el suministro controlado de gases anestésicos. La compresión y expansión de gases en la fabricación de medicamentos se basa en sus principios, al igual que en la industria química para controlar y monitorear gases en reactores químicos.
En la atmósfera, la Ley de Boyle se emplea en física y meteorología para comprender cambios en la presión atmosférica con la altitud. En la ingeniería de motores de combustión, es crucial para el funcionamiento de cilindros, donde la compresión del aire y su mezcla con combustible son esenciales. Los buceadores deben comprenderla, ya que la presión del aire varía con la profundidad y afecta la respiración desde tanques de aire comprimido.
La calibración de instrumentos de medición de presión, la exploración espacial con sistemas de soporte vital, y la aplicación en la industria alimentaria para controlar gases en fermentación y conservación, son ejemplos adicionales. En sistemas de control de fluidos y gases, como válvulas y tuberías, se utilizan los principios de la Ley de Boyle para regular el flujo y la presión.
(11.2) Ejercicios resueltos de la ley de Boyle
Ejemplo. Hallar V2 de un gas ideal a 12.3 L y 40 mmHg que pasa a estar a 60 mmHg || química de gases Ejemplo. Hallar P2 de un gas a 400 ft3 y 1 atm que debe pasa a 3.00 ft3 || química de gases
Matamala y Gonzalez Ejercicio 7.1. Cierta masa de gas ocupa 45 ml a 0°C y 650 mm de Hg. ¿Qué volumen ocuparía en CN?
Química de Chang 10 Ejemplo 5.5. Se permite que un globo de helio inflado con un volumen de 0.55 L al nivel del mar (1.0 atm) se eleve a una altura de 6.5 km, donde la presión es de aproximadamente 0.40 atm. Suponiendo que la temperatura permanece constante, ¿cuál es el volumen final del globo? Química de Chang 10 Práctica 5.5. Una muestra de cloro gaseoso ocupa un volumen de 946 mL a una presión de 726 mmHg. Calcule la presión del gas (en mmHg) si el volumen se reduce a temperatura constante a 154 mL
Química de Chang 10 Problema-5.19. Un gas que ocupa un volumen de 725 mL a una presión de 0.970 atm se deja expandir a temperatura constante hasta alcanzar una presión de 0.541 atm. ¿Cuál es su volumen final? Química de Chang 10 Problema-5.20. Una muestra de amoniaco gaseoso ejerce una presión de 5.3 atm a 468C. ¿Cuál es la presión cuando el volumen del gas se reduce a una décima parte (0.10) de su valor inicial a la misma temperatura? Química de Chang 10 Problema-5.21. El volumen de un gas es de 5.80 L, medido a 1.00 atm. ¿Cuál es la presión del gas en mmHg si el volumen cambia a 9.65 L? (La temperatura permanece constante.)
Química de Chang 10 Problema-5.22a. Una muestra de aire ocupa un volumen de 3.8 L cuando la presión es de 1.2 atm. a) ¿Qué volumen ocuparía a 6.6 atm? (La temperatura se mantiene constante.) Química de Chang 10 Problema-5.22b. Una muestra de aire ocupa un volumen de 3.8 L cuando la presión es de 1.2 atm. b) ¿Cuál es la presión requerida para comprimirlo a 0.075 L? (La temperatura se mantiene constante.)
Química la ciencia central 13. Ejercicio 10.25a. Tiene un gas a 25 °C confinado a un cilindro con un pistón móvil. ¿Cuál de las siguientes acciones duplicaría la presión del gas? (a) Levantar el pistón para duplicar el volumen mientras se mantiene constante la temperatura. Química la ciencia central 13. Ejercicio 10.25c. Tiene un gas a 25 °C confinado a un cilindro con un pistón móvil. ¿Cuál de las siguientes acciones duplicaría la presión del gas? (c) Empujar hacia abajo el pistón para reducir a la mitad el volumen mientras se mantiene constante la temperatura. Química la ciencia central 13. Ejercicio 10.26a. Una cantidad fija de gas a 21 °C exhibe una presión de 752 torr y ocupa un volumen de 5.12 L. (a) Calcule el volumen que ocupará el gas si la presión se incrementa a 1.88 atm mientras la temperatura se mantiene constante.
Hipertexto. Ejemplo 1. En un recipiente se tienen 30 litros de nitrógeno a 20 °C y a una atmósfera de presión. ¿A qué presión es necesario someter el gas para que su volumen se reduzca a 10 litros? Asuma que la temperatura no cambia 3 atm Hipertexto. Ejemplo 2. ¿Cuál será el volumen final ocupado por 50 litros de oxígeno cuya presión inicial es de 560 mm de Hg y es comprimido hasta que la presión es de 2 atm? 18.42 L
(11.3) La constante molar de Boyle y la gráfica
Dado que la constante de Boyle es el producto de la cantidad de sustancia, la temperatura y la constante R. Podemos obtener su forma molar para valores estándar como 1 mol y 273 K DEMOSTRACIÓN. Calcular la constante de la ley de Boyle a 273 K y 1 mol de gas
Con lo que obtenemos un valor de 22.4 atm L, y con esta constante, es posible crear una gráfica predictiva. Si asumimos una situación experimental como un émbolo o un pistón de vapor en el que se manipula la presión para obtener un volumen, podemos determinar que la presión es la variable independiente y el volumen la dependiente. Dado que es una constante y no un problema de lápiz y papel, usaremos la calculadora. Con la constante molar de Boyle podemos graficar, asumamos una mol de gas en condiciones estándar de temperatura, pero presión variable.
Figura 11.1. Curva de la ley de Boyle. Se obtiene al graficar la ecuación 6.1, con la constante 22.4 atm L. Tenga en cuenta que la única diferencia con el volumen molar, son sus unidades, pues en el volumen molar lo que tenemos es 22.4 L / mol.
Es posible predecir la gráfica sin el valor de la constante, pues se tiene una ecuación de la forma y=1/x, que en cálculo se sabe que arroja una curva inversa. De hecho, la ley de Boyle es la única de las leyes de los gases que tiene esta forma notable.
(12) La ley de Charles, P constante
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
Definiremos matemáticamente la Ley de Charles como la consecuencia que se deriva de mantener la cantidad de sustancia y la presión constantes en la ecuación de estado. DEMOSTRACION. Obtener la ley de Charles a partir de la ecuación de estado o ley de los gases ideales P V = n R T, empleando como condición un sistema en el que el volumen cambia en función de la temperatura a presión constante.
|
\[V=k \cdot T\] |
Eq 12.1. Forma estática de la ley de Charles. |
|
\[\frac{T_o}{V_o}=\frac{T}{V}\] |
Eq 12.2. Forma dinámica de la ley de Charles. |
(12.1) Aplicaciones de la ley de Charles.
Nos encontramos con esta ley muchas veces en nuestra vida diaria. Comencemos con un ejemplo muy simple; Cuando abres una lata fría simplemente ves burbujas, pero si abres una lata más caliente, las burbujas derraman la bebida. ¿Por qué crees que esto ocurre? Definitivamente por la ley de Charles. En una lata más cálida, el volumen de gases aumenta y al abrir la lata, las moléculas de gas encuentran su salida empujando al refresco.
En los productos de panadería, la levadura se usa para la fermentación. La levadura produce dióxido de carbono y cuando horneamos pan / pastel, el dióxido de carbono se expande debido al aumento de la temperatura y da esponjosidad a nuestro pan y pasteles al empujar la masa desde adentro.
A veces tenemos que estar alertas ante los efectos de esta ley. ¿Has leído las advertencias escritas en la botella de desodorante? Sugieren almacenarlo por debajo de 50 ° C y también advierten de mantenerlo alejado de la luz solar directa y el encendido. Porque a temperaturas más altas, el volumen de gases aumenta y si llega al límite puede reventar la botella.
Si quiere presenciar la ley de Charles, puede hacer un experimento con el globo usted mismo. Elija un día soleado para su experimento, salga a una temperatura más cálida y llene un globo con gas. Luego llévalo a un lugar más frío. Verá que su globo se reduce de tamaño a medida que lo coloca en un lugar más frío y reanuda su tamaño original al salir. En un lugar más frío, el volumen de gas se reduce, lo que resulta en la contracción del globo. Cuando te diriges afuera, la temperatura aumenta y también lo hace el volumen de gas, por lo que el globo recupera su tamaño. Un globo cuyo gas este a una temperatura mayor que la del medio circundante se expandirá hasta tener una menor densidad, por lo que tenderá a elevarse, este es el principio de los globos aerostáticos.
(12.1) Ejercicios resueltos de la ley de Charles
Ejemplo. Calcular el volumen final de un globo si este se encuentra a 27 °C y 25 L si se lo calienta hasta llegar a los 227 °C Ejemplo. Una máquina térmica tiene un gas originalmente a 27 °C y 20 L, ¿Cuál será la temperatura en °C si el volumen se expande a 500 L? Ejemplo. El dióxido de carbono se forma generalmente cuando se quema la gasolina. Si se producen 30.0 L de CO2 a una temperatura de 1.00 × 103 °C y se les permite alcanzar la temperatura ambiente (25.0 ° C) sin ningún cambio de presión, ¿cuál es el nuevo volumen de dióxido de carbono? Ejemplo. Una muestra de 600.0 mL de nitrógeno se calienta de 77.0 ° C a 86.0 ° C. Encuentra su nuevo volumen si la presión permanece constante. Ejemplo. Cuando 50.0 litros de oxígeno a 20.0 ° C se comprimen a 5.00 litros, ¿cuál debe ser la nueva temperatura para mantener una presión constante? Exprese el resultado en grados celsius y el kelvins.
Química de Chang 10. Problema-5.23. Un volumen de 36.4 L de gas metano se calienta de 25 °C a 88 °C a presión constante. ¿Cuál es el volumen final del gas? Química de Chang 10. Problema-5.24. En condiciones de presión constante, una muestra de gas hidrógeno inicialmente a 88 ° C y 9.6 L se enfría hasta que su volumen final es 3.4 L. ¿Cuál es su temperatura final? Química de Chang 10. Problema-5.36. La temperatura de 2.5 L de un gas, inicialmente a TPE, se eleva a 250°C a volumen constante. Calcule la presión final del gas en atm.
Química la ciencia central 13. Muestra 10.03a. Supongamos que tenemos un gas confinado en un cilindro con un pistón móvil que está sellado para que no haya fugas. ¿Cómo afectará cada uno de los siguientes cambios (i) la presión del gas, (ii) el número de moles de gas en el cilindro, (iii) la distancia promedio entre las moléculas: al calentar el gas manteniendo una presión constante. Química la ciencia central 13. Práctica 10.05.2. La presión en un tanque de gas natural se mantiene a 2.20 atm. En un día en que la temperatura es de -15 °C, el volumen de gas en el tanque es de 3.25 x 103 m3. ¿Cuál es el volumen de la misma cantidad de gas en un día cuando la temperatura es de 31 °C?
Hipertexto. Problemas básicos 10a. Un recipiente contiene 5 L de nitrógeno gaseoso a 225 °C. Calcula el volumen que ocupará este gas a presión constante y a las siguientes temperaturas: 1 °C Hipertexto. Problemas básicos 10b. Un recipiente contiene 5 L de nitrógeno gaseoso a 225 °C. Calcula el volumen que ocupará este gas a presión constante y a las siguientes temperaturas: 210 K Hipertexto. Problemas básicos 10c. Un recipiente contiene 5 L de nitrógeno gaseoso a 225 °C. Calcula el volumen que ocupará este gas a presión constante y a las siguientes temperaturas: 15 °F Hipertexto. Problemas básicos 10d. Un recipiente contiene 5 L de nitrógeno gaseoso a 225 °C. Calcula el volumen que ocupará este gas a presión constante y a las siguientes temperaturas: 20 °F
(12.2) Calculando la constante molar de Charles y la gráfica
Enunciado: Hallar el valor de la constante en la ley de Charles a 1.00 atm y 1.00 mol de gas ideal.
Figura 12.1. Curva de la ley de Charles. La gráfica de la ley de Charles es una línea recta, a menor temperatura, el volumen de un gas disminuye.
(12.3) Consecuencias de la ley de Charles
Esta ley nos trae ciertas consecuencias, el volumen de un gas depende de las vibraciones, no del volumen de sus moléculas, por lo que es teóricamente posible reducir el volumen de un gas hasta el mínimo paralizando sus vibraciones, si conseguimos disminuir su temperatura lo suficiente. Para hacer esto, los científicos determinaron las rectas para varios gases diferentes y analizaron sus pendientes para ver a que temperaturas teorías debería congelarse un gas para lograr el volumen casi cero. La sorpresa fue que dicha temperatura siempre era la misma sin importar el gas que se estaba trabajando, -273.15 °C, valor denominado el cero absoluto.
(13) La ley de Gay-Lussac, V constante
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
Definiremos matemáticamente a la primera Ley de Gay-Lussac como la consecuencia que se deriva de mantener la cantidad de sustancia y el volumen constantes en la ecuación de estado. DEMOSTRACION. Obtener la ley de Gay-Lussac a partir de la ecuación de estado o ley de los gases ideales P V = n R T, empleando como condición un sistema en el que la presión cambia en función de la temperatura a volumen constante.
|
\[P=k\cdot T\] |
Eq 13.1. Forma estática para la ley de Gay-Lussac. |
|
\[\frac{T_o}{P_o}=\frac{T}{P}\] |
Eq 13.2. Forma dinámica de la ley de Gay-Lussac. |
Emplearemos la ley de Gay-Lussac para este caso, tenga en cuenta que las temperaturas deben convertirse a kelvins, sin importar que formen cocientes homogéneos.
(13.1) Aplicaciones de la ley de Gay-Lussac
La ley de Gay-Lussac encuentra numerosas confirmaciones en situaciones de la vida cotidiana. Un ejemplo evidente es el comportamiento de los neumáticos calientes en climas cálidos, donde las altas temperaturas provocan un aumento en la presión interna del neumático, superando su límite de tolerancia. Como resultado, cuando la presión del gas supera la capacidad elástica del neumático, este puede llegar a explotar.
La olla a presión es otro ejemplo que respalda la ley de Gay-Lussac. Al aumentar la temperatura en su interior, la presión se eleva por encima de la atmosférica, lo que resulta beneficioso para la cocción de alimentos. Esta elevada presión impide que el agua se evapore a la temperatura usual de ebullición de 100°C, evitando así que los alimentos se sequen. Además, permite que el agua líquida alcance temperaturas superiores a los 100°C, lo que acelera el proceso de cocción.
En la industria de los aerosoles, la ley de Gay-Lussac es fundamental para garantizar que los productos en aerosol funcionen correctamente. Los aerosoles, como los desodorantes o los productos para el cabello, contienen gases comprimidos en el interior del envase. Cuando se presiona la válvula, se libera el contenido en forma de spray. El aumento de la temperatura ambiente puede aumentar la presión dentro del envase, lo que afecta la dispensación del producto. Las empresas que fabrican estos productos deben tener en cuenta la variación de la presión debido a la temperatura para diseñar envases seguros y eficientes que eviten fugas o explosiones.
En la aviación, la ley de Gay-Lussac desempeña un papel vital en el diseño y funcionamiento de las aeronaves. A medida que una aeronave gana altitud, la temperatura en la atmósfera disminuye. Esto tiene un impacto directo en la presión del aire en el interior y exterior de la aeronave. Para mantener un ambiente seguro y confortable para los pasajeros y tripulación, las aeronaves cuentan con sistemas de regulación de presión y temperatura. Estos sistemas compensan las variaciones en la presión y la temperatura para garantizar un vuelo seguro y agradable, lo que demuestra la aplicación práctica de la ley de Gay-Lussac en la industria de la aviación.
(13.2) Problemas resueltos de la ley de Gay-Lussac
Ejemplo. Un gas está en un recipiente rígido de 2 L a 20 °C y 560 mmHg. ¿A qué temperatura en °C llegará el gas si aumenta la presión interna hasta 760 mmHg? Ejemplo. Un gas ocupa un volumen de 10.0 L a una temperatura de 300 K. Si la temperatura se incrementa a 400 K, el volumen se mantiene constante y la presión a 1.00 atm, ¿cuál será la nueva presión del gas? a. 1.33 atm b. 2.00 atm c. 3.00 atm d. 4.00 atm Ejemplo. Una muestra de 30.0 L de nitrógeno dentro de un contenedor rígido de metal a 20.0 °C se coloca dentro de un horno cuya temperatura es 50.0 °C. La presión dentro del contenedor a 20.0 ° C fue de 6.00 atm. ¿Cuál es la presión del nitrógeno después de aumentar su temperatura a 50.0 °C? || Pulse aquí
Matamala y Gonzalez. Ejercicio 7.3. Se tiene 2 L de gas a 27°C ¿Cuánto habrá que elevar la temperatura para que la presión aumente un 20%, si el volumen se mantiene constante? Matamala y Gonzalez. Ejercicio 7.4. Una botella contiene gas carbónico a 27 °C y 12 atmósferas. ¿Cuál será la presión del gas si se calienta el recipiente a 100°C?
Química de Chang 10. Ejemplo 5.6. El argón es un gas inerte que se utiliza en bombillas para retardar la vaporización del filamento de tungsteno. Cierta bombilla que contiene argón a 1.20 atm y 18 °C se calienta a 85 °C a volumen constante. Calcule su presión final (en atm). Química de Chang 10. Práctica 5.6. Una muestra de oxígeno gaseoso inicialmente a 0.97 atm se enfría de 21 °C a -68 °C a volumen constante. ¿Cuál es su presión final (en atm)?
Química de Chang 10. Problema-5.38. Un gas liberado durante la fermentación de glucosa (en la manufactura de vino) tiene un volumen de 0.78 L a 20.1°C y 1.00 atm. ¿Cuál es el volumen del gas a la temperatura de fermentación de 36.5°C y 1.00 atm de presión? Química de Chang 10. Problema-5.25. El amoníaco se quema en oxígeno gaseoso para formar óxido nítrico (NO) y vapor de agua. ¿Cuántos volúmenes de NO se obtienen de un volumen de amoníaco a la misma temperatura y presión? Química de Chang 10. Problema-5.26. El cloro molecular y el flúor molecular se combinan para formar un producto gaseoso. En las mismas condiciones de temperatura y presión, se encuentra que un volumen de Cl2 reacciona con tres volúmenes de F2 para producir dos volúmenes del producto. ¿Cuál es la fórmula del producto?
Química La ciencia central 13. Muestra 10.05. La presión del gas en una lata de aerosol es de 1.5 atm a 25 °C. Suponiendo que el gas obedece la ecuación del gas ideal, ¿cuál es la presión cuando la lata se calienta a 450 °C? 3.6 atm Química La ciencia central 13. Práctica 10.05.1. Si llena la llanta de su automóvil a una presión de 32 psi (libras por pulgada cuadrada) en un día caluroso de verano cuando la temperatura es de 35 °C (95 °F), ¿cuál es la presión (en psi) en un día frío de invierno cuando la temperatura es -15 °C (5 °F)? Suponga que no hay fugas de gas entre las mediciones y que el volumen de la llanta no cambia. (a) 38 psi, (b) 27 psi, (c) -13.7 psi, (d) 1.8 psi, (e) 13.7 psi Química La ciencia central 13. Ejercicio 10.25b. Tiene un gas a 25 °C confinado a un cilindro con un pistón móvil. ¿Cuál de las siguientes acciones duplicaría la presión del gas? (b) Calentar el gas para que su temperatura suba de 25 °C a 50 ° C, mientras se mantiene constante el volumen. Química La ciencia central 13. Ejercicio 10.44c. Muchos gases se envían en contenedores de alta presión. Considere un tanque de acero cuyo volumen es de 55.0 galones que contiene gas O2 a una presión de 16500 kPa a 23 °C. ¿A qué temperatura la presión en el tanque sería igual a 150.0 atm? Química La ciencia central 13. Ejercicio 10.69. Un recipiente rígido que contiene una proporción molar de dióxido de carbono y vapor de agua de 3:1 se mantiene a 200 °C donde tiene una presión total de 2.00 atm. Si el recipiente se enfría a 10 °C para que todo el vapor de agua se condense, ¿cuál es la presión del dióxido de carbono? Desprecie el volumen del agua líquida que se forma al enfriarse.
Hipertexto. Ejemplo 3. Un gas está en un recipiente de 2 L a 20 °C y 560 mmHg. ¿A qué temperatura en °C llegará el gas si aumenta la presión interna hasta 760 mmHg?
(13.3) Graficando la ley de Gay-Lussac
Figura 13.1. Curva de la ley de Gay-Lussac. La ley de Gay-Lussac también se relaciona con el cero absoluto, pues a esa temperatura, la presión de cualquier gas debería ser casi cero.
(14) La segunda ley de Gay-Lussac
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
En 1808, Gay-Lussac comunicó uno de sus logros más destacados, a menudo subestimado por muchos profesores de química. A través de sus propios experimentos y los de otros científicos, dedujo que los gases, bajo condiciones constantes de temperatura y presión, se combinan en proporciones numéricas simples por volumen. Además, los productos resultantes, cuando son gases, también mantienen proporciones simples en volumen respecto a los volúmenes de los reactivos. Esta conclusión posteriormente fue reconocida como la ley de Gay-Lussac de los volúmenes de combinación. Aunque esta ley pueda parecer compleja o incluso trivial en primera instancia, se revela que los valores de los volúmenes de combinación, al expresarse en las relaciones de enteros más simples posibles, coinciden con lo que hoy conocemos como coeficientes estequiométricos.
Gay-Lussac colaboró en una serie de experimentos con el naturalista prusiano Alexander von Humboldt (1769-1859), enfocándose en la generación de vapor de agua mediante la introducción de chispas en mezclas de gases de hidrógeno y oxígeno. Durante estas investigaciones, Gay-Lussac observó una relación específica: para cualquier volumen dado de oxígeno consumido por completo en la reacción, se requería precisamente el doble de ese volumen en hidrógeno. Los resultados de las mediciones fueron notablemente precisos, indicando una relación de 2:1 con una exactitud cercana al 0.1% (Dalton, von Humboldt, & Thenard, n.d.).
Con todos los volúmenes medidos a una temperatura y presión constantes, se observa que los volúmenes de reactantes gaseosos y productos gaseosos son fracciones pequeñas de números enteros, o números enteros, siempre y cuando se seleccione de manera adecuada el reactivo limitante, es decir, que no existen sobrantes o faltantes en la reacción. Gay-Lussac extendió su investigación a las relaciones de volumen de diversas sustancias gaseosas, identificando patrones significativos. Por ejemplo, propuso la Ley de Volúmenes de Combinación para el amoníaco, donde un volumen de nitrógeno reacciona con 3 volúmenes de hidrógeno para producir dos volúmenes de amoníaco. Otro caso es la aplicación de la Ley de Volúmenes de Combinación en la síntesis del cloruro de hidrógeno, donde se necesita un volumen de hidrógeno y un volumen de gas cloro para generar un volumen de cloruro de hidrógeno.
(14.1) Modelo matemático
Aunque los volúmenes absolutos difieren, al calcular los cocientes o ratios de volúmenes, obtenemos valores constantes. Por ejemplo, al realizar mediciones para la síntesis de agua utilizando 1 L de oxígeno, luego 2 L y finalmente 4 L, observamos que la cantidad de hidrógeno consumido siempre es el doble. De esta manera, el ratio de volúmenes de hidrógeno a oxígeno sigue consistentemente un patrón de 2:1. A este cociente lo denominamos como ratio estequiométrico. La elección de este nombre se fundamenta en la intuición compartida por Dalton, Gay-Lussac y Avogadro, quienes percibieron que estos volúmenes estaban relacionados con el número de moléculas involucradas. En otras palabras, al escalar el sistema a nivel molecular, los volúmenes de combinación representaban la cantidad de moléculas de cada sustancia.
No obstante, antes de adentrarnos en consideraciones teóricas más profundas, procederemos a definir el ratio estequiométrico mediante la letra griega lambda minúscula (λ). Este símbolo representa el cociente de volúmenes entre dos sustancias gaseosas en una reacción química donde no existen ni excesos ni déficits de ninguna de ellas.
|
\[\lambda_{ij}=\frac{V_i}{V_j}\] |
Eq 14.1. Forma estática de la ley de volúmenes de combinación. |
La forma en que se plantea actualmente, la ley de volúmenes de combinación guarda similitud con la ley de Proust, aunque en este escenario, la proporción definida o ratio estequiométrico afecta a múltiples sustancias en una reacción química. Desde esta perspectiva, sería razonable anticipar la necesidad de elaborar tablas de equivalencias con volúmenes estándar para calcular volúmenes experimentales. Esta posibilidad es plausible debido a que, al tratarse de una relación lineal, se puede aplicar de manera directa una regla de tres simple.
Retomando la intuición de Avogadro y sus colegas, surgió un dilema. Dalton sostenía la idea de que los gases elementales de hidrógeno y oxígeno estaban constituidos por átomos libres, y que la molécula de agua se formaba con un átomo de cada uno. Esto llevaba a prever que los volúmenes de combinación generarían un ratio estequiométrico de 1:1. Sin embargo, los resultados de Gay-Lussac no concordaban con esta perspectiva, desconcertando a Dalton. Fue Avogadro quien resolvió ambas posiciones al proponer que los gases elementales estaban compuestos por dos átomos unidos en una molécula diatómica, y que la cantidad de átomos en los reactivos debía ser igual a la presente en los productos. De esta manera, se necesitaban 2 moléculas de hidrógeno, cada una formada por dos átomos, lo que daba un total de cuatro átomos de hidrógeno. Estos reaccionaban con una molécula diatómica de oxígeno para formar dos moléculas de agua, siguiendo la conocida fórmula con un átomo de oxígeno por cada dos de hidrógeno.
Bajo esta perspectiva molecular, los valores que, en la visión macroscópica, representan volúmenes de combinación, adquieren el significado de números de moléculas. Cuando ajustamos estos números de moléculas de manera que reflejen los patrones de enteros más pequeños posibles para completar un solo evento de reacción química, los denominamos números estequiométricos o coeficientes estequiométricos, simbolizados por la letra griega nu minúscula (ν). Es importante recordar que, aunque cuentan con un símbolo independiente, los números estequiométricos se derivan de la cantidad de entidades y, por lo tanto, son adimensionales. Esta consideración implica también que el ratio estequiométrico es equivalente al cociente de los números estequiométricos.
Lo cual posibilita la igualación de ambos cocientes en una formulación más dinámica de la Ley de Volúmenes de Combinación, que denominaremos como la Ley Estequiométrica de Volúmenes de Combinación. Es importante tener en cuenta que, dado que los volúmenes de combinación se registran a presión y temperatura constantes, cualquier teorema derivado de esta ley debe considerar dicha limitación.
|
\[\frac{V_i}{V_d}=\frac{\nu_i}{\nu_d}\] |
Eq 14.2. Forma estática de la ley de volúmenes de combinación. |
En muchas ocasiones, los números estequiométricos se presentan en las ecuaciones químicas, es decir, son proporcionados por el enunciado, desempeñando un papel similar al de las tablas de equivalencias de Richter. Cuando esto sucede, afirmamos que la ecuación química está ajustada, balanceada, o, en otras palabras, cumple con la ley de la conservación de la masa. Miremos primero como extraer los números estequiométricos de ecuaciones químicas ajustadas.
Ejemplo. Identifique los números estequiométricos en la siguiente ecuación química balanceada 2 H2O → 2 H2 + O2. Ejemplo. Identifique los números estequiométricos de las sustancias en la siguiente ecuación química balanceada 3 Hg(OH)2 + 2 H3PO4 → Hg3(PO4)2 + 6 H2O Ejemplo. Identifique los números estequiométricos de las sustancias en la siguiente ecuación química balanceada 8 CO + 17 H2 → C8H18 + 8 H2O
Ahora que sabemos leer los números estequiométricos, si podemos aplicar la ley estequiométrica de volúmenes de combinación.
Ejemplo Si se descomponen 40 litros de amoníaco, calcule el volumen de hidrógeno y nitrógeno que se deberían generar. Utilice la siguiente ecuación química: 2 NH₃ → 3 H₂ + N₂. Ejemplo. Calcular el volumen de oxígeno requerido para completar la combustión de 0.25 dm3 de metano, teniendo en cuenta la ecuación química: CH4 + 2O2 → CO2 + 2H2O
Matamala y Gonzalez. Ejercicio 7.17. Hallar el volumen de nitrógeno a 0°C y 38 cm de Hg requerido para reaccionar completamente con 1.8 L de hidrógeno en CN. Matamala y Gonzalez. Ejercicio 7.26. Cuantos litros de O2 se necesitan para la combustión completa de 30 litros de sulfuro de hidrógeno según la reacción: 2 H2S + 3 O2 → 2 SO2 + 2 H2O. Matamala y Gonzalez. Ejercicio 7.30. Determinar el volumen de dióxido de carbono CO2 que resulta de la combustión completa de 65 L de monóxido de carbono CO. ¿Qué volumen de oxígeno requirió?
Química de Chang 10. Ejemplo 5.11. Calcule el volumen de O2 (en litros) necesario para la combustión completa de 7.64 L de acetileno (C2H2) medido a la misma temperatura y presión. 2C2H2 (g) + 5O2 (g) → 4CO2 (g) + 2H2O (l) Química de Chang 10. Práctica 5.11. Suponiendo que no hay cambios en la temperatura y la presión, calcule el volumen de O2 (en litros) necesario para la combustión completa de 14.9 L de butano (C4H10): 2C4H10 (g) + 13O2 (g) → 8CO2 (g) + 10H2O (l) Química de Chang 10. Problema-5.51. Considere la formación de dióxido de nitrógeno a partir de óxido nítrico y oxígeno: 2NO (g) + O2 (g) → 2NO2 (g) Si se hacen reaccionar 9.0 L de NO con exceso de O2 en STP, ¿cuál es el volumen en litros del NO2 producido?
Para concluir, es importante tener en cuenta que en cualquier teorema se le denomina estequiométrico si el ratio \(\lambda= \nu_i \ / \ \nu_j\) aparece como uno de sus términos. Debido en parte a la oposición de Dalton, pasaron casi cincuenta años antes de que el compatriota italiano de Avogadro, Stanislao Cannizzaro (1826 a 1910), lograra persuadir a la comunidad química de que la hipótesis de Avogadro era correcta. El hecho de que los químicos hayan mostrado inicialmente resistencia a aceptar las ideas de Avogadro durante un período prolongado nos ofrece una indicación sobre la actitud arraigada en la comunidad química. Existe una notoria reticencia a cambiar métodos, nomenclaturas y algoritmos, revelando un fuerte apego a la tradición que a veces roza una postura anticientífica. Por lo tanto, como químicos en formación, es crucial ser conscientes de distinguir entre aspectos fundamentales y simples algoritmos elegidos entre varias posibilidades. Individualmente, debemos estar abiertos a considerar alternativas diferentes a las que comúnmente se presentan en la tradición y los libros de texto. Esta, mis estudiantes, es una actitud científica y crítica que debemos cultivar constantemente.
(15) Las leyes de Avogadro
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
Aunque en la historiografía científica convencional se hace referencia principalmente a una única ley de Avogadro, y en ocasiones se menciona la hipótesis de Avogadro como un corolario, la realidad es un tanto más compleja. Lo que comúnmente se conoce como la hipótesis de Avogadro ha evolucionado a lo largo del tiempo y, en la actualidad, se considera una ley. Esto se debe a que sus valores han sido medidos con precisión, y, sobre todo, hay certeza acerca de la existencia del átomo, aspecto que en la época de Avogadro era bastante incierto y por lo tanto su enunciado fue inicialmente llamado hipótesis.
En nuestro curso de química general, distinguiremos tres leyes estrechamente vinculadas. La primera ley, anteriormente conocida como la hipótesis de Avogadro, la segunda ley, que es la más conocida y está relacionada con la ecuación de estado, y la tercera ley, que define el propio número de Avogadro. Este enfoque nos permitirá explorar de manera más completa y precisa las contribuciones y desarrollos conceptuales asociados con las leyes de Avogadro en la comprensión moderna de la química.
(15.1) Primera ley
En 1811, Amedeo Avogadro presentó su famosa hipótesis, la cual postula que volúmenes iguales de gases, mantenidos a una presión y temperatura constantes, contienen el mismo número de moléculas. A pesar de que inicialmente no la expresó utilizando lenguaje matemático, hoy en día podemos representarla de manera lineal. La expresión matemática correspondiente establece que el volumen de un sistema gaseoso es igual al producto de una constante por el número de entidades del gas, es decir, su cantidad de moléculas. En este contexto, la constante es el volumen que ocupa una sola molécula del gas a una determinada presión y temperatura (Avogadro, 1811; Becker, 2001; Morselli, 1984).
|
\[V=V_N \cdot N\] |
Eq 15.1. Hipótesis de Avogadro de 1811. |
Es importante recordar que este volumen es el volumen vibracional, el cual es considerablemente mayor que el volumen ocupado por la propia molécula. Sin embargo, la rápida vibración de la molécula en ese espacio genera un campo de fuerza que experimentamos como la presión individual de la molécula.
La expresión anterior será denominada la Primera Ley de Avogadro, ya que es cronológicamente la primera relación asociada al número de entidades y fue la única que él propuso explícitamente en palabras. Sin embargo, a partir de esta ley, emergen otras dos relaciones, siendo una de ellas la que más se vincula con Avogadro, a pesar de que él nunca las propuso directamente. Es fascinante observar cómo la Primera Ley de Avogadro sienta las bases para el desarrollo de otras relaciones, contribuyendo a nuestro entendimiento de las propiedades de los gases y la naturaleza molecular de la materia. Aunque Avogadro no haya formulado explícitamente todas estas leyes, su contribución inicial marcó el camino para futuros desarrollos en la comprensión de la física y la química de los gases.
Las otras dos expresiones, estrechamente relacionadas con la obra de Avogadro, surgieron necesariamente después de 1961, momento en el cual Edward Guggenheim introdujo el parámetro cantidad de sustancia (n), que resulta crucial en la formulación de las otras dos leyes de Avogadro. Guggenheim desempeñó un papel fundamental al establecer el concepto de cantidad de sustancia, proporcionando un marco teórico más preciso para comprender las relaciones entre volúmenes de gases y el número de moléculas. A partir de este avance, se pudieron formular otras leyes que expandieron y refinaron la comprensión de Avogadro sobre las propiedades de los gases y las interacciones moleculares. Aunque estas leyes puedan haberse desarrollado posteriormente a la época de Avogadro, su legado sigue siendo fundamental en la evolución de la química.
(15.2) Segunda ley
La segunda ley de Avogadro se define como la consecuencia de mantener constante la presión y la temperatura en la ecuación de estado. En este contexto, la constante obtenida tiene un símbolo propio y se denomina volumen molar. Entre todas las constantes molares mencionadas anteriormente, el volumen molar en la segunda ley de Avogadro adquiere una importancia destacada, ya que a través de ella se definió históricamente el mol, antes de que este se asociara al número de entidades.
Es crucial recordar que el volumen molar a condiciones normales o estándar, es decir, a 1 atmósfera de presión y 0°C, es de 22.41 litros. Estas condiciones fueron inicialmente asociadas por Ostwald con la expresión "molécula-gramo" y posteriormente se simplificó a simplemente "mol". Ahora, exploremos la demostración de la obtención de la segunda ley de Avogadro a partir de la ecuación de estado, lo cual nos permitirá comprender cómo el volumen molar desempeña un papel central en esta ley. Demostración: Obtener la segunda ley de Avogadro a partir de la ecuación de estado, asumiendo presión y temperatura constantes, indique una variante de la anterior que permita hacer cálculos con la masa. También indica la fórmula para calcular el volumen molar en cualquier condición.
|
\[V=V_m \cdot n\] |
Eq 15.2. Segunda ley de Avogadro. |
|
\[V=V_m \cdot \frac{m}{M}\] |
Eq 15.3. Segunda ley de Avogadro usando la masa. |
|
\[V_m=R \cdot \frac{T}{P}=\frac{V}{n}\] |
Eq 15.4. Volumen molar para cualquier condición. |
Ejemplo. ¿Cuál es el volumen que ocupa 10 mol oxígeno en condiciones estándar de presión y temperatura? Ejemplo. ¿Cuál es el volumen que ocupa 24 g oxígeno molecular O2 en condiciones estándar de presión y temperatura? Ejemplo. En condiciones normales un gas desconocido de 2.156 g ocupa 680 mL. Calcule la masa molar e indique su identidad más probable asumiendo que es un gas elemental diatómico. Ejemplo. Calcule el volumen molar a 1500 mmHg y 200 °C. (a) 10 L/mol (b) 20 L/mol (c) 40 L/mol (d) 80 L/mol
Matamala y Gonzalez. Ejercicio 7.7. ¿Qué volumen ocupan 12 g de oxígeno en condiciones normales? Matamala y Gonzalez. Ejercicio 7.8. ¿Qué volumen ocuparán, a C.N. 3 kg de gas cloro? Matamala y Gonzalez. Ejercicio 7.13. En condiciones normales, 1,078 g de un gas ocupan 340 ml. Hallar la masa molar. Matamala y González. Ejercicio 7.28. ¿Qué peso de oxígeno ocupará el mismo volumen que 35 g de nitrógeno y cuantas moléculas hay en ese volumen?
Química de Chang 10. Ejemplo 5.4. Calcule el volumen (en litros) ocupado por 7.40 g de NH3 en STP Química de Chang 10. Práctica 5.4. ¿Cuál es el volumen (en litros) ocupado por 49.8 g de HCl en STP? Química de Chang 10. Problema-5.40. Calcule el volumen (en litros) de 88.4 g de CO2 a TPE Química de Chang 10. Problema-5.41. Un gas a 772 mmHg y 35.0 °C ocupa un volumen de 6.85 L. Calcule su volumen en condiciones estándar de presión y temperatura. Química de Chang 10. Problema-5.42. El hielo es dióxido de carbono sólido. Se coloca una muestra de 0.050 g de hielo seco en un recipiente evacuado de 4.6 L a 30 °C. Calcule la presión dentro del recipiente después de que todo el hielo seco se haya convertido en gas CO2. Química de Chang 10. Problema-5.43. En condiciones estándar de presión y temperatura 0.280 L de un gas pesan 0.400 g. Calcula la masa molar del gas. Química de Chang 10. Problema-5.44. A 741 torr y 44 °C, 7.10 g de un gas ocupan un volumen de 5.40 L. ¿Cuál es la masa molar del gas?
Química la ciencia central 11. Ejercicio 10.40b. Una lata de aerosol con un volumen de 250 ml contiene 2.30 g de gas propano C3H8 como propulsor. (b) ¿Qué volumen ocuparía el propano en STP?
(15.3) Tercera ley
La tercera ley de Avogadro constituye la definición del número de Avogadro y, esencialmente, representa la conjunción de la primera y la segunda ley. Entre todas las leyes, la tercera reviste una importancia fundamental, ya que posibilita la transición del universo molar al universo molecular.
Los químicos han acuñado la expresión "universo molar" para describir el mundo que percibimos con nuestros sentidos, donde la materia aparenta ser continua, sólida y sin vacíos. En contraste, el universo molecular es más peculiar, conformado por partículas que vibran en el vacío generando campos. En este universo, las partículas están sujetas tanto a las leyes de Newton como a las leyes cuánticas. Un ejemplo de esta dualidad es que, aunque podemos modelar el movimiento promedio de las partículas de un gas como si fueran balas de cañón newtonianas, a las cuales se les calcula su velocidad promedio, las moléculas y átomos también pueden experimentar fenómenos cuánticos como el efecto túnel cuántico (Merzbacher, 2002).
El efecto túnel cuántico es un fenómeno que puede experimentar cualquier partícula cuántica, como electrones, átomos y moléculas. Se refiere a la probabilidad de que una partícula atraviese una barrera de energía, incluso cuando clásicamente no tendría suficiente energía para hacerlo. En términos simples, es como si la partícula "atravesara" una pared sin la necesidad de tener energía suficiente para superarla. Este fenómeno es fundamental en la mecánica cuántica y se manifiesta en diversas áreas, desde la conductividad eléctrica en semiconductores hasta reacciones químicas en moléculas, donde las partículas pueden superar barreras de energía potencial mediante el efecto túnel cuántico (Merzbacher, 2002).
La tercera ley está inherentemente relacionada con las dos anteriores, por lo que observaremos cómo se interconectan, aunque en esencia, su comprensión es fácil de memorizar. Demostración: Obtener la definición del número de Avogadro a partir de la hipótesis de Avogadro y la ley de Avogadro, indique una variante de la anterior que permita hacer cálculos con la masa.
|
\[N=N_A \cdot n\] |
Eq 15.5. Tercera ley de Avogadro para cantidad de sustancia. |
|
\[N=N_A \cdot \frac{m}{M}\] |
Eq 15.6. Tercera ley de Avogadro para cantidad de sustancia. |
(15.4) Movimiento browniano
El movimiento browniano se refiere al movimiento aleatorio y caótico observado en partículas microscópicas suspendidas en un fluido, como el constante y vibrante desplazamiento de partículas de polvo en un líquido. Este fenómeno fue intuitivamente descrito por el filósofo-poeta romano Lucrecio en el siglo I a.C., quien, al observar el movimiento de partículas de polvo iluminadas por la luz solar, interpretó la danza caótica como una indicación de la existencia de átomos en constante movimiento. Aunque Jan Ingenhousz y Robert Brown, en 1785 y 1827 respectivamente, observaron irregularidades en el movimiento de partículas, fue Brown quien, al estudiar granos de polen bajo un microscopio, notó el movimiento caótico característico, sin poder explicar su origen (Cattani & Salvadori, 1714; Zhao, Guo, Wu, & Xiao, n.d.).
Einstein proporcionó una descripción analítica sólida del movimiento browniano en 1905. Basándose en la observación de Brown, Einstein desarrolló una teoría que relacionaba el movimiento errático de partículas con la agitación molecular inherente en los fluidos. Al introducir conceptos estadísticos y probabilísticos, Einstein derivó ecuaciones que describían cuantitativamente el comportamiento de las partículas en movimiento browniano, confirmando indirectamente la existencia de átomos y moléculas. Su teoría fue posteriormente respaldada experimentalmente por Jean Baptiste Perrin en 1908, consolidando el concepto del movimiento browniano en la comprensión científica de la materia (Bigg, 2008; Perrin, 1901, 1909, 1911, 1913).
Jean Perrin desempeñó un papel fundamental en la demostración de la existencia del átomo a principios del siglo XX, centrándose en sus investigaciones sobre el movimiento browniano. Utilizando el fenómeno de Brownian motion, que describe el movimiento constante y caótico de partículas microscópicas en un líquido o gas, Perrin propuso una conexión tangible entre el mundo macroscópico y el sub-microscópico. A través de sus experimentos en la década de 1900, Perrin empleó la técnica del ultramicroscopio, un instrumento innovador desarrollado por Richard Zsigmondy y Henry Siedentopf, para observar partículas coloidales individuales en suspensión. Al rastrear la trayectoria de estas partículas mediante un diagrama detallado, Perrin presentó una evidencia visual convincente del movimiento browniano, que, según él, solo podía entenderse y ser una prueba experimental de la existencia de átomos si se observaba de la manera correcta. Su trabajo pionero y las representaciones visuales resultantes, incluyendo la famosa traza de partículas sobre papel cuadriculado, contribuyeron significativamente a consolidar la aceptación de la realidad atómica en la comunidad científica, culminando en el reconocimiento de Jean Perrin con el Premio Nobel de Física en 1926 por haber puesto fin a la larga controversia sobre la existencia real de las moléculas (Rodgers, 2019).
Además, Perrin no se limitó a demostrar el movimiento browniano como evidencia de la existencia del átomo, sino que también enfatizó la importancia de la visualización en sus argumentos científicos. Reconoció que, aunque los átomos y las moléculas nunca se observaron directamente, las representaciones visuales, como los diagramas y películas que produjo, jugaron un papel crucial en la persuasión y en la comprensión de la realidad sub-microscópica. Su enfoque en la visualidad y las estrategias para hacer que el mundo sub-microscópico fuera accesible a los sentidos contribuyó significativamente a la consolidación de la noción de realidad molecular en la transición del siglo XIX al XX, marcando un hito en la historia de la física y la aceptación generalizada de la existencia de átomos.
(15.5) El número de Avogadro o de Perrin
El término "número de Avogadro" fue acuñado antes de la aparición del concepto de cantidad de sustancia. La primera formulación de este número en su forma más primitiva se remonta a una serie de artículos de Jean Perrin entre 1908 y 1911. Por otro lado, el concepto de cantidad de sustancia se estableció alrededor de 1961. Esto revela que, aunque ambos elementos estén presentes en una misma ecuación simple, su relación no resultó inmediatamente evidente. Hacia 2019, el número de Avogadro fue fijado arbitrariamente como una constante fundamental del universo, crucial para definir otras importantes constantes como la constante de los gases ideales. Su valor es de 6.022 140 76 x 1023 mol-1 (BIPM, 2018; Güttler, Bettin, et al., 2019; Güttler, Rienitz, et al., 2019; Marquardt, 2019).
En mi perspectiva, Perrin tenía la opción y, desde mi punto de vista, la oportunidad de recibir reconocimiento por la constante; sin embargo, decidió atribuirla a Avogadro. Es crucial tener en cuenta que, para un científico, la reputación es fundamental, incluso más relevante que la ocupación inmediata. La reputación le permite atraer a jóvenes investigadores talentosos a su órbita de influencia, lo que le asegura aún más prestigio, asegurar financiamiento para la investigación y trasladarse entre instituciones educativas con relativa facilidad. Fue debido a este gesto de humildad que, con el tiempo, se originó un error muy extendido, ya que muchas personas creen erróneamente que fue Amadeo Avogadro quien propuso la constante.
Recuerda que, según las reglas del Libro de Oro y el Sistema Internacional de Unidades, los números de entidades no poseen unidades. A pesar de ello, existe una tradición entre los químicos de desafiar esta convención, optando por asignar pseudounidades asociadas a la entidad contada, como huevos, átomos o moléculas. Si consideráramos la cuenta de huevos, el número de Avogadro indicaría cuántos huevos caben en una mol de huevos. Dado que la notación científica tiende a ser grande, esto implicaría una cantidad considerable de huevos, alrededor de 602 mil trillones de huevos sería necesarios para completar una sola mol de huevos.
(15.6) La tercera ley y la ley de Proust
En algunas situaciones, se nos solicita determinar el número de átomos presentes en una masa de sustancia para cada elemento específico. Para lograr esto, es necesario derivar una fórmula que relacione el número de moléculas con el número de átomos. Esta fórmula se obtiene de manera axiomática, es decir, surge a partir de un análisis directo de la definición teórica de molécula. Además, sirve como un medio para interpretar de manera molecular la ley de Proust sobre proporciones definidas.
Recuerda que la ley de Proust establece que las proporciones de cada elemento en una molécula son constantes. En este contexto, interpretamos esta proporción como el subíndice. De manera axiomática, afirmamos que el número de átomos J en una molécula j es igual al número de moléculas j multiplicada por el subíndice del elemento J en esa molécula j. En términos matemáticos, expresamos esto como
|
\[N(J)_j=si(J)_j \cdot N_j\] |
Eq 15.7. Interpretación molecular de la ley de Proust de Proporciones definidas. |
Ejemplo. Calcule el número de átomos de cada elemento presente en (a) 1 molécula y (b) 4 moléculas de hexacloroplatinato(IV) de amonio, cuya fórmula es (NH₄)₂[PtCl₆]. Esta definición carece de utilidad si no la vinculamos con el concepto molar, por lo que es necesario realizar una demostración. Demostración: ajustar la interpretación molecular de la ley de Proust de manera que podamos calcular el número de átomos de cualquier elemento a partir de la cantidad de sustancia o la masa de la molécula. Ejemplo. Cuantos átomos de Oxígeno, 20 moles de sulfato de amonio (NH3)2SO4. Ejemplo. Cuantos átomos de Oxígeno hay en 92 g de CO2.
(16) La técnica de Cannizzaro
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
El método de Cannizzaro, desarrollado por el químico italiano Stanislao Cannizzaro en 1858, fue un avance crucial en la determinación de masas atómicas relativas, un problema fundamental en la química del siglo XIX (Brock, 1985; Kauffman, 1994). En ese período, la estequiometría y la relación entre las masas de los elementos en una reacción química eran mal comprendidas. El método de Cannizzaro se basa en la idea de que los gases a temperaturas y presiones conocidas ocupan volúmenes definidos, lo que permitió establecer la relación entre las masas de los elementos. La técnica se Cannizzaro se sostiene en:
(a) Uso de la hipótesis de Avogadro: Cannizzaro respaldó la hipótesis de Avogadro, que sostiene que volúmenes iguales de gases, en las mismas condiciones de temperatura y presión, contienen el mismo número de moléculas. Esta hipótesis resultó fundamental para establecer conexiones entre las masas atómicas de distintos elementos.
(b) El hidrógeno como unidad relativa: Dado que Cannizzaro también adoptó la hipótesis de los gases diatómicos de Avogadro, tenía la intención de que el hidrógeno gaseoso registrara una masa de 2 gramos. Así, el hidrógeno monoatómico se asignaría a una masa relativa de 1, siendo el elemento más ligero y sirviendo como referencia para las demás masas. Sin embargo, el hidrógeno solo alcanzó los 2 gramos a 1 atm y 0°C cuando se completaron 22.41 litros.
(c) Uso del volumen 22.41 Litros. Una vez establecido el volumen estándar donde el hidrógeno gaseoso pesa 2 y el hidrógeno monoatómico pesa 1, se aplicó el mismo procedimiento para determinar los pesos de otros elementos. De esta manera, el oxígeno gaseoso registró un peso de 32, y consecuentemente, el monoatómico registró 16. De manera similar, el cloro gaseoso registró 71 y su forma monoatómica registró 35.5, y así sucesivamente para otros elementos gaseosos.
(16.1) Modelo matemático
El método de Cannizzaro allanó el camino para la determinación más precisa de las masas atómicas y la formulación de la tabla periódica de los elementos. Su trabajo ayudó a establecer las bases de la estequiometría moderna y la química, y su contribución fue de gran importancia para la química del siglo XIX. Aunque Cannizzaro no disponía de nuestro moderno sistema de parámetros matemáticos, el propósito de este curso es transformar la narración anterior en una fórmula que nos habilite para calcular la masa molar. Esta masa molar representa el valor de los pesos atómicos expresados en unidades de g/mol (gramos sobre mol). Demostración. A partir de la ecuación de estado encuentre un modelo matemático que describa la técnica de Cannizzaro.
|
\[M_i= V_m \cdot \rho^o\] |
Eq 16.1. Modelo matemático de la técnica de Cannizzaro, masa molar como función de la densidad de un gas en condiciones normales por el volumen molar 22.41 L/mol. |
La densidad estándar de un gas se refiere a la densidad de ese gas en condiciones normales (CN), que son 0 °C (273.15 K) y 1 atmósfera (101.3 kPa) de presión. En estas condiciones, un mol de cualquier gas ocupa un volumen de aproximadamente 22.4 litros. La densidad estándar de un gas se expresa en gramos sobre litro (g/L) o kilogramos sobre metro cúbico (kg/m³) a condiciones normales. A continuación, te proporciono las densidades estándar para algunos gases elementales, el dióxido de carbono (CO2), en gramos sobre litro:
Hidrógeno: 0.0899; Helio: 0.179; Nitrógeno: 1.250; Oxígeno: 1.429; Flúor: 1.696; Cloro: 3.213; Neón: 0.900; Argón: 1.784; Kriptón: 3.733 g/L; Xenón (Xe): 5.894. En el caso del dióxido de carbono (CO2), su densidad estándar es de alrededor de 1.977 g/L a condiciones normales. Estas densidades son útiles para realizar cálculos estequiométricos y para comparar las masas de diferentes sustancias gaseosas bajo condiciones estándar.
Ejemplo. Calcule el peso atómico del nitrógeno atómico empleando la densidad del nitrógeno molecular 1.250 g/L. Ejemplo. Calcular la densidad del cloro molecular en condiciones normales. Matamala y González Ejercicio 7.9. Hallar la densidad del oxígeno en C.N. Química la ciencia central 13. Práctica 10.08.1. ¿Cuál es la masa molar de un hidrocarburo desconocido cuya densidad se mide en 1.97 g/L en STP? (a) 4.04 g/mol, (b) 30.7 g/mol, (c) 44.1 g/mol, (d) 48.2 g/mol. Hipertexto. Analiza y resuelve 5. ¿Qué relación existe entre la densidad y el peso molecular de los gases?
(16.2) Hacia la tabla periódica
La contribución de Cannizzaro al establecer los pesos atómicos relativos representó un avance que casi pasó desapercibido, dado que se basaba en la entonces frágil hipótesis atómica. A pesar de las dudas que existían en torno a dicha hipótesis, los químicos de los elementos optaron por emplearla como una herramienta para resolver problemas concretos. Durante décadas, los químicos se esforzaron por organizar los elementos recién descubiertos, encontrándose con la dificultad de no hallar patrones de organización generales, sino más bien pequeñas agrupaciones conocidas como familias (Chapman, 2021; Dias, 2020; Egdell & Bruton, 2020; Rouvray & King, 2004; E. Scerri, 2012; E. R. Scerri, 2006).
Las familias consistían comúnmente en grupos de tres elementos que compartían patrones de reacción similares. Por ejemplo, el potasio, el sodio y el litio pertenecen a una familia de metales blandos que reaccionan de manera violenta con el agua. Aunque la intensidad de las reacciones puede variar, presentan similitudes fundamentales. Del mismo modo, otra familia significativa incluía a los metales nobles oro, plata y cobre, así como la familia de los halógenos, representada por el flúor, cloro y bromo.
Los pesos atómicos establecidos por Cannizzaro inicialmente se utilizaron para determinar directamente los pesos relativos de elementos gaseosos. Sin embargo, también se podían aplicar mediante técnicas estequiométricas para inferir los pesos atómicos de otros elementos, como se explorará en capítulos subsiguientes. Lo crucial fue la pronta generación de una lista de pesos atómicos, proporcionando a los químicos un segundo criterio de organización. Con estos datos a su disposición, varios científicos intentaron organizar los elementos en un patrón de pesos crecientes, estructurándolos en columnas que reflejaran sus propiedades químicas como familias.
Entre los diversos intentos, la propuesta más exitosa fue la de Dmitri Mendeléyev, ya que dejaba espacios para elementos no reportados y, mediante el análisis de los elementos vecinos, incluso permitía prever aproximadamente las propiedades de esos elementos. El germanio emergió como uno de los elementos más significativos en la construcción de la tabla periódica de Mendeléyev. Este metal asumió las propiedades previstas para un elemento hipotético llamado "aka-silicio", que Mendeléyev había predicho ocuparía un espacio vacío en la tabla periódica. La inclusión exitosa del germanio no solo dotó a la tabla periódica de una estructura organizativa, sino que también le confirió un carácter predictivo notable.
La Ley Periódica establece que, al organizar los elementos según su número atómico creciente y por familias, deben distribuirse en filas periódicas. A pesar de que, como hemos visto, el peso atómico fue la propiedad organizativa más importante, no estaba exenta de fallas. A principios del siglo XX, cuando se descubrieron las propiedades radioeléctricas del núcleo, el criterio pasó del peso atómico al número atómico. La periodicidad implica que, al comenzar una nueva fila, las propiedades químicas de los elementos en las columnas empiezan a repetirse de manera regular. Este patrón de repetición se incrementa: la primera fila consta solo de dos elementos, las siguientes dos de ocho elementos cada una, las subsiguientes dos de diez y dieciocho elementos, y las dos últimas de 32 elementos para completar los 118 elementos conocidos. Es crucial señalar que, en la época de Mendeléyev, muchos elementos aún no habían sido aislados. Además, es probable que su tabla periódica no incluya la última actualización de la IUPAC, que incorpora elementos como el Nihonio y el Oganesson.
Abordaremos en futuras lecciones detalles más profundos sobre la tabla periódica. Por ahora, lo crucial es reconocer que la química, al cuantificar numéricamente las propiedades de los gases, pudo expandirse hacia otras áreas de investigación, incluyendo la Ley Periódica y proyectos relacionados con la estructura del átomo. Vale la pena destacar que, aunque la existencia del átomo era motivo de escepticismo para muchos científicos, otros se aventuraron a explorar su estructura eléctrica, donde los gases desempeñarían un papel significativo, pero ahora como plasmas eléctricamente cargados. Peso eso también lo analizaremos en secciones futuras.
(17) Usando la ecuación de estado
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
En lecciones anteriores, exploramos la definición de la ecuación de estado de los gases ideales \(P \cdot V = n \cdot R \cdot T\) y cómo utilizarla para derivar otras leyes importantes de los gases, incluyendo las leyes empíricas clásicas, así como las técnicas de Cannizzaro y la ley de Avogadro. Ahora, nos adentraremos en una comprensión más utilitaria de esta ecuación.
La ley de los gases ideales, expresada como la ecuación de estado \(P \cdot V = n \cdot R \cdot T\), contiene cinco términos en total: la presión (P), el volumen (V), la cantidad de sustancia (n), la constante de los gases ideales (R) y la temperatura (T).
Dado que la constante R se mantiene invariable, nos encontramos con solo cuatro términos variables. Esta condición conlleva a que los ejercicios de ecuaciones de estado estática presenten cuatro variantes, una para cada uno de los parámetros expresados en función de los demás y la constante. Por ende, resulta crucial que adquieras la habilidad de despejar la ecuación de estado en cualquiera de sus cuatro formas, prescindiendo de la necesidad de recurrir a una tabla o formulario. Posteriormente, es imperativo que seas capaz de operar con estas variantes. Cabe recordar que, en este contexto, el uso de una regla de tres resulta inviable. DEMOSTRACION. Exprese la ecuación de estado de los gases ideales para poder calcular el volumen, la presión, la cantidad de sustancia y la temperatura absoluta respectivamente
|
\[P_i =R \cdot T_i \cdot\frac{n_i}{V_i}\] |
Eq 17.1. Presión en función de las variables de estado de un gas ideal. |
|
\[V_i =R \cdot T_i \cdot\frac{n_i}{P_i} \] |
Eq 17.2. Volumen en función de las variables de estado de un gas ideal. |
|
\[n_i = \frac{P_i \cdot V_i}{R \cdot T_i}\] |
Eq 17.3. Cantidad de sustancia en función de las variables de estado de un gas ideal. |
|
\[T_i = \frac{P_i \cdot V_i}{R \cdot n_i}\] |
Eq 17.4. Temperatura en función de las variables de estado de un gas ideal. |
Ejemplo. Si tienes un gas con un volumen de 3.0 L, una cantidad de sustancia de 2.5 mol, y a una temperatura de 300 K, ¿cuál es la presión del gas? Ejemplo. Si un gas a una presión de 2.0 atm, una cantidad de sustancia de 1.5 mol, y a una temperatura de 400 K, ¿cuál es el volumen del gas? Ejemplo. Un gas ocupa un volumen de 1000 mL a una presión de 1.2 atm y a una temperatura de 77 °C. ¿Cuántas moles de gas hay en el sistema? Ejemplo. Un gas tiene una presión de 303.9 kPa, un volumen de 4000 mL, y una cantidad de sustancia de 0.80 mol. ¿Cuál es la temperatura del gas en °C?
(17.1.1) Despejar a presión
Química de Chang 10. Ejemplo 5.3. El hexafluoruro de azufre (SF6) es un gas incoloro, inodoro y muy poco reactivo. Calcule la presión (en atm) ejercida por 1.82 moles de gas en un recipiente de acero de 5.43 L de volumen a 69.5°C. Química de Chang 10. Problema-5.32. Dado que hay 6.9 moles de gas monóxido de carbono en un recipiente de 30.4 L de volumen, ¿cuál es la presión del gas (en atm) si la temperatura es de 62 °C? Química de Chang 10. Problema Problema-5.42. El hielo es dióxido de carbono sólido. Se coloca una muestra de 0.050 g de hielo seco en un recipiente evacuado de 4.6 L a 30 °C. Calcule la presión dentro del recipiente después de que todo el hielo seco se haya convertido en gas CO2. Química la ciencia central 11. Ejercicio 10.33d. Hallar la presión de un gas a 585 mL 0.250 mol y 295 K
(17.1.2) Despejar el volumen
Matamala y Gonzalez. Ejercicio 7.10. ¿Qué volumen ocupará 8,8 g de gas carbónico, CO2, a 12 °C y 720 mm Hg? Matamala y Gonzalez. Ejercicio 7.18. ¿Qué volumen ocupan 5,7 g de flúor, F2, a 27°C y ½ atm? Matamala y Gonzalez. Ejercicio 7.20. Hallar el volumen ocupado por 0,1 mol de un gas ideal a 0°C y 0,25 atm de presión. Química de Chang 10. Práctica 5.3. Calcule el volumen (en litros) ocupado por 2.12 moles de óxido nítrico (NO) a 6.54 atm y 76°C. Química de Chang 10. Problema-5.33. ¿Qué volumen ocuparán 5.6 moles de gas hexafluoruro de azufre (SF6) si la temperatura y la presión del gas son 128 ° C y 9.4 atm? Química la ciencia central 11. Ejercicio 10.33c. Hallar el volumen de un gas a 650 torr 0.333 mol 350 K Química la ciencia central 11. Ejercicio 10.34a. Calcule el volumen del gas, en litros, si 1.50 mol tiene una presión de 1.25 atm a una temperatura de -6 ° C. Hipertexto. Ejemplo 4. Una masa gaseosa ocupa un volumen de 2.5 litros a 12 °C y 2 atm de presión. ¿Cuál es el volumen del gas si la temperatura aumenta a 38 °C y la presión se incrementa hasta 2.5 atm? Hipertexto. Problemas básicos 8.1. Determinar el volumen de 1.20 moles de oxígeno gaseoso, O2, a 27 °C y 1 atmósfera de presión. Hipertexto. Problemas básicos 11. Un gas ocupa un volumen de 800 mL a una presión de 650 mmHg. Calcula el volumen que ocupará a temperatura constante y a los siguientes valores de presión: a) 1 atm b) 800 torr c) 320 mmHg d) 100 torr
(17.1.3) Despejar la cantidad de sustancia
Matamala y Gonzalez. Ejercicio 7.21. A 380 mmHg de presión y 0°C, un reciente de 11,2 L de gas contendrá un numero de moles de: Química de Chang 10. Problema-5.31. Una muestra de nitrógeno gaseoso almacenada en un recipiente de 2.3 L de volumen y a una temperatura de 32 °C ejerce una presión de 4.7 atm. Calcule el número de moles de gas presentes. Química la ciencia central 11. Ejercicio 10.33b. Hallar los moles de un gas a 0.300 atm 0.250 L y 27 °C. Química la ciencia central 11. Ejercicio 10.34d. Calcule la cantidad de gas, en moles, si 126.5 L a 54 °C tiene una presión de 11.25 kPa. Hipertexto. Ejemplo 5. Calcula el número de moles de un gas que se encuentran en un recipiente cerrado de 2,0 litros; sometido a una presión de 2,3 atm y a 25 °C. Hipertexto. Problemas básicos 8.2. Determinar el número de moles en 10 L de CO2 a 20 °C y 800 torr.
(17.1.4) Despejar la temperatura
Matamala y Gonzalez. Ejercicio 7.11. Tres moles de un gas perfecto ocupan 100 litros a 1 atmósfera. ¿Cuál es su temperatura? Química de Chang 10. Problema-5.34. Cierta cantidad de un gas está contenida en un recipiente de vidrio a 25°C y a una presión de 0.800 atm. Suponga que el recipiente soporta una presión máxima de 2.00 atm. ¿Cuánto se puede elevar la temperatura del gas sin que se rompa el recipiente? Química la ciencia central 11. Ejercicio 10.33a. Hallar la temperatura de un gas a 2.00 atm, 1.00 L, y 0.500 mol. Química la ciencia central 11. Ejercicio 10.34b. Calcule la temperatura absoluta del gas a la cual 3.33x10-3 mol ocupa 478 mL a 750 torr.
(18) Ecuación de estado combinada
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
Al igual que las leyes de Avogadro y otras leyes empíricas de gases, la ley de los gases ideales puede modificarse para estado, identidad de la sustancia, pureza, masa, densidad, y número de entidades, así como ser adaptada para sistemas no gaseosos, pero que se describen como ideales por comportarse de manera tal que pueden operarse como si fueran gases.
Al igual que con la ley de Avogadro, la ecuación de estado estático puede modificarse, ya sea para un cambio de estado o para un cambio de identidad de gas, ya sea dos gases mezclados, o un gas al interior de un conjunto total o mezcla de gases. DEMOSTRACION. Modificar la ecuación de estado para volumen molar, masa, densidad, número de entidades, y concentración molar
|
\[ \frac{P_i}{P_{oi}} \cdot \frac{V_i}{V_{oi}} = \frac{n_i}{n_{oi}} \cdot \frac{T_i}{T_{oi}} \] |
Eq 18.1 Ley combinada de gases ideales para un cambio de estado.
|
|
\[ V_m = \frac{R \cdot T}{P} \] |
Eq 18.2 Ecuación de estado estático definida para el volumen molar. |
|
\[ \frac{V_m}{V_{o,m}} = \frac{T}{T_o} \cdot \frac{P_o}{P} \] |
Eq 18.3 Ecuación de estado dinámico definida para el volumen molar. |
|
\[ P_i \cdot V_i = \frac{m_i}{M_i} \cdot R \cdot T_i \] |
Eq 18.4 Ecuación de estado estático definida para la masa
|
|
\[ \frac{P_i}{P_{oi}} \cdot \frac{V_i}{V_{oi}} = \frac{m_i}{m_{oi}} \cdot \frac{T_i}{T_{oi}} \] |
Eq 18.5 Ecuación de estado dinámico definida para la masa.
|
|
\[ P_i \cdot M_i = \rho_i \cdot R \cdot T_i \] |
Eq 18.6 Ecuación de estado estático definida para la densidad. |
|
\[ \frac{P_i}{P_{oi}} = \frac{\rho_i}{\rho_{oi}} \cdot \frac{T_i}{T_{oi}} \] |
Eq 18.7 Ecuación de estado dinámico definida para la densidad.
|
|
\[ P_i \cdot V_i = N_i \cdot k_B \cdot T_i \] |
Eq 18.8 Ecuación de estado estático definida para el número de entidades. |
|
\[ \frac{P_i}{P_{oi}} \cdot \frac{V_i}{V_{oi}} = \frac{N_i}{N_{oi}} \cdot \frac{T_i}{T_{oi}} \] |
Eq 18.9 Ecuación de estado dinámico definida para el número de entidades. |
|
\[ P_i = c_i \cdot R \cdot T_i \] |
Eq 18.10 Ecuación de estado estático definida para la concentración molar. |
|
\[ \frac{P_i}{P_{oi}} = \frac{c_i}{c_{oi}} \cdot \frac{T_i}{T_{oi}} \] |
Eq 18.11 Ecuación de estado dinámico definida para la concentración molar. |
Ejemplo. Un gas, inicialmente a una presión de 10 atmósferas y una temperatura de 300 K, ocupando un volumen de 20 litros, experimenta un cambio en sus condiciones. Se nos pide determinar el volumen final cuando la presión se triplica y la temperatura final es la mitad de la inicial Ejemplo. Un sistema gaseoso compuesto por 4.00 x 10^25 moléculas de gas ideal, inicialmente a una presión de 10 atmósferas y a una temperatura de 270 K, experimenta cambios en sus condiciones. Si el volumen se mantiene constante, se busca determinar cuántas moléculas de gas habrá cuando el sistema se somete a una presión diez veces mayor que la inicial y a una quinta parte de la temperatura inicial
(18.1) Ejemplos de la forma combinada simple
Matamala y González. Ejercicio 7.5. Cierta masa de gas ocupa 20 litros a 27 °C y 380 mm de presión ¿Qué volumen ocupará en C.N.? Matamala y González. Ejercicio 7.6. ¿Cuántos globos de 6 L de capacidad cada uno, en condiciones normales, pueden llenarse con 250 L de hidrógeno, medidos a 68 °F y 587 mm de presión? ¿sobra gas? Química de Chang 10. Ejemplo 5.7. Una pequeña burbuja se eleva desde el fondo de un lago, donde la temperatura y la presión son 8 °C y 6.4 atm, hasta la superficie del agua, donde la temperatura es 25 °C y la presión es 1.0 atm. Calcule el volumen final (en mL) de la burbuja si su volumen inicial fue de 2.1 mL. Química de Chang 10. Práctica 5.7. Un gas inicialmente a 4.0 L, 1.2 atm y 66 °C sufre un cambio de modo que su volumen y temperatura finales son 1.7 L y 42 °C. ¿Cuál es su presión final? Suponga que el número de lunares permanece sin cambios. Química de Chang 10. Problema-5.35. Un globo lleno de gas, que tiene un volumen de 2.50 L a 1.2 atm y 25°C, se eleva en la estratosfera (unos 30 km sobre la superficie de la Tierra), donde la temperatura y la presión son de -23°C y 3.00 x 10-3 atm, respectivamente. Calcule el volumen final del globo. Química de Chang 10. Problema-5.37. La presión de 6.0 L de un gas ideal en un recipiente flexible se reduce a un tercio de su presión original, y su temperatura absoluta disminuye a la mitad. ¿Cuál es el volumen final del gas?
Química de Chang 10. Problema-5.39. Un gas ideal originalmente a 0.85 atm y 66°C se expande hasta que su volumen final, presión y temperatura son de 94 mL, 0.60 atm y 45°C, respectivamente. ¿Cuál era su volumen inicial?
Química la ciencia central 13. Muestra 10.06. Un globo inflado tiene un volumen de 6.0 L al nivel del mar (1.0 atm) y se le permite ascender hasta que la presión sea de 0.45 atm. Durante el ascenso, la temperatura del gas cae de 22 °C a -21 °C. Calcula el volumen del globo en su altura final. Química la ciencia central 13. Práctica 10.06.1. Un gas ocupa un volumen de 0.75 L a 20 °C a 720 torr. ¿Qué volumen ocuparía el gas a 41 °C y 760 torr? (a) 1.45 L, (b) 0.85 L, (c) 0.76 L, (d) 0.66 L, (e) 0.35 L. Química la ciencia central 13. Ejercicio 10.43c. El cloro se usa ampliamente para purificar los suministros municipales de agua y para tratar las aguas de piscinas. Suponga que el volumen de una muestra particular de gas Cl2 es 8.70 L a 895 torr y 24 °C. (c) ¿A qué temperatura será el volumen 15,00 L si la presión es 8,76x102 torr? Química la ciencia central 13. Práctica 10.06.2. Una muestra de oxígeno gaseoso de 0.50 mol se encuentra confinada a 0 °C y 1.0 atm en un cilindro con un pistón móvil. El pistón comprime el gas de modo que el volumen final es la mitad del volumen inicial y la presión final es de 2.2 atm. ¿Cuál es la temperatura final del gas en grados Celsius? Hipertexto. Problemas básicos 9. Un gas ocupa un volumen de 520 mL a 25 °C y 650 mmHg de presión. Calcula el volumen que ocuparía el gas a 700 mmHg y 32 °C.
(18.2) Ejemplos con volumen molar
Matamala y González Ejercicio 7.19. El volumen molar del acetileno, C2H2, a 300 K y 0,45 atm, es:
(18.3) Ejemplos con masa y masa molar
Matamala y González. Ejercicio 7.12. ¿Cuál es el peso molecular de un gas de 1 g, si el mismo ocupa 200 ml a 150°C y 760 mmHg? Matamala y González. Ejercicio 7.14. Hallar el peso molecular de un gas, si 725 ml del mismo, a 20°C y 562 mmHg, pesan 0,983 g. Matamala y González. Ejercicio 7.16. ¿Cuánto pesan 0,75 L de cloro, Cl2, medidos a 20°C y 0,25 atm de presión? }
Química de Chang 10. Ejemplo 5.9. Un químico ha sintetizado un compuesto gaseoso de color amarillo verdoso de cloro y oxígeno y encuentra que su densidad es de 7.71 g / L a 36°C y 2.88 atm. Calcule la masa molar del compuesto y determine su fórmula molecular. uímica de Chang 10. Práctica 5.9. La densidad de un compuesto orgánico gaseoso es 3.38 g / L a 40°C y 1.97 atm. ¿Cuál es su masa molar?
Química la ciencia central 13. Ejercicio 10.31. Suponga que le dan dos matraces de 1 L y le dicen que uno contiene un gas de masa molar 30, el otro un gas de masa molar 60, ambos a la misma temperatura. La presión en el matraz A es X atm, y la masa de gas en el matraz es 1.2 g. La presión en el matraz B es 0.5 X atm, y la masa de gas en ese matraz es 1.2 g. ¿Qué matraz contiene el gas de la masa molar 30 y cuál contiene el gas de la masa molar 60? Química la ciencia central 13. Ejercicio 10.32. Suponga que le dan dos matraces a la misma temperatura, uno de volumen 2 L y el otro de volumen 3 L. El matraz de 2 L contiene 4,8 g de gas y la presión del gas es X atm. El matraz de 3 litros contiene 0,36 g de gas, y la presión del gas es 0,1X. ¿Los dos gases tienen la misma masa molar? Si no, ¿cuál contiene el gas de mayor masa molar? Química la ciencia central 13. Ejercicio 10.35. Los dirigibles Goodyear, que con frecuencia vuelan sobre eventos deportivos, contienen aproximadamente 175000 pies3 de helio. Si el gas está a 23 °C y 1.0 atm, ¿qué masa de helio hay en un dirigible? Química la ciencia central 13. Ejercicio 10.39a. El tanque de un buzo contiene 0.29 kg de O2 comprimido en un volumen de 2.3 L. Calcule la presión de gas dentro del tanque a 9 °C. Química la ciencia central 13. Ejercicio 10.39b. El tanque de un buzo contiene 0.29 kg de O2 comprimido en un volumen de 2.3 L. ¿Qué volumen ocuparía 0.29 kg de O2 a 26 °C y 0.95 atm? Química la ciencia central 13. Ejercicio 10.40a. Una lata de aerosol con un volumen de 250 ml contiene 2.30 g de gas propano C3H8 como ropulsor. Si la lata está a 23 °C, ¿cuál es la presión en la lata? Química la ciencia central 13. Ejercicio 10.40c. Una lata de aerosol con un volumen de 250 ml contiene 2.30 g de gas propano C3H8 como propulsor. La etiqueta de la lata dice que la exposición a temperaturas superiores a 130 °F puede hacer que la lata explote. ¿Cuál es la presión en la lata a esta temperatura? Química la ciencia central 13. Ejercicio 10.43a. El cloro se usa ampliamente para purificar los suministros municipales de agua y para tratar las aguas de piscinas. Suponga que el volumen de una muestra particular de gas Cl2 es 8.70 L a 895 torr y 24 ° C. ¿Cuántos gramos de Cl2 hay en la muestra? Química la ciencia central 13. Ejercicio 10.51b. Calcule la masa molar de un gas si 2,50 g ocupa 0,875 L a 685 torr y 35 ° C. Química la ciencia central 13. Ejercicio 10.52b. Calcule la masa molar de un vapor que tiene una densidad de 7,135 g/L a 12 ° C y 743 torr. Química la ciencia central 13. Ejercicio 10.53. En la técnica del bulbo de Dumas para determinar la masa molar de un líquido desconocido, se vaporiza la muestra de un líquido que hierve por debajo de 100 ° C en un baño de agua hirviendo y se determina la masa de vapor necesaria para llenar el bulbo. A partir de los siguientes datos, calcule la masa molar del líquido desconocido: masa de vapor desconocido, 1,012 g; volumen de bulbo, 354 cm3; presión, 742 torr; temperatura, 99 ° C. Química la ciencia central 13. Ejercicio 10.54. La masa molar de una sustancia volátil se determinó mediante el método del bulbo de Dumas descrito en el ejercicio 10.53. El vapor desconocido tenía una masa de 0,846 g; el volumen del bulbo era de 354 cm3, la presión de 752 torr y la temperatura de 100 °C. Calcule la masa molar del vapor desconocido. Química la ciencia central 13. Ejercicio 10.74a. Una muestra de 3.00 g de SO2(g) originalmente en un recipiente de 5.00 L a 21 °C se transfiere a un recipiente de 10.0 L a 26 °C. Una muestra de 2.35 g de N2(g) originalmente en un recipiente de 2.50 L a 20 °C se transfiere a este mismo recipiente de 10.0 L. ¿Cuál es la presión parcial de SO2(g) en el recipiente más grande? Química la ciencia central 13. Ejercicio 10.74b. Una muestra de 3.00 g de SO2(g) originalmente en un recipiente de 5.00 L a 21 °C se transfiere a un recipiente de 10.0 L a 26 °C. Una muestra de 2.35 g de N2(g) originalmente en un recipiente de 2.50 L a 20 °C se transfiere a este mismo recipiente de 10.0 L. (b) ¿Cuál es la presión parcial de N2(g) en este recipiente? Hipertexto. Problemas de profundización 12. Calcula el volumen de un tanque de 40 kg de metano (CH4) a 25 °C y 1 atm. ¿Qué sucederá si se aumenta la temperatura y la presión?
(18.4) Ejemplos con la densidad
Ejemplo. La densidad de un compuesto orgánico gaseoso es 3.38 g / L a 40°C y 1.97 atm. ¿Cuál es su masa molar? || Pulse aquí. Matamala y Gonzalez Ejercicio 7.15. Hallar la densidad del amoníaco, NH3, a 640 mmHg y 27°C. Matamala y González Ejercicio 7.24 ¿Cuántas moléculas hay en 11,2 litros de un gas a 273 °C y 380 mmHg? Si el gas es nitrógeno, ¿Cuántos átomos hay?, si el gas es amoníaco ¿Cuántos átomos de H hay? Química de Chang 10. Ejemplo 5.8. Calcule la densidad del dióxido de carbono (CO2) en gramos por litro (g / L) a 0.990 atm y 55°C. Química de Chang 10. Práctica 5.8. ¿Cuál es la densidad (en g / L) del hexafluoruro de uranio (UF6) a 779 mmHg y 62ºC? Química de Chang 10. Problema-5.47. Un recipiente de 2.10 L contiene 4.65 g de un gas a 1.00 atm y 27.0 ° C. (a) Calcule la densidad del gas en gramos por litro (b) ¿Cuál es la masa molar del gas? Química de Chang 10. Problema-5.48. Calcule la densidad del gas bromuro de hidrógeno (HBr) en gramos por litro a 733 mmHg y 46 °C.
Química la ciencia central 13. Muestra 10.07. ¿Cuál es la densidad del vapor de tetracloruro de carbono a 714 torr y 125 °C? Química la ciencia central 13. Práctica 10.07.1. ¿Cuál es la densidad del metano, CH4, en un recipiente donde la presión es de 910 torr y la temperatura es de 255 K? (a) 0.92 g/L, (b) 697 g/L, (c) 0.057 g/L, (d) 16 g/L, (e) 0.72 g/L. Química la ciencia central 13. Práctica 10.07.2. La masa molar media de la atmósfera en la superficie de Titán, la luna más grande de Saturno, es de 28.6 g/mol. La temperatura de la superficie es de 95 K y la presión es de 1.6 atm. Suponiendo un comportamiento ideal, calcule la densidad de la atmósfera de Titán. Química la ciencia central 13. Muestra 10.08. Un matraz vacío grande inicialmente tiene una masa de 134.567 g. Cuando el matraz se llena con un gas de masa molar desconocida a una presión de 735 torr a 31 °C, su masa es de 137.456 g. Cuando se vuelve a evacuar el matraz y luego se llena con agua a 31 °C, su masa es de 1067.9 g. (La densidad del agua a esta temperatura es de 0.997 g/mL). Suponiendo que se aplica la ecuación del gas ideal, calcule la masa molar del gas Química la ciencia central 13. Práctica 10.08.2. Calcula la masa molar promedio del aire seco si tiene una densidad de 1.17 g/L a 21 °C y 740.0 torr. Química la ciencia central 13. Ejercicio 10.47. ¿Qué gas es más denso a 1,00 atm y 298 K: CO2, N2O o Cl2? Explique. Química la ciencia central 13. Ejercicio 10.48. Clasifique los siguientes gases del menos denso al más denso a 1,00 atm y 298 K: SO2, HBr, CO2. Explique. Química la ciencia central 13. Ejercicio 10.51a. Calcule la densidad del gas NO2 a 0,970 atm y 35 °C. Química la ciencia central 13. Ejercicio 10.52a. Calcule la densidad del gas hexafluoruro de azufre a 707 torr y 21 °C. Hipertexto Problemas básicos 7. ¿Cómo se puede calcular el número de moléculas de un gas con un volumen de 10 ml? Hipertexto Problemas básicos 8.3. Determinar el peso molecular de un gas cuya densidad es 1.62 g/L a 200 K y 1.89 atmósferas de presión
(18.5) Ejemplos con número de entidades
Matamala y González. Ejercicio 7.25. En un tubo de 820 ml con gas enrarecido, la presión es de 1,9x10-6 mmHg. Si la temperatura es de 0°C, ¿Cuántas moléculas de gas hay en el tubo? Química de Chang 10. Problema-5.45. Las moléculas de ozono en la estratosfera absorben gran parte de la radiación dañina del sol. Normalmente, la temperatura y la presión del ozono en la estratosfera son 250 K y 1,0 x 10-3 atm, respectivamente. ¿Cuántas moléculas de ozono hay en 1.0 L de aire en estas condiciones? Química de Chang 10. Problema-5.46 Suponiendo que el aire contiene 78 por ciento de N2, 21 por ciento de O2 y 1 por ciento de Ar, todo en volumen, ¿cuántas moléculas de cada tipo de gas están presentes en 1.0 L de aire en STP? Química la ciencia central 13. Ejercicio 10.37a. Calcule el número de moléculas en una respiración profunda de aire cuyo volumen es 2.25 L a temperatura corporal, 37 °C y una presión de 735 torr.
(19) La ley de Dalton y ecuación de estado
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
La ley de las presiones parciales de Dalton establece que, en una mezcla de gases, la presión total P ejercida por la mezcla es igual a la suma (sigma Σ) de las presiones parciales de cada gas individual Pj presente en la mezcla (Pickover, 2008). En otras palabras, cada gas en una mezcla contribuye de manera independiente a la presión total, como si los demás gases no estuvieran presentes, o como si todos los gases fueran uno y el mismo gas, el gas ideal.
|
\[P=\Sigma P_i\] |
Eq 19.1 Forma básica de la ley de Dalton. |
Un ejemplo práctico de la ley de las presiones parciales sería una mezcla de gases en un recipiente cerrado. Imagina un recipiente que contiene oxígeno y nitrógeno. Según la ley de Dalton, la presión total dentro del recipiente sería la suma de la presión parcial del oxígeno y la presión parcial del nitrógeno. Si se introduce más oxígeno al recipiente, la presión total aumentará debido a la contribución adicional de la presión parcial del oxígeno. Lo mismo ocurriría si se añade más nitrógeno. En resumen, la presión total es la suma de las presiones parciales individuales de cada gas presente en la mezcla.
Figura 26.19.1. John Dalton (6 de septiembre de 1766 - 27 de julio de 1844) fue un químico, físico y meteorólogo inglés. Es mejor conocido por introducir la teoría atómica en la química y por su investigación sobre la ceguera al color, a veces denominado Daltonismo en su honor.
Ejemplo. Se captura hidrógeno mediante el desplazamiento de agua a una presión atmosférica de 560 mmHg. Al alcanzar el equilibrio, observamos que, a la temperatura del día, la tabla de presiones de vapor de agua señala un valor de 24 mmHg. Calcular la presión parcial del hidrógeno recogido. Ejemplo. Un matraz de 2.5 L a 15°C contiene una mezcla de N2, He y Ne a presiones parciales de 0.32 atm para N2, 0.15 atm para He y 0.42 atm para Ne. a) Calcule la presión total de la mezcla. Química de Chang 10. Problema-5.66. Se recoge una mezcla de gases de helio y neón sobre agua a 28.0 °C y 745 mmHg. Si la presión parcial del helio es 368 mmHg, ¿cuál es la presión parcial del neón? (Presión de vapor de agua a 28 °C 5 28.3 mmHg.) Química la ciencia central 13. Muestra 10.10. Una mezcla de 6.00 g de O2(g) y 9.00 g de CH4(g) se coloca en un recipiente de 15.0 L a 0 °C. ¿Cuál es la presión parcial de cada gas y cuál es la presión total en el recipiente?
Química la ciencia central 13. Ejercicio 10.64. Un buzo de aguas profundas usa un cilindro de gas con un volumen de 10.0 L y un contenido de 51.2 g de O2 y 32.6 g de He. Calcula la presión parcial de cada gas y la presión total si la temperatura del gas es de 19 °C. Química la ciencia central 13. Ejercicio 10.67. Un trozo de hielo seco (dióxido de carbono sólido) con una masa de 5,50 g se coloca en un recipiente de 10,0 L que ya contiene aire a 705 torr y 24 °C. Después de que el dióxido de carbono se ha sublimado por completo, ¿cuál es la presión parcial del gas CO2 resultante y la presión total en el recipiente a 24 °C? Química la ciencia central 13. Ejercicio 10.68. Una muestra de 5.00 mL de éter dietílico (C2H5OC2H5, densidad = 0.7134 g/mL) se introduce en un recipiente de 6.00 L que ya contiene una mezcla de N2 y O2, cuyas presiones parciales son P(N2) = 0.751 atm y P(O2) = 0.208 atm. La temperatura se mantiene a 35.0 °C y el éter dietílico se evapora totalmente. (a) Calcule la presión parcial del éter dietílico. (b) Calcule la presión total en el recipiente.
(19.1) El aire
La ley de las presiones parciales de Dalton es particularmente relevante cuando se aplica al aire. El aire es una mezcla gaseosa compuesta principalmente de nitrógeno, oxígeno, argón, dióxido de carbono y otros gases en proporciones más pequeñas. Según la ley de Dalton, cada uno de estos componentes contribuye de manera independiente a la presión total del aire.
La capacidad de los gases para mezclarse homogéneamente en todas las proporciones es un concepto clave. Esto significa que los gases en el aire se dispersan y distribuyen uniformemente entre sí. En otras palabras, no hay límites precisos entre las partículas de los diferentes gases; están intercalados de manera que la composición es constante en cualquier parte de la mezcla. Esta propiedad es lo que hace que el aire parezca ser una sustancia única y pura, a pesar de estar compuesto por varios gases.
En términos de mezclas, podemos distinguir entre mezclas homogéneas y heterogéneas. Una mezcla homogénea, también llamada solución o disolución, es aquella en la que los componentes están completamente mezclados, y no se pueden distinguir a simple vista. El aire es un ejemplo de una mezcla homogénea en el estado gaseoso. Por otro lado, una mezcla heterogénea tiene componentes que se pueden identificar visualmente porque no están completamente mezclados.
(19.2) Otras formas aditivas
Aunque la Ley de Dalton sobre las presiones parciales, representada como, es ampliamente conocida y reconocida, es importante destacar que prácticamente todos los parámetros de una ecuación de estado pueden ser expresados de manera aditiva bajo las condiciones adecuadas.
|
\[V=\Sigma V_j\] |
Eq 19.2 Ley de los volúmenes parciales. |
|
\[n=\Sigma n_j\] |
Eq 19.3 Ley de la cantidad de sustancia parcial |
|
\[m=\Sigma m_j\] |
Eq 19.4 Ley de la conservación de la masa |
Esta idea de expresar propiedades termodinámicas de forma aditiva es fundamental en la teoría de mezclas y en la comprensión del comportamiento de sistemas gaseosos y líquidos en diversos contextos. Bajo las condiciones adecuadas, es posible descomponer y calcular las propiedades de un sistema complejo en función de las contribuciones de sus componentes individuales, como sumas simples. Este enfoque es esencial en la termodinámica y la química, donde se estudian y se diseñan sistemas que involucran mezclas de sustancias diversas.
Es importante recordar que la aditividad de estos parámetros se debe a la naturaleza del estado gaseoso, en el cual cada gas, con su propia identidad, parece comportarse como si fueran un único gas ideal con propiedades comunes y monótonas. Esto da lugar a patrones en las ecuaciones que también son comunes y monótonos, lo que facilita el estudio y la comprensión de sistemas gaseosos en términos termodinámicos. El uso de una ley aditiva está condicionado, por el contexto del ejercicio, y normalmente se usan en combinación con la ley de los gases ideales que veremos a continuación con mayor profundidad.
(19.3) Concentración de un gas
La concentración de un gas se refiere a la cantidad de ese gas presente en una mezcla o en un volumen específico. Puede expresarse de diversas maneras, como la fracción molar, la fracción de volumen, la presión parcial o la densidad, y proporciona información sobre la cantidad relativa de un gas en relación con los demás componentes o con el volumen total de la mezcla gaseosa. La concentración es esencial para comprender y calcular las propiedades y el comportamiento de las mezclas de gases en diferentes situaciones.
La fracción molar se define como el ratio o fracción simple entre la cantidad de sustancia de un gas particular nj contenido en las fronteras del recipiente y la cantidad total de sustancia en la mezcla n. Es fundamental recordar que, en la medida de lo posible o práctico, empleamos notaciones sin subíndices para los totales con el fin de evitar una proliferación excesiva de símbolos. .Similar a otras unidades de concentración, la fracción molar actúa como una medida de la actividad del gas, indicando su presencia en el sistema y, por ende, su predisposición para participar en reacciones químicas. Así como ocurre con otras propiedades aditivas, la actividad de un gas en una mezcla puede expresarse en términos de fracción de volumen (phi ϕ) y fracción de masa (w).
|
\[\chi_j =\frac{n_j}{n}\] |
Eq 19.5 Fracción molar de un gas. |
|
\[\phi_j =\frac{V_j}{V}\] |
Eq 19.6 Fracción de volumen de un gas. |
La ecuación de estado puede ser formulada tanto para un gas específico como para una mezcla de gases, y suele ser establecida bajo condiciones de presión y temperatura constantes. Cuando tomamos el cociente de dos ecuaciones de estado, las constantes se eliminan, resultando en que el cociente de volúmenes, conocido como fracción en volumen, es igual al cociente de la cantidad de sustancia, denominado fracción molar. Es importante destacar que esta igualdad es válida únicamente en el estado gaseoso, donde estas relaciones emergen de la ecuación de estado de un gas. En líquidos y sólidos, estas equivalencias no se mantendrán.
|
\[\psi_j =\chi_j \] |
Eq 19.7 Identidad de concentración de volumen y molar de un gas |
Los tres tipos de fracciones se caracterizan por ser números que van de cero a uno, y tradicionalmente se expresan en porcentajes multiplicando el valor de la fracción por 100%. Es importante tener en cuenta que "%" es esencialmente una forma diferente de decir "centi" o \(10^{-2}\), por lo que 100% es igual a 1. En otras palabras, una fracción decimal es esencialmente el mismo número que una fracción porcentual. Aunque, curiosamente, los humanos tienden a encontrar más intuitivo visualizar una escala de 0 a 100 en lugar de 0 a 1.
Las fracciones, ya sea en forma porcentual o decimal, siguen cumpliendo con la ley de aditividad. En este caso, tanto en porcentajes como en fracciones, la suma de todas las fracciones en una mezcla es igual a 1 o 100%. Esto permite determinar el porcentaje de un gas en una mezcla si conocemos los porcentajes de todos los demás componentes.
Química la ciencia central 13. Muestra 10.11b. Un estudio de los efectos de ciertos gases en el crecimiento de las plantas requiere una atmósfera sintética compuesta de 1.5 % mol de CO2, 18.0 % mol de O2 y 80.5 % mol de Ar. (b) Si esta atmósfera se va a mantener en un espacio de 121 L a 295 K, ¿cuántos moles de O2 se necesitan si se mantiene la presión total de 745 torr? Química la ciencia central 13. Ejercicio 10.38b. El dióxido de carbono constituye aproximadamente el 0.04% de la atmósfera de la Tierra. Si recolecta una muestra de 2.0 L de la atmósfera al nivel del mar (1.00 atm) en un día cálido de (27 °C), ¿cuántas moléculas de CO2 hay en su muestra? Química la ciencia central 13. Ejercicio 10.45. En un experimento publicado en la literatura científica, se hizo que las cucarachas machos corrieran a diferentes velocidades en una cinta de correr en miniatura mientras se medía su consumo de oxígeno. En 1 hora, la cucaracha promedio corriendo a 0,08 km/h consumió 0,8 mL de O2 a una presión de 1 atm y 24 °C por gramo de masa de insecto. (a) ¿Cuántos moles de O2 se consumirían en 1 hora por una cucaracha de 5,2 g que se mueve a esta velocidad? (b) Esta misma cucaracha es atrapada por un niño y colocada en un frasco de fruta de 1 cuarto con una tapa hermética. Suponiendo el mismo nivel de actividad continua que en la investigación, ¿la cucaracha consumirá más del 20% del O2 disponible en un período de 48 horas? (El aire es 21 mol % O2.). Química la ciencia central 13. Ejercicio 10.65. La concentración atmosférica de gas CO2 es actualmente de 390 ppm (partes por millón, en volumen; es decir, 390 L de cada 106 L de la atmósfera son CO2). ¿Cuál es la fracción molar de CO2 en la atmósfera? Química La ciencia central 13. Muestra 10.11a. Un estudio de los efectos de ciertos gases en el crecimiento de las plantas requiere una atmósfera sintética compuesta de 1.5 % mol de CO2, 18.0 % mol de O2 y 80.5 % mol de Ar. (a) Calcule la presión parcial de O2 en la mezcla si la presión total de la atmósfera debe ser de 745 torr. Química La ciencia central 13. Ejercicio 10.63. Una mezcla que contiene 0.765 mol de He(g), 0.330 mol de Ne(g) y 0.110 mol de Ar(g) está confinada en un recipiente de 10.00 L a 25 °C. (a) Calcule la presión parcial de cada uno de los gases en la mezcla. (b) Calcule la presión total de la mezcla. Química La ciencia central 13. Ejercicio 10.71. A una profundidad submarina de 250 pies, la presión es de 8.38 atm. ¿Cuál debe ser el porcentaje molar de oxígeno en el gas de buceo para que la presión parcial de oxígeno en la mezcla sea de 0.21 atm, la misma que en el aire a 1 atm? Química La ciencia central 13. Ejercicio 10.72a. ¿Cuáles son las fracciones molares de cada componente en una mezcla de 15.08 g de O2, 8.17 g de N2 y 2.64 g de H2? Química La ciencia central 13. Ejercicio 10.72b. ¿Cuál es la presión parcial en atm de cada componente de esta mezcla si se mantiene en un recipiente de 15.50 L a 15 °C? asuma que las fracciones molares de los componentes son 0.227 O2, 0.141 N2 y 0.633 H2 y que la casntidad de sustancia total es de 2.07 mol.
Química de Chang 10. Ejemplo 5.14. Una mezcla de gases contiene 4.46 moles de neón (Ne), 0.74 moles de argón (Ar) y 2.15 moles de xenón (Xe). Calcule las presiones parciales de los gases si la presión total es 2.00 atm a cierta temperatura. Química de Chang 10. Práctica 5.14. Una muestra de gas natural contiene 8.24 moles de metano (CH4), 0.421 moles de etano (C2H6) y 0.116 moles de propano (C3H8). Si la presión total de los gases es 1.37 atm, ¿cuáles son las presiones parciales de los gases? Química de Chang 10.Una mezcla de gases contiene 0.31 moles de CH4, 0.25 moles de C2H6 y 0.29 moles de C3H8. La presión total es 1.50 atm. Calcule las presiones parciales de los gases. Química de Chang 10. Problema-5.64a. Un matraz de 2.5 L a 15°C contiene una mezcla de N2, He y Ne a presiones parciales de 0.32 atm para N2, 0.15 atm para He y 0.42 atm para Ne. a) Calcule la presión total de la mezcla. Química de Chang 10. Problema-5.65a. El aire seco cerca del nivel del mar tiene la siguiente composición en volumen: N2, 78.08 por ciento; O2, 20.94 por ciento; Ar, 0.93 por ciento; CO2, 0.05 por ciento. La presión atmosférica es de 1.00 atm. Calcule (a) la presión parcial de cada gas en atm Química de Chang 10. Problema-5.65b. El aire seco cerca del nivel del mar tiene la siguiente composición en volumen: N2, 78.08 por ciento; O2, 20.94 por ciento; Ar, 0.93 por ciento; CO2, 0.05 por ciento. La presión atmosférica es de 1.00 atm. Calcule (b) la concentración de cada gas en moles por litro a 0 °C. (Sugerencia: debido a que el volumen es proporcional al número de moles presentes, las fracciones molares de gases se pueden expresar como proporciones de volúmenes a la misma temperatura y presión). Química de Chang 10. Problema-5.69. El helio se mezcla con oxígeno gaseoso para los buceadores de aguas profundas. Calcule el porcentaje en volumen de oxígeno gaseoso en la mezcla si el buzo tiene que sumergirse a una profundidad en la que la presión total sea de 4.2 atm. La presión parcial de oxígeno se mantiene a 0.20 atm a esta profundidad.
Ejemplo. Se tiene una muestra de gas metano de 1.80 g en un cilindro de 500 ml, determinar la densidad y la concentración molar. La masa molar del metano es 16 g/mol. Ejemplo. Una muestra de H2 tiene una cantidad de sustancia de 80 moles en CN, los cuales están contenidos en un recipiente rígido de 6.0 litros. Determinar la concentración molar de este gas.
(19.4) Efecto de la ley de Dalton y otras formas aditivas en la ley de los gases ideales.
Dado lo anterior deberíamos preguntarnos, cual es el efecto de las leyes aditivas en la ecuación de los gases ideales. DEMOSTRACION. Obtener la ecuación de estado de los gases ideales en términos de una mezcla de gases donde tenemos varias (a) presiones (b) cantidades de sustancia (c) masas (d) volúmenes.
|
\[ \Sigma P_i \cdot V=n \cdot R \cdot T \] |
Eq 19.1. Ecuación de estado con ley de Dalton |
|
\[ P \cdot \Sigma V_i=n \cdot R \cdot T \] |
Eq 19.2. Ecuación de estado con el de volúmenes parciales |
|
\[ P \cdot V=\Sigma n_i \cdot R \cdot T \] |
Eq 19.3. Ecuación de estado con ley de cantidad de sustancia parcial |
|
\[ P \cdot V=\sum (\frac{m_i}{M_i}) \cdot R \cdot T \] |
Eq 19.4. Ecuación de estado con ley de cantidad de sustancia parcial expresada en masa |
Ejemplo. Si se combinan 88 g de CO2 y 64 g de SO2 a una presión de 2.0 atmósferas y una temperatura de 300 K, ¿cuál será el volumen resultante? Matamala y González. Ejercicio 7.29. Se mezclan 16 g de SO2 y 5,5 de CO2 en un recipiente de 5,6 L, a una temperatura de 27°C. Hallar la presión en mmHg.
Química la ciencia central 13. Práctica 10.10.1. Un cilindro de 15 L contiene 4.0 g de hidrógeno y 28 g de nitrógeno. Si la temperatura es de 27 °C, ¿cuál es la presión total de la mezcla? (a) 0.44 atm, (b) 1.6 atm, (c) 3.3 atm, (d) 4.9 atm, (e) 9.8 atm. Química la ciencia central 13. Práctica 10.10.2. ¿Cuál es la presión total ejercida por una mezcla de 2.00 g de H2(g) y 8.00 g de N2(g) a 273 K en un recipiente de 10.0 L? Química la ciencia central 13. Ejercicio 10.62b. Considere una mezcla de dos gases, A y B, confinada en un recipiente cerrado. Se agrega una cantidad de un tercer gas, C, al mismo recipiente a la misma temperatura. ¿Cómo afecta la adición de gas C a lo siguiente: la presión total en el recipiente. Química la ciencia central 13. Ejercicio 10.74c. Una muestra de 3.00 g de SO2(g) originalmente en un recipiente de 5.00 L a 21 °C se transfiere a un recipiente de 10.0 L a 26 °C. Una muestra de 2.35 g de N2(g) originalmente en un recipiente de 2.50 L a 20 °C se transfiere a este mismo recipiente de 10.0 L. (c) ¿Cuál es la presión total en el recipiente?
(19.5) Los gases que se expanden y mezclan
Visualicemos una serie de recipientes conectados a través de conductos y separados por válvulas de cierre. En el inicio, estas válvulas están cerradas, lo que implica que los gases están contenidos en volúmenes individuales y variables, con presiones y temperaturas que pueden diferir entre sí. Al abrir las válvulas de cierre, los volúmenes de todos los recipientes se amalgaman en uno solo, posibilitando la mezcla de los gases entre sí. La difusión de un gas en otro, al abrir la válvula, conlleva alteraciones en la temperatura, volumen y presión. Nos enfrentamos, por tanto, a un caso clásico de cambio de estado térmico, transitando desde un estado inicial hacia otro final. DEMOSTRACION. Obtener la ecuación que permite calcular la presión total y cantidad de sustancia total en términos de dos o más gases en contenedores de tamaño y presión diferente que se mezclan a temperatura constante.
|
\[P=\frac{T}{V}\cdot \sum (\frac{ P_{oi}\cdot V_{oi}}{T_{oi}})\] |
Eq 19.5. Presión total final en términos de presiones, volúmenes y temperaturas iniciales de gases mezclados en un volumen total final a temperatura de mezcla final. |
Ejemplo. Tres frascos, cada uno con una capacidad de 100 mL, están conectados por válvulas cerradas. A una temperatura ambiente de 27 °C, el primer frasco contiene 10 atmósferas de CO2, el segundo 20 atmósferas de N2, y el último 4 atmósferas de F2. Si se abren los frascos, ¿cuál será la presión final del sistema? Química la ciencia central 13. Ejercicio 10.61c. Considere el aparato que se muestra en el siguiente dibujo. ¿Cuál es la presión total en el recipiente después de que se mezclan los gases? Química la ciencia central 13. Ejercicio 10.62a. Considere una mezcla de dos gases, A y B, confinada en un recipiente cerrado. Se agrega una cantidad de un tercer gas, C, al mismo recipiente a la misma temperatura. ¿Cómo afecta la adición de gas C a lo siguiente: la presión parcial del gas A, Química la ciencia central 13. Ejercicio 10.73. Una cantidad de gas N2 originalmente mantenida a 5.25 atm de presión en un recipiente de 1.00 L a 26 °C se transfiere a un recipiente de 12.5 L a 20 °C. Una cantidad de gas O2 originalmente a 5.25 atm y 26 °C en un recipiente de 5.00 L se transfiere a este mismo recipiente. ¿Cuál es la presión total en el nuevo recipiente?
(20) Ley de los gases reales
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
Los gases, a primera vista, son considerados sustancias químicas con propiedades individuales, es decir, poseen identidad química. Sin embargo, la teoría cinética y las leyes macroscópicas simplifican la realidad al tratar a los gases como partículas físicas uniformes, sin identidad química, una aproximación que no refleja completamente la naturaleza de las moléculas gaseosas. La mayoría de los postulados básicos de la teoría cinética niegan su identidad química, tratándolas como esferas inertes sin volumen propio y sin interacciones moleculares. Aunque estos supuestos son útiles para describir un gas ideal, surge la pregunta de si esta representación siempre es válida, especialmente cuando se trata de gases reales con propiedades más complejas.
Figura 20.1. Johannes Diderik van der Waals. (Leiden, Países Bajos, 23 de noviembre de 1837 - Ámsterdam, 8 de marzo de 1923) fue un profesor universitario y físico neerlandés galardonado con el Premio Nobel de Física en 1910. Es conocido por su trabajo en la ecuación del estado de los gases y los líquidos por el cual ganó el Premio Nobel de Física en 1910.
(20.1) Historia
La ecuación de Van der Waals, una expresión termodinámica fundamental, parte de la premisa de que los fluidos consisten en partículas con volúmenes no nulos y están sometidos a fuerzas de atracción entre ellas (no necesariamente en pares). Este modelo teórico se fundamenta en los trabajos de Johannes Diderik van der Waals a finales del siglo XIX, quien también exploró la fuerza de atracción que hoy lleva su nombre. La ecuación se deriva de conjuntos tradicionales de fórmulas relacionadas con los esfuerzos de Van der Waals y otros, así como de derivaciones basadas en la termodinámica estadística. Un marco integral que ha demostrado su eficacia en la descripción de comportamientos de sustancias en condiciones no ideales. (Wisniak, 2000).
\[(P_i + \frac{a_i \cdot n_i^2}{V_i^2}) \cdot (V_i - b_i \cdot n_i) = n_i \cdot R \cdot T_i\] | Eq 30.1 Ecuación de van der Waals |
Los primeros intereses de Van der Waals estaban principalmente en el campo de la termodinámica, donde una primera influencia fue el trabajo publicado de Rudolf Clausius sobre el calor en 1857; otras influencias significativas fueron los escritos de James Clerk Maxwell, Ludwig Boltzmann y Willard Gibbs (Johannes D Van der Waals, 1910). Después de la búsqueda inicial de credenciales docentes, el trabajo de grado de Van der Waals en matemáticas y física en la Universidad de Leiden en los Países Bajos condujo (con obstáculos significativos) a su aceptación para realizar estudios de doctorado en Leiden con Pieter Rijke. Si bien su disertación ayuda a explicar la observación experimental en 1869 por parte del profesor irlandés de química Thomas Andrews (Queen's University Belfast) de la existencia de un punto crítico en los fluidos (Andrews, 1869), el historiador de la ciencia Martin J. Klein afirma que no está claro si Van der Waals estaba al tanto de los resultados de Andrews cuando comenzó su trabajo de doctorado (Klein, 1974). La investigación doctoral de Van der Waals culminó en una disertación de 1873 que proporcionó una teoría semicuantitativa que describe el cambio de estado gas-líquido y el origen de una temperatura crítica, On the Continuity of the Gas- and Liquid-State; fue en esta disertación que aparecieron las primeras derivaciones de lo que ahora llamamos la ecuación de Van der Waals (Johannes Diderik Van der Waals, 1873). James Clerk Maxwell revisó y elogió su contenido publicado en la revista científica británica Nature (Clerk-Maxwell, 1874; Maxwell, 1874), y Van der Waals comenzó un trabajo independiente que resultaría en su recepción del Premio Nobel en 1910, que enfatizó la contribución de su formulación de esta "ecuación de estado para gases y líquidos".
(20.2) Gases en condiciones extremas
Debido a las interacciones moleculares, las partículas gaseosas reales no chocan de manera perfectamente elástica, y por consiguiente la energía de impacto de la partícula con la pared es menor o mayor, dependiendo de la identidad química de la sustancia. Dado que en la realidad siempre tratamos con sustancias químicas con identidad, entonces siempre tenemos desviaciones del comportamiento ideal, ya que el gas ideal no existe realmente. Sin embargo, a presiones y volúmenes normales, las desviaciones reales son despreciables, y, por lo tanto, al carecer de impacto matemático, normalmente asumimos que el gas ideal es un buen modelo para los gases reales, de allí que es el estado de la materia más fácil de entender.
Figura 20.2. Gases reales en condiciones extremas Gráfica de comparación de un gas ideal y varios gases reales en base a la relación presión (eje x) y el producto de PV/RT (eje y).
Las desviaciones significativas del comportamiento ideal ocurren en condiciones de alta presión o baja temperatura, donde las sustancias reales cambian de fase gaseosa a fase acuosa, y las interacciones químicas comienzan a hacerse más importantes. Pongamos solo un detalle, los gases ideales NUNCA SE LICUAN, y cuando me refiero a eso, es a que pasan de un estado gaseoso a uno líquido. En otras palabras, un gas ideal sigue estando en estado gaseoso por muy infinitamente cerca que se encuentre al cero absoluto o a la presión más aplastante que uno pueda imaginarse. Pero las sustancias químicas no obedecen este patrón, los puntos de fusión funcionan en ambos sentidos, a ciertas temperaturas y presiones cualquier gas cambia de estado.
En resumen, los gases tienden a comportarse idealmente solo a ciertos rangos de temperatura y presión, y por debajo o por encima de ellos, comenzaran a mostrar signos de desviación, si no es que directamente cambiaran a estado líquido, sólido o exóticos. Todo esto se deberá a la capacidad de las moléculas de establecer interacciones moleculares. A mayor cantidad de interacciones o más fuertes estas, el gas se desviará del comportamiento ideal más rápido pasando a estado líquido y/o sólido con mayor facilidad.
(20.3) Presión límite o crítica
La reducción extrema de la densidad de un gas provoca su rarefacción. Aunque podría pensarse que esto no tiene un impacto significativo, en realidad facilita su transición al estado de plasma al establecer una diferencia de potencial eléctrico entre dos puntos. En otras palabras, un gas rarefacto conduce la electricidad de manera similar a un cable en un circuito. Por otro lado, cuando aumentamos considerablemente la presión, las interacciones atractivas entre las moléculas comienzan a superar a las repulsivas, dando lugar a un cambio de estado hacia el líquido.
\[P_{i,\text{ideal}} = P_{i,\text{real}} + \frac{a_i \cdot n_i^2}{V_i^2}\] | Eq 30.2 presión de van der Waals |
En la ecuación de los gases reales, el término de corrección para la presión (P) incluye la constante "a". Esta constante tiene un significado importante, ya que representa la fuerza de las interacciones atractivas entre las moléculas del gas, teniendo en cuenta la identidad del gas, es decir, “a” depende de la química de la sustancia. Cuando se tiene en cuenta esta corrección, la presión real del gas es ajustada para considerar las fuerzas intermoleculares. El término corrector (a veces el cuadrado de cantidad de sustancia sobre el cuadrado de volumen) actúa como una medida de la desviación del comportamiento de un gas respecto al modelo ideal. A medida que la cantidad de sustancia de gas disminuye o el volumen que ocupa aumenta, el término corrector tiende a acercarse a cero, lo que indica una mayor similitud entre la presión real y la presión ideal. Esto implica que los gases rarificados tienden a comportarse de manera más cercana a un gas ideal. Es importante destacar que esta ecuación solo aborda esta desviación específica y no tiene en cuenta otras propiedades que puedan surgir en gases rarificados, como la conductividad eléctrica. En resumen, la idea fundamental es que los gases dispersos o poco concentrados, de baja densidad, tienden a comportarse de manera más semejante a un gas ideal.
(20.4) Temperatura crítica
A medida que la temperatura disminuye, las vibraciones moleculares y el movimiento cinético, que contribuyen a las fuerzas repulsivas entre las moléculas, disminuyen. Como resultado, las fuerzas atractivas se vuelven más predominantes, lo que conduce a que el gas experimente una transición hacia el estado líquido. Cuando elevamos la temperatura de un gas cerca de su punto crítico, se produce la disociación de los átomos de las moléculas del gas en átomos libres ionizados. En otras palabras, no solo los átomos se separan, sino que también liberan sus electrones, generando un plasma incandescente muy caliente, similar al que se observa en la corona del Sol.
\[V_{i,\text{ideal}} = V_{i,\text{real}} -b_i \cdot n_i\] | Eq 30.2 presión de van der Waals |
En términos de corrección del volumen, es similar al ajuste aplicado a la presión en el sentido de que la constante refleja las fuerzas atractivas entre las moléculas. Desde una perspectiva molecular, las atracciones moleculares provocan el agrupamiento de las moléculas, lo que resulta en un aumento de la presión y, por ende, en una corrección positiva en ese aspecto. Sin embargo, al mismo tiempo que estas interacciones moleculares congregan a las moléculas, también hacen que el sistema ocupe menos espacio del que teóricamente debería, generando así una disminución en el volumen. Este fenómeno tiene sentido al considerar el aumento de la presión.
La corrección indica que "b" es una constante dependiente de la identidad química de cada gas específico, y su impacto se hace más evidente a medida que aumenta la cantidad de moléculas de gas en el sistema. En resumen, la ecuación de los gases reales sugiere que estos gases, debido a las interacciones moleculares, exhiben presiones mayores y volúmenes menores en comparación con un gas ideal.
(20.4) Constantes de los gases reales
Como resultado, las constantes "a" y "b" son análogas a la masa molar, ya que, al ser constantes químicas, no son universales y varían según cada gas en particular. Por lo tanto, es necesario calcularlas experimentalmente y registrarlas en tablas estandarizadas, como la siguiente.
Tabla 20.1. Constantes de los gases reales.
| Gas | a (L^2·atm/mol^2) | b (L/mol) |
| H₂ | 0.244 | 0.0266 |
| N₂ | 1.39 | 0.0391 |
| O₂ | 0.138 | 0.0319 |
| F₂ | 0.295 | 0.0296 |
| Cl₂ | 6.49 | 0.0562 |
| H₂O | 5.46 | 0.0305 |
| CO₂ | 3.59 | 0.0427 |
| CO | 3.59 | 0.0427 |
| SO₂ | 8.64 | 0.0562 |
Referencias bibliográficas
Inicio: ⟨Cursos⟩: ⟨Química⟩: {La materia y el átomo}: [Gases]: (1) Introducción, (2) Generalidades, (3) Propiedades, (4) Temperatura, (5) Volumen, (6) Presión, (7) Presión atmosférica, (8) Masa, (9) Historia de las leyes empíricas, (10) Historia de la ecuación de estado, (11) Ley de Boyle, (12) Ley de Charles, (13) Ley de Gay-Lussac, (14) Volúmenes de combinación, (15) Leyes de Avogadro, (16) Técnica de Cannizzaro, (17) Usando la ecuación de estado, (18) Ecuación de estado combinada, (19) Ley de Dalton, (20) Ley de los gases reales, (R) Referencias.
Adcock, L. H. (1998). The egg in the bottle revisited: Air pressure and Amontons’ law (Charles’ law). Journal of Chemical Education, 75(12), 1567.
Andrews, T. (1869). XVIII. The Bakerian Lecture.—On the continuity of the gaseous and liquid states of matter. Philosophical Transactions of the Royal Society of London, (159), 575–590.
Avogadro, A. (1811). Essay on a manner of determining the relative masses of the elementary molecules of bodies, and the proportions in which they enter into these compounds. Resonance, 11(01). Retrieved from https://www.ias.ac.in/public/Volumes/reso/011/01/0090-0095.pdf
Becker, P. (2001). History and progress in the accurate determination of the Avogadro constant. Reports on Progress in Physics, 64(12), 1945.
Bigg, C. (2008). Evident atoms: Visuality in Jean Perrin’s Brownian motion research. Studies in History and Philosophy of Science Part A, 39(3), 312–322.
BIPM. (2018). The mole. Retrieved November 1, 2019, from https://www.bipm.org/en/measurement-units/
Boas, M. (1949). Hero’s Pneumatica: a study of its transmission and influence. Isis, 40(1), 38–48.
Boyle, R. (1911). The Sceptical Chymist: The Classic 1661 Text. Courier Dover Publications.
Brock, W. H. (1985). Chemical atomism in the nineteenth century: from Dalton to Cannizzaro.
Brown, T. L., LeMay, H. E. J., Bursten, B. E., Murphy, C. J., & Woodward, P. (2009). Chemistry the central science (11th ed.). Pearson; Prentice Hall.
Brown, T. L., LeMay, H. E. J., Bursten, B. E., Murphy, C. J., Woodward, P. M., & Stoltzfus, M. W. (2017). Chemistry, the central science (13th ed.). Boston: Pearson.
Cattani, M., & Salvadori, M. C. (1714). Diffusion Process and Brownian Motion. Publicação IF, 1(08), 2019.
Chang, R. (2010). Chemistry (10th ed.). McGraw-Hill New York.
Chapman, K. (2021). Element Discovery and the Birth of the Atomic Age. In 150 Years of the Periodic Table: A Commemorative Symposium (pp. 329–342). Springer.
Clerk-Maxwell, J. (1874). O ver de continuiteit van den gas-en vloeistofiocstand Academisch proefschrift. Nature, 10(259), 477–480.
Coulston, C. (1960). The Edge of Objectivity: An Essay in the History of Scientific Ideas.
Dalton, J.-B. B., von Humboldt, A., & Thenard, L. J. (n.d.). GAY-LUSSAC’S LAW OF COMBINING GAS VOLUMES. SELECTED BOOKS BY, 190.
Deslattes, R. D. (1980). The avogadro constant. Annual Review of Physical Chemistry, 31(1), 435–461.
Dias, J. R. (2020). Teaching of chemistry before and after the periodic table. Foundations of Chemistry, 22(1), 99–106.
Egdell, R. G., & Bruton, E. (2020). Henry Moseley, X-ray spectroscopy and the periodic table. Philosophical Transactions of the Royal Society A, 378(2180), 20190302.
Farmer, E. E. (2010). Jean Senebier’s thoughts on experimentation. ARCHIVES DES SCIENCES, 63, 185–192.
Furio, C., Azcona, R., & Guisasola, J. (2002). The learning and teaching of the concepts ‘amount of substance’and ‘mole’: A review of the literature. Chemistry Education Research and Practice, 3(3), 277–292.
Furio, C., Azcona, R., Guisasola, J., & Ratcliffe, M. (2000). Difficulties in teaching the concepts of’amount of substance’and’mole’. International Journal of Science Education, 22(12), 1285–1304. Retrieved from https://www.tandfonline.com/doi/abs/10.1080/095006900750036262
Gay-Lussac, J. L. (1802). Recherches sur la dilatation des gaz et des vapeurs. In Annales de chimie (Vol. 43, pp. 137–175).
Georgakellos, N. L. (2019). Empedocles of Acragas: His Theory and the Exact Sciences (1st ed.). Cambridge Scholars Publishing. Retrieved from https://books.google.com.co/books?id=nFyJDwAAQBAJ&pg=PA75&dq=empedocles+hourglass+clepsydra+air&hl=es-419&sa=X&ved=2ahUKEwjSpqa4o7f4AhW5ZTABHRupAOcQ6AF6BAgCEAI#v=onepage&q=empedocles hourglass clepsydra air&f=false
Grigull, U. (1984). Newton’s temperature scale and the law of cooling. Wärme-Und Stoffübertragung, 18(4), 195–199.
Güttler, B., Bettin, H., Brown, R. J. C., Davis, R. S., Mester, Z., Milton, M. J. T., … Wielgosz, R. I. (2019). Amount of substance and the mole in the SI. Metrologia, 56(4), 44002.
Güttler, B., Rienitz, O., & Pramann, A. (2019). The Avogadro constant for the definition and realization of the mole. Annalen Der Physik, 531(5), 1800292.
Hauksbee, F. (2017). An Account of an Experiment Touching the Different Densities of the Air, from the Greatest Natural Heat, to the Greatest Natural Cold in This Climate. Philos. Trans. R. Soc. Lond, 26, 313–324.
Jensen, W. B. (2003). The universal gas constant R. Journal of Chemical Education, 80(7), 731.
Jensen, W. B. (2004). The origin of the mole concept. Journal of Chemical Education, 81(10), 1409.
Kauffman, G. B. (1994). Before and After Cannizzaro: A Philosophical Commentary on the Development of the Atomic and Molecular Theories. American Scientist, 82(4), 395–397.
Kelvin, Lord. (1848). On an Absolute Thermometric Scale. Phil. Mag.
Kirk, W. (1953). The geographical significance of Vitruvius’ de architectura. Scottish Geographical Magazine, 69(1), 1–10.
Klein, M. J. (1974). The historical origins of the van der Waals equation. Physica, 73(1), 28–47.
Marquardt, R. (2019). The mole and IUPAC: a brief history. Chemistry International, 41(3), 50–52.
Matamála, M., & Gonzalez, P. (1976). Química General. Cultural.
Matthiesen, S. (2022). A short history of temperature measurements and temperature scales - Stephan Matthiesen. Retrieved June 18, 2022, from https://www.stephan-matthiesen.de/en/texts-blog/49-texts-blog/138-a-short-history-of-temperature-measurements-and-temperature-scales.html
Maxwell, J. C. (1874). Van der Waals on the continuity of the gaseous and liquid states. Nature, 10(259), 477–480.
Merzbacher, E. (2002). The early history of quantum tunneling. Physics Today, 55(8), 44–50.
Morselli, M. (1984). The Molecular Hypothesis: After the Karlsruhe Congress. In Amedeo Avogadro (pp. 194–271). Springer.
Perrin, J. (1901). Les hypothèses moléculaires. Revue Scientifique, 15, 449–461.
Perrin, J. (1909). Mouvement brownien et réalité moléculaire. In Annales de Chimie et de Physique (Vol. 18, pp. 5–104). Retrieved from https://djalil.chafai.net/docs/M2/history-brownian-motion/Perrin - 1909 - French.pdf
Perrin, J. (1911). La réalité des molécules. Revue Scientifique, 25(16), 774–784.
Perrin, J. (1913). Les atomes. Alcan.
Pickover, C. (2008). Archimedes to Hawking: laws of science and the great minds behind them. Oxford University Press.
Priestley, J. (1772). XIX. Observations on different kinds of air. Philosophical Transactions of the Royal Society of London, (62), 147–264.
Rodgers, G. E. (2019). Questioning the reality of Atoms on the ground: Loschmidt, mach, boltzmann, and ostwald (germany and Austria). Traveling with the Atom: A Scientific Guide to Europe and Beyond, 244.
Rouvray, D. H., & King, R. B. (2004). The periodic table: Into the 21st century. Research Studies Press Baldock, UK.
Safley, T. M. (2018). Mercury mining and miners: the transition from boutique metal to strategic commodity in the 16th century. In Labor Before the Industrial Revolution (pp. 198–231). Routledge.
Scerri, E. (2012). Mendeleev’s periodic table is finally completed and what to do about group 3. Chem. Int. July-Aug, 28–31.
Scerri, E. R. (2006). The periodic table: its story and its significance. Oxford University Press.
Shapiro, S. (1964). The origin of the suction pump. Technology and Culture, 5(4), 566–574.
Singh, J. (2021). Oxygen: Risk assessment, environmental, and health hazard. In Hazardous Gases (pp. 289–299). Elsevier.
Soentgen, J. (2010). On the history and prehistory of CO2. Foundations of Chemistry, 12(2), 137–148.
Solari, G. (2019). The Wind and the New Science. In Wind Science and Engineering (pp. 87–167). Springer.
Sparavigna, A. C. (2011). Water, Air and Fire at work in Hero’s machines. ArXiv Preprint ArXiv:1101.3470.
Van der Waals, Johannes D. (1910). The equation of state for gases and liquids. Nobel Lectures in Physics, 1, 254–265.
Van der Waals, Johannes Diderik. (1873). Over de Continuiteit van den Gas-en Vloeistoftoestand (Vol. 1). Sijthoff.
West, J. B. (2014). Henry Cavendish (1731–1810): hydrogen, carbon dioxide, water, and weighing the world. American Journal of Physiology-Lung Cellular and Molecular Physiology, 307(1), L1–L6.
Wisniak, J. (2000). Johannes Diderik van der Waals: A Life of Achievements. The Chemical Educator, 5(3), 149–155.
Zhao, H.-J., Guo, Z.-H., Wu, X.-Y., & Xiao, Y. (n.d.). Machine Learning to Classify Electrostatic Plasma Turbulence in Tokamaks.












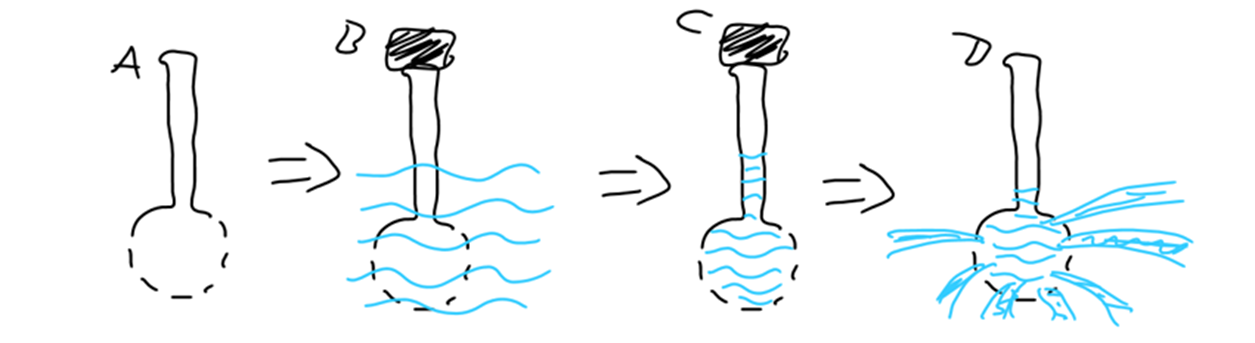










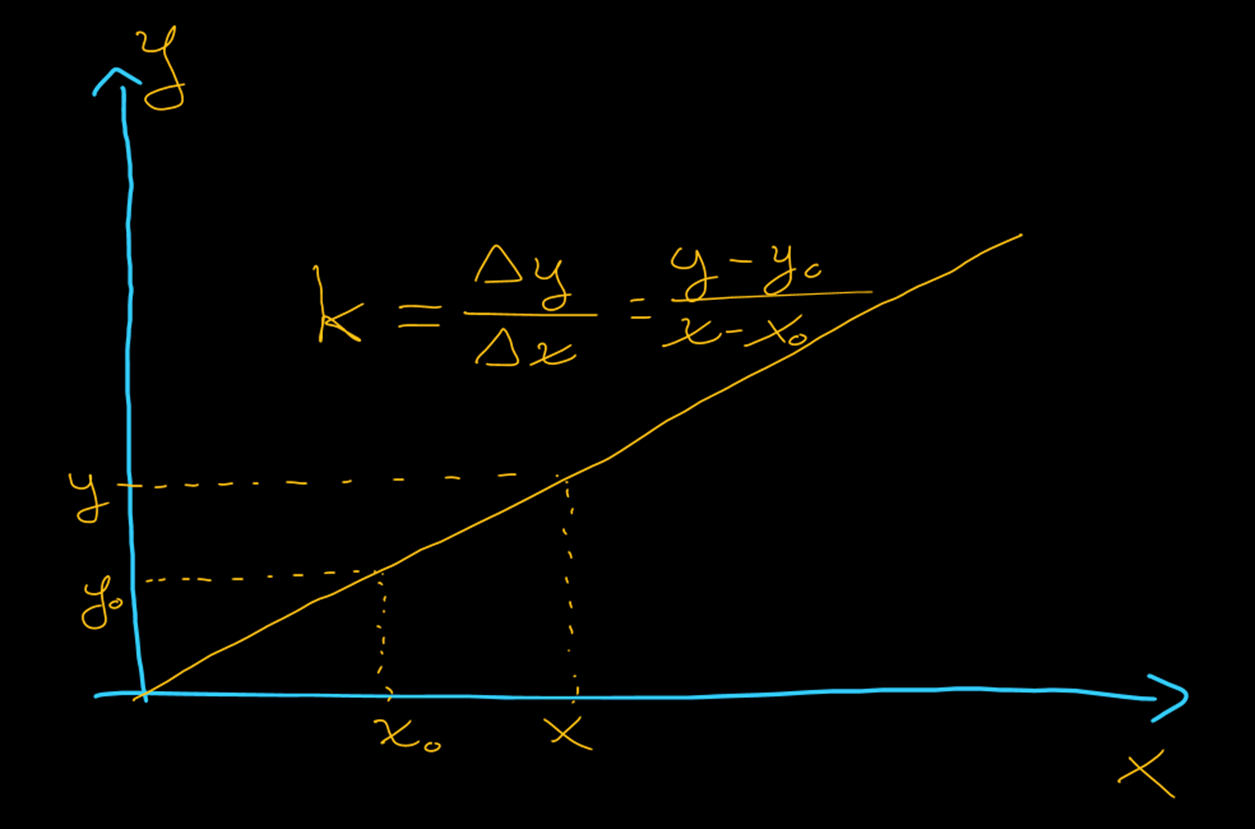











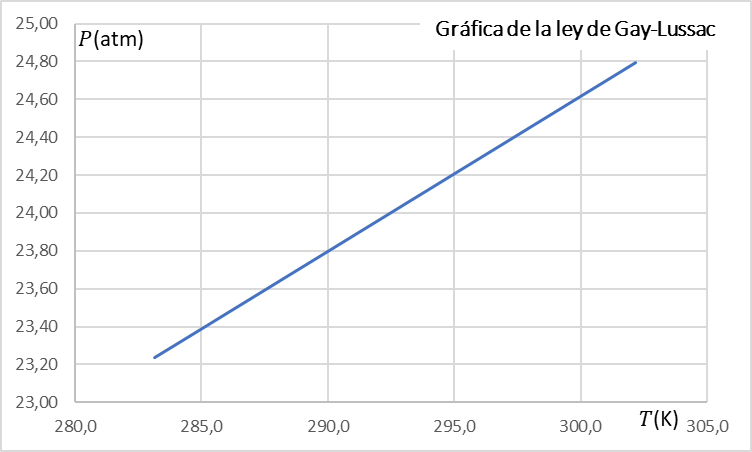








No hay comentarios:
Publicar un comentario