Índice
|
|| 0|| Índice || p|| Portada || E|| Ejercicios resueltos || R|| Referencias Bibliográficas || 1|| Introducción || 2|| Generalidades || 3|| El átomo filosófico || 4|| Introducción a las leyes ponderales || 5|| La ley de la conservación de la masa || 6|| Ley de las proporciones definidas || 7|| Ley de las proporciones recíprocas || 8|| Ley de las proporciones múltiples || 9|| La teoría atómica de Dalton || 10|| Postulado de composición |
|| 11|| Postulado de identidad atómica || 12|| Postulado de cambio de identidad molecular || 13|| Postulados de asociación || 14|| Postulado de la ecuación química || 15|| Pesos atómicos en la teoría de Dalton || 16|| Las hipótesis de Avogadro || 17|| El método de Cannizzaro || 18|| Del molécula-gramo al mol || 19|| Del mol a la cantidad de sustancia || 20|| Historia de la teoría cinética de gases || 21|| Modelo matemático de la teoría cinética de gases || 22|| Estequiometría de composición || 23|| La ley de Dulong y Petit |
Portada
1. Introducción
|| REGRESAR AL INDICE ||
La teoría atómica postula que la materia está hecha de pequeñas partículas llamadas átomos, sin embargo, si la cosa fuera tan simple como solo una idea, no tendría que dividir el estudio del átomo entres grandes capítulos, del cual este es el primero, el átomo químico.
Definiremos al átomo químico como una partícula sin estructura interna que posee propiedades fijas dependiendo del elemento al que pertenece como una masa propia, y patrones de reactividad que le permite combinarse con otros átomos del mismo elemento o de otros elementos formando moléculas elementales o moléculas compuestas.
Estos átomos entendidos como partículas pueden por lo tanto parametrizarse en una serie de cantidades como su número absoluto (N), su número relativo (n) su masa absoluta (ma) o masa relativa (Ar)(M), entre otras. La historia del átomo químico es también la historia de otros grandes capítulos de la química, como son gases, estequiometría y mezclas, de allí que algunos conceptos, pasajes históricos y protagonistas se repiten constantemente.
1.1 Stanislao Cannizzaro
Cannizzaro nació en Palermo, hijo de Mariano Cannizzaro y Anna Di Benedetto. En 1841, ingresó en la universidad de su ciudad natal con la intención de hacer de la medicina su profesión, pero pronto se dedicó al estudio de la química. En 1845 y 1846, trabajó como asistente de Raffaele Piria (1815-1865), conocido por su trabajo en el salicinato, y que era entonces profesor de química en Pisa y que posteriormente ocupó el mismo cargo en Turín.
Durante la Revolución siciliana de 1848, Cannizzaro sirvió como oficial de artillería en Messina y también fue elegido diputado por Francavilla en el Parlamento de Sicilia. Tras la caída de Messina, en septiembre de 1848, permaneció en Taormina. Aprovechando el colapso de los insurgentes, Cannizzaro escapó a Marsella en mayo de 1849, y, después de visitar varias ciudades francesas, alcanzó París en octubre. Allí pudo ingresar en el laboratorio de Michel Eugène Chevreul, y en conjunción con F.S. Cloez (1817-1883) hizo su primera contribución a la investigación química en 1851, cuando prepararon cianamida por la acción de amoníaco en cloruro de cianógeno en solución de éter. En el mismo año, Cannizzaro aceptó un puesto en el Colegio Nacional de Alessandria, como profesor de química y física. En Alessandria, descubrió que los aldehídos aromáticos se descomponen por una solución alcohólica de hidróxido de potasio en una mezcla del ácido correspondiente y alcohol. Por ejemplo, el benzaldehído se descompone en ácido benzoico y alcohol bencílico, en la denominada reacción de Cannizzaro.
En el otoño de 1855, se convirtió en profesor de química en la Universidad de Génova, y después de obtener nuevas cátedras en Pisa y Nápoles, aceptó la cátedra de química orgánica e inorgánica en Palermo. Allí pasó diez años estudiando compuestos aromáticos y siguió trabajando en las aminas, hasta 1871, cuando fue nombrado para la cátedra de química en la Universidad de Roma.
Aparte de su trabajo en la química orgánica, Cannizzaro prestó un gran servicio a la química con su artículo de 1858 "Sunto di un corso di Filosofia Chimica" (Bosquejo de un curso de filosofía química), en el que insistió en la distinción entre peso atómico y peso molecular, acabando de fijar la hipótesis previamente efectuada por Avogadro. Cannizzaro mostró cómo los pesos atómicos de los elementos contenidos en compuestos volátiles se pueden deducir de los pesos moleculares de los compuestos, y cómo los pesos atómicos de elementos de cuyos compuestos las densidades de vapor son desconocidas pueden determinarse a partir del conocimiento de sus calores específicos. Por estos logros, de importancia fundamental para la teoría atómica, fue galardonado con la Medalla Copley por la Royal Society en 1891 (de haber existido permio Nobel en esa época seguro se lo hubieran dado).
En 1871, el prestigio científico de Cannizzaro le aseguró su ingreso en el Senado italiano, del que fue vicepresidente, y como miembro del Consejo de Instrucción Pública, prestando importantes servicios a la causa de la educación científica en Italia.
Es principalmente conocido por su contribución al debate entonces existente respecto a los átomos, las moléculas y los pesos atómicos. Defendió la noción de Amedeo Avogadro de que volúmenes iguales de gas a la misma presión y temperatura contienen el mismo número de moléculas o átomos, y la noción de que volúmenes iguales de gas podrían ser utilizados para calcular los pesos atómicos. De este modo, Cannizzaro proporcionó una nueva comprensión de la química.
2. Generalidades
|| REGRESAR AL INDICE ||
Epistemológicamente diferenciaremos entre la teoría atómica y el modelo del átomo. La teoría atómica es un concepto general, siendo un paradigma sombrilla bajo el cual diversos programas de investigación fueron creados, antes y después de John Dalton y que en palabras simples establece que la materia está hecha de átomos (Clary, 2013). El desarrollo de la teoría atómica antes y después de Dalton es un proceso mucho más complejo en el cual dos corrientes disciplinares y filosóficas han chocado constantemente y aun lo hacen. Algunas de ellas son el platonismo y el aristotelismo, el realismo científico contra el instrumentalismo, incluso los modos de pensar desde la química y desde la física. Hablando concretamente de la interpretación química o física el escritor del presente artículo no toma partido por ninguna de las dos posturas, ya que, en sus campos específicos, cada visión ha demostrado ser útil y ha dado resultados, por consecuencia ambas cumplen el compromiso racionalista con el Materialismo Metodológico (Blanco, 2012), lo cual define mi postura como instrumentalista, ya que imperan los resultados por sobre la posibilidad de describir acertadamente una realidad física. En últimas, la verdad real del modelo es irrelevante “realismo científico”, lo que importa es su utilidad pragmática “instrumentalismo”.
2.1 El problema de la sustancia, elementos y compuestos
La química es una ciencia experimental y como tal damos por presupuestos principios que provienen desde la experimentación a la hora de definir elemento, compuesto y sustancia. De lo que el estudiante, el químico o el filósofo pueden dar cuenta en el mundo sensible y tangible de lo macroscópico es de sustancias continuas, las cuales al combinarse parecen transmutar en otras sustancias nuevas. En este sentido la transmutación hace referencia al cambio de las propiedades de las sustancias iniciales a las finales. De aquí que la teoría atómica tenga como fin último –al menos en la química –dar una explicación metodológicamente útil al asunto de la reacción/transmutación de las sustancias al inicio del cambio químico en las sustancias al final. El asunto es que al menos en principio tal explicación es contra intuitiva, ¿cómo partículas no conectadas pueden generar fenómenos con apariencia continua?
Uno de los aspectos que permitiría la definición de los átomos fue la definición de elemento o sustancia simple. Boyle fue el primero en dar una definición de elemento que cortaba con las tradiciones de la alquimia y el flogisto, y posteriormente Lavoisier la retomaría (Paneth, 2003). Para ellos un elemento era:
Ser sustancias que no pueden dividirse en otras por métodos químicos.
Esto es, a pesar de que muchas sustancias cambian sus propiedades y presentación en el mundo macroscópico, algunas parecían estar compuestas por las mismas sustancias simples. Sin el presunto de una sustancia elemental, es imposible pensar posteriormente en los átomos. Ahora el problema estaría definido por las posibilidades experimentales para poder identificar correctamente las sustancias simples de las compuestas, ya que al nivel de lo macroscópico son indistinguibles. Un ejemplo es el aire, por milenios se lo consideró como un elemento, pero para el siglo XVIII-XIX los adelantos tecnológicos permitieron dar cuenta de los componentes del aire, haciéndolo una sustancia compuesta y no un elemento. El propio Dalton tendría problemas con este asunto experimental.
2.2 Objeciones a la teoría atómica
Tal vez de todas las objeciones a la teoría atómica la más importante fuese que no era tan necesaria, de hecho, muchos adelantos químicos fueron realizados de forma independiente a pretender crear un modelo de átomo. De hecho, muchos científicos prominentes del siglo XIX no creían en la existencia de los átomos, o que tan siquiera fueran una hipótesis científica seria, tildándolos de ser una ficción conveniente. Autores que sostenían esta postura son por ejemplo Faraday “A” (Burwell Jr, 1894) y Ostwald “B” (Swackhamer, 2005). De hecho, la hipótesis del átomo solo vendría a aceptarse de forma extendida hasta 1904 (Colyvan, 1998). De hecho, el propio Mendeleev “C” dudaba de la existencia real del átomo, empleándolo como una simple convención metodológica. De hecho, en alguna ocasión afirmó que la teoría Atómica era inútil para el establecimiento del sistema periódica, el cual se basaba en pesos de los elementos y de sus propiedades (Scerri, 2006).
2.3 Definición básica de la teoría atómica
Tomando en cuenta las objeciones de la época de Dalton y los cambios que ha sufrido el concepto de átomo cabe preguntarse ¿Cuál es el fundamento primordial de la teoría atómica? En este sentido vale la pena reducirlo a la noción con la cual inició el atomismo desde la Grecia antigua. La materia regular está compuesta por partículas microscópicas llamadas átomos, las cuales se caracterizan por no poder dividirse, la palabra átomo en el contexto griego significa lo indivisible. A pesar de que la mayor parte de los postulados del modelo atómico de Dalton fueron refutados con el avance de los métodos físicos, comenzando por el propio significado de la palabra “átomo = indivisible” lo que es relevante para todos los modelos del átomo, es que son el fundamento para explicar gran parte de las propiedades de los elementos.
La teoría atómica no sería aceptada de forma inmediata y tendría una evolución paralela a la del propio modelo atómico, de hecho, aún para la época en que Thomson describió su modelo atómico de pastel con pasas, la existencia del átomo seguía siendo controversial (Van Melsen, 2004) y muchos científicos prominentes se murieron negando su existencia.
2.4 Modelos atómicos
Bien, los postulados de la teoría atómica de Dalton son un poco difíciles de digerir si no contamos con una manera de “visualizarlos”, con lo que caemos en un pequeño problema para este punto de nuestro pequeño relato. Dalton no tenía ni idea de cómo se veía un átomo, o de si tenía alguna estructura en especial, es más, es posible que como Demócrito aun pensara realmente que los átomos eran en verdad partículas individuales, únicas y eternas. Allí es donde entra la expresión MODELO atómico. Para poder explicar de una mejor manera los postulados de la teoría atómica debemos visualizarlos, pero al no tener una idea de cómo se ve un átomo debemos realizar una aproximación de COMO PODRIA verse el átomo en base a la mejor información con la que contemos en un momento de tiempo determinado.
Esa es precisamente la definición de un modelo atómico: una representación gráfica aproximada de cómo podría verse un átomo, de forma tal que pueda explicar sus propiedades físicas y/o químicas. Un modelo atómico no es una foto de un átomo, tampoco pretende ser la “verdad” sobre como “verdaderamente” se ve la forma “real” de un átomo, es tan solo una aproximación que explica los fenómenos relacionados con los átomos. La certeza sobre un modelo atómico recae en su capacidad para poder explicar la realidad, predecir fenómenos y por lo tanto para generar tecnologías que nos permitan aprovechar de manera intencionada dichas propiedades. En otras palabras, el nivel de certeza de un modelo atómico es directamente proporcional a su utilidad es un contexto específico, es lo que Bohr llamaba instrumentalismo científico (Maleeh & Amani, 2013).
Para poner un ejemplo, los mapas también son modelos que representan a la realidad, son una aproximación a cómo debería verse un área geográfica desde determinado punto de vista. Pero si te pones en ese punto de vista, te das cuenta de que la realidad se ve un poco diferente a como se representa en el papel. ¿Significa entonces que los mapas son falsos?, la respuesta es no, porque son ÚTILES para poder predecir los fenómenos, en este caso, poder predecir cómo se comporta el terreno a medida que avanzamos desde un punto (A) a un punto (B). En otras palabras, los mapas son una representación de la realidad de un área geográfica, no la realidad misma del área geográfica. Lo mismo sucede con los modelos atómicos. Un modelo atómico es una representación de la realidad del átomo, no la realidad misma del átomo. El patrón para juzgar a un modelo científico, sea un mapa, un modelo o una teoría es su utilidad.
2.5 El átomo químico, físico-clásico y físico-cuántico
Los modelos atómicos se pueden distinguir en tres categorías principales, el átomo de los químicos, los modelos atómicos clásicos y los modelos atómicos cuánticos.
El átomo químico es una categoría que agrupa al modelo atómico de Dalton y todas las correcciones hechas Avogadro, Cannizzaro entre otros, de forma tal que es posible realizar predicciones sobre el comportamiento de la materia desde el punto de vista de reacciones químicas, con la característica principal de modelar a cada átomo como si se tratara de una partícula sin estructura interna.
Los modelos físicos por su parte buscan estudiar la estructura interna del átomo apoyándose en dos teorías de la física, la mecánica clásica, y la mecánica cuántica.
Los modelos atómicos de física clásica se caracterizan porque debían cumplir las leyes de Newton, debido a que la física de Newton se denomina mecánica clásica, los modelos atómicos que cumplen las leyes newtonianas reciben el nombre de clásicos (Pais, 1991). A pesar del conflicto que pueda existir entre la noción de átomo físico y átomo químico un aspecto común a los modelos clásicos es que sus propiedades no son diferentes a las de los objetos macroscópicos. Esto es cierto desde las primeras nociones del átomo griego hasta el átomo de Rutherford, donde los átomos poseen propiedades mecánicas. En esta primera etapa del desarrollo del átomo se generan varias cuestiones:
👉 la existencia del átomo,
👉 las propiedades de los átomos y finalmente
👉 la estructura interna de los átomos que quedará casi definida cuando al modelo de Rutherford se le adiciona el concepto de Neutrón.
El último modelo atómico clásico fue el modelo de Rutherford, lo cual trajo consigo una serie de paradojas relacionadas con la luz, los colores y las orbitas electrónicas que contribuyeron al surgimiento de una nueva física, con nuevas reglas, una física que negaba el concepto más básico de Newton, la continuidad del movimiento a través del espacio, dando lugar a un concepto descabellado en nuestra realidad inmediata, el salto cuántico que puede traducirse solo con el concepto de teletransportación. Todos los modelos que acogen el salto cuántico, es decir el movimiento de un electrón entre dos puntos sin recorrer el espacio intermedio se denominarán como cuánticos, y de ellos el modelo estándar moderno es el modelo atómico mecánico-cuántico-ondulatorio relacionado a autores como Erwin Schrödinger, aunque a él contribuyeron muchos autores más, y lo más paradójico es que todos lo detestaron, pero ninguno pudo refutarlo debido al criterio instrumentalista, la maldita teoría cuántica ondulatoria funciona aunque a nadie le guste y prácticamente nadie la endiente completamente.
3. El átomo filosófico
|| REGRESAR AL INDICE ||
Aunque en los textos de química el primer modelo del átomo que se representa es la esfera de Dalton y se mencionan solo de pasada las ideas griegas, hay que resaltar que dichos filósofos pensaron bastante sobre el problema, y un autor generalmente excluido es Platón aun cuando es el primero en dibujar un posible modelo del átomo para los diferentes tipos de sustancia. Aunque dicho intento pueda parecer risible, en el fondo la idea de la tabla periódica vista a través de los modelos del átomo es la misma idea, explicar las sustancias a través de la posible estructura de un átomo.
3.1 El átomo griego
Figura 3.1. Leucipo (en griego, Λεύκιππος, "Leúkippos") fue un filósofo griego (Mileto, Jonia) del siglo V a.C. a quien se atribuye la fundación del atomismo, al parecer fue "el primero en poner en tela de juicio la suposición aparentemente natural que afirma que cualquier trozo de materia, por muy pequeño que sea, siempre puede dividirse en otros trozos aún más pequeños". Él afirmaba que llegaba un momento en que dicha división llegaba a un fin.
Figura 3.2. Demócrito (en griego: Δημόκριτος; Abdera, Tracia, c. 460 a. C.-c. 370 a. C.) conocido también como El filósofo risueño, fue un filósofo y matemático griego que vivió entre los siglos V-IV a. C.12 Discípulo de Leucipo, se le llama también «el filósofo que ríe». Pensador con un amplio campo de intereses, es especialmente recordado por su concepción atomista de la materia.
👉 Leucipo, Epicuro y Demócrito
En el siglo V antes de cristo, Leucipo y su discípulo Demócrito propusieron que: Toda la materia está compuesta por partículas pequeñas e indivisibles llamadas átomos. Este es el fundamento de toda teoría atómica, sin embargo, ellos la postularon para poder reconciliar dos escuelas filosóficas que ya hemos tratado con anterioridad, la escuela de Heráclito y el cambio constante; y la escuela de Parménides y la esencia eterna. Básicamente los átomos son esa esencia eterna, que nunca cambia, que no se crea ni se destruye, pero a diferencia de Parménides, Demócrito y su maestro sostienen que el vacío existe. Los átomos al moverse en el vacío pueden cambiar sus asociaciones permitiendo el cambio constante del que hablaba Heráclito. En resumen, los átomos de Demócrito eran las partículas esenciales de Parménides cuyos movimientos en el vacío explicaban las ideas de Heráclito (Van Melsen, 2004).
👉 El átomo de Platón
Pocos conocen que Platón postuló un modelo del átomo –con partículas subatómicas incluidas –así como un intento de descripción matemático-filosófica.
Figura 3.3. Los átomos platónicos o stoicheias.
El atomismo de Platón era mecánico-materialista, es decir, átomos que estaban compuestos por partículas más fundamentales. Esta noción indica que los griegos estaban ya abiertos a la posibilidad de que el átomo “que significa indivisible” no fuera tan indivisible después de todo. En el Timeo, Platón (Friedlander, 2015) sostiene que los cuatro elementos estaban formados por cuatro tipos de átomos cuyas formas mecánicas explicaban las propiedades de los elementos que los componían –idea que será retomada en el siglo XVIII con poco éxito. Los átomos de platón son sólidos geométricos:
👉 El Cubo (A) conformaba los sólidos, es decir la Tierra debido a que la base sólida conferiría estabilidad.
👉 El Tetraedro (B) fue asignado al Fuego debido a que sus puntas penetrantes podrían descomponer las uniones de los átomos de la Tierra.
👉 El Octaedro (C) fue asignado al Agua debido a que sus bordes menos prominentes lo hacen menos estable para formar estructuras fijas.
👉 El Icosaedro (D) fue asignado al Aire debido a que posee puntas aún más redondeadas y por lo tanto seria menos estable que el octaedro.
Cada átomo de los cuatro elementos platónicos estaba a su vez compuesto por partículas subatómicas, en este caso triángulos. Los triángulos se convertían en la verdadera esencia de las cosas, los átomos podían descomponerse, y de esta forma explicarse porque lo sólido podía convertirse en líquido –ofreciendo una explicación para la transmutación/reacción química (Cornford, 2000; Lloyd, 2012).
👉 El átomo vs Aristóteles
De cierta forma Carl Sagan fue bastante injusto con Aristóteles sobre el asunto del átomo (Malone, Sagan, Druyan, & Soter, 1980). Por muchos años yo también años juzgué los argumentos de Aristóteles sobre el atomismo solo como aseveraciones basadas en la Autoridad. Sin embargo, el punto de vista de Aristóteles es evidentemente pragmático y atento a la experiencia sensible, es decir, la visión de Aristóteles debería ser el punto de vista intuitivo con el que debería llegar cualquier individuo que nunca ha estado expuesto a la idea del átomo por películas o educación básica.
Figura 3.4. Platón En griego antiguo: Πλάτων, Plátōn; Atenas o Egina, c. 427-347 a. C.) fue un filósofo griego seguidor de Sócrates y maestro de Aristóteles. En 387 fundó la Academia, institución que continuaría su marcha a lo largo de más de novecientos años y a la que Aristóteles acudiría desde Estagira a estudiar filosofía alrededor del 367, compartiendo, de este modo, unos veinte años de amistad y trabajo con su maestro
Aristóteles no aceptó la idea de Platón a cerca del mundo de las ideas, es decir del mundo alejado de los sentidos, y todo lo perteneciente a este mundo –como sus átomos mecánicos –fue desechado. Para Aristóteles la materia era tal y como se manifestaba, es decir continua, cuando uno ve un bloque de hierro, uno no ve segmentos de hierro, todo es continuo, sin partículas evidentes. Esta postura opuesta al mecanicismo discreto se denomina hilomorfismo (Verdejo, 2012). El hiloformismo dice que la materia es continua y sus transformaciones se explican por el cambio de la manifestación de los potenciales de la materia (Hesse & Anderson, 1992; Lloyd & Lloyd, 1968; Pohle, 1971).
Figura 3.5. Aristóteles. (En griego antiguo: Ἀριστοτέλης Aristotélēs; Estagira, 384 a. C.-Calcis, 322 a. C.) fue un filósofo, polímata y científico nacido en la ciudad de Estagira, al norte de Antigua Grecia aunque manteniendo fuertes lazos con Macedonia. Es considerado junto a Platón, el padre de la filosofía occidental. Sus ideas han ejercido una enorme influencia sobre la historia intelectual de Occidente por más de dos milenios.
En el contexto griego no había posibilidad de poner a prueba el atomismo, para ello se requeriría un mejor desarrollo en la neumática, que es la tecnología que permite la manipulación de los gases. Estas tecnologías no estaban de hecho lejos de su alcance, pero las guerras helenísticas y factores sociales como la esclavitud en la Alejandría egipcia impidieron en su tiempo (Ferguson, 2015). Debido a la imposibilidad de poner a prueba el atomismo o de obtener aplicaciones prácticas de esta idea, esta fue olvidada por muchos años en favor del hiloformismo aristotélico, que impulsó vanamente la investigación alquímica por siglos (Eliade, & Ledesma, 1974). En paralelo, la teoría de Aristóteles sobre la manifestación del potencial de la materia dio apoyo a las ideas de transmutación de cuerpos materiales continuos, lo que conllevó al desarrollo de la alquimia en las culturas donde su filosofía fue influyente: el Cristianismo y el Islam (Eliade, & Ledesma, 1974).
3.2 El átomo en el renacimiento
En clase, cuando vas describiendo la historia del átomo por lo general hay un hecho notable, y es un salto cualitativo entre Demócrito y Aristóteles hasta Dalton, como si la palabra de Aristóteles se hubiese tomado al dedillo durante la edad media y el renacimiento hasta llegar mágicamente a Dalton. Aunque esta idea va en consonancia con la leyenda de un autoritarismo severo por parte de los académicos eclesiásticos que tomaron a Aristóteles como la gran autoridad de la antigüedad, la verdad –por lo menos para el atomismo –no fue tan severa, después de todo los átomos no reñían con las doctrinas cristianas –por lo menos hasta donde tengo entendido. En consecuencia, el atomismo como escuela de pensamiento siguió viva, y sus principales defensores empiezan a ser ev identes ya en el siglo XVII, y autores tan importantes como Galileo Galilei o René Descartes dedicaron tiempo a la idea del átomo.
👉 El átomo de Galileo
Figura 3.6. Galileo Galilei (Pisa, Toscana; 15 de febrero de 15644-Arcetri, Toscana; 8 de enero de 1642) fue un astrónomo, filósofo, ingeniero, matemático y físico italiano, relacionado estrechamente con la revolución científica. Eminente hombre del Renacimiento, mostró interés por casi todas las ciencias y artes (música, literatura, pintura). Sus logros incluyen la mejora del telescopio, gran variedad de observaciones astronómicas, la primera ley del movimiento y un apoyo determinante a la «Revolución de Copérnico». Ha sido considerado como el «padre de la astronomía moderna», el «padre de la física moderna» y el «padre de la ciencia».
Aunque en principio el atomismo no pareciera plantear un problema serio para la doctrina cristiana sí que lo hacía. La Transmutación y la transubstanciación eran fenómenos filosóficamente similares que eran explicados por la teoría de Aristóteles. El problema con el atomismo es que niega una transubstanciación radical de los materiales ya que los átomos son eternos y no cambian –según las ideas de Demócrito. Algunos autores sostienen que las ideas de Galileo sobre el atomismo y la transubstanciación fueron las que lo mandaron con la inquisición y no el asunto del sistema copernicano. Esto se debe a que la doctrina cristiana dictaminaba literalmente que la hostia y el vino durante la eucaristía literalmente se transformaban con toda su esencia en el cuerpo y la sangre de Cristo (Glausser, 1991; Meinel, 1988). Sea como fuere los instrumentos de Galileo le impidieron encontrar evidencia experimental de los átomos.
👉 El átomo de Descartes
La filosofía mecanicista de Descartes plantea que todo lo que existe resulta de la unión mecánica de partes que conforman el todo, en este sentido es una filosofía muy similar al atomismo y es considerada en varios sentidos otra versión de la misma (Lennon, 2014).
Figura 3.7. René Descartes También llamado Renatus Cartesius (en escritura latina) (La Haye en Touraine, 31 de marzo de 1596-Estocolmo, Suecia, 11 de febrero de 1650), fue un filósofo, matemático y físico francés, considerado como el padre de la geometría analítica y de la filosofía moderna, así como uno de los epígonos con luz propia en el umbral de la revolución científica.
Descartes pensaba que toda la materia debía estar compuesta de pequeños vórtices de materia, al igual que los primeros atomistas Descartes pensaba que las propiedades macroscópicas de la materia eran solo ilusiones causadas por las estructuras de estos vórtices de materia. Sin embargo, existen dos diferencias entre el atomismo clásico y el atomismo de Descartes. La primera es el concepto de vacío que para Descartes era imposible, para Descartes la materia se mueve a través de otra materia
Otro aspecto importante del pensamiento de Descartes es que no es completamente materialista, de esta forma en su teoría da espacio para fenómenos idealistas como el alma y Dios (Garber, 1987; Glausser, 1991; Lennon, 1993; Meinel, 1988; Zepeda, 2009).
👉 El átomo de Gassendi
Figura 3.8. Pierre Gassendi (Champtercier, Provenza; 22 de enero de 1592-París, 24 de octubre de 1655) fue un sacerdote católico francés, filósofo, astrónomo y matemático.
Pierre Gassendi fue un sacerdote Católico de Francia que también era un curioso filósofo natural (Lennon, 2014). Gossendi se encontraba trabajando en paralelo con Descartes a cerca de la composición última de la materia intrigado por el atomismo clásico, se puso a la tarea de liberarlo de sus conclusiones filosóficas heréticas y ateísticas para de esta forma hacerlo concordante con la doctrina cristiana (Dijksterhuis & Dikshoorn, 1969).
Gassendi formuló una teoría atomista de la filosofía mecanicista parcialmente en respuesta a Descartes, oponiéndose particularmente a la idea reduccionista de que solo las explicaciones mecánicas son válidas en la filosofía natural (Clericuzio, 2000).
👉 El átomo newtoniano
El Corpuscularianismo –átomo newtoniano –es una filosofía similar al atomismo, excepto que donde los átomos se suponían indivisibles, los corpúsculos se los asumía como divisibles. De esta forma se ofrecía otra explicación para la transmutación, ya que un material como el mercurio podría en principio alterar los corpúsculos del plomo y convertirlo en oro (Newton, 1718). Gran parte de los problemas del átomo Newtoniano fue su pretensión de reducir las propiedades de la materia continua a formas geométricas del corpúsculo, lo que con frecuencia llevaba a formar modelos atómicos tan complejos que resultaban inviables. La física de los newtonianos estaba especialmente organizada para lidiar con fenómenos simples y relaciones entre variables no selectivas, por el contrario las relaciones químicas son muy selectivas y modelar esto resultaba muy complejo (Bernal & Daza, 2010).
Figura 3.9. Isaac Newton (Woolsthorpe, Lincolnshire; 25 de diciembre de 1642jul./ 4 de enero de 1643greg.-Kensington, Londres; 20 de marzojul./ 31 de marzo de 1727greg.) fue un físico, teólogo, inventor, alquimista y matemático inglés. Es autor de los Philosophiæ naturalis principia mathematica, más conocidos como los Principia, donde describe la ley de la gravitación universal y estableció las bases de la mecánica clásica mediante las leyes que llevan su nombre. Entre sus otros descubrimientos científicos destacan los trabajos sobre la naturaleza de la luz y la óptica (que se presentan principalmente en su obra Opticks), y en matemáticas, el desarrollo del cálculo infinitesimal.
En cualquier caso el “átomo newtoniano” se mantuvo como la teoría dominante por casi 100 años reteniendo sus vínculos con la alquimia en los trabajos de filósofos naturales como Robert Boyle e Isaac Newton (Levere, 2001). Un ejemplo de esto, es que Newton empleó la teoría corpuscular para crear una teoría corpuscular de la luz (Sabra, 1981) o mucho más básico para crear el modelo reduccionista del móvil corpuscular sobre el cual se crea la cinemática. Boyle asumió un modelo híbrido entre las propuestas de Newton, Descartes y Gassendi demostrando que algunos problemas provenientes de la nueva rama de la neumática podían explicarse mediante una teoría corpuscular-atómica (Boyle, 1911).
4. Introducción a las leyes ponderales
|| REGRESAR AL INDICE ||
Las leyes químicas son aquellas leyes de la naturaleza relevantes para la química, entre ellas, las más fundamentales son las que se agrupan bajo el concepto de ponderales. Sin embargo, antes de enunciarlas vale la pena preguntarnos, ¿Cuál es el significado de ponderal?
El significado que emerge de la palabra ponderal corresponde a un valor relacionado con el peso, es decir, lo que actualmente denominamos la masa de un objeto, por consiguiente, las leyes ponderales dependen de nuestra capacidad para medir de manera precisa la masa de los sistemas de estudio, sean estos: entidades físicas, o entidades químicas en reacción; lo cual nos traslada a entender los instrumentos de medida de masa, es decir, la balanza.
4.1 Historia de la balanza
Las reliquias más antiguas de una balanza se han descubierto en el valle del río Indo, cerca del actual Pakistán, que datan de alrededor del año 2000 a.C. A medida que se desarrollaba el comercio durante la antigüedad, los mercaderes desarrollaron la necesidad de evaluar el valor de bienes tales como cosechas, ropa y oro, con el fin de intercambiar sus bienes. Esto también implica la necesidad de evaluar proporciones de cambio para poder hacer trueques, o usar monedas de metales preciosos (Petruso, 1981).
Figura 4.1. Representaciones en jeroglíficos de la balanza, en estas destaca el juicio del alma, en la cual el dios Anubis mide el corazón del alma con respecto a la pluma de la justicia divina o maat, para ver si el alma es digna de pasar al paraíso, o de lo contrario ser alimento por Ammyt.
Los primeros dispositivos usaban un sistema simple, pero efectivo, que se basaba en equilibrar bienes. Consistían en dos placas unidas a una viga superior que estaba fijada en un poste central. Las medidas se tomaron colocando el objeto medido en un plato y piedras de peso en el otro, hasta que se alcanzara un equilibrio. Los arqueólogos han descubierto cubos de piedra pulidos y uniformes en los primeros asentamientos comerciales. En China, la balanza de pesaje más antigua excavada estaba hecha de madera y usaba masas de bronce. Se encontró en una tumba que data del siglo III al IV a. C. en el monte Zuojiagong, cerca de Changsha, Hunan. Cuando los romanos invadieron Gran Bretaña, las pesas de piedra fueron reemplazadas por pesas de metal más precisas y se impuso un sistema de medición para eliminar las prácticas de pesaje deshonestas por parte de los comerciantes (Petruso, 1981).
Figura 4.2. La imagen a la izquierda muestra el gabinete de pesas en el Museo de Nápoles, que representa los tipos de balanzas de metal utilizadas durante la época romana, y a la derecha hay una talla romana que muestra a un carnicero con su balanza detrás de él. Estas prácticas primero habilitaron el mercado de productos básicos y las ruedas de la industria que conocemos hoy.
Este sistema podía ser preciso, pero también se podía engañar fácilmente, siendo el ejemplo más famoso de una balanza manipulada cuando el cacique celta Brennus capturó Roma alrededor del 390 a. C. y exigió un rescate de 1000 libras de oro, por lo que fue acusado de usar pesas adulteradas (Norwood, 1950). Los comerciantes solían llevar sus propios pesos inexactos para trabajar a su favor, lo que llevó a la necesidad de un sistema más preciso, y la estandarización de los pesos fue una preocupación de los gobiernos durante este período. Una serie de variedades de balanzas, cada una con ventajas y mejoras entre sí, aparecen a lo largo de la historia registrada, con inventores como Leonardo da Vinci ayudando personalmente en su desarrollo .
A pesar de esto, hasta el siglo XVII d.C., los avances en el diseño y desarrollo de básculas fueron esencialmente todas las variaciones de la balanza. No surgió un método de pesaje más preciso hasta finales del siglo XVII, cuando la revolución industrial comenzaba a traer importantes mejoras tecnológicas. Tras la invención de la báscula de resorte por el fabricante de balanzas británico Richard Salter, alrededor de 1770, la balanza de pesaje ya no dependía de contrapesos. La báscula de resorte utilizó los efectos de la gravedad para calcular el peso, como se define en la Ley de Hooke, que determina el desplazamiento de la fuerza en el resorte. Funciona midiendo la presión ejercida sobre un resorte para deducir el peso de un objeto. La plausibilidad científica de las básculas de resorte llevó a que se convirtieran en la forma de báscula comercial y doméstica más utilizada y todavía son comunes hoy en día debido a su bajo costo (Bedini, 1965; Büttner & Renn, 2016).
Este vínculo entre la ciencia, la tecnología, la técnica y la artesanía de precisión ya había alcanzado un grado de interacción muy avanzado en el siglo XVIII, por ejemplo, Antoine Laurent de Lavoisier considerado el padre de la química moderna. El realizó experimentos que condujeron a la identificación del oxígeno, la ley de conservación de la masa ("nada se pierde, nada se crea, todo se transforma") y la síntesis del agua fueron hitos en la historia de la química (Donovan, 1996; Golinski, 1994).
Figura 4.3. Representación del laboratorio de Lavoisier.
Para llevar a cabo con éxito sus experimentos, Lavoisier utilizó unos trece mil instrumentos y aparatos, incluidos termómetros, barómetros, areómetros, relojes de arena, crisoles, reglas, bombas de vacío, balanzas y espejos reflectores. Trabajó en estrecha colaboración con los fabricantes para construir los instrumentos necesarios para sus experimentos. Con Nicolás Fortin ideó balanzas con una precisión hasta entonces desconocida para determinar la equivalencia del kilogramo . También creó gasómetros para la síntesis de agua y calorímetros para medir la cantidad de calor de un cuerpo. Administrador de la Ferme Générale, fue guillotinado en 1794, pero su esposa se encargó de la custodia de su laboratorio. Su sobrina nieta, Madame de Chazelles, donó algunas de las piezas más prestigiosas a la Académie des Sciences, y fueron trasladadas al Conservatorio en 1866. En 1956, la empresa Du Pont de Nemours adquirió unos quinientos aparatos para el museo, que dan testimonio a la química en tiempos de Lavoisier. De hecho, el fabricante Nicolás Fortin debería ser reconocido para muchas de las leyes que se mencionan en este capítulo y en el capítulo de gases, pues diseñó instrumentos para científicos tan prestigiosos como Gay-Lussac, François Arago, y Pierre Dulong (Beretta, 2014; Beretta & Brenni, 2022b, 2022a; Levere, 1990).
4.2 La balanza de Fortin
A medida que avanzaba el trabajo de Lavoisier para cuantificar la química, se hizo evidente que las balanzas que estaba usando no eran lo suficientemente precisas. Para compensar esto, Lavoisier había adoptado el pesaje doble, donde cada medición se hacía dos veces, intercambiando el matraz y los pesos entre las dos bandejas y tomando el valor promedio. Ahora, sin embargo, Lavoisier necesitaba un equilibrio con un nivel de precisión diferente al que había tenido antes. En el verano de 1788 recurrió a Fortin para el trabajo (Beretta, 2014; Beretta & Brenni, 2022b, 2022a; Levere, 1990).
Fortin entregó algo verdaderamente exquisito que sentó las reglas para futuros balances analíticos. La balanza en sí estaba encerrada en una gran caja de palisandro con paredes de vidrio y puertas corredizas para protegerla de la menor corriente de aire; Lavoisier ordenó que se sentara en una habitación separada para evitar la influencia de los vapores corrosivos del laboratorio. Dos cacerolas grandes colgaban de los extremos de una viga de acero dulce de un metro de largo. Una gran palanca en la base de la caja podía levantar la viga usando dos brazos conectados al poste central, de modo que la viga se bloqueaba mientras se cargaba. Al deslizar la palanca, la viga descendió suavemente sobre un filo de cuchillo hecho de acero templado (martensítico) resistente al desgaste. Un pequeño microscopio permitía al experimentador leer un puntero desde el exterior de la caja cerrada. La balanza operaba con una precisión de alrededor de una parte por millón. Con él, Lavoisier pudo sacar la conclusión que sustenta toda la química (pero que en realidad nunca escribió): Rien ne se perd. Rien ne se crée. Tout se transforma. (Nada se pierde. Nada se crea. Todo cambia) (Beretta, 2014; Beretta & Brenni, 2022b, 2022a; Levere, 1990).
Fortin también entregó otras dos balanzas con vigas más pequeñas. Lavoisier estaba encantado y los describió en detalle en su Traité Elementaire de Chimie, señalando que “combinan todas las correcciones y comodidades que uno podría desear. No puedo imaginar ningún otro, con la posible excepción de uno hecho por [Jesse] Ramsden, que pueda compararse tanto en exactitud como en precisión”. Había costado 600 libras pero valía su peso en oro. Durante los próximos 30 años, Fortin haría varias otras balanzas en la misma línea para químicos como Louis-Jacques Thénard, Joseph-Louis Gay-Lussac y Michel-Eugène Chevreul. Al menos dos aún sobreviven (Beretta, 2014; Beretta & Brenni, 2022b, 2022a; Levere, 1990).
4.3 Números absolutos y números relativos
Un concepto relativo o una cantidad es lo que se define en relación con otra cosa, de tal manera que una descripción significativa del concepto o de la cantidad implica necesariamente una referencia a la otra cosa en relación con la cual se ha definido. Por ejemplo, si te dijera que tengo el doble de dientes que mi abuela, entonces te he dado una descripción relativa de la cardinalidad de mis dientes.
En otras palabras, para saber de manera significativa cuántos dientes tengo, debes referirte a cuántos dientes tiene mi abuela. Sin embargo, si les digo que tengo 32 dientes, entonces es una descripción absoluta de la cardinalidad de mis dientes porque se define significativamente en sí mismo y no necesita referirse a otra cosa.
Tres de las cuatro leyes ponderales siempre estarán expresadas como magnitudes relativas, mientras que la última, la ley de la conservación de la masa puede estarlo o no estarlo dependiendo del modo en que la estemos expresando, pues esta última ley tiene una amplia gama de formas matemáticas posibles.
Hay varios significados y contextos ligeramente diferentes en los que las palabras relativo o absoluto pueden usarse en física, pero el impulso básico detrás de la idea sigue siendo el mismo. Daré un par de ejemplos, uno de los cuales ya se ha mencionado en otras respuestas:
👉 En un sentido básico, todas las descripciones de cantidades que tienen unidades dimensionales son necesariamente relativas. ¡En particular, transmiten información significativa solo en relación con sus unidades estandarizadas! Por ejemplo, cuando te digo que mi bolsa pesa 20 kg, te digo que su inercia es 20 veces mayor que la de la masa patrón de kilogramo.
👉 Un ejemplo más obvio de una cantidad relativa es la gravedad específica de una sustancia. Se define como la relación entre la densidad de dicha sustancia y la densidad del agua. Como puedes ver, esta es una cantidad relativa porque se define explícitamente en relación con la densidad del agua. Tenga en cuenta que la gravedad específica no tiene unidades, pero sigue siendo una cantidad relativa debido a la forma en que se define (en otras palabras, el hecho de que algo sea un número puro no significa que sea absoluto).
En general podemos concluir que cualquier magnitud que se defina como un cociente de otras dos, como la densidad o la masa molar son números relativos, mientras que las magnitudes que solo dependen de su unidad de referencia las consideraremos como absolutas. Por ejemplo, medir la masa de un objeto nos dará su masa absoluta, pero el cociente de la masa entre su volumen nos dará una masa relativa llamada densidad.
4.5 Resumen de las cuatro leyes ponderales
Como se mencionó anteriormente, las cuatro leyes ponderales se definen en cuanto a que son medidas de masa (o peso como se la denomina en textos de química)y a que la mayoría son números ponderales o relativos. Las leyes ponderales son leyes clásicas de la química que se refieren a los aspectos cuantitativos de las masas de diferentes elementos que se combinan para formar otros compuestos en reacciones químicas. Las leyes ponderales son:
👉 la ley de la conservación de la masa de Lavoisier 1774.
👉 la ley de proporciones equivalentes de Richter 1792.
👉 la ley de las proporciones definidas de Proust 1794.
👉 la ley de las proporciones múltiples de Dalton 1804.
Muchas fuentes normalmente excluyen la ley de proporciones recíprocas, ya que para ser justos su definición es algo confusa, y los ejercicios de lápiz y papel que se desprenden de ella son complicados al principio. En las siguientes secciones discutiremos con mayor profundidad cada una de estas leyes.
5. La ley de la conservación de la masa
|| REGRESAR AL INDICE ||
En física y química, la ley de conservación de la masa o principio de conservación de la masa establece que, para cualquier sistema cerrado a todas las transferencias de materia y energía, la masa del sistema debe permanecer constante en el tiempo, ya que la masa del sistema no puede cambiar, por lo que la cantidad no se puede agregar ni quitar. Por lo tanto, la cantidad de masa se conserva en el tiempo.
La ley implica que la masa no puede crearse ni destruirse, aunque puede reorganizarse en el espacio, o las entidades asociadas con ella pueden cambiar de forma. Por ejemplo, en las reacciones químicas, la masa de los componentes químicos antes de la reacción es igual a la masa de los componentes después de la reacción. Así, durante cualquier reacción química y proceso termodinámico de baja energía en un sistema aislado, la masa total de los reactivos o materiales de partida debe ser igual a la masa de los productos.
El concepto de conservación de la masa se usa ampliamente en muchos campos, como la química, la mecánica y la dinámica de fluidos. Históricamente, la conservación de la masa en las reacciones químicas fue demostrada de forma independiente por Mikhail Lomonosov y luego redescubierta por Antoine Lavoisier a fines del siglo XVIII. La formulación de esta ley fue de crucial importancia en el progreso de la alquimia a la moderna ciencia natural de la química.
En realidad, la conservación de la masa solo se mantiene aproximadamente y se considera parte de una serie de supuestos en la mecánica clásica. La ley debe modificarse para cumplir con las leyes de la mecánica cuántica y la relatividad especial bajo el principio de equivalencia masa-energía, que establece que la energía y la masa forman una cantidad conservada. Para sistemas muy energéticos, se muestra que la conservación de solo la masa no se cumple, como es el caso de las reacciones nucleares y la aniquilación de partículas-antipartículas en la física de partículas.
La masa tampoco se conserva generalmente en los sistemas abiertos. Tal es el caso cuando se permiten varias formas de energía y materia dentro o fuera del sistema. Sin embargo, a menos que estén involucradas la radiactividad o las reacciones nucleares, la cantidad de energía que escapa (o ingresa) a sistemas como el calor, el trabajo mecánico o la radiación electromagnética generalmente es demasiado pequeña para medirse como una disminución (o aumento) en la masa del sistema. Para sistemas que incluyen grandes campos gravitatorios, se debe tener en cuenta la relatividad general; por tanto, la conservación de masa-energía se convierte en un concepto más complejo, sujeto a diferentes definiciones, y ni la masa ni la energía se conservan tan estricta y simplemente como en el caso de la relatividad especial.
5.1 Los filósofos hindúes y griegos
Ya en el año 520 a. C., la filosofía jainista, una filosofía no creacionista basada en las enseñanzas de Mahavira (Bose, 2015), afirmó que el universo y sus componentes, como la materia, no se pueden destruir ni crear. Una idea importante en la filosofía griega antigua era que "Nada viene de la nada", por lo que lo que existe ahora siempre ha existido: ninguna materia nueva puede surgir donde antes no existía. Una declaración explícita de esto, junto con el principio adicional de que nada puede convertirse en nada, se encuentra en Empédocles (c. Siglo IV a. C.): "Porque es imposible que algo venga a ser de lo que no es, y no puede ser". ser provocado o oído hablar de que lo que es debe ser completamente destruido" (Kirk, Raven, & Schofield, 1983). Epicuro declaró otro principio de conservación alrededor del siglo III a. C., quien escribió al describir la naturaleza del Universo que "la totalidad de las cosas siempre fue tal como es ahora, y siempre será" (Leroux, 1992).
5.2 Primeros estudios científicos
En el siglo XVIII, el principio de conservación de la masa durante las reacciones químicas se usaba ampliamente y era una suposición a priori importante durante los experimentos, incluso antes de que se estableciera formalmente una definición o una prueba, como se puede ver en los trabajos de Joseph Black, Henry Cavendish y Juan Rey (Whitaker, 1975). El primero en esbozar el principio fue Mikhail Lomonosov en 1756 (Pomper, 1962). Es posible que lo haya demostrado mediante experimentos y ciertamente discutió el principio en 1748 en correspondencia con Leonhard Euler (Pismen, 2018), aunque su afirmación sobre el tema a veces es cuestionada (Usitalo, 2013).
5.3 Lavoisier
Posteriormente, Antoine Lavoisier llevó a cabo una serie de experimentos más refinados, quien expresó su conclusión en 1773 y popularizó el principio de conservación de la masa (Barrotta, 2000; de Andrade Martins, n.d.; Holmes, 1985). Las demostraciones del principio desmintieron la entonces popular teoría del flogisto que decía que se podía ganar o perder masa en los procesos de combustión y calor.
La conservación de la masa fue oscura durante milenios debido al efecto de flotabilidad de la atmósfera terrestre sobre el peso de los gases emitidos en muchas reacciones de combustión y desplazamiento ácido-base, por lo que, a parte de una balanza, se requiere que la reacción ocurra en un sistema que impida el escape de materia.
Por ejemplo, un trozo de madera pesa menos después de quemarlo; esto parecía sugerir que parte de su masa desaparece, o se transforma o se pierde en forma de calor, lo cual constituía parte de la teoría del flogisto.
5.4 El experimento de Landolt
Sin embargo, y aunque los libros de texto no lo indiquen, la cuestión de la ley de la conservación de la masa quedó abierta un par de años más después de los experimentos de Lavoisier, pues los diseños experimentales hechos hasta ese momento caían en razonamientos circulares (Jensen, 2019).
Figura 5.1. (A) Hans Landolt (1831-1910) (B) Una fotografía de la balanza de Landolt con dos de sus tubos de reacción contrapesados: el de la izquierda antes de la reacción y el de la derecha después de la reacción. Los tubos siempre se pesaron uno contra el otro en pares para compensar la flotabilidad-boyancia del aire. (C ) Los dos reactivos, A y B, estaban en brazos separados del tubo antes de la inversión para iniciar la reacción química.
No fue sino hasta 1893 que el químico físico suizo-alemán Hans Landolt llevó a cabo una serie de experimentos diseñados para probar explícitamente la ley. Usando una balanza especialmente diseñada y tubos de reacción sellados herméticamente, Landolt probó cuatro sistemas de reacción diferentes para la conservación de la masa (Jensen, 2019):
👉 La reacción entre el sulfato de hierro y el sulfato de destilación para producir plata y trisulfato de dihierro, donde el acto de reacción se indicó visualmente mediante la formación de un espejo de plata :
2Fe(SO4)(aq) + Ag2(SO4)(aq) ➝ 2Ag(s) + Fe2(SO4)3(ac)
👉 La reacción entre el yodato de hidrógeno y una mezcla de ácido sulfúrico/yoduro de potasio para producir diyodo, hidrogenosulfato de potasio y agua, donde el acto de reacción se indicó visualmente por la formación del color marrón del diyodo acuoso:
H(IO3)(aq) + 5H2(SO4)(aq) + 5KI(aq) ➝ 3I2(aq) + 5K(HSO4)(aq) + 3H2O(l)
👉 La reacción entre el sulfito disódico y el diyodo para producir yoduro de sodio y ditonato disódico, donde el acto de reacción se indicó visualmente por la desaparición del color marrón del diyodo acuoso:
2Na2(SO3)(aq) + I2(aq) ➝ 2NaI(aq ) + Na2(S2O6)(ac)
👉 La reacción entre el hidrato de cloral y el hidróxido de potasio para producir cloroformo, formiato de potasio y agua, donde el acto de reacción se indicó visualmente por la formación de una capa de cloroformo insoluble en agua:
CCl3CH(OH)2(aq) + K(OH) (aq) ➝ HCCl3(l) + K(CHOO)(aq) + H2O(l)
Se encontró que las diferencias de masa antes y después de la reacción eran siempre del orden de entre 10-4 y 10-6 gramos y, por lo tanto, eran el posible resultado de un error experimental, lo que lleva a Landolt a concluir que: Ninguna de las reacciones empleadas muestra un cierto cambio de peso. Si, después de todo, ocurrieran tales cambios, deben ser tan pequeños que no tengan importancia práctica para el químico (Jensen, 2019). En este orden de ideas, el lector siempre debe tener en cuenta que los experimentos verdaderos, por muy bien diseñados que estén, siempre tienen cierto ruido debido a errores experimentales, por ejemplo, que el operario mida de manera incorrecta la masa de los reactivos, es por esto que actualmente los experimentos siempre se hacen con un mínimo de tres réplicas y se aplican métodos estadísticos.
Figura 5.2. Variación escolar idealizada del experimento de Landolt. El contenedor cerrado evita que los gases de la combustión invisibles escapen, permitiendo medir la masa final total sin que escape materia.
5.5 Consecuencias
Una vez comprendida, la conservación de la masa fue de gran importancia en el progreso de la alquimia a la química moderna. Una vez que los primeros químicos intuyeron a priori que las sustancias químicas nunca desaparecían, sino que solo se transformaban en otras sustancias con el mismo peso, estos científicos pudieron por primera vez embarcarse en estudios cuantitativos de las transformaciones de las sustancias. La idea de la conservación de la masa más la suposición de que ciertas "sustancias elementales" tampoco podían transformarse en otras mediante reacciones químicas, a su vez condujo a una comprensión de los elementos químicos, así como a la idea de que todos los procesos y transformaciones químicos (como la quema de y reacciones metabólicas) son reacciones entre cantidades o pesos invariantes de estos elementos químicos.
Siguiendo el trabajo pionero de Lavoisier, los exhaustivos experimentos de Jean Stas y Landolt avalaron la consistencia de esta ley en las reacciones químicas (Wang, 2017), aunque se realizaron con otras intenciones. La ley de la conservación de la masa en la actualidad se emplea para sistemas no relativistas y no nucleares, los cuales afortunadamente constituyen la inmensa mayoría de procesos químicos experimentales e industriales. Por lo anterior, la ley de la conservación de la masa puede definirse para un sistema no nuclear/relativista como: La masa no se crea ni se destruye, solo se transforma.
5.6 Propiedades aditivas de la conservación de la masa
La ley de la conservación de la masa tiene una multitud de definiciones y consecuencias que se retomarán en capítulos posteriores, por el momento la definiremos como: la masa total de un sistema m es igual a la suma de las masas individuales de los componentes mi de dicho sistema.
Eq. 5.7. Ley de la conservación de la masa de un sistema compuesto por partes de masa variable.
Al ser una suma, es importante recalcar que la ley de la conservación de la masa está sometida a todas las propiedades de la adición tales como:
👉 conmutación: dos sistemas pueden tener la misma masa total, aunque sus partículas individuales tengan masas diferentes.
👉 asociación total: podemos agrupar algunas partes del sistema para sumarlas de manera acelerada, esto es particularmente cierto si las partículas poseen la misma masa, en cuyo caso podemos usar una multiplicación. Así, por ejemplo, si todas las masas de la ecuación 4.1 tuvieran el mismo valor, entonces podemos reescribir la expresión como el producto del número de partes (N) por la masa común (mi):
Eq. 5.8. Ley de la conservación de la masa de un sistema compuesto por partes de masa constante, donde (x) representa la cantidad de partes del sistema.
👉 asociación parcial: Un sistema puede estar dividido en partes asociables por masa, es decir un sistema tiene varios tipos de partes, cada una rexpidiéndose una cierta cantidad de veces.
Eq. 5.9. Ley de la conservación de la masa de un sistema compuesto por grupos de partes de masa constante. Cuando esto sucede la multiplicación se convierte en una alternativa aritmética más sencilla que la suma simple.
De lo anterior se concluye que la forma matemática de ley de la conservación de la masa cambia dependiendo de cómo se organizan las partículas que componen a un sistema, y puede variar entre sumas simples y multiplicaciones.
5.10 Propiedad de suma cero para un cambio de estado
Otra consecuencia de la ley de la conservación de la masa es que la masa total de un sistema cerrado no cambia, aunque el sistema cambie su estado desde un momento inicial a un momento final, por lo que se puede igual a cero.
Eq. 5.11. La diferencia de masa total es cero.
5.12 Conservación de la masa en una reacción química ideal
Aplicando las propiedades generales anteriores, definiremos que una reacción química es un cambio en el estado de un sistema, donde la masa se reacción inicial es la suma de las masas de cualquier sustancia al principio de la reacción, y la masa de reacción final es la suma de las masas de cualquier sustancia al final de la reacción.
Figura 5.3. (Izquierda) Masa inicial total en términos de las masas de las sustancias al principio de la reacción. (Derecha) Masa inicial total en términos de las masas de las sustancias al principio de la reacción.
En un sistema complejo como los de equilibrio químico, la diferencia entre productos y reactivos es ambigua, por lo que se debe tener en cuenta a todas las sustancias de reacción posibles presentes en el sistema, sin embargo, dado que estamos iniciando, asumiremos una reacción no reversible sin sobrantes o faltantes, donde la masa de reacción inicial está definida únicamente por las masas iniciales de los reactivos, y la masa de reacción final está definida únicamente por la masa final de los productos. En estas situaciones ideales, las marcas de inicio y final se hacen innecesarias, y simplemente nos referimos a las masas de reactivos y productos.
Figura 5.4. (Izquierda) Masa inicial total en términos de las masas de las sustancias al principio de la reacción. (Derecha) Masa inicial total en términos de las masas de las sustancias al principio de la reacción.
En un sistema complejo como los de equilibrio químico, la diferencia entre productos y reactivos es ambigua
Por lo que la ley de la conservación de la masa de este tipo de reacciones puede escribirse de dos formas:
Figura 5.5. (Izquierda) Masa inicial total en términos de las masas de las sustancias al principio de la reacción. (Derecha) Masa inicial total en términos de las masas de las sustancias al principio de la reacción.
Tenga en cuenta que las ecuaciones de la ley de la conservación de la masa fallaran para reacciones donde ser produce grandes cantidades de calor, y en su lugar se debe emplear la forma más general llamada ley de la conservación de la energía de Einstein, sin embargo, las diferencias para la mayoría de las reacciones químicas es tan pequeña que podemos despreciarla.
Matamala y Gonzáles
Ejercicio 1.8. En el óxido férrico Fe2O3 ¿cuantos moles de oxígeno atómico entran por cada 2,8 gramos de hierro?
Química la ciencia central 13
Ejercicio 2.1-página-91. En un experimento, 7.0 g de nitrógeno reaccionaron con exactamente 16.0 g de oxígeno para formar un solo compuesto. ¿Cuál sería la masa total del compuesto? (a) 7.0 g (b) 16 g (c) 23 g
5.19 Conservación de la masa en una reacción química no-ideal
Si la ley de la conservación de la masa se aplica únicamente a situaciones ideales, pues aplicarla es muy sencillo, sin embargo, la realidad dista mucho de la idealidad, por ejemplo, en una reacción química, puede ocurrir que:
👉 el reactor tenga contaminantes de productos de una reacción previa, por lo que la masa de reacción inicial contendrá cierta masa de producto diferente de cero.
👉 uno de los reactivos se encuentra en exceso, por lo que la masa final del reactivo es diferente de cero.
👉 o las dos situaciones simultáneas anteriores.
Para estas situaciones si es importante usar la simbología de estado inicial-final que introdujimos en el capítulo de gases.
Eq. 5.20. Ley de la conservación de la masa para una reacción química incompleta que inicia con cierta cantidad de producto generada por una reacción previa.
En la ecuación anterior tenemos dos términos que normalmente no tenemos en cuenta ya que los asumimos idealmente como ceros, que son la masa final de los reactivos (mr) y la masa inicial de los productos (mo,p). De hecho, igualando estos dos términos a cero recuperaremos la ecuación 5.17. Aunque la ecuación 5.20 parece innecesariamente complicada, nos permite evaluar sistemas que se desvían de la idealidad, es decir, sistemas donde la mezcla de reactivos NO se consume completamente, que ocurren en reactores que no se limpian adecuadamente.
6. Ley de las proporciones definidas
|| REGRESAR AL INDICE ||
En química, la ley de las proporciones definidas –algunas veces denominada ley de Proust –establece que un compuesto químico contiene siempre cantidades fijas en proporciones semejantes de las masas de los elementos que lo componen.
6.1 Modelos matemáticos no moleculares
Matemáticamente hablando, la ley de Proust modela reacciones de descomposición o de síntesis. La expresión matemática de la ley de Proust se puede plantear de dos formas, la primera y más común es la del cociente de masas de los elementos que conforman al compuesto.
Figura 6.1. Interpretaciones macroscópicas de la ley de Proust de proporciones definidas empleando el parámetro masa, sin embargo dependiendo los tipos de masas analizados, podemos expresar el ratio de masas de dos elementos en él compuesto (Eq. 6.2.), o el ratio de masas de un elemento contra la masa total del compuesto (Eq. 6.3.).
La segunda manera es visualizar a un compuesto como una mezcla homogénea de proporciones invariantes, por lo que podemos aplicar cualquiera de las unidades de concentración que se ven en mezclas, solo que en lugar de estar definidas para un compuesto j-qualquiera estarán definidas para el elemento J-cualquiera, y en lugar de arrojar concentraciones variables, la concentración del elemento en el compuesto nunca cambia.
👉 La constante permite crear regla de tres
Dado que el ratio de masas o la fracción de masas del elemento contra el compuesto es una constante, hoy podemos igualar dos expresiones s donde las masas se obtienen de experimentos diferentes, hoy ya sea que tengamos una relación de masa experimental a masa estándar, o una relación de dos masas experimentales de dos muestras diferentes.
Figura 6.2. Reglas de tres analíticas para la ley de Proust empleando el parámetro masa, hoy a la izquierda tendríamos la relación entre masa inicial y masa final de los dos elementos, y a la derecha la relación que existiría entre la masa estándar de los dos elementos y la masa experimental. aunque el concepto de masa inicial y más estándar es diferente en términos experimentales, ambos funcionan exactamente igual al nivel matemático, y por consiguiente ambos tipos de ejercicios, aunque conceptualmente distintos se pueden resolver con una regla de tres aritmética.
👉 Porcentuales
Hoy cuando expresamos una fracción como un porcentaje en realidad estamos multiplicando por uno, eso se debe a que el símbolo de porcentual (%) hoy es equivalente al prefijo centi (10-2), Por lo que la expresión (100 %) que empleamos para convertir una fracción a un porcentaje es equivalente a la unidad. lo anterior implica que un porcentaje de una fracción son en esencia el mismo número, sólo son diferentes modos de visualizarlos, y por consiguiente el porcentaje no es otra cosa que un reemplazo limitado de la notación científica.
Matamala y González
Ejercicio 1.6. ¿Qué peso de nitrógeno se combina con 50 g de oxígeno en un compuesto en el cual hay 2 átomos de N por cada átomo de O?
Recuerde que normalmente las fracciones de masa se expresan como porcentaje, así, por ejemplo, el porcentaje en peso del carbono en el dióxido de carbono se expresa como 27.27%. Este porcentaje debe calcularse experimentalmente, por ejemplo, determinando cuanto carbono mineral se requiere para consumir una determinada masa de oxígeno puro:C(s) + O2(g) → CO2(g). Existen técnicas teóricas para predecir el porcentaje, pero estas involucran interpretaciones teóricas de la ley de Proust a la luz de la teoría atómica, que no veremos en esta sección debido a que sería una interpretación anacrónica, pues aún no hemos introducido la propia teoría atómica.
Lo anterior nos lleva a una paradoja de tiempo. Todos los procesos que nos permite hacer la ley de proporciones definidas ya están presentes en la ley de proporciones recíprocas de Ricther, pero esta es 2 años más antigua como mínimo. Por tal razón, aunque cronológicamente, la ley de Proust es posterior a la ley de Ricther, conceptualmente, y matemáticamente, solo podemos explicar la ley de Ricther en base a los procedimientos de la ley de Proust.
Figura 6.3. Joseph Louis Proust (Angers, 26 de septiembre de 1754 – ibídem, 5 de julio de 1826) fue un farmacéutico y químico francés y uno de los fundadores de la química moderna.
6.7 La controversia Proust Bertholet
Recuerdan que matemáticamente podemos usar las unidades de concentración de las mezclas homogéneas para describir una proporción definida? Pues resulta que históricamente existió un conflicto con respecto a ese detalle, pues los químicos no distinguían entre sustancias puras compuestas y mezclas homogéneas.
El problema es que los químicos tenían dos tipos de sustancias macroscópicas, aquellas que, si cumplen la ley de Proust y arrojan cocientes de masa constantes, y otras que no lo hacen. Este problema lo tenemos resuelto mediante la primera gran separación de la materia que tenemos en la siguiente figura
Figura 6.4. Diagrama de clasificación de la materia. Este diagrama nos indica que las sustancias puras compuestos como por ejemplo una muestra pura de H2O, poseen una apariencia semejante de una mezcla homogénea como por ejemplo el agua azucarada, sin embargo, al descomponerlas, las mezclas generan proporciones variables, mientras que los compuestos generan proporciones fijas.
La materia se divide en dos grandes grupos, aquellas en el que el cociente de masas es constante, y que actualmente llamamos sustancias puras compuestas, y aquellas en las que el cociente de masas es variable, y denominamos mezclas. El problema es que en la época de Proust las técnicas para separar mezclas en sustancias puras, y posteriormente, las sustancias puras en elementos, aún estaban en pleno perfeccionamiento, por lo que algunos químicos contemporáneos como Claude Louis Berthollet dudaban que en verdad los cocientes de masa se hicieran constantes en algún momento (Fujii, 1986; Hartog, 1894; Kapoor, 1965), lo cual implica que para la época, la diferencia entre elemento, compuesto, sustancia pura y mezcla, tan intuitiva para nosotros, aun no era aceptada completamente. (Daubeny, 1850).
También debemos tener en cuenta que la idea de proporciones definidas en Proust corresponde a cantidades macroscópicas de sustancias, cosas que pueden medirse con balanzas, de allí que es una ley ponderal, sin embargo, la idea moderna de proporciones definidas se vincula más a la teoría atómica de Dalton. Aunque actualmente podemos plantear ecuaciones que vinculan estas dos formas tan diferentes de entender la materia, algunos autores sugieren que la idea de proporciones definidas de Dalton es muy diferente de la de Proust a tal punto que puede que no sean tan directamente compatibles como plantean los libros de texto normalmente (Fujii, 1986).
No sería Dalton, sino Berzelius quien encontraría el vínculo entre la ley de proporciones definidas y la teoría atómica de Dalton hasta 1811.
7. Ley de las proporciones recíprocas
|| REGRESAR AL INDICE ||
La ley de las proporciones recíprocas fue propuesta por Jeremias Richter en 1792. Establece que, "si dos elementos diferentes se combinan por separado con el mismo peso de un tercer elemento, la relación de las masas en las que lo hacen es la misma o un simple múltiplo de la relación de masa en la que se combinan". En otras palabras, la ley de las proporciones recíprocas dice que, si conocemos la proporción de elementos en el compuesto AB y la proporción de elementos en los compuestos BC, podemos determinar la proporción de elementos en el compuesto AC. ¿Pero que es una proporción? Cuando hablamos de proporciones en química generalmente hablamos de radios o cocientes, en este caso cocientes de masa.
Esta es la menos conocida de las leyes ponderales, a tal grado de haber sido expulsada del libro de química general moderno, probablemente debido a que su algoritmo de resolución matemático es complejo. La ley de Ricther plantea dos cosas implícitas:
1- las proporciones de masa de los reactivos y productos en una reacción química son fijas o iguales a una constante que denominaremos cociente de masas y que representaremos con la letra griega “zeta ζ”. Esta idea es semejante a la ley de Proust, pues en ambos casos estamos hablando de una proporción de finida, pero en la ley de Proust nos limitamos a reacciones de descomposición de un compuesto a elementos, o de una reacción de síntesis desde elementos a un compuesto. La ley de proporciones recíprocas se plantea para grupos de reacciones con reactivos o productos semejantes que no necesariamente involucran elementos puros.
2- es posible usar información conocida de dos reacciones químicas estándar para inferir información desconocida de una tercera ecuación química.
Normalmente tendremos tres cocientes de masa experimentales, que son los que se calculan directamente. Una de las reacciones normalmente se selecciona arbitrariamente para ser calculada indirectamente a través de la información de las otras dos reacciones, y luego se compara el cociente experimental con el cociente calculado indirectamente.
DEMOSTRACIÓN: Demostrar las ecuaciones que sirven para contrastar la ley de proporciones recíprocas o ley de Richter.
Figura 7.1. Ecuaciones básicas para resolver un ejercicio de ley de Richter: Eq. 7.1. Cociente de masas de la reacción 1 Eq.7.2. Cociente de masas de la reacción 2. Eq. 7.3. Cociente de masas de la reacción 3. Eq. 7.4. Cociente de masas de la reacción 3 calculado.
Para que las ecuaciones anteriores funcionen, la sustancia II debe ser aquella que se repite en las reacciones 1 y 2, y que no aparece en la reacción 3. Algunas variantes del enunciado de la ley de proporciones recíprocas emplean la unidad de fracción de masas o su porcentaje. Sin embargo, la fracción de masas solo es una forma de expresar las proporciones de masa.
Richter dirigió sus intereses a las reacciones de neutralización ácido-base. En estos experimentos, midió exactamente cuánto ácido se requería para neutralizar una determinada cantidad de base y viceversa. Lo que encontró fue que se requerían cantidades fijas y definidas de cada uno. Publicó esta idea de "peso equivalente" en 1792. La idea fue rápidamente adoptada por dos químicos franceses que lógicamente preguntaron si la proporción en masas se mantenía constante para otros tipos de reacción química, en especial las reacciones de síntesis y descomposición, ya que esto permitiría estudiar la composición de sustancias químicas y permitir separar o categorizar tipos de sustancias.
7.9 Origen del concepto de estequiometría
El término “estequiometría” es de origen griego; stoicheion = elemento y metron = medida, por lo que stoicheion + metron significa: medida del elemento. La ley de proporciones recíprocas representa uno de los primeros intentos de hacer medidas de elementos siendo introducida por el químico alemán Jeremias Benjamin Richter (1762-1807) en su tesis doctoral “De usu matheseos in chemia” (Sobre el uso de matemáticas en química, 1789), su trabajo de 3 volúmenes titulado Anfangsgrunde der St ¨ ochiometrie oder ¨ Meßkunst chemischer Elemente (Fundamentos de la estequiometría o el arte de medir elementos químicos) publicado en 1792–1793 (Richter, 1968) y 11 pequeños volúmenes titulados Ueber die ¨ neuen Gegenstande der Chemie ¨ (Sobre los nuevos temas de la química) publicados entre 1791 y 1802 (Michałowska-Kaczmarczyk, Asuero, & Michałowski, 2015).
Richter descubrió que la proporción en peso de los compuestos consumidos en una reacción química completan en la que no hay residuos de un reactivo excedente era siempre la misma, sin importar que la masa absoluta de partida fuera diferente. La ley de proporciones recíprocas se formuló bajo supuestos de que se cumple la ley de composición constante, para estos compuestos, lo cual implica que la ley de proporciones definidas antecedió a su reconocimiento generalizado por Proust, lo cual explica la paradoja matemática en la que aunque la ley de Ricther es “más antigua” también es matemáticamente mas compleja de la ley de Proust (Michałowska-Kaczmarczyk et al., 2015).
Cabe señalar que Richter estudió filosofía y matemáticas en la Universidad de Konigsberg, donde enseñó el gran filósofo Immanuel Kant. El joven Richter estuvo fuertemente influenciado por la afirmación kantiana de que “cualquier disciplina entre las ciencias naturales es una verdadera ciencia solo en la medida en que contiene matemáticas”. Su fascinación por el papel de las matemáticas en la química se expresó en su tesis doctoral. Richter creía implícitamente en el libro bíblico La Sabiduría de Salomón (XI:22), por lo que tomó en sus escritos sobre estequiometría el lema “Dios ha ordenado todas las cosas en función del peso, el número y la medida” (Michałowska-Kaczmarczyk et al., 2015).
El nivel de "matemáticas químicas" utilizado por Richter para explicar los principios de la estequiometría ciertamente no era congruente con el nivel sofisticado demostrado por los primeros matemáticos y físicos y los contemporáneos de Richter (Lagrange, Laplace). Sin embargo, las matemáticas químicas utilizadas por Richter no eran comprensibles (consideradas “oscuras y torpes”) por los químicos contemporáneos y sus ideas pasaron inicialmente desapercibidas. Como dijo Thomson: "Richter, en cierta medida, fue anterior a la época en que vivió..." (Michałowska-Kaczmarczyk et al., 2015).
7.10 Origen de las proporciones recíprocas
En 1792, Richter observó que la neutralidad se conserva cuando se mezclan soluciones de dos sales neutras, aunque se produzca una doble descomposición. Escribió: "De esto no pude sacar ninguna inferencia directa aparte de que deben existir relaciones cuantitativas fijas entre los constituyentes de las sales neutras. Por lo tanto, se sigue que si se conocen las proporciones de combinación en los compuestos originales, las de los compuestos recién formados también son conocidos". Determinó los pesos de varias bases requeridas para neutralizar un peso dado de un ácido y encontró que la proporción de estos pesos era constante, sin importar el ácido, y viceversa, la misma relación se mantiene cuando un peso fijo de una base es neutralizado por varios ácidos. En otras palabras, las cantidades de ácidos y bases equivalentes en una neutralización lo son en todas. Desafortunadamente, Richter expresó sus generalizaciones en un estilo extremadamente complicado y confuso, sus escritos no fueron leídos cuidadosamente y el crédito por sus conclusiones se le dio al precursor de Richter, Carl Friedrich Wenad (1740-1793) (Darmstaedter & Oesper, 1928).
Berzelius fue el responsable de este error y su rectificación se debió a G. H. Hess, quien en 1840 señaló que Wenzel no tiene ningún derecho real al mérito de sentar las bases de la equivalencia química. La tardía apreciación de la obra de Richter se debió a varias causas. Aunque no era defensor del flogisto, Richter usó a menudo este marco de referencia flogística, y este compromiso no solo oscureció sus conclusiones, sino que no complació a ninguna escuela de química moderna. La controversia del flogisto-oxígeno estaba ocupando las mentes del mundo químico. Además, la cuestión de la composición constante de las sales no había sido resuelta, por lo que cualquier juicio sobre la validez de las conclusiones de Richter quedó necesariamente en suspenso.
El propio Richter no tenía ninguna duda sobre la verdad y la importancia de su teorema y al discutir su ley de equivalentes afirmó: "Esta proposición es una verdadera piedra de toque de los experimentos que tratan con relaciones de neutralización, porque si las relaciones encontradas experimentalmente no se ajustan a la ley los cambios de gobierno ocasionados por la doble descomposición sin cambio en la neutralidad, los resultados deben ser rechazados como erróneos, y los experimentos ciertamente contienen una fuente de error". Los datos se reunieron en tablas de equivalentes de neutralización, una tabla separada para cada ácido y cada base, pero en 1802 G. E. Fischer recopiló los valores numéricos dispersos de Richter y los combinó en una sola tabulación. Richter reconoció el valor de esta compilación y en 1803 él mismo publicó una tabla más completa que contenía los pesos equivalentes de 18 ácidos y 30 bases. En esto se revisaron muchos de sus pesos equivalentes anteriores. Las cifras no son muy precisas, ya que Richter admitió que no era un buen analista. "No soy un manipulador hábil. Nunca puedo terminar un análisis sin perder algo antes de que se completen todas las operaciones. Cuando hago determinaciones estequiométricas, nunca intento trabajar con tan solo 100 granos. Necesito 500".
Richter consideraba la química como una rama de las matemáticas aplicadas y estudiaba sus resultados experimentales con la esperanza de descubrir regularidades aritméticas y encontrarlas a pesar de su inexistencia. Creía que los pesos combinados de los ácidos formaban una serie geométrica, mientras que los de las bases estaban en progresión aritmética. Estaba tan obsesionado con este postulado, que se ha afirmado que no dudó en alterar sus datos para ajustarse a esta noción, y este prejuicio puede haberle impedido percibir el significado real de su ley de proporciones recíprocas. Algunos afirman que sostuvo que la especulación era la más importante de las dos. Sus medidas de los pesos de los metales que se disolvieron en pesos fijos de ácido para formar sales neutras lo llevaron a deducir la afirmación de que los pesos de varias bases que saturan un peso constante de un ácido contienen el mismo peso de oxígeno, y del mantenimiento de neutralidad cuando un metal precipita otro de una sal neutra, también concluyó que las cantidades de dos metales que se disuelven en el mismo peso de un ácido también se unen en sus óxidos con el mismo peso de oxígeno. En sus tabulaciones de estos experimentos, representó los metales por los símbolos alquímicos entonces vigentes, pero su trabajo también incluyó algunos de los metales recién descubiertos y para estos escribió las dos primeras letras de los nombres, anticipándose así a Berzelius, quien más tarde amplió esta idea a todos los elementos.
Completamente convencido de la verdad de la ley de proporcionalidad, profetizó que llegaría el momento en que "se romperá el muro que separa las matemáticas de la química y se descubrirá que las primeras gobiernan aún otros fenómenos de las ciencias naturales". . . . Como dice Lowig: "De hecho, toda la industria química se colocó por primera vez sobre una base racional con la introducción de las leyes de Richter, y los miles de millones ahorrados son incalculables". Richter creía implícitamente en la verdad del Libro de la Sabiduría XI, 22, y lo colocó como lema guía al comienzo de sus escritos estequiométricos: "Dios ha ordenado todas las cosas por medida, número y peso".
8. Ley de las proporciones múltiples
|| REGRESAR AL INDICE ||
Algunas veces también se la denomina como la ley de Dalton en honor a su descubridor, el químico Inglés John Dalton (Bernatowicz, 1970). La formulación de la ley establece: Si dos elementos forman más de un compuesto entre ellas, cuando se analizan los radios/proporciones de las masas dejando uno de los elementos fijos, el segundo se combina en múltiples masas fijas de acuerdo con radios expresables en números enteros pequeños.
Esto implica que una misma pareja de elementos puede generar diferentes compuestos, cada uno con su propio cociente de masa, por consiguiente, si el porcentaje en masa (o sus fracciones o cocientes) de un elemento es diferente entre dos muestras analizadas, entonces las muestras son de compuestos diferentes, pero si por el contrario el valor es igual, entonces probablemente las dos muestras pertenecen al mismo compuesto.
De lo anterior se desprende que emplearemos las mismas ecuaciones que usamos para la ley de Proust. Por tradición, los cocientes de masa se expresan a pocos decimales, los necesarios para encontrar una proporción de números enteros pequeños.
La ley de las proporciones múltiples fue una prueba clave de la teoría atómica, pero no está claro si Dalton descubrió la ley de las proporciones múltiples por accidente y luego usó la teoría atómica para explicarla, o si su ley fue una hipótesis que propuso para investigar. la validez de la teoría atómica(Roscoe & Harden, 1896).
En 1792, Bertrand Pelletier descubrió que cierta cantidad de estaño se combina con cierta cantidad de oxígeno para formar un óxido de estaño, o el doble de oxígeno para formar un óxido diferente. Joseph Proust confirmó el descubrimiento de Pelletier y proporcionó medidas de la composición: un óxido de estaño tiene 87 partes de estaño y 13 partes de oxígeno, y el otro tiene 78.4 partes de estaño y 21.6 partes de oxígeno. Probablemente eran óxido de estaño (II) (SnO) y dióxido de estaño (SnO2), y sus composiciones reales son 88.1 % de estaño, 11.9 % de oxígeno y 78.7 % de estaño, 21.3 % de oxígeno.
Los estudiosos que han revisado los escritos de Proust descubrieron que tenía suficientes datos para haber descubierto la ley de las proporciones múltiples por sí mismo, pero de alguna manera no lo hizo. Con respecto a los óxidos de estaño antes mencionados, si Proust hubiera ajustado sus cifras para un contenido de estaño de 100 partes para ambos óxidos, habría notado que 100 partes de estaño se combinarán con 14.9 o 27.6 partes de oxígeno. 14.9 y 27.6 forman una relación de 1:1.85, que es 1:2 si se perdona el error experimental. Parece que esto no se le ocurrió a Proust, pero se le ocurrió a Dalton (Roscoe & Harden, 1896).
9. La teoría atómica de Dalton
|| REGRESAR AL INDICE ||
La teoría atómica es una de las piedras angulares de la ciencia moderna, pues referencias a ella se pueden hallar en la física, la química e incluso, la biología, y en su núcleo central es bastante sencilla, pudiéndose reducir a la siguiente expresión: Toda la materia está compuesta de pequeñas partículas llamadas átomos (Bell, 2005; Brady & Humiston, 1986; Brown, LeMay, Bursten, Murphy, & Woodward, 2009; Chang, 2010; Chang & Overby, 2011; Jespersen, Brady, & Hyslop, 2012; Matamála & Gonzalez, 1976; Petrucci, Herring, Madura, & Bissonnette, 2010; Zumdahl & Zumdahl, 2007). Sin embargo, existe un espacio entre la idea fundamental y el modo en que la ponemos en el papel. Esta corporación de la teoría atómica en algo tangible se denomina modelo atómico, y aunque la teoría atómica ha permanecido relativamente constante desde la época de los filósofos Leucipo y Demócrito, los modelos atómicos han cambiado mucho a lo largo del tiempo, pero eso no implica que uno reemplace al otro.
Figura 9.1. John Dalton (Eaglesfield, Cumberland (Reino Unido), 6 de septiembre de 1766-Mánchester, 27 de julio de 1844) fue un naturalista, químico, matemático y meteorólogo británico. Entre sus trabajos destacan el modelo atómico y su tabla de pesos relativos de los elementos, que contribuyeron a sentar las bases de la química moderna. También es conocido por haber descrito el daltonismo, defecto visual relativo a la percepción de los colores que padecía y que lleva su nombre.
El modelo atómico de Dalton se diferencia de otras ideas anteriores en que se basa en las leyes ponderales para argumentar o inferir la existencia de los átomos, en lugar de intentar deducir una estructura atómica que explicaría las propiedades de la materia. Sin embargo, algo que todos los modelos atómicos tienen en común es que son principalmente construcciones numéricas que luego se trasladan a dibujitos para poder enseñar sus fundamentos rápido, pero estos dibujitos no son realmente la esencia de cada modelo. Las matemáticas de cada modelo nuevo sí que se hacen más complejas con el tiempo, sin embargo, algo que quedará demostrado en estas presentaciones, es que dicho modelo matemático para el modelo de Dalton es el que en verdad le es útil a la química cuantitativa.
9.1 Desde kilogramos a átomos
El descubrimiento del gas hidrógeno surgió de las dudas planteadas por las observaciones de científicos y filósofos. No creían que el agua y el oxígeno fueran elementos básicos. El hidrógeno fue identificado por primera vez por el científico británico Henry Cavendish, quien demostró a la Royal Society of London en 1766 que había dos tipos diferentes de aire: "aire fijo" o dióxido de carbono y "aire inflamable" o hidrógeno empleando la electrólisis, una corriente eléctrica sobre agua, que la separa en hidrógeno y oxígeno. Cavendish también demostró que el hidrógeno era mucho más liviano que el aire cuando se toman iguales volúmenes, y fue el primero en producir agua a partir de hidrógeno y oxígeno con la ayuda de una chispa eléctrica. El químico francés Antoine Laurent Lavoisier repitió los experimentos de Cavendish. Los experimentos de 1785 de Lavoisier, realizados frente a numerosos científicos, se consideraron definitivos. El francés también fue el primer científico en asignar nombres al hidrógeno y al oxígeno.
Figura 9.2. Henry Cavendish (1731-1810) fue un físico y químico británico y francés. Como físico, es conocido por el experimento de Cavendish (mediante el que posteriormente se determinó la constante de gravitación universal); y como químico, por el descubrimiento del hidrógeno y de la composición del agua. Parte de su popularidad posterior deriva de su singular carácter personal (extremadamente reservado) y de las múltiples anécdotas que jalonan su biografía.
Después de este, otros experimentos permitieron descomponer otras sustancias, como el amoníaco en nitrógeno he hidrógeno entre muchos otros. La pregunta es ¿Cómo llegamos de la idea de masa medible con una balanza de pesar cualquiera a átomos y sus respectivos pesos que no podemos medir directamente? ¿si la ciencia se basa en lo observable y medible entonces porque tantos científicos se apasionaron con la defensa de algo que no podía ser observado ni medido? Los debates sobre esto se acaloraron tanto que se arruinaron carreras, se generaron enemistades, y hasta uno se suicidó, el célebre Ludwig Eduard Boltzmann.
Para entender estos razonamientos, exploraremos los postulados de la teoría atómica, y los traduciremos a expresiones matemáticas que usan los símbolos modernos de cada concepto, ya que, en su época, estos químicos usaban técnicas aritméticas sin fórmulas generales.
9.2 Resumen de los postulados de la teoría atómica
👉 Postulado de composición: Toda la materia consta de partículas indivisibles llamadas átomos. Este postulado implica que los átomos son entidades discretas que en teoría podrían contarse, pero son muchos y muy pequeños, lo cual lo hace difícil.
👉 Postulado de identidad: Todos los átomos de un mismo elemento son idénticos entre sí, poseen igual tamaño, masa y comportamiento físico y químico. El postulado de identidad ha sido el que más ha cambiado a lo largo de la historia de la química, pues, aunque los átomos de un elemento se definen por su comportamiento químico, su masa no es exactamente igual en todos los casos, sin embargo, para los ejercicios de lápiz y papel enmarcados en la teoría atómica clásica asumiremos que las masas de los elementos indican su identidad.
👉 Postulado de cambio de identidad: Los átomos no se pueden crear ni destruir. Este es otro de los postulados que han cambiado, actualmente sabemos que los átomos pueden cambiar su identidad a otros átomos o incluso descomponerse en energía pura. Pero, para las reacciones ordinarias estos son eventos exóticos o que afectan de manera insignificante los cálculos, por lo que podemos ignorarlos.
👉 Postulado de asociación 1 moléculas: Los átomos de diferentes elementos pueden combinarse entre sí en proporciones de números enteros simples y fijos para formar átomos compuestos. Dalton expresó el concepto de átomo compuesto a lo que nosotros llamamos moléculas, en otras palabras, los átomos forman moléculas. Un detalle a tener en cuenta es que las moléculas de Dalton siempre eran formadas por átomos de identidad diferente, por lo que no concibió, y hasta se opuso a la idea, de moléculas de átomos con la misma identidad. Este postulado es una interpretación molecular de la ley de las proporciones definidas.
👉 Postulado de asociación 2 poder de enlace: Los átomos del mismo elemento pueden combinarse en más de una proporción para formar dos o más compuestos. Esto implica que los elementos poseen poderes de enlace diferentes, que pueden cambiar dependiendo de las cantidades relativas de los reactivos o de las condiciones físicas como la temperatura o la presión. Este postulado es una interpretación molecular de la ley de las proporciones múltiples.
👉 Postulado de representación de la reacción química: El átomo es la unidad de materia más pequeña que puede participar en una reacción química, y por consiguiente puede usarse para representar una reacción química en su expresión mas pequeña posible, el evento de reacción. Por tradición, expresamos las reacciones químicas representando un solo evento de reacción para poder trabajar con los números enteros mas pequeños posibles, lo cual mantiene la aritmética química lo mas simple posible.
9.3 Incongruencias
La principal incongruencia de la teoría atómica de Dalton concierne a su apego de representar los elementos (que son sustancia) como entidades de un solo átomo, lo cual, vuelve y juega, mantendría la aritmética simple, pero entra en conflicto con otras leyes de la química, específicamente, la ley de los volúmenes de combinación de Gay-Lussac. Sería el Conde Avogadro quien armonizaría la teoría atómica con la ley de volúmenes de combinación, pero para hacerlo fue necesario romper con el apego de Dalton a elementos monoatómicos, pues Avogadro debió introducir la noción de elementos compuestos no por átomos libres, sino por moléculas diatómicas. Al usar moléculas diatómicas todo el sistema matemático entre la teoría atómica y las leyes de gases calzó perfectamente, pero aun no se contaba con la tecnología para poner a prueba directamente estas ideas, por lo que el asunto de la teoría atómica quedó pendiente durante casi todo el siglo XIX.
Otras incongruencias del modelo de Dalton surgieron con el avance de la investigación científica, siendo los más importantes:
👉 Se demostró que la indivisibilidad de un átomo era incorrecta: un átomo se puede subdividir en protones, neutrones y electrones. Sin embargo, un átomo es la partícula más pequeña que participa en las reacciones químicas.
👉 Según Dalton, los átomos de un mismo elemento son similares en todos los aspectos. Sin embargo, los átomos de algunos elementos varían en sus masas y densidades. Estos átomos de diferentes masas se llaman isótopos. Por ejemplo, el cloro tiene dos isótopos con números de masa 35 y 37.
👉 Dalton también afirmó que los átomos de diferentes elementos son diferentes en todos los aspectos. Se ha demostrado que esto es incorrecto en ciertos casos: los átomos de argón y calcio tienen cada uno una masa atómica de 40 uma. Estos átomos se conocen como isóbaros.
👉 Según Dalton, los átomos de diferentes elementos se combinan en proporciones simples de números enteros para formar compuestos. Esto no se observa en compuestos orgánicos complejos como el azúcar (C12H22O11), los lípidos, las proteínas o el ADN, sustancias cuya composición absoluta aun no podía medirse en su época.
👉 La teoría no logra explicar la existencia de alótropos; no tiene en cuenta las diferencias en las propiedades del carbón vegetal, el grafito y el diamante.
9.4 Legado
Aunque los postulados de Avogadro tardaron mucho en aceptarse, sus modificaciones le permitieron ofrecer estimaciones más precisas de la masa atómica del oxígeno y varios otros elementos, e hizo una distinción clara entre moléculas y átomos. Una molécula puede estar compuesta por átomos de este o de diferentes elementos.
En 1827, el botánico británico Robert Brown observó que las partículas de polvo dentro de los granos de polen que flotan en el agua se movían constantemente sin razón aparente. En 1905, Albert Einstein teorizó que este movimiento browniano era causado por las moléculas de agua que golpeaban continuamente los granos y desarrolló un modelo matemático hipotético para describirlo (Einstein, 1905). Este modelo fue validado experimentalmente en 1908 por el físico francés Jean Perrin (Bigg, 2008; Perrin, 1901, 1909, 1911, 1913), lo que proporcionó una validación adicional para la teoría de partículas (y, por extensión, para la teoría atómica).
Aunque la teoría atómica que aceptándose gradualmente durante el curso del siglo XIX no fue sino hasta el experimento de Perrin que los últimos negacionistas del átomo verdaderamente prestigiosos se convencieron de la realidad científica de su existencia (Bigg, 2008).
En las secciones siguientes analizaremos a mayor profundidad los postulados de la teoría atómica de Dalton.
10. Postulado de composición
|| REGRESAR AL INDICE ||
“Toda la materia consta de partículas indivisibles llamadas átomos.”
Este postulado es evidente en sí mismo para la teoría atómica, pero nos permite ingresar a nuestra serie de magnitudes físicas el número de entidades N (IUPAC, 2019). La entrada del libro de oro para el parámetro número de entidades N dice: Número entero obtenido por conteo de entidades, que suelen ser moléculas, átomos o iones.
10.1 Un parámetro sin unidades
A diferencia de la mayoría de las cantidades físicas, el número de entidades N es una cantidad adimensional. Una cantidad adimensional (también conocida como cantidad simple, pura o escalar, así como cantidad de dimensión uno) es una cantidad a la que no se le asigna ninguna dimensión física, con una unidad de medida SI correspondiente de uno (o 1), que no se muestra explícitamente. Las cantidades adimensionales se utilizan ampliamente en muchos campos, como las matemáticas, la física, la química, la ingeniería y la economía. Las cantidades adimensionales son distintas de las cantidades que tienen dimensiones asociadas, como el tiempo (medido en segundos).
10.2 Definición de la cantidad de una sustancia
El número de entidades N es una propiedad extensiva, ya que es directamente proporcional al tamaño del sistema en consideración y, por lo tanto, solo tiene significado para sistemas cerrados. De hecho, podemos considerarlo como el parámetro que mide directamente la cantidad de una sustancia, pues cuando hablamos que hay mas sustancia, implícitamente hablamos de un mayor número de entidades de esa sustancia. El problema es que los átomos no son las únicas entidades de tamaño reducido a tener en cuenta.
10.3 Otras entidades
Existen muchas partículas a ser consideradas, pero dado que número de entidades N es adimensional, uno debe calcularlas por el contexto, aunque normalmente en un curso de química general, las únicas partículas que se consideran normalmente son los átomos y las moléculas.
Pero esto nos trae un problema de notación moderno. Tradicionalmente en los libros de texto se usan pseudounidades para diferencia átomos de moléculas, pero si deseamos seguir las recomendaciones del SI, entonces no podemos usar pseudounidades, por ende, a partir de este punto,
👉 el número de moléculas de la sustancia (i) se notará como Ni, o como N(i). El símbolo i puede reemplazarse por el nombre de la sustancia o por su fórmula química, así para el número de moléculas de agua podemos indicarlo como N(agua), N(H2O), Nagua o NH2O.
👉 el número de átomos del elemento (I) se notará como NI o como N(I). El símbolo I en este caso no es yodo sino cualquier elemento incógnita, el cual puede ser reemplazado por el nombre del elemento en la tabla periódica o por su símbolo atómico, así por ejemplo para el número de átomos de hidrógeno tendremos los símbolos N(hidrógeno), N(H), Nhidrógeno, NH.
En futuros modelos atómicos nos encontraremos con otras entidades que también se expresan como número de entidades. El tamaño extremadamente pequeño de los átomos y moléculas hacía que, en época de Dalton, calcular el parámetro (N) fuera inviable, pero bueno, apenas estamos definiendo cosas en términos muy ideales. Por otro lado, en la actualidad este postulado debe ser matizado, pues ni toda la materia consta de átomos, ni estos son indivisibles, sin embargo, la materia con masa ordinaria si está hecha de átomos y las reacciones químicas ordinarias no involucran rompimiento o fusión de estos.
11. Postulado de identidad atómica
|| REGRESAR AL INDICE ||
Todos los átomos de un mismo elemento son idénticos entre sí, poseen igual tamaño, masa y comportamiento físico y químico
Al igual que 1 es diferente de 2 o una pera es diferente de una manzana, un átomo de hidrogeno es diferente de un átomo de oxígeno en propiedades físicas como la masa, o en propiedades químicas como sus posibles reacciones y productos con otros elementos. Esto se traslada pictóricamente al hecho de que el átomo de cada elemento se representa con un símbolo propio, que originalmente eran esferas.
11.1 Colores de las esferas daltonianas
Debido a que John Dalton era daltónico “ceguera a algunos colores” el código original para los elementos eran esferas con símbolos internos. Por lo que podemos representar el átomo daltoniano como una esfera sólida sin estructura interna que se diferencia de otras por sus propiedades, siendo la masa la más relevante.
Figura 11.1. Modelo atómico de Dalton. La identidad del átomo de Dalton estaba dictada por su masa y por ende, por su tamaño. Dalton sin embargo los diferenció por símbolo, siendo estos arbitrarios.
Durante la etapa introductoria del curso de química general, los textos también emplean círculos o esferas, pero como la mayoría no somos daltónicos “como si lo era Dalton” en lugar de símbolos generalmente empleamos un código de colores. Estos colores se denominan código CPK. Es probable que los colores de CPK se hayan inspirado en modelos del siglo XIX. Aparentemente, August Wilhelm von Hofmann fue el primero en introducir modelos moleculares en la química orgánica, luego de la introducción de la teoría de la estructura química de August Kekule en 1858 y la introducción de fórmulas estructurales impresas de Alexander Crum Brown en 1861. En un discurso de viernes por la noche en la Royal Institution de Londres el 7 de abril de 1865, mostró modelos moleculares de sustancias orgánicas simples como metano, etano y cloruro de metilo, que había construido a partir de bolas de croquet de mesa de diferentes colores conectadas entre sí con tubos delgados de latón. El esquema de color original de Hofmann (carbono = negro, hidrógeno = blanco, nitrógeno = azul, oxígeno = rojo, cloro = verde y azufre = amarillo) ha evolucionado hacia los esquemas de color posteriores (Ollis, 1972).
Figura 11.2. Código de colores CPK. Existen otras versiones de este código, por ejemplo, la más común es que todos los halógenos se representan verdes.
Varios de los colores CPK se refieren mnemotécnicamente a colores de elementos puros o compuestos notables. Por ejemplo, el hidrógeno es un gas incoloro, el carbono como carbón, grafito o coque es negro, el azufre en polvo es amarillo, el cloro es un gas verdoso, el bromo es un líquido rojo oscuro, el yodo en el éter es violeta, el fósforo amorfo es rojo, el óxido de hierro III es rojo anaranjado oscuro, etc. Para algunos colores, como los de oxígeno y nitrógeno, la inspiración es menos clara. Quizás el rojo para el oxígeno esté inspirado en el hecho de que normalmente se requiere oxígeno para la combustión o que el químico que contiene oxígeno en la sangre, la hemoglobina, es de color rojo brillante, y el azul para el nitrógeno en el hecho de que el nitrógeno es el componente principal de la atmósfera terrestre. que aparece a los ojos humanos como de color azul cielo. La nomenclatura CPK es muy empleada para la elaboración de modelos moleculares de plástico o figuras con esferas.
Figura 11.3. Juego de modelos moleculares de plástico empleando la nomenclatura CPK básica, em la caja tenemos nitrógeno (azules) hidrógeno (blancas), carbono (negras) azufre (amarillas) halógenos (verdes) y oxígeno (rojas).
Figura 11.4. La nomenclatura CPK también es empleada para representar pictóricamente los átomos en dibujos sencillos.
11.2 Símbolo atómico
Sin embargo, dibujar esferas de colores es molesto a la hora de hacer u modelo matemático, por lo que un elemento en general se representa actualmente mediante el símbolo atómico, un conjunto de una o dos letras que normalmente es el nombre del elemento, aunque puede que el nombre usado no sea el de su idioma, y por eso elementos como sodio se representan con Na, pues se usa el nombre en latín Natrum. Recuerde que la mayúscula y la minúscula cuentan, una combinación de una mayúscula y una minúscula como en Ni representa un solo símbolo atómico, en este caso níquel, pero una combinación de dos mayúsculas NI representa dos símbolos atómicos consecutivos, pero de elementos distintos, en este caso nitrógeno y yodo.
11.3 Modelo matemático
¿Cómo se lee el principio de identidad atómica matemáticamente? Hay dos opciones, la primera es una suma de átomos que tienen la misma identidad.
El número total de átomos del elemento (J) es igual a la suma de átomos de ese mismo elemento en cada una de las partes del sistema (x).
Recuerde que una suma solo me permite sumar cosas con la misma identidad, si tengo una manzana más otra manzana, pues obtengo dos manzanas, pero no puedo sumar una manzana y una pera, pues sus identidades son distintas.
Una segunda ecuación que podemos desprender del principio de identidad es que un átomo de un elemento dado tiene una masa atómica específica para ese elemento (I), entonces, la masa de un cuerpo puro dependerá de la cantidad de átomos, y de la masa de un solo átomo de ese mismo elemento.
La masa de un elemento puro mJ es igual al producto de su masa atómica absoluta en gramos mpJ por el número de átomos de ese elemento presente en el sistema.
La masa atómica mp(J) es propia de cada elemento, del mismo modo en que cada elemento parecía tener una masa relativa propia cuando se la ponderaba con otras magnitudes como el volumen. Eso se sabía desde la época clásica cuando Arquímedes empleó la densidad como una medida para identificar la identidad y pureza del oro con respecto a aleaciones de plata menos valiosas. Aunque Dalton y los atomistas solo podían soñar con hacer los cálculos siguientes:
12. Postulado de cambio de identidad molecular
|| REGRESAR AL INDICE ||
Los átomos no se pueden crear ni destruir.
Aunque actualmente esta afirmación es incorrecta, debemos tener en cuenta que solo es inválida en situaciones especiales, que son de hecho, las mismas de la ley de la conservación de la masa, por ende, para la mayoría de las reacciones químicas es una afirmación correcta.
Este postulado adicionalmente forma la base de lo que denominamos balanceo de reacciones químicas, pues si los átomos no se crean o destruyen en una reacción química, eso significa que la suma de átomos al principio de una reacción química, debe ser la misma cantidad de átomos presentes al final de una reacción química.
12.1 La reacción química
Dado que introducimos el concepto de reacción química o cambio químico, debemos describirlo un poco mejor. En una reacción química usamos sustancias iniciales que llamaremos los reactivos, los cuales se consumen al reorganizar sus átomos, para formar sustancias nuevas llamadas productos.
12.2. Reacción química generalizada, las sustancias estan referidas por sus nombres sin indicación de sus números estequiométricos.
La flecha indica el evento de cambio, el cual está involucrado al tiempo, aunque en este caso solo nos interesa el momento donde están los reactivos como momento inicial, y cuanto están los productos como comento final. Normalmente asumiremos reacciones que;
👉 no se revierten
👉 cantidades de reactivo que no dejan sobrantes
👉 y la cantidad de productos inicial es cero.
En una reacción química cambian las identidades de las sustancias, pero los átomos que componen a las sustancias no cambian ni en identidad ni en número, por lo que el número de átomos de cada elemento y el número de átomos total se mantiene constante.
12.3 Prueba de balance de masa
Ahora bien, ¿cómo justificamos que los átomos no se crean ni se destruyen matemáticamente? Pues simplemente es aplicar la ley de la conservación de la masa, pues si la masa total es constante, entonces la suma de masas de productos debe ser igual a la suma de masas de reactivos para cada elemento analizado.
Aunque la forma larga es más general, la forma corta es más práctica para resolver los ejercicios de tipo conteo de átomos como los siguientes:
Ejemplo. Demuestre que la siguiente figura es congruente con la ley de la conservación de la masa.
13. Postulados de asociación
|| REGRESAR AL INDICE ||
13.1 Postulado de asociación
Los átomos de diferentes elementos pueden combinarse entre sí en proporciones de números enteros simples y fijos para formar átomos compuestos.
Lo anterior implica que dos átomos de diferentes elementos se combinan para formar un átomo compuesto “como lo llamaba Dalton” o una molécula de una sustancia compuesta como la llamamos nosotros. Nuevamente, el modo original de expresarlo era con círculos:
Figura 13.1. Representación pictórica de las moléculas de diferentes sustancias compuestas empleando el modelo atómico de Dalton, (izquierda )con los símbolos propuestos por el propio Dalton (derecha) con el código de colores CPK.
👉 Fórmula molecular
En la Figura 13‑1 podemos notar que debajo del modelo CPK de la molécula existe un nombre y un símbolo compuesto por símbolos atómicos y subíndices numéricos, este código es lo que se conoce en química como la fórmula molecular. La fórmula molecular es el equivalente al símbolo atómico, pues permite representar a la molécula de manera abstracta sin tener que dibujar esferas de colores CPK todo el tiempo.
Las primeras fórmulas químicas fueron algo diferentes de como las representamos actualmente, por ejemplo, la teoría equivalentista manejaba una mezcla entre fórmulas y símbolos específicos, como si fueran códigos más o menos arbitrarios para indicar los pesos equivalentes de las sustancias, mientras que las primeras versiones de las fórmulas químicas que conocemos expresaban las cantidades de átomos (relativas o absolutas) como superíndices en lugar de subíndices:
Tabla 13.1. Diferentes fórmulas químicas dependientes de la teoría que se asumiera como correcta (Padilla & Furio-Mas, 2008).
El subíndice en la fórmula molecular representa el número absoluto o verdadero de átomos de un elemento en una molécula. En ocasiones el subíndice será un parámetro importante a tener en cuenta algebraicamente por lo que lo representaremos con el símbolo siI.
Química la ciencia central 13
👉 Fórmula empírica
En química, la fórmula empírica de un compuesto químico es la proporción más simple de números enteros de átomos presentes en un compuesto. Un ejemplo simple de este concepto es que la fórmula empírica del monóxido de azufre, o SO, sería simplemente SO, al igual que la fórmula empírica del dióxido de azufre, S2O2. Así, el monóxido de azufre y el dióxido de disulfuro, ambos compuestos de azufre y oxígeno, tienen la misma fórmula empírica. Sin embargo, sus fórmulas moleculares, que expresan el número de átomos en cada molécula de un compuesto químico, no son las mismas. Una fórmula empírica no menciona la disposición o el número de átomos verdadero y por ende no permite calcular la masa molar verdadera. Es
estándar para muchos compuestos iónicos, como el cloruro de calcio (CaCl2), y para macromoléculas, como el dióxido de silicio (SiO2).
Ejemplo. La fórmula molecular del dimetiléter de etanol es C4H12O2. Determinar la fórmula empírica.
👉 Subíndices no enteros
Existen dos razones para obtener subíndices no enteros, la primera es porque la sustancia es un bertólido o no estequiométrico, categoría de sustancias que discutiremos más adelante. La segunda razón es porque la serie de números enteros más pequeños posee subíndices diferentes de 1. Para tal caso debemos tomar el subíndice no entero y encontrar o
👉 El número fraccionario o racional que más se acerca a él y luego multiplicar todos los subíndices por el denominador.
👉 Encontrar un número que multiplicado por el decimal genere un número fácilmente redondeable a un entero, y nuevamente multiplicar todos los subíndices por ese valor.
👉 Sustancias no estequiométricas
El hecho de que estemos calculando subíndices como números enteros se debe a que asumimos dos cosas implícitamente, que la teoría atómica es correcta y que la ley de Proust es correcta, el problema es algunos tipos de compuestos iónicos, no se pueden escribir con fórmulas empíricas enteramente de números enteros. Un ejemplo es el carburo de boro, cuya fórmula de CBn es una proporción variable de números no enteros con n que van desde más de 4 a más de 6,5. Otro ejemplo es el mineral de hierro llamado wüstita que puede contener un intervalo de hierro de entre 0.83 a 0.95 hierro por cada oxígeno (Gusev, 2014; Park, Kim, Lee, & Kim, 1999). Por suerte para Proust medir esto hubiera sido imposible con la tecnología disponible en su tiempo. Sin embargo, cuando se descubrieron estas sustancias que no siguen la ley de Proust, se les dio el nombre de bertólidos, en honor a Claude Louis conde de Berthollet, quien se opuso a la idea de las proporciones definidas (Padilla & Furio-Mas, 2008). Otras especies químicas como los biopolímeros de proteína y ADN poseen composiciones moleculares altamente variables por lo que no sirven para realizar cálculos estequiométricos.
Figura 13.2. La wustita o wüstita es un mineral de la clase de los minerales óxidos de composición FeO. Fue descubierto en 1924 cerca de Stuttgart (Alemania), siendo nombrado así en honor de Ewald Wüst (1875-1934), geólogo y paleontólogo alemán. Otros sinónimos para denominar a este mineral son wuestita, iozita o iosiderita.
Las razones para esto radican en que, aunque la teoría atómica es siempre correcta, la ley de Proust tiene dos excepciones principales
👉 Algunos cristales pueden encerrar cantidades variables de átomos, lo que genera una composición variable como en la wustita.
👉 La identidad de algunas sustancias no se enmarca a una proporción definida de átomos, sino a una estructura general y a propiedades químicas más o menos semejantes. Esto sucede en macromoléculas, donde hay tantos átomos que la presencia o ausencia de unos cuantos no afecta mucho, que es el caso normal del ADN y los isómeros enzimáticos.
👉 La proporción definida
Tomando cuenta la estructura de una fórmula molecular podemos vincular el número de átomos de un elemento cualquiera NJ,j con el número de moléculas donde reside ese elemento Nj empleando el subíndice del elemento siJ,j en la fórmula molecular.
Interpretación molecular de la ley de Proust de proporciones definidas dónde él número de átomos de un elemento-J en un compuesto-j N(J,j) es una función del número de moléculas del compuesto-j N(J,j) y el subíndice de dicho elemento si(J,j) en la fórmula molecular del compuesto-j.
Donde el subíndice (siJ,j) es la constante de proporcionalidad. Decimos que () representa a la proporción definida porque su valor es constante para un elemento dado en una molécula dad, si dos muestras arrojan valores divergentes de (siJ,j) dirémos que son sustancias diferentes, al menos para compuestos simples, pues en compuestos complejos esta idea no funciona. Es por esto por lo que se dice que la ley de Proust se aplica a compuestos pequeños o de bajo peso molecular. Aunque la ecuación 13.1., parece trivial a primera vista, nos permitirá calcular el número de átomos en un número de moléculas arbitrario, así como poder determinar las relaciones de proporción en situaciones de estequiometría complejas como el análisis de combustión y el análisis de composición porcentual.
Ejemplo. Cuantos átomos hay en 92.93 g de fosforo
Ejemplo. Cuantos átomos de hidrógeno y oxígeno hay en una molécula de agua
Ejemplo. Cuantos átomos de carbono hay en una molécula de C2H2
Ejemplo. Cuantos átomos de carbono hay en una molécula de acetona.
Ejemplo. Cuantos átomos hay en 5 moléculas de hidróxido de sodio NaOH.
Ejemplo. Cuantos átomos hay en 5 moléculas de ácido sulfúrico H2SO4.
Ejemplo. Cuantos átomos hay en 6 moléculas de propano C3H8.
Ejemplo. Cuantos átomos de hidrogeno hay en una molécula de acetona C3H6O
Ejemplo. Cuantos átomos de carbono hay en 350 moléculas de acetona C3H6O
Ejemplo. Cuantos átomos de carbono hay en 3.78 x 1028 moléculas de acetona C3H6O
13.3 Poder de enlace variable
Los átomos del mismo elemento pueden combinarse en más de una proporción para formar dos o más compuestos.
Eso implica, por ejemplo, para una sustancia compuesta por los elementos cualquiera A y B, cuya fórmula química estará dada por AaBb, los valores de los subíndices no son siempre constantes, pero cuando los subíndices cambian, también cambia la identidad del compuesto, así, por ejemplo, el agua H2O es una sustancia diferente del agua oxigenada o peróxido de hidrógeno H2O2.
Lo anterior constituye la interpretación atómica de las leyes de proporciones definidas y múltiples, que podemos expresar de este modo.
👉 Ley de las proporciones definidas: Los subíndices de una fórmula química de una molécula no cambian.
👉 Ley de las proporciones múltiples: dos elementos pueden tener más de un conjunto de subíndices, pero cada conjunto de subíndices le da identidad a una sustancia diferente.
14. Postulado de la ecuación química
|| REGRESAR AL INDICE ||
El átomo es la unidad de materia más pequeña que puede participar en una reacción química.
Para Dalton los elementos eran monoatómicos es decir átomos libres, y las moléculas siempre eran polielementales, es decir, compuestas por distintos elementos. Por lo anterior la síntesis de agua por combustión de hidrógeno se representaba como:
Figura 14.1. Síntesis de agua usando el modelo atómico de Dalton original. Recuerde que para Dalton los elementos como hidrógeno (gris/pequeño) y oxígeno (rojo/grande) estaban compuestos por un solo átomo.
14.1 Uso de los símbolos atómicos
En la actualidad sabemos que los átomos libres rara vez existen en la naturaleza, sin embargo, el postulado de la ecuación química puede entenderse como que los átomos no cambian su identidad en la ecuación química, por lo que esta se entiende como una reorganización de las posiciones de los átomos y del modo en que se unen a otros átomos, pero la cantidad de átomos total, así como la cantidad de átomos de cada elemento se conserva.
Dado que emplear colores y esferas se hace inconveniente, las ecuaciones químicas normalmente se traducen a un modelo simbólico que reemplaza las esferas daltonianas por el símbolo atómico.
Figura 14.2. Desplazamiento del hidrógeno por el zinc en la ecuación química Zn + H2S → ZnS + H2.
14.2 El número estequiométrico y el número de eventos de reacción
Cuando analizamos una reacción química, normalmente el número de átomos de un determinado elemento es algo más complicado, esto debido a que el número de moléculas no está dado en una medida absoluta, sino en una medida relativa a un evento de reacción.
Un evento de reacción (Nξ = 1) representa el conjunto mínimo de átomos y moléculas necesario para que la reacción ocurra una vez como mínimo, asumiendo una interpretación molecular de la materia. Por ejemplo:
Figura 14.3. Síntesis de agua en la hipótesis de Avogadro. Aunque Dalton no la modelo de este modo, es el ejemplo más simple para introducir el concepto de número estequiométrico. El número estequiométrico es el número de veces que una molécula se repite en un solo evento de reacción, por ende, el número estequiométrico del hidrógeno es 2, el del oxígeno es 1, y del del agua es 2. Al contar números estequiométricos contamos moléculas, pero su composición atómica es irrelevante.
14.3 Número estequiométrico
El número de veces que se repite una determinada molécula se conoce como número estequiométrico o coeficiente estequiométrico, su símbolo moderno es (vi). El número estequiométrico es fácil de identificar en las reacciones anteriores, pues en el desplazamiento de zinc a hidrógeno todos los números estequiométricos son uno, mientras que en la síntesis de agua tenemos v(H2)=2, v(O2)=1 y v(H2O)=2. El número estequiométrico es adimensional, y se encuentra en ecuaciones químicas como el número que está a la izquierda de la fórmula molecular, por ejemplo:
Una reacción real no ocurre una sola vez, existe una cantidad indeterminada de eventos de reacción, que deben tomarse en cuenta, aunque sea de manera teórica por medio del parámetro número de eventos de reacción (Nξ). El número de moléculas mínimo involucrado en un solo evento de reacción lo expresaremos como el número estequiométrico.
Número de moléculas Nj en términos del número estequiométrico de la molécula vj y el número de eventos de reacción Nξ.
Química la Ciencia Central
Por lo tanto, podemos reescribir la ecuación del número de átomos de un elemento como:
Número de átomos de un elemento N(J,j) en términos del número estequiométrico de la molécula v(i), el subíndice del elemento en la molécula y el número de eventos de reacción N(ξ).
Número de átomos de un elemento en términos del número estequiométrico de la molécula , el subíndice del elemento en la molécula y el número de eventos de reacción si el elemento se encuentra en mas de una molécula.
15. Pesos atómicos en la teoría de Dalton
|| REGRESAR AL INDICE ||
Las ecuaciones que dedujimos en las secciones anteriores como: Masa de un elemento en términos de su masa atómica y el número de átomos (mJ = mpJ NJ); Número de moléculas en términos del número estequiométrico y el número de veces que se repite una reacción química (NJ = vJ Nξ); y el número de átomos de un elemento insertados en una molécula en términos del subíndice del elemento en dicha molécula y el número de moléculas (NJ,j = vJ,j Nj); no son útiles por separado pues requieren conocer parámetros que no se pueden contar, o que no se podían contar en la época de Dalton como el número de átomos NJ, el número de moléculas Nj, la masa atómica absoluta mpJ o la masa molecular absoluta mpj. Sin embargo, veremos cómo al combinarlas emergen expresiones nuevas o teoremas que, si pueden ponerse a prueba experimentalmente, aunque algunas requieren presupuestos que no son del todo correctos. Tenga en cuenta, nuevamente, que Dalton no hizo este argumento algebraico, pero sí tuvo que seguir la línea de pensamiento aquí descrita de manera intuitiva y/o con técnicas aritméticas.
15.1 Masas atómicas relativas (ArJ)
En la época de Dalton no se podía saber la masa atómica en unidades absolutas maJ de un solo átomo de nadie (ni tampoco podían saber que un mismo elemento podría tener valores de mpJ ligeramente variables), y tampoco contar átomos NJ, o moléculas Nj, por lo que las ecuaciones Eq. 11.4 y Eq 11.5 eran imprácticas. Estas ecuaciones son ejemplos que leyes que surgen de un análisis abstracto de una teoría, y se diferencian de las leyes empíricas como las leyes de gases que emergen de experimentos e instrumentos.
La imposibilidad de calcular la masa absoluta de los átomos conllevo a una de las mayores infelicidades en la historia de la química cuantitativa, la generación de dos escalas de masa de elementos, aquella que debería medirse en escala absoluta de unidades de masa como kilogramos, y aquella relativa a una masa de referencia estándar elegida por acuerdo. En la actualidad ambas escalas se relacionan mediante la siguiente expresión.
Donde la masa atómica relativa “sin unidades o adimensional” Ar(J) es el cociente entre la masa atómica absoluta del elemento mp(J) ponderada a una masa atómica de referencia o estándar mu. Los pesos “masas” atómicas que encontramos en una tabla periódica estándar están dadas en unidades relativas a una masa de ponderación conocida como la constante de masa atómica (mu), pero que originalmente correspondió a la masa atómica de un elemento, el hidrógeno, sin embargo, en la actualidad la masa de ponderación es la doceava parte de 12 g de carbono-12 puro (por lo que su masa en gros es 12.00 g) dividido entre el número de Avogadro.
La masa atómica de referencia que pondera a las demás masas atómicas es un acuerdo, por ello la escala relativa es arbitraria. Concentrémonos ahora en el problema de la masa relativa, pues aparentemente ahora tenemos un problema más grande, pues la masa relativa sigue estando definida en términos de masas atómicas microscópicas que no se pueden medir con balanzas macroscópicas como las disponibles en el siglo XIX, así que, debemos encontrar un modo de calcular la masa relativa con masas que no sean las atómicas.
La masa atómica relativa de un elemento J-cualquiera Ar(J) con respecto a la masa atómica relativa del hidrógeno Ar(H) en términos del cociente de masas y el cociente inverso del número de átomos El radio de masas puede medirse fácilmente, pues es básicamente la forma macroscópica de la ley de Proust-Dalton, pero la clave está en el radio de número de átomos, ¿Cómo encontrar el valor del cociente para los subíndices?
15.4 Masas atómicas relativas al hidrógeno
Lo único de podemos decir del cociente subíndices es que, según la teoría atómica de Dalton, los subíndices son propios de cada sustancia “siendo una manifestación atómico-molecular de la ley de proporciones definidas”, y a falta de más información decidió asumir la hipótesis más sencilla. Dalton decidió resolver esta situación con dos ideas básicas, la primera, usar al
👉 hidrógeno como masa atómica igual a 1 exacto, y
👉 asumir que los subíndices de sustancias simples como el agua también eran igual a 1 exacto,
de hecho, su fórmula para el agua es HO (la verdadera es H2O) y para el amoníaco HN (la verdadera es NH3) siguen estos postulados. Sin embargo, al simplificar las fórmulas se generaba una ecuación que, si se puede resolver, aunque sea incorrecta, tomando al hidrógeno como masa de ponderación, lo cual cancela convenientemente el cociente de número de átomos y permite definir la masa relativa en términos de un cociente de masas macroscópicas que si pueden medirse con balanzas.
Fórmula para hallar la masa relativa de un elemento cualquiera en términos de la masa de esta sustancia con respecto a la masa equivalente de hidrógeno.
Usando esta técnica (empleando razonamiento aritmético en lugar de algebraico) Dalton generó una primera tabla de pesos atómicos hipotéticos, y digo hipotéticos, porque su elección para el radio de subíndices de los dos elementos no era correcta.
Figura 15.1. Lista con los símbolos, nombres y pesos atómicos dados por Dalton originalmente.
A parte de no elegir correctamente los subíndices, se puede notar que Dalton cometió errores experimentales al medir la masa equivalente de hidrógeno a oxígeno, pues si se hace bien la medición el valor obtenido debe ser de 7.92 oxígeno con respecto al hidrógeno, lo cual tradicionalmente se redondea a 8. En 1803, Dalton se refirió esta lista de pesos atómicos relativos al hidrógeno para varias sustancias en una charla ante la Sociedad Filosófica y Literaria de Manchester sobre la solubilidad de varios gases, como el dióxido de carbono y el nitrógeno, en agua.
Pero, tal como nos pasa en este punto de la discusión, a Dalton aun le faltaban conceptos o herramientas matemáticas, por lo que llegó a conclusiones imprecisas (Kauffman, 1994), o dicho de otro modo, la Eq. 15.6 es incorrecta, debido a que es una simplificación arbitraria de Eq. 15.4, el problema es que aún faltaba un medio para acceder a los subíndices por una ruta diferente de las leyes ponderales y de la medición de la masa. A demás, la masa atómica de un solo átomo de hidrógeno no es exactamente uno, pero esas son cosas que nadie podía prever pues, nuevamente faltaban conceptos y tecnologías. No es como si una teoría científica esté obligada a nacer con una matemática perfecta de inmediato. Y lo anterior es un detalle general a tener en cuenta, los científicos asumimos siempre que toda teoría compuesta por un modelo matemático dado es imperfecta, y por ende perfeccionable.
15.6 Átomos y moléculas
Los primeros resultados de Dalton fueron presentados en 1803 en una conferencia (Nash, 1956), pero el artículo correspondiente a esta primera intervención no fue publicado sino hasta 1805, pero sin discutir el factor más relevante, es decir, como es que obtuvo las figuras (Dalton, 1805). El método no fue revelado sino hasta 1807 por un conocido suyo llamado Thomas Thomson en la tercera edición de su libro de texto, Un Sistema para la Química (Thomson, 1820). Dalton se vio forzado a publicar sus métodos en su propio libro de texto llamado, Un Nuevo Sistema de la Filosofía de la Química (Dalton, 2010) entre los años de 1808 y 1810, y secciones del mismo son públicas, por ejemplo (https://web.lemoyne.edu/giunta/DALTON.HTML).
En sus escritos, Dalton usó el término "átomo" para referirse a la partícula básica de cualquier sustancia química, sin importar que fueran conjuntos de átomos pegados o átomos libres unitarios. Dalton no usó la palabra "molécula"; en su lugar, utilizó los términos "átomo compuesto" y "átomo elemental" para lo que actualmente llamaríamos compuesto y elemento con átomos libres, y no todos los elementos se componen de átomos libres, pero eso no podía saberlo Dalton en su época (Dalton, 2010). En la actualidad una molécula es un conjunto de átomos del mismo o de diferentes elementos que viajan juntos debido a sus enlaces químicos.
15.7 Consecuencias del modelo atómico de Dalton
En comparación de lo rápido que nos movemos del modelo de Dalton al modelo de Thomson en el tablero, el proceso histórico para aceptar al átomo, una entidad no visible, como un concepto científico fue largo, de hecho, el asunto completo no sería resuelto sino hasta el siglo XX por dos de los más grandes científicos de todos los tiempos, Albert Einstein (1879-1955) y Jean Perrin (1870-1942). El modelo de Dalton y su teoría atómica subyacente terminó de ser propuesta de forma firme para 1808 mediante la publicación del primer volumen de “Nuevos Sistemas de la Filosofía de la Química” (Dalton, 2010).
La teoría atómica contó con el apoyo de científicos famosos como Jöns Jakob Berzelius (1779-1848), pero no todos estaban convencidos, por ejemplo, Humphry Davy (1748-1829) y Claude-Louis Berthollet (1748-1822) argumentaban en torno al hecho de que los átomos no podían ser evidenciados de forma directa. La evidencia del átomo era de naturaleza sumamente indirecta, pero no por ello poco convincente, de hecho, lograba dar una explicación para la estequiometria –y gracias al trabajo de Avogadro – al explicar las proporciones de combinación y facilitar los cálculos.
La aceptación de la teoría atómica de Dalton creció bajo el eslogan de ser “una ficción útil”, se trataba de un modelo sin pretensiones ontológicas, muchos de los científicos que lo usaban no lo asumían como algo verdadero, pero debido a su utilidad, el lenguaje cotidiano fue calando poco a poco a través de la formación de químicos, físicos y biólogos desde 1810 hasta 1910 fecha en la que los últimos negacionistas del átomo murieron –negándolo hasta la tumba. Ejemplos famosos de negacionistas del átomo fueron Marcellin Berthelot (1827-1907) y Wilhelm Ostwald (1853-1932).
15.8 La aceptación final de la teoría atómica por la ciencia moderna
Durante la misma década el propio Albert Einstein publicó un artículo en el que empleaba el modelo del átomo para explicar el fenómeno del movimiento Browniano (Einstein, 1905). El artículo de Einstein era teórico –como todo lo que hizo- por lo que su modelo debió ser validado experimentalmente.
Figura 15.2. Albert Einstein. (Ulm, Imperio alemán, 14 de marzo de 1879-Princeton, Estados Unidos, 18 de abril de 1955) fue un físico alemán de origen judío, nacionalizado después suizo, austriaco y estadounidense. Se lo considera el científico más importante, conocido y popular del siglo XX.
El encargado de demostrar finalmente la existencia de los átomos fue Jean Perrin (1870-1942) quien realizó medidas de un sistema real (Perrin, 1909, 1911, 1913), precisamente el mismo empleado por Einstein de forma teórica –un cilindro con una solución que podía ser descrita en términos de las leyes de los gases, la presuposición de la existencia de átomos/moléculas y las suficientes modificaciones –obteniendo resultados que concordaban con el supuesto de la existencia de átomos y moléculas. Gracias a este trabajo recibió el premio Nobel en 1926. Resulta bastante conmovedor que, a pesar de que muchos contemporáneos e historiadores de las ciencias le acreditan a Perrin el ser el primero en dar una prueba directa de la existencia de la realidad discontinua de la materia (Bigg, 2008), al mismo tiempo hubiera terminado por ser excluido del libro de texto y de la historiografía estándar del átomo en la escuela (Haw, 2005).
De hecho, Perrin también trabajo alrededor del modelo atómico de Thomson, pero esto es algo que discutiremos en la sección respectiva. En cualquier caso, la aceptación del átomo demuestra algo, el mito científico de los momentos de eureka, desde que Dalton publicara su propuesta, hasta que Perrin aportara el aspecto más importante para aceptar su realidad pasaron más de 100 años de debates, controversias, descalificaciones y puntos de vista sobre el átomo.
También se resalta que pueden existir premios Nobel, expertos en el tema –como Ostwald – que son negacioncitas minoritarios de un modelo o teoría aceptada por el resto de la comunidad, en este caso lo que valida a la teoría no es la apelación a las mayorías, sino al hecho de que el programa de investigación mayoritario se demuestra fructífero y aplicable a aspectos que originalmente no venían incluidos por los proponentes originales, esto es lo que puede ser denominado como un programa de investigación progresivo (Lakatos, 1978). Cabe resaltar que la década en la que Perrin obtiene el Nobel también es la década en la que el modelo del átomo cuántico queda establecido, y el camino hacia el mundo de las partículas cuánticas y la física de partículas lleva a la física moderna, con el modelo estándar y los grandes aceleradores de partículas.
Figura 15.3. Jean Baptiste Perrin (Lille, 30 de septiembre de 1870-Nueva York, 17 de abril de 1942) fue un químico físico francés galardonado con el Premio Nobel de Física en 1926 por sus trabajos sobre los rayos catódicos y sobre el equilibrio de sedimentación.
16. Las hipótesis de Avogadro
|| REGRESAR AL INDICE ||
El hecho de que hallamos terminado de exponer los principios de la teoría atómica de Dalton, no significa que su modelo hubiera quedado entre comillas perfecto, aún quedaban ciertos problemas en los cuales la química de gases fue fundamental para poder corregir la hipótesis atómica empleando la hipótesis de Avogadro y la ley de volúmenes de combinación de Gay-Lussac, y convertirla en una ruta de investigación válida. Tenga en cuenta que Avogadro es mejor conocido por su ley moles a volumen:
Expresión que de hecho el jamás postuló realmente, ya que la magnitud cantidad de sustancia solo fue confirmada hasta la década de 1970. En realidad, su importancia radica en dos hipótesis diferentes, la hipótesis volumen a número de moléculas y la hipótesis de los gases diatómicos.
16.2 Volúmenes de combinación
En 1808, Joseph Louis Gay-Lussac (1778-1850), al realizar el experimento Cavendish de formación de agua, observó que los volúmenes de hidrógeno y oxígeno se combinaron en una proporción de 2:1, con un error experimental de menos del 0.1%. Además de esto, cuando realizó diferentes experimentos con otros gases, notó que el volumen del producto resultante en la reacción, que en el caso del agua era vapor o gas a la temperatura experimental, estaba relacionado con los volúmenes de los elementos reactivos en una proporción simple:
Figura 16.1 Equivalencia de volúmenes para la síntesis del agua. Para que en la síntesis de agua no quedaran sobrantes, se determinó experimentalmente que se necesitaba medio volumen de oxígeno gaseoso por cada volumen de hidrógeno gaseoso. Estos volúmenes fueron medidos por Gay-Lussac.
De esta manera, llegó a la siguiente conclusión: ‘‘Me parece que los gases siempre se combinan en las proporciones más simples cuando actúan entre sí".
Dalton no aceptó los resultados de Gay-Lussac, porque no se obtuvieron números enteros en esos experimentos de volúmenes de combinación. Esto se debe a que la hipótesis de Dalton para la descomposición no explicaba la razón por la cual solo se consumía medio volumen equivalente de oxígeno, los volúmenes equivalentes deberían ser 1:1. Dado lo anterior podemos indicar que la ley de Gay-Lussac de volúmenes de combinación también adquiere una forma de radio de volúmenes.
A presión y temperatura constantes los volúmenes de combinación mantienen la proporción, por lo que en un calculo de proporciones de volúmenes de una pareja cualquiera de gases en la reacción química el valor será una constante sin importar que en unos experimentos tengamos mas materia que en otros experimentos.
Donde el cociente de volúmenes será constante siempre y cuando las condiciones de presión y volumen sea constantes, y que los dos volúmenes estén vinculados en una misma reacción de síntesis o descomposición.
16.5 La hipótesis molécula a volumen
Si ponemos el hallazgo de Gay-Lussac en matemáticas, esto implica que el volumen de un gas es una propiedad que depende solo del número de partículas libres que pueden ser átomos o moléculas, pero no de la identidad de estos.
Una forma moderna de expresar la hipótesis de Avogadro es que el volumen de un gas j-cualquiera Vj a temperatura y presión constante depende del número de entidades de dicho gas-j Nj y una constante de proporcionalidad que representa el volumen de un solo átomo/molécula en vibración Vp.
Por lo que dos números de átomos de elementos distintos ocuparían el mismo volumen. Fue en 1811, que Amedeo Avogadro (1778-1856) formuló precisamente esta idea. ‘‘En las mismas condiciones de temperatura y presión, volúmenes iguales de diferentes gases tienen el mismo número de moléculas”. Tenga en cuenta que muchas de las leyes naturales que usamos en la parte numérica no fueron enunciadas originalmente como ecuaciones, o incluso, las ecuaciones originales pueden ser indistinguibles de sus formas modernas. En aras de un uso práctico de las leyes naturales hemos estado usando y continuaremos usando lenguaje moderno. La Ecuación 16.3 tradicionalmente se denomina la hipótesis de Avogadro, pero actualmente debería recibir el nombre de la ley molecular de Avogadro para volúmenes. Esta ecuación puede usarse para calcular el volumen que ocupa una sola molécula vibrando como en el siguiente ejemplo.
Dado que el volumen de partículas es literalmente una constante, cualquier molécula ocupará 3.72x10-2 zeptolitros. Sin embargo, igual que en otros cálculos que hemos hecho, en época de Avogadro este tipo de cálculos sería imposible ya que no les era posible contar el número de átomos en un determinado volumen a presión y temperatura constantes.
16.7 El radio estequiométrico
Tradicionalmente se nos dice que el radio estequiométrico es una cantidad óptima en proporción de una sustancia en una reacción química. En la práctica el radio estequiométrico es el cociente que ocurre entre dos números estequiométricos para sustancias diferentes, que normalmente llamaremos la incógnita (i) y el dato (d) o sustancia 1 y sustancia 2. Normalmente este cociente no tiene un símbolo propio, pero (Kulikovsky, 2004) propuso emplear la letra delta:
El radio estequiométrico λ(j,i) se define como el cociente de números estequiométricos de una sustancia v(j) entre el número estequiométrico de otra sustancia v(i) en una misma ecuación química que cumple con la ley de la conservación masa.
Si tomamos la ecuación que vincula el número de moléculas con el número de eventos de reacción Nj = vj Nξ y sacamos un cociente para una segunda sustancia dentro de la misma reacción entonces el parámetro de número de eventos de reacción será constante, por lo tanto:
Forma dinámica de la ley eventos de reacción, La cual indica que el cociente de número de moléculas es igual al cociente números estequiométricos.
O interesante es que si obtenemos un cociente para la hipótesis de Avogadro.
Forma dinámica de la hipótesis de Avogadro.
Podremos expresar los números estequiométricos en términos de los volúmenes de combinación ajustados a números enteros pequeños.
Ley de volúmenes de combinación.
16.12 La hipótesis de los gases diatómicos
Solo había un pequeño problema con esto, al aplicar los volúmenes de combinación como coeficientes a las fórmulas moleculares de Dalton para el agua, se incumplía la ley de la conservación de la masa.
Figura 16.2. Incumplimiento aparente de la ley de conservación de la masa en la ecuación química de Dalton para la síntesis de agua.
Si evaluamos el número de hidrógenos hay dos a ambos lados, pero si evaluamos el número de oxígenos, la cosa ya no funciona pues tenemos un oxígeno de un lado y dos del otro. Lo anterior implica que hay algo malo, pues la ley de la conservación de la masa es una ley que es muy difícil de romper. Así que solo hay dos cosas que pueden estar mal:
👉 Que el modelo matemático que llevamos hasta el momento sea solo una fumada mental, y por ende hemos perdido el tiempo desde la lección de teoría atómica.
👉 Que las fórmulas químicas para las sustancias estén mal, lo cual es más fácil de corregir.
Avogadro eligió la ruta fácil, así que, en lugar de reevaluar todas las hipótesis de la teoría atómica, se decantó por modificar los subíndices del hidrógeno, el oxígeno y el agua, hasta que concordaran simultáneamente con la ley de la conservación de la masa y los volúmenes de combinación de Gay-Lussac. El proceso debe haber sido manual, así que para ahorrarnos tiempo solo expondremos el resultado correcto.
Figura 16.3. Representación de un evento de reacción molecular para la síntesis del agua (2H2+O2→2H2O), note que los números estequiométricos indican cuantas moléculas están presentes, mientras que los subíndices indican cuantos átomos están pegados en una molécula. En la imagen podemos ver que hay 4 átomos de hidrógeno azules a ambos lados de la reacción, y dos átomos de oxígeno a ambos lados de la reacción.
Esta hipótesis se conoce como la hipótesis de los gases diatómicos debido a que los elementos que hasta ese momento se pensaba eran átomos libres como hidrógeno, oxígeno, flúor, cloro entre otros, en realidad se comportaban como moléculas compuestas por dos átomos, siendo el segundo gran aporte de Avogadro a la teoría atómica. Cuando se aplicaron las hipótesis de gases diatómicos a otras reacciones de gases, se dieron cuenta que tanto la ley de la conservación del número de átomos como la ley de volúmenes de combinación de Gay-Lussac se cumplía. Esto también implica que las primeras ecuaciones químicas se balancearon primero constando con los volúmenes experimentales, y la hipótesis de gases de combinación para poder hipotetizar la fórmula molecular de algunas sustancias, por ejemplo.
Observe que el balanceo de ecuaciones químicas hecho originalmente se realizaba con los coeficientes estequiométricos conocidos, y una hipótesis para la fórmula de los elementos gaseosos, y con esto se infería hipotéticamente la fórmula de los compuestos. Matemáticamente esto fue extremadamente armonioso y permitió hacer cálculos predictivos, pero los fundamentos de los cuales emergían, como la existencia de átomos, y que los elementos fueran moléculas diatómicas no lo fue, se trataba a la vista de muchos atomistas tibios o antiatomistas como una ficción útil. Los que, si se creyeron que los fundamentos que sostenían a estas ecuaciones útiles debían tener algo de verdadero, empezaron a usar estas fórmulas químicas hipotéticas para empezar a dar nombres sistemáticos a las sustancias, y desligarse definitivamente de nombres arcaicos heredados de la alquimia como el azote o el aceite de vitriolo.
Ejemplo. Cuantos átomos de calcio nitrógeno y oxigeno hay en un mol de Ca(NO3)2
17. El método de Cannizzaro
|| REGRESAR AL INDICE ||
La hipótesis atómica, y su corrección con las dos hipótesis de Avogadro, es decir, la de gases diatomicos, y la de volumen a número de partículas eran eso, meras hipótesis que no podían probar, especialmente porque en la época la teoría de la química era la de equivalentes, que sostenía que las sustancias se transmutaban en cantidades fijas en masa llamadas equivalentes, pero que la transmutación se basaba en entidades continuas de sustancia medibles fácilmente mediante la forma dinámica de la ecuación para la ley de Proust y la ley de Richter. Aquí es donde entra Stanislao Cannizzaro quien se encargaría de resolver la confusión entre las masas de las moléculas y las masas de los átomos, claro, asumiendo como verdaderas las hipótesis de Avogadro y la teoría atómica.
Figura 17.1. Stanislao Cannizzaro (13 de julio de 1826-10 de mayo de 1910) fue un químico italiano. Es famoso por la reacción de Cannizzaro y por su papel influyente en las deliberaciones de peso atómico del Congreso de Karlsruhe en 1860. Él defendió la noción de Amedeo Avogadro de que volúmenes iguales de gas a la misma presión y temperatura tenían el mismo número de moléculas o átomos, y la noción de que se podrían usar volúmenes iguales de gas para calcular pesos atómicos. Al hacerlo, Cannizzaro proporcionó una nueva comprensión de la química.
17.1 La nueva masa atómica del oxígeno.
Ahora que tenemos la hipótesis de Avogadro para la fórmula del agua podemos usar la ecuación Demostrada aquí:
Masa relativa de un elemento usando al hidrógeno como masa ponderadora.
… para calcular su masa atómica, nuevamente, asumiendo que un solo átomo de hidrógeno tiene una masa de igual a 1 exacto.
Por lo tanto, la nueva masa atómica del oxígeno debía ser 16, y por lo tanto la masa de la molécula de oxígeno O2 debía ser 32.
17.2 La masa molecular relativa
Dado que los elementos forman moléculas, se hace necesario diferenciar el concepto de masa atómica (mp(J)) del de masa molecular (mp(i)), por medio de la ley de la conservación de la masa. La masa molecular debe ser igual al aporte en masa de todos los átomos presentes, los cuales se agrupan por elementos, por lo que la suma de masas adquiere la estructura de una suma ponderada, y lo mismo debe ocurrir con la masa molecular relativa.
En las fórmulas anteriores debemos indicar que un compuesto cualquiera (j) como, por ejemplo, la cafeína, puede tener una fórmula molecular dada y compleja como C8H10N4O2. Dado que existe una cantidad casi infinita de fórmulas moleculares, representaremos cualquier fórmula molecular con la expresión AaBb…Zz donde (A) es el primer elemento y (a) su subíndice, (B) el segundo elemento y (b) su subíndice, así sucesivamente hasta llegar hasta el último elemento del conjunto. El problema con esta expresión sigue siendo el mismo que hemos tenido desde la introducción de la teoría atómica de Dalton, en esa época no era posible medir las masas atómicas o moleculares en unidades de masa como gramos o kilogramos, de allí que, en lugar de emplear al kilogramo como unidad de medida, se empleara la masa del elemento más ligero conocido, y eso convierte a la medición de masa en algo relativo (Ecuación 17.2). Si sienten que este tipo de cálculos ya lo han hecho, están en lo correcto, pues lo empleamos en el capítulo de química de gases, pues las masas molares son una magnitud estrechamente vinculada a la masa molecular y a la masa relativa, solo que con diferentes unidades. Miremos unos ejemplos simples:
17.5 De una masa estándar a un volumen estándar
En primera instancia debemos tener en cuenta que el número de moléculas de un sistema es directamente proporcional a su masa, es evidente que, a mayor cantidad de átomos, la masa va a ser más grande, y que ambas se relacionan con la masa de una sola molécula mediante el modelo lineal 17.4. La constante que relaciona la masa y el número de moléculas, llamada masa molecular mpj, no podía ser calculada con la tecnología disponible en la época de Cannizzaro. Pero si la dividimos entre la hipótesis de Avogadro obtenemos, un cociente masa a volumen, es decir, de densidades (Ecuación 17.5):
|
Por un lado, tendremos una densidad microscópica entre la masa molecular y el volumen de una sola partícula, sin embargo, ese valor será igual a la densidad macroscópica, medida con la masa y el volumen que se pueden medir fácilmente en el laboratorio bajo condiciones arbitrariamente elegidas de presión y temperatura que en su época eran conocidas como la densidad de vapor. Esta ecuación implica que, si se estandariza una masa dada de un gas conocido en condiciones estándar de presión y temperatura, debería generarse un volumen estándar. Si la masa estándar elegida para cada elemento contenía el mismo número de moléculas asumiendo que el volumen atómico es constante sin importar la identidad de la sustancia, entonces el volumen generado debería ser el mismo sin importar la identidad de la sustancia. Lo importante de esta ruta de pensamiento radica en que podía generarse un diseño experimental accesible a la tecnología del momento, empleando básicamente el mismo diseño experimental empleado para inferir la ley de Boyle, un cilindro con un pistón que permite el cambio de volumen, manteniendo la presión constante, un termómetro y un baño en frio para medir el volumen del gas al llegar a 0°C y una balanza para medir la masa del gas elemental empleado.
Figura 17.2. La temperatura elegida fue 0 °C y 1 atm de presión. Evidentemente en lugar de una llama, se usaría un baño de hielo.
Las masas se estandarizarían del siguiente modo:
👉 Completar 2 gramos de hidrógeno, pues es la masa molecular del hidrógeno expresada en gramos y determinar el volumen a 1 atm y 0 °C, que fue de 22.42 L.
👉 Completar 32 gramos de oxígeno y determinar nuevamente el volumen bajo las mismas condiciones, y el resultado fue, nuevamente 22.37 L.
Al redondear a tres cifras se puede ver claramente que el volumen en efecto se estandarizaba a 22,4 L, siempre y cuando se eligiera correctamente la masa estándar como predecía la hipótesis de Avogadro de gases diatómicos (Wisniak, 2000). El volumen estándar con presión estándar y temperatura estándar actuaría como una caja de huevos, en su interior siempre habría el mismo número significativo de moléculas “pues asumimos como correcta la hipótesis de Avogadro de relación volumen a número de moléculas”, aunque no pudieran contarse. Ahora era posible determinar las masas atómicas relativas y las masas moleculares relativas, siempre y cuando pudiéramos convertir una sustancia en un gas en condiciones estándar de presión y temperatura.
17.8 De un volumen estándar a una masa estándar
Con el volumen estandarizado con hidrogeno y oxígeno ahora sería posible recorrer el camino inverso, y usar el volumen estándar de 22.4 L., con la presión estándar de 1 atm y la temperatura estándar de 0 °C, para hallar la masa estándar de otras sustancias diferentes de hidrógeno y oxígeno. Actualmente esta historia está secretamente condensada en la ley de Avogadro para gases expresada para una densidad, cuya demostración hicimos en el capítulo de gases, y su fórmula es la siguiente:
Masa molar en términos de la densidad y el volumen molar.
Nuevamente, debemos recordar que la simbología aquí expresada es anacrónica, en su tiempo no existía masa molar, sino la masa de un elemento estandarizada al contener su materia a 22.4 L en condiciones normales de presión y temperatura, idea que luego fue acortada a la expresión molécula-gramo, y que finalmente se acortó a mol. A su vez debemos tener en cuenta que la masa molar es una masa relativa con unidades de g/mol, por lo que al despojarla de sus unidades Mi se convierte en Ari. Para adicionar o quitar las unidades g/mol se diseñó una constante llamada constante de masa molar Mu que es igualo a 1 g/mol, lo cual permite definir la masa molar en términos de masa relativa.
Masa molar en términos de la masa molecular relativa.
En la práctica la ecuación anterior se aplica de manera instintiva o explícita.
Aunque las masas atómicas relativas también se pueden calcular por medio de reacciones de síntesis o descomposición, por ejemplo:
Ejemplo. Calcular la masa molar de un gas X2 sí sabemos que en C.N. su densidad específica es 1.696 g/L
Por ende, hay dos rutas o diseños experimentales diferentes que convergen en el mismo valor de masa atómica relativa o peso atómico relativo. El problema de ambas técnicas radica en que se pueden hacer cálculos para elementos volátiles que se convierten en gases, pero elementos como los metales no pueden convertirse en gases fácilmente, por lo que debemos hacernos la pregunta ¿Cómo se determina la masa atómica relativa de los metales en esta época? La respuesta viene con la ley de Dulong y Petit que veremos más adelante, pero que permitió generar las primeras tablas de pesos atómicos como la de Berzelius.
Figura 17.3. Pesos atómicos para varios elementos conocidos a finales del siglo XIX calculados por medio de la técnica de Cannizzaro.
Nuevamente, esto traería impactos, con las tablas de pesos atómicos y los patrones de reactividad se hizo necesario una forma de organizar los elementos conocidos, es decir, estos cálculos serian el cimiento para la construcción de las primeras tablas periódicas.
Figura 17.4. Tabla periódica de Mendeleev generada al combinar la reactividad de los elementos junto con sus pesos estandarizados.
18. Del molécula-gramo al mol
|| REGRESAR AL INDICE ||
El volumen estandarizado o 22.4 L en 1 atm y 0°C fue denominado como el molécula-gramo, pues la masa de un gas en esas condiciones era reconocida como la masa estándar, aunque nuevamente, era denominada como molécula-gramo, y su conversión dividiendo entre 2 para los gases diatómicos como el átomo-gramo. Sin embargo, ya actualmente no usamos el molécula-gramo o el átomo-gramo emergen dos preguntas: ¿Por qué desaparecieron? ¿Algo más los reemplazó? Para responder estas preguntas, primero debemos reiniciar donde nos quedamos la última vez, y es con la técnica de Cannizzaro, pues, aunque él hubiera desarrollado el modo de calcular los molécula-gramo y los átomo-gramo, aún quedaba una parte del método científico, y era publicar tus resultados ante una comunidad de expertos que estén dispuestos a escucharte.
18.1 El Congreso de Karlsruhe
En 1860, August Kekule, Adolf Wurtz y Karl Weltzien convocaron una reunión en Karlsruhe (Alemania) que se convirtió en el primer Congreso Internacional de Química. El objetivo principal era llegar a un acuerdo sobre la nomenclatura química. Se discutieron diferentes temas. Una de estas cuestiones era la necesidad de distinguir claramente conceptos tales como átomo, molécula y equivalente, al dar definiciones más precisas a cada uno, pues los pesos relativos de Dalton aun eran empleados bajo la etiqueta de equivalentes, pues la hipótesis de los gases diatómicos no era tan reconocida, y los que la conocían no la aceptaban en muchas ocasiones (Padilla & Furio-Mas, 2008).
Hermann Franz Moritz Kopp abrió la discusión indicando que los pesos equivalentes (por ejemplo, la relación de masa hidrógeno a oxígeno en el agua de 1 a 8) era algo que se medía directo sin la necesidad de fumadas mentales de moléculas diatómicas. Después de una larga sesión de discusión, nunca se llegó a una decisión final. Sin embargo, la ciencia no es una democracia, y no se esperaba que se decidiera el asunto por votaciones, la utilidad del congreso recayó en que Cannizzaro pudo popularizar su método de cálculo de los molécula-gramo y los átomo-gramo frente a todos los sujetos que importaban, la élite de la química, la crème de la crème, pero con resultados limitados, básicamente se aceptaron los cálculos, pero no las ideas que los sostienen,, es decir el átomo no se asumió como una cosa que estaba afuera y alrededor, sino como una conjetura platónica que solo existía en la cabeza de los científicos, igual que los números.
De hecho, fue algo muy semejante a las primeras definiciones de gen, Gregor Mendel también pensaba que sus factores generadores o genes como los llamamos actualmente no tenían una base física real, sino que se trataba de una idea matemática que solo existía en la mente humana. La aceptación paulatina de que los átomos debían existir fue gradual y ocurrió “parafraseando a Max Planck” a medida que los ancianos químicos equivalentistas iban estirando la pata, y sus plazas de enseñanza en universidades y colegios se llenaban con sucesores atomistas (Padilla & Furio-Mas, 2008).
Figura 18.1. Jan o Johann Joseph Loschmidt (15 de marzo de 1821 - 8 de julio de 1895), químico y físico (termodinámica, óptica, electrodinámica, formas cristalinas). Fue uno de los primeros investigadores de la teoría de la valencia atómica y del tamaño molecular. Escribió un tratado, Estudios químicos I, donde interpretaba correctamente la naturaleza de los compuestos azucarados como compuestos parecidos al éter, y afirmaba que el ozono es O3 y el benceno una molécula cíclica. Aceptó la existencia de valencias variables para ciertos átomos como el azufre y valencia fija para otros como hidrógeno, carbono y oxígeno. Este tratado tuvo tan escasa repercusión que su segunda parte, proyectada por el autor mientras escribía la primera, nunca fue publicada. Posteriormente trabajó sobre la teoría cinética de los gases, donde calculó por primera vez el valor exacto del tamaño de las moléculas del aire. Con este valor estimó erróneamente el número de moléculas que hay en un centímetro cúbico de aire. No obstante, fue el primer intento de medir el número de Avogadro, constante que a veces también se denomina número de Loschmidt.
18.2 La constante de Loschmidt
A pesar de este ambiente hostil, otros científicos si opinaban que los átomos y las moléculas debían existir, y que la hipótesis de Avogadro representaba una relación real en la naturaleza más allá de permitir el cálculo de una tabla de pesos atómicos relativos.
Tal como se escribe la hipótesis de Avogadro debería poder permitir el cálculo del número de moléculas en un volumen determinado, el problema era la tecnología de la época, pero aunque no pudiera calcularse el número real, si era posible realizar una estimación. La primera persona en estimar el número real de partículas en una cantidad determinada de una sustancia fue Josef Loschmidt, un profesor de secundaria austríaco que más tarde se convirtió en profesor en la Universidad de Viena (Wiswesser, 1989). En 1865 Loschmidt utilizó la teoría cinética molecular para estimar el número de partículas en un centímetro cúbico de gas en condiciones estándar, con un valor de 1.81 x 1024 m-3, el valor moderno es de 2.69 x 1025 m-3, aunque bastante diferente si sacáramos una estimación de error absoluto, por lo menos fue una aproximación, antes de eso el número de átomos en un volumen dado podía ser cualquier cosa.
Tenga en cuenta que el modo original para esta estimación es diferente, debido a que actualmente contamos con el número de Avogadro o la constante de Boltzman, lo cual facilita la deducción, por lo que dejaremos la demostración “moderna” de este cálculo para más adelante. A parte del intento de Loschmidt, pocos se enfocaron en calcular el número de partículas en el volumen estándar, pues la teoría equivalentista funcionaba bien sin asumir números extravagantes de moléculas que no se podían ver.
18.3 Mol como diminutivo de molécula-gramo
Sin embargo, la expresión molécula-gramo y átomo-gramo era problemática para los antiatomistas ya que era teóricamente sesgada, al usarla los alumnos eran inducidos a pensar que átomos y moléculas existían. Para evitar este sesgo ideológico, uno de los más grandes antiatomistas, el célebre Friedrich Wilhelm Ostwald acuña el término mol, como unidad de medida en 1893 para su libro de texto como una abreviatura de la expresión molécula-gramo, y esto trajo dos consecuencias, la primera era que acortaba la carga simbólica de la aritmética de factores de conversión, y la segunda era que desligaba del lenguaje la mención implícita a átomos y moléculas, que, en su opinión, no existían. Así pues, la primera definición del mol fue como la masa de referencia en STP mas un volumen de 22.41 L.
Sin embargo, por algún tiempo y hasta libros de texto de 1970 se mantuvo la expresión átomo-gramo y molécula-gramo para átomos y moléculas por separado en los capítulos introductorios de la teoría atómica clásica, lo que ayudaba a aumentar la confusión conceptual (Matamála & Gonzalez, 1976). Esta mención quedó finalmente suprimida en textos modernos que usan mol como reemplazo tanto del molécula-gramo como del átomo-gramo. De esta manera se enfatizaba una ruptura que venía dándose desde el tiempo de Dalton, la química era una ciencia con dos mundos a parte:
👉 El primer mundo era el mundo molar (o real según algunos) de los moles, gramos y volúmenes, era algo así como el mundo realmente accesible por los químicos, y en lo único que estaban de acuerdo en que existía,
👉 El segundo era el mundo el molecular (o hipotético), con sus átomos, moléculas, formulas moleculares, y cosas que, para muchos, e incluso buena parte de los atomistas, solo existía en la mente humana.
De hecho, esta tendencia es tan fuerte que muchos de los cálculos de masa rutinarios no tienen en cuenta argumentos moleculares. Los libros de texto moderno de hecho fuerzan una única interpretación del número estequiométrico, y es que se deben describir como los moles teóricos o estándar de una sustancia.
18.4 El número de Avogadro y la aceptación del átomo
A finales del siglo XIX los físicos comenzaron a encontrar argumentos para defender la teoría atómica. Hacia 1871 Ludwig Boltzmann desarrolló la teoría cinético-molecular, que es básicamente la explicación de las leyes de los gases en base a la teoría atómica, aunque en su época muchos físicos aun no tomaban en serio la teoría atómica (Flamm, 1997; Rodgers, 2019; Wilholt, 2002). Lamentablemente Boltzmann se suicidaría en 1906 por causas relacionadas precisamente a este ambiente hostil contra la teoría atómica.
Figura 18.2. Un tubo de rayos catódicos es un tuvo casi vacío por donde pasa una corriente eléctrica.
Otros físicos comenzaron a estudiar a los átomos con propiedades diferentes de la masa y su reactividad, por ejemplo, gracias a los rayos catódicos, el físico J J Thomson logró desarrollar un modelo atómico nuevo, el gastronómico pudin de pasas, sin embargo, esta receta culinaria del átomo esconde unas matemáticas realmente elevadas, dentro de las cuales destaca la relación carga masa con respecto al movimiento de una partícula en el vacío la cual modelaba el movimiento de los rayos de electrones en un tubo casi al vacío. Para acortar la historia, la masa en la ecuación era la masa del electrón, y con la determinación de la dirección, pudo crearse una nueva tecnología llamada espectrometría de masas, en la cual podía emplearse la relación entre carga y movimiento de un elemento para calcular su átomo-gramo sin necesidad de usar el volumen de referencia (Münzenberg, 2013), convirtiéndose en una técnica secundaria que corroboraba los datos de pesos relativos calculados por técnicas químicas.
Años más tarde Albert Einstein emplearía las propiedades coligativas para introducir la hipótesis de Avogadro de manera evidente, el problema es que los símbolos que usamos actualmente aun no estaban estandarizados, por lo que resulta difícil reconocer estas ecuaciones con sus contrapartes modernas (Milton, 2011). Sin embargo gracias al uso de los parámetros de número de partículas en las propiedades coligativas propuesta por Einstein combinadas con la teoría cinética, 6 años más tarde Jean Perrin podría deducir ecuaciones nuevas que sugerían un diseño experimental que permitía medir el valor del número de partículas contenido en el molécula gramo (Perrin, 1901, 1909, 1911, 1913). Uno de los primeros valores fue 6.70 x 1023 moléculas en un mol de sustancia.
Aunque un poco diferente del valor actual o del valor dado por Losdmidt, la diferencia radicaba en que la demostración de Perrin si era convincente para los antiatomistas, tanto así que fue capaz de convencer a Ostwald que estaba equivocado y que la teoría atómica era más que una fumada mental, sin embargo, vale la pena recalcar que Perrin no reclamó la gloria para sí mismo, reconoció que la primera persona en intuir la existencia de este número fue el Conde Lorenzo Romano Amedeo Carlo Avogadro, y por ende y cito “Este número es una constante universal, que se puede designar apropiadamente como constante de Avogadro. Si se conoce esta constante, se conoce la masa de cualquier molécula”, la comunidad científica aceptó la recomendación y desde entonces se conoce a la variable como El número de Avogadro simbolizado como NA.
Figura 18.3. Friedrich Wilhelm Ostwald (en letón, Vilhelms Ostvalds) (Riga, Letonia; 2 de septiembre de 1853-Grossbothen, Alemania; 3 de abril de 1932) fue un químico, eugenista, profesor universitario y filósofo alemán, premio Nobel de Química en 1909 «por su trabajo en la catálisis y por sus investigaciones sobre los principios fundamentales que rigen los equilibrios químicos y las velocidades de reacción» Inicialmente se opuso a la teoría atómica, pero luego de que se realizaran medidas del movimiento browniano y se comprobase que coinciden con las ecuaciones calculadas por Albert Einstein (medidas realizadas por Jean Perrin), cambió de opinión.
Finalmente, el libro de oro de la IUPAC sostiene que las variables discretas de conteos, como un numero de partículas dado, no tiene unidades, pero el número de Avogadro al ser un numero ponderado a 1 mol tendrá unidades de uno sobre mol, o mol a la menos uno, y por tradición memorizamos este número con cuatro cifras significativas NA = 6.022 x 1023 mol-1 = 6.022 x 1023 / mol. En la actualidad se emplean técnicas más sofisticadas para hallar el número de Avogadro, pero son técnicas de índole físico en los cuales no se emplean reacciones químicas, sino el modo en que se modifica la dirección de un rayo de alta energía, con lo cual se ha logrado aumentar el nivel de precisión del número de Avogadro a nueve cifras significativas NA = 6.02214076 x 1023 mol-1. Tenga en cuenta que esto sigue siendo una aproximación, pues el verdadero número de Avogadro debe tener exactamente 23 cifras significativas, ya llevamos 9 al menos.
19. Del mol a la cantidad de sustancia
|| REGRESAR AL INDICE ||
En 1961 Edward Guggenheim introdujo una serie de modificaciones al lenguaje que se había heredado desde el siglo XIX (Guggenheim, 1961). Pues varios conceptos relacionados se venían acumulando de manera intrincada, siendo estos:
👉 el mol,
👉 el átomo-gramo / el molécula-gramo,
👉 el peso atómico relativo / el peso molecular relativo,
👉 el peso atómico / el peso molecular,
Una absoluta desgracia, o como dicen los historiadores de la ciencia, una infelicidad fruto del devenir histórico del proceso de investigación. El problema es que, en lugar de simplificar el lenguaje, Guggenheim introdujo una nueva magnitud, la masa molar para reemplazar al átomo-gramo y al molécula-gramo, pero su introducción no se aceptó unánimemente, pues, por ejemplo, las tablas periódicas siguen estando expresadas con el concepto de pesos relativos. Esto demuestra que poner de acuerdo con los químicos es muy, pero muy, difícil.
Figura 19.1. Edward Armand Guggenheim FRS (11 de agosto de 1901 en Manchester - 9 de agosto de 1970) fue un químico físico inglés, conocido por sus contribuciones a la termodinámica.
19.1 Masa relativa
Las masas que aparecen en la tabla periódica carecen de unidades pues son masas relativas asociadas a la unidad de masa atómica o dalton (mu = 1 uma = 1 u = 1.661 × 10−24 g). Cada unidad de masa atómica es igual a una constante de masa atómica, así que es posible calcular la masa absoluta de un elemento multiplicando por la constante de masa atómica. La masa relativa de un compuesto sigue la ley de la conservación de la masa, por lo que se puede calcular como la suma ponderada de las masas relativas y los subíndices.
Evidentemente existen relaciones con la masa molar, pero no vale la pena expresarlas en ecuaciones, simplemente se trata de retirar o agregar la constante de masa atómica y agregar o retirar las unidades de la constante de masa molar para hacer las conversiones entre estas tres escalas de masa que tienen los mismos valores.
Química de Chang 10
Ejemplo 3.5a. Calcular la masa molecular en uma para el dióxido de azufre, usando los pesos atómicos a cuatro cifras significativas.
Ejemplo 3.5b. Calcular la masa molecular en uma para la cafeína (C8H10N4O2), usando los pesos atómicos a cuatro cifras significativas.
Problema 3.23a. Calcule la masa molecular o la masa de fórmula (en uma) de CH4
Problema 3.23b. Calcule la masa molecular o la masa de fórmula (en uma) de NO2
Problema 3.23c. Calcule la masa molecular o la masa de fórmula (en uma) de SO3
Problema 3.23d. Calcule la masa molecular o la masa de fórmula (en uma) de C6H6
Problema 3.23e. Calcule la masa molecular o la masa de fórmula (en uma) de NaI
Problema 3.23f. Calcule la masa molecular o la masa de fórmula (en uma) de K2SO4
Problema 3.24a. Calcular la masa molecular o masa de la fórmula en uma de Li2CO3
Problema 3.24b. Calcular la masa molecular o masa de la fórmula en uma de CS2
Problema 3.24c. Calcular la masa molecular o masa de la fórmula en uma de CHCl3
Problema 3.24d. Calcular la masa molecular o masa de la fórmula en uma de C6H8O6 ácido ascórbico o vitamina C.
Problema 3.24e. Calcular la masa molecular o masa de la fórmula en uma de KNO3
Problema 3.24f. Calcular la masa molecular o masa de la fórmula en uma de Mg3N2
Problema 3.25. Calcular la masa molar de un compuesto si 0.372 mol tienen una masa de 152 g.
Química la ciencia central
Muestra 3.5a. Calcule el peso fórmula de la sacarosa, C12H22O11 (azúcar de mesa)
Muestra 3.5b. Calcule el peso fórmula de nitrato de calcio, Ca(NO3)2.
Práctica 3.5.1. ¿Cuál de los siguientes es el peso fórmula correcto para el fosfato de calcio? (a) 310.2 uma. (b) 135.1 uma. (c) 182.2 uma. (d) 278.2 uma. (e) 175.1 uma.
Práctica 3.5.2a. Calcule el peso fórmula de Al(OH)3
Práctica 3.5.2b. Calcule el peso fórmula de CH3OH
Práctica 3.5.2c. Calcule el peso fórmula de TaON
Ejercicio 3.23a. Determine los pesos fórmula del ácido nítrico, HNO3.
Ejercicio 3.23b. Determine los pesos fórmula del KMnO4.
Ejercicio 3.23c. Determine los pesos fórmula del Ca3(PO4)2.
Ejercicio 3.23d. Determine los pesos fórmula del cuarzo, SiO2.
Ejercicio 3.23e. Determine los pesos fórmula del sulfuro de galio.
Ejercicio 3.23f. Determine los pesos fórmula del sulfato de cromo (III).
Ejercicio 3.23g. Determine los pesos fórmula del tricloruro de fósforo.
Ejercicio 3.24a. Determine los pesos fórmula del óxido nitroso, N2O, conocido como gas hilarante y utilizado como anestésico en odontología.
Ejercicio 3.24b. Determine los pesos fórmula del ácido benzoico; HC7H5O2, sustancia utilizada como conservante de alimentos.
Ejercicio 3.24c. Determine los pesos fórmula del Mg(OH)2, el ingrediente activo de la leche de magnesia.
Ejercicio 3.24d. Determine los pesos fórmula del urea, (NH2)2CO, un compuesto utilizado como fertilizante nitrogenado.
Ejercicio 3.24e. Determine los pesos fórmula del acetato de isopentilo, CH3CO2C5H11, responsable del olor de los plátanos.
19.4 La masa molar y cantidad de sustancia
La masa molar es la relación de masa de una sustancia o elemento en un mol de esta, medida directa o indirectamente. Normalmente definimos la masa molar para sustancias.
|
Ejemplo. Cuantos moles hay en 20 g de cobre. Ejemplo. Cuantos moles hay en 14.0 g de N2.
Ejemplo. Cuantos moles hay en 10 gramos de agua Ejemplo. Cuantos moles hay en 10 ng de H2SO4.
Ejemplo. Cuantos moles hay en 14.9 g de H2. Ejemplo. Cuantos moles hay en 14.9 mg de Cl2.
Ejemplo. Cuantos moles hay en 100 g de CO2. Ejemplo. Cuantos moles hay en 100 gramos de sodio.
Ejemplo. Cuantos moles hay en una libra de azucar. Ejemplo. Cuantos moles hay en 60 g de cobre.
Ejemplo. Cuantos moles hay en 12 g de carbono. Ejemplo. Cuantos moles hay en 160 g de NH3.
Ejemplo. Cuantos moles hay en 100 ml de agua. Ejemplo. Cuantos moles hay en 18 g de agua.
Ejemplo. Cuantos moles hay en 244 g de aluminio. Ejemplo. Cuantos moles hay en 25 g de cobre.
Ejemplo. Cuantos moles hay en 250 g de agua. Ejemplo. Cuantos moles hay en 200 g de CaCO3.
Ejemplo. Cuantos moles hay en 294 g de ácido sulfúrico.Ejemplo. Cuantos moles hay en 220 g de CO2.
Ejemplo. Cuantos moles hay en 200 g de agua. Ejemplo. Cuantos moles hay en 2 L de agua.
Ejemplo. Cuantos moles hay en 20 gramos de SO2. Ejemplo. Cuantos moles hay en 20 nanogramos de H2O2.
Ejemplo. Cuantos moles hay en 28.7 g de Na2SO4. Ejemplo. Cuantos moles hay en 28.7 mg de FeSO4.
Ejemplo. Cuantos moles hay en 24 gramos de carbono. Ejemplo. Cuantos milimoles hay en 25 mg de NaCl.
Ejemplo. Cuantos moles hay en 25 g de H2SO4. Ejemplo. Cuantos moles hay en 25 dg de H2SO3.
Ejemplo. Cuantos moles hay en 30 g de helio. Ejemplo. Cuantos moles hay en 30 g de H2SO4.
Ejemplo. Cuantos moles hay en 350 g de hierro. Ejemplo. Cuantos moles hay en 3 gramos de carbono.
Ejemplo. Cuantos moles hay en 3 g de helio. Ejemplo. Cuantos moles hay en 300 g de H2SO4.
Ejemplo. Cuantos moles hay en 350 g de NaNO3. Ejemplo. Cuantos moles hay en 36 g de agua.
Ejemplo. Cuantos moles hay en 360 g de agua. Ejemplo. Cuantos moles hay en 40 g de agua.
Ejemplo. Cuantos moles hay en 35 g de NaCl. Ejemplo. Cuantos moles hay en 36 g de CO2.
Ejemplo. Cuantos moles hay en 4 gramos de agua. Ejemplo. Cuantos moles hay en 4 microgramos de H2O2.
Ejemplo. Cuantos moles hay en 40 gramos de sodio, manual. Ejemplo. Cuantos moles hay en 48 g de CH4, manual.
Ejemplo. Cuantos moles hay en 45 g de NaCl. Ejemplo. Cuantos moles hay en 44 g de CO2.
Ejemplo. Cuantos moles hay en 400 g de Na3PO4. Ejemplo. Cuantos moles hay en 400 g de Na2SO3.
Ejemplo. Cuantos moles hay en 400 g de CO2, manual. Ejemplo. Cuantos moles hay en 400 mg de SO2.
Ejemplo. Cuantos moles hay en 43 g de NH3. Ejemplo. Cuantos moles hay en 40 g de Fe2O3.
Ejemplo. Cuantos moles hay en 49 g de H2SO4. Ejemplo. Cuantos moles hay en 45 g de F2.
Ejemplo. Cuantos moles hay en 54 g de agua. Ejemplo. Cuantos moles hay en 5.00 g de Li.
Ejemplo. Cuantos moles hay en 5.1 g de P4. Ejemplo. Cuantos moles hay en 54 g de PCl5.
Ejemplo. Cuantos moles hay en 50 g de H2O. Ejemplo. Cuantos moles hay en 507.25 g de NH3.
Ejemplo. Cuantos moles hay en 5 g de agua oxigenada. Ejemplo. Cuantos moles hay en 5 g de cloruro de sodio.
Ejemplo. Cuantos moles hay en 50 g de NaCl. Ejemplo. Cuantos moles hay en 54.7 g de CaCO3.
Ejemplo. Cuantos moles hay en 50 g de CaCO3. Ejemplo. Cuantos moles hay en 56 g de KMnO4, manual.
Ejemplo. Cuantas moles hay en 56 mg de HCN, manual Ejemplo. Cuantas moles hay en 56 g de NO2 manual.
Ejemplo. Cuantos moles hay en 500 g de CO2, manual. Ejemplo. Cuantos moles hay en 500 mg de agua, manual.
Ejemplo. Cuantos moles hay en 50 g de H2SO4. Ejemplo. Cuantos moles hay en 6 g de oro.
Ejemplo. Cuantos moles hay en 60 g de NaOH. Ejemplo. Cuantos moles hay en 64 g de metano CH4.
Ejemplo. Cuantos moles hay en 60 gramos de carbono. Ejemplo. Cuantos moles hay en 60 g de agua.
Ejemplo. Cuantos moles hay en 60 gramos de etano C2H6. Ejemplo. Cuantas moles hay en 63 mg de CO2.
Ejemplo. Cuantos moles hay en 600 g de oxígeno. Ejemplo. Cuantos moles hay en 64 g de O2.
Ejemplo. Cuantos moles hay en 6.46 g de helio. Ejemplo. Cuantos moles hay en 600 g de butano C4H10.
Ejemplo. Cuantos moles hay en 600 gramos de MgSO4 Ejemplo. Cuantos moles hay en 600 mg de FeSO4
Ejemplo. Cuantos moles hay en 63 g de SnCl4. Ejemplo. Cuantos moles hay en 64 g de S.
Ejemplo. Cuantos moles hay en 75 g de ZnSO4. Ejemplo. Cuantos moles hay en 72 gramos de agua.
Ejemplo. Cuantos moles hay en 7.58 mg de CCl4. Ejemplo. Cuantos moles hay en 70 g de cloro molecular.
Ejemplo. Cuantos moles hay en 7.0 g de Na Ejemplo. Cuantos moles hay en 7.0 kg de boro.
Ejemplo. Cuantos moles hay en 7.0 gramos de He Ejemplo. Cuantos moles hay en 7.0 nanogramos de Ar
Ejemplo. Cuantos moles hay en 72 gramos de agua Ejemplo. Cuantos moles hay en 75 g de ZnSO4
Ejemplo. Cuantos moles hay en 72 g de CaCO3 Ejemplo. Cuantos moles hay en 78 g de NaCl
Ejemplo. Cuantos moles hay en 75.0 g de SO2. Ejemplo. Cuantos moles hay en 788 g de oro.
Ejemplo. Cuantos moles hay en 75 g de hierro. Ejemplo. Cuantos moles hay en 7.5 g de CO2.
Ejemplo. Cuantos moles hay en 7.5 gramos de NaCl Ejemplo. Cuantos moles hay en 7.5 microgramos CaCl2
Ejemplo. Cuantos moles hay en 76.0 g de ácido sulfúrico. Ejemplo. Cuantos moles hay en 7.46 g de litio.
Ejemplo. Cuantos moles hay en 750 g de H2SO4. Ejemplo. Cuantos moles hay en 88 g de CO2.
Ejemplo. Cuantos moles hay en 8 g de O2. Ejemplo. Cuantos moles hay en 80 g de NaOH.
Ejemplo. Cuantos moles hay en 800 g de MgCl2. Ejemplo. Cuantos moles hay en 88 g de C12H22O11.
Ejemplo. Cuantos moles hay en 870 g de cobre. Ejemplo. Cuantos moles hay en 80 g de amoníaco.
Ejemplo. Cuantos moles hay en 80 g de calcio. Ejemplo. Cuantos moles hay en 80 g de O2.
Ejemplo. Cuantos moles hay en 80 gramos de CH4Cl Ejemplo. Cuantos moles hay en 80 gramos de Cu(OH)2
Ejemplo. Cuantos moles hay en 90 g de H2O. Ejemplo. Cuantos moles hay en 980 g de H2SO4.
Ejemplo. Cuantos moles hay en 9 g de H2O. Ejemplo. Cuantos moles hay en 900 g de H2O2.
Ejemplo. Cuantos moles hay en 96 g de oro. Ejemplo. Cuantos moles hay en 94.5 g de HNO3.
Ejemplo. Cuantos moles hay en 90 g de glucosa C6H12O6. Ejemplo. Cuantos moles hay en 90 g de amoniaco
Ejemplo. Cuantos moles hay en 987 g de KMnO4. Ejemplo. Cuantos moles hay en 987 mg de LiMnO4.
Ejemplo. Calcula la masa en gramos de 1.5 moles de Na
Ejemplo. Cuántos gramos de sodio hay en 4 moles de sodio
Ejemplo. Calcula la masa en gramos de 11 moles de NaCl
Ejemplo. Calcular masa en gramos de 1.73 mol de CaH2
Ejemplo. Calcular la masa en gramos de 2.80 moles de Ca
Ejemplo. Cuantos gramos hay en 2 moles de agua
Ejemplo. Calcular la masa en gramos de 3.52 moles de MgBr2
Ejemplo. Calcular la masa en gramos de 3.00 mol de CaS
Ejemplo. Calcular la masa en gramos de 3.09 moles de carbonato de amonio
Ejemplo. Calcular la masa en gramos de 0.30 moles de ácido sulfúrico
Ejemplo. Calcular la masa en gramos en 4.0 mol de CO2
Ejemplo. Calcular la masa en gramos en 4.0 mol de O2
Ejemplo. Calcular la masa en gramos en 5.02 mol de oro
Ejemplo. Calcular la masa en gramos en 6.0 moles de magnesio
Ejemplo. Calcular la masa en gramos en 7.81 mol de sodio
Ejemplo. Calcular la masa en gramos en 80 mol de H2
Ejemplo. Calcular la masa en gramos en 80 mol de Cl2
Ejemplo. Calcular la masa en gramos en 80 mol de P
Ejemplo. Calcular la masa en gramos en 80 mol de agua
Ejemplo. Calcular la masa en gramos en 9.00 mol de Na2CO3
Ejemplo. Calcular la masa en gramos en 9.00 mol de magnesio
Ejemplo. Cuantos gramos de helio hay en 100 moles de helio
Matamala y González
Química de Chang 10
Problema 3.9a-b. Defina el término "mol". ¿Cuál es la unidad del mol en los cálculos?
Problema 3.9c-d. ¿Qué tiene el mol en común con el par, la docena y el gross? ¿Qué representa el número de Avogadro?
Práctica 3.2. ¿Cuántos moles de magnesio (Mg) hay en 87.3 g de Mg?
Práctica 3.3. Calcular la cantidad de gramos de plomo (Pb) en 12.4 moles de plomo.
Práctica 3.6. Calcular el número de moles de cloroformo (CHCl3) en 198 g de cloroformo.
Problema 3.15. ¿Cuántos moles de átomos de calcio (Ca) hay en 77,4 g de Ca?
Problema 3.16. ¿Cuántos gramos de oro (Au) hay en 15.3 moles de Au?
Química la ciencia central 13
Muestra 3.9. ¿Cuál es la masa molar de la glucosa, C6H12O6?
Práctica 3.9.2. Calcular la masa molar de Ca(NO3)2.
Muestra 3.10. Calcular el número de moles de glucosa C6H12O6 en 5.380 g de C6H12O6.
Práctica 3.10.1. ¿Cuántos moles de bicarbonato de sodio NaHCO3 hay en 508 g de NaHCO3?
Práctica 3.10.2. ¿Cuántos moles de agua hay en 1.00 L de agua, cuya densidad es de 1.00 g/mL?
Muestra 3.11. Calcula la masa, en gramos, de 0.433 mol de nitrato de calcio.
Práctica 3.11.1a. ¿Cuál es la masa, en gramos, de 6.33 mol de NaHCO3?
Práctica 3.11.1b. ¿Cuál es la masa, en gramos, de 3.0 x 10-5 mol de ácido sulfúrico?
Práctica 3.11.2a. ¿Cuál es la masa, en gramos, de 0.50 mol de diamante (C)?
Práctica 3.11.2b. ¿Cuál es la masa, en gramos, de 0.155 mol de cloruro de amonio?
Ejercicio 3.30. (a) ¿Cuál es la masa, en gramos, de un mol de 12C? (b) ¿Cuántos átomos de carbono hay en un mol de 12C?
Ejercicio 3.35a. Calcular la masa, en gramos, de 0.105 mol de sacarosa C12H22O11.
Ejercicio 3.35b. Calcular los moles de Zn(NO3)2 en 143.50 g de esta sustancia.
Ejercicio 3.35c. Calcular el número de moléculas en 1.0 x 10-6 mol CH3CH2OH.
Ejercicio 3.35d. Calcular el número de átomos de N en 0.410 mol NH3.
Ejercicio 3.36a. Calcular la masa, en gramos, de 1.50 x 10-2 mol CdS.
Ejercicio 3.36b. Calcular el número de moles de NH4Cl en 86.6 g de esta sustancia.
Ejercicio 3.36c. Calcular el número de moléculas en 8.447 x 10-2 mol C6H6.
Ejercicio 3.36d. Calcular el número de átomos de O en 6.25 x 10-3 mol Al(NO3)3.
Ejercicio 3.37a. ¿Cuál es la masa, en gramos, de 2.50x10-3 mol de fosfato de amonio?
Ejercicio 3.37b. ¿Cuántos moles de iones de cloruro hay en 0.2550 g de cloruro de aluminio?
Ejercicio 3.37c. ¿Cuál es la masa, en gramos, de 7.70x1020 moléculas de cafeína, C8H10N4O2?
Ejercicio 3.37d. ¿Cuál es la masa molar de colesterol si 0.00105 mol tiene una masa de 0.406 g?
Ejercicio 3.38a. ¿Cuál es la masa, en gramos, de 1.223 mol de sulfato de hierro (III)?
Ejercicio 3.38b. ¿Cuántos moles de iones de amonio hay en 6.955 g de carbonato de amonio?
Ejercicio 3.38c. ¿Cuál es la masa, en gramos, de 1.50 x 1021 moléculas de aspirina, C9H8O4?
Ejercicio 3.38d. ¿Cuál es la masa molar de diazepam (Valium®) si 0,05570 mol tiene una masa de 15.86 g?
Ejercicio 3.39a. La fórmula molecular de la alicna, el compuesto responsable del olor característico del ajo, es C6H10OS2. a) ¿Cuál es la masa molar de alicina?
Ejercicio 3.40a. La fórmula molecular del aspartamo, el edulcorante artificial comercializado como NutraSweet®, es C14H18N2O5. (a) ¿Cuál es la masa molar del aspartamo?
Otro aporte de Edward Guggenheim radica en darle un símbolo de variable medida en moles, es decir (nj) que Guggenheim bautizó como Stoffmenge que significa cantidad de sustancia (Marquardt, 2019). Tenga en cuenta que la unidad mol se había usado desde principios de siglo, pero su nombre y símbolo de variable no se estandarizaron realmente por la IUPAC sino hasta los años 70, y lo que es peor, estos conceptos convivieron con sus versiones viejas como el átomo-gramo hasta bien entrada la década de 1970, y tengo un libro que lo atestigua, la química de Matamala y Gonzalez (1976), escrita en esa época.
19.7 Calculando la cantidad de átomos en una masa arbitraria de sustancia pura
En 1971 la IUPAC redefinió al mol en base a las leyes de Avogadro.
La tercera ley de Avogadro
Con el valor del número de Avogadro y su relación con número de átomos o moléculas, ya podemos hacer cierto tipo de cálculos que antes no eran posibles con nuestras herramientas, por ejemplo, calcular el número de Loschmidt, pues este será igual al número de átomos sobre un volumen de 1 metro cúbico.
La ecuación anterior es la definición moderna del número de Avogadro, la cual al derivase de la hipótesis de Avogadro con la ley de Avogadro bien puede denominarse la tercera ley de Avogadro, pues ya sabemos que darle el nombre a una ecuación, no implica que esa persona la hubiera formulado directamente o en su forma moderna. La tercera ley de Avogadro nos permite resolver un escenario común y es el de contar el número de átomos en una masa de sustancia pura. Lo anterior implica que el cociente de masa del elemento a la masa del compuesto puede expresarse en términos de subíndices y masas molares, que son constantes para una sustancia dada, lo cual es la justificación última de la ley de Proust de Proporciones Definidas.
Existen otras modificaciones a la ley de proporciones definidas de Proust como:
Donde Na (at,T) es el número de átomos total, si(T) el subíndice total.
Ejemplo. Cuantos moles hay en 1.25 x 1015 moléculas de NH3.
Ejemplo. Cuantas moléculas hay en 79.68 mol de NaF.
Ejemplo. Cuantas moléculas hay en 0.75 moles de CO2.
Ejemplo. Cuantas moléculas hay en 0.95 moles de sulfuro de sodio.
Ejemplo. Cuantas moléculas hay en 0.03 moles de H2.
Ejemplo. Cuantas moléculas hay en 0.5 moles de oxígeno y CO2.
Ejemplo. Cuantas moléculas hay en 0.25 moles de metano CH4.
Ejemplo. Cuantas moléculas hay en 10 moles de agua y metano.
Ejemplo. Cuantas moléculas hay en 1.5 moles de CO
Ejemplo. Cuantas moléculas hay en 1.75 moles de NH4OH.
Ejemplo. Cuantas moléculas hay en 2 moles de agua, NH3
Ejemplo. Cuantas moléculas hay en 3 moles de NH3 y CO2.
Ejemplo. Cuantas moléculas hay en 3.6 moles de Al(OH)3 hidróxido de alumino.
Ejemplo. Cuantas moléculas hay en 4 moles de CaO, CO2, nitrígeno líquido y H2SO4.
Ejemplo. Cuantas moléculas hay en 5.4 mol de H2SO4.
Ejemplo. Cuantas moléculas hay en 5 moles de CO2.
Ejemplo. Cuantas moléculas hay en 54 moles de H2O.
Ejemplo. Cuantas moléculas hay en 6.0 moles de H2SO4 y CO2.
Ejemplo. Cuantas moléculas hay en 7.0 moles de H2SO4, agua y NH3.
Ejemplo. Cuantas moléculas hay en 8.3 mol de Ca3PO4.
Ejemplo. Cuantas moléculas hay en 8.0 moles de H2O y FeCl3.
Ejemplo. Cuantas moléculas hay en 9.0 moles de agua.
Ejemplo. Cuantas moléculas hay en 0.746 gramos de agua.
Ejemplo. Cuantas moléculas hay en 0.056 g de HCN.
Ejemplo. Cuantas moléculas hay en 10 g de H2O2.
Ejemplo. Cuantas moléculas hay en 100 g de decaoxido de tetrafosforo.
Ejemplo. Cuantas moléculas hay en 100 g de agua.
Ejemplo. Cuantas moléculas hay en 125 g de cloruro de hidrógeno.
Ejemplo. Cuantas moléculas hay en 18 g de agua.
Ejemplo. Cuantas moléculas de CO2 hay en 200 gramos de CO2.
Ejemplo. Cuantas moléculas hay en 20 g de decoxido de tetrafosforo
Ejemplo. Cuantas moléculas hay en 20 g de O2.
Ejemplo. Cuantas moléculas hay en 25 g de dióxido de carbono
Ejemplo. Cuantas moléculas hay en 25 g de HCl
Ejemplo. Cuantas moléculas hay en 25 g de hidrógeno.
Ejemplo. Cuantas moléculas existen en 272 g de ácido sulfúrico.
Ejemplo. Cuántas moléculas hay en 286 g de Cr2O3.
Ejemplo. Cuántas moléculas hay en 260 g de NH4OH.
Ejemplo. Cuantas moléculas hay en 30 gramos de trioxido de azufre SO3.
Ejemplo. Cuantas moléculas hay en 30 gramos de dióxido de carbono.
Ejemplo. Cuantas moléculas hay en 30 g de urea.
Ejemplo. Cuantas moléculas hay en 400 g de Na2SO4.
Ejemplo. Cuantas moléculas hay en 5.0 gramos de agua.
Ejemplo. Cuantas moléculas hay en 60 gramos de HCl.
Ejemplo. Cuantas moléculas hay en 64 g de O2.
Ejemplo. Cuantas moléculas y átomos hay en 6.31 moles de O2
Ejemplo. Cuantas moléculas hay en 60 gramos de H2O.
Ejemplo. Cuantas moléculas hay en 600 g de CaCO3.
Ejemplo. Cuantas moléculas hay en 8 gramos se sacarosa C12H22O11.
Ejemplo. Cuantas moléculas hay en 8 gramos de oxígeno.
Ejemplo. Cuantas moléculas hay en 8 g de metano CH4.
Ejemplo. Cuantas moléculas hay en 900 gramos de agua.
Ejemplo. Cuantas moléculas hay en 96 g de SO2.
Ejemplo. Cuantas moléculas hay en 9 gramos de agua.
Ejemplo. Calcular el número de moléculas existentes en 1.30 moles de KOH
Ejemplo. Calcular el número de moléculas de SO2 en 1.28 moles de SO2
Ejemplo. ¿Cuántas moléculas de agua se encuentran en 36 gramos de esta?
Ejemplo. ¿Cuántas moléculas de agua se encuentran en 500 ml de esta?
Ejemplo. ¿Cuántas moléculas de H2O están presentes en 4.00 moles de esta?
Ejemplo. Cuantos moles hay en 5.25 x 1020 átomos de Cu.
Ejemplo. Cuantos átomos hay en 12.7 mol de Ca.
Ejemplo. ¿Cuántas moléculas de agua se encuentran en 3.00 moles de esta?
Ejemplo. Calcular el número de átomos de H en 36 g de H2O. La masa molar del agua es 18 g/mol.
Ejemplo. Cuantos átomos hay en 0.025 moles de hierro
Ejemplo. Cuantos átomos hay en 0.350 mol de P4
Ejemplo. Cuantos átomos hay en 47.5 g de platino
Ejemplo. Cuantos átomos hay en 98.5 g de calcio
Ejemplo. Cuantos gramos de oxígeno hay en 1.052 g de glucosa
Ejemplo. Cuantos átomos hay de KCl en 0.1 mol
Ejemplo. Cuantos átomos hay en 0.1 mol de magnesio
Ejemplo. Cuantos átomos hay en 0.100 moles de CaCO3
Ejemplo. Cuantos átomos hay en 0.1 g de hierro
Ejemplo. Cuantos átomos hay en 0.20 g de bromo (Br)
Ejemplo. Cuantos átomos hay en 0.20 mg de cromo (Cr)
Ejemplo. Cuantos átomos hay en 0.50 gramos de aluminio
Ejemplo. Cuantos átomos hay en 0.60 mg de magnesio
Ejemplo. Cuantos átomos hay en 16.3 g de S.
Ejemplo. Cuantos átomos hay en 12 g de carbono.
Ejemplo. Cuantos átomos hay en 1.0 g de plata
Ejemplo. Cuantos átomos hay en 1 gramo de oxígeno
Ejemplo. Cuantos átomos hay en 2.0 g de potasio
Ejemplo. Cuantos átomos hay en 2.0 gramos de cobre
Ejemplo. Cuantos átomos hay en 10 g de oxígeno.
Ejemplo. Cuantos átomos hay en 100 g de oro.
Ejemplo. Cuantos átomos hay en 100 gramos de hidrógeno
Ejemplo. Cuantos átomos de helio hay en 100 kg
Ejemplo. Cuantos átomos hay en 10 gramos de hierro
Ejemplo. Cuantos átomos hay en 10 mg de cloro
Ejemplo. Cuantos átomos hay en 16.3 mg de cobre
Ejemplo. Cuantos átomos hay en 16.3 kg de silicio
Ejemplo. Cuantos átomos hay en 120 g de magnesio.
Ejemplo. Cuantos átomos hay en 15 g de hierro.
Ejemplo. Cuantos átomos hay en 100 g de carbono.
Ejemplo. Cuantos átomos hay en 12 g de fósforo.
Ejemplo. Cuantos átomos hay en 186 g de magnesio.
Ejemplo. Cuantos átomos hay en 10 g de calcio.
Ejemplo. Cuantos átomos hay en 28 g de hierro.
Ejemplo. Cuantos átomos hay en 224 g de azufre.
Ejemplo. Cuantos átomos hay en 240 g de carbono.
Ejemplo. Cuantos átomos hay en 20 g de boro.
Ejemplo. Cuantos átomos hay en 25 gramos de Al2(SO4)3
Ejemplo. Cuantos átomos hay en 25 kg de H2O
Ejemplo. Cuantos átomos hay en 250 g de hierro.
Ejemplo. Cuantos átomos hay en 20 g de calcio.
Ejemplo. Cuantos átomos hay en 24 g de carbono.
Ejemplo. Cuantos átomos hay en 23 g de sodio.
Ejemplo. Cuantos átomos hay en 20 g de aluminio.
Ejemplo. Cuantos átomos hay en 300 g de arsénico.
Ejemplo. Cuantos átomos hay en 25 g de H2O2.
Ejemplo. Cuantos átomos hay en 25 g de H2SO3.
Ejemplo. Cuantos átomos hay en 3.52 g de magnesio.
Ejemplo. Cuantos átomos hay en 326 g de bromo.
Ejemplo. Cuantos átomos hay en 30 g de hierro.
Ejemplo. Cuantos átomos hay en 30 g de mercurio.
Ejemplo. Cuantos átomos hay en 32 g de azufre.
Ejemplo. Cuantos átomos hay en 3.14 g de cobre.
Ejemplo. Cuantos átomos hay en 3.5 g de nitrógeno.
Ejemplo. Cuantos átomos hay en 47.5 g de platino.
Ejemplo. Cuantos átomos hay en 3.5 g de sodio.
Ejemplo. Cuantos átomos hay en 3.5 kg de estaño.
Ejemplo. Cuantos átomos hay en 40 g de calcio.
Ejemplo. Cuantos átomos hay en 46 g de sodio.
Ejemplo. Cuantos átomos hay en 40 g de nitrógeno
Ejemplo. Cuantos átomos hay en 45 g de hierro
Ejemplo. Cuantos átomos hay en 4 gramos de helio.
Ejemplo. Cuantos átomos hay en 4 gramos de carbono.
Ejemplo. Cuantos átomos hay en 4.0 g de irido.
Ejemplo. Cuantos átomos hay en 5.0 gramos de oxígeno.
Ejemplo. Cuantos átomos hay en 50 g de oro.
Ejemplo. Cuantos átomos hay en 50 g de helio.
Ejemplo. Cuantos átomos hay en 50 g de aluminio
Ejemplo. Cuantos átomos hay en 50 g calcio
Ejemplo. Cuantos átomos de magnesio hay en 500 g
Ejemplo. Cuantos átomos de mendelevio hay en 500 μg
Ejemplo. Cuantos átomos hay en 5 g magnesio
Ejemplo. Cuantos átomos hay en 5 kg manganeso
Ejemplo. Cuantos átomos hay en 5 moles de hierro
Ejemplo. Cuantos átomos hay en 5 gramos de hierro
Ejemplo. Cuantos átomos hay en 5 miligramos de paladio
Ejemplo. Cuantos átomos hay en 5.0 gramos de oro
Ejemplo. Cuantos átomos hay en 6.0 g de carbono.
Ejemplo. Cuantos átomos hay en 60 g de calcio.
Ejemplo. Cuantos átomos hay en 6.0 gramos de azufre.
Ejemplo. Cuantos átomos hay en 6.0 moles de CO2
Ejemplo. Cuantos átomos hay en 6.0 moles de manganeso
Ejemplo. Cuantos átomos hay en 6.0 mmoles de hierro
Ejemplo. Cuantos moles hay en 6.0 gramos de oro
Ejemplo. Cuantos átomos hay en 6.0 mmol de polonio
Ejemplo. Cuantos átomos hay en 64 g de azufre.
Ejemplo. Cuantos átomos hay en 64 g de selenio.
Ejemplo. Cuantos átomos hay en 64 g de oxígeno.
Ejemplo. Cuantos átomos hay en 65 g de sodio.
Ejemplo. Cuantos átomos hay en 64 g de CH4.
Ejemplo. Cuantos átomos totales hay en 65 g de HBr
Ejemplo. Cuantos átomos hay en 7.4 g de silicio.
Ejemplo. Cuantos átomos hay en 70 g de nitrógeno.
Ejemplo. Cuantos átomos hay en 70 g de cloro.
Ejemplo. Cuantos átomos hay en 700 mg de hidrógeno.
Ejemplo. Cuantos átomos hay en 7 moles de Fe
Ejemplo. Cuantos átomos hay en 7 mmol de Na
Ejemplo. Cuantos átomos hay en 72 g de cromo.
Ejemplo. Cuantos átomos hay en 7.0 g de fósforo.
Ejemplo. Cuantos átomos hay en 710 g de cloro.
Ejemplo. Cuantos átomos hay en 7.95 g de cloro.
Ejemplo. Cuantos átomos hay en 800 g de plomo
Ejemplo. Cuantos átomos hay en 800 g de estaño
Ejemplo. Cuantos átomos hay en 800 g de oxígeno
Ejemplo. Cuantos átomos existen en 80 g de calcio
Ejemplo. Cuantos átomos hay en 8.4 g de silicio
Ejemplo. Cuantos átomos hay en 8.4 mg de selenio
Ejemplo. Cuantos átomos hay en 8 g de hierro
Ejemplo. Cuantos átomos hay en 8 g de azufre
Ejemplo. Cuantos átomos existen en 80 g de oro
Ejemplo. Cuantos átomos existen en 80 kg de osmio
Ejemplo. Cuantos átomos hay en 90 g de agua
Ejemplo. Cuantos gramos de carbono están presentes en 440 gramos de gas propano
Ejemplo. Cuantos átomos hay en 750 libras de KMnO4.
Ejemplo. Cuantos gramos de oxígeno hay en 800 gramos de carbonato de calcio
Ejemplo. Cuantos gramos de carbono hay en 34 gramos de propano
Ejemplo. Cuantos gramos de oxígeno hay en 37 g de Ca(OH)2
Ejemplo. Cuantos gramos de hidrogeno hay en 0.254 g de propano
Ejemplo. Cuantos gramos de nitrógeno hay en 20.42 g de riboflavina.
Ejemplo. Cuantos gramos de oxígeno hay en 15.8 moles de ácido sulfúrico.
Ejemplo. Cuantos gramos de hidrogeno hay en 2.12 g de naftaleno.
Ejemplo. Cuantos gramos de carbono hay en 3 moles C6H6.
Ejemplo. Cuantos gramos de carbono hay en 25 gramos de CO2
Ejemplo. Cuantos gramos de nitrógeno hay en 28 g de Cu(NO3)2
Ejemplo. Cuantos átomos de fósforo hay en 0.25 moles de P2O5
Ejemplo. Cuantos átomos de nitrógeno hay en 0.25 moles de nitrato de calcio
Ejemplo. Cuantos átomos de hidrógeno hay en 90 g de agua
Matamala y González
Ejemplo 1.8.2. ¿Cuántos átomos hay presentes en 7 g de hierro?
Ejemplo 1.9.1. ¿Cuántas moléculas y cuantos moles hay en 0.007 gramos de nitrógeno molecular N2?
Ejercicio 1.4. Demuestre que en 3.5 g de N hay el mismo número de átomos que en 4 g de O.
Ejercicio 1.5. ¿Cuantos átomos hay en 0.8 g de Ca?
Ejercicio 1.11. Seleccione la respuesta correcta. 0,2 mol de Cu es lo mismo que: (a) 0,2 mol de O (b) 318 g de Cu (c) 3 x 1024 átomos de Cu (d) 1 x 1023 átomos de Cu.
Ejercicio 1.12b. El aluminio tiene una masa atómica de 27 uma. ¿Cuántos moles y cuantos átomos hay en 8.1 g de aluminio?
Ejercicio 1.14. ¿Cuál de las siguientes masas es mayor? (a) 48 g de Zn, (b) 4 moles de N, (c) 0.1 moles de Bi, (d) 2 x 1023 átomos de Cd.
Ejercicio 1.24a. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos moles de hidrógeno hay en cada mol del ácido?
Ejercicio 1.24b. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de hidrógeno hay en cada mol del ácido?
Ejercicio 1.24d. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos mol de hidrógeno hay en cada mol del oxígeno?
Ejercicio 1.24e. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de azufre hay por cada mol de O?
Ejercicio 1.24f. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de azufre hay por cada gramo de hidrógeno?
Ejercicio 1.24g. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de H por cada 9.8 gramos de H2SO4?
Ejercicio 1.24h. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de azufre por cada átomo de oxígeno?
Ejercicio 1.24i. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos átomos de oxígeno por mol de H2SO4?
Ejercicio 1.24j. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos mol de O por gramo de H2SO4?
Ejercicio 1.24k. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de H por gramo de H2SO4?
Química de Chang 10
Problema 3.9c-d. ¿Qué tiene el mol en común con el par, la docena y el gross? ¿Qué representa el número de Avogadro?
Problema 3.13. ¿Cuántos átomos hay en 5.10 moles de azufre (S)?
Problema 3.14. ¿Cuántos moles de cobalto (Co) se encuentran en 6.00 x 109 (6 mil millones) átomos de Co?
Práctica 3.4. Calcular el número de átomos en 0.551 g de potasio (K).
Ejemplo 3.6. El metano (CH4) es un componente principal del gas natural. Cuantas moles de metano están presentes en 6.07 g de CH4?
Práctica 3.7. ¿Cuántos átomos de H hay en 72.5 g de isopropanol (alcohol isopropílico), C3H8O?
Ejemplo 3.10. La calcopirita (CuFeS2) es un mineral principal de cobre. Calcule el número de kilogramos de Cu en 3.71 x 103 kg de calcopirita.
Práctica 3.10. Calcule el número de gramos de Al en 371 g de Al2O3.
Problema 3.19. ¿Cuál es la masa en gramos de 1.00 X 1012 átomos de plomo (Pb)?
Problema 3.20. ¿Cuántos átomos hay en 3.14 g de cobre (Cu)?
Problema 3.21. ¿Cuál de los siguientes tiene más átomos: 1.10 g de átomos de hidrógeno o 14.7 g de átomos de cromo?
Problema 3.22. ¿Cuál de los siguientes tiene mayor masa? 2 átomos de plomo o 5.1 x 10-23 moles de helio.
Problema 3.26. ¿Cuántas moléculas de etano (C2H6) hay en 0.334 g de C2H6?
Problema 3.27. Calcule el número de átomos de C, H y O en 1.50 g de azúcar glucosa C6H12O6.
Problema 3.28. La urea [(NH2)2CO] se usa como fertilizante y muchas otras cosas. Calcule el número de átomos de N, C, O y H en 1.68 x 104 g de urea.
Problema 3.30. La densidad del agua es de 1.00 g/mL a 48 °C. ¿Cuántas moléculas de agua hay en 2.56 mL de agua a esta temperatura?
Problema 3.45. La fórmula del óxido puede ser representada por Fe2O3. Cuantos moles de Fe están presentes en 24.6 g del compuesto?
Problema 3.46. ¿Cuantos gramos de azufre (S) se necesitan para reaccionar completamente con 246 g de mercurio (Hg) y formar HgS?
Problema 3.47. Calcular la masa en gramos de yodo (I2) que reaccionará completamente con 20.4 g de aluminio (Al) para formar yoduro de aluminio (AlI3)
Química la ciencia central 13
Práctica 3.7.2. Sin usar una calculadora, organice estas muestras en orden creciente de átomos de O: 1 mol H2O, 1 mol CO2, 3 x 1023 moléculas de O3.
Muestra 3.8. Calcular el número de átomos de H en 0.350 mol de C6H12O6.
Práctica 3.8.1a. Cuántos átomos de azufre hay en 0.45 mol de BaSO4.
Práctica 3.8.1b. ¿Cuántos átomos de azufre hay en 1.10 mol de sulfuro de aluminio?
Práctica 3.8.2a. ¿Cuántos átomos de oxígeno hay en 0.25 mol de Ca(NO3)2?
Práctica 3.8.2b. ¿Cuántos átomos de oxígeno hay en 1.50 mol de carbonato de sodio?
Muestra 3.12a. ¿Cuántas moléculas de glucosa hay en 5.23 g de C6H12O6?
Muestra 3.12a. ¿Cuántos átomos de oxígeno hay en 5.23 g de C6H12O6?
Práctica 3.12.1. ¿Cuántos átomos de cloro hay en 12.2 g de CCl4? (a) 4.77 x 1022. (b) 7.34 x 1024. (c) 1.91 x 1023. (d) 2.07 x 1023.
Práctica 3.12.2a. ¿Cuántas moléculas de ácido nítrico hay en 4.20 g de HNO3?
Práctica 3.12.2b. ¿Cuántos átomos de O hay en 4.20 g de HNO3?
Ejercicio 3.41a. Una muestra de glucosa, C6H12O6, contiene 1.250x1021 átomos de carbono. (a) ¿Cuántos átomos de hidrógeno contiene?
Ejercicio 3.41b. Una muestra de glucosa, C6H12O6, contiene 1.250x1021 átomos de carbono. (b) ¿Cuántas moléculas de glucosa contiene?
Ejercicio 3.41c. Una muestra de glucosa, C6H12O6, contiene 1.250x1021 átomos de carbono. (c) ¿Cuántos moles de glucosa contiene?
Ejercicio 3.41c. Una muestra de glucosa, C6H12O6, contiene 1.250x1021 átomos de carbono. (d) ¿Cuántos gramos de glucosa contiene? (d) 0.06228 g.
19.27 Calculando la masa de una molécula o un átomo
Con las ecuaciones anteriores es posible poder determinar las masas absolutas de partículas como átomos o moléculas, claro está, asumiendo a priori que la masa molar de un elemento mide partículas con estructura y masa igual, lo cual como veremos mas adelante no es necesariamente cierto.
Masa absoluta de una partícula mp(j) sea esta átomo o molécula en términos de la masa molar de dicha partícula (M(j)) y el número de Avogadro (NA).
Matamala y González
Ejemplo 1.8.1. ¿Cuál es la masa de un átomo de hidrógeno?
Ejercicio 1.12. El aluminio tiene una masa molar de 27 g/mol. ¿cuál es la masa en gramos de un solo átomo de aluminio?
Química de Chang 10
Problema 3.10. ¿Cuál es la masa molar de un átomo? ¿Cuáles son las unidades de masa molar más utilizadas?
Práctica 3.5. ¿Cuál es la masa molecular del metanol (CH4O)? usar los pesos atómicos a cuatro cifras significativas.
Problema 3.17a. ¿Cuál es la masa en gramos de un solo átomo de mercurio Hg?
Problema 3.17b. ¿Cuál es la masa en gramos de un solo átomo de neón Ne?
Problema 3.18a. ¿Cuál es la masa en gramos de un solo átomo de arsénico As?
Problema 3.18b. ¿Cuál es la masa en gramos de un solo átomo de níquel Ni?
19.29 Volumen molar de un sólido
El volumen molar y el volumen de una sola partícula también pueden calcularse para sólidos, pero a diferencia de los gases, sus valores no son constantes.
Donde Vm(j) es el volumen molar de un sólido no constante y VA(j) es el volumen atómico.
Matamala y González
Ejercicio 1.13a. El Bi tiene una masa molar de 209 g/mol y una densidad de 9,8 g/cc. ¿Qué volumen ocupa un mol de bismuto?
Ejercicio 1.13b. El Bi tiene una masa molar de 209 g/mol y una densidad de 9,8 g/cc. ¿Cuál será el volumen promedio que ocupa un solo átomo de bismuto?
Ejercicio 1.13c. Suponiendo que el átomo de bismuto tiene forma esférica, ¿Cuál será su radio en cm y en Å si su volumen atómico promedio es 3.54 x 10-23 cm3?
20. Historia de la teoría cinética de gases
|| REGRESAR AL INDICE ||
Deja de decirle a Dios que hacer con sus dados.
La teoría cinética de los gases es un modelo simple e históricamente significativo del comportamiento termodinámico de los gases, con el que se establecieron muchos conceptos principales de termodinámica y que dio indicios de que la hipótesis atómica era más flexible que la teoría de equivalentes. El modelo describe un gas como una gran cantidad de partículas submicroscópicas idénticas (átomos o moléculas), todas las cuales están en movimiento aleatorio, rápido y constante. Se supone que su tamaño es mucho menor que la distancia promedio entre las partículas. Las partículas sufren colisiones elásticas aleatorias entre ellas y con las paredes circundantes del contenedor. La versión básica del modelo describe el gas ideal y no considera otras interacciones entre las partículas.
La teoría cinética de los gases explica las propiedades macroscópicas de los gases, como el volumen, la presión y la temperatura, así como las propiedades de transporte como la viscosidad, la conductividad térmica y la difusividad de la masa. El modelo también tiene en cuenta fenómenos relacionados, como el movimiento browniano.
Esta es una teoría importante que generalmente se cubre desde el principio en los planes de estudios científicos y de ingeniería. Nos permite relacionar propiedades observables macroscópicas medibles, como la presión y la temperatura, con el comportamiento microscópico del medio gaseoso asumiendo que los átomos y las moléculas son cosas reales.
20.1 Presupuestos
Al igual que toda teoría deductiva, las matemáticas se fundamentan en una serie de presupuestos básicos, a saber:
1- El gas consiste en partículas muy pequeñas conocidas como moléculas o átomos en gases de los gases nobles. Esta pequeñez de su tamaño es tal, que el volumen total de las moléculas de gas individuales sumadas es insignificante en comparación con el volumen total. Esto es equivalente a afirmar que la distancia promedio que separa las partículas de gas es grande en comparación con su tamaño.
2- Estas partículas tienen la misma masa.
3- El número de moléculas es tan grande que se puede aplicar un tratamiento estadístico.
4- Las partículas que se mueven rápidamente chocan constantemente entre sí y con las paredes del contenedor. Las colisiones son elásticas sin atracciones o repulsiones debidas a la naturaleza química de la sustancia. Esto significa que las moléculas se consideran de forma perfectamente esférica y de naturaleza elástica.
5- Excepto durante las colisiones, las interacciones entre las moléculas son insignificantes. (Es decir, no ejercen fuerzas entre sí).
20.2 Consecuencias de los presupuestos
1- Los efectos relativistas son insignificantes.
2- Los efectos de la mecánica cuántica son insignificantes. Esto significa que la distancia entre partículas es mucho mayor que la longitud de onda térmica de Broglie y las moléculas se tratan como objetos clásicos.
3- Debido a los dos anteriores, su dinámica se puede tratar de forma clásica. Esto significa que las ecuaciones de movimiento de las moléculas son reversibles en el tiempo.
4- La energía cinética promedio de las partículas de gas depende solo de la temperatura absoluta del sistema. La teoría cinética tiene su propia definición de temperatura, no idéntica a la definición termodinámica.
5- El tiempo transcurrido de una colisión entre una molécula y la pared del recipiente es insignificante en comparación con el tiempo entre colisiones sucesivas.
6- Hay una fuerza gravitacional insignificante sobre las moléculas.
Desarrollos más modernos relajan estos supuestos y se basan en la ecuación de Boltzmann. Sin embargo, nuestros intereses en la teoría cinética no son tan profundos. Existen muchas formas de ahondar en sus matemáticas, pero solo veremos la que traen algunos libros de texto y sus consecuencias.
Figura 20.1. Modelo gráfico de la teoría cinética de gases. Las partículas representan átomos y moléculas que se mueven al azar en el vacío chocando con las paredes y entre ellas mismas de manera completamente elástica.
20.3 Historia de la teoría cinética
Aproximadamente en el 50 a. C., el filósofo romano Lucrecio propuso que los cuerpos macroscópicos aparentemente estáticos se componían en una pequeña escala de átomos que se movían rápidamente, todos rebotando entre sí (James Clerk Maxwell, 1867), la pregunta es ¿por qué no estamos hablando de Demócrito o Leucipo? Lucrecio hipotetizó algo más allá de la existencia de átomos, el punto con la teoría cinética es el estudio del movimiento de dichos átomos, en otras palabras, mientras que la teoría atómica estudia al átomo, la teoría cinético molecular estudia cómo es que se mueven átomos y moléculas. Este punto de vista atomista rara vez se consideró en los siglos posteriores, cuando las ideas aristotélicas eran dominantes.
👉 Constitución de un gas
En 1738 Daniel Bernoulli publicó Hydrodynamica, que sentó las bases para la teoría cinética de los gases. En este trabajo, Bernoulli postuló el argumento de que los gases consisten en un gran número de moléculas que se mueven en todas direcciones, que su impacto sobre una superficie provoca la presión del gas y que su energía cinética media determina la temperatura del gas. La teoría no fue aceptada de inmediato, en parte porque aún no se había establecido la conservación de la energía, y no era obvio para los físicos cómo las colisiones entre moléculas podían ser perfectamente elásticas (Ponomarev & Kurchatov, 1993).
Figura 20.2. Daniel Bernoulli (Groninga, 29 de enerojul./ 8 de febrero de 1700greg. - Basilea, 17 de marzo de 1782) fue un matemático, estadístico, físico y médico suizo. Destacó no solo en matemática pura, sino también en las llamadas aplicadas, principalmente estadística y probabilidad. Hizo importantes contribuciones en hidrodinámica y elasticidad.
En 1856, August Krönig (probablemente después de leer un artículo de Waterston) creó un modelo cinético de gas simple, que solo consideraba el movimiento de traslación de las partículas (Krönig, 1856).
En 1857, Rudolf Clausius desarrolló una versión similar, pero más sofisticada, de la teoría, que incluía movimientos moleculares de traslación y, contrariamente a Krönig, también rotacionales y vibracionales. En este mismo trabajo introdujo el concepto de camino libre medio de una partícula (Clausius, 1857).
👉 Velocidades moleculares
En 1859, después de leer un artículo sobre la difusión de moléculas de Clausius, el físico escocés James Clerk Maxwell formuló la distribución de Maxwell de velocidades moleculares, que dio la proporción de moléculas que tienen una cierta velocidad en un rango específico (J C Maxwell, 1860; James Clerk Maxwell, 1860). Esta fue la primera ley estadística de la física (Mahon, 2004). Maxwell también dio el primer argumento mecánico de que las colisiones moleculares implican una igualación de temperaturas y, por lo tanto, una tendencia hacia el equilibrio (Gyenis, 2017). En su artículo de 1873 de trece páginas llamado 'Moléculas', Maxwell afirma: "Se nos dice que un 'átomo' es un punto material, invertido y rodeado por 'fuerzas potenciales' y que cuando las 'moléculas voladoras' chocan contra un cuerpo sólido en constante sucesión causa lo que se llama presión de aire y otros gases " (Maddox, 2002).
En 1871, Ludwig Boltzmann generalizó el logro de Maxwell y formuló la distribución de Maxwell-Boltzmann. También él estableció por primera vez la conexión logarítmica entre entropía y probabilidad. Boltzmann dedicó un gran esfuerzo en sus últimos años a defender sus teorías (Cercignani, 2000). No se llevaba bien con algunos de sus colegas en Viena, en particular con Ernst Mach, que se convirtió en profesor de filosofía e historia de las ciencias en 1895. Ese mismo año, Georg Helm y Wilhelm Ostwald presentaron su posición sobre la energía en una reunión en Lübeck. Vieron la energía, y no la materia, como el componente principal del universo. La posición de Boltzmann triunfó entre otros físicos que apoyaron sus teorías atómicas en el debate (Planck, 1896).
Figura 20.3. Rudolf Julius Emmanuel Clausius (Koszalin, Prusia, 2 de enero de 1822- Bonn, 24 de agosto de 1888), fue un físico y matemático alemán, considerado uno de los fundadores centrales de la ciencia de la termodinámica. En su nueva formulación del principio de Sadi Carnot, conocido como ciclo de Carnot, además propuso la teoría del calor sobre una base más sólida y más verdadera. En su trabajo más importante sobre la teoría mecánica del calor, publicado en 1850, estableció por primera vez las ideas básicas de la segunda ley de la termodinámica. En 1865 introdujo el concepto de entropía.
Figura 20.4. James Clerk Maxwell FRS FRSE (Reino Unido: 13 de junio de 1831-5 de noviembre de 1879) fue un científico escocés especializado en el campo de la física matemática. Su mayor logro fue la formulación de la teoría clásica de la radiación electromagnética, que unificó por primera vez la electricidad, el magnetismo y la luz como manifestaciones distintas de un mismo fenómeno. Las ecuaciones de Maxwell, formuladas para el electromagnetismo, han sido ampliamente consideradas la “segunda gran unificación de la física”, siendo la primera aquella realizada por Isaac Newton.
👉 La realidad del átomo y el anti-atomismo
La teoría cinética de los gases de Boltzmann parecía presuponer la realidad de los átomos y las moléculas, pero casi todos los filósofos alemanes y muchos científicos como Ernst Mach y el químico físico Wilhelm Ostwald no creían en su existencia. Durante la década de 1890, Boltzmann intentó formular una posición de compromiso que permitiría tanto a los atomistas como a los anti-atomistas hacer física sin discutir sobre los átomos. Su solución fue utilizar la teoría de Hertz de que los átomos eran modelos o imágenes mentales, entidades semejantes a números que solo existían en la cabeza del científico, pero que, sin ellas, no se puede hacer ciencia. Los atomistas podían pensar que las imágenes eran los átomos reales, mientras que los anti-atomistas podían pensar que las imágenes representaban un modelo útil pero irreal, pero esto no satisfizo completamente a ninguno de los grupos. Además, Ostwald y muchos defensores de la "termodinámica pura" se esforzaban por refutar la teoría cinética de los gases y la mecánica estadística debido a las suposiciones de Boltzmann sobre átomos y moléculas y especialmente a la interpretación estadística de la segunda ley de la termodinámica.
Figura 20.5. Ludwig Eduard Boltzmann (Viena, 20 de febrero de 1844-Duino, 5 de septiembre de 1906) fue un físico austríaco pionero de la mecánica estadística, a quien debe su nombre la llamada constante de Boltzmann, concepto fundamental de la termodinámica, y que halló la expresión matemática de la entropía desde el punto de vista de la probabilidad (la relación entre estados macroscópicos y microscópicos). Se suicidó en Trieste en 1906. Aunque las causas no están claras, se baraja el poco reconocimiento académico a sus ideas como una de ellas. Al poco tiempo de su muerte, llegaron las pruebas de que sus ideas eran ciertas y fueron aceptadas de forma generalizada, lo que zanjó definitivamente la disputa entre los atomistas y sus opositores los equivalentistas.
👉 Filosofía y experimentos sobre la realidad del átomo
Hacia el cambio de siglo, la ciencia de Boltzmann se vio amenazada por otra objeción filosófica. Algunos físicos, incluido el estudiante de Mach, Gustav Jaumann, interpretaron que todo el comportamiento electromagnético es continuo, como si no hubiera átomos ni moléculas, y de la misma manera como si todo el comportamiento físico fuera en última instancia electromagnético. Este movimiento alrededor de 1900 deprimió profundamente a Boltzmann ya que podría significar el fin de su teoría cinética y la interpretación estadística de la segunda ley de la termodinámica.
Después de la renuncia de Mach en Viena en 1901, Boltzmann regresó allí y decidió convertirse él mismo en filósofo para refutar las objeciones filosóficas a su física, pero pronto se desanimó nuevamente. En 1904, en una conferencia de física en St. Louis, la mayoría de los físicos parecían rechazar los átomos y ni siquiera fue invitado a la sección de física. Más bien, estaba atrapado en una sección llamada "matemáticas aplicadas", atacó violentamente la filosofía, especialmente sobre bases supuestamente darwinianas, pero en realidad en términos de la teoría de Lamarck de la herencia de las características adquiridas de que la gente heredaba la mala filosofía del pasado y que era difícil para que los científicos superen tal herencia.
En 1905, Boltzmann mantuvo una extensa correspondencia con el filósofo austro-alemán Franz Brentano con la esperanza de obtener un mejor dominio de la filosofía, aparentemente, para poder refutar mejor su relevancia en la ciencia, pero también se desanimó con este enfoque.
En 1906, el deterioro de la condición mental de Boltzmann lo obligó a renunciar a su cargo y sus síntomas indican que experimentó lo que hoy sería diagnosticado como trastorno bipolar (Cercignani, 2000). Cuatro meses después murió por suicidio el 5 de septiembre de 1906, ahorcándose mientras estaba de vacaciones con su esposa e hija en Duino, cerca de Trieste (entonces Austria).
Irónicamente, la realidad de la existencia del átomo estaba solo a unos 4 años de ser aceptada por la comunidad científica gracias al trabajo de Jean Perrin (Bigg, 2008; Perrin, 1901, 1909, 1911, 1913).
21. Modelo matemático de la teoría cinética de gases
|| REGRESAR AL INDICE ||
21.1 La constante de Boltzman
La constante de Boltzmann (kB) es el factor de proporcionalidad que relaciona la energía cinética relativa promedio de las partículas en un gas con la temperatura termodinámica del gas, y es igual a:
Definición de la constante de Boltzmann
Ocurre en las definiciones de kelvin y la constante de gas, y en la ley de Planck de la radiación de cuerpo negro y la fórmula de entropía de Boltzmann. La constante de Boltzmann tiene dimensiones de energía divididas por temperatura, lo mismo que la entropía. Lleva el nombre del científico austriaco Ludwig Boltzmann. Como parte de la redefinición de las unidades base del SI de 2019, la constante de Boltzmann es una de las siete "constantes universales" a las que se les han dado definiciones exactas. Se utilizan en varias combinaciones para definir las siete unidades básicas del SI. La constante de Boltzmann se define como exactamente 1.380649 x 10−23 J K−1 (Stock, Davis, de Mirandés, & Milton, 2019).
21.3 Energía cinética de un gas y temperatura
Uno de los aspectos más importantes de la teoría cinética es que nos permite describir a los gases en términos de una nueva variable, la energía. Recordemos que la energía E se define mecánicamente, como la capacidad de realizar un trabajo mecánico W, y mecánicamente es la fuerza empleada F para mover a un objeto a una distancia determinada ∆x en la fórmula E = W = F ∆x.
Promedio del cuadrado de la velocidad promedio de la partícula de un gas en términos de la masa y temperatura del sistema.
Según la teoría cinética molecular, la presión del gas P es el resultado de colisiones entre las moléculas y las paredes de su contenedor. Depende de la frecuencia de la colisión por unidad de área y de cuán "duras" son las moléculas que golpean la pared. La teoría también proporciona una interpretación molecular de la temperatura. En la demostración anterior la temperatura absoluta de un gas T es una medida de la energía cinética promedio de las moléculas Ēk. En otras palabras, la temperatura absoluta es una indicación del movimiento aleatorio de las moléculas: cuanto mayor es la temperatura, más enérgicas son las moléculas. Debido a que está relacionado con la temperatura de la muestra de gas, el movimiento molecular aleatorio a veces se denomina movimiento térmico.
21.5 Las leyes de los gases y la energía cinética
A pesar de que la teoría cinético-molecular de los gases se basa en un principio relativamente simple, los detalles matemáticos son muy complejos. Sin embargo, bajo una base cualitativa, es posible utilizar la teoría para describir las propiedades generales de las sustancias en el estado gaseoso. Los siguientes ejemplos ilustran su rango de utilidad.
👉 Compresibilidad de los gases
La gran compresibilidad de los gases se explica en términos del primer principio de la teoría cinético-molecular, las moléculas en la fase gaseosa son partículas de volumen matemáticamente despreciable, separadas por distancias de muchos órdenes de magnitud superiores a su propio volumen. Los gases pueden comprimirse porque las moléculas pueden disminuir grandemente las distancias que las separan sin que empiecen a generar interacciones moleculares entre sí.
👉 Ley de Boyle
La presión ejercida por un gas resulta del promedio de impacto de las moléculas por unidad de área por unidad de tiempo en las paredes del contenedor. La tasa de colisión es proporcional a la densidad de un gas “lo cual tienen sentido, ya que al haber más partículas por unidad de volumen habrá más oportunidad para que estas choquen con la pared del contenedor viceversa”. Es por esto por lo que la presión es inversamente proporcional al volumen del gas, al haber más volumen las partículas pasaran más tiempo desplazándose en el espacio interno del gas que impactando en las paredes del contenedor.
👉 Ley de Charles
Debido a que la energía cinética promedio de las moléculas de un gas, son proporcionales a la temperatura, el incremento de la temperatura incrementa la energía cinética del gas. En consecuencia, las partículas colisionarán con las paredes del contenedor más frecuentemente y con mayor impacto si el gas es calentado. Esto tiene sentido, ya que la variable que se afecta al incrementar la temperatura es la velocidad de la partícula “ya que la masa permanece constante”, si la partícula se desplaza más rápido en el espacio vacío del contenedor, esto implica que chocara más veces por unidad de tiempo contra las paredes del contenedor. Si el contenedor posee un volumen expandible, al calentarlo, las partículas comenzaran a golpear las paredes con una fuerza determinada. La expansión solo se detiene cuando la presión interna es igualada por la presión externa del ambiente, o cuando el contenedor explota.
👉 Ley molar de Avogadro para volúmenes
Debido a que el volumen de la partícula es despreciable así mismo como su masa. Las variables de estado se ven afectadas solo por la cantidad de partículas, no por el tipo de partículas. De allí se explica porque, la ley de Avogadro establece que el volumen molar de cualquier gas es el mismo. En otras palabras, cualquier molécula tiene una masa y un volumen despreciable, y lo que importa es su cantidad. Y, por lo tanto, una misma cantidad de cualquier gas genera unas mismas variables de estado. Es por ello que, cualquier gas a la misma temperatura y a la misma presión tendrá un mismo volumen.
👉 Ley de Dalton
La ley de Dalton se explica de manera similar a la ley de Avogadro, nuevamente, lo único especifico de cada tipo de gas sería el volumen de esta y su masa, pero ambas son valores matemáticamente despreciables, es por ello que matemáticamente las moléculas de cualquier gas se describen del mismo modo, se ven como partículas iguales. Es por ello que adicionar un tipo de gas a otro tipo de gas es solo desde el punto de vista matemático, agregar más partículas al contenedor, que afectan del mismo modo “aditivo” a las variables de estado.
21.6 Velocidades moleculares
La teoría cinética de los gases nos permite investigar el movimiento molecular en más detalle. Supongamos que tenemos un gran número de moléculas de gas, digamos 1 mol que es la cantidad de sustancia estándar. Mientras que no se alteren las variables de estado y en especial la temperatura, la energía cinética y a su vez, la velocidad de las partículas del gas permanecerá sin cambiar. Como se espera, el movimiento de las partículas es completamente aleatorio e impredecible. En un instante dado, ¿cuántas moléculas se estarán moviendo a una velocidad dada? Para resolver esta respuesta Maxwell “si el mismo Maxwell de las ecuaciones ondulatorias” analizó a varios gases para determinar su comportamiento de velocidad promedio a diferentes temperaturas.
Primero analizó un mismo gas “nitrógeno” a diferentes temperaturas Figura 21.1-a. A una temperatura dada, tenemos una curva de distribución probabilística “campana Gaussiana” que nos dice la cantidad de partículas moviéndose a una velocidad determinada. El pico de la curva como en todas las curvas gaussianas representa el promedio de la velocidad, es decir la velocidad más probable, la cual la mayoría de las partículas tiene. Podemos notar que, a medida que la temperatura se incrementa, la velocidad promedio de las partículas aumenta, pero el promedio en si disminuye, en otras palabras, al aumentar la temperatura algunas partículas empiezan a moverse más rápido. También al aumentar el rango de movimiento, existe una mayor diversidad de velocidades posibles para las partículas, y, por lo tanto, el promedio deja de ser tan claro.
Figura 21.1. Curvas de velocidad promedio dependientes de la temperatura y la masa experimentales. (a) La distribución de velocidades para el gas nitrógeno a tres temperaturas diferentes. A temperaturas más altas, más moléculas se mueven más rápido. (b) La distribución de velocidades para tres gases diferentes a la misma temperatura. En promedio, las moléculas más ligeras se mueven más rápido que las moléculas más pesadas.
El segundo análisis se realizó con varios gases a temperatura constante Figura 40-b. Aquí se encontró que entre más ligera la molécula esta se mueve más rápido en promedio “aunque también, entre más ligera la molécula esta impacta más débilmente en la pared del contenedor, en otras palabras, la velocidad y la masa de la partícula se equilibran entre sí para que su efecto común sea exactamente el mismo sin importar el gas que estemas trabajando”.
Figura 21.2. Medición de la velocidad promedio. (a) Aparato para estudiar la distribución de la velocidad molecular a cierta temperatura. La bomba de vacío hace que las moléculas viajen de izquierda a derecha como se muestra. (b) La extensión del depósito en el detector proporciona el rango de velocidades moleculares, y la densidad del depósito es proporcional al número de moléculas que se mueven a diferentes velocidades.
Velocidad molecular promedio en términos de la temperatura y la masa molar. Para usar la ecuación recuerde que 1 atm L = 1 J y que 1 J = 1 kg m2 / s2.
Química de Chang
Ejemplo 5.16. Calcular la velocidad promedio de una partícula de nitrógeno molecular a 25 °C.
Práctica 5.16. Calcular la velocidad cuadrática promedio de una partícula de cloro molecular a 20 °C.
La Eq. 21.3 muestra la velocidad molecular promedio es directamente proporcional a la temperatura absoluta e inversamente proporcional a la masa molar de la sustancia, lo que concuerda con las mediciones dadas en la Figura 21.1 a y b. Esta ecuación tiene consecuencias interesantes, pues explica la razón de la composición de la atmósfera de los planetas: Los gases muy ligeros tendrán una velocidad promedio alta, que es mayor a la velocidad de escape mínima dada por la atracción gravitacional de planetas pequeños como la Tierra, de allí que los gases ligeros tienden a escaparse en promedio, con algunas moléculas de velocidades promedio bajas aun atrapados. En planetas supermasivos como Júpiter, la velocidad mínima de escape es colosal, lo que mantiene atrapados a la mayoría de las moléculas de los gases ligeros.
21.8 Difusión y efusión de un gas
Ahora discutiremos dos fenómenos basados en el movimiento gaseoso.
👉 Difusión de un gas
Una demostración del movimiento aleatorio de los gases es proveída por el fenómeno de la difusión. La difusión se describe como una mezcla gradual de las moléculas de un gas en otro debido a sus propiedades cinéticas “o sea que se mueven solos”. A pesar del hecho de que las velocidades moleculares son muy grandes, el proceso de difusión tarda relativamente bastante tiempo en completarse. Por ejemplo, cuando se abre un frasco de amoniaco, este le toma bastante tiempo para difundirse entre las moléculas del aire lo suficiente como para llegar a la nariz de quien la destapó y ser olfateado.
La respuesta está nuevamente en el movimiento aleatorio y en el hecho de que las moléculas experimentan numerosas colisiones que obstruyen su camino con bastante frecuencia. Otro fenómeno que podemos rescatar, es que la difusión de un gas ligero será mucho más rápida de la difusión de un gas pesado, debido a que los parámetros que afectan a la difusión son la masa de la partícula y su velocidad. Como vimos en temas anteriores, la velocidad promedio de las partículas depende de la masa molar del gas, gases con moléculas más pesadas se mueven más lento.
Ahora bien, debido a que la difusión de los gases se realiza en un mismo contenedor, asumimos como mínimo que ambos gases están a la misma temperatura. Desde aquí podemos construir la ley de Graham. Dividimos la velocidad promedio entre sí misma para dos gases de identidad diferente.
DEMOSTRACIÓN. Demostrar la ley de Graham con la ley de velocidad molecular promedio.
Ley de Graham
👉 Efusión de un gas
Mientras que la difusión de un gas es un proceso en el que un gas se mezcla con otro en un mismo contenedor. La efusión es un proceso en el que un gas bajo una presión escapa de un contenedor hacia otro pasando por una abertura pequeña. La ecuación de efusión es similar a la ley de Graham y se deriva de esta, pero en este caso asumiremos que los dos gases se mueven iguales distancias, y lo que cambia es el tiempo. Por lo que emplearemos la definición de velocidad promedio.
DEMOSTRACIÓN. Expresar la ley de Graham en términos del cociente de tiempo en lugar del cociente de velocidad molecular promedio.
Efusión de un gas
Química de Chang
Matamala y González
Ejercicio 7.23. A través de un recipiente poroso se escapan 220 ml de H2 en 15 minutos. ¿Qué volumen de O2 se escapará en ese tiempo?
Ejercicio 7.26. La velocidad de difusión del hidrógeno con respecto al helio es: (a) la mitad (b) 4 veces mayor (c) 2 veces mayor (d) 1.4 veces mayor.
22. Estequiometría de composición
|| REGRESAR AL INDICE ||
La estequiometría de composición hace referencia a situaciones en las que no necesitamos conocer los números estequiométricos de una ecuación química balanceada para resolver el cálculo. Recuerde que la información clave que emerge de una ecuación química son los números estequiométricos, sin embargo, en la estequiometría de composición podemos usar los subíndices de los elementos como un reemplazo para hacer los cálculos de masa. Dichos subíndices están relacionados con las cantidades de sustancia del elemento y el compuesto a través de la interpretación molecular de la ley de Proust.
22.1 Modificaciones a la ley de proporciones definidas
En secciones anteriores vimos algunas modificaciones a la ley de las proporciones definidas entre un solo elemento y el compuesto, sin embargo también podemos encontrarnos con situaciones que requieren analizar dos elementos en el mismo compuesto.
DEMOSTRACIÓN. Obtenga fórmulas para poder calcular las cantidades de sustancia y masas de dos elementos al interior de un mismo compuesto.
Química la ciencia central 13
22.5 Análisis de combustión
El análisis de combustión es un método utilizado tanto en química orgánica como en química analítica para determinar la composición elemental (más precisamente, la fórmula empírica) de un compuesto orgánico puro mediante la combustión de la muestra en condiciones en las que los productos de combustión resultantes pueden analizarse cuantitativamente. Una vez que se ha determinado el número de moles de cada producto de combustión, se puede calcular la fórmula empírica o una fórmula empírica parcial del compuesto original.
Las aplicaciones para el análisis de combustión involucran solo los elementos de carbono (C), hidrógeno (H), nitrógeno (N) y azufre (S) ya que la combustión de los materiales que los contienen convierten estos elementos en su forma oxidada (CO2, H2O, NO o NO2, y SO2) en condiciones de alta temperatura y alto oxígeno. Los intereses notables para estos elementos implican medir el nitrógeno total en los alimentos o piensos para determinar el porcentaje de proteína, medir el azufre en los productos derivados del petróleo o medir el carbono orgánico total (TOC) en el agua.
El método fue inventado por Joseph Louis Gay-Lussac. Justus von Liebig estudió el método mientras trabajaba con Gay-Lussac entre 1822 y 1824 y mejoró el método en los años siguientes a un nivel que podría usarse como procedimiento estándar para el análisis orgánico.
Las fórmulas empíricas y moleculares para compuestos que contienen solo carbono e hidrógeno (CaHb) o carbono, hidrógeno y oxígeno (CaHbOc) se pueden determinar con un proceso llamado análisis de combustión. Pese una muestra del compuesto a analizar y colóquelo en el aparato que se muestra en la imagen a continuación.
Figura 22.1. Aparato para análisis de combustión. Un compuesto que contiene carbono e hidrógeno (CaHb) o carbono, hidrógeno y oxígeno (CaHbOc) se quema por completo para formar H2O y CO2. Los productos se dibujan a través de dos tubos. El primer tubo absorbe agua y el segundo tubo absorbe dióxido de carbono.
Quema el compuesto completamente. Los únicos productos de la combustión de un compuesto que contiene solo carbono e hidrógeno (CaHb) o carbono, hidrógeno y oxígeno (CaHbOc) son dióxido de carbono y agua. El H2O y el CO2 se extraen a través de dos tubos. Un tubo contiene una sustancia que absorbe agua y el otro contiene una sustancia que absorbe dióxido de carbono. Pese cada uno de estos tubos antes y después de la combustión. El aumento de masa en el primer tubo es la masa de H2O que se formó en la combustión, y el aumento de masa para el segundo tubo es la masa de CO2 formada.
Para el modelo matemático del análisis de combustión debemos tener en cuenta que no necesitamos la ecuación química balanceada, lo que si vamos a necesitar es la ley de las proporciones definidas interpretada molecularmente.
|
En caso de que el ejercicio no proporcione la masa molar del reactivo Mr asuma una masa de 100 g/mol, los subíndices generados deberán dividirse por aquel de menor valor, con lo que obtendremos los subíndices de la fórmula empírica.
Chem team
Matamala y Gonzáles
Ejercicio 1.18. 3,01 x 1023 átomos del elemento A se combinan con 16 g de oxígeno. La fórmula del compuesto será: (a) AO, (b) A2O3, (c) A2O5, (d) AO2, (e) A2O.
Química de Chang 10
Química la ciencia central 13
22.13 Análisis de composición porcentual
DEMOSTRACION: Simplificar la ecuación de análisis de combustión masa a masa para poder hacer un análisis de composición porcentual.
Eq. 22.11.
Análisis de composición porcentual.
Ejemplo. Calcular la fórmula empírica de un hidrocarburo que tiene 85.63 % de carbono y 14.3% de hidrógeno.
Matamala y Gonzáles
Ejercicio 1.15 Un compuesto de hierro y oxígeno contiene 70% del metal, determinar la fórmula correcta: (a) FeO, (b) Fe3O4, (c) FeO2, (d) Fe2O3.
Ejercicio 1.16. Determinar la fórmula empírica de un compuesto de Na 42,08%, P 18,98 %, y O 39,03%. (a) NaPO2, (b) Na2PO3, (c) Na3PO4, (d) NaPO3, (e) Na4P2O7.
Ejercicio 1.25. Un óxido de manganeso contiene 63,2% de metal. Hallar su fórmula empírica.
Ejercicio 7.31. Un hidrocarburo contiene 82,76% de carbono y 17,24% de hidrógeno. Si su densidad a C.N. es de 2,59 g/L, hallar la fórmula molecular.
Química de Chang 10
Problema 3.49a. Cual es la fórmula empírica de 2.1 porciento de H, 65.3 por ciento de O, 32.6 porciento de S.
Problema 3.49b. Cual es la fórmula empírica de 20.2 porciento de Al, 79.8 por ciento de Cl.
Problema 3.50a. Cual es la fórmula empírica de 40.1 porciento de C, 6.6 por ciento de H y 53.3 por ciento de O.
Problema 3.50b. Cual es la fórmula empírica de 18.4 porciento de C, 21.5 por ciento de N y 60.1 por ciento de K.
Química la ciencia central 13
Ejercicio 3.45a. Dé la fórmula empírica: 0,0130 mol C; 0,0390 mol H; y 0.0065 mol O.
Ejercicio 3.45b. Dé la fórmula empírica de 11.66 g de hierro y 5.01 g de oxígeno.
Ejercicio 3.45c. Dé la fórmula empírica de 40.0% C, 6.7% H y 53.3% O en masa.
Ejercicio 3.46a. Determine la fórmula empírica de 0,104 mol K; 0,052 mol C; y 0,156 mol O.
Ejercicio 3.46b. Determine la fórmula empírica de 5,28 g de Sn y 3,37 g de F.
Ejercicio 3.46c. Determine la fórmula empírica de 87.5% de N y 12.5% de H en masa.
Ejercicio 3.47a. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 10.4% C; 27.8% S; y 61.7% Cl.
Ejercicio 3.47b. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 21,7% C; 9,6% O; y 68,7% F.
Ejercicio 3.47c. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 32,79% Na; 13,02% Al; y el resto F.
Ejercicio 3.48a. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 55,3% K; 14,6% P; y 30,1% O.
Ejercicio 3.48b. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 24,5% Na; 14,9% Si; y 60.6% F.
Ejercicio 3.48c. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 62,1% C; 5,21% H; 12,1% N; y el resto O.
Ejercicio 3.49. Un compuesto cuya fórmula empírica es XF3 consiste en 65% de F en masa. ¿Cuál es la masa atómica de X?
Ejercicio 3.50. El compuesto XCl4 contiene 75.0% de Cl en masa. ¿Cuál es el elemento X? R= Titanio.
22.15 Calculando el porcentaje de un elemento en un compuesto
DEMOSTRACION: Deducir la fórmula para calcular el porcentaje en masa de un elemento en un compuesto.
Fracción o riqueza de un elemento en un compuesto
La fracción de masas para un compuesto puro es constante, pues una representación moderna de la ley de las proporciones definidas, por tal razón, si la fracción de masas medida es diferente de la fracción de masas esperada, se concluye que la muestra no es pura.
Ejemplo. Hallar la composición centesimal del nitrato de bario Ba(NO3)2.
Ejemplo. Hallar la composición centesimal del ácido sulfúrico H2SO4.
Ejemplo. Hallar la composición centesimal del agua H2O.
Ejemplo. Hallar la composición centesimal del peróxido de hidrógeno H2O2.
Ejemplo. Hallar la composición centesimal del ácido nítrico HNO3.
Ejemplo. Hallar la composición centesimal del permanganato de potasio KMnO4.
Ejemplo. Hallar la composición centesimal del cloruro de potasio KCl.
Ejemplo. Hallar la composición centesimal del hipoclorito de potasio KClO.
Ejemplo. Hallar la composición centesimal del clorito de potasio KClO2.
Ejemplo. Hallar la composición centesimal del clorato de potasio KClO3.
Ejemplo. Hallar la composición centesimal del perclorato de potasio KClO4.
Ejemplo. Hallar la composición centesimal de la glucosa C6H12O6.
Ejemplo. Hallar la composición centesimal del carbonato de sodio Na2CO3.
Ejemplo. Hallar la composición centesimal del bicarbonato de sodio NaHCO3.
Ejemplo. Hallar la composición centesimal del hidróxido de sodio NaOH.
Ejemplo. Hallar la composición centesimal del ácido fosfórico H3PO4.
Matamala y Gonzalez
Ejercicio 1.17. Analizando una muestra de la sustancia llamada clorato sódico NaClO3, se obtuvo 31% de cloro. ¿es pura la muestra?
Ejercicio 1.26. Hallar la composición centesimal del nitrato de bario Ba(NO3)2
Química de Chang 10
Práctica 3.8. Calcule la composición porcentual en masa de cada uno de los elementos en ácido sulfúrico (H2SO4).
Problema 3.39. El estaño (Sn) existe en la corteza terrestre como SnO2. Calcular el porcentaje de composición en masa de Sn y O en SO2.
Química la ciencia central
Muestra 3.6. Calcula el porcentaje de carbono, hidrógeno y oxígeno (en masa) en C12H22O11.
Práctica 3.6.1. ¿Cuál es el porcentaje de nitrógeno, en masa, en el nitrato de calcio? (a) 8.54%. (b) 17.1%. (c) 13.7%. (d) 24.4%. (e) 82.9%.
Práctica 3.6.2. Calcular el porcentaje de potasio, en masa, en K2PtCl6.
Ejercicio 3.25a. Calcular el porcentaje en masa de oxígeno en la morfina, C17H19NO3.
Ejercicio 3.25b. Calcular el porcentaje en masa de oxígeno en la codeína, C18H21NO3
Ejercicio 3.25c. Calcular el porcentaje en masa de oxígeno en la cocaína, C17H21NO4
Ejercicio 3.25d. Calcular el porcentaje en masa de oxígeno en la tetraciclina, C22H24N2O8
Ejercicio 3.25e. Calcular el porcentaje en masa de oxígeno en la digitoxina, C41H64O13
Ejercicio 3.25f. Calcular el porcentaje en masa de oxígeno en la vancomicina, C66H75Cl2N9O24
Ejercicio 3.26a. Calcular el porcentaje en masa del carbono en acetileno, C2H2, gas utilizado en soldadura.
Ejercicio 3.26b. Calcular el porcentaje en masa del hidrógeno en ácido ascórbico, HC6H7O6, también conocido como vitamina C.
Ejercicio 3.26c. Calcular el porcentaje en masa del hidrógeno en sulfato de amonio, (NH4)2SO4, una sustancia utilizada como fertilizante nitrogenado.
Ejercicio 3.26d. Calcular el porcentaje en masa del platino en PtCl2(NH3)2, un agente de quimioterapia llamado cisplatino.
Ejercicio 3.26e. Calcular el porcentaje en masa del oxígeno en la hormona sexual femenina estradiol, C18H24O2.
Ejercicio 3.26f. Calcular el porcentaje en masa del carbono en capsaicina, C18H27NO3, el compuesto que le da el sabor picante a los chiles.
Ejercicio 3.27a. Con base en la siguiente fórmula estructural del benzaldehido, calcule el porcentaje de carbono en masa.
Ejercicio 3.27b. Con base en la siguiente fórmula estructural de la vanilina, calcule el porcentaje de carbono en masa.
Ejercicio 3.27c. Con base en la siguiente fórmula estructural del acetato de isopentilo, calcule el porcentaje de carbono en masa.
Ejercicio 3.28a. Con base en la siguiente fórmula estructural del dióxido de carbono, calcule el porcentaje de carbono en masa.
Ejercicio 3.28b. Con base en la siguiente fórmula estructural del metanol, calcule el porcentaje de carbono en masa.
Ejercicio 3.28c. Con base en la siguiente fórmula estructural del etano, calcule el porcentaje de carbono en masa.
Ejercicio 3.28d. Con base en la siguiente fórmula estructural de la tiourea, calcule el porcentaje de carbono en masa.
22.17 Relación entre fórmulas moleculares y empíricas con sus masas molares
DEMOSTRACION: Deducir una fórmula que permite calcular la fórmula molecular con la fórmula empírica y la masa molar verdadera de la sustancia.
Interpretación empírico-molecular de la ley de proporciones definidas entre una fórmula empírica que posee una masa molar empírica Mj° y subíndices empíricos sij°, con la fórmula molecular o verdadera.
Química de Chang 10
Problema 3.53. La masa molar de la cafeína es de 194.19 g. ¿La fórmula molecular de la cafeína es C4H5N2O o C8H10N4O2?
Química de Chang 13
Ejercicio 3.51a. ¿Cuál es la fórmula molecular del siguiente compuesto? fórmula empírica CH2, masa molar = 84 g/mol.
Ejercicio 3.51b. ¿Cuál es la fórmula molecular del siguiente compuesto? fórmula empírica NH2Cl, masa molar = 51,5 g/mol.
Ejercicio 3.52a. ¿Cuál es la fórmula molecular del siguiente compuesto? fórmula empírica HCO2, masa molar = 90,0 g/mol. R= H2C2O4.
Ejercicio 3.52b. ¿Cuál es la fórmula molecular del siguiente compuesto? fórmula empírica C2H4O, masa molar = 88 g/mol. R= C4H8O2.
22.19 Calculando el nivel de hidratación
Cuando se preparan las sales, se puede retener algo de agua dentro de la estructura de la sal durante el proceso de cristalización, esto afecta la forma y el color del cristal. Las sales que contienen agua dentro de su estructura se denominan sales hidratadas, mientras que las sales anhidras son aquellas que no contienen agua en su estructura. Un ejemplo común es el sulfato de cobre (II) que cristaliza formando el sulfato de cobre (II) hidratado con sal, que es azul, cuando se calienta, se elimina el agua de su estructura, formando sulfato de cobre (II) anhidro, que es de color blanco, por lo que la sal hidratada se ha deshidratado para formar la sal anhidra. Esta reacción se puede revertir agregando agua al sulfato de cobre (II) anhidro.
Las moléculas de agua incluidas en la estructura de algunas sales durante el proceso de cristalización se conocen como agua de cristalización. Un compuesto que contiene agua de cristalización se llama compuesto hidratado. Al escribir la fórmula química de los compuestos hidratados, el agua de cristalización se separa de la fórmula principal por un punto, por ejemplo, el sulfato de cobre (II) hidratado es CuSO4∙5H2O y el cloruro de cobalto(II) hidratado es CoCl2∙6H2O. La fórmula muestra el número de moles de agua contenidos en un mol de sal hidratada P.ej. sulfato de cobre (II) hidratado, CuSO4∙5H2O, contiene 5 moles de agua en 1 mol de sal hidratada. Un compuesto que no contiene agua de cristalización se llama compuesto anhidro como el sulfato de cobre (II) anhidro es CuSO4, el cloruro de cobalto (II) anhidro es CoCl2. La conversión de compuestos anhidros a compuestos hidratados es reversible al calentar la sal hidratada:
👉 Sal anhidra a hidratada CuSO4 + 5H2O → CuSO4∙5H2O
👉 Hidratado a sal anhidra (por calentamiento) CuSO4∙5H2O → CuSO4 + 5H2O
Nivel de hidratación (x) en términos de las cantidades de sustancia del agua (nH2O) y la sal anhidro (nah) y sus respectivas masas (mH2O) (mah) y masas molares (MH2O) (Mah).
Química la ciencia central 13
23. La ley de Dulong y Petit
|| REGRESAR AL INDICE ||
Hasta el momento hemos empleado la técnica de Cannizzaro para calcular la masa relativa (que es la misma masa molar si la multiplicamos por la constante de masa molar) de elementos no metálicos fácilmente volatilizables, es decir, de gases. Sin embargo, la mayoría de los elementos son metales no volatilizables mediante tecnologías disponibles en la época de Cannizzaro, así que debe emerger la pregunta ¿Cómo podemos calcular las masas relativas/molares de elementos no volatilizables?
La respuesta es por medio de la ley de Dulong-Petit, es una ley termodinámica propuesta en 1819 por los físicos franceses Pierre Louis Dulong y Alexis Thérèse Petit, la cual establece la expresión clásica para la capacidad calorífica específica molar de ciertos elementos químicos.
Sin embargo, como otras expresiones que hemos visto como la ley de Avogadro o la ley de los gases ideales, la forma original de la ley de Dulong y Petit es muy diferente de la forma moderna, que es la que vamos a emplear en este curso de química general.
23.1 Tres capacidades de calor
En términos generales, la ley de Dulong-Petit indica que el producto entre la masa molar de un gas y su capacidad calorífica es una constante, la pregunta es ¿Cuál de las capacidades caloríficas es la que se usa y en que unidades?
👉 Capacidad calorífica
La capacidad calorífica o capacidad térmica (Ci no confundir con la concentración molar cuyo símbolo es una c minúscula) es una propiedad física de la materia, definida como la cantidad de calor (Qi) que se suministra a una masa determinada de un material (mi) para producir un cambio unitario en su temperatura (Ti). La unidad SI de capacidad calorífica es julio por kelvin (J / K). La capacidad calorífica es una propiedad extensiva pues entre masas masa involucrada se requiere más calor para provocar un cambio en la temperatura. La propiedad intensiva correspondiente es la capacidad calorífica específica y la capacidad calorífica molar.
👉 Capacidad calorífica específica
En termodinámica, la capacidad calorífica específica (símbolo Csi) de una sustancia es la capacidad calorífica de una muestra de la sustancia dividida por la masa de la muestra. De manera informal, es la cantidad de energía que debe agregarse, en forma de calor, a una unidad de masa de la sustancia para provocar un aumento de una unidad en la temperatura.
La unidad SI de calor específico es, J⋅kg−1⋅K−1. Por ejemplo, el calor necesario para elevar la temperatura de 1 kg de agua en 1 K es 4184 julios, por lo que la capacidad calorífica específica del agua es 4184 J⋅kg−1⋅K−1.
👉 Capacidad calorífica molar
La capacidad calorífica molar (Cmi) de una sustancia química es la cantidad de energía que debe agregarse, en forma de calor, a un mol de la sustancia para provocar un aumento de una unidad en su temperatura. Alternativamente, es la capacidad calorífica de una muestra de la sustancia dividida por la cantidad de sustancia de la muestra; o también la capacidad calorífica específica de la sustancia multiplicada por su masa molar. La unidad SI de calor específico es, J⋅K−1⋅mol−1.
23.5 Relación entre capacidad calorífica y masa molar
La forma moderna de la ley de Dulong y Petit se debe a una reinterpretación hecha a la luz de la teoría cinética de los gases y a trabajos de Albert Einstein. Dulong y Petit no establecieron su ley en términos de la constante de gas ideal R (que entonces no se conocía). En cambio, midieron los valores de las capacidades caloríficas (por peso) de las sustancias, y ajustaron a una constante arbitraria dadas en otras unidades a las que empleamos actualmente.
23.6 No es precisa
La ley de Dulong y Petit no es tan precisa como la técnica de Cannizzaro para los gases, sin embargo, usada en conjunto con una ecuación auxiliar estequiométrica permite aproximarse al valor de masa molar, lo cual a su vez permite manipular cualitativamente la ecuación estequiométrica para inferir la fórmula molecular de la sustancia problema, y la verdadera masa molar del metal involucrado.
A pesar de su simplicidad, la ley de Dulong-Petit ofrece una predicción bastante buena de la capacidad calorífica de muchos sólidos elementales con una estructura cristalina relativamente simple a altas temperaturas, pero falla a temperatura ambiente para los átomos livianos fuertemente unidos entre sí, como en el berilio metálico y en el carbono como el diamante. Aquí, predice capacidades de calor más altas de las que realmente se encuentran.
En la región de temperatura muy baja (criogénica) esta ley falla para todas las sustancias.
23.7 Modelo matemático
DEMOSTRACIÓN: Inferir la ley de Dulong y Petit a través de la teoría cinética de los gases
|
Matamala y González
Ejemplo 1.6.2. 11.17 g de un metal se combinan con 4.8 g de oxígeno. El calor específico del metal es 0,112 cal/(g ºC). Hallar su masa molar.
Ejercicio 1.20. 7.122 g de un metal se combinan con 1,92 g de oxígeno. El calor específico del metal es 0,053 cal / (g ºC). Hallar su peso atómico exacto.
Ejercicio 1.21. Hallar la masa molar de un metal sabiendo que 13,15 g del mismo se combinan con 2,00 g de oxígeno y su calor específico es 0,04 cal / (g ºC).
23.11 Legado de la ley Dulong-Petit
Berzelius usó la ley para corregir algunos, pero no todos, los pesos atómicos que había medido con el método de Cannizzaro. Lo que Berzelius no pudo aceptar en absoluto, sin embargo, fue la ley propuesta en 1811 por Amedeo Avogadro, que establecía que un volumen dado de cualquier gas, para valores fijos de temperatura y presión, siempre contenía el mismo número de moléculas. Cuando se combina con los pesos atómicos de los gases obtenidos por Dumas, la ley de Avogadro implicaba de hecho que incluso los gases simples como el hidrógeno o el nitrógeno tenían que estar hechos de moléculas diatómicas.
Figura 23.1. Jöns Jacob Berzelius (Östergötland, Suecia, 20 de agosto de 1779 - Estocolmo, 17 de agosto de 1848) fue un químico sueco. Ideó el moderno sistema de notación química, y junto con John Dalton, Antoine Lavoisier, y Robert Boyle, es considerado el padre de la química moderna. Es reconocido por haber sido el primer analista del siglo XIX. Descubrió el torio, el cerio y el selenio y fue el primero en aislar el circonio, el silicio y el titanio. También perfeccionó la tabla de los pesos atómicos de los elementos publicada por Dalton, corrigiendo sus errores.
Para Berzelius, que creía que los enlaces entre átomos siempre se derivan de fuerzas eléctricas, esto era claramente insostenible y casi absurdo: ¿cómo podían unirse dos átomos idénticos con la misma carga? De hecho, las ideas de Avogadro permanecieron en el olvido durante mucho tiempo hasta que Stanislao Cannizzaro, el mayor químico italiano del siglo XIX, que había estudiado calorimetría con Regnault en el Coll`ege de France les dio el lugar que merecen (Piazza, 2018).
En una carta al secretario de Il Nuovo Cimento Salvatore De Luca, titulada Sunto di un corso di Filosofia Chimica, Cannizzaro, admitiendo la hipótesis de Avogadro, hizo un amplio uso de la ley DP para evaluar pesos atómicos y moleculares precisos (Piazza, 2018). Esto lo llevó a formular su resultado fundamental, un gran paso hacia dar realidad física a los átomos:
Las diversas cantidades de un mismo elemento contenidas en diferentes moléculas son todas múltiplos de la misma cantidad que, entrando siempre como un todo, debe llamarse átomo. (Piazza, 2018).
Figura 23.2. Alexis Thérèse Petit (2 de octubre de 1791 - 21 de junio de 1820) fue un físico francés, célebre por su trabajo sobre la eficiencia de las máquinas de aire y vapor, publicado en 1818. Sus discusiones técnicas con el físico francés Sadi Carnot, fundador de la termodinámica, pudieron haber estimulado a Carnot a desarrollar las teorías sobre eficiencia termodinámica en máquinas térmicas.
Figura 23.3. Pierre Louis Dulong fue un químico francés, (Ruan, 12 de febrero de 1785 - París, 19 de julio de 1838), que encontró la relación entre el calor específico de un elemento y su masa molar. A parte de sus grandes logros, debemos recalcar que al principio de su labor profesional no fue muy afortunado, En sus comienzos ejerció la medicina sin cobrar nada por sus servicios especialmente entre los más necesitados, por lo que no parece extraño que fracasara en esta profesión. Posteriormente se dedicó a la Química, arruinándose al gastarse todo el dinero que poseía en comprar el instrumental apropiado. En 1813 tuvo la mala suerte de descubrir de forma accidental el tricloruro de nitrógeno, un compuesto altamente explosivo y muy delicado de manejar, que le costó la pérdida de la vista en un ojo y casi una mano en dos explosiones, a pesar de lo cual continuó sus experimentos.
Cannizzaro presentó sus ideas en la primera conferencia mundial de químicos, celebrada en Karlsruhe en 1860. Uno de los participantes de la conferencia fue un joven estudiante de química ruso, Dmitrii Ivanovich Mendeleev, quien, junto con todos los asistentes, recibió una copia del documento por Cannizzaro. Inmediatamente después de leer el documento, Mendeleev escribió una carta entusiasta a su maestro A. A. Voskresenskii en San Petersburgo, mencionándole que descubrió que todos los valores de Cannizzaro satisfacían la ley del PD. La apreciación del trabajo de Cannizzaro y de la importancia de la ley DP tuvo una consecuencia crucial en la construcción de la tabla periódica. De hecho, Mendeleev usó la ley DP para corregir los pesos atómicos de indio, cerio y uranio, que estaban equivocados en su primera tabla de 1869 permitiéndole producir la notable tabla de 1871 que duró básicamente sin cambios durante casi 70 años (Piazza, 2018).
Referencias Bibliográficas
|| REGRESAR AL INDICE ||
Barrotta, P. (2000). Scientific Dialectics in Action. Scientific Controversies: Philosophical and Historical Perspectives, 153.
Bedini, S. A. (1965). Weighing and Its Instruments: Scales and Weights: A Historical Outline (Yale Studies in the History of Science and Medicine, vol. 1). Bruno Kisch. Yale University Press, New Haven, Conn., 1965. xxi+ 297 pp. Illus. $15. Science, 150(3693), 203–204.
Bell, J. A. (2005). Chemistry: A General Chemistry Project of the American Chemical Society. (American Chemical Society, Ed.) (1st ed.). Freeman.
Beretta, M. (2014). Between the workshop and the laboratory: Lavoisier’s network of instrument makers. Osiris, 29(1), 197–214.
Beretta, M., & Brenni, P. (2022a). Lavoisier’s Approach to Chemical Instrument Making. In The Arsenal of Eighteenth-Century Chemistry (pp. 18–49). Brill.
Beretta, M., & Brenni, P. (2022b). The Arsenal of Eighteenth-Century Chemistry: The Laboratories of Antoine Laurent Lavoisier (1743-1794). Brill.
Bernal, A., & Daza, E. E. (2010). On the epistemological and ontological status of chemical relations. HYLE–International Journal for Philosophy of Chemistry, 16(2), 80–103.
Bernatowicz, A. J. (1970). Dalton’s rule of simplicity. Journal of Chemical Education, 47(8), 577.
Bigg, C. (2008). Evident atoms: Visuality in Jean Perrin’s Brownian motion research. Studies in History and Philosophy of Science Part A, 39(3), 312–322.
Blanco, D. (2012). Aristas controversiales en la caja negra de Darwin. Lógoi, (8).
Bose, S. K. (2015). The atomic hypothesis. Current Science, 108(5), 998–1002.
Boyle, R. (1911). The Sceptical Chymist: The Classic 1661 Text. Courier Dover Publications.
Brady, J. E., & Humiston, G. E. (1986). General Chemistry: Principles and Structure. Wiley & Sons.
Brown, T. L., LeMay, H. E. J., Bursten, B. E., Murphy, C. J., & Woodward, P. (2009). Chemistry the central science (11th ed.). Pearson; Prentice Hall.
Brown, T. L., LeMay, H. E. J., Bursten, B. E., Murphy, C. J., Woodward, P. M., & Stoltzfus, M. W. (2017). Chemistry, the central science (13th ed.). Boston: Pearson.
Burwell Jr, R. L. (1894). Heterogeneous catalysis before 1934. Catalysis, (2).
Büttner, J., & Renn, J. (2016). The early history of weighing technology from the perspective of a theory of innovation. ETopoi: Journal for Ancient Studies, 6, 757–776.
Cercignani, C. (2000). Ludwig Boltzmann: the man who trusted atoms. American Association of Physics Teachers.
Chang, R. (2010). Chemistry (10th ed.). McGraw-Hill New York.
Chang, R., & Overby, J. (2011). General Chemistry,Th e Essential Concepts (11th ed.). McGraw-Hill New York.
Clary, D. C. (2013). 100 Years of Atomic Theory. Science, 341(6143), 244–245.
Clausius, R. (1857). Ueber die Art der Bewegung, welche wir Wärme nennen. Annalen Der Physik, 176(3), 353–380.
Clericuzio, A. (2000). Elements, principles and corpuscles: A study of atomism and chemistry in the seventeenth century (Vol. 171). Springer.
Colyvan, M. (1998). In defence of indispensability. Philosophia Mathematica, 6(1), 39–62.
Cornford, F. M. (2000). Plato’s cosmology: the Timaeus of Plato (Vol. 4). Psychology Press.
Dalton, J. (1805). On the absorption of gases by water and other liquids. S. Russell.
Dalton, J. (2010). A new system of chemical philosophy (Vol. 1). Cambridge University Press.
Darmstaedter, L., & Oesper, R. E. (1928). Jeremias Benjamin Richter. Journal of Chemical Education, 5(7), 785.
Daubeny, C. (1850). Supplement to the Introduction to the atomic theory: comprehending a sketch of certain opinions and discoveries bearing upon the general principles of chemical philosophy, which have been brought into notice since the publication of that work. University Press.
de Andrade Martins, R. (n.d.). A PRIORI COMPONENTS OF SCIENCE: LAVOISIER AND THE LAW OF CONSERVATION OF MASS IN CHEMICAL REACTIONS.
Dijksterhuis, E. J., & Dikshoorn, C. (1969). The mechanization of the world picture. Oxford University Press Oxford.
Donovan, A. (1996). Antoine Lavoisier: Science, administration and revolution (Vol. 5). Cambridge University Press.
Einstein, A. (1905). Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Annalen Der Physik, 4.
Eliade, M., & Ledesma, M. P. (1974). Herreros y alquimistas. Alianza Madrid.
Ferguson, L. (2015). Control Systems as Used by the Ancient World.
Flamm, D. (1997). Ludwig Boltzmann--A Pioneer of Modern Physics. ArXiv Preprint Physics/9710007.
Fujii, K. (1986). The Berthollet-Proust Controversy and Dalton’s Chemical Atomic Theory 1800-1820. The British Journal for the History of Science, 177–200.
Garber, D. (1987). How God causes motion: Descartes, divine sustenance, and occasionalism. JSTOR.
Glausser, W. (1991). Atomistic Simulacra in the Enlightenment and in Blake’s Post-Enlightenment. The Eighteenth Century, 73–88.
Golinski, J. (1994). Precision instruments and the demonstrative order of proof in Lavoisier’s chemistry. Osiris, 9, 30–47.
Guggenheim, E. A. (1961). The mole and related quantities. Journal of Chemical Education, 38(2), 86. Retrieved from https://pubs.acs.org/doi/pdf/10.1021/ed038p86
Gusev, A. I. (2014). Nonstoichiometry and superstructures. Physics-Uspekhi, 57(9), 839.
Gyenis, B. (2017). Maxwell and the normal distribution: A colored story of probability, independence, and tendency toward equilibrium. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics, 57, 53–65.
Hartog, P. J. (1894). The Berthollet-Proust Controversy and the Law of Definite Proportions. Nature, 50(1285), 149–150.
Haw, M. (2005). Einstein’s random walk. Physics World, 18(1), 19–22.
Hesse, J. J., & Anderson, C. W. (1992). Students’ conceptions of chemical change. Journal of Research in Science Teaching, 29(3), 277–299.
Holmes, F. L. (1985). Lavoisier and the chemistry of life: An exploration of scientific creativity. Univ of Wisconsin Press.
IUPAC. (2019). Compendium of Chemical Terminology the “Gold Book.” (S. J. Chalk, Ed.) (2nd ed.). Compiled by A. D. McNaught and A. Wilkinson. Blackwell Scientific Publications, Oxford. Retrieved from http://goldbook.iupac.org/
Jensen, W. B. (2019). Hans Landolt and the Conservation of Mass: Notes from the Oesper Collections, No. 55, March/April 2019.
Jespersen, N. D., Brady, J. E., & Hyslop, A. (2012). Chemistry The Molecular Nature of Matter (6th ed.). Wiley Online Library.
Kapoor, S. C. (1965). Berthollet, Proust, and proportions. Chymia, 10, 53–110.
Kauffman, G. B. (1994). Before and After Cannizzaro: A Philosophical Commentary on the Development of the Atomic and Molecular Theories. American Scientist, 82(4), 395–397.
Kirk, G. S., Raven, J. E., & Schofield, M. (1983). The presocratic philosophers: A critical history with a selection of texts. Cambridge university press.
Krönig, A. (1856). Grundzüge einer theorie der gase.
Kulikovsky, A. A. (2004). The effect of stoichiometric ratio λ on the performance of a polymer electrolyte fuel cell. Electrochimica Acta, 49(4), 617–625.
Lakatos, I. (1978). The methodology of scientific research programmes. Cambridge University Press.
Lennon, T. M. (1993). The battle of the gods and giants: the legacies of Descartes and Gassendi, 1655-1715. Princeton University Press Princeton.
Lennon, T. M. (2014). The battle of the gods and giants: the legacies of Descartes and Gassendi, 1655-1715. Princeton University Press.
Leroux, G. (1992). The Hellenistic Philosophers Volume 1: Translations of the Principal Sources with Philosophical Commentary Volume 2: Greek and Latin Texts with Notes and BibliographyA. A. Long et DN Sedley Cambridge, Cambridge University Press, 1987, vol. 1, xvi, 512 p.; Dialogue: Canadian Philosophical Review/Revue Canadienne de Philosophie, 31(1), 121–123.
Levere, T. H. (1990). Lavoisier: Language, instruments, and the chemical revolution. In Nature, Experiment, and the Sciences (pp. 207–223). Springer.
Levere, T. H. (2001). Transforming matter: a history of chemistry from alchemy to the buckyball. JHU Press.
Lloyd, G. E. R. (2012). Early greek science: Thales to Aristotle. Random House.
Lloyd, G. E. R., & Lloyd, G. E. (1968). Aristotle: the growth and structure of his thought. Cambridge University Press Cambridge.
Maddox, J. (2002). Maxwell’s demon: Slamming the door. Nature, 417(6892), 903.
Mahon, B. (2004). The man who changed everything: the life of James Clerk Maxwell. John Wiley & Sons.
Maleeh, R., & Amani, P. (2013). Pragmatism, Bohr, and the Copenhagen interpretation of quantum mechanics. International Studies in the Philosophy of Science, 27(4), 353–367.
Malone, A., Sagan, C., Druyan, A., & Soter, S. (1980). Cosmos: A Personal Voyage: The Lives of the Stars. United States: PBS.
Marquardt, R. (2019). The mole and IUPAC: a brief history. Chemistry International, 41(3), 50–52.
Matamála, M., & Gonzalez, P. (1976). Química General. Cultural.
Maxwell, J C. (1860). On the Motions and Collisions of Perfectly Elastic Spheres. 19.
Maxwell, James Clerk. (1860). II. Illustrations of the dynamical theory of gases. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 20(130), 21–37.
Maxwell, James Clerk. (1867). IV. On the dynamical theory of gases. Philosophical Transactions of the Royal Society of London, (157), 49–88.
Meinel, C. (1988). Early Seventeenth-Century Atomism: Theory, Epistemology, and the Insufficiency of Experiment. Isis, 68–103.
Michałowska-Kaczmarczyk, A. M., Asuero, A. G., & Michałowski, T. (2015). “Why Not Stoichiometry” versus “Stoichiometry—Why Not?” Part I: General Context. Critical Reviews in Analytical Chemistry, 45(2), 166–188.
Milton, M. J. T. (2011). A new definition for the mole based on the Avogadro constant: a journey from physics to chemistry. Phil. Trans. R. Soc. A, 369(1953), 3993–4003. Retrieved from https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2011.0176
Münzenberg, G. (2013). Development of mass spectrometers from Thomson and Aston to present. International Journal of Mass Spectrometry, 349, 9–18.
Nash, L. K. (1956). The origin of Dalton’s chemical atomic theory. Isis, 101–116.
Newton, I. (1718). Opticks (2003rd ed.). Prometheus Books.
Norwood, G. (1950). Interruptions. The Classical Bulletin, 27(1), 1.
Ollis, W. D. (1972). Models and Molecules. Proceedings of the Royal Institution of Great Britain, 45, 1–31.
Padilla, K., & Furio-Mas, C. (2008). The importance of history and philosophy of science in correcting distorted views of ‘amount of substance’and ‘mole’concepts in chemistry teaching. Science & Education, 17(4), 403–424. Retrieved from https://www.researchgate.net/profile/Kira-Padilla/publication/225927861_The_Importance_of_History_and_Philosophy_of_Science_in_Correcting_Distorted_Views_of_%27Amount_of_Substance%27_and_%27Mole%27_Concepts_in_Chemistry_Teaching/links/5563b91808ae9963a11e
Pais, A. (1991). Niels Bohr’s times: in physics, philosophy, and polity. Clarendon Press Oxford.
Paneth, F. A. (2003). The epistemological status of the chemical concept of element. Foundations of Chemistry, 5(2), 113–145.
Park, J.-C., Kim, D., Lee, C.-S., & Kim, D.-K. (1999). A new synthetic route to wüstite. BULLETIN-KOREAN CHEMICAL SOCIETY, 20, 1005–1009.
Perrin, J. (1901). Les hypothèses moléculaires. Revue Scientifique, 15, 449–461.
Perrin, J. (1909). Mouvement brownien et réalité moléculaire. In Annales de Chimie et de Physique (Vol. 18, pp. 5–104). Retrieved from https://djalil.chafai.net/docs/M2/history-brownian-motion/Perrin - 1909 - French.pdf
Perrin, J. (1911). La réalité des molécules. Revue Scientifique, 25(16), 774–784.
Perrin, J. (1913). Les atomes. Alcan.
Petrucci, R. H., Herring, F. G., Madura, J. D., & Bissonnette, C. (2010). General Chemistry Principles and Modern Applications (10th ed.). Pearson.
Petruso, K. M. (1981). Early weights and weighing in Egypt and the Indus Valley. M Bulletin (Museum of Fine Arts, Boston), 79, 44–51.
Piazza, R. (2018). The strange case of Dr. Petit and Mr. Dulong. ArXiv Preprint ArXiv:1807.02270.
Pismen, L. (2018). The Swings of Science: From Complexity to Simplicity and Back. Springer.
Planck, M. (1896). Gegen die neuere Energetik. Annalen Der Physik, 293(1), 72–78.
Pohle, W. (1971). The mathematical Foundations of Plato’s atomic Physics. Isis, 36–46.
Pomper, P. (1962). Lomonosov and the Discovery of the Law of the Conservation of Matter in Chemical Transformations. Ambix, 10(3), 119–127.
Ponomarev, L. I., & Kurchatov, I. V. (1993). The quantum dice. CRC Press.
Rodgers, G. E. (2019). Questioning the reality of Atoms on the ground: Loschmidt, mach, boltzmann, and ostwald (germany and Austria). Traveling with the Atom: A Scientific Guide to Europe and Beyond, 244.
Roscoe, H. E., & Harden, A. (1896). A New View of the Origin of Dalton’s Atomic Theory: A Contribution to Chemical History, Together with Letters and Documents Concerning the Life and Labours of John Dalton, Now for the First Time Published from Manuscript in the Possession of the Literary . Macmillan and Company.
Sabra, A. I. (1981). Theories of light, from Descartes to Newton. CUP Archive.
Stock, M., Davis, R., de Mirandés, E., & Milton, M. J. T. (2019). The revision of the SI—the result of three decades of progress in metrology. Metrologia, 56(2), 22001.
Swackhamer, G. (2005). Cognitive resources for understanding energy.
Thomson, T. (1820). A System of Chemistry: In Four Volumes (Vol. 1). Baldwin, Cradock, and Joy.
Usitalo, S. (2013). The invention of Mikhail Lomonosov: a Russian national myth. Academic Studies Press.
Van Melsen, A. G. (2004). From atomos to atom: The history of the concept atom. Courier Dover Publications.
Verdejo, M. E. (2012). La realidad última: átomos y vínculos sustanciales. Eikasia: Revista de Filosofía, (43), 47–60.
Wang, L. J. (2017). A critique on Einstein’s mass-energy relationship and Heisenberg’s uncertainty principle. Physics Essays, 30(1), 75–87.
Whitaker, R. D. (1975). An historical note on the conservation of mass. Journal of Chemical Education, 52(10), 658.
Wilholt, T. (2002). Ludwig Boltzmann’s mathematical argument for atomism. In History of Philosophy of Science (pp. 199–211). Springer.
Wisniak, J. (2000). Amedeo Avogadro the man, the hypothesis, and the number. The Chemical Educator, 5(5), 263–268.
Wiswesser, W. J. (1989). Johann Josef Loschmidt (1821-1895): a forgotten genius. Aldrichim. Acta, 22, 17–19.
Zepeda, J. R. (2009). Descartes and His Critics on Space and Vacuum. University of Notre Dame.
Zumdahl, S. S., & Zumdahl, S. A. (2007). Chemistry (7th ed.). Boston: Houghton Mifflin Company.
Ejercicios resueltos
|| REGRESAR AL INDICE ||
👉 Demostraciones <Ejercicios analíticos para demostrar las respuestas analíticas o algoritmos de solución> (Pulse aquí)
👉 Ejemplos <Ejercicios Propios de la página> (Pulse aquí)
👉 Matamala y González <Libro de texto Ediciones Cultural - 1976> (Pulse aquí)
👉 Química general de Chang <Libro de texto de Raymond Chang> (Pulse aquí)
👉 Química la ciencia central <Libro de texto de Theodore E. Brown> (Pulse aquí)
Demostraciones
DEMOSTRACIÓN. Demostrar las ecuaciones que sirven para contrastar la ley de proporciones recíprocas o ley de Richter
DEMOSTRACIÓN. Demostrar la ley de Graham con la ley de velocidad molecular promedio.
DEMOSTRACIÓN. Expresar la ley de Graham en términos del cociente de tiempo en lugar del cociente de velocidad molecular promedio.
DEMOSTRACIÓN. Deducir la fórmula para calcular el porcentaje en masa de un elemento en un compuesto.
DEMOSTRACIÓN. Deducir una fórmula que permite calcular la fórmula molecular con la fórmula empírica y la masa molar verdadera de la sustancia.
DEMOSTRACIÓN. Inferir la ley de Dulong y Petit a través de la teoría cinética de los gases
Ejemplos
Ejemplo. Demuestre que la siguiente figura es congruente con la ley de la conservación de la masa.
Ejemplo. La fórmula molecular del dimetiléter de etanol es C4H12O2. Determinar la fórmula empírica.
Ejemplo. Cuantos átomos de hidrogeno hay en una molécula de acetona C3H6O
Ejemplo. Cuantos átomos de carbono hay en 350 moléculas de acetona C3H6O
Ejemplo. Cuantos átomos de carbono hay en 3.78 x 1028 moléculas de acetona C3H6O
Ejemplo. Cuantos átomos de calcio nitrógeno y oxigeno hay en un mol de Ca(NO3)2
Ejemplo. Calcular la masa molar de un gas X2 sí sabemos que en C.N. su densidad específica es 1.696 g/L
Ejemplo. Cuantos moles hay en 20 g de cobre. Ejemplo. Cuantos moles hay en 14.0 g de N2.
Ejemplo. Cuantos moles hay en una libra de azucar. Ejemplo. Cuantos moles hay en 60 g de cobre.
Ejemplo. Cuantos moles hay en 12 g de carbono. Ejemplo. Cuantos moles hay en 160 g de NH3.
Ejemplo. Cuantos moles hay en 100 ml de agua. Ejemplo. Cuantos moles hay en 18 g de agua.
Ejemplo. Cuantos moles hay en 244 g de aluminio. Ejemplo. Cuantos moles hay en 25 g de cobre.
Ejemplo. Cuantos moles hay en 250 g de agua. Ejemplo. Cuantos moles hay en 200 g de CaCO3.
Ejemplo. Cuantos moles hay en 294 g de ácido sulfúrico. Ejemplo. Cuantos moles hay en 220 g de CO2.
Ejemplo. Cuantos moles hay en 200 g de agua. Ejemplo. Cuantos moles hay en 2 L de agua.
Ejemplo. Cuantos moles hay en 30 g de helio. Ejemplo. Cuantos moles hay en 30 g de H2SO4.
Ejemplo. Cuantos moles hay en 350 g de hierro. Ejemplo. Cuantos moles hay en 3 gramos de carbono.
Ejemplo. Cuantos moles hay en 3 g de helio. Ejemplo. Cuantos moles hay en 300 g de H2SO4.
Ejemplo. Cuantos moles hay en 350 g de NaNO3. Ejemplo. Cuantos moles hay en 36 g de agua.
Ejemplo. Cuantos moles hay en 360 g de agua. Ejemplo. Cuantos moles hay en 40 g de agua.
Ejemplo. Cuantos moles hay en 45 g de NaCl. Ejemplo. Cuantos moles hay en 44 g de CO2.
Ejemplo. Cuantos moles hay en 400 g de Na3PO4. Ejemplo. Cuantos moles hay en 400 g de Na2SO3.
Ejemplo. Cuantos moles hay en 43 g de NH3. Ejemplo. Cuantos moles hay en 40 g de Fe2O3.
Ejemplo. Cuantos moles hay en 49 g de H2SO4. Ejemplo. Cuantos moles hay en 45 g de F2.
Ejemplo. Cuantos moles hay en 54 g de agua. Ejemplo. Cuantos moles hay en 5.00 g de Li.
Ejemplo. Cuantos moles hay en 50 g de H2O. Ejemplo. Cuantos moles hay en 507.25 g de NH3.
Ejemplo. Cuantos moles hay en 5 g de agua oxigenada. Ejemplo. Cuantos moles hay en 5 g de cloruro de sodio.
Ejemplo. Cuantos moles hay en 50 g de NaCl. Ejemplo. Cuantos moles hay en 54.7 g de CaCO3.
Ejemplo. Cuantos moles hay en 50 g de H2SO4. Ejemplo. Cuantos moles hay en 6 g de oro.
Ejemplo. Cuantos moles hay en 60 g de NaOH. Ejemplo. Cuantos moles hay en 64 g de metano CH4.
Ejemplo. Cuantos moles hay en 600 g de oxígeno. Ejemplo. Cuantos moles hay en 64 g de O2.
Ejemplo. Cuantos moles hay en 6.46 g de helio. Ejemplo. Cuantos moles hay en 600 g de butano C4H10.
Ejemplo. Cuantos moles hay en 63 g de SnCl4. Ejemplo. Cuantos moles hay en 64 g de S.
Ejemplo. Cuantos moles hay en 75 g de ZnSO4. Ejemplo. Cuantos moles hay en 72 gramos de agua.
Ejemplo. Cuantos moles hay en 75.0 g de SO2. Ejemplo. Cuantos moles hay en 788 g de oro.
Ejemplo. Cuantos moles hay en 75 g de hierro. Ejemplo. Cuantos moles hay en 7.5 g de CO2.
Ejemplo. Cuantos moles hay en 76.0 g de ácido sulfúrico. Ejemplo. Cuantos moles hay en 7.46 g de litio.
Ejemplo. Cuantos moles hay en 750 g de H2SO4. Ejemplo. Cuantos moles hay en 88 g de CO2.
Ejemplo. Cuantos moles hay en 8 g de O2. Ejemplo. Cuantos moles hay en 80 g de NaOH.
Ejemplo. Cuantos moles hay en 800 g de MgCl2. Ejemplo. Cuantos moles hay en 88 g de C12H22O11.
Ejemplo. Cuantos moles hay en 870 g de cobre. Ejemplo. Cuantos moles hay en 80 g de amoníaco.
Ejemplo. Cuantos moles hay en 80 g de calcio. Ejemplo. Cuantos moles hay en 80 g de O2.
Ejemplo. Cuantos moles hay en 90 g de H2O. Ejemplo. Cuantos moles hay en 980 g de H2SO4.
Ejemplo. Cuantos moles hay en 9 g de H2O. Ejemplo. Cuantos moles hay en 900 g de H2O2.
Ejemplo. Cuantos moles hay en 96 g de oro. Ejemplo. Cuantos moles hay en 94.5 g de HNO3.
Ejemplo. Cuantos moles hay en 90 g de glucosa C6H12O6. Ejemplo. Cuantos moles hay en 98 g de H2SO4.
Ejemplo. Cuantos moles hay en 1.25 x 1015 moléculas de NH3.
Ejemplo. Cuantos moles hay en 5.25 x 1020 átomos de Cu. Ejemplo. Cuantos átomos hay en 12.7 mol de Ca.
Ejemplo. ¿Cuántas moléculas de agua se encuentran en 3.00 moles de esta?
Ejemplo. Calcular el número de átomos de H en 36 g de H2O. La masa molar del agua es 18 g/mol.
Ejemplo. Cuantos átomos hay en 16.3 g de S. Ejemplo. Cuantos átomos hay en 12 g de carbono.
Ejemplo. Cuantos átomos hay en 10 g de oxígeno. Ejemplo. Cuantos átomos hay en 100 g de oro.
Ejemplo. Cuantos átomos hay en 120 g de magnesio. Ejemplo. Cuantos átomos hay en 15 g de hierro.
Ejemplo. Cuantos átomos hay en 100 g de carbono. Ejemplo. Cuantos átomos hay en 12 g de fósforo.
Ejemplo. Cuantos átomos hay en 186 g de magnesio. Ejemplo. Cuantos átomos hay en 10 g de calcio. Ejemplo. Cuantos átomos hay en 28 g de hierro. Ejemplo. Cuantos átomos hay en 224 g de azufre.
Ejemplo. Cuantos átomos hay en 240 g de carbono. Ejemplo. Cuantos átomos hay en 20 g de boro.
Ejemplo. Cuantos átomos hay en 250 g de hierro. Ejemplo. Cuantos átomos hay en 20 g de calcio.
Ejemplo. Cuantos átomos hay en 24 g de carbono. Ejemplo. Cuantos átomos hay en 23 g de sodio.
Ejemplo. Cuantos átomos hay en 20 g de aluminio. Ejemplo. Cuantos átomos hay en 300 g de arsénico.
Ejemplo. Cuantos átomos hay en 3.52 g de magnesio. Ejemplo. Cuantos átomos hay en 326 g de bromo.
Ejemplo. Cuantos átomos hay en 30 g de hierro. Ejemplo. Cuantos átomos hay en 30 g de mercurio.
Ejemplo. Cuantos átomos hay en 32 g de azufre. Ejemplo. Cuantos átomos hay en 3.14 g de cobre.
Ejemplo. Cuantos átomos hay en 3.5 g de nitrógeno. Ejemplo. Cuantos átomos hay en 47.5 g de platino.
Ejemplo. Cuantos átomos hay en 40 g de calcio. Ejemplo. Cuantos átomos hay en 46 g de sodio.
Ejemplo. Cuantos átomos hay en 4 gramos de helio. Ejemplo. Cuantos átomos hay en 4 gramos de carbono.
Ejemplo. Cuantos átomos hay en 4.0 g de irido. Ejemplo. Cuantos átomos hay en 5.0 gramos de oxígeno.
Ejemplo. Cuantos átomos hay en 50 g de oro. Ejemplo. Cuantos átomos hay en 50 g de helio.
Ejemplo. Cuantos átomos hay en 6.0 g de carbono. Ejemplo. Cuantos átomos hay en 60 g de calcio.
Ejemplo. Cuantos átomos hay en 64 g de azufre. Ejemplo. Cuantos átomos hay en 64 g de selenio.
Ejemplo. Cuantos átomos hay en 64 g de oxígeno. Ejemplo. Cuantos átomos hay en 65 g de sodio.
Ejemplo. Cuantos átomos hay en 7.4 g de silicio. Ejemplo. Cuantos átomos hay en 70 g de nitrógeno.
Ejemplo. Cuantos átomos hay en 72 g de cromo. Ejemplo. Cuantos átomos hay en 7.0 g de fósforo.
Ejemplo. Cuantos átomos hay en 71 g de cloro. Ejemplo. Cuantos átomos hay en 7.95 g de cloro.
Ejemplo. Cuantas moléculas en 6.31 moles de O2
Ejemplo. Calcular el número de moléculas existentes en 1.30 moles de KOH
Ejemplo. Calcular el número de moléculas de SO2 en 1.28 moles de SO2
Ejemplo. ¿Cuántas moléculas de agua se encuentran en 36 gramos de esta?
Ejemplo. ¿Cuántas moléculas de agua se encuentran en 500 ml de esta?
Ejemplo. ¿Cuántas moléculas de H2O están presentes en 4.00 moles de esta?
Ejemplo. Hallar la composición centesimal del nitrato de bario Ba(NO3)2.
Ejemplo. Hallar la composición centesimal del ácido sulfúrico H2SO4.
Ejemplo. Hallar la composición centesimal del agua H2O.
Ejemplo. Hallar la composición centesimal del peróxido de hidrógeno H2O2.
Ejemplo. Hallar la composición centesimal del ácido nítrico HNO3.
Ejemplo. Hallar la composición centesimal del permanganato de potasio KMnO4.
Ejemplo. Hallar la composición centesimal del cloruro de potasio KCl.
Ejemplo. Hallar la composición centesimal del hipoclorito de potasio KClO.
Ejemplo. Hallar la composición centesimal del clorito de potasio KClO2.
Ejemplo. Hallar la composición centesimal del clorato de potasio KClO3.
Ejemplo. Hallar la composición centesimal del perclorato de potasio KClO4.
Ejemplo. Hallar la composición centesimal de la glucosa C6H12O6.
Ejemplo. Hallar la composición centesimal del carbonato de sodio Na2CO3.
Ejemplo. Hallar la composición centesimal del bicarbonato de sodio NaHCO3.
Ejemplo. Hallar la composición centesimal del hidróxido de sodio NaOH.
Ejemplo. Hallar la composición centesimal del ácido fosfórico H3PO4.
Ejemplo. Cuantos átomos hay en 5 moléculas de hidróxido de sodio NaOH.
Ejemplo. Cuantos átomos hay en 5 moléculas de ácido sulfúrico H2SO4.
Ejemplo. Cuantos átomos hay en 6 moléculas de propano C3H8.
Matamala y González
Ejemplo 1.6.2. 11.17 g de un metal se combinan con 4.8 g de oxígeno. El calor específico del metal es 0,112 cal/(g ºC). Hallar su masa molar.
Ejemplo 1.8.1. ¿Cuál es la masa de un átomo de hidrógeno?
Ejercicio 1.6. ¿Qué peso de nitrógeno se combina con 50 g de oxígeno en un compuesto en el cual hay 2 átomos de N por cada átomo de O?
Ejercicio 1.8. En el óxido férrico Fe2O3 ¿cuantos moles de oxígeno atómico entran por cada 2,8 gramos de hierro?
Ejercicio 1.11. Seleccione la respuesta correcta. 0,2 mol de Cu es lo mismo que: (a) 0,2 mol de O (b) 318 g de Cu (c) 3 x 1024 átomos de Cu (d) 1 x 1023 átomos de Cu.
Ejercicio 1.12a. El aluminio tiene una masa molar de 27 g/mol. ¿cuál es la masa en gramos de un solo átomo de aluminio?
Ejercicio 1.12b. El aluminio tiene una masa atómica de 27 uma. ¿Cuántos moles y cuantos átomos hay en 8.1 g de aluminio?
Ejercicio 1.13a. El Bi tiene una masa molar de 209 g/mol y una densidad de 9,8 g/cc. ¿Qué volumen ocupa un mol de bismuto?
Ejercicio 1.13b. El Bi tiene una masa molar de 209 g/mol y una densidad de 9,8 g/cc. ¿Cuál será el volumen promedio que ocupa un solo átomo de bismuto?
Ejercicio 1.13c. Suponiendo que el átomo de bismuto tiene forma esférica, ¿Cuál será su radio en cm y en Å si su volumen atómico promedio es 3.54 x 10-23 cm3?
Ejercicio 1.14. ¿Cuál de las siguientes masas es mayor? (a) 48 g de Zn, (b) 4 moles de N, (c) 0.1 moles de Bi, (d) 2 x 1023 átomos de Cd.
Ejercicio 1.15. Un compuesto de hierro y oxígeno contiene 70% del metal, determinar la fórmula correcta: (a) FeO, (b) Fe3O4, (c) FeO2, (d) Fe2O3.
Ejercicio 1.16. Determinar la fórmula empírica de un compuesto de Na 42,08%, P 18,98 %, y O 39,03%. (a) NaPO2, (b) Na2PO3, (c) Na3PO4, (d) NaPO3, (e) Na4P2O7.
Ejercicio 1.17. Analizando una muestra de la sustancia llamada clorato sódico NaClO3, se obtuvo 31% de cloro. ¿es pura la muestra?
Ejercicio 1.18. 3,01 x 1023 átomos del elemento A se combinan con 16 g de oxígeno. La fórmula del compuesto será: (a) AO, (b) A2O3, (c) A2O5, (d) AO2, (e) A2O.
Ejercicio 1.20. 7.122 g de un metal se combinan con 1,92 g de oxígeno. El calor específico del metal es 0,053 cal / (g ºC). Hallar su peso atómico exacto.
Ejercicio 1.21. Hallar la masa molar de un metal sabiendo que 13,15 g del mismo se combinan con 2,00 g de oxígeno y su calor específico es 0,04 cal / (g ºC).
Ejercicio 1.24a. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos moles de hidrógeno hay en cada mol del ácido?
Ejercicio 1.24b. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de hidrógeno hay en cada mol del ácido?
Ejercicio 1.24d. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos mol de hidrógeno hay en cada mol del oxígeno?
Ejercicio 1.24e. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de azufre hay por cada mol de O?
Ejercicio 1.24f. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de azufre hay por cada gramo de hidrógeno?
Ejercicio 1.24g. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de H por cada 9.8 gramos de H2SO4?
Ejercicio 1.24h. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de azufre por cada átomo de oxígeno?
Ejercicio 1.24i. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos átomos de oxígeno por mol de H2SO4?
Ejercicio 1.24j. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos mol de O por gramo de H2SO4?
Ejercicio 1.24k. Considerando la fórmula molecular del ácido sulfúrico como H2SO4: ¿Cuántos gramos de H por gramo de H2SO4?
Ejercicio 1.25. Un óxido de manganeso contiene 63,2% de metal. Hallar su fórmula empírica.
Ejercicio 1.26. Hallar la composición centesimal del nitrato de bario Ba(NO3)2
Ejercicio 7.23. A través de un recipiente poroso se escapan 220 ml de H2 en 15 minutos. ¿Qué volumen de O2 se escapará en ese tiempo?
Ejercicio 7.26. La velocidad de difusión del hidrógeno con respecto al helio es: (a) la mitad (b) 4 veces mayor (c) 2 veces mayor (d) 1.4 veces mayor.
Ejercicio 7.31. Un hidrocarburo contiene 82,76% de carbono y 17,24% de hidrógeno. Si su densidad a C.N. es de 2,59 g/L, hallar la fórmula molecular.
Ejemplo 5.16. Calcular la velocidad promedio de una partícula de nitrógeno molecular a 25 °C.
Práctica 5.16. Calcular la velocidad cuadrática promedio de una partícula de cloro molecular a 20 °C.
Química de Chang
Problema 3.9a-b. Defina el término "mol". ¿Cuál es la unidad del mol en los cálculos?
Problema 3.9c-d. ¿Qué tiene el mol en común con el par, la docena y el gross? ¿Qué representa el número de Avogadro?
Problema 3.10. ¿Cuál es la masa molar de un átomo? ¿Cuáles son las unidades de masa molar más utilizadas?
Práctica 3.2. ¿Cuántos moles de magnesio (Mg) hay en 87.3 g de Mg?
Práctica 3.3. Calcular la cantidad de gramos de plomo (Pb) en 12.4 moles de plomo.
Práctica 3.4. Calcular el número de átomos en 0.551 g de potasio (K).
Ejemplo 3.5a. Calcular la masa molecular en uma para el dióxido de azufre, usando los pesos atómicos a cuatro cifras significativas.
Ejemplo 3.5b. Calcular la masa molecular en uma para la cafeína (C8H10N4O2), usando los pesos atómicos a cuatro cifras significativas.
Práctica 3.5. ¿Cuál es la masa molecular del metanol (CH4O)? usar los pesos atómicos a cuatro cifras significativas.
Ejemplo 3.6. El metano (CH4) es un componente principal del gas natural. Cuantas moles de metano están presentes en 6.07 g de CH4?
Práctica 3.6. Calcular el número de moles de cloroformo (CHCl3) en 198 g de cloroformo.
Práctica 3.7. ¿Cuántos átomos de H hay en 72.5 g de isopropanol (alcohol isopropílico), C3H8O?
Práctica 3.8. Calcule la composición porcentual en masa de cada uno de los elementos en ácido sulfúrico (H2SO4).
Ejemplo 3.10. La calcopirita (CuFeS2) es un mineral principal de cobre. Calcule el número de kilogramos de Cu en 3.71 x 103 kg de calcopirita.
Práctica 3.10. Calcule el número de gramos de Al en 371 g de Al2O3.
Problema 3.13. ¿Cuántos átomos hay en 5.10 moles de azufre (S)?
Problema 3.14. ¿Cuántos moles de cobalto (Co) se encuentran en 6.00 x 109 (6 mil millones) átomos de Co?
Problema 3.15. ¿Cuántos moles de átomos de calcio (Ca) hay en 77,4 g de Ca?
Problema 3.16. ¿Cuántos gramos de oro (Au) hay en 15.3 moles de Au?
Problema 3.17a. ¿Cuál es la masa en gramos de un solo átomo de mercurio Hg?
Problema 3.17b. ¿Cuál es la masa en gramos de un solo átomo de neón Ne?
Problema 3.18a. ¿Cuál es la masa en gramos de un solo átomo de arsénico As?
Problema 3.18b. ¿Cuál es la masa en gramos de un solo átomo de níquel Ni?
Problema 3.19. ¿Cuál es la masa en gramos de 1.00 X 1012 átomos de plomo (Pb)?
Problema 3.20. ¿Cuántos átomos hay en 3.14 g de cobre (Cu)?
Problema 3.21. ¿Cuál de los siguientes tiene más átomos: 1.10 g de átomos de hidrógeno o 14.7 g de átomos de cromo?
Problema 3.22. ¿Cuál de los siguientes tiene mayor masa? 2 átomos de plomo o 5.1 x 10-23 moles de helio.
Problema 3.23a. Calcule la masa molecular o la masa de fórmula (en uma) de CH4
Problema 3.23b. Calcule la masa molecular o la masa de fórmula (en uma) de NO2
Problema 3.23c. Calcule la masa molecular o la masa de fórmula (en uma) de SO3
Problema 3.23d. Calcule la masa molecular o la masa de fórmula (en uma) de C6H6
Problema 3.23e. Calcule la masa molecular o la masa de fórmula (en uma) de NaI
Problema 3.23f. Calcule la masa molecular o la masa de fórmula (en uma) de K2SO4
Problema 3.24a. Calcular la masa molecular o masa de la fórmula en uma de Li2CO3
Problema 3.24b. Calcular la masa molecular o masa de la fórmula en uma de CS2
Problema 3.24c. Calcular la masa molecular o masa de la fórmula en uma de CHCl3
Problema 3.24d. Calcular la masa molecular o masa de la fórmula en uma de C6H8O6 ácido ascórbico o vitamina C.
Problema 3.24e. Calcular la masa molecular o masa de la fórmula en uma de KNO3
Problema 3.24f. Calcular la masa molecular o masa de la fórmula en uma de Mg3N2
Problema 3.25. Calcular la masa molar de un compuesto si 0.372 mol tienen una masa de 152 g.
Problema 3.26. ¿Cuántas moléculas de etano (C2H6) hay en 0.334 g de C2H6?
Problema 3.27. Calcule el número de átomos de C, H y O en 1.50 g de azúcar glucosa C6H12O6.
Problema 3.28. La urea [(NH2)2CO] se usa como fertilizante y muchas otras cosas. Calcule el número de átomos de N, C, O y H en 1.68 x 104 g de urea.
Problema 3.30. La densidad del agua es de 1.00 g/mL a 48 °C. ¿Cuántas moléculas de agua hay en 2.56 mL de agua a esta temperatura?
Problema 3.39. El estaño (Sn) existe en la corteza terrestre como SnO2. Calcular el porcentaje de composición en masa de Sn y O en SO2.
Problema 3.45. La fórmula del óxido puede ser representada por Fe2O3. Cuantos moles de Fe están presentes en 24.6 g del compuesto?
Problema 3.46. ¿Cuantos gramos de azufre (S) se necesitan para reaccionar completamente con 246 g de mercurio (Hg) y formar HgS?
Problema 3.47. Calcular la masa en gramos de yodo (I2) que reaccionará completamente con 20.4 g de aluminio (Al) para formar yoduro de aluminio (AlI3)
Problema 3.49a. Cual es la fórmula empírica de 2.1 porciento de H, 65.3 por ciento de O, 32.6 porciento de S.
Problema 3.49b. Cual es la fórmula empírica de 20.2 porciento de Al, 79.8 por ciento de Cl.
Problema 3.50a. Cual es la fórmula empírica de 40.1 porciento de C, 6.6 por ciento de H y 53.3 por ciento de O.
Problema 3.50b. Cual es la fórmula empírica de 18.4 porciento de C, 21.5 por ciento de N y 60.1 por ciento de K.
Problema 3.53. La masa molar de la cafeína es de 194.19 g. ¿La fórmula molecular de la cafeína es C4H5N2O o C8H10N4O2?
Química la ciencia central 13
Muestra 3.5a. Calcule el peso fórmula de la sacarosa, C12H22O11 (azúcar de mesa)
Muestra 3.5b. Calcule el peso fórmula de nitrato de calcio, Ca(NO3)2.
Práctica 3.5.1. ¿Cuál de los siguientes es el peso fórmula correcto para el fosfato de calcio? (a) 310.2 uma. (b) 135.1 uma. (c) 182.2 uma. (d) 278.2 uma. (e) 175.1 uma.
Práctica 3.5.2a. Calcule el peso fórmula de Al(OH)3
Práctica 3.5.2b. Calcule el peso fórmula de CH3OH
Práctica 3.5.2c. Calcule el peso fórmula de TaON
Muestra 3.6. Calcula el porcentaje de carbono, hidrógeno y oxígeno (en masa) en C12H22O11.
Práctica 3.6.1. ¿Cuál es el porcentaje de nitrógeno, en masa, en el nitrato de calcio? (a) 8.54%. (b) 17.1%. (c) 13.7%. (d) 24.4%. (e) 82.9%.
Práctica 3.6.2. Calcular el porcentaje de potasio, en masa, en K2PtCl6.
Práctica 3.7.2. Sin usar una calculadora, organice estas muestras en orden creciente de átomos de O: 1 mol H2O, 1 mol CO2, 3 x 1023 moléculas de O3.
Muestra 3.8. Calcular el número de átomos de H en 0.350 mol de C6H12O6.
Práctica 3.8.1a. Cuántos átomos de azufre hay en 0.45 mol de BaSO4.
Práctica 3.8.1b. ¿Cuántos átomos de azufre hay en 1.10 mol de sulfuro de aluminio?
Práctica 3.8.2a. ¿Cuántos átomos de oxígeno hay en 0.25 mol de Ca(NO3)2?
Práctica 3.8.2b. ¿Cuántos átomos de oxígeno hay en 1.50 mol de carbonato de sodio?
Muestra 3.9. ¿Cuál es la masa molar de la glucosa, C6H12O6?
Práctica 3.9.2. Calcular la masa molar de Ca(NO3)2.
Muestra 3.10. Calcular el número de moles de glucosa C6H12O6 en 5.380 g de C6H12O6.
Práctica 3.10.1. ¿Cuántos moles de bicarbonato de sodio NaHCO3 hay en 508 g de NaHCO3?
Práctica 3.10.2. ¿Cuántos moles de agua hay en 1.00 L de agua, cuya densidad es de 1.00 g/mL?
Muestra 3.11. Calcula la masa, en gramos, de 0.433 mol de nitrato de calcio.
Práctica 3.11.1a. ¿Cuál es la masa, en gramos, de 6.33 mol de NaHCO3?
Práctica 3.11.1b. ¿Cuál es la masa, en gramos, de 3.0 x 10-5 mol de ácido sulfúrico?
Práctica 3.11.2a. ¿Cuál es la masa, en gramos, de 0.50 mol de diamante (C)?
Práctica 3.11.2b. ¿Cuál es la masa, en gramos, de 0.155 mol de cloruro de amonio?
Muestra 3.12a. ¿Cuántas moléculas de glucosa hay en 5.23 g de C6H12O6?
Muestra 3.12a. ¿Cuántos átomos de oxígeno hay en 5.23 g de C6H12O6?
Práctica 3.12.1. ¿Cuántos átomos de cloro hay en 12.2 g de CCl4? (a) 4.77 x 1022. (b) 7.34 x 1024. (c) 1.91 x 1023. (d) 2.07 x 1023.
Práctica 3.12.2a. ¿Cuántas moléculas de ácido nítrico hay en 4.20 g de HNO3?
Práctica 3.12.2b. ¿Cuántos átomos de O hay en 4.20 g de HNO3?
Ejercicio 3.23a. Determine los pesos fórmula del ácido nítrico, HNO3.
Ejercicio 3.23b. Determine los pesos fórmula del KMnO4.
Ejercicio 3.23c. Determine los pesos fórmula del Ca3(PO4)2.
Ejercicio 3.23d. Determine los pesos fórmula del cuarzo, SiO2.
Ejercicio 3.23e. Determine los pesos fórmula del sulfuro de galio.
Ejercicio 3.23f. Determine los pesos fórmula del sulfato de cromo (III).
Ejercicio 3.23g. Determine los pesos fórmula del tricloruro de fósforo.
Ejercicio 3.24a. Determine los pesos fórmula del óxido nitroso, N2O, conocido como gas hilarante y utilizado como anestésico en odontología.
Ejercicio 3.24b. Determine los pesos fórmula del ácido benzoico; HC7H5O2, sustancia utilizada como conservante de alimentos.
Ejercicio 3.24c. Determine los pesos fórmula del Mg(OH)2, el ingrediente activo de la leche de magnesia.
Ejercicio 3.24d. Determine los pesos fórmula del urea, (NH2)2CO, un compuesto utilizado como fertilizante nitrogenado.
Ejercicio 3.24e. Determine los pesos fórmula del acetato de isopentilo, CH3CO2C5H11, responsable del olor de los plátanos.
Ejercicio 3.25a. Calcular el porcentaje en masa de oxígeno en la morfina, C17H19NO3.
Ejercicio 3.25b. Calcular el porcentaje en masa de oxígeno en la codeína, C18H21NO3
Ejercicio 3.25c. Calcular el porcentaje en masa de oxígeno en la cocaína, C17H21NO4
Ejercicio 3.25d. Calcular el porcentaje en masa de oxígeno en la tetraciclina, C22H24N2O8
Ejercicio 3.25e. Calcular el porcentaje en masa de oxígeno en la digitoxina, C41H64O13
Ejercicio 3.25f. Calcular el porcentaje en masa de oxígeno en la vancomicina, C66H75Cl2N9O24
Ejercicio 3.26a. Calcular el porcentaje en masa del carbono en acetileno, C2H2, gas utilizado en soldadura.
Ejercicio 3.26b. Calcular el porcentaje en masa del hidrógeno en ácido ascórbico, HC6H7O6, también conocido como vitamina C.
Ejercicio 3.26c. Calcular el porcentaje en masa del hidrógeno en sulfato de amonio, (NH4)2SO4, una sustancia utilizada como fertilizante nitrogenado.
Ejercicio 3.26d. Calcular el porcentaje en masa del platino en PtCl2(NH3)2, un agente de quimioterapia llamado cisplatino.
Ejercicio 3.26e. Calcular el porcentaje en masa del oxígeno en la hormona sexual femenina estradiol, C18H24O2.
Ejercicio 3.26f. Calcular el porcentaje en masa del carbono en capsaicina, C18H27NO3, el compuesto que le da el sabor picante a los chiles.
Ejercicio 3.27a. Con base en la siguiente fórmula estructural del benzaldehido, calcule el porcentaje de carbono en masa.
Ejercicio 3.27b. Con base en la siguiente fórmula estructural de la vanilina, calcule el porcentaje de carbono en masa.
Ejercicio 3.27c. Con base en la siguiente fórmula estructural del acetato de isopentilo, calcule el porcentaje de carbono en masa.
Ejercicio 3.28a. Con base en la siguiente fórmula estructural del dióxido de carbono, calcule el porcentaje de carbono en masa.
Ejercicio 3.28b. Con base en la siguiente fórmula estructural del metanol, calcule el porcentaje de carbono en masa.
Ejercicio 3.28c. Con base en la siguiente fórmula estructural del etano, calcule el porcentaje de carbono en masa.
Ejercicio 3.28d. Con base en la siguiente fórmula estructural de la tiourea, calcule el porcentaje de carbono en masa.
Ejercicio 3.30. (a) ¿Cuál es la masa, en gramos, de un mol de 12C? (b) ¿Cuántos átomos de carbono hay en un mol de 12C?
Ejercicio 3.35a. Calcular la masa, en gramos, de 0.105 mol de sacarosa C12H22O11.
Ejercicio 3.35b. Calcular los moles de Zn(NO3)2 en 143.50 g de esta sustancia.
Ejercicio 3.35c. Calcular el número de moléculas en 1.0 x 10-6 mol CH3CH2OH.
Ejercicio 3.35d. Calcular el número de átomos de N en 0.410 mol NH3.
Ejercicio 3.36a. Calcular la masa, en gramos, de 1.50 x 10-2 mol CdS.
Ejercicio 3.36b. Calcular el número de moles de NH4Cl en 86.6 g de esta sustancia.
Ejercicio 3.36c. Calcular el número de moléculas en 8.447 x 10-2 mol C6H6.
Ejercicio 3.36d. Calcular el número de átomos de O en 6.25 x 10-3 mol Al(NO3)3.
Ejercicio 3.37a. ¿Cuál es la masa, en gramos, de 2.50x10-3 mol de fosfato de amonio?
Ejercicio 3.37b. ¿Cuántos moles de iones de cloruro hay en 0.2550 g de cloruro de aluminio?
Ejercicio 3.37c. ¿Cuál es la masa, en gramos, de 7.70x1020 moléculas de cafeína, C8H10N4O2?
Ejercicio 3.37d. ¿Cuál es la masa molar de colesterol si 0.00105 mol tiene una masa de 0.406 g?
Ejercicio 3.38a. ¿Cuál es la masa, en gramos, de 1.223 mol de sulfato de hierro (III)?
Ejercicio 3.38b. ¿Cuántos moles de iones de amonio hay en 6.955 g de carbonato de amonio?
Ejercicio 3.38c. ¿Cuál es la masa, en gramos, de 1.50 x 1021 moléculas de aspirina, C9H8O4?
Ejercicio 3.38d. ¿Cuál es la masa molar de diazepam (Valium®) si 0,05570 mol tiene una masa de 15.86 g?
Ejercicio 3.45a. Dé la fórmula empírica: 0.0130 mol C; 0.0390 mol H; y 0.0065 mol O.
Ejercicio 3.45b. Dé la fórmula empírica de 11.66 g de hierro y 5.01 g de oxígeno.
Ejercicio 3.45c. Dé la fórmula empírica de 40.0% C, 6.7% H y 53.3% O en masa.
Ejercicio 3.46a. Determine la fórmula empírica de 0.104 mol K; 0.052 mol C; y 0,156 mol O.
Ejercicio 3.46b. Determine la fórmula empírica de 5.28 g de Sn y 3.37 g de F.
Ejercicio 3.46c. Determine la fórmula empírica de 87.5% de N y 12.5% de H en masa.
Ejercicio 3.47a. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 10.4% C; 27.8% S; y 61.7% Cl.
Ejercicio 3.47b. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 21,7% C; 9,6% O; y 68,7% F.
Ejercicio 3.47c. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 32,79% Na; 13,02% Al; y el resto F.
Ejercicio 3.48a. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 55,3% K; 14,6% P; y 30,1% O.
Ejercicio 3.48b. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 24,5% Na; 14,9% Si; y 60.6% F.
Ejercicio 3.48c. Determine la fórmula empírica del compuesto con la siguiente composición en masa: 62,1% C; 5,21% H; 12,1% N; y el resto O.
Ejercicio 3.49. Un compuesto cuya fórmula empírica es XF3 consiste en 65% de F en masa. ¿Cuál es la masa atómica de X?
Ejercicio 3.50. El compuesto XCl4 contiene 75.0% de Cl en masa. ¿Cuál es el elemento X?.
Ejercicio 3.51a. ¿Cuál es la fórmula molecular del siguiente compuesto? fórmula empírica CH2, masa molar = 84 g/mol.
Ejercicio 3.51b. ¿Cuál es la fórmula molecular del siguiente compuesto? fórmula empírica NH2Cl, masa molar = 51,5 g/mol.
Ejercicio 3.52a. ¿Cuál es la fórmula molecular del siguiente compuesto? fórmula empírica HCO2, masa molar = 90,0 g/mol.
Ejercicio 3.52b. ¿Cuál es la fórmula molecular del siguiente compuesto? fórmula empírica C2H4O, masa molar = 88 g/mol.
Chemteam



















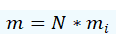





























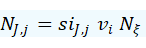

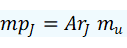

















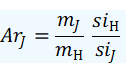
















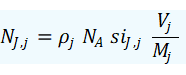























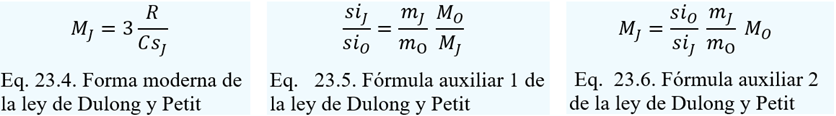



No hay comentarios:
Publicar un comentario