Índice
||
Portada
1. Introducción
|| REGRESAR AL INDICE ||
Por genética clásica o mendelismo entenderemos una teoría científica que intentó entender la genética o herencia de los seres vivos mediante una abstracción matemática simple y mediante la suposición experimental o teórica de una herencia discreta en la que los rasgos de cada carácter eran fáciles de distinguir y matematizar.
Tenga en cuenta que una cosa es el modelo teórico “Genética Clásica o Mendelismo” y otra el fenómeno de la genética como tal, Los fenómenos regularmente son demasiado complejos, por lo que regularmente los reducimos a modelos que buscan determinar los rasgos clave, es decir, sus características más importantes. Es importante entender que la genética clásica no es el modelo más preciso que podamos encontrar y ha sido superada por otros modos de entender la herencia, en la actualidad la genética se modela en base a la Teoría Sintética de la Evolución, que tiene un punto de vista más amplio, en cuanto a matemáticas, métodos de investigación químicos y tipos de herencia que pueden ser continuos o discretos. La genética clásica se enmarcará desde la publicación de Gregor Mendel (Mendel, 1866) sobre hibridación hasta el descubrimiento por parte de Arne Wilhelm Kaurin Tiselius de la electroforesis en 1931 (Jorgenson & Lukacs, 2009), aunque ya en 1916 el paradigma que distinguía la herencia continua de la discreta ya había sido refutado por T. H. Morgan.
El año 1900 marcó el "redescubrimiento de Mendel" por Hugo de Vries, Carl Correns y Erich von Tschermak, aunque existe debate histórico sobre la verdadera importancia de Tschermak y de Mendel, así como un conflicto de prioridades entre Hugo de Vries y Carl Correns. En 1915 los principios básicos de la genética mendeliana se aplicaron a una amplia variedad de organismos, sobre todo la mosca de la fruta Drosophila melanogaster. Liderados por Thomas Hunt Morgan y sus colegas "drosophilistas", los genetistas desarrollaron el modelo mendeliano, que fue ampliamente aceptado en 1925. Junto con el trabajo experimental, los matemáticos desarrollaron el marco estadístico de la genética de poblaciones, llevando las explicaciones genéticas al estudio de la evolución.
¿Porque unos individuos son más altos? ¿Por qué unas personas tienden a engordar con facilidad y otras se mantienen delgadas sin esfuerzo? ¿La inteligencia se hereda o se entrena? ¿por qué algunas cualidades parecen heredarse de padres a hijos y otras no? Desde la antigüedad estas preguntas habían sido un misterio, y debido a la incapacidad para responder tales preguntas, nuestros ancestros desarrollaron creencias socialmente aceptadas a cerca de la herencia de rasgos y habilidades. La aristocracia, por ejemplo, se basa en la creencia de que los miembros de una familia noble heredan habilidades complejas, como gobernar bien o combatir con habilidad, siendo los miembros de estas castas de alguna forma superiores y esa superioridad se pasaba de padres a hijos. En otros casos se trataba de maldiciones de los dioses o los demonios.
Por siglos existieron intentos académicos para explicar el problema de la herencia, pero todos fallaron debido a la naturaleza compleja del problema. En esta serie de lecciones examinaremos el primer intento de explicar la herencia en términos cuantitativos que ha influido de forma profunda en la forma en que entendemos la naturaleza de la herencia en la actualidad. A este primer intento de explicación lo denominaremos como la genética mendeliana (Stubbe, 1972).
Trabajaremos el modelo de herencia mendeliano, como este explica los resultados de un diseño experimental muy concreto, como afectó a las comunidades científicas de su momento y como nos afecta ahora. Sin embargo, lo anterior plantea un problema espinoso, tendemos a aplicar los conceptos del presente a los conceptos en el pasado, juzgamos al pasado como algo de ignorantes y atrasados, sin entender sus contextos, problemas y limitaciones. Debido a esto he decidido cortar con todas las referencias a la biología molecular que generalmente son aplicadas a la genética clásica, preocupándome únicamente del modelo matemático y su coherencia con respecto a los resultados experimentales.
1.1 Thomas Hunt Morgan
(25 de septiembre de 1866 - 4 de diciembre de 1945) fue un biólogo evolutivo, genetista, embriólogo y autor científico estadounidense que ganó el Premio Nobel de Fisiología o Medicina en 1933 por sus descubrimientos que aclararon el papel que desempeña el cromosoma en la herencia.
Morgan recibió su Ph.D. de la Universidad Johns Hopkins en zoología en 1890 e investigó embriología durante su mandato en Bryn Mawr. Tras el redescubrimiento de la herencia mendeliana en 1900, Morgan comenzó a estudiar las características genéticas de la mosca de la fruta Drosophila melanogaster. En su famosa Fly Room en el Schermerhorn Hall de la Universidad de Columbia, Morgan demostró que los genes se transportan en los cromosomas y son la base mecánica de la herencia. Estos descubrimientos formaron la base de la ciencia moderna de la genética.
Durante su distinguida carrera, Morgan escribió 22 libros y 370 artículos científicos. Como resultado de su trabajo, Drosophila se convirtió en un organismo modelo importante en la genética contemporánea. La División de Biología que estableció en el Instituto de Tecnología de California ha producido siete premios Nobel (Hartl, 1979).
2. Genética premendeliana 1, Grecia y jude
|| REGRESAR AL INDICE ||
Para poder entender cuál fue el efecto de la revolución mendeliana, debemos comprender cuál era la visión del problema de la herencia por las culturas que influyeron en la tradición del pensamiento occidental.
2.1 Herencia, cultura, mito y religión
No existe una tendencia general sobre cómo ve cada cultura el modo en que se heredan los rasgos, sin embargo, podemos afirmar con pocas dudas que el mito y la religión jugaron y tal vez aun juegan parte importante. Algunos rasgos hereditarios disminuyen las capacidades con las cuales los individuos se relacionan con su medioambiente, es decir se perciben como defectos. Para explicar los defectos algunas culturas pueden optar por el concepto de maldiciones divinas o demoníacas causadas por pecados contra la moral o contra los dioses “hubris”.
Figura 2.1. Las causas de estas maldiciones dejan de ser fenómenos de la naturaleza y comienzan a interpretarse como la base de un discurso moral, mitológico o religioso; en varias ocasiones excluyente. No es raro encontrar denominaciones religiosas que ven los defectos físicos, ya sea estos heredados o adquiridos como causa de menosprecio, discriminación y exclusión.
En otras ocasiones ocurre lo opuesto, en el que rasgos anómalos son vistos de forma positiva por parte de la sociedad como en el caso de Lakshmi Tatma (Tubbs, Ditty, Bosmia, & Bosmia, 2015) quien al nacer un gemelo siamés incompleto que creció desde su pelvis fue tomada como la diosa de la fortuna y en consecuencia bautizada con el mismo nombre. El ejemplo anterior nos da la pista para entender las ideas de la herencia en sociedades pasadas, y es que hay que entender sus religiones para entender su modo de razonar.
2.2 La Grecia antigua y la herencia premendeliana
Desde la antigua Grecia dos tipos de pensamiento sobre la naturaleza han permanecido con competición, y aun hoy siguen asiéndolo, estos son el pensamiento internalista y el pensamiento externalista (Benfey, 2007). Con pensamiento internalista se hace referencia a aquel en el que el fenómeno natural es generado por causas internas del sistema, por sus componentes físicos, estos factores originadores dan sentido a la palabra genética que significa “el estudio del origen”. El pensamiento opuesto es percibir a los fenómenos naturales como originados por las relaciones externas a él, por las condiciones expuestas e impuestas por su medio ambiente. En este caso el ambiente esta sobre los factores internos. En la actualidad esta perspectiva se conoce como epigenética.
2.3 El preformacionismo
Uno de los modelos genéticos más antiguos es el prefomacionismo, que proponía que los descendientes ya están preformados en las semillas como si se trataran de muñecas rusas, cada una más pequeña que la siguiente.
Figura 2.2. Por años se pensó que la semilla masculina contenía al individuo preformado.
Los proponentes del preformacionismo fueron famosos filósofos como Aristóteles y Anaxágoras, donde percibía al hombre como arado y la mujer como una especie incubadora o campo. Nuevamente una reminiscencia al mito de Uranos y Gaia (Preus, 1977). El preformacionismo es internalista ya que la herencia viene preformada en los homúnculos encerrados al interior de la semilla masculina.
2.4 Problemas del preformacionismo
Uno de los problemas del preformacionismo masculino era que las mujeres también aportaban al desarrollo de sus descendientes. Aristóteles menciona un caso de una mujer que fue infiel con un etíope “un hombre de africano de poblaciones de piel negra”, la hija producto del adulterio no manifestó rasgos etíopes, pero los nietos sí. Esta inconcordancia produjo dos explicaciones. En la primera el preformacionismo fue modificado por influencias externas a la semilla paterna, y en la segunda se propuso la idea de una segunda semilla que afectaba a la paterna.
2.5 Influencia del externalismo al preformacionismo
Una interpretación externalista al preformacionismo planteaba que el útero de la mujer no poseía semilla alguna, las modificaciones eran causadas por factores externos a la semilla que la afectaban. Para esta perspectiva la mujer solo era un receptáculo donde se plantaba la semilla y así esta podía desarrollarse. De este modo existían fenómenos que actuaban “sobre” los “factores originadores” de la semilla. La dicotomía internalista y externalista es lo que actualmente puede denominarse como el debate de lo heredado vs lo ambiental o genética vs epigenética. ¿La inteligencia se hereda o se desarrolla? Esta y otras preguntas sobre al talento vs el esfuerzo diario aún siguen siendo un tópico candente. La propuesta de la semilla paterna deformada por el ambiente materno se la atribuye a Aristóteles (Marinella, 2007).
Figura 2.3. Etíopes del período clásico griego. Memnón en la Ilíada es etíope, el único igual a Aquiles. Etíope significa "cara quemada" en griego en referencia al tono de piel general de los africanos subsaharianos. Se pensaba que eran las personas más puras, las únicas entre las que los dioses caminaban abiertamente. Perseo también rescató a la mujer más hermosa del mundo de ser sacrificada a un monstruo marino. Ella era la hija del rey de Etiopía, la princesa Andrómeda.
2.6 Las dos semillas
No todos los griegos concordaban con la visión del preformacionismo, Empédocles de Agrigento por ejemplo fue el primer filósofo occidental en ir en contra de sus creencias culturales y atreverse a proponer que la herencia dependía de forma igualitaria de los dos padres, elevando a la mujer a una posición igualitaria a la del hombre (Whaley, 2003). El problema con la propuesta de Empédocles era que las semillas no tenían una estructura interna, esto es porque la expresión semilla era una alegoría filosófica, no una entidad experimental como si lo fueron en siglos posteriores el óvulo y el espermatozoide. A falta de experimentación, Empédocles no podía explicar las diferencias de origen entre hombres y mujeres, y esto se convirtió en el blanco de críticos de los preformacionistas como Aristóteles (Whaley, 2003).
2.7 Resumen de la herencia en la Grecia antigua
En la Grecia antigua se encuentra el fundamento de la actual discusión heredado contra aprendido; talento contra esfuerzo. Esta discusión puede plantearse en términos generales como la discusión entre la causa internalista y la externalista. La causa internalista depende solo de los factores internos de un sistema, “lo que le da inicio” es lo más importante, es decir su genética. La causa externalista depende de las relaciones del sistema con su ambiente, el ambiente se encuentra por encima de lo que le “da inicio”. Dos hipótesis de la Grecia antigua concuerdan con las dos posturas.
La hipótesis de las dos semillas postulaba que cada ancestro da dos semillas que interactúan internamente sin importar las condiciones del vientre materno, defendida por Empédocles de Agrigento. La hipótesis externalista proponía que la semilla era dada por el padre y el ambiente del vientre corrompía a la semilla alterándola para generar mujeres y otras deformidades según Aristóteles.
Sin embargo, la filosofía griega tubo un problema endémico que dificultó su ulterior avance, la falta de experimentación controlada para indagar más en las observaciones hechas en el ambiente natural, los filósofos contaban con anécdotas locales y los escritos de sus predecesores, pero en muy raras ocasiones diseñaron experimentos controlados con instrumentación especializada. Con el dominio romano las posturas del preformacionismo y las dos semillas permanecieron en espera, y al establecerse el cristianismo en occidente, las posturas de Aristóteles se convirtieron en el estándar universal. No sería sino hasta el renacimiento que las ideas sobre la herencia serian retomadas con un nuevo punto de vista, la nueva ciencia empirista.
2.8 La ley mosaica y la herencia premendeliana
A lo largo de los estudios de genética nos daremos cuenta de que la hemofilia es la enfermedad favorita de los genetistas. La hemofilia es una enfermedad cuyo síntoma más importante, es la imposibilidad que tiene la sangre para formar coágulos y tapas las heridas. Un enfermo de hemofilia grave sangrará por un corte leve incluso hasta la muerte. Esto es un problema para los judíos, ya que los niños varones debe pasar por un ritual llamado circuncisión. ¿Cómo le hacen los judíos hemofílicos? En el desierto del cercano oriente hace 1800 años un rabí enfrentaba un problema.
Una mujer judía había dado a luz a un varón. La ley judía establecía por orden de Dios mismo que el niño a su octavo día debía asistir al ritual de circuición. Ahora, ese no era el problema, el problema era que los dos hijos varones previos que esta misma mujer había dado a luz, había sagrado hasta la muerte después de ser circuncidados. Pero, aun así, la ley seguía en pie, el niño no podría ser contado entre el pueblo elegido a menos que pasara por tal ritual. Después de una larga consulta con otros Rabí se decidió exceptuar al bebé del ritual.
Figura 2.4. La circuncisión consiste en cortar una porción del prepucio del pene que cubre al glande “es una cubierta de piel”, dejándolo permanentemente al descubierto.
Figura 2.5. Maimónides fue un médico, rabino y teólogo judío de al-Ándalus, la actual España. Tuvo importancia como filósofo en el pensamiento medieval.
Casi mil años más tarde, el médico y comentador bíblico Maimones revisó numerosos casos en la literatura rabínica estableciendo que en tales casos el tercer hijo no debía ser circuncidado. Adicionalmente la excepción debía aplicar, aunque el tercer hijo de la mujer fuera de un esposo diferente. Maimónides razonó que el desorden que causaba el desangrado estaba claramente asociado a la mujer, el cual lo pasaba inevitablemente a todos sus hijos. Sin saber nada de genética moderna, estos sabios antiguos lograron vincular un desorden físico con un patrón de herencia (Sadava, Berenbaum, & Hillis, 2014)
3. Genética mendeliana 2, domesticación
|| REGRESAR AL INDICE ||
El estudio de la herencia biológica ha sido de vital importancia desde los albores de la civilización, de hecho, el mundo agrícola y ganadero se basó en la selección de ciertos grupos de organismos con características deseadas como la docilidad y el fácil manejo, y en cuanto al grano aquellos que dieran mejores cosechas.
Figura 3.1. Las bananas o plátanos poseen una estructura conveniente no porque así se presenten en la naturaleza, sino porque han sido domesticadas. Las versiones salvajes de la familia de los plátanos "género Musa" son realmente inconvenientes, tienen poca pulpa y huelen mal.
El proceso ha sido tan exitoso que las especies producidas por nuestra mano prácticamente son irreconocibles de sus parientes que aún son salvajes. Uno de los casos más emblemáticos son los pastos que sirven de alimento, como el maíz.
Figura 3.2. A la izquierda el teosinto o maíz salvaje, es una especie de pasto que puede arreglárselas muy bien en el ambiente sin ningún cuidado. A la derecha el cultivar empleado para producir maíz, las diferencias en el fruto y la forma de la planta son evidentes, pero arqueológicamente se sabe que el teosinto es el ancestro a partir se domesticó el maíz.
El maíz es una especie de pasto seleccionado a partir de pastos salvajes semejantes al actual teosintio. El fruto del teosintio es más pequeño y duro, pero al mismo tiempo es más resistente al ambiente y a las enfermedades (Arriaga, 1987). Otro caso es el banano, muchas personas piensan que las plantas de plátano o banano son salvajes, “la típica imagen del mono comiendo bananas en ambiente salvaje”. Sin embargo, las bananas salvajes son prácticamente irreconocibles, frutos duros y pequeños (S. B. Edwards, 1991).
3.1 La cría selectiva y la aplicación de la ciencia
La cría selectiva se basa en reservar para la reproducción aquellos ejemplares con los rasgos más deseables de toda una generación. El proceso ha sido empleado por la humanidad casi desde el año 5 000 antes de Cristo, pero se ha hecho, mucho más rápido desde la introducción a la agricultura de los conocimientos generados por la ciencia de la genética (Doebley, Gaut, & Smith, 2006). Y esto es el quid de la cuestión, la genética ha servido para incrementar la productividad de las cosechas, o para aplicaciones médicas que generan riqueza. En otras palabras, la genética es una herramienta para producir más capital económico.
3.2 La cría selectiva en el contexto de Mendel y Darwin
Para el siglo XIX la cría selectiva de plantas ya era una actividad con milenios de historia y documentación. Los métodos de Mendel no eran para nada novedoso en términos de procedimiento. Cualquier granjero era capaz de emplearlos. Incluso ya era empleada en los diseños experimentales de otros académicos como Charles Darwin contemporáneo suyo, pero con quien nunca pudo establecer contacto también empleaba la cría selectiva como un mecanismo para poder estudiar sus hipótesis. En una carta de Darwin a Wallace podemos leer (Williams, 2003):
“Mi querido Wallace,
Me parece que no entiendes a lo que me refiero cuando hablo de que ciertas variedades no se mezclan entre sí. Mi comentario no tiene nada que ver con la fertilidad, y un ejemplo lo puede explicar.
He cruzado entre sí plantas de arveja de las variedades Painted Lady y Purple, que presentan coloraciones muy diferentes, y he obtenido, incluso en la misma vaina, alverjas de ambas variedades, pero ninguno intermedio.
Figura 3.3. Flores de arveja dulce, variedades Painted Lady “izquierda” y Purple “derecha”.
Me parece que algo similar debe estar ocurriendo con tus mariposas y con las tres formas de Lythrum que mencionas. Aunque estos casos parecen sorprendentes, en realidad se trata del mismo fenómeno que hace que cada hembra en el mundo produzca descendencia tanto masculina como femenina.
Con mi afecto más sincero, Ch. Darwin”
En esta carta se puede ver que Darwin y Wallace estaban cerca de uno de los puntos preponderantes del modelo de Mendel, la idea básica de una falta de mezcla, pero para aclarar esta idea debemos entender como entendían la mezcla en ese contexto.
3.3 La cría selectiva depende de factores de ambos progenitores
Cada padre contribuye de manera igual a las características de la descendencia. Aunque actualmente se piensa que la idea proviene de Mendel, en realidad esto ya rondaba los círculos académicos desde mucho antes que Darwin, Wallace y Mendel. Ya antes de Mendel las hipótesis Aristotélicas a cerca de la herencia eran cuestionadas profundamente a base de datos empíricos, en la década de 1770, lo botánico Alemán Josef Gottlieb Kolreuter estudió la descendencia de cruces recíprocos en las cuales, las plantas eran cruzadas en direcciones opuestas (Mayr, 1986). Por ejemplo, en un cruce los machos que tenían flores blancas se cruzaban con hembras de flores rojas. Mientras que en el cruce complementario machos de flores rojas se cruzaban con hembras de flores blancas. Los resultados demostraban que ambos padres contribuían de manera equitativa a los caracteres de la descendencia.
3.4 La herencia continua contra la herencia discreta
Los determinantes hereditarios se mezclan en los descendientes. Por ejemplo, si tenemos una flor roja y una flor azul, se suponía que, los descendientes con flores purpuras resultaban de una mezcla indivisible, algo así como cuando mezclas pintura de diferentes colores. El problema específico con esta hipótesis era la presunción de que una vez mezclados los caracteres no podían volver a separarse. Como bien puede intuirse en la carta de Darwin a Wallace en el artículo anterior, para el siglo XIX las hipótesis de la mezcla de caracteres ya empezaba a cuestionarse, y el mecanismo que impedía la mezcla fue relacionado con aquel que genera la diferencia de sexos. El problema es que nadie intentó formalizar ese mecanismo de forma matemática antes de la llegada de Mendel. Por dos razones:
1- a la mayoría de los filósofos naturales y primeros biólogos no se les daba bien las matemáticas, de lo contrario hubieran sido físicos que era algo más prestigioso.
2- por otro lado, los caracteres que exhibían la falta de mezcla eran raros, lo más común era ver que los rasgos se mezclaban en estados intermedios.
3.5 Resumen de la cría selectiva premendeliana
Para la época de Mendel los naturalistas sabían que algunos rasgos no se heredaban de forma mezclada, se mantenían de una generación a otra, pero también reconocían que estos rasgos eran pocos en comparación a los que, si se mezclaban, y estos últimos eran en los que se enfocaban para explicar. Las explicaciones para los rasgos complejos fueron muchas, pero debido a los límites de la época la mayoría terminó por aceptar al lamarckismo como la explicación dominante, y cuando digo todos eso incluyó a Darwin (Kutschera & Niklas, 2004). Este es el punto de partida del trabajo de Mendel y al mismo tiempo la causa de que no fuera reconocido en su tiempo, pero eso es parte de la siguiente lección.
4. Gregor Mendel
|| REGRESAR AL INDICE ||
Antes de hablar de Gregor Mendel vale la pena mencionar algunas generalidades sobre las tendencias de las ciencias de la naturaleza en el siglo XIX, las cuales estaban enmarcadas en el éxito del programa de investigación newtoniano basado en el reduccionismo y la matematización de la naturaleza.
Figura 4.1. Gregor Johann Mendel (Heinzendorf, Imperio austriaco, actual Hynčice, distrito Nový Jičín, República Checa; 20 de julio de 18221-Brno, Imperio austrohúngaro; 6 de enero de 1884) fue un monje agustino católico y naturalista. Formuló, por medio de los trabajos que llevó a cabo con diferentes variedades del guisante o arveja (Pisum sativum), las hoy llamadas leyes de Mendel que dieron origen a la herencia genética.
4.1 La fisicalización de las ciencias
En el siglo XIX una gran cantidad de académicos tenían un objetivo en mente, transformar sus campos de estudio de forma tal que se parecieran lo más posible a la gran ciencia del momento, la física, todo lo demás sería un arte de coleccionistas, ideología que se mantendría hasta bien entrado el siglo XX –cita de Erns Rutheford cuando le dieron el nobel de Química (Cahoone, 2013). Uno de los métodos de la física de la época era el reduccionismo, encontrar un modelo teórico simple, elegante y hermoso “pero irreal” que relacionara de forma matemática dos variables simples de un sistema complejo. El modelo teórico debería representarse por medio de una fórmula matemática sencilla a la cual se la llamaría ley natural.
4.2 La matematización de la biología
Para fisicalizar una ciencia era necesario matematizarla, desarrollar alguna forma para transformar los fenómenos que se trabajaban en el laboratorio o en el campo en números. Los números serian luego susceptibles de ser transformados en fórmulas matemáticas que los englobarían, o a la inversa, los principios naturales deberían ser idealizados en un modelo con fórmulas matemáticas que luego serían medidas en experimentos. No todos los científicos NO-físicos estaban de acuerdo con esta noción, ya fuera porque al igual que ahora odiaban las matemáticas, y por ende se habían dedicado a estudiar cualquier cosa que no fura “matemática o física” pero que tuviera que ver con las ciencias de la naturaleza; o por fundamentos filosóficos mucho más profundos.
En la química, por ejemplo, se creó una gran resistencia a aplicar métodos matemáticos, y gran parte de su comunidad siguió trabajando en términos cualitativos. En la biología sucedió algo similar, los que querían emplear matemáticas y asemejar la biología a la física, y los que abogaban por emplear principios independientes a los de la física que fueron agrupados bajo el título de vitalistas (Benton, 1974).
En cualquier caso, una cosa es segura, el trabajo de Mendel es evidentemente fiscalista ya que es uno de los primeros que aplica un cuerpo matemático robusto en un fenómeno biológico dado. De hecho se puede afirmar que la brillantes de su trabajo radica más en la matematización de la herencia (Teicher, 2014) que en el hecho de señalar que habían rasgos que no se mezclaban, cuestión que ya era conocida en su tiempo por otros naturalistas como Darwin, Wallace (Williams, 2005) y probablemente otros miembros de la Royal Society de Londres.
Figura 4.2. Franz Joseph Unger, fue un médico, botánico, paleontólogo, y especialista en fisiología vegetal austríaco.
4.3 Preparación académica de Gregor Mendel
Gregor Mendel “1822-1884” era un moje que nació en el Imperio de Austra-Hungría. Al igual que muchos de los que leemos esto, Mendel no era rico, sus padres eran humildes campesinos, por lo que Mendel no podía aspirar a una vida aislada de la lucha por la subsistencia para estudiar la naturaleza a menos que… se dedicara al sacerdocio. En 1850 falló un examen para obtener una certificación para poder enseñar ciencias naturales, y, de hecho, sus calificaciones más bajas fueron en biología (Henig, 2001). A pesar de ello, el llevó a cabo estudios de matemáticas, física-química y varios aspectos de la biología en la universidad de Viena entre “1851-1853” gracias al auspicio de la iglesia Católica (Henig, 2001). También estudió química y biología. En este último ramo se aproximó a la botánica de la mano de una de las más grandes autoridades en este ramo en la época, Franz Joseph Unger "1800-1870" un fisiólogo vegetal que llevaba varios años trabajando en la obtención de nuevas variedades de plantas mediante la fertilización artificial (Henig, 2001). A parte de sus deberes monásticos, Mendel también fue profesor de básica secundaria en colegios locales y es recordado por ser un profesor amable (Henig, 2001).
4.4 Una abadía o un centro de investigación
Mendel realizó su trabajo en la abadía de Santo Tomas de Brno, una elección peculiar para quien piensa que los sacerdotes solo hacen oraciones y cosas religiosas. La Abadia de San Tomás de Brno era un sitio peculiar.
Figura 4.3. La Abadía de San Tomás de Brno. es un monasterio de los agustinos (OSA.), situado en Brno, en la República Checa. Fue el hogar del genetista y abad Gregor Mendel, que entre 1856 y 1863 llevó a cabo, en las huertas de la abadía, sus famosos experimentos con guisantes que le llevaron a proponer lo que después se conocieron como leyes de la herencia de Mendel. Es la única abadía agustiniana en el mundo. Alberga un museo dedicado a Mendel.2 La iglesia está dedicada a la Asunción de la Virgen María.
Gracias a una larguísima carta a la Asamblea Imperial de Austria solicitando la extensión de los derechos civiles al interior de las órdenes monásticas y solicitando para la comunidad de Brno el permiso para dedicarse exclusivamente a la docencia y a la investigación científica, solicitud que les fue concedida (Henig, 2001). El monasterio adquirió los recursos necesarios para transformarse en un verdadero centro de investigación. La carta fue escrita por varios monjes dentro de los cuales figuraba el propio Mendel (Henig, 2001).
4.5 El laboratorio de Mendel
Esto ocurrió poco después de 1848 cuando e nuevo emperador de Austria llamado Francisco José I tomó el trono. El monasterio contaba ya antes del ingreso de Mendel con un pequeño observatorio astronómico, una biblioteca bastante buena y con un vivero dedicado a la investigación botánica (Henig, 2001). En otras palabras, a diferencia de la imagen romántica general, Mendel no era una excepción en un jardín, el ingresó a una comunidad académica y prosiguió con un programa de investigación que le precedía (Henig, 2001).
4.6 Mendel fue olvidado
Mendel publicó en alemán, el idioma nacional del imperio de Austrai-Hugría sus resultados bajo el título “Versuche über Pflanzenhybriden” o Experimentos sobre hibridación de las plantas (Mendel, 1866) en dos simposios de la Sociedad de Historia Natural de Brno, sin embargo la interpretación de sus resultados por parte de sus pares se enfocó más en la cuestión de hibridación, y no llamó mucho la atención por 34 años (Moore, 2001). Los historiadores de la ciencia aun debaten sobre esto y han formulado una serie de hipótesis:
👉 la comunidad científica de biólogos no estaba preparada para matematizar su ciencia
👉 que simplemente tenía malas relaciones con los posibles contactos de entrada a las comunidades científicas de la época
👉 tuvo que esperar a que la comunidad científica documentara la mitosis, meiosis y cromosomas para poder aceptar los factores hereditarios mendelianos como material físico y no un simple artefacto matemático pitagórico “en otras palabras, una fumada mental”
👉 que su trabajo fue reinterpretado de formas que el propio Mendel no tuvo en mente por autores de eras posteriores.
Lo cierto es que después de publicar sus resultados pocas referencias hay de el en la literatura científica por más de tres décadas. Adicionalmente, el sucesor de Mendel en la abadía ordenó la destrucción de sus archivos. Sin embargo, entre los pocos documentos y libros que lograron sobrevivir se encuentra un ejemplar del Origen de las Especies y de otros libros de Darwin, en los que hay una gran cantidad de anotaciones manuscritas (Henig, 2001). Gracias al testimonio de uno de sus amigos, sabemos que Mendel “estaba muy interesado en las ideas evolutivas, y ciertamente no era un adversario de la teoría evolutiva —aunque afirmaba que algo seguía faltando” (Henig, 2001).
Durante los 34 años de olvido, los científicos prosiguieron sus investigaciones descriptivas, piezas del rompecabezas como las descripciones de la mitosis “1882” y meiosis “1876” fueron fundamentales para una facilitación de la reinterpretación del trabajo de Gregor Mendel, en tal marco conceptual, los descubrimientos cuantitativos de Mendel adquirieron un sentido biológico completo. El trabajo de Mendel fue redescubierto independientemente por tres genetistas. Hugo De Vries "1848-1835", redescubrió las leyes de la herencia por si solo en la década de 1890 pero durante el desarrollo final de su artículo encontró el articulo original de Mendel, por lo que modifico la terminología para que concordara. Sin embargo, en 1900 al publicar originalmente su ensayo omitió ese pequeño detalle, aunque después de críticas por parte de Carl Correns "1864-1833", la preeminencia del descubrimiento fue adjudicada a Mendel.
5. El mito de Mendel
|| REGRESAR AL INDICE ||
El contexto histórico inmediato a Mendel es el de la historia natural y el conflicto del fisicalismo y el vitalismo. Mucho de la biología en el siglo XIX era realizado en términos de historia natural, observación de la naturaleza, observación de estructuras, coleccionismo y clasificación de especímenes, en ultimas lo que el físico Ernest Rutherford "1871-1937" llamaba con un tono algo despectivo, un arte de coleccionistas. En el siglo XIX también se enfrentan continuamente la postura vitalista “teleológica y basada en fuerzas metafísicas como el principio vital, la entelequia y porque no, la mano divina” en contra de los fisicalistas que veían como causas de las cosas a sus componentes últimos, en otras palabras a sus genes y átomos (Cahoone, 2013). Para el siglo XX en sus inicios, las hipótesis atómicas comenzaban a ganar fuerza (Van Melsen, 2004). De las tres grandes ramas de las ciencias de la naturaleza la física comenzó a adquirir un nuevo prestigio del cual no gozaba desde los tiempos en que el trabajo de Newton "1643-1727"" fue valorado. De hecho, muchos de los trabajos más importantes en física provienen de las décadas de 1890 a 1910. Un ejemplo es el trabajo que le valió a Albert Einstein "1879-1955" su premio Nobel, el cual fue publicado en 1904 (Einstein, 1905)
La física adquirió un enorme impulso, así como la postura fisicalista de causas internas o genéticas, en oposición a fuerzas externas. En biología esta postura fue reforzada cuando Weismann "1834-1914" propuso su famosa teoría de línea germinal y línea somática con sus famosos experimentos de la cola de los ratones (Kutschera & Niklas, 2004). La meiosis fue descrita entre "1876-1883" y en la década de 1900 a 1910 fue conectada por los principios hereditarios o leyes de segregación y distribución independiente por Walter Sutton (McKusick, 1960). Para la primera década del siglo XX las nociones vitalistas habían sido abandonadas por gran parte de la comunidad de biólogos, y de esta forma estaban preparados para abrazar una teórica de causas internas, de causas genéticas para la forma y función de los seres vivos.
Al igual que los países, las comunidades científicas gozan con elevar a ciertos individuos por sobre sus comunidades, convirtiéndolos en paladines de la razón, en héroes de la ciencia. Gregor Mendel (1822-1884) solo puede ser opacado por Charles Darwin al interior de la escala de héroes de la biología en la segunda mitad del siglo XIX.A él se le atribuye ser el Padre de la Genética y generalmente se lo ilustra como un individuo aislado en, un jardín, resaltando poco su labor monacal y su vida algo frustrante. En cualquier caso. su trabajo se ha convertido en la base de lo que actualmente denominamos genética clásica o genética mendeliana, aunque en esta serie de escritos no las tratamos como sinónimos. La genética mendeliana está relacionada con el trabajo de Mendel hasta el dihibrido en el pódelo biológico de Pisum sativum, mientras que la genética clásica o escolarizada inicia con el “redescubrimiento de Mendel” en el cambio de siglo.
En consecuencia, Mendel junto con Darwin es incluido en todos los cursos de introducción a la biología. Sin embargo, es esta breve serie de artículos veremos como mucho de lo que hoy llamamos genética mendeliana, fue desarrollada especialmente por dos autores que se disputaban la prioridad histórica, Carl Correns y Hugo de Vries.
5.1 Características del artículo de Mendel
Pocas veces me he sentado a pensar detalladamente en el modo en que aprendemos, leemos y enseñamos a Mendel, ya sea en el contexto de la ciencia del bachillerato o de la universidad. Tal vez la excusa de siempre con respecto a las limitaciones de tiempo o al peso de la tradición. Sin embargo si el trabajo de la ciencia es indagar para dar luz sobre los mitos, es bueno realizar ese mismo ejercicio sobre los mitos propios de la labor científica (S. J. Gould, 1982). Tal vez el primer autor de divulgación científica adepto estos ejercicios fue Stiphen J. Gould, y de sus lecturas aprendí algo muy significativo.
Que el hecho de develar el mito no mina los fundamentos teóricos, epistemológicos o empíricos sobre los que se fundamenta una ciencia, por el contrario, la hace más sólida; la ciencia es una labor humana y como tal está influida por sesgos, costumbres y límites de los instrumentos que empleamos para trabajar. En esta serie de artículos procederé a realizar una traducción y comentarios de autores que han indagado sobre el mito de Mendel y el mendelismo. Esto con el objeto de comprender mejor como se desarrolló la genética postmendeliana en la primera década del siglo XX.
5.2 Mendel trabajaba sobre especiación, no sobre herencia
Como se mencionó anteriormente, Mendel estaba interesado en la teoría de la evolución, aunque afirmaba que algo seguía faltando. Probablemente lo que faltaba era el problema que siempre tuvo Darwin con su teoría y era precisamente el condenado “origen de las especies”, si ya se, ese es el nombre de libro, pero paradójicamente ese problema es evadido de forma monumental en toda su obra. El trabajo de Darwin y Wallace no es acerca del origen sino de la selección de variedades que se diferencia entre sí, dejando el problema del verdadero origen de las especies muy abierto a discusión. De esta forma es posible reconciliar todo el proyecto de investigación mendeliano.
Según Moore (2001) el artículo original de Mendel trataba sobre el proceso de especiación, y de hecho no incluía palabras traducibles por herencia. Por el contrario, Mendel intentaba descubrir las leyes que gobiernan la formación y desarrollo de híbridos. De hecho las discusiones que prosiguieron a la exposición de los resultados experimentales de Mendel a la Sociedad de Ciencias Naturales de Brunn en 1865 fueron a cerca del problema de la hibridación y no de la herencia (Monaghan & Corcos, 1990). Otro aspecto paradójico es que Mendel tampoco menciona el radio 9:3:3:1 de la F2 del cruce dihíbrido con la que generalmente se describe la así llamada Ley de Distribución Independiente “independent assortment”. De cierta forma podemos señalar que Mendel no fue mendeliano (Olby, 1979)
5.3 Mendel nunca habló de 9:3:3:1
De Mendel no nos llegan sus palabras o modos de representación, aunque su artículo de 1865 es extremadamente famoso y algo largo “45 páginas” (Mendel, 1866, 1996) aparentemente es muy poco leído a la hora de escribir libros de texto. De hecho, lo que aprendemos de Mendel es en realidad el mendelismo creado a partir de los descubrimientos a principios de siglo XX y su interpretación en el trabajo de Mendel de lo que se trabajaba en el siglo XX. Como se mencionó en el artículo anterior, Mendel no expresó la ley de la distribución independiente en la forma de proporción 9:3:3:1, sino que la expresó de forma textual: “El comportamiento de cada par de caracteres diferentes en la asociación de un híbrido es independiente de todas las diferencias en las dos plantas parentales” (Monaghan & Corcos, 1990; Moore, 2001; Olby, 1979).
Esa frase es el clímax del artículo original, y fue posteriormente desarrollada por los redescubridores del siglo XX como la ley de distribución independiente. Moore (2001) señala que, de hecho, en el artículo de Mendel, no se expresan las famosas leyes de Mendel, o al menos no como las conocemos, aprendemos, estudiamos y enseñamos actualmente.
El núcleo fundamental sobre el cual construimos el modelo matemático de la genética mendeliana se basa en la equivalencia de un carácter en una pareja de factores particulados. A pesar de que la influencia del trabajo de Mendel es grande, aparentemente sus resultados no son tan grandes como la tradición ha adjudicado. El trabajo de Mendel no da evidencias que el manejara los conceptos de homocigo dominante (AA) y homocigoto recesivo (aa) en términos algebráicos estándar.
Mendel jamás trabajó la naturaleza de los genes y tampoco describió la equivalencia entre la pareja de rasgos y la pareja de factores heredables sobre la que se construye el modelo matemático mendeliano. En otras palabras, Mendel no era mendeliano. Carl Correns fue el primero es introducir la equivalencia entre par de rasgos y par de factores (Monaghan & Corcos, 1990; Moore, 2001; Olby, 1979).
Mendel empleó la teoría celular de fertilización para explicar porque los descendientes de los linajes híbridos formaban linajes puros y otros no. El deseaba esclarecer la composición de los así llamados gametos en los híbridos. Mendel no empleó su teoría para localizar genes no menciona ninguna palabra que se acerque a tal concepto. Mendel estaba estudiando el número y tipo de progenie producida por híbridos autofertilizados, no la herencia de los caracteres. De ser así y si Moore y colaboradores están en lo correcto, la mayor parte del modelo matemático que actualmente llamamos mendeliano, es un producto de los redescubridores y no del propio Mendel.
5.4 Verdaderas definiciones mendelianas
A pesar de que Mendel no manejaba el concepto de gen, si es posible rastrear dos conceptos y dos palabras asociadas a lo que manejamos como “carácter-factor” o más contemporáneamente “fenotipo-genotipo” y es el concepto de Merkmal y Elemente. Merkmal se define como lo que es posible ver, la apariencia externa, en este sentido los redescubridores lo tradujeron como caracteres y actualmente lo llamaríamos fenotipo (Monaghan & Corcos, 1990; Moore, 2001; Olby, 1979).
La otra palabra es elemente, la cual sería entendida como aquello que se movía entre las generaciones. Aunque actualmente lo podríamos entender como genotipo, en aquella época con la discusión entre fisicalistas y vitalistas podría entenderse en términos de una fuerza inmaterial (Monaghan & Corcos, 1990; Moore, 2001; Olby, 1979). De hecho, la definición de elemente era tan diferente a la que se maneja en el modelo matemático “mendeliano” que por ejemplo los individuos de linaje puro no se describían con parejas (AA o aa) sino con una sola letra.
El cruce F2 del monohíbrido mendeliano se describe en la actualidad de la forma algebraica AA + 2Aa + aa, la cual es dechecho la respuesta del caso de factorización suma de cuadrados fue descrita originalmente como A+2Aa+a (Mendel, 1866, 1996). Lo cual implica que Mendel tampoco manejaba concepto de monocigoto y heterocigoto, lo cual a su vez explica la razón de no existir una palabra mendeliana para esos conceptos. Tal vez Mendel creía que los linajes puros “o monocigotos” solo poseían un elemente, o mucho más probablemente, pensaba que su modelo solo era una entelequia, un modelo únicamente instrumentalista que no representaba para nada las estructuras reales, “una fumada mental que funcionaba” (Monaghan & Corcos, 1990; Moore, 2001; Olby, 1979).
Esto último es un rasgo muy común de los modelos matemáticos de la ciencia de Prusia y Austria. De hecho, el modelo actual del átomo se basa en ese mismo principio, un modelo matemático que no busca representar una realidad estructural, pero que no fue tomado en cuenta por muchos físicos por la misma razón, durante muchos años solo fue una inferencia matemática para explicar fenómenos, y no es que eso hubiera cambiado actualmente, lo que sucede es que actualmente parecemos confiar más en las matemáticas.
5.5 ¿Por qué es famoso?
La pregunta que emerge de este panorama es, si Mendel no construyó todo el modelo matemático que le adjudicamos, ¿cómo es que lo llegamos a adjudicar? La respuesta viene en el momento en que las matemáticas irrumpieron realmente en toda una comunidad científica y no en un solo individuo, lo cual fue en la generación de científicos activa en el cambio de siglo cerca del año 1900. En ese momento varios científicos con entrenamiento matemático se avocaron a trabajar problemas semejantes a los de Mendel pero con un enfoque más en la herencia que en la hibridación, y en base a ese conflicto la figura de Mendel fue fabricada para combatir en un conflicto de prioridades científicas, pero eso lo veremos en el siguiente capítulo (Monaghan & Corcos, 1990; Moore, 2001; Olby, 1979).
6. Principios de estadística básica para genética
|| REGRESAR AL INDICE ||
Según Galileo Galilei 1564-1642 las matemáticas poseen una autoridad que solo podría ser superada por la de Dios en persona, mientras que Lord Kelvin 1824-1907 opinaba que la única manera de conocer algo de manera satisfactoria era a través de las matemáticas, prácticamente una ciencia solo se reconoce como tal, al emplear un núcleo matemático, que es en principio simple. De hecho, la biología no fue reconocida como una ciencia a la par de la física hasta que se logró un fundamento matemático fuerte, sin embargo, los biólogos pre-mendelianos se oponían a este esfuerzo, pues consideraban que la física y la biología eran ciencias completamente diferentes. Los primeros en cuestionar esta separación fueron los mendelianos, que iniciaron con el arduo trabajo de introducir una teoría matemática en los fenómenos de la vida. El primero en hacer esto fue Gregor Mendel 1822-1884, aunque el enfoque de su investigación y la actitud anti-matemática en la biología de la época hicieron que su trabajo fuera irrelevante por 34 años.
Justo al inicio del siglo XX la comunidad científica se dio cuenta de las posibilidades que ofrecía el cálculo de probabilidades y el álgebra simple para entender el comportamiento de la herencia de rasgos de caracteres en los seres vivos. Este esfuerzo fue posteriormente llevado a su máxima expresión en la Teoría Sintética de la Evolución, punto en el cual el modelo matemático se extendió a la herencia y cambio de los caracteres en poblaciones completas. En la actualidad, si bien los principios siguen siendo simples, la enorme cantidad de interacciones hace que los procesos matemáticos sean más pesados, por lo que se requieren de supercomputadoras para hacer el trabajo predictivo que inicialmente era realizado con lápiz y papel.
Hay dos conceptos que nos importan a la hora de formular modelos matemáticos son los del azar y el determinismo. El determinismo se define generalmente como eventos que pueden predecirse de manera determinada, sin embargo, esta noción solo es correcta para sistemas simples donde se tiene el control de todas las variables, cuando un sistema determinista se hace complejo, la interacción de sus componentes lo hacen caótico y difícil de predecir, dando nacimiento a procesos azarosos de tipo clásico. El azar por otro lado se define como un sistema difícil de predecir, pero nuevamente esto solo aplica para sistemas simples con pocos eventos, ya que cuando se analiza un sistema complejo con muchos eventos, pero perfectamente aleatorio, este se hace predecible hasta cierto punto.
La fluidez de los anteriores conceptos hace que sea muy importante la formulación de medios para medirlos sin tantas ambigüedades, y la ciencia que se encarga de esto es la estadística, la cual a su vez se fundamenta en el cálculo diferencial.
6.1 Número de entidades
El número de entidades (Nj) es el número entero (cuantizado o sin decimales) obtenido por conteo de entidades, que suelen ser moléculas, átomos o iones; pero que puede ser cualquier entidad discreta cuantizada por el número de papas, el número de personas, o el número de semillas de un determinado color. El parámetro número de entidades se considera adimensional, y por ende no le vamos a asociar unidades.
Figura 6.1. Un parámetro dado o medición puede realizarse a una amplia variedad de entidades u objetos, de allí que se requiera del símbolo de entidad contada y medida para indicar cual es el objeto al cual estamos haciendo referencia.
No todas las áreas de conocimiento manejan el mismo tipo de nomenclatura, por ejemplo en estadística el parámetro se denomina como frecuencia absoluta, de la cual tendremos dos divisiones dependiendo de cómo estemos analizando el sistema.
👉 la frecuencia absoluta total, frecuencia acumulativa o número de entidades total (N): representa la suma de objetos que pueden ser contados.
👉 la frecuencia absoluta de subgrupo o número de entidades j-ésimo (NJ): representa la cantidad de objetos que cumplen una determinada característica que los distingue de otros objetos semejantes al interior del sistema de estudio.
Ejemplo. Cuente los siguientes objetos y exprese su valor como un parámetro matemático.
Ejemplo. Cuente los siguientes objetos y exprese su valor como un parámetro matemático.
Ejemplo. Cuente los siguientes objetos y exprese su valor como un parámetro matemático.
Ejemplo. Cuente los siguientes objetos y exprese su valor como un parámetro matemático.
La frecuencia absoluta total y la frecuencia absoluta de un subgrupo se relacionan por medio de la siguiente ecuación:
(Eq. 6.1) Frecuencia acumulativa/total experimental absoluta.
Frecuencia relativa empírica
La probabilidad empírica (PJ), la frecuencia relativa o la probabilidad experimental de un evento es el cociente entre la frecuencia de subgrupo (NJ) sobre la frecuencia acumulativa (N). Un problema que nos encontraremos frecuentemente con las frecuencias relativas, es el hecho de que el símbolo P se empezará a repetir mucho, sin portar información relevante, lo que aumenta de manera innecesaria la carga simbólica de algunos axiomas, es por eso que podemos emplear una solución semejante a la que se usa en química del equilibrio con la concentración molar, y emplear corchetes para inferir de manera implícita que estamos calculando una frecuencia relativa o probabilidad.
(Eq. 6.2) Frecuencia relativa experimental o probabilidad experimental en términos del número racional o fraccionario número de entidades sobre número total.
La probabilidad empírica estima las probabilidades a partir de la experiencia y la observación. Dado un evento A en un espacio muestral j (ejemplo, evento: semilla amarilla; en espacio muestral: color de semilla), la frecuencia relativa de A será un cociente entre el número de objetos que cumple la cualidad A dividido en el número total de objetos, siendo un valor que va desde 0 a 1.
Ejemplo. Determine la frecuencia o probabilidad experimental mediante la siguiente figura.
Ejemplo. Determine la frecuencia o probabilidad experimental mediante la siguiente figura.
Ejemplo. Determine la frecuencia o probabilidad experimental mediante la siguiente figura.
6.2 Frecuencia teórica o estándar
Las frecuencias no solo se obtienen de contar objetos, sino al realizar un proceso analítico sobre un sistema antes de realizar el propio experimento o conteo real. Simbolizaremos las frecuencias teóricas adicionando el símbolo 0 o 0 que deberá leerse como teórico o estándar para evitar adicionar símbolos como (teo) que aumentan la carga simbólica de los términos algebraicos. La frecuencia absoluta de subgrupo teórico (Nj°) representa el número de veces que se repite una opción dentro de un conjunto de posibilidades de un sistema. En este caso la frecuencia acumulativa teórica vuelve a ser la suma de las frecuencias de subgrupo teóricas.
(Eq. 6.3) Frecuencia acumulativa/total teórica absoluta.
El cociente de las frecuencias teóricas de subgrupo y la frecuencia acumulativa teórica genera la frecuencia relativa teórica, o simplemente la probabilidad teórica.
(Eq. 6.4) Frecuencia relativa experimental o probabilidad experimental.
6.3 Porcentajes y radios
Las probabilidades pueden expresarse de tres maneras:
👉 Frecuencias relativas: son valores con un rango entre 0 y 1, donde 0 representa que el evento no puede suceder y 1 que el evento es inevitable. Aunque tendemos a pensar que los números entre 0 y 1 son todos decimales, es conveniente tener en cuenta que algunos números fraccionarios representarán probabilidades comunes, por lo que es importante memorizarse algunos de estos cocientes notables y su interconversión a valores decimales.
Tabla 6.1. Tabla de cocientes aritméticos notables, se resalta en fondo verde algunos valores que son particularmente comunes en el curso de genética clásica. En fondo rojo se resaltan los cocientes base, memorizando el cociente base es posible obtener cualquier cociente de su serie respectiva multiplicando por el entero respectivo.
|
Decimal |
Fracciones equivalentes |
||||||
|
1 |
20/20 |
16/16 |
10/10 |
5/5 |
4/4 |
3/3 |
2/2 |
|
0.95 |
19/20 |
|
|
|
|
|
|
|
0.90 |
18/20 |
|
9/10 |
|
|
|
|
|
0.85 |
17/20 |
|
|
|
|
|
|
|
0.80 |
16/20 |
|
8/10 |
4/5 |
|
|
|
|
0.75 |
15/20 |
12/16 |
|
|
3/4 |
|
|
|
0.70 |
14/20 |
|
7/10 |
|
|
|
|
|
0.666666666 |
|
|
|
|
|
2/3 |
|
|
0.65 |
13/20 |
|
|
|
|
|
|
|
0.60 |
12/20 |
|
6/10 |
3/5 |
|
|
|
|
0.5625 |
|
9/16 |
|
|
|
|
|
|
0.55 |
11/20 |
|
|
|
|
|
|
|
0.50 |
10/20 |
8/16 |
5/10 |
|
2/4 |
|
1/2 |
|
0.45 |
9/20 |
|
|
|
|
|
|
|
0.40 |
8/20 |
|
4/10 |
2/5 |
|
|
|
|
0.35 |
7/20 |
|
|
|
|
|
|
|
0.333333333 |
|
|
|
|
|
1/3 |
|
|
0.30 |
6/20 |
|
3/10 |
|
|
|
|
|
0.25 |
5/20 |
4/16 |
|
|
1/4 |
|
|
|
0.20 |
4/20 |
|
2/10 |
1/5 |
|
|
|
|
0.1875 |
|
3/16 |
|
|
|
|
|
|
0.15 |
3/20 |
|
|
|
|
|
|
|
0.125 |
|
2/16 |
|
|
|
|
|
|
0.10 |
2/20 |
|
1/10 |
|
|
|
|
|
0.0625 |
|
1/16 |
|
|
|
|
|
|
0.05 |
1/20 |
|
|
|
|
|
|
👉 Porcentajes: Los porcentajes representan la frecuencia aplicada a una frecuencia acumulativa estándar de 100 unidades, por ende, se define matemáticamente como el producto entre la frecuencia relativa por la constante de porcentaje que es 100 %, donde el símbolo % es igual a 10-2. Debido a que 100 % es igual a 100 (10-2) y por ende igual a 1, podemos concluir que una frecuencia relativa 1 adimensional es igual a 100 %.
Los porcentajes son la forma más común de representar una probabilidad en textos de todo tipo, sin embargo, son términos complejos en manipulaciones algebraicas, es por ende que se aconseja convertir los porcentajes a frecuencias cuando se hacen manipulaciones con las leyes de la probabilidad dividiendo los porcentajes entre 100 %.
Ejemplo. Convierta los siguientes porcentajes a frecuencias: 75 % 25 % 33 % 50 %.
Ejemplo. Convierta la siguiente frecuencia relativa a porcentaje: 2/4, 2/8, 6/8, 4/6, 2/6, 4/16.
👉 Radio: son comparaciones de frecuencias absolutas de subgrupo, sean estas teóricas o experimentales. Por ejemplo, para la moneda teórica el radio de cara a sello se expresa como 1:1. Para el dado de cuatro caras teórico el radio de expresa como 1:1:1:1. Un radio se puede expresar también como un evento dado con respecto a la suma de las más posibilidades, así el radio de la cara II del dado de 6 caras teórico será de 1:5. En ocasiones los radios pueden expresarse como polinomios, donde los coeficientes algebraicos representan el número de entidades. Tenga en cuenta que, por reglas del álgebra, los coeficientes 1 están implícitos, por lo que no se muestran, pero si estarán presentes.
7. Propiedades de las probabilidades
|| REGRESAR AL INDICE ||
Las probabilidades vistas hasta el momento son individuales, sin embargo, cuando tenemos sistemas compuestos por más de un elemento aleatorio, podemos expresar propiedades emergentes que surgen de su interacción de las partículas en el sistema. Tenga en cuenta que dependiendo de la interacción deberemos ejecutar diferentes operaciones matemáticas, desde sumas y restas hasta potencias y factoriales. Adicionalmente, dado que estructuralmente las probabilidades teóricas y experimentales poseen ecuaciones semejantes, definiremos las siguientes probabilidades solo para las probabilidades experimentales, pero estas aplicarán de igual forma a las probabilidades teóricas.
7.1 La probabilidad total.
Al igual que la frecuencia absoluta aditiva o total es la suma de las frecuencias de subgrupo, la frecuencia relativa aditiva o total (P) es la suma (∑) a las frecuencias relativas parciales (Pj). Sin embargo, a diferencia de la frecuencia absoluta aditiva que puede tener un valor arbitrario que dependerá del sistema de estudio, la frecuencia relativa aditiva siempre tiene un valor de 1 o del 100% cuando se expresa como un porcentaje.
(Eq. 7.1) Probabilidad total (P) en términos de las probabilidades parciales (Pj).
La probabilidad total igual a 1 es un instrumento de corrección útil a la hora de finalizar un ejercicio de lápiz y papel, pues si la suma de probabilidades parciales no es 1 o significativamente cercana a 1 (ejemplo 0.9999, o 1.0001) entonces significa que se cometieron errores en los cálculos.
7.2 Probabilidad de dos o más eventos opcionales.
En este caso, queremos saber qué tan probable es que dos eventos independientes sucedan sin importar que sea simultáneo, en este orden de ideas planteamos los dos eventos buscados como opciones, y queremos saber qué tan probable es acertar a cualquiera de las dos opciones. En este caso se emplea generalmente el conector “o” de opción “P(A o B)”. Para este caso, la solución aritmética es la suma de probabilidades, por lo que también podemos emplear la notación “P(A más B)”, lo cual implica que debemos sumar las probabilidades del evento A y del evento B. En caso de que el valor de P sea un decimal o un porcentaje se efectúa una suma simple, pero en el caso de que P sea un fraccionario, debemos ejecutar una suma de fraccionarios, aunque por lo general dado que ambas P tienen el mismo denominador, la expresión de la suma es sencilla.
(Eq. 7.2)Probabilidad de dos eventos opcionales.
(Eq. 7.3) Probabilidades de dos o más eventos opcionales.
7.3 Probabilidad de que no ocurra j.
Evidentemente el conector aquí es el “no”. Estos casos se basan en determinar qué tan probable es que no aparezca un determinado subgrupo j. Y para hacerlo aplicamos la siguiente fórmula.
(Eq. 7.4) Probabilidades de no ocurrencia del subgrupo j.
7.4 Probabilidad de dos eventos simultáneos o dependientes.
En este caso, queremos saber qué tan probable es que dos eventos independientes-simultáneos o dependientes sucedan al mismo tiempo, simultáneamente, para esto generalmente empleamos el conector “y” de inclusión, y para resolver esto, debemos multiplicar las dos probabilidades involucradas, de allí que la notación sea P(AB)
(Eq. 7.5) Probabilidad de dos eventos simultáneos.
(Eq. 7.6) Probabilidad de dos o mas eventos simultáneos.
Ejemplo. ¿Cuál es la probabilidad de que al arrojar dos dados de 4 caras ideales me aparezca un doble III?
Ejemplo. ¿Cuál es la probabilidad de que al arrojar tres dados de 6 caras ideales me aparezca un triple VI?
7.5 Recuperar un número de eventos buscados i calculados a partir de una probabilidad teórica y el número total experimental.
Resulta común tener que comparar probabilidades, pero algunas técnicas de comparación nos exigirán emplear número de entidades en lugar de las frecuencias relativas. En tal caso, debemos poder expresar una frecuencia relativa teórica ([j]0) como una frecuencia absoluta teórica (Nj°) empleando la frecuencia aditiva experimental (N).
(Eq. 7.7) Número de entidades teórico calculado a partir del número de entidades aditivo experimental.
Ejemplo. Si la probabilidad de un dado ideal para la cara II es de 1/4, y además lo lanzara unas 60 veces, ¿Cuál sería el número de veces que debería aparecer el número II?
7.6 Probabilidades ordinales y permutaciones.
Las probabilidades condicionales encierras más trucos que el solo hecho de tener que multiplicarlas, por ejemplo, si tenemos tres subgrupos, y nos piden calcular las probabilidades de A B C en ese orden, entonces la probabilidad no podrá calcularse con la mera multiplicación, úes la multiplicación de probabilidades solo nos dará la probabilidad de los tres subgrupos en cualquier orden si una organización predeterminada.
Para poder calcular la probabilidad de una determinada serie organizada deberemos emplear una permutación. La permutación es una técnica de conteo que permite calcular las posibles ordenaciones de los elementos de un conjunto o número de elementos del espacio muestral de un experimento aleatorio. En esta técnica de conteo se considera que existe el orden en la muestra, pero no es posible repetir ningún elemento de la población en su conformación.
La fórmula de la permutación nos permitirá obtener la probabilidad de una determinada serie organizada dentro de un conjunto de series posibles, sin tener que realizar un proceso de descarte manual:
(Eq. 7.8) Probabilidad de que una de las posibles series se manifieste al azar dentro de un conjunto posible de permutaciones.
8. Pisum sativum
|| REGRESAR AL INDICE ||
8.1 Elección del organismo modelo
Elegir un organismo modelo adecuado para las necesidades experimentales es crucial, si se elige mal se pueden obtener falsos resultados, o resultados demasiado complejos para crear un modelo viable, o puede hacerse demasiado costoso económicamente de mantener. Básicamente, todo el éxito de Mendel se debió a la elección de la planta de un modelo biológico fácil de simplificar, y que era económico de mantener, el guisante o arveja “Pisum sativum” (Sadava et al., 2014). Algunas ventajas de la alverja como organismo modelo son:
👉 La alverja es fácil y por ende, económico, de cultivar.
👉 Genera una gran cantidad de descendientes por generación “aspecto vital para los análisis estadísticos”.
👉 Sus caracteres poseen rasgos diferenciables cualitativamente.
👉 Son autofertilizables y soportan la endogamia.
👉 La fertilización puede manipularse artificialmente ofreciendo control sobre los cruces entre los individuos.
8.2 Control sobre la reproducción
La polinización artificial se podía hacer sin ningún problema con la ayuda de un pincel que trasladaba el polen de una flor a otra. Por lo que podía conocer cuáles eran los caracteres de los parentales con respecto a sus descendientes. Sin embargo, los primero que hizo Mendel fue un proceso de purificación de caracteres (Sadava et al., 2014).
8.3 Anacronismo
Emplearemos lo más posible las definiciones mendelianas, pues sus equivalentes no fueron desarrollados hasta después de su muerte.
👉 Caracteres: Característica física a observar, como tamaño, textura, color o forma.
👉 Rasgos: Es el estado en que aparece un solo carácter, ya sea amarillo o verde, liso o rugoso, largo o corto.
Esto es porque las definiciones mendelianas están más relacionadas con lo que percibimos de las plantas, y no parten del presupuesto teórico que por cierto AUN NO HEMOS INTRODUCIDO.
8.4 Caracteres y rasgos de P. sativum
Mendel buscada caracteres con rasgos fácilmente contrastables, es decir que tuvieran una relación 0:1, blanco:negro etc. (Sadava et al., 2014). Los caracteres elegidos se observan en la Figura 8.1.
Figura 8.1. Los siete caracteres y sus correspondientes parejas de rasgos dominante y recesivo
9. Diseño experimental mendeliano
|| REGRESAR AL INDICE ||
Muchas veces cometemos el pecado de analizar directamente los resultados que obtuvo Mendel y damos poca importancia al diseño experimental, el cual da muestras de una serie de presupuestos subyacentes a las ciencias de su época, especialmente en lo concerniente al reduccionismo matemático puesto de moda por Isaac Newton ya en 1687, casi 170 años antes (Falk, 2001, 2006).
9.1 Una teoría de la herencia discreta
El mendelismo es una teoría de la herencia que busca explicar los fenómenos hereditarios mediante un modelo matemático que asume factores discretos que hoy en día llamamos genes y alelos para predecir estadísticamente las características físicas de los seres vivos. El objetivo es que los números obtenidos experimentalmente sean los mismos que han sido predichos teóricamente. Por lo anterior, se puede decir que el objeto último de un ejercicio mendeliano matematizado es comparar dos cantidades numéricas, una experimental y otra teórica (Cleophas & Zwinderman, 2017; Pilgrim, 1986).
9.2 Purificación de los linajes experimentales
En la naturaleza, las poblaciones de las especies experimentan altos niveles de diversidad, flores de colores y formas diferentes, textura de la semilla, tamaños de la planta entre otros. El método newtoniano de hacer ciencia implicaba abandonar todo este ruido ambiental y/o encontrar un sistema de variables reducidas.
Por lo anterior era necesario que Mendel purificara su sistema de estudio. Para hacer esto, Mendel tuvo que autopolinizar artificialmente las flores de cada uno de sus linajes por varias generaciones sin permitir la producción de semilla no planificada. En el proceso algunos rasgos de las plantas se perdieron de forma tal que llegó a un sistema simple de dos rasgos por cada carácter (Sadava et al., 2014).
A pesar del popular mito de Newton y la manzana, en el texto que él escribió llamado “Principios Matemáticos de Filosofía Natural” se puede interpretar que el proceso fue deductivo. Newton imaginó un sistema NO-natural más simple sobre el cual podía extraer sus hipótesis. El proceso también fue empleado por Mendel pero en el diseño experimental (Müller-Wille, 2007). Es por esto que podemos juzgar a la genética clásica como incapaz de dar cuenta de la variabilidad encontrada en la naturaleza, pero este no era su objetivo, lo que buscaba era regularidades expresables en términos de fórmulas matemáticas simples de fenómenos elegidos.
Figura 9.1. Evidentemente hay muchos morados aquí, y es muy probable que Mendel hubiera tenido que eliminar algunos colores de flor para tener un sistema simple, el punto es que los textos no son claros en cual fue el tono de morado empleado por Mendel, lo único claro es que su sistema solo tenía dos colores, mientras que la variación real es más diversa, lo mismo ocurre con otros caracteres.
9.3 Procedimiento experimental
👉 Tener un linaje puro de dos rasgos diferentes para un carácter, a esta generación se la denomina parental o P.
👉 Cortar los anteridios de las flores femeninas para evitar posibles autofecundaciones no deseadas.
👉 Tomar polen de los anteridios de las flores masculinas y desecharlas, luego pasar el polen a las flores femeninas a las que se les ha retirado los anteridios, esta flor femenina madre de una generación y su compañero desechado serán la generación parental o P.
👉 La primera generación se la denomina primer filial o F1. Los caracteres de la generación F1 son cuidadosamente consignados.
En algunas plantas F1 se deja auto-polinizar para producir una segunda generación filial, también llamada F2. Los datos de la segunda generación son cuidadosamente consignados. (Sadava et al., 2014).
9.4 Nomenclatura entre las generaciones
La primera generación de plantas de linajes puros se llamarán generación parental, y se simboliza con la letra P. La primera generación de hijos se simboliza con la letra F1 que se lee como filial 1. La segunda generación de descendientes “nietos” se los simboliza como F2. Que se lee como filial 2. La tercera generación será F3. La razón para esta nomenclatura es evidentemente un aspecto a posteriori de los primeros ensayos de Mendel y algo que se sabía desde la antigüedad, algunos rasgos de carácter desaparecían en la primera filial y regresaban en filiales posteriores como de la nada, por esto el modelo matemático mendeliano debía abarcar más de una generación.
9.5 Símbolos para los sexos
A parte de las generaciones, otra variable a tener en cuenta es el sexo, por lo que es conveniente introducir su simbología. El escudo y la lanza de Ares (♂), que simboliza la guerra, la sangre, la violencia, al planeta Marte “rojo” y la masculinidad. El espejo de Afrodita (♀), que simboliza al amor, la feminidad "y la vanidad", al planeta Venus “la estrella de la mañana”. Aunque las plantas de alverja son hermafroditas, resulta conveniente tener en cuenta estos símbolos. Ahora bien, no es que se trate de mantener un estereotipo de comportamiento, sin embargo, negar la historia de dichos símbolos sería algo inconsecuente.
9.6 Definición de cruce monohíbrido, dihíbrido y más allá
Un híbrido es el resultado de la mezcla de los linajes puros, la hibridación es el proceso por el cual se toma a un individuo puro para un rasgo y se lo fecunda con el material reproductivo de un individuo con otro rasgo puro (Sadava et al., 2014). Dependiendo de cuantos caracteres se estudian los cruces híbridos pueden clasificarse como:
👉 El cruce mohíbrido busca contrastar un solo carácter, por ejemplo, color de la flor. En matemática estadística equivale a tener una sola variable categórica.
👉 El cruce dihíbrido busca contrastar dos caracteres de forma simultánea, por ejemplo, color de la flor y forma de la semilla. En matemática estadística corresponde a tener dos variables categóricas.
👉 El cruce trihíbrido busca contrastar tres caracteres de forma simultánea, por ejemplo, forma de la semilla, forma de la vaina, y tamaño de la planta. En matemática estadística corresponde a tener tres variables categóricas.
En la medida que la cantidad de caracteres se incrementa la complejidad matemática lo hace de forma exponencial. Por esta razón iniciaremos con el sistema de estudio más sencillo, el cruce monohíbrido (Sadava et al., 2014).
9.7 El modelo teórico general, obtención de hipótesis de trabajo
El modelo de herencia entre los cultivadores, y de hecho con el que trabajaban en casi todas partes en Europa era continuo. Se percibía a las características como tarros de pintura de diferentes colores, cuando se generaba el hibrido las características se mezclaban en un nivel intermedio. Si bien incluso el propio Darwin encontró casos en los que este modelo no aplica, vale la pena iniciar con él (Sadava et al., 2014).
👉 Condición: generación parental con individuos cuyas características son diferentes y puras. Los rasgos de cada carácter son cualitativamente diferenciables, por ejemplo: (liso contra arrugado; alto contra bajo; verde contra amarillo).
👉 Hipótesis nula: Los rasgos de cada carácter a estudiar en la F1 son una mezcla intermedia de los rasgos de la generación P. Como hemos visto existen flores con tono rosado tenue, morado oscuro y blancas, por lo que es una hipótesis que tiene sentido.
👉 Hipótesis alternativa: Los rasgos de cada carácter a estudiar en la F1 son los mismos de alguno de los parentales sin experimentar una mezcla.
10. Resultados experimentales del cruce monohíbrido y ley de dominancia completa
|| REGRESAR AL INDICE ||
El cruce monohíbrido se puede modelar matemáticamente como una variable categórica “carácter” que puede adquirir diferentes valores “rasgos”, y en este sentido solo hay un carácter con dos rasgos. Su simplicidad matemática obedece a un trabajo de purificación previo a la intervención experimental y no a un comportamiento natural, pues como vimos en capítulos anteriores la variabilidad natural es mucho más grande (Sadava et al., 2014).
10.1 Resultados de la F1 experimentales
En la F1 uno de los rasgos en cada uno de los caracteres de estudio invariablemente desapareció completamente, mientras que el otro rasgo era evidente en todos los miembros F1. De allí surge la simbología dominante y recesiva. Tradicionalmente se ha empleado la letra mayúscula para el dominante y la minúscula para el recesivo, pero hay que tener en cuenta que eso solo funciona para un sistema mendeliano en el cual solo hay dos rasgos por cada carácter que es el sistema más simple de todos. Matemáticamente se puede definir que la probabilidad de que el dominante experimental [A] se manifiesta, es certera o de frecuencia 1, mientras que la probabilidad del recesivo experimental [a] es imposible o de frecuencia cero.
10.2 Resultados de la F2 experimentales y la primera ley de la herencia
A diferencia de lo que sucedía en la primera generación de crías F1, la segunda generación de crías F2 manifestó el rasgo desaparecido, pero en menor proporción. Este rasgo débil que desaparece o posee una proporción menor fue denominado el recesivo.
Tabla 10.1. Resultados mendelianos para la F2. Observe que las probabilidades experimentales siempre oscilan en una proporción de 0.75:0.25 también llamada 3:1. Se emplea la letra (D) para representar los rasgos dominantes y (r) para los rasgos recesivos
|
|
N(D) Número experimental de dominantes |
N(r) Número experimental de recesivos |
N Número total experimental |
Probabilidad experimental de dominantes |
Probabilidad experimental de recesivos |
|
Color de la flor |
705 |
224 |
929 |
0.76 |
0.24 |
|
Color de la semilla |
6022 |
2001 |
8023 |
0.75 |
0.25 |
|
Textura de la semilla |
5474 |
1850 |
7324 |
0.75 |
0.25 |
|
Color de la vaina |
428 |
152 |
580 |
0.74 |
0.26 |
|
Textura de la vaina |
882 |
299 |
1181 |
0.75 |
0.25 |
|
Nacimiento de la flor |
651 |
207 |
858 |
0.76 |
0.24 |
|
Longitud del tallo |
787 |
277 |
1064 |
0.74 |
0.26 |
|
Promedios |
|
0.75 =3/4 |
0.25 =1/4 |
||
Evidentemente Mendel realizó el proceso para todos sus caracteres experimentales. Ahora analizaremos sus respectivas probabilidades. Con la reaparición constante del caracter perdido en la F2 Mendel propone su primera ley de la herencia, que se denomina la Ley de la Dominancia. La ley de la dominancia se puede definir como: "en un cruce de parentales puros para un carácter solo uno de los dos aparecerá en la F1, de este modo los híbridos F1 expresarán solo uno de los fenotipos de los parentales". El promedio de las probabilidades del dominante es del 0.75 y del recesivo es del 0.25 lo cual equivale a un radio de tres dominantes por cada recesivo aproximadamente. Las desviaciones estándar de ambas series de datos, aunque no las mostramos son interiores al límite de significancia elegido que fue de dos decimales, por lo que la solidez de los datos muestra una tendencia clara por el radio 3:1.
10.3 Contrastación del modelo cualitativo y continuo de la herencia
Al contrastar los resultados de F1 y F2 con el modelo continuo emerge una conclusión. Los rasgos de los caracteres empleados en el modelo experimental mendeliano no se mezclan. Pueden desaparecer en una generación y reaparecer en la siguiente, pero no se mezclan. Con estos resultados se podía concluir que el modelo continuo de la herencia no aplicaba específicamente para el organismo modelo empleado por Mendel. Hay que destacar que esto no implica que todos los rasgos sean discretos o categóricos, simplemente implicaba que el modelo purificado con el que trabajaba Mendel si lo era. El problema ahora era concebir un modelo matemático que explicara los resultados desde la generación parental hasta la filial.
10.4 Diferencia entre genotipo y fenotipo
Para poder entender como se modeló teóricamente el sistema matemático, debemos distinguir dos conceptos:
👉 Fenotipo: es la forma evidente, forma manifestada o macroscópica. Denominaremos fenotipo dominante al que se manifiesta completamente en un cruce de variedades puras. Denominaremos fenotipo recesivo a que desaparece en el cruce de dos variedades puras. Para simbolizarlos plantearemos como dominante a la letra D y al recesivo la letra r.
👉 Genotipo: es la forma inferida estadísticamente, que genera la forma del cuerpo pero que no puede verse directamente. Los símbolos de los genotipos son letras, siendo originalmente mayúsculas para dominantes, minúsculas para recesivas y binomios para híbridos. Sin embargo e4n la actualidad usamos la notación de Correns que plantea tres tipos de genotipos: AA Homocigoto dominante o puro dominante; Aa heterocigoto; aa homocigoto recesivo o puro recesivo.
10.5 Ley de la dominancia completa
La ley de la dominancia completa establece que, en una pareja de rasgos de un carácter, uno es dominante y otro recesivo, más concretamente, el dominante es generado por dos tipos de genotipos.
Tabla 10.2. Expresión de la relación fenotipo genotipo en la ley de la dominancia completa.
|
Genotipo Lo que NO se observa, modelo algebraico. |
Fenotipo Lo que se observa, lo que se cuenta experimentalmente. |
|||
|
Nombre |
Símbolo |
Nombre |
Símbolo |
Ejemplo |
|
Homocigoto dominante |
AA |
Fenotipo Dominante |
|
Semilla amarilla |
|
Heterocigoto |
Aa |
|||
|
Homocigoto recesivo |
aa |
Fenotipo Recesivo |
|
Semilla verde |
Aunque parece evidente en sí misma, enunciar la ley de la dominancia completa al principio de cualquier ejercicio de lápiz y papel de genética clásica es crucial, ya que funciona como un instrumento de traducción
👉 desde el enunciado hacia el álgebra, y
👉 desde la solución numérica a una conclusión en texto.
11. El cuadro de Punnett y la ley de segregación independiente
|| REGRESAR AL INDICE ||
Hoy el contexto aquí planteado no es el del monje aaustríaco Gregor Mendel, recordemos que él es una figura casi mítica y su trabajo no contiene prácticamente nada del lenguaje que usamos para la construcción de dicha teoría. por ejemplo, para la explicación fundamental de la ley de segregación independiente conocida como su segunda ley, debemos emplear conceptos que se desarrollaron en microscopía por parte de científicos alemanes que contaban con los mejores microscopios de la época, juguetes con los que no podía contar Gregor Mendel.
11.1 Gametos y meiosis
Hoy el ciclo vital de un ser vivo con célula eucariota como las plantas y los animales se fundamenta en dos procesos importantes, la meiosis y la fecundación.
👉 meiosis es un tipo de reproducción celular especial que se especializa en la disminución de la cantidad de cromosomas estándar de el cuerpo de una especie a la mitad, hoy el producto principal de la meiosis es la células gameto. en general vamos a clasificar a los gametos en 2 variedades dependiendo del sexo que los produce, el gameto femenino lo denominamos huevo u óvulo, y el gameto masculino esperma o espermatozoide.
👉 fecundación es el proceso opuesto de la meiosis, aquí 2 gametos se fusionan para producir una célula con la cantidad estándar de cromosomas de la especie.
11.2 haploide y diploide
Denominaremos a una célula con la cantidad estándar de cromosomas como célula diploide simbolizada como 2n, pues las células diploides cuentan con cromosomas homólogos o en parejas que contienen la misma información genética. Por el contrario una célula haploide es aquella que cuenta con un solo juego de cromosomas sin repeticiones.
11.3 Cromosomas
La palabra significa cuerpos coloreados o cuerpos que absorben color, son paquetes de ADN que se forman al principio de una reproducción celular como la mitosis o la meiosis, y sirven para organizar a la información genética de forma tal que se pueda repartir fácilmente en las células hijas de una reproducción celular.
11.4 Ley de la segregación independiente
La ley de la segregación independiente plantea que los factores que constituyen un genotipo y que denominaremos alelo se separan independientemente durante la formación de gametos, como si viajaran en cada cromosoma homólogo, de forma tal que cuando se generan gametos, cada gameto haploide hereda sólo un alelo de las células madre que lo produjo.
11.5 Algoritmos para representar la formación de gametos y la fecundación
Muchas veces ponemos más énfasis en los algoritmos que en los objetivos últimos de los conceptos a enseñar. Uno de los ejemplos es precisamente el cuadro de Punnett. En todo libro de texto, desde los de nivel de básica secundaria hasta los universitarios introducen el cuadro de Punnett a la hora de realizar los cálculos mendelianos clásicos, incluso artículos de investigación solo emplean el cuadro de Punnett como si fuera la única alternativa (Castillo Murillo, 2011; Rivas Mosquera, n.d.).
Figura 11.1. Reginald Punnett, junto con William Bateson, Punnett ayudó al establecimiento de la Genética como una nueva ciencia en Cambridge. Juntos descubrieron el fenómeno de ligamiento, una auténtica excepción a las leyes de Mendel.
Lo interesante es que la obra de Mendel no fue expresada en términos de un cuadro, si no lo llamaríamos el cuadro de Mendel (Mendel, 1996), ya que el autor del cuadro llamado Reginald Punnett “1875-1967” nació casi una década más tarde de que Mendel publicara su trabajo. La obra de Punnett que probablemente popularizó su visión de la genética fue un libro de texto llamado mendelismo (1905) justo la década en la que las comunidades científicas empezaron a emplear con seriedad y a expandir los trabajos de Gregor Mendel. Punett también se acredita junto con William Bateson “1861-1962” y Rebecca Saunders “1865-1945” descubrieron que la hipótesis alternativa a la segunda ley de Mendel “conocida como la ley de la distribución independiente” podía presentarse en algunos modelos biológicos como los pollos. En otras palabras, que el ligamiento de caracteres por factores “ya en esta época llamados genes” si ocurría.
El propio cuadro no fue un invento del propio Punnett, sino que hace parte de uno de los instrumentos o algoritmos clásicos de la enseñanza del álgebra escolar, y recibe el nombre general de Modelo de Área o baldosas algebraicas (Area Tiles).
11.6 Los modelos de área en álgebra
Las baldosas algebraicas son manipuladores matemáticos que permiten a los estudiantes comprender mejor las formas de pensamiento algebraico y los conceptos de álgebra. Se ha demostrado que estos mosaicos proporcionan modelos concretos para estudiantes de introducción al álgebra de la escuela primaria, secundaria, preparatoria y de nivel universitario. También se han utilizado para preparar a los presos para sus exámenes de Desarrollo Educativo General (GED) (Leitze & Kitt, 2000). Las baldosas algebraicas permiten un enfoque tanto algebraico como geométrico de los conceptos algebraicos. Brindan a los estudiantes otra forma de resolver problemas algebraicos además de la simple manipulación abstracta (Leitze & Kitt, 2000). El Consejo Nacional de Profesores de Matemáticas (NCTM) recomienda un menor énfasis en la memorización de las reglas de álgebra y la manipulación de símbolos de álgebra en sus Estándares de Currículo y Evaluación de Matemáticas. De acuerdo con los estándares NCTM 1989, " la relación de los modelos entre sí genera una mejor comprensión de cada uno".
Las baldosas algebraicas forman parte de la historia del álgebra, pues fueron los instrumentos de trabajo de los matemáticos antes de la invención del álgebra simbólica (Hopkins, 2021).
Figura 11.2. En este minidocumental podremos darnos cuenta de la transcendental importancia que tuvieron las baldosas geométricas y sus versiones tridimensionales, los cubos geométricos para la resolución del problema de las ecuaciones de tercer grado (Enlace).
Figura 11.3. Representación de los caso de factorización de producto de monomios (a x a), (a x b) y el producto de dos binomios iguales (a x b)2 dado por el álgebra de Baldor (Baldor, 2008).
Como matemático es evidente que Punnett debió estar familiarizado con esta técnica pedagógica de factorización, por lo que al popularizar el estudio del mendelismo entre los biólogos no dados a las matemáticas empleó este instrumento para realizar algunas demostraciones simples.
11.7 El cuadro
El cuadro de Punnett apareció originalmente en un texto de enseñanza escrito por Reginald Punnett llamado mendelismo (Reginald Crundall Punnett, 1905). El cuadro de Punnett en realidad es una forma de expresar dos casos de factorización, el factor común y el binomio cuadrado perfecto. Se trata de una introducción a una matematización de la biología para no matemáticos. El cuadro de Punnett es quizá la herramienta más básica para ilustrar la ley de la segregación independiente de los factores mendelianos “alelos”, sin embargo, no es ni la única ni la más potente, simplemente se trata del modelo más tradicional al haber aparecido en el primer primerísimo texto de genética.
El cuadro de Punnett para el cruce monohíbrido consta de dos columnas y dos filas En las columnas se distribuyen por separado los factores del padre y en las filas los factores de la madre. En las intersecciones de columnas y filas se copian y pegan los factores de los parentales de forma tal que se crean genotipos nuevos, que pueden ser iguales o diferentes a los parentales.
Figura 11.4. Cuadro de Punnett (izquierda) y factorización del trinomio cuadrado perfecto (derecha), ambos son solo algoritmos empleados para resolver la misma situación.
Esto implica que los genotipos mendelianos pueden ser representados algebraicamente, pero retornaremos a eso posteriormente, por el momento nos concentraremos en el funcionamiento básico del cuadro de Punnett para los no iniciados en álgebra.
11.8 Segregación independiente y segregación dependiente
La primera ley de Mendel y el título de este capítulo se denominan segregación independiente, pero ¿Qué quiere decir eso? La segregación independiente hace referencia a que las mezclas entre todos los factores es completamente al azar, sin sesgo o correlación alguna con la variable sexo que acompaña a cada uno de los factores mendelianos (Sadava et al., 2014). Evidentemente existen rasgos que, si están asociados al sexo y se denominan ligamiento al sexo, pero el tratamiento matemático de estos jamás fue abordado por Gregor Mendel y debió ser trabajado en el contexto de la genética clásica casi 36 años después de que Mendel publicara sus trabajos sobre el monohíbridos y el dihíbrido con las arvejas. En el cuadro de Punnett la segregación independiente se manifiesta al colocar los factores de cada parental en columnas independientes.
11.9 Método algebraico
Para resolver los ejercicios de Punnett podemos simplemente usar el álgebra, lo cual a su vez nos otorgará la capacidad de programar los cálculos en una hoja de cálculo como Excel. Para ello tenga en cuenta que los casos de factorización para tener en cuenta son el factor común y el binomio cuadrado perfecto.
La simbolización algebraica nos permite entre otras cosas obtener un formalismo diferente para el genotipo y para los gametos, distinción importante a la hora de plantear los problemas de genética clásica. En consecuencia, la resolución de un problema de genética se convierte en plantear el formalismo de los gametos y resolver el problema algebraico respectivo.
11.10 Resolver un ejercicio no es igual a completar el cuadro de Punnett
Como menciona esta sección, un error común de los estudiantes es pensar que el ejercicio mendeliano acaba en el momento en que completas el cuadro, sin embargo, la cosa es un poco más complicada, pues el cuadro es solo un instrumento transitorio, dentro de un problema completo, en otras palabras, hay tareas que realizar antes para poder dibujar el cuadro, y tares que realizar después para poder extraer la información relevante al interior del cuadro, pero eso lo veremos en la siguiente sección.
12. Como resolver el cruce monohíbrido
|| REGRESAR AL INDICE ||
Resolver un problema mendeliano monohíbrido generalmente se confunde con resolver un cuadro de Punnett, sin embargo, eso es solo una herramienta de factorización, en realidad usted puede resolver el cuadro de Punnett y no llegar a nada, pues el objetivo de un problema contextualizado depende del tipo de pregunta.
12.1 Traducir del texto al modelo
Uno de los mayores inconvenientes que tienen los estudiantes y en general cualquier persona que enfrenta un problema de genética clásica, es el hecho de que no nos advierten que el paso más importante es la traducción del texto al modelo matemático.
Traducir del texto al modelo matemático involucra un ejercicio mental importante y por sobre todas las cosas la aplicación de la ley de la dominancia completa o cualquier ley de genética de traducción que estemos empleando en el contexto dado.
Tenga en cuenta que la ley de la dominancia completa no siempre se cumple, y por ende la herramienta de traducción de texto a modelo matemático puede cambiar.
La herramienta de traducción para la dominancia completa puede materializarse de diversas maneras, una puede ser implícita, es decir que usted instintivamente sepa lo que está haciendo, pero asumamos que no. Entonces vamos a necesitar un instrumento que sea evidente. Una segunda opción es dibujar una tabla con las relaciones como las que hemos establecido anteriormente y que volveremos a dibujar a continuación para la dominancia completa
(Eq. 12.1) Plantear la ley de dominancia permite generar un instrumento que traduce la información cualitativa en el texto enunciado en parámetros algebraicos a resolver por cuadro de Punnett o factorización directa.
Adicionalmente usted debe estar muy atento a sutiles indicaciones que aparecen en el enunciado, por ejemplo, si nos dicen que un fenotipo dominante es híbrido, impuro o mezclado, significa que el genotipo va a ser heterocigoto (Aa); pero si por el contrario el enunciado indica que el fenotipo dominante es puro o no mezclado su genotipo será homocigoto dominante (AA).
12.2 Usando el modelo matemático
En general se preguntan por probabilidades que pueden ser expresadas como fracciones, frecuencias o porcentajes; además se puede preguntas por los genotipos de los gametos, por los genotipos de la siguiente generación o por los fenotipos de la siguiente generación. En el contexto de los primeros mendelianos, los genetistas no tenían acceso al contenido del genotipo de gametos o de las siguientes generaciones, por lo que la pregunta más habitual es por los fenotipos posibles. El cruce monohíbrido solo tiene seis variantes algebraicas a saber.
👉 Cruce de dominantes puros AA x AA.
👉 Cruce de recesivos puros aa x aa
👉 Cruce de un dominante puro con un recesivo puro AA x aa
👉 Cruce de un heterocigoto con un dominante puro Aa x AA
👉 Cruce de un heterocigoto con un recesivo puro Aa x aa
👉 Cruce de dos heterocigotos Aa x Aa
Por tradición mendeliana, los dos problemas que vienen plasmados como ejemplos en los libros de texto son el cruce de un dominante puro con un recesivo puro; y el cruce de dos heterocigotos, siendo este último el más complejo. En los siguientes ejemplos mostraremos las soluciones para cada uno de estos casos, desde el más complicado al más sencillo en un problema con contexto.
12.3 Interpretación moderna de la ley de la segregación independiente
Actualmente concebimos a los factores mendelianos como alelos o formas alternativas de un gen, los genes se encuentran en una posición fija en un cromosoma. Los humanos, las plantas y otros eucariotas poseen en alguna de sus etapas del ciclo de vida dos copias de cada gen en cromosomas homólogos, estado denominado diploide y que explica la razón por la que el modelo mendeliano emplea dos copias de cada factor. Existe otra etapa del ciclo de vida en la que se tiene una sola copia de cada cromosoma y por ende de cada gen, estado llamado homocigoto y que se representa como la generación de gametos en nuestros modelos matemáticos.
La segregación independiente se iguala al momento de generación de gametos, es decir la meiosis donde las células diploides con dos copias de cada cromosoma, se transforma en células haploides de gametos con una sola copia de cada cromosoma. Mendel jamás realizó dicha asociación ya que el trabajo con la meiosis prosiguió caminos independientes al de la genética matematizada por la mayor parte del siglo XIX (McKusick, 1960). Sería un biólogo menos conocido llamado Walter Sutton quien asociaría la segregación de factores mendelianos con la segregación de cromosomas homólogos durante la meiosis (McKusick, 1960).
12.4 Interpretación algebraica de la ley de la segregación independiente
La ley de la segregación independiente es una ley que nos sirve para generar los gametos de un determinado genotipo, y puede aplicarse de manera análoga al cuadro o de manera analítica para facilitar el álgebra. En este texto aplicaremos la segunda interpretación.
👉 Gametos de un homocigoto Un homocigoto solo puede generar un tipo de gameto, por ejemplo, AA genera solo gametos tipo A, o un aa solo genera gametos tipo a.
👉 Gametos de un heterocigoto Un heterocigoto genera dos tipos de gametos modelados como binomio Aa genera gametos tipo (A+a)
12.5 La fecundación independiente como una ley oculta
La ley de la segregación independiente solo es posible de determinar si hay otra condición, y es que exista una fecundación independiente o al azar de los gametos generados al azar. La fecundación al azar se modela como una multiplicación algebraica de polinomios o monomios.
Los tipos de fecundación literalmente han de condicionar las preguntas que pueden hacerse, y siguiendo las reglas matemáticas, para un mohíbrido solo podemos tener 6 casos.
Tenga en cuenta que el resultado de multiplicar los gametos se denomina genotipo de la siguiente generación.
DEMOSTRACIÓN. Factorizar todos los casos del cruce monohíbrido empleando el cuadro de Punnett.
DEMOSTRACIÓN. Factorizar todos los casos del cruce monohíbrido empleando técnicas de factorización.
13. Contrastación experimento vs teoría
|| REGRESAR AL INDICE ||
El método científico generalmente se enseña como un proceso lineal y progresivo, aunque la verdad puede ser un poco más complicada. Muchas de las grandes teorías de la ciencia no se inducen posterior a un experimento, sino que se deducen antes o durante la realización del mismo, y en ocasiones experimentos clave no necesariamente conllevan a consolidar un modelo claro. De cualquier modo, lo que hoy nos trae es un paso del método científico y es el que vincula al modelo teórico con los datos experimentales, pues en muchas ocasiones la simetría entre ambos no es total.
13.1 El ruido
Toda serie de datos experimentales está sometida a ruidos experimentales, debido a variables menores que deben ignorarse para que el modelo no sea demasiado complejo, o a errores de medición intrínsecos a los procesos experimentales, por lo que los científicos deben plantear un rango de tolerancia de desviación a los valores teóricos. El proceso de contrastación entre datos teóricos y experimentales para discernir el ruido o azar es uno de los factores más importantes de la biología moderna, ya que los primeros genetistas debieron realizar comparaciones intuitivas o al ojímetro para decir que sus proporciones teóricas concordaban con las experimentales.
13.2 Midiendo el ruido de lo que no lo es
Sin embargo, este ojímetro es bastante difuso, por ejemplo, se dice que Hugo de Vries acopló sus resultados experimentales a las proporciones del monohibrido 3:1, cuando sus resultados experimentales realmente apoyarían a una proporción de 2:1 en la segunda generación del análisis de monohíbrido, sin embargo, lo más probable es que esto se deba a que en su tiempo los estadísticos para realizar esas comparaciones no se habían formulado. En la actualidad contamos con dos pruebas estadísticas para poder trabajar este problema de contrastación, la chi cuadrado de Pearson y los tests exactos de Fisher. En la lección de hoy nos concentraremos en el uso de la chi cuadrado, propuesta alrededor de 1900 precisamente para resolver el dilema de la contrastación, precisamente en el modelo mendeliano.
La chi cuadrado es una prueba de contrastación de valores experimentales y valores teóricos, y nos determina una prueba de dos hipótesis:
👉 la primera hipótesis conocida como hipótesis nula establece que no existen diferencias significativas entre las dos series de datos
👉 la hipótesis alternativa establece que si existen diferencias significativas entre las dos series de datos.
13.3 Los mendelianos estadísticos y eugenistas
La Prueba de Chi cuadrado fue propuesta por Karl Pearson, uno de los primeros mendelianos matemáticos, que hizo sus aportes desde la estadística, aunque también hay que destacar que también era un eugenista acérrimo. Durante su carrera, Pearson desarrolló teorías estadísticas y las aplicó a la exploración de datos biológicos. Sin embargo, sus innovaciones no fueron bien recibidas y se enfrentó a una ardua lucha para convencer a otros científicos de que aceptaran la idea de que las matemáticas deberían aplicarse a la biología. Por ejemplo, durante la época de Pearson, la Royal Society, que es la academia de ciencias del Reino Unido, aceptaría artículos y otros documentos que se referían a matemática o biología, pero se negaba a aceptar trabajos de ambos temas. En respuesta, Pearson, junto con Francis Galton y W. F. R. Weldon, fundaron una nueva revista llamada Biometrika en 1901 para promover el análisis estadístico de los datos sobre la herencia. La persistencia de Pearson valió la pena (Inman, 1994; Magnello, 1998).
Tabla 13.1. Datos de la chi cuadrada teórica o de la tabla (Xo)2, que representan el límite de tolerancia de diferencias acumuladas, el valor dependerá de un límite de confianza que generalmente es el 95% y de los grados de libertad que dependen de la cantidad de parejas menos uno.
|
Grados de libertad |
(Xo)2 |
|
1 |
3.84 |
|
2 |
5.99 |
|
3 |
7.81 |
|
4 |
9.49 |
|
5 |
11.07 |
|
6 |
12.59 |
|
7 |
14.07 |
|
8 |
15.51 |
|
9 |
16.92 |
|
10 |
18.31 |
Hoy, las pruebas estadísticas son esenciales para examinar datos biológicos. En términos prácticos la prueba de Chi cuadrado se basa en determinar un valor crítico o de frontera empleando unos grados de libertad que dependen de la cantidad de categorías o parejas de datos que se deben comparar. La chi cuadrada de la tabla o limite (X02) se compara con una chi cuadrada calculada (X2) a través de la siguiente fórmula general.
(Eq. 13.1) Fórmula del parámetro chi cuadrada calculada X2, que debe compararse con la chi cuadrada estándar, de la tabla o teórica (Xo)2 .
Para poder encontrar la tabla de chi cuadrado tenemos tres opciones: buscarla en internet, buscarla en un libro de estadística universitaria o extraerla de Excel a través de la fórmula correspondiente. La frontera de la chi cuadrada está definida por un valor llamado alfa o límite de confianza, aunque las tablas de los libros tienen todos los valores, por tradición en biología solo empleamos la columna con el alfa del 95% que presentamos a continuación para grados de libertad desde 1 hasta 10.
13.4 Resolviendo una situación de contraste experimento-teoría
Ahora miremos un ejemplo. Para poder hacer una prueba chi cuadrado requerimos datos experimentales, como los de Mendel, estos resultados fueron los que obtuvo Mendel para la F2 de un análisis monohíbrido de líneas puras como el que se modeló en él, por lo que la probabilidad del rasgo dominante es de ¾ y la del recesivo es de ¼, se supone que debemos comparar estos datos teóricos con los datos experimentales de la segunda tabla de la presente guía, así que los sacaremos en limpio (Tabla 13.2).
Tabla 13.2. Tabla para solucionar manualmente para un monohíbrido. Los conteos calculados se obtienen al multiplicar el total de conteos experimentales (929) por las probabilidades teóricas respectivas. Los grados de libertad se obtienen como el número de parejas analizadas menos 1.
Como el Χ2 = 0.40 es menor a la frontera de tolerancia Χ02 = 3.84, que se encuentra en la Tabla 13.1 buscando con los grados de libertad indicados como número de parejas -1, es decir gl = 2 - 1 =1. Decimos que no existen diferencias significativas entre los datos teóricos y experimentales, ya que la acumulación de diferencias no supera a las de la tabla, por lo que podemos tolerar la desviación entre ambas series de datos con un 95% de confianza. Cabe destacar que los datos mendelianos se ajustan tan bien al modelo teórico que algunos autores han sospechado por años sobre la posibilidad de que Mendel hubiera maquillado sus resultados de forma artificial mediante sesgos de muestreo (Franklin, 2008; Franklin, Edwards, Fairbanks, & Hartl, 2008; Pires & Branco, 2010). Sea cual sea el caso con esto completamos nuestro estudio del cruce monohíbrido.
13.5 Error absoluto y relativo, cuando no tenemos la chi cuadrado
Existe una alternativa “mas económica” a la chi cuadrado en caso de que necesitemos estimar la distancia que hay entre el valor esperado y el valor calculado, que llamaremos como el error relativo.
(Eq. 13.2). Fórmula del error relativo. El resultado es una frecuencia que va desde 0 hasta 1, por lo que normalmente se la multiplica por la constante 100 % en las conclusiones.
Al aplicar la ecuación anterior a la Tabla 13.2 obtenemos que ε(dominante) = 1.15 % y ε(recesivo) = 3.45 %, lo cual indica errores relativos bajos, lo cual concuerda con el cálculo de Chi cuadrado que concluyó que no existían diferencias significativas. El error absoluto estimará la distancia entre un valor esperado y otro experimental, pero no ofrecerá un promedio de diferentes valores esperados. Recuerde que en un ejercicio mendeliano típico tendremos como mínimo dos estimaciones teórico-experimentales, como son dominante contra recesivo, por lo que puede emplearse otro estadístico de estimación poco complejo como el error absoluto promedio.
(Eq. 13.3). Fórmula del error relativo promedio.
Si aplicamos la fórmula del erro relativo promedio obtendremos un valor del 1.72 %, que es un valor bajo que concuerda con las otras estimaciones de error.
14. La ley de la distribución independiente
|| REGRESAR AL INDICE ||
La ley de la distribución independiente se encuentra estrechamente ligada al cruce dihíbrido. El cruce dihíbrido significa un híbrido doble. Esto hace referencia a que el modelo experimental toma en cuenta dos caracteres, cada uno con dos rasgos diferentes. Este es otro punto donde el modelo experimental de Mendel resultó ser afortunado. Ninguno de los 7 caracteres empleados se encuentra ligado, y esto afecta mucho las presuposiciones del modelo matemático empleado para formular la tercera ley de Mendel. Sin embargo Mendel no tenía ni idea del concepto de ligamiento en un cromosoma, por lo que nuevamente su propuesta fue una apuesta en un modelo matemático aleatorio (Sadava et al., 2014).
Tabla 14.1. Expresión de la relación fenotipo genotipo en la ley de la dominancia completa en un análisis de cruce dihíbrido. Recuerde que el genotipo era solo un modelo matemático, y lo que en verdad se veía era el fenotipo.
La segunda ley de Mendel se da al interior de los rasgos en un solo carácter. La tercera ley de Mendel involucra dos o más caracteres y sus correspondientes rasgos. Del mismo modo en que podía proponerse que los factores que generaban los rasgos se segregaban de forma independiente; Mendel empezó a trabajar que sucedía cuando analizaba dos caracteres y sus correspondientes cuatro rasgos. ¿Cómo se combinarían?
El modelo que Mendel aplicó volvió a ser una propuesta por el azar. Del mismo modo que los factores se segregan de forma azarosa, entonces los factores que generan los rasgos se distribuirían de forma independiente y azarosa. En base a esta ley proponemos el modelo matemático (Sadava et al., 2014). El azar es tomado en cuenta por el modelo como la obligación de generar todas las combinaciones posibles, y eso es justo lo que vamos a realizar para los cruces F1 y F2 del dihíbrido "color de semilla X forma de la semilla" tanto por los cuadros de Punnett, la cadena de Markov y el formalismo algebraico.
14.1 Simbolización de un dihíbrido
Los dihíbridos se simbolizan con cuatro factores, de a dos parejas. Cada pareja es la combinación que genera un rasgo fenotípico como se observa en la Tabla 14.1, si hay dos parejas entonces se generan dos rasgos. Mendel empleó linajes puros dobles, un doble homocigoto dominante y un doble homocigoto recesivo. En total tenemos 9 genotipos diferentes que dan lugar a cuatro fenotipos que es lo que en verdad se contrasta. La pareja de caracteres puede ser cualquiera ya que se encuentran segregados aleatoriamente. Sin embargo, Mendel mismo no fue quien creó el modelo matemático que vemos en la Tabla 14.1, el verdadero proponente fue Carl Correns.
Figura 14.1. Carl Correns, fue un biólogo, genetista y botánico alemán. Junto a Erich von Tschermak y Hugo de Vries, redescubren, a comienzos del s. XX, las leyes de Mendel, o eso es lo que nos dicen los libros de texto.
Dado que un cruce dihíbrido es estadística y algebraicamente el producto de multiplicar dos monohíbridos todo aumenta exponencialmente al cuadrado. En lugar de tres genotipos ahora serán nueve y el lugar de dos fenotipos ahora serán cuatro. Esto también afectará al cuadro de Punnett completo que en lugar de tener 4 casillas internas tendrá 16. Sin embargo, en este texto emplearemos cuadros de Punnett resumidos o el método algebraico para ahorrar tiempo e intentar una menor inducción al error. Recuerde que el cuadro de Punnett en sí mismo no responde nunca un problema contextualizado de genética, es solo una herramienta de varias posibles para resolver un problema de factorización, la cual en el caso del cruce dihíbrido empieza a ser ya una factorización polinómica de nivel intermedio. La clave fundamental para resolver por una u otra ruta es simplemente ser muy ordenados y mantener la calma.
14.2 El cuadro de Punnett del dihíbrido
Los cruces dihíbridos son mucho más numerosos que los monohíbridos. Si contando los ejercicios monótonos y no monótonos hay 6 posibles combinaciones de monohíbrido en sus genotipos, para el dihíbrido la cantidad de combinaciones será 62=36 combinaciones geneticas posibles. Adicionalmente, el cuadro de Punnett para este tipo de situaciones es mucho más complejo.
Tabla 14.1. Cuadro de Punnett para un cruce dihíbrido de dos dobles heterocigotos. Como se pueden dar cuenta el cuadro es más complejo, por lo que es en este contexto donde el método algebraico es más útil al simplificar el razonamiento..
Tenga en cuenta que completar un cuadro de Punnett no es el objetivo sino solo una herramienta, después de completarlo debemos extraer los genotipos y las veces que cada uno se repite: AABB + aaBB + AAbb + Aabb + 4AaBb + 2aaBB + 2AABb + 2aaBb + 2 Aabb. Posteriormente se usa la ley de la dominancia completa para ver los fenotipos generados y las veces que cada uno se repite.
Con la información de la Tabla 14.2 se espera que usted sea capaz de traducir los genotipos a fenotipos. sin embargo, esa tarea puede convertirse en algo un poco molesto en especial cuando tenemos una colección de genotipos compleja como en el cruce de 2 híbridos como se muestra en la Tabla 14.3.
Sin embargo, existe una alternativa para resolver estos ejercicios de manera más sencilla y es visualizar la ley de la distribución independiente no sólo como una separación azarosa de los genotipos sino como el hecho de que podemos interpretar un híbrido como 2 mono híbridos independientes.
Ejemplo. Resolver el cruce mendeliano AaBb por AaBb con el cuadro de Punnett.
14.3 El dihíbrido como dos monohíbridos independientes
Esta es la encarnación de la ley de distribución independiente, ya que como su nombre indica, si los factores de cada carácter se distribuyen independientemente, podemos analizarlos como monohíbridos y luego factorizar para obtener la forma dihíbrida. La razón de que esta técnica es más rápida se basa en la propia definición de la multiplicación como una suma abreviada, por lo que multiplicar siempre será más rápido que sumar.
En este caso retomaremos el caso más complejo el cruce de 2 heterocigotos (AaBb x AaBb). En este caso vamos a interpretar la ley de la distribución independiente distribuyendo independientemente los factores de cada carácter para generar dos monohíbridos (Aa x Aa)(Bb x Bb). La solución de un mono híbrido es mucho más sencilla, por ejemplo, en este cruce de un monohíbrido de dos heterocigotos el genotipo de la F1 es el trinomio cuadrado perfecto (AA+2Aa+aa) y su respectivo fenotipo es (3D1+r1).
Como el segundo carácter tiene exactamente la misma estructura, pero con símbolos diferentes podemos copiar las respuestas esto significa que el genotipo de la F1 va a volver a ser un trinomio cuadrado perfecto (BB+2Bb+bb) y su respectivo fenotipo será (3D2+r2)
De esta manera las dos soluciones principales de un dihíbrido se reducen a hacer la factorización de las dos soluciones de un monohíbrido.
Primero vamos a hacer el genotipo que ya como es una factorización un poco más compleja vamos a hacer un cuadro de factorización:
Tabla 14.3. Tabla de factorización de dos trinomios que genera un polinomio de nueve términos, que representan los genotipos de la F1 de un cruce dihíbrido de dos dobles heterocigotos.
|
|
AA |
2Aa |
aa |
|
BB |
AABB |
2 AaBB |
aaBB |
|
2Bb |
2 AABb |
4 AaBb |
2 aaBb |
|
Bb |
AAbb |
2 Aabb |
aabb |
El punto es que no es necesario traducir la tabla de genotipos a la de fenotipos tampoco, pues al igual que hicimos anteriormente, los fenotipos del dihíbrido pueden obtenerse factorizando los fenotipos de los dos monohíbridos.
Ejemplo. Resolver el cruce mendeliano AaBb por AaBb con la factorización algebraica.
14.4 Todos los fenotipos posibles
Al combinar las técnicas de las celdas algebraicas (cuadros de Punnett extendidos por llamarlos de un modo familiar) con la factorización de polinomios obtenemos una técnica aun más potente que nos permitirá predecir las posibles combinaciones de fenotipos de un cruce dihíbrido asumiendo distribución independiente. Para ello solo debemos tener en cuenta que los fenotipos posibles de un cruce monohíbrido son 4, ni mas ni menos:
👉 Todos dominantes (D),
👉 Todos recesivos (r),
👉 La mitad dominantes y la mitad recesivos (D + r),
👉 El 75% dominantes y el 25% recesivos (3D + r),
Por lo anterior, si sacamos el producto de estos cuatro posibles fenotipos del carácter 1 con sus recíprocos en el carácter 2 obtendremos una hipótesis general de todas las combinaciones de fenotipos:
DEMOSTRACION. Cuales son todos los fenotipos posibles de un cruce dihíbrido con distribución independiente
Tabla 14.4. Tabla de factorización de los fenotipos de cualquier cruce dihíbrido con distribución independiente. Con el dihíbrido la factorización combinada con el cuadro de Punnett nos permite predecir TODOS los tipos de enunciado y su solución para un dihíbrido aun antes de enfrentarlos. Este tipo de predicciones son lo que en ciencia conocemos como las hipótesis.
Es mas que evidente que la mayoría de los ejercicios de lápiz y papel estarán diseñados para poner a prueba las hipótesis más complejas como el cruce de dos dihíbridos que da como resultado la proporción 9:3:3:1.
15. Resolviendo dihíbridos y trihíbridos
|| REGRESAR AL INDICE ||
Normalmente los libros de texto nos obligan a resolver el dihíbrido en bloque, sin embargo, tal aproximación es desgastante e innecesaria, en esta lección veremos una combinación de una interpretación alternativa de la ley de distribución independiente más el uso consciente de reglas del álgebra para factorizar polinomios, que nos ayudan a resolver dihíbridos y trihíbridos de manera analítica, más eficiente y especialmente, de manera más elegante.
15.1 El inicio y el final
Recuerde que el inicio y el final de un ejercicio contextualizado de genética clásica con híbridos siempre estará sometido a una ley de dominancia, en este caso no es necesario plantear una tabla tan compleja como la que se vio en la tabla 6, pues podemos seguir argumentando que los dos caracteres son independientes hasta cierto punto. Por ende, la ley de la dominancia completa en un híbrido se enunciará simplemente como dos leyes de dominancia completa para dos monohíbridos independientes:
(Eq. 15.1) Plantear la ley de dominancia permite generar un instrumento que traduce la información cualitativa en el texto enunciado en parámetros algebraicos a resolver por cuadro de Punnett o factorización directa.
15.2 Ejercicios
El método algebraico se fundamenta en la propia ley de la distribución independiente, pues su cada gen se distribuye independientemente, podemos modelar matemáticamente cada gen como un monohíbrido independiente y luego unir la respuesta como una multiplicación de polinomios.
15.3 El trihíbrido
Digamos que queremos resolver el cruce trihíbrido de la forma AaBbCc x AaBbCc, es decir el triple heterocigoto, en un cuadro de Punnett nos saldría una matriz de 64 celdas que no es práctica. Sin embargo, con el método algebraico resulta viable. Si asumimos que los tres genes no están ligados entonces la ley de distribución independiente nos permite resolverlos parcialmente como tres monohíbridos independientes. El procedimiento es exactamente igual a como se realizó con el dihíbrido.
16. Los microscopistas
|| REGRESAR AL INDICE ||
Austria la patria de Mendel no era el centro de la investigación biológica en el siglo XIX, pues tal título era rivalizado por Inglaterra y algunos estados germánicos, especialmente la belicosa Prusia. Durante este siglo los principales avances en la biología se dieron en los campos de la geología, paleontología y proposición de la primera teoría de la evolución, lo cual nos lleva a Charles Darwin (Kutschera & Niklas, 2004) y los ingleses; la aparición de la bioquímica y microbiología por medio de los estudios de Pasteur , lo cual nos lleva principalmente a Francia (Löwy, 1994); el último campo es el de la fisiología celular y los microscopistas, lo cual nos lleva a los alemanes (Pickstone, 1973).
Resulta más que evidente que los trabajos de los microscopistas, los microbiólogos y los naturalistas convergerían con el trabajo de Mendel, sin embargo, esta unión no se produjo nunca en el siglo XIX. La unión a la que hacemos referencia adquiriría el nombre de la Teoría Sintética de la Evolución (Kutschera & Niklas, 2004). En consecuencia, las líneas de pensamiento en el siglo XIX permanecen un poco separadas. A continuación, realizaremos un breve sondeo del estado de la biología celular en el siglo XIX y su asociación a los reinos germánicos.
16.1 Europa en el siglo XIX un breve resumen
El evento que forjó la historia del siglo XIX en Europa fueron las guerras napoleónicas. Cuando Napoleón fue derrotado las naciones contra las que se enfrentó terminaron todas en un estado de guerra fría de todos contra todos. Este conflicto no era únicamente militar, también era cultural, de orgullo, y por lo tanto transferido a otras esferas de la vida pública como la academia y las ciencias (Bernal, 1953; Crosland, 1977; Olesko, 2006). En esta época se pueden citar por lo menos 4 grandes potencias:
👉 El imperio británico que reforzó su poderío marítimo:
👉 Las naciones de habla alemana, dos de ellas particularmente fuertes, Prusia y Austria. Aunque ambas intentaron crear un super-estado germánico, nunca se logró. Aunque Austria tenía un mayor prestigio histórico, Prusia era más poderosa militarmente.
👉 Finalmente, Prusia quien afianzó sus dominios en el oriente.
El centro de investigación más fuerte en términos de biología en Europa durante el siglo XIX fue Prusia en cuanto al desarrollo de instrumentos como microscopios, sin embargo las dos ideas más revolucionarias no surgirían allí: la “Selección Natural” fue propuesta por dos naturalistas del Imperio británico (Kutschera & Niklas, 2004), mientras que la matemática de los patrones de herencia discontinuos fue propuesta en el Imperio Austro-Húngaro por un sacerdote bastante humilde (Stubbe, 1972). A pesar de ello Prusia la cual posterior al año de 1871 será conocido como Estado Alemán formaría a muchos de los biólogos más importantes del siglo XIX.
Figura 16.1. Eduard Strasburger (A), Walther Flemming (B), Heinrich von Waldeyer (C) y el belga Edouard Van Beneden (D).
16.2 La biología del segundo Reich Alemán
Durante la mayor parte del siglo XIX Alemania no existía como tal, en su lugar existían una serie de reinos y principados beligerantes entre sí. Posteriormente en 1871 gracias a las hábiles maniobras del primer ministro de uno de dichos reinos llamado Prusia, los reinos combatientes pactaron la unificación en el segundo imperio Alemán (Pflanze, 2014). A pesar de las turbulencias políticas la academia de Prusia y Alemania floreció durante este periodo de tiempo, entre los años de 1860 y 1910 se desarrolló una de las subteorias más importantes dentro de la biología, la cual refutaba las afirmaciones originales de Darwin, pero que al mismo tiempo las reconstruyó en un cuerpo nuevo de conocimiento, a lo cual se conoce como la segunda teoría evolutiva o también llamado neo-Darwinismo (Kutschera & Niklas, 2004).
Las anomalías “si empleamos la terminología de Kuhn” (Kuhn, 1970) que empezaron a descubrirse se relacionaban especialmente con la descripción de los mecanismos de reproducción celular, es decir la mitosis y meiosis que ya hemos estudiado. Todos los descubrimientos en esta área fueron realizados por pruso-alemaes y un belga colado.
Figura 16.2. Oscar Hertwig y August Weismann.
Eduard Strasburger, Walther Flemming, Heinrich von Waldeyer y el belga Edouard Van Beneden fundaron las bases de la citología y la citogénesis del siglo XIX, pero paradójicamente son muy poco conocidos (Barnett & Robinow, 2002; Cherif, Roze, & Movahedzadeh, n.d.; Cremer & Cremer, 1988; Zacharias, 2001), lo cual nos recuerda que quienes proponen las grandes teorías son más fácilmente recordados que quienes se encargan del trabajo “sucio” de la ciencia, recolectar los datos individuales básicos.
Strasburger “1844-1912” uno de los más importantes fisiólogos botánicos “estudia cómo funcionan las plantas” acuñó los términos nucleoplasma y citoplasma para señalar a la parte al interior de las membranas nuclear y celular respectivamente. Van Beneden “1846-1910” descubrió como los cromosomas se combinaban durante la meiosis, durante la producción de los gametos, también identificó y nombro la cromatina. Walther Flemming “1843-1905” fundó los estudios en citogenética y acuñó el término mitosis (Barnett & Robinow, 2002; Cherif et al., n.d.; Cremer & Cremer, 1988; Zacharias, 2001). Los descubrimientos de la mitosis y la meiosis se cuentan entre los 100 descubrimientos científicos más importantes de todos los tiempos, y es uno de los 10 más importantes de la biología celular.
La meiosis fue descubierta y descrita por primera vez por otro biólogo pruso-alemán llamado Oscar Hertwig “1849-1922” en 1876 y confirmada posteriormente en 1883 al nivel de los cromosomas por Van Beneden en huevos de áscaris “un gusano parasítico” (Churchill, 1970; Hamoir, 2003). Pero estos descubrimientos solo son procesos relativamente mecánicos, si no se los hila en una teoría que genere consecuencias lógicas y explique fenómenos más allá. El proceso de convertir a la mitosis y la meiosis en las armas para destruir a la primer teoría de la evolución y recrearla de una forma nueva fueron hechas por el biólogo francfortés-alemán August Weismann (Churchill, 1970; Winther, 2001)
16.3 La hipótesis de Weissman
La hipótesis de los caracteres adquiridos avanzó desde Jean-Baptiste de Lamarck (1744–1829) y fue aceptada por Darwin (1859, 1872) fue vigorosamente refutada por August Weismann (1834–1914). Durante la época en que Weismann y otros realizaron los experimentos que desacreditaron la noción de herencia blanda, los genetistas mendelianos habían desarrollado una base firme para explicar la variación entre los individuos en una población tal y como lo requería la teoría de Darwin (Johnston, 1995; Mayr, 1985; Winther, 2001). Desde 1960 los genetistas moleculares demostraron que los cambios en la composición de pares de bases en el ADN se traducían en cambios en la estructura de las proteínas. Lo anterior demostró que la noción de Weismann de herencia dura era un hecho irrefutable. El término “Hipótesis de Weismann” ahora se concentra en la proposición explicita de que la reproducción sexual funciona como un proveedor de variación para la selección natural (Kutschera & Niklas, 2004)
A pesar de la importancia adaptativa del sexo (y el cómo el sexo evolucionó) ha permanecido como un área de considerable debate debido al costo del 50% en la aptitud, lo que en teoría debería favorecer a la reproducción asexual (Kutschera & Niklas, 2004). Nótese que, durante la reproducción sexual, cada progenitor solo le hereda el 50% de su genoma a su descendencia. El resultado de la vacación genómica introducido de esta forma puede conllevar a la aparición de individuos mal adaptados. En contraste, la reproducción asexual, asegura que los nuevos individuos están adaptados como sus padres al ambiente, lo que conllevaría a que cada miembro de la población generase clones de sí mismo. Por lo cual la pregunta del millón es ¿Por qué es tan común entre los eucariontes, la reproducción sexual? De acuerdo con Mayr el dilema de la perdida de la aptitud en un 50% debido a la reproducción sexual se puede resolver si consideramos el hecho de que el ambiente al que estaban adaptados los padres cambia a través del tiempo y puede que no sea el mismo que enfrentara la descendencia (Mayr, 1982).
Niklas señaló que la reproducción sexual y asexual no son mutuamente excluyentes, una combinación de ambas se puede observar en plantas, hongos y un sin fin de organismos eucariontes microscópicos (Niklas, 1997). La descendencia variable producida por la reproducción sexual puede contener (y debido al número, contiene) algunos individuos mejor adaptados a nuevos ambientes, mientras que la reproducción asexual produce organismos que retienen los caracteres adaptativos para un ambiente estable
De hecho, muchos hongos poseen ambos tipos de reproducción, cuando llegan a un ambiente rico en recursos ellos empiezan a generar una población clonal generada por reproducción asexual, cuando las condiciones del ambiente se hacen menos favorables, los hongos entran en un estado que induce la generación de gametos y estructuras secundarias que sirven para dispersar a largas distancias los cigotos producidos por la reproducción sexual. Esta estrategia no es única de los hongos, y la reproducción sexual siempre emerge como un fenómeno de emergencia, cuando las condiciones del ambiente se ponen poco favorables (Carlile, Watkinson, & Gooday, 2001).
Hamilton, Axelrod, y Tanese (1990) propusieron que la variabilidad genética que la reproducción sexual provee ayuda a las plantas, animales, hongos entre otros a lidiar contra parásitos y enfermedades. En la carrera armamentista evolutiva, los organismos patogénicos pueden crecer y adaptarse rápidamente debido a su gran número y corto ciclo de vida, lo que les permite evadir las defensas del organismo huésped. Rice y Chippindale (2001) han mostrado evidencia de que la reproducción sexual es ventajosa debido a que acelera la evolución genotípica sin el riesgo de la mutación aleatoria que puede generar tanto alelos ventajosos como perjudiciales (Chippindale & Rice, 2001; W R Rice & Chippindale, 2001; William R Rice & Chippindale, 2001). Todas estas ideas y experimentos soportan el concepto original de Weismann de que la reproducción sexual produce una progenie variable lo que promueve la evolución adaptativa. El problema seguía siendo encontrar la naturaleza básica de la herencia, sin embargo, su asociación directa a los cromosomas solo se hizo patente hasta que el mendelismo de popularizó.
16.4 El descubrimiento de los cromosomas
Todo estudio sobre la reproducción celular hace referencia de manera inevitable a los cromosomas, sin embargo, resulta un poco extraño realizar tantas referencias a ellos sin indagar sobre la historia de su descubrimiento, o de manera más específica, que ocurre con su contenido genético durante la primera etapa de la meiosis. Nuestra introducción a este problema inicia a mediados del siglo XIX cuando C Correns y otros construyeron el mendelismo cerca de la existencia de factores discretos que determinan la morfología de los seres vivos.
Basados en lo anterior debemos recordar dos cosas:
👉 a nadie le interesó su trabajo por casi 34 años
👉 la propuesta de Mendeliana era completamente teórica.
El modelo Mendeliano permitía explicar fenómenos, pero no proveía evidencia experimental de la ubicación física de estos factores hereditarios. En otras palabras, los trabajos de los Mendelianos están desligados de manera absoluta a la naturaleza física de los genes. Entre los años entre la propuesta de Mendel y su redescubrimiento, un periodo de tiempo aproximado de 50 años varios biólogos especialmente pruso-alemanes se involucraron en la indagación de la naturaleza física del material hereditario.
Durante la década de 1880 varios biólogos europeos estaban siguiendo las actividades del desarrollo experimental, especialmente en lo concerniente al desarrollo de nuevos instrumentos. Esta tendencia fue desarrollada de manera más marcada en el continente, especialmente en Francia y el recién formado estado alemán. En lo que concierne a la biología el desarrollo de instrumentos se centró en los microscopios ópticos, que fueran capaces de obtener mayor resolución reduciendo el número de artefactos “machas debidas a imperfecciones del manejo de la luz y las lentes”. Estos nuevos instrumentos permitieron discernir nuevas estructuras celulares, así se pudieron distinguir eventos al interior de las células, en otras palabras, las primeras evidencias del ciclo celular. No es que los trabajos de Mendel fueran despreciados por todo el mundo, tal vez fuera el hecho de que no tuvieron el impacto necesario. En cuanto a impacto nos referimos a la cantidad de veces que el trabajo de un autor es citado por otros.
Figura 16.3. Los dibujos de W. Flemming con respecto a la mitosis muestran el grado de perfeccionamiento de los microscopios del siglo XIX y el nivel exquisito de detalles en las observaciones realizadas en esta época.
Ninguno de los biólogos que trabajaban en microscopia tuvo acceso a los trabajos de Mendel, pero aun así entendía que cualquier cosa que gobernara las características hereditarias debía pasarse de una célula a otra de generación en generación. Esta conclusión por sí misma es una idea crucial: toda la información genética necesaria para construir y mantener una planta o animal complejos tienen que caber en el interior de las fronteras de una sola célula. Aquí ingresa Walter Flemming uno de los más grandes biólogos celulares, fue quien acuñó la palabra cromatina y mitosis. Al igual que otros biólogos que estudiaron la citología Flemming era prusiano “sirvió como médico en la guerra franco-prusiana”.
El hecho de que todos estos citólogos sean pruso-alemanes no es coincidencia debido a que la ciencia continental tuvo un enfoque empirista-instrumentalista más marcado que el de Inglaterra durante la misma época, y la citología es algo que solo puede investigarse con instrumentos. En los primeros años de la década de 1880 Walter Flemming revelaron que los contenidos citoplasmáticos eran repartidos de una célula a otra al azar dependiendo del plano de división de la célula. En contraste las células parecían embarcarse en muchos problemas para dividir sus contenidos nucleares de manera altamente organizada. Durante las divisiones celulares el material que se condesaba al interior del núcleo se hacía altamente organizado en fibras visibles, las cuales fueron denominadas cromosomas, que significa cuerpos color.
16.5 Primeras observaciones de la fertilización manipulada
Durante el periodo de tiempo de las investigaciones celulares “segunda mitad del siglo XIX” el proceso de fertilización fue observado y descrito por dos biólogos llamados T. Boveri y J. Zeit en 1888. A pesar de que la célula espermática es particularmente pequeña rápidamente se descubrió que era igual de importante en términos genéticos al mucho más grande óvulo. ¿Qué es lo que estas dos células tienen en común?, la característica más evidente es la del núcleo y los cromosomas.
Figura 16.4. Theorore Boveri, embriólogo alemán. Junto con Wilhelm Roux y Hans Driesch es considerado uno de los grandes fundadores de la embriología experimental.
La importancia de los cromosomas que son aportados por el gameto masculino se hizo evidente por estudios posteriores realizados nuevamente por Theorore Boveri en huevos de erizo de mar. Estos estudios también involucran unos de los primeros procedimientos de fertilización artificial. La manipulación en este caso involucró la fertilización de un solo óvulo por dos espermatozoides en lugar de solo uno como sería normalmente el caso.
Esta condición denominada poliespermia se caracteriza por divisiones celulares abortivas que condicen a la muerte temprana del embrión en formación. La pregunta en su contexto fue ¿Por qué la presencia de una célula tan pequeña en comparación con un óvulo mucho más grande tiene consecuencias tan drásticas? El Segundo espermatozoide dona un juego extra de cromosomas en estado haploide, generando una célula en estado (3n) junto con un centriolo extra. Estos componentes adicionales conllevan a divisiones celulares anormales en el embrión durante la división celular. Lo anterior conlleva a que las células hijas reciban cantidades variables de cromosomas, lo cual conlleva a su muerte por falta o exceso de ciertos componentes celulares producidos de manera anormal.
Boveri y su grupo de investigación concluyeron que el proceso de desarrollo normal era dependiente de una combinación particular de cromosomas; y esto solo puede significar que los cromosomas individuales debían poseer cualidades hereditarias que alteran la función celular. Esta fue la primera evidencia de una diferencia cualitativa entre los cromosomas y otros componentes celulares.
16.6 Primeros modelos biológicos en la biología celular
A parte del erizo de mar, otro organismo modelo que fue ampliamente empleado por los microscopios disponibles en el siglo XIX fue el de los gusanos parasíticos nematodos del género Ascaris. Los gametos de áscaris se caracterizan por tener pocos cromosomas (n=2; 2n=4) que son grandes y fáciles de observar. Estas características son ideales para microscopios con baja resolución como los disponibles en el siglo XIX o en los cursos de introducción a la biología en muchas universidades modernas. En 1883 el biólogo belga Edouard van Beneden se dio cuenta de que las células de estos gusanos poseen cuatro cromosomas, pero que en los gametos masculino y femenino solo se detectaba la presencia de dos cromosomas justo antes de la fertilización.
Pocos años después el proceso de la meiosis fue descrito y finalmente el 1887 el biólogo pruso-alemán August Weismann concluyó que durante la meiosis existía un evento que reducía a la mitad la cantidad de cromosomas presentes en los gametos en formación. Si la fase de reducción no ocurriera, con cada generación la cantidad de cromosomas de la especie se duplicaría, evento que no ocurre “al menos no con frecuencia”.
16.7 Todos pasan por alto a Mendel en el siglo XIX
El hecho de que su trabajo fuera incinerado por el sucesor en la abadía nos da ya una idea de lo que le sucedió a Mendel. El impacto de una genética reduccionista e internalista no se dio por casi 34 años en los que, si bien su trabajo estuvo al acceso de las comunidades científicas, este fue ignorado. Posiblemente la genética reduccionista no podía explicar muchos otros casos de variabilidad en otras especies de plantas, animales y en el hombre; las cuales mostraban claros patrones de herencia continua, para los cuales la herencia mendeliana es inútil. Es por esto que el trabajo de Mendel publicado en 1866 en un libro llamado “Experimentos en hibridación de plantas: Versuche über Pflanzen-Hybriden” escrito en alemán (Mendel, 1866, 1996); no fue tenido en cuenta para los programas de investigación en genética más holista que buscaba encontrar explicaciones para la herencia continua.
El trabajo de Mendel solo comenzó a tomarse en serio 34 años después por sus tres redescubridores más notables: Carl Correns, Hugo de Vries y Eric von Tschermak. Este redescubrimiento coindice con el cambio de siglo y una nueva actitud hacia la biología mucho más enfocada hacia las matemáticas duras. Una vez redescubierto Mendel, la genética postmendeliana dio inicio con varios objetivos en mente (Harwood, 2000; Moore, 2001; Stubbe, 1972).
👉 Expandir las leyes reduccionistas de la genética clásica para explicar otros patrones de herencia; especialmente la herencia continua.
👉 Encontrar la naturaleza física de los factores mendelianos, hasta entonces meros artefactos de la imaginación matemática para explicar fenotipos.
👉 Crear un nuevo vocabulario para distinguir los fenómenos genéticos y su base celular.
16.8 La búsqueda de la naturaleza física de los factores mendelianos
El redescubrimiento de las leyes de la genética clásica y su confirmación triple influyó notablemente en la investigación sobre la biología celular a partir de la primera década del siglo XX. Este aspecto de la historia es muy importante ya que iría en contra de la concepción de ciencia popularizada por el circulo de Viena cerca del mismo periodo de tiempo, donde se proponía que la ciencia procedía de forma acumulativa e inductiva, de los datos a la teoría. Para el caso de Mendel, las observaciones que el realizó conllevaron a una construcción teórica que presuponía de estructuras al interior de los seres vivos que no podían ser observadas de manera directa, es decir la ubicación física y química de sus factores hereditarios, es decir los genes. En la primera década, del silo XX las leyes mendelianas se convirtieron en la guía teórica a la cual debía atenerse la investigación sobre la naturaleza física de los genes, es decir cualquiera que fuera la unidad hereditaria estas deberían comportarse físicamente en base a las leyes mendelianas.
17. Los mendelianos 1, el mito del redescubrimiento
|| REGRESAR AL INDICE ||
Por genética clásica podemos entender a la rama de la genética que se basa únicamente en el fenotipo, es decir la biométrica y en los cruces de hibridación selectiva que abarca desde el trabajo de Mendel hasta el descubrimiento de los métodos moleculares que dan acceso a las manifestaciones físicas de los alelos, es decir las proteínas. En un sentido más estricto podemos entender como aquella parte de la genética biométrica que fue transpuesta a la enseñanza escolar y que fue construida por los mendelianos –más NO por Mendel –en la primera mitad de la década de 1900, junto con algunos detalles de estudios posteriores. La mayoría de estos primeros mendelianos provenían de dos campos diferentes, unos eran especialistas en botánicos, y otros eran matemáticos puros.
La genética clásica parte de un problema, las leyes mendelianas parecían aplicar bien a un selecto conjunto de casos, pero no servían para la mayoría de eventos naturales, problema que paradójicamente evitó que tanto Darwin como Wallace estudiaran más profundamente la herencia discreta o mendeliana, por considerarla muy rara y simple, como bien se lee en sus cartas. Sin embargo, eso no evitó que muchos mendelianos se enamoraran del modelo de herencia discreta, e intentaran expandirla una vez fue popularizada por Carl Correns y Hugo de Vries en 1900.
A estos primeros genetistas mendelianos les debemos también la creación de un nuevo vocabulario, el vocabulario de la genética clásica, del cual se nos heredan conceptos como genética, gen, alelo, genotipo, fenotipo, mutación, homocigoto o heterocigoto.
¿Es la ciencia un área donde se relacionan caballeros elegantes? O en realidad ¿se trata de la confrontación como perros y gatos por la gloria y la fama?
El redescubrimiento de Mendel es una historia bastante compleja, y lo es más, si nuestra visión de la ciencia es la de caballeros elegantes que discuten todo en un estirado tono de condescendencias, como elegantes caballeros británicos tomando te de forma sofisticada. Mendel y su obra fueron reinterpretados a la luz de los debates a cerca de la herencia especialmente por Hugo de Vries y Carl Correns. Mendel fue elevado a la categoría de padre de la genética no por una condescendencia caballeresca de sus redescubridores (Monaghan & Corcos, 1990; Moore, 2001; Olby, 1979).
De hecho, gran parte del modelo mendeliano que aprendemos en los libros de texto es adjudicarle específicamente a Carl Correns y él lo sabía, pero para evitar que Hugo de Vries se quedara con la prioridad del descubrimiento y con el título de padre de la genética, pues había publicado primero en el tema pero no de forma tan completa como Correns, decidió abandonar el mismo la esperanza de adquirir la inmortalidad del título de Padre de la Genética para sí mismo y otórgaselo a Mendel muerto ya hace décadas antes de ceder ante de Vries (Monaghan & Corcos, 1990; Moore, 2001; Olby, 1979).
Más allá de las luchas por la gloria, la fama y el dinero, de los redescubridores de Mendel o más apropiadamente de los fabricadores del mito de Mendel, podemos afirmar una cosa, ellos son el verdadero origen del mendelismo, y aunque resulte paradójico, cuando nos referiremos a los mendelianos de aquí en adelante nos referiremos a estos señores y otros tantos científicos de la primera década del siglo XX pero excluyendo al propio Mendel, quien ya llevaba muerto y enterrado por unos cuantos años (Fairbanks & Rytting, 2001; Olby, 1979).
17.1 La obra de Tschermak
Mendel murió en 1884, y su trabajo permaneció en una relativa oscuridad debido a que su objeto era en realidad la especiación por medio de hibridación estable, no el estudio de la herencia. Según Moore (2001) de los tres redescubridores el que menos entendió el trabajo de Mendel fue Tschermak quien llegó incluso a afirmar la aparición de mezclas de rasgos, justo en oposición del núcleo fundamental del trabajo de mendelismo clásico en donde se afirmaba que los rasgos no se mezclaban, uno se hacía dominante y el otro recesivo. De hecho estos dos conceptos si los acuñó Mendel con el formalismo A +2ab + a (Mendel, 1866, 1996).
Figura 17.1. Erich von Tschermak, fue un biólogo, botánico, genetista y agrónomo austríaco codescubridor de las Leyes de Mendel de manera independiente de los otros dos científicos Hugo de Vries y Carl Correns. Von Tschermak publicó sus hallazgos en junio de 1900. Tschermak era nieto del profesor que enseñó botánica en Viena a Gregor Mendel.
Tschermak tampoco discutió la proporción 3:1 con la cual se ejemplifica actualmente la primera ley de Mendel o ley de la segregación independiente. Las menciones de Tschermak sobre la proporción 9:3:3:1 de los fenotipos en la F2 del cruce dihíbrido empleado para enunciar la segunda ley de Mendel o ley de la distribución de caracteres, se realizaron en base a las referencias que hacía de ella Carl Correns, y de hecho sus resultados experimentales no concordaban con esa proporción (Monaghan & Corcos, 1987).
17.2 La obra de De Vries
El trabajo de de Vries ha sido sometido a grandes controversias a lo largo de los años (Meijer, 1985). A pesar de no mencionar a Mendel como referencia de su trabajo, la organización de los artículos de de Vries son semejantes a los de Mendel (Moore, 2001). La terminología difería originalmente, por ejemplo en lugar de emplear el concepto de dominante y recesivo como posteriormente hizo, al principio hablaba de activo y latente respectivamente (Darden, 1985). Aunque no citar a Mendel sería la debilidad por la cual Carl Correns lo criticaría posteriormente, el trabajo de de Vries también tenía otra debilidad, una que tal vez a nuestros ojos puede parecer muy grave en términos de ética científica (Moore, 2001).
Asumiendo que de Vries estaba enterado del trabajo de Mendel y del radio 3:1 que el mismo referencia como una Ley Natural, estaba estancado en un feo problema. Sus datos no concordaban con aquel modelo teórico. Como se vio en los problemas con genética mendeliana, las proporciones teóricas que se asumen bajo un azar perfecto no se traducen de forma exacta a las proporciones obtenidas experimentalmente, siempre existen ruidos que favorecen algunos rasgos sobre otros.
Figura 17.2. Hugo Marie de Vries, fue un botánico neerlandés y uno de los primeros genetistas. Nacido en Haarlem y fallecido en Lunteren, es uno de los tres biólogos, junto a Carl Correns y Erich von Tschermak que en 1900 redescubrieron las leyes fundamentales de la genética publicadas primero por Gregor Mendel en 1866.
Para resolver aquel problema se empleaba el método de análisis de gráficas o las pruebas de hipótesis como el chi cuadrado. El problema para la época es que precisamente en esas fechas estaba comenzando a desarrollarse las teorías estadísticas sobre las cuales se crearían las pruebas de hipótesis, en otras palabras, en aquella época para determinar si sus datos experimentales concordaban con los teóricos solo tenían regla y escuadra para hacer las gráficas de barras y el ojímetro.
Por ejemplo, las pruebas del tipo chi cuadrado fueron desarrolladas entre los años de 1900 a 1920 por Karl Pearson “1857-1936” (Plackett, 1983); o las pruebas de análisis de varianza ANOVA por Ronald Fisher “1890-1962” en 1925 (R. Gould, 2011). Hugo de Vries estiró sus conclusiones, pero no maquilló los datos, por eso es fácil pescarle. Aunque en sus conclusiones habla de una proporción 3:1 sus datos aportarían más a una proporción 2:1. Lo anterior implicaría que de Vries estaba interesado en ajustar sus datos experimentales a la fuerza con el modelo teórico propuesto por Mendel aun cuando no le estaba dando el crédito por el radio 3:1 (Moore, 2001). Pero siendo justos lo mismo nos pasa a la mayoría de los profesores de genética, cuando tratamos de ajustar a las malas los datos de Mendel sobre color y textura de la semilla de la arveja a la proporción 9 3 3 1, cuando en realidad los datos apoyan más una proporción 10:3:3:1.
Hugo de Vries puede ser recordado como quien inició el concepto de gen, aunque él lo llamó pangen que literalmente significa: lo que da origen a todo. Para de Vries, los pangenes vendrían en formas activas e inactivas. En 1903 de Vries afirmó que los pangenes no podían cambiar o variar, aunque posteriormente sería recordado por proponer la teoría mutacionista que establece precisamente que los factores hereditarios cambian (Dobzhansky, 1959). Las hipótesis de de Vries sobre los pangenes cambiaron a lo largo de su vida. Inicialmente pensaba que las células reproductoras recibían la totalidad de pangenes de sus ancestros. Sin embargo, después de 1900 ya afirmaba en consonancia del modelo matemático mendeliano que ha llegado a nuestros días, que cada célula reproductora “gametos” recibían solo la mitad de los pangenes de los parentales (Moore, 2001).
17.3 La obra de Correns
De todos los redescubridores de Mendel fue Correns único en citar su artículo original poco antes del año 1900 aunque varios autores proponen que de Vries si lo conocía y evidencia de ello es su intento de estirar sus datos a la proporción 3:1 (Moore, 2001). Es por esta razón que es poco creíble la afirmación de que los tres realizaron sus descubrimientos de forma independiente, más bien los tres bebieron de la misma fuente, aunque con interpretaciones, propósitos y conclusiones diferentes de la que tuvo el propio Mendel, por ejemplo, Mendel jamás menciona la proporción 9:3:3:1, entre otras porque sus datos no se ajustaban a ella.
De los tres, tal vez la interpretación más afortunada y el desarrollo teórico más sólido fue la dada por Carl Corres quien bien puede ser llamado el padre no reconocido de la genética clásica (Hans-Jorg Rheinberger, 1995; Hans-Jörg Rheinberger, 2000). Mucho de lo que trabajamos como genética mendeliana proviene de su trabajo. En primera instancia Correns destruyó cualquier noción vitalista, o espirituoso-filosófica a cerca de los factores mendelianos que eran llamados originalmente como elemente/merkmal, señalando que lo que fuera que era pasado de una generación a otra, se localizaba en el núcleo de la célula, justo el lugar donde poco tiempo atrás habían sido descubiertos los cromosomas (McKusick, 1960). Correns fue el primero en expresar el resultado 9:3:3:1 aunque no lo relacionó explícitamente con la capacidad que tenía cada rasgo de ser distribuido independientemente “tercera ley de Mendel”.
17.4 De Merkmal a Anlage, codificación
Correns propuso una serie de conceptos que son actualmente el núcleo de la teoría mendeliana, entre otros la correlación de dos factores para cada rasgo. Correns también acuñó su propia terminología, por ejemplo, la palabra Anlage que significa preparar algo para su desarrollo. Para Correns Anlage era un código diferente al rasgo observable, por lo que aquí ya puede verse una diferenciación clara entre lo que actualmente llamamos fenotipo “lo que se ve” y genotipo “lo que genera”. Correns fue el primero en asociar de forma explícita los factores de herencia con rasgos; el primero en reportar claramente el radio 9:3:3:1; en expresar excepciones a este radio promedio de ligamientos y mucho más importante, relacionar a la meiosis como el mecanismo primordial que dirigía el proceso de generación de gametos. La codificación en parejas de factores “Anlagens” tal como es expresada en el modelo matemático mendeliano también fueron propuestas originales de Correns, por ejemplo para el monohíbrido: AA+ 2Aa + aa; la cual contrastaba con la forma mendeliana: A + 2Aa + a (Moore, 2001)
17.5 La disputa de Correns y de Vries
De los tres redescubridores Correns es el que entiende de forma más detallada el trabajo de Mendel el que genera resultados más sólidos y concordantes; y finalmente el que expresa el mejor modelo explicativo tanto en lo teórico como en el vínculo con procesos biológicos observables para el momento como la meiosis. Ahora el problema que Correns tenía entre manos era la prioridad, aunque de Vries no tenía resultados experimentales sólidos, sí que mencionaba la proporción 3:1, justo uno de sus propios resultados, repetir esto tenía que venir con una cita apropiada. Si Correns hubiera citado a de Vries, este último hubiera adquirido la prioridad sobre todos los trabajos que se deriva de la ley de la segregación independiente.
En base a ello, Correns decidió citar a Mendel y otorgarle tal vez más crédito del que realmente merecía, lo que ha conllevado a errores históricos como afirmar que Mendel propuso la 9:3:3:1, lo que evitó efectivamente de de Vries se quedara con el crédito, pero a costa de que Correns también se convirtiera en un fantasma más a la sombra de Mendel, creando así un mito fundacional para una nueva rama de la ciencia, que a la postre sería llamada la genética. Sin embargo, fue el contexto del siglo XX la que originó realmente el mendelismo y la que extendió el mendelismo más allá de las leyes de dominancia, segregación y distribución. Y esto fue particularmente rápido, solo diez años después los fundamentos postmendelianos ya habían sido descritos, entre los que hay que destacar la recombinación genética, uno de los pilares de la posterior síntesis de la teoría de la evolución.
18. Los mendelianos 2, la comunidad científica
|| REGRESAR AL INDICE ||
William Bateson “1861-1962” un famoso zoólogo de Cambridge famoso por proponer el concepto de aloforma la cual más tarde conllevaría a la definición de alelo, pero es menos famoso por otra cosa, oponerse a la idea darwinista de variación continua. Bateson pensaba que la herencia mendeliana le daría el golpe definitivo al neodarwinismo de la época.
Figura 18.1. William Bateson, fue un biólogo y genetista inglés, uno de los redescubridores del trabajo de Mendel, razón por la que es considerado uno de los fundadores de la genética humana. Bateson fue muy crítico con la concepción exclusivamente cromosómica de la herencia y defendió una teoría saltacionista de la evolución, en oposición a la teoría de Darwin de la evolución por medio de la selección natural.
Figura 18.2. El mendelismo y el neodarwinismo de principio del siglo XX parecen opuestos e irereconciliables, el mendelismo se basa en el supuesto de que los rasgos son discontinuos con diferencias cualitativas evidentes “izquierda”, mientras que el mendelismo se basaba en caracteres cuyos estados cambian sutilmente de un individuo a otro “derecha”. Aunque ambos eventos suceden en la naturaleza, la herencia continua “derecha” es mucho más común que la discreta “izquierda”, eso lo reconocieron Darwin y Wallace, y por eso no estudiaron la herencia discreta, aunque esta última era más fácil de convertir a un formalismo matemático.
Eso se debía a que el mendelismo construido por Correns y de Vries se basaba en herencia discontinua, es decir a saltos, justo lo opuesto a la propuesta de Darwin de herencia continua. De hecho, una vez que conoció la teoría mendeliana, Bateson se puso a la tarea de extenderla al reino animal creyendo que el trabajo mendeliano confirmaría su teoría de herencia discontinua. Bateson acuñó en nombre del campo, GENÉTICA, y adicionalmente afirmó que esta se oponía a la teoría de la evolución de Darwin y seguidores.
Tal vez de Vries no estaba de acuerdo, aunque el desarrollo del mendelismo fue un paso importante en el desarrollo de la genética, no podía explicar toda la variación de los seres vivos. Ya fuera por resultados de sus propios experimentos, o por su propia reticencia a darle más crédito a Mendel, de Vries decisión subestimar lo más posible los descubrimientos realizados por Mendel y por el desarrollo del mendelismo que el mismo había ayudado a construir.
Según de Vries en una carta a Bateson: “el Mendelismo es una excepción, más que una regla”, en realidad de Vries señalaba el problema del trabajo de Mendel, es tan reduccionista que nunca pudo extenderse a más que unos casos contados dentro de los seres vivos. En cualquier caso, la repulsión de de Vries por todo lo mendeliano lo llevó a despreciar una invitación a la conmemoración de Mendel (Moore, 2001).
18.1 La hipótesis de la mutación
Esta historia de autores poco valorados nos regresa ahora a Darwin y su teoría de la evolución. Actualmente el proceso de mutación es indispensable para explicar, pero ni el propio Darwin la propuso, su trabajo fue sobre selección. De Vries es el padre de la teoría de la mutación. El concepto de mutación se opone a la propuesta original de Darwin, ya que la mutación afecta a un factor hereditario de forma discontinua. La propuesta original es que la variación era absolutamente gradual, como si se tratara de un fluido que cambia paulatinamente de color. La mutación por más pequeña que fuera es un proceso puntual y discontinuo. Es por esto que el proceso de eliminación de mutantes no fue llamado selección natural por autores como Thomas H. Morgan “1866-1945” aun cuando actualmente así lo hacemos.
18.2 El concepto matemático del gen
Los factores que generan un mismo carácter y se simbolizan con la misma letra independientemente de si es mayúscula o minúscula se denominarán genes.
Figura 18.3. Edith Rebecca Saunders, fue una genetista británica y anatomista de plantas. Descrita por JBS Haldane como la "Madre de la genética de plantas británica", ella jugó un papel activo en el redescubrimiento de las leyes de herencia de Mendel, la comprensión de la herencia de rasgos en las plantas, y fue la primera colaboradora del genetista William Bateson.
Figura 18.4. Wilhelm Ludvig Johannsen, fue un botánico, genetista, fisiólogo vegetal danés. Trabajó para el Instituto agrícola de Copenague antes de convertirse en catedrático de agricultura a la universidad de la ciudad. En 1909 acuñó el término gen (a partir del griego "que origina...") como abreviatura de la palabra pangen, acuñada por Hugo de Vries en 1889. También acuñó las palabras "genotipo" y fenotipo" en 1911.
La expresión gen también fue acuñada a principios del siglo XX con los estudios de redescubrimiento de Mendel por parte del botánico danés Wilhelm Johannsen "1857-1927" en 1909, quién también acuñó los términos genotipo y fenotipo (Churchill, 1974). Los factores que generan un mismo carácter, pero diferentes rasgos serán denominados alelos y se simbolizan con letras mayúsculas o minúsculas, aunque existen otras posibilidades como emplear subíndices y superíndices como números o comillas. La palabra Alelo fue acuñada por William Bateson y Rebecca Saunders en 1902 aunque originalmente emplearon el término alelomorfo (Onaga, 2010).
Hasta ahora no había diferencia explícitamente entre los factores para rasgo y para carácter, contentándonos únicamente con la expresión factor que era el término más aproximado a lo que empleaba Mendel. Resulta curioso como dos términos que en libros de texto son tan inmediatos tardaron casi una década en formularse uno del otro.
18.3 Otros conceptos de genética en la década de 1900-1910
La década de 1900 es una completa locura, pues se presenta una efervescencia de investigaciones impulsadas por los trabajos de los “redescubridores” aunque con pocos factores unificadores y bastante resistencia. Sin embargo, en aquella década se desarrollaron otros conceptos como:
La chi cuadrada para comparar series experimentales y series teóricas (Plackett, 1983). Ligamiento genético, descubierto por Bateson, Saunders y Punnett en 1904 (Bateson, Saunders, & Punnett, 1904). La pleiotropía en 1910 por Ludwig Plate (Stearns, 2010)
El principio de Hardy-Weinberg por Karl Pearson. Reginald Punnett, Wilhelm Weinberg, William E. Castle y Godfrey Harold Hardy en 1908 (A. W. F. Edwards, 2008).
Adicionalmente los genetistas se dan cuenta que los resultados que obtuvo Mendel son una rareza, por lo que era difícil determinar si sus resultados concordaban con proporciones experimentales, por lo que comenzaron a emplearse las primeras pruebas de hipótesis de variables categóricas como la Chi cuadrada, instrumento desarrollado por Carl Pearson (Plackett, 1983).
19. La teoría cromosómica y la distribución dependiente
La asociación entre cromosomas y unidades hereditarias “genes” no se realizó sino hasta el redescubrimiento de las leyes de Mendel, pero cuando las leyes de la genética clásica fueron redescubiertas la asociación de los genes y los cromosomas fue casi que inmediata. Ya en 1903 en la misma década en que los trabajos de los re-descubridores de la genética clásica impactaron a otro biólogo llamado Walter Sutton un joven graduado de la Universidad de Columbia publicó un artículo que ligaba directamente a los cromosomas como los portadores físicos de los factores genéticos propuestos de manera teórica por Mendel para explicar los fenómenos observados al nivel macroscópico (Sutton, 1903).
Figura 19.1. Walter Sutton, fue un médico y genetista estadounidense cuya contribución más significativa a la biología fue su teoría de que las leyes mendelianas de la herencia podían ser aplicadas a los cromosomas a nivel celular.
En este caso tenemos una interacción compleja de la teoría, la razón y lo empírico en el desarrollo de la ciencia.
19.1 Relación mitosis y meiosis
Cuando Sutton examinó los cromosomas en las células justo al inicio de la meiosis encontró que los miembros de cada pareja de cromosomas se asociaban unos con otros formando estructuras complejas que reciben diferentes nombres actualmente, como bivalentes o tétradas ya sea su se observa desde los cromosomas homólogos o desde las cromátides hermanas y homólogas respectivamente (Crow & Crow, 2002; McKusick, 1960). Dado que en este punto de microscopia se los observa desde el punto de vista de cromosomas emplearemos la expresión bivalente.
Figura 19.2. Por el momento solo nos debemos concentrar en la imagen de arriba ya que el modelo de abajo vino varios años después. Los microscopios de principios del siglo XX difícilmente podían tener la resolución necesaria para distinguir las cromátides hermanas al interior de los cromosomas, por esto el nombre bivalente es más acertado en este contexto.
Sutton observó la presencia de 11 bivalentes en los cuales cada una de las 11 parejas de cromosomas homólogos se encontraban asociadas de manera intima. El resultado de la primera división meiótica conllevaba a la separación de los cromosomas homólogos en células independientes. Esta era la primera división reductora propuesta por Weismann 15 años antes en base a una propuesta puramente teórica. Esta también era la base física para la propuesta de los factores hereditarios de Mendel, los cuales también se encontraban en parejas al interior de la célula y cuando esta genera gametos se separaban. La división reductora observada por Sutton explicó varios de los hallazgos que Mendel había encontrado:
👉 Los gametos presentan un solo alelo = los gametos contienen un solo cromosoma de cada clase.
👉 El número de células que contiene un tipo de alelo es el mismo de los que contiene el otro tipo de alelo = el número de células que contiene un cromosoma es el mismo al que contiene a su versión homóloga.
👉 La fertilización de los gametos completa la cantidad de alelos originales = la fertilización completa la cantidad de cromosomas originales.
A pesar de que las propuestas de Sutton con respecto a los cromosomas y los factores
de mendelianos parecían encajar, existían aun cuestiones que no concordaban totalmente. Por ejemplo ¿cómo era que los genes se organizaban al interior de los cromosomas?, ¿sería posible encontrar la ubicación de los genes en los cromosomas?
Sin embargo, el problema más claro que Sutton encontró a su propia propuesta tenía que ver con la Ley de Distribución Independiente, en la que los caracteres hereditarios se distribuyen de manera independiente y aleatoria unos de otros. En base a los trabajos de los mendelianos ningún carácter estaba ligado a otro durante los cruces di-híbridos, pero la propuesta cromosomal de Sutton predecía la existencia de grupos de genes ligados en los mismos cromosomas.
Figura 19.3. La formación de gametos mendelianos como abstracción matemática tenía un comportamiento semejante a la meiosis observada al microscopio en el sentido de que ambas disminuía el con tenido genético a la mitad.
La respuesta a ambas preguntas se encuentra posiblemente en la naturaleza independiente de los cromosomas, si los genes se encuentran todos en diferentes cromosomas se comportarían de manera mendeliana clásica, distribuyéndose de manera independiente y aleatoria entre las células hijas. Pero la otra opción era que los genes se encontraran ubicados en un mismo cromosoma. Sutton no se amilanó, y en lugar de intentar hacer encajar toda la propuesta de los mendelianos propuso y predijo la existencia de caracteres que se debían heredar de manera no-mendeliana debido al ligamiento físico de sus genes en un mismo cromosoma, concepto al cual se le ha denominado grupo de ligamiento.
La profecía de Sutton a cerca de los grupos de ligamiento se cumplió poco tiempo después cuando se encontró que en los guisantes dulces dos caracteres independientes uno de color de la flor y otro de la forma del polen se comportaban como grupos de ligamiento. Al poco tiempo otros ejemplos se acumularon (Karp, 2013). Lo anterior es interesante debido a que el redescubrimiento de las leyes de Mendel a los inicios de siglo XX también conllevó casi de manera inmediata al desarrollo de la genética evolutiva, y uno de sus principales precursores seria Thomas Hunt Morgan (Thomas Hunt Morgan, 1916). Otro detalle de la era postmendeliana es que el foco de la historia se transfiere desde la Alemania de segundo Reich a la nueva potencia en florecimiento los Estados Unidos de América.
19.2 Hacia la comunidad
William Bateson, Edith Rebecca Saunders y Reginald C. Punnett en 1905, en su trabajo con plantas de guisantes, notaron que no todos sus cruces arrojaron resultados cumplieran la ley de la distribución independiente. Recuerde que la ley de la distribución independiente es aquella que nos obliga a generar todas las combinaciones de gametos posibles para construir el cuadro de Punnett o aquella que nos permite resolver un problema dihíbrido como si fueran dos monohíbridos independientes que al final se combinan por una factorización polinómica. Específicamente, algunos fenotipos aparecieron con mucha más frecuencia de lo que la genética mendeliana tradicional predecía, pero que la hipótesis de Walther Sutton acerca de que los cromosomas transportaban los genes si postulaba.
Figura 19.4. Sutton predice la existencia de genes ubicados en un mismo cromosoma que altera las frecuencias y tipos de gametos esperables.
Con base en estos hallazgos, el trío propuso que ciertos alelos de alguna manera deben estar acoplados entre sí, aunque no estaban seguros de cómo se produjo este vínculo hasta que se adicionaron las predicciones de Sutton. La respuesta a esta pregunta se produjo siete años más tarde, cuando Thomas Hunt Morgan utilizó moscas de la fruta para demostrar que los genes vinculados deben ser objetos físicos reales que se encuentran muy cerca del mismo cromosoma, confirmándose así la teoría cromosómica de la herencia suttoniana (Crow & Crow, 2002).
19.3 Primeras desviaciones de la segregación independiente
En 1905, William Bateson, Edith Rebecca Saunders y Reginald Punnett examinaban el color de la flor y la forma del polen en las plantas de guisante (Bateson et al., 1905) realizando cruces dihíbridos similares a los llevados a cabo por Gregor Mendel y que se ven en cualquier libro de texto. En particular, estos investigadores cruzaron plantas de guisante homocigóticas que tenían flores de color púrpura y largos granos de polen con plantas homocigóticas que tenían flores rojas y granos redondos de polen (Pierce, 2005). Antes del cruce, el trío notó que las flores moradas (P) dominaban sobre las flores rojas (p), y que los granos largos de polen (L) dominaban sobre los granos redondos de polen (l). La generación F1 de plantas resultantes del cruce PPLL x ppll fue, por lo tanto, doblemente heterocigótica (PpL1), y todas las plantas F1 tenían flores moradas y granos largos de polen, tal cual se esperaba teóricamente, hasta este punto nada raro (Lobo, 2008a).
A continuación, Bateson, Saunders y Punnett decidieron cruzar las plantas F1 entre sí. Después de este cruce, los investigadores esperaban que la generación F2 tuviera una proporción de 9: 3: 3: 1 (nueve plantas con flores de color púrpura y largos granos de polen, tres plantas con flores de color púrpura y granos de polen redondo, tres plantas con flores rojas y granos largos de polen, a una planta con flores rojas y granos redondos de polen). En su lugar, observaron los resultados que se muestran en la Tabla 19.1 (Bateson et al., 1905), y se encontró que existen diferencias significativas entre las proporciones esperadas y las observadas (Lobo, 2008a).
Como lo indica la Tabla 19.1, Bateson, Saunders y Punnett observaron que sus cruces producían una desviación de las proporciones de la distribución independiente (Bateson et al., 1905). Los investigadores consideraron varias explicaciones para este resultado, incluida la epistasis, e incluso trataron de ajustar sus datos con una proporción de 7: 1: 1: 7. Sin embargo, la epistasis en las generaciones F2 generalmente da como resultado una relación mendeliana modificada y se observa cuando los genes afectan el mismo rasgo, como el color de la flor, por lo que la epistasis no podría explicar la desviación que se ve aquí, ya que estamos hablando de dos caracteres, color de la flor y forma del polen (Lobo, 2008a).
Tabla 19.1. Tabla para solucionar manualmente la para un dihíbrido. Los contetos calculados se obtienen al multiplicar el total de conteos experimentales (929) por las probabilidades teóricas respectivas. Los grados de libertad se obtienen como el número de parejas analizadas menos 1.
Durante su análisis, los investigadores se dieron cuenta de que había un exceso en el número de fenotipos parentales (violeta // largo y redondo) en los resultados de F2. En particular, de las 2.132 plantas F2, se esperaba que 1.199 tuvieran flores de color púrpura y granos largos de polen, pero en su lugar, había un enorme 1.528 de plantas con este fenotipo. De manera similar, se esperaba que solo 133 plantas tuvieran flores rojas y granos redondos de polen, pero los investigadores observaron casi tres veces ese número (381). Ahora se entiende que las diferencias entre los resultados esperados y observados fueron estadísticamente significativas (P <0.005), lo que significa que los datos no pueden ser explicados únicamente por casualidad (Lobo, 2008a).
Debido a que los fenotipos parentales reaparecieron con más frecuencia de lo esperado, los tres investigadores supusieron que había un acoplamiento, o conexión, entre los alelos parentales para el color de la flor y la forma del grano de polen (Bateson et al., 1905), y que este acoplamiento resultó en la desviación observada de la distribución independiente. De hecho, la Figura 19.5 muestra un ejemplo de un cruce entre plantas de guisante homocigóticas con flores de color púrpura y largos granos de polen y plantas homocigóticas con flores rojas y granos de polen redondo que exhibe el enlace de los alelos parentales. Pero, ¿por qué se relacionan ciertos alelos? Bateson, Saunders y Punnett no estaban seguros. De hecho, no fue hasta el último trabajo del genetista Thomas Hunt Morgan que este acoplamiento, o vinculación, podría explicarse por completo (Lobo, 2008a).
A principios del siglo XX, la famosa "sala de las moscas" de Thomas Hunt Morgan en la Universidad de Columbia fue el sitio de muchos descubrimientos y momentos "eureka" en el campo de la genética. Morgan eligió usar la mosca de la fruta prolífica Drosophila melanogaster como modelo para estudiar genética. Luego, durante un período de tres años, Morgan y sus alumnos lucharon por encontrar una forma de crear una mosca que se viera diferente a las moscas normales al tratar estas moscas con calor, frío, rayos X, ácidos, bases, azúcares y otros químicos (Lobo, 2008a).
Finalmente, en 1910, Morgan descubrió fortuitamente una sola mosca con ojos blancos que no resultó de ninguno de sus tratamientos.
Figura 19.5. Cuando las plantas de guisantes que tienen flores de color púrpura con largos granos de polen se cruzan con plantas de guisantes que tienen flores rojas con granos de polen redondos, la progenie resultante se designa como la generación F1. Todas las plantas en la generación F1 tienen el mismo fenotipo: flores de color púrpura y granos largos de polen. Cuando se permite que estas plantas F1 se autofecundan, la progenie resultante se designa como la generación F2. La expectativa es que los siguientes fenotipos se observarán en una proporción de 9: 3: 3: 1 en la generación F2: plantas púrpuras con granos largos de polen, plantas púrpuras con granos redondos de polen, plantas rojas con granos largos de polen y plantas rojas con redondo de granos de polen. Sin embargo, la generación F2 producida en este cruce no se ajusta a la relación esperada de 9: 3: 3: 1. En cambio, hay muchas más plantas púrpuras con largos granos de polen y plantas rojas con granos redondos de polen de lo predicho.
(Las moscas normales de la fruta tienen ojos rojos, no ojos blancos.) Morgan cruzó inmediatamente esta mosca blanca de ojos blancos a sus hermanas de ojos rojos (Morgan & Bridges, 1916). Cuando Morgan cruzó la mosca ojos blancos con la de ojos rojos sin tomar en cuenta un segundo carácter encontró que seguía el patrón mendeliano. Sin embargo, cuando se analizó el vínculo entre el color de ojos y el sexo la cosa fue diferente, Morgan esperaba una relación de 1: 1: 1: 1 de hembras de ojos rojos, machos de ojos rojos, machos de ojos blancos y hembras de ojos blancos. En cambio, observó los siguientes fenotipos en su generación F2 (Lobo, 2008a):
👉 2459 hembras de ojos rojos
👉 1011 hombres de ojos rojos
👉 782 machos de ojos blancos
No había hembras de ojos blancos, y Morgan se preguntó si esto era porque el rasgo estaba vinculado al sexo y solo se expresaba en moscas macho. Para probar si este era realmente el caso, Morgan completó un segundo cruce entre la mosca macho de ojos blancos original y algunas de sus hijas de F1. Estos cruces produjeron una generación F2 con los siguientes fenotipos:
👉 129 hembras de ojos rojos
👉 132 machos de ojos rojos
👉 88 mujeres de ojos blancos
👉 86 machos de ojos blancos
19.4 Reglas de ligamiento de genotipo a cariotipo
Por lo tanto, los resultados de este cruce sí produjeron hembras de ojos blancos, y los grupos tenían números aproximadamente iguales. Por lo tanto, Morgan formuló la hipótesis de que el rasgo del color de los ojos estaba relacionado con el factor sexo. Esto a su vez llevó a la idea de la vinculación genética, lo que significa que cuando dos genes están estrechamente asociados en el mismo cromosoma, no se distribuyen de forma independiente (Morgan & Bridges, 1916).
La propuesta de Morgan fue una sugerencia temprana de que los genes eran objetos físicos reales que estaban ubicados en los cromosomas. De hecho, el conocimiento de la vinculación genética fue fundamental para demostrar que los genes eran objetos reales que podían heredarse, someterse a recombinación y asignarse a ubicaciones específicas en los cromosomas. Por ejemplo, después de la publicación de los hallazgos de Morgan, Reginald C. Punnett utilizó esta información para identificar los grupos de ligamiento en sus estudios previos con plantas, y asoció estos grupos de ligamiento con cromosomas (Punnett, 1923; Punnett, 1927). Además, con este conocimiento en su lugar, Morgan y Alfred H. Sturtevant, su alumno, llevaron a cabo más estudios de vinculación que proporcionaron información sobre la ubicación de los genes en los cromosomas y finalmente dieron como resultado el mapeo de genes (Lobo, 2008a).
19.5 Modelando el ligamiento
Modelaremos a un determinado cromosoma con el símbolo Ii--, por ejemplo, si el cromosoma 1 porta los dos alelos dominantes de dos genes de interés I1AB, mientras el cromosoma dos las dos versiones recesivas I2ab. Aunque parece más complejo, el problema se reduce a la solución de monohíbridos.
20. El señor de las moscas
|| REGRESAR AL INDICE ||
Thomas Hunt Morgan es un punto de inflexión en la historia de la genética, ya que el destruye de forma definitiva el darwinismo y neodarwinismo de Weismann y lo reconstruye a una nueva imagen, la imagen de la genética, después de él y de su libro Una Crítica a la Teoría de la Evolución (Thomas Hunt Morgan, 1916), hablan de evolución y hablar de genética equivaldrán a la misma ciencia, quienes le sucedieron se encargaron de proseguir esa senda la cual concluyó con el establecimiento de la Teoría Sintética de la Evolución (Brooks, 2011; Carroll, 2008; Kutschera & Niklas, 2004; Pigliucci, 2009).
Figura 20.1. Thomas Hunt Morgan, fue un genetista estadounidense. Estudió la historia natural, zoología, y macromutación en la mosca de la fruta Drosophila melanogaster. Sus contribuciones científicas más importantes fueron en el campo de la Genética. Fue galardonado con el Premio Nobel de Fisiología y Medicina en 1933 por la demostración de que los cromosomas son portadores de los genes, lo que se conoce como la teoría cromosómica de Sutton y Boveri. Gracias a su trabajo, Drosophila melanogaster se convirtió en uno de los principales organismos modelo en Genética. También dejo sentada la base de la Teoría Sintética de la Evolución.
Adicionalmente en el laboratorio de Morgan la genética de los años 1910-1920 toma forma completando muchos otros conceptos como la epistasis, la corroboración experimental de la mutación, el ligamiento al sexo y el mapeo de los genes al interior de los cromosomas. De aquí en adelante ya no podrá decirse de los factores mendelianos que son entelequias, sino entidades reales, entidades químicas que se encuentran al interior de las células (Allen, 1985; Thomas Hunt Morgan, 1919a).
20.1 Morgan y Darwin
Una de las cosas que deberemos comprender a lo largo de estas lecturas es que la Teoría de la Evolución no es un sinónimo de darwinismo, puede que Charles Darwin "1809-1882" enunciara por vez primera un mecanismo que permitía la adaptación en condiciones ambientales estables, pero más allá de ello el resto de la comunidad científica continuó haciéndose preguntas e incluso cuestionando algunos planteamientos suyos (Kutschera & Niklas, 2004).
Uno de ellos fue el excesivo gradualismo sobre el que debería operar la selección natural. Este gradualismo acérrimo se asemejaba al concepto de mezcla de pinturas que generan un gradiente de decoloración suyos (Kutschera & Niklas, 2004).
En este se genera un patrón continuo de tonos imposibles de distinguir el uno del otro. Uno de los principales críticos a esta noción continua de la variabilidad natural fue Thomas Hunt Morgan “1866-1945” biólogo evolutivo, genetista y embriología quien sería uno de los fundadores de la genética y la evolución tal como los entendemos en la actualidad suyos (Kutschera & Niklas, 2004).
¿Cómo ser un biólogo evolutivo y al mismo tiempo criticar el trabajo de Darwin?, por el simple hecho de que los modelos teóricos no pertenecen al autor, sino por el contrario son trabajados por las comunidades científicas, y estos pueden ser criticados para ser modificados y mejorados; o incluso desechados (Kuhn, 1970). Morgan criticó el sentido gradualista de la variabilidad darwiniana y en contraposición postuló basándose en trabajos previos de Weismann y de Vries que pequeños eventos discontinuos eran los que engendraban la diversidad, y estos eventos discontinuos serían las mutaciones (Allen, 1968).
20.2 Morgan en el contexto del redescubrimiento de Mendel
T. H. Morgan es un caso interesante dentro de la biología debido a que en sus inicios era altamente escéptico de muchas cosas que nosotros damos por sentadas como la selección natural, el ligamiento al sexo y la genética mendeliana (Allen, 1975). El modelo teórico sobre el cual Morgan inició su proyecto de investigación fue la teoría mutacionista de de Vries alrededor de la década de 1900. A finales de la década, en 1908 Morgan adoptó la propuesta de C. W. Woodworth y William E. Castl para emplear a la mosca de la fruta “Drosophila melanogaster” como principal organismo modelo de experimentación en evolución y genética (Allen, 1975).
Figura 20.2. Drosophila melanogaster, «amante del rocío de vientre negro», también llamada mosca del vinagre o mosca de la fruta, es una especie de díptero braquícero de la familia Drosophilidae. Recibe su nombre debido a que se alimenta de frutas en proceso de fermentación tales como manzanas, bananas, uvas, etc.
Figura 20.3. El mutante ojos blancos vs la forma normal de ojos rojos, el patrón de herencia era el de un mendeliano típico donde ojos rojos presenta dominancia completa.
Durante todo ese año junto a Fernandus Payne “1881-1977” intentaron mutar a las moscas de la fruta de todas las formas posibles mediante métodos físicos y químicos, aunque inicialmente tuvieron poco éxito. Finalmente en el año siguiente 1909 la primera mutación apareció “mosca de ojos blancos” (Kohler, 1994). La mutación blanca para su gran sorpresa fue la que lo convirtió hacia el mendelismo ya que esta reproducía de forma clara las predicciones teóricas. Las moscas de ojos normales eran dominantes sobre las moscas de ojos blancos, lo cual generaba las proporción 3:1 de moscas de ojos rojos contra moscas de ojos blancas (Karp, 2013).
Adicionalmente contra su escepticismo identificó otras mutaciones ligadas a los cromosomas sexuales lo cual implicaba que los genes se ubicaban en los cromosomas. Estos descubrimientos fueron publicados en una de las dos revistas más prestigiosas del mundo de las ciencias de la naturaleza, la revista Science (Kohler, 1994).
20.3 Del redescubrimiento de Mendel a la genética evolutiva
La genética demuestra uno de los mayores problemas de la biología y es la necesidad de emplear modelos biológicos “seres vivos fáciles de estudiar” en los cuales las conclusiones obtenidas se extrapolan más o menos a otros seres vivos como los humanos. Las características de los modelos biológicos son generalmente tiempos cortos para completar su ciclo de vida y una elevada tasa reproductiva que permite obtener resultados confiables al nivel estadístico.
Figura 20.4. Macho y hembra de la mosca de la fruta, la hembra es más grande y gorda que el macho.
Sin embargo, ya hacia finales de la primera década del siglo XX un organismo modelo comenzó a destacar sobre el resto, una especie de mosca de la fruta. Las moscas de la fruta poseen todas las características de un organismo modelo, son fáciles de manipular, son resistentes a los ambientes de laboratorio, no exigen alimento costoso, completan su ciclo de vida en 10 días y las hembras producen 1000 huevos durante un ciclo de vida completo (Karp, 2013; Kohler, 1994).
Figura 20.5. Mutante alas vestigiales, la mutación ubicada en el cromosoma dos (somático) y es de tipo recesivo es decir que para que la mosca sea fenotípicamente vestigial debe portar los dos alelos mutantes. se caracteriza por tener alas poco desarrolladas que no le sirven para volar.
El empleo de las moscas de la fruta como organismo modelo experimental fue popularizado por Thomas Hunt Morgan de la Universidad de Columbia, lo cual daría inicio a una era completamente nueva en la genética post-mendeliana (Karp, 2013; Kohler, 1994). Morgan y sus estudiantes se hicieron poco a poco más hábiles en la manipulación experimental de la mosca de la fruta descubriendo cientos de mutaciones describibles mediante las leyes de la genética clásica, así como por fenómenos postmendelianos como el ligamiento al sexo, la epistasis, la codominancia entre otros. Con esta materia prima se embarcaron en el análisis de patrones de herencia complejos “que no son descritos de la genética escolar”. Uno de los patrones de herencia complejos fue denominado recombinación genética, la cual tendrá implicaciones profundas en la teoría de la evolución durante las siguientes décadas.
20.4 La mutación como instrumento de investigación
El concepto de mutación ya había estado en boga en la biología desde que la hipótesis de Weismann con respecto al plasma germinal fue aceptada por la mayor parte de la comunidad científica. Sin embargo, son los trabajos de T.H. Morgan los primeros en emplear la mutación como herramienta de investigación prácticamente desde 0. Si Morgan hubiera esperado que todas las mutaciones fueran letales, las moscas de la fruta no le hubieran servido de mucho.
Bajo las condiciones de selección de la naturaleza solo existe una variante del tipo de mosca de la fruta que decidió emplear para sus investigaciones. Pero Morgan se basó en un planteamiento neodarwiniano y decidió que simplemente debería esperar a generar sus propios mutantes y para ello lo único que debía hacer es reproducir las moscas muchas generaciones y esperar. Morgan reprodujo sus moscas de tipo natural o cómo se las llama en genética post-mendeliana de “tipo silvestre” y en menos de un año obtuvo su primer mutante distinguible con claridad del tipo silvestre. El primer mutante se caracterizaba por una alteración de los ojos, mientras que los ejemplares de tipo silvestre poseen ojos rojos, el primer mutante de Morgan poseía ojos blancos. Cerca de 5 años de investigación le bastaron a Morgan y sus colaboradores para obtener, identificar y mantener a 85 tipos mutantes de moscas con una amplia gama de alteraciones morfológicas heredables (Karp, 2013.
De esto se hizo claro que las mutaciones, aunque raras aparecen cuando se las asume desde un punto de vista de las poblaciones, que las mutaciones una vez aparecen se pueden mantener al interior de la población siempre y cuando las condiciones de selección así lo permitan. Para el caso de los mutantes de laboratorio las condiciones son ejercidas artificialmente, mientras que en la naturaleza muchos de estos mutantes serian eliminados al no poder competir tan efectivamente como los ejemplares silvestres (Karp, 2013).
Los trabajos de Morgan en las moscas de la fruta son coyunturales ya que poseían impactos en varias líneas de investigación biológicas durante el periodo de tiempo correspondiente a la primer y segunda década del siglo XX. Por un lado, la demostración experimental de la existencia de mutaciones espontáneas, heredables en el genoma de la mosca de la fruta tenía implicaciones al nivel del genoma de todos los seres vivientes incluyendo al ser humano. Sugería que el mecanismo que originaba la variabilidad existe al interior de las poblaciones, una evidencia vital que aportaba a la tercera teoría de la evolución que se venía gestando durante la misma época. Si los genes variantes podían emerger de manera espontánea, entonces las poblaciones aisladas podían separarse de otras a medida que el tiempo y las condiciones ecológicas específicas seleccionaran las variantes que iban apareciendo (Karp, 2013).
El cambio morfológico al fin tenía un motor de inicio independiente al de selección natural y sobre esta base seria propuesta la tercera teoría de la evolución unas décadas más tarde y es a la que se le denomina la Síntesis Evolutiva ya que conjuga a la selección natural de Darwin con la genética desarrollada a inicios del siglo XX (Karp, 2013).
Independientemente a las implicaciones teóricas las mutaciones rápidamente se convirtieron en herramientas de investigación genética ya que proveían contrastes estadísticos al tipo silvestre, además de poder ampliar variaciones a las leyes estadísticas obtenidas por Mendel en el siglo XIX. La otra coyuntura del trabajo de Morgan se dio con las propuestas de Sutton no mucho tiempo antes, Morgan encontró de todos los mutantes de la mosca de la fruta no se segregaban de manera independiente, por el contrario, se segregaban en cuatro grupos de ligamiento teóricos que concordaban con los cuatro cromosomas identificados con el microscopio lo cual corroboró que los cromosomas son el lugar de reposo de las unidades hereditarias que regulan la forma de los seres vivos (Karp, 2013).
20.5 Efecto de la recombinación genética
La primera evidencia que se encontró de la recombinación genética vino del laboratorio de T. H. Morgan durante la segunda década del siglo XX gracias a las investigaciones realizadas en las moscas de la fruta. Posteriormente las observaciones en este organismo modelo fueron extrapoladas y confirmadas en otros modelos eucariotas capaces de realizar la reproducción sexual vía la meiosis como lo somos los seres humanos. La recombinación genética altera las proporciones mendelianas clásicas y por eso hace parte de la genética post-mendeliana. La recombinación genética también confirma otra de las grandes hipótesis de A. Weismann y es concerniente al concepto de la reina roja y la utilidad evolutiva del sexo.
En resumen, el sexo es costoso biológicamente, por lo que debería presentar una utilidad evolutiva muy grande, y esa utilidad es dada por la recombinación genética. La recombinación es un mecanismo que incrementa la variabilidad de las poblaciones de manera independiente a las mutaciones espontáneas. Con una mayor variabilidad las poblaciones toleran con mayor facilidad los cambios ambientales y las presiones ejercidas por los parásitos, los competidores y los depredadores.
Adicionalmente, la reducción del número de cromosomas requeridos para la reproducción sexual, la meiosis incrementa la diversidad genética de una población de organismos eucariotas con reproducción sexual de una generación a la siguiente de manera independiente a la segregación independiente de los cromosomas durante la anafase I. La recombinación genética permite crear nuevas cromátides independientes a las que fueron heredadas por los padres del individuo. Mediante la mezcla del material genético, los alelos de los cromosomas homólogos pueden intercambiarse generando nuevos genotipos.
La variabilidad en el fenotipo y el genotipo en poblaciones de plantas, animales hongos “entre otros” se genera mediante recombinación genética (intercambio de brazos cromosomales en la segunda fase de la meiosis) resultado de la reproducción sexual y de las mutaciones aleatorias a través de la secuencia (parental – descendencia). La cantidad de variación genética que una población que se reproduce sexualmente puede producir es enorme. Considere a un solo progenitor con un numero N de genes, cada uno con solo 2 alelos. El ser humano posee alrededor de 25.000 a 30.000 genes cada uno con entre 10 y 20 alelos, algunos genes pueden tener 100 alelos todos funcionales en la población, recuerden que cada individuo solo puede llevar 2. Este individuo “ideal” produce una cantidad diferente de gametos (óvulos y espermatozoides) igual a 2N. Debido a que la reproducción sexual envuelve a dos progenitores, cada combinación de gametos puede producir una cantidad de cigotos igual a 4N con diferentes genotipos. Si cada progenitor tuviera solo 150 genes con solo 2 alelos (una subestimación grosera del genoma de un eucarionte como el ser humano), cada pariente puede dar lugar a 1045 diferentes espermatozoides u óvulos; y solo una pareja de padres podría producir teóricamente más de 1090 de diferentes cigotos con genomas únicos (un número que es bastante cercano al estimado de partículas totales en todo el universo) (Karp, 2013).
20.6 Descubrimiento de la recombinación genética
A pesar de que la asociación de los genes en grupos de ligamiento fue confirmada por los trabajos de Morgan a mediados de la segunda década del siglo XX, el problema es que el ligamiento aparecía de forma estadísticamente incompleta, existía algo que seguía alterando las frecuencias mendelianas al nivel estadístico.
Figura 20.6. La recombinación genética permite aumentar la biodiversidad con menos riesgo que la mutación (YouTube).
En otras palabras, los alelos de dos genes diferentes como los que codifican para alas cortas y cuerpo negro que originalmente se presentaban ligadas en un mismo cromosoma, no siempre permanecían unidos durante la producción de los gametos.
Por lo tanto, las características maternales y paternales heredadas por in individuo en cromosomas homólogos separados podían ser cruzadas y terminar presentes en el mismo cromosoma de un solo gameto. Alternativamente, dos características que se heredaron unidas en un mismo cromosoma parental podían terminar separadas una de la otra en diferentes gametos. En 1911 Morgan ofreció una explicación para el rompimiento del ligamiento. Dos años antes F. A. Janssens había observado que los cromosomas homólogos de los bivalentes se envolvían entre si durante la primera fase de la meiosis I (Thomas Hunt Morgan, 1919b).
Si los cromosomas pasaran intactos se generarían grupos de ligamiento como en este ejemplo hipotético. Sin recombinación solo existirían 2 tipos de cromosomas con identidades genéticas bien definidas que se heredarían de manera mendeliana en grupo. Janssens había propuesto que esta interacción entre los cromosomas paternos y maternos generaba un rompimiento e intercambio de los brazos cromosomales.
20.7 Propiedades de los porcentajes de recombinación
El cruzamiento tiene el potencial de generar cuatro cromátides con identidades genéticas diferentes, dos que son las originales y dos que son recombinantes. De la imagen se puede anticipar que los genes que están cerca unos de otros tienen altas posibilidades de ser transferidos en grupos ligados cuando el cromosoma recombina, mientras que los genes en posiciones lejanas tienen altas posibilidades de combinarse con alelos alternativos generando cromosomas nuevos. Capitalizando esta propuesta, Morgan sugirió que este fenómeno que acuñó como entrecruzamiento o recombinación genética podía explicar la aparición de descendientes con fenotipo recombinante. Los análisis de los descendientes al nivel estadístico de una alta cantidad de individuos adultos cargan una variedad de alelos en el mismo cromosoma indicando que (Karp, 2013):
👉 el porcentaje de recombinación entre un par de genes en un cromosoma como color de ojos o longitud de ala era constante entre diferentes ciclos generados
👉 los porcentajes de recombinación entre los diferentes pares de genes como el color de ojos y la longitud de del ala contra otro par de color de ojos y longitud de alas puede variar mucho.
Figura 20.7. Alfred Henry Sturtevant, fue un genetista estadounidense, construyó el primer mapa genético de un cromosoma en 1913. Durante su carrera trabajó con el organismo modelo Drosophila melanogaster con Thomas Hunt Morgan.
20.8 El concepto de locus
El hecho de que un par de genes dado da aproximadamente la misma frecuencia de recombinación en cada cruce sugiere fuertemente que las posiciones de los genes a lo largo de los cromosomas son fijas y no varía de una generación a otra. A esta posición fija se la denominó Locus “singular” o Loci “plural”. Si el locus de cada gen es fijo, entonces la frecuencia de recombinación entre dos genes depende de la lejanía o cercanía relativa entre este par de genes, es decir entre más recombinación más lejos y entre menos recombinación más cerca. En 1911 A. Sturtevant un estudiante del laboratorio de Morgan concibió la idea de que las frecuencias de recombinación podían ser empleadas para dibujar mapas de distancia relativa entre los diferentes genes al interior de un mismo cromosoma (Donis-Keller et al., 1987; Lobo & Shaw, 2008; Sturtevant, 1965). La ubicación física de un gen será llamada locus en singular, si hablamos de varios genes diferentes sus ubicaciones físicas serán llamadas loci.
El concepto de recombinación genética le permitió a Morgan realizar un modelo predictivo y deductivo magistral, crear los mapas de la ubicación relativa de un gen al interior de un cromosoma. La recombinación es causada por el entrecruzamiento de los brazos de un cromosoma siendo estos intercambiados. Entre más cercanos están los loci de un par de genes menos probable
es que sean recombinados por lo que experimentan un ligamiento fuerte. Por el contrario, si un par de loci está lejos su probabilidad de recombinar es alta y no son distribuidos de forma independiente “como en la ley de distribución independiente”. Otros loci pueden ubicarse de forma intermedia, siendo que en ocasiones son recombinados y en otras no.
Figura 20.8. Calvin Blackman Bridges, fue un científico estadounidense, conocido por sus contribuciones al campo de la genética. Junto con Alfred Sturtevant y H. J. Muller, Bridges fue parte de la famosa sala de moscas de Thomas Hunt Morgan en la Universidad de Columbia.
Figura 20.9. Hermann Joseph Muller, fue un biólogo y genetista estadounidense. Renovador de la genética. Autor de notables estudios acerca de la acción de los rayos X como productores de mutación la acción de las radiaciones sobre células; por estos trabajos le fue concedido el Premio Nobel de Fisiología o Medicina en 1946.
Si se estimaban muchas veces la recombinación o no de varios loci es posible determinar cuáles están más cerca y cuales más lejos. El estudiante de Morgan llamado Alfred Sturtevant “1891-1970” sería el primer investigador en crear un mapa de genes en 1913. (Donis-Keller et al., 1987; Lobo & Shaw, 2008; Sturtevant, 1965).
20.9 Análisis de complementariedad
El análisis de complementariedad permite determinar si dos mutaciones aisladas de forma independiente se encuentran localizadas en el mismo gen, o si por el contrario obedecen a genes diferentes. En otras palabras, se busca responder la pregunta: ¿Son dos mutaciones que convergen en un fenotipo semejante pertenecientes a un mismo locus o se encuentran en diferentes loci? Para encontrar la respuesta se realiza un cruce de dos cepas mutantes y se analiza su generación F1.
En el caso 1 se tiene un cruce monohíbrido típico “aa x aa”, en el cual los 4 posibles cruces darán como resultado el mismo genotipo homocigoto recesivo y en consecuencia el 100% de las crías presentarán el fenotipo mutante de genotió aa.
En el caso 2 se tiene un cruce dihíbrido epistático, en el cual dos genes afectan un solo fenotipo “aaBB x AAbb”. En este caso los cruces complementarios crean un doble heterocigoto con fenotipo dominante “AaBb”. Si la mutación afecta un solo gen de forma que el alelo nuevo es recesivo, al cruzar ambas cepas todos los descendientes aparecen sin alas; pero si la mutación recesiva se ubica en dos genes diferentes al cruzar las cepas todos los descendientes aparecen con el fenotipo normal, asumiendo que las mutaciones son de tipo recesivo.
20.10 La síntesis entre la teoría cromosómica de la herencia y el mendelismo
La entendemos así en el sentido de que T. H. Morgan logró a través de la mosca de la fruta relacionar a los cromosomas con los patrones de herencia mendelianos así como múltiples modificaciones. En 1915 los alumnos de Morgan Alfred Sturtevant “1891-1970”, Calvin Bridges “1889-1938” y Hermann Joseph Muller “1890-1967” escribieron un de los libros de texto que más influirían en la comprensión de la genética mendeliana y postmendeliana llamado Mecanismos de Herencia Mendeliana (T H Morgan, Sturtevant, Muller, & Bridges, 1972; Thomas Hunt Morgan, 1915).
En los años siguientes la mayoría de la comunidad científica adoptó la teoría mendeliana cromosómica de la herencia, la cual había sido intuida teóricamente por biólogos alemanes como Walter Sutton “1877-1916” y Theodor Boveri “1862-1915” alrededor de 1902-1903. El desarrollo experimental fue realizado por Morgan entre 1908 y 1915. Aun así seguían existiendo críticos como W. E. Castle y R. Goldschmidt (Karp, 2013).
20.11 Morgan y la teoría de la evolución
A pesar de que los trabajos de Weismann intentaron corregir las deficiencias darwinianas acuñado el término de neodarwinismo, no es hasta que Morgan identifica caramente el rol de los mecanismos internos de los seres vivos para variar que el asunto no fue zanjado en la forma en que lo entendemos actualmente. En su libro Morgan da sus roles a la variabilidad aleatoria en forma de las mutaciones y la recombinación de forma independiente a la selección natural que es antialeatoria. Mientras que la variación crea nuevas variantes la selección las elimina. Mientras que una especie logre el equilibrio entre ambos fenómenos seguirá existiendo, pero si por ejemplo no se produce suficiente variación, la selección aplasta a la población generando el fenómeno de la extinción.
Más que rechazar a la Evolución como lo sugeriría retóricamente el título de su obra de 1916 Morgan le dio su forma casi moderna a la teoría de la evolución (Thomas Hunt Morgan, 1916), sin embargo aún pasarían dos décadas hasta que otros fenómenos relacionados se conjugarían en la Teoría Sintética de la Evolución (Kutschera & Niklas, 2004). Una vez afianzado el modelo teórico clásico, Morgan procedió a retomar sus cuestionamientos contra Darwin, y especialmente su problema con el concepto de selección natural. Estos cuestionamientos fueron depositados en un libro denominado Una Crítica a la Teoría de la Evolución (1916) en el que Morgan discutió preguntas tales como (Morgan, 1916):
👉 ¿La selección natural realmente juega un papel en la evolución?
👉 ¿En verdad la selección natural tiene algún poder creativo?
Estas críticas a la selección natural procedían de la gran debilidad de la primera teoría de la evolución, al no poder explicar el origen de la variación, Darwin recurrió a la teoría de Lamark convirtiendo al ambiente en fuente de variación y selección simultáneamente, lo cual conllevó a ver a la selección natural como una especie de mecanismo omnipotente creador y destructor (Kutschera & Niklas, 2004).
Con el trabajo de Morgan se afianza la etapa denominada Clásica de la genética, y sus conclusiones se abarcan en los libros de texto como las “extensiones a las leyes de Mendel”. Sin embargo, el logro más importante es pavimentar el camino de la reconciliación entre el neodarwinismo y el mendelismo, cuestiones que aparentemente estaban en conflicto y que lo habían estado patentemente desde el inicio del siglo XX en una sola y única ciencia. A partir de aquí nuestro próximo gran capítulo de la historia de la genética convergerá con el de la teoría sintética de la evolución, aunque debemos empezar con un concepto propuesto en la década mendeliana de 1900-1910 y es el equilibrio Hardy-Weinberg.
21. Extralimitación del modelo mendeliano
|| REGRESAR AL INDICE ||
El trabajo de los mendelianos originales “Correns y de Vries” era sólido, o al menos eso parecía a los principios de 1900, por lo que varios científicos se lanzaron a la tarea de ver su aplicación a otros modelos biológicos incluyendo la especie humana. Los resultados no fueron tan alentadores, pues la herencia mendeliana solo era aplicable a unos pocos casos contados de herencia discontinua. Algunos caracteres anatómicos fueron descritos como de herencia dominante o de herencia recesiva. Ciertas enfermedades también fueron identificadas como de herencia mendeliana, pero no todas (Klug, Cummings, Spencer, & Palladino, 2009).
Por otra parte, los conceptos de gen y alelo comenzaban a acarrear problemas filosóficos, ya que desde la perspectiva materialista de las ciencias de la naturaleza no podían ser entidades abstractas, platónicas o vitalistas; en otras palabras, debían tener una existencia física y material. Es por esto por lo que esta época también se resalta por la búsqueda de la base física del gen, cosa que resolvieron Morgan y sus colaboradores.
21.1 Limitaciones del modelo mendeliano en genética humana
¿Cómo es que las leyes de Mendel pueden aplicarse a los seres humanos? Cuando Mendel trabajó con alverjas tenía varios lujitos que no tienen los genetistas humanos:
👉 Poseía líneas puras para caracteres. Las poblaciones humanas nunca son “puras” aunque clamen serlo, por lo general un individuo sano posee un alto grado de heterocigocidad en muchos de sus genes.
👉 Cada carácter había sido reducido a dos rasgos fácilmente diferenciables entre sí. Los seres humanos, así como las alverjas no reducidas para la experimentación poseen muchos más rasgos para cada carácter que solo dos. Adicionalmente la mayoría de los caracteres son de herencia continua y no discreta como la que empleó Mendel para experimentar. Es por esto que la herencia mendeliana es tan excepcional en el modelo humano o cualquier modelo biológico no purificado para experimentación.
👉 Cada cruce daba como resultado una descendencia de cientos a miles de individuos. Los seres humanos tenemos pocas crías, por lo que el análisis estadístico no aplica de forma tan sólida y debe recurrirse más al razonamiento deductivo clásico.
Si los genetistas humanos no pueden aplicar el método estadístico para analizar casos puntuales, ¿Cómo pueden ser diagnosticadas las enfermedades o rasgos hereditarios de tipo mendeliano? Recuerde que, aunque pocas, si han sido reportados rasgos y enfermedades con herencia mendeliana clásica (Klug, Cummings, Spencer, & Palladino, 2012; Pierce, 2008).
21.2 Falsos caracteres con herencia Mendeliana
Muchas veces nuestro deseo por hacer encajar una teoría con la experimentación nos lleva a eliminar variabilidad que existe. Un ejemplo es el supuesto carácter mendeliano de dedos de ángulo negativo “yo tengo ese carácter”.
Figura 21.1. Visión mendeliana de los estados del carácter de ángulo negativo del pulgar.
El problema resulta en que no son pocas las fuentes que señalan que este es un carácter mendeliano con dos rasgos, el dedo recto y en dedo en ángulo negativo. En 1953 Glass y Kistler propusieron que el ángulo del dedo era un rasgo mendeliano (Glass & Kistler, 1953), aun cuando sus valores de medida daban cuenta de una distribución continua entre los rasgos.
Figura 21.2. Aunque el histogreama de Glass y Kistler era evidentemente continuo y darwiniano, lo hicieron encajar a las malas en un modelo mendeliano.
Figura 21.3. El ángulo negativo del pulgar en la realidad muestra patrón de herencia darwiniano o neodarwiniano con muchos rasgos difíciles de distinguir uno del otro.
De hecho, unos años antes otro estudio de Harris y Joseph había encontrado una distribución mucho más normal y continua entre el ángulo del dedo (Harris & Joseph, 1949). Glass y Kistler aparentemente decidieron emplear una división arbitraria para designar a todos los rasgos desde cierto ángulo hacia atrás como de ángulo negativo, sin ofrecer una explicación para elegir ese ángulo y no otro. Básicamente nos encontramos aquí ante el patrón típico de la herencia de Mendel nunca estudió y nunca pudo explicar, el patrón de herencia continua con múltiples rasgos.
Otros caracteres de falsa herencia mendeliana son (McDonald, 2011).
👉 La lengua enroscarle y la lengua no enroscarle
👉 Los colores de los ojos, lo cual ha llegado a incluir falsos cuadros de Punnett
👉 El pico de bruja.
👉 Sensibilidad al fenylthiocarbamida (PTC) y al propiltiouracilo.
👉 Hoyuelos de las mejillas.
👉 El cabello rojo.
👉 Longitud de los dedos de los pies.
De hecho, muchos de los rasgos humanos empleados para ejemplificar la genética clásica a nivel escolar “e incluso en cursos de introducción a la genética universitarios” ¡son un mito!: el pico de bruja, los hoyuelos en las mejillas, la capacidad de saborear PTC o el mentón partido. Cuando se examina con mayor claridad, muchos de estos rasgos son en realidad parte de un patrón de herencia continua. Es por esto que antes de iniciar nuestro estudio de con los pedigrís es bueno señalar que varios de los rasgos empleados allí son solo ejercicios de lápiz y papel; y que probablemente ellos también hacen parte de patrones de herencia continua, la clase de herencia para la cual la genética clásica no es muy útil.
21.3 Consideraciones sobre el modelo humano y la enseñanza de la genética clásica
Una de las motivaciones más grandes del estudio de la genética es la de poder entender porque y como es que presentamos los rasgos que tenemos, más allá de enseñarla en modelos biológicos como alverjas, moscas o gatos, la preocupación siempre va dirigida a nuestro propio ser, es decir el organismo modelo humano. Una de las grandes ventajas que tiene la genética es que potencialmente no requeriría instrumentación compleja, solo una vista aguda para observar los caracteres y sus respectivos rasgos.
Desafortunadamente durante la transposición didáctica “usando la terminología de Yves Chevallard” (Chevallard, 1985; Chevallard & Perrenoud, 1998) algo se pierde. Cosas que, NUNCA HAN SIDO REPORTADAS en las revistas científicas o que poseen poca evidencia aparecen en libros de texto como si fueran fenómenos absolutos, y eso es lo que vimos en varios artículos anteriores. Muchos de los caracteres que se emplean para enseñar genética clásica aplicada al hombre son en realidad de herencia NO MENDELIANA.
Desafortunadamente los libros de texto, los manuales de laboratorio y varias fuentes de internet siguen empleando estos caracteres, lo cual perpetúa los mitos. En otras palabras, el organismo modelo humano es muy malo para poder ejemplificar la genética clásica al nivel de las leyes de los mendelianos, y la mayoría de sus rasgos, como en cualquier especie no purificada para experimentación, se describen en términos de la herencia continua, cuestión que no se abarcaría seriamente sino hasta la aparición de la Teoría Sintética Evolutiva, específicamente en la rama de la genética de poblaciones, cuestión que abarcaría la década de 1920-1930 (Sarkar, 2004).
Sobresimplificar la genética humana trae graves consecuencias para la construcción de conocimiento posterior, especialmente para la teoría de la evolución, ya que esta depende de entender a los modelos reales como sistemas de herencia no-mendeliana. La genética clásica se construyó sobre un organismo modelo tratado previamente para eliminar su herencia continua, generando artificialmente una herencia discreta. La transposición forzada de este modelo experimental a un modelo real como el humano fuerza a creer que todos los patrones de herencia en los sistemas reales se comportan de forma mendeliana, lo cual suma a errores conceptuales a cerca de la evolución, después de todo el modelo gradual de la evolución se monta sobre la base de patrones de herencia continuos. La genética moderna posee métodos conceptuales para lidiar con la herencia continua, por lo que muchos de los rasgos humanos deberían ser expuestos en los conceptos evolutivos de la genética de poblaciones, pues allí es donde pertenecen.
Algunos docentes pueden argumentar “basándose en conceptos como la transposición didáctica” que el empleo de caracteres en el modelo humano para enseñar la genética clásica es un modo de motivar a los estudiantes a estudiar la genética, haciéndola ver como algo pertinente para conocer sus propios cuerpos. De cierta forma es como un guiño, una mentira para niños estilo “la cigüeña”. En cierto sentido es como en el estudio del átomo, donde se les enseña a los estudiantes los modelos atómicos históricos dejando que el modelo moderno sea estudiado por quienes deseen estudiarlo en sus cursos de física cuántica más especializados. Lo mismo le sucede a la genética evolutiva, la cual es vista como parte de la clásica “pero no toda”, u omitida del todo en cursos básicos o introductorios, dejando cosas como penetrancia, epistasis, multigenéticos y multialélicos para cursos más avanzados. Personalmente no estoy de acuerdo con esta postura, ni para la enseñanza del átomo ni para la genética. Si se va a simplificar se tiene que hacer evidente, explicita y conscientemente que lo estamos haciendo. El estudiante debe ser consciente que el ejemplo empleado es solo una “pinturita” para poder aplicar el modelo matemático, de lo contrario no seríamos más que perpetuadores de mitos no diferentes a lo que hacen ciertas denominaciones religiosas.
La genética es un conocimiento peligroso en niveles escolares, y entre más jóvenes los estudiantes es peor. La razón es que estadísticamente es probable que en alguno de los grupos de trabajo se encuentren estudiantes que han sido adoptados, o que llaman "papi" a quien no lo es por un affaire de la madre u otras cuestiones familiares que caen en lo humano y no en lo científico. Aunque puede parecer cómico, esto es problemático en términos del desarrollo psicológico del estudiante, más aún si los ejemplos que se enseñan no poseen realmente una herencia mendeliana clásica. Qué pasa si el estudiante comprende el modelo matemático cabalmente y emplea un falso carácter mendeliano y concluye erróneamente ¿qué es adoptado? o ¿qué su madre engañó a su padre? Esto tiene ramificaciones humanas a tenerse en cuenta.
Las mismas ramificaciones éticas deben tenerse en cuenta, aunque se empleen ejemplos de marcadores genéticos más apropiados, como las pruebas de ADN o el más potencialmente empleable factor Rhesus “o el HB0 si ya se está tratando con multialélicos”. De los dos ejemplos el más grave es el primero, que el estudiante llegue a falsas conclusiones provenientes de una ciencia escolar sobresimplificada. Aunque ambos tienen el mismo problema, el potencial de interferir de forma negativa con lo humano y el desarrollo psicológico del estudiante.
21.4 El concepto de raza humana
Dado que la mayoría de los caracteres humanos varían en patrones continuos y que los rasgos no tienen una asociación concreta con una población particular, por ejemplo, la asociación piel negra, ojos azules y cabello rubio no pertenecen a grupos raciales dispersos, un individuo humano puede ser en efecto de piel oscura, ojos azules
y cabello rubio “aunque sea poco frecuente”, el concepto de raza biológica en la especie humana no se sostiene por lo menos en la actualidad. En especies como los perros, los seres humanos mantienen la asociación de características concretas con poblaciones concretas por selección artificial, sin embargo, en la actualidad las poblaciones humanas están altamente mestizadas y no hay una correlación fuerte de grupos de rasgos fenotípicos o genéticos con una raza en concreto. Sin embargo, el racismo y el mendelismo favorecieron la imagen forzada de clasificar a la variación humana en solo cuatro categorías raciales arbitrarias. La variación genética humana es predominantemente intrapoblacional, continua y de estructura compleja, lo cual es inconsistente con el concepto de razas humanas genéticas (Goodman, 2000). Desde la década de 1970, se hizo evidente que:
👉 la mayoría de las diferencias humanas eran culturales
👉 lo que no era cultural era principalmente polimórfico o de herencia continua darwiniana, es decir, se encontraba en diversos grupos de personas a diferentes frecuencias.
👉 lo que no era cultural o polimórfico era principalmente clinal, es decir, gradualmente variable sobre la geografía
👉 lo que quedaba -el componente de la diversidad humana que no era cultural, polimórfico o clinal- era muy pequeño.
Figura 21.4. Algunas combinaciones de rasgos fenotípicos que la cultura popular consideraría imposibles y que los mendelianos o racistas consideran inexistentes.
Un consenso consecuentemente desarrollado entre los antropólogos y genetistas que la raza como la generación anterior lo había conocido, como grupos de genes en gran parte discretos, geográficamente distintos, no existía. El término raza en biología se usa con precaución porque puede ser ambiguo. Generalmente, cuando se usa, es efectivamente un sinónimo de subespecie.
Figura 21.5. Solo a través del racismo se pueden dibujar fronteras arbitrarias en un estado de carácter darwiniano de herencia continua.
Para los animales, la única unidad taxonómica debajo del nivel de la especie suele ser la subespecie; hay rangos infraespecíficos más estrechos en botánica, y la raza no corresponde directamente con ninguno de ellos. Tradicionalmente, las subespecies se consideran geográficamente aisladas y genéticamente poblaciones diferenciadas en agrupaciones matemáticamente significativas por pruebas estadísticas como las ANOVAs. Los estudios de la variación genética humana muestran que las poblaciones humanas no están geográficamente aisladas, y sus diferencias genéticas son mucho más pequeñas que las de subespecies comparables (Goodman, 2000). De lo anterior se desprende que el concepto de raza solo puede ser entendida por genéticas no-clásicas, es decir, por la Teoría Sintética de la Evolución, que es después de todo la verdadera teoría de la genética moderna y que veremos en el capítulo siguiente.
22. Polimorfismo genético
|| REGRESAR AL INDICE ||
La genética clásica como vimos anteriormente es el periodo en que se reinterpreta el trabajo de Mendel a la luz de una actitud nueva de las matemáticas en la biología. De hecho, los cruces que tradicionalmente adjudicamos a Mendel son matemáticamente interpretados bajos las conclusiones de Carl Correns. Esta interpretación se basará en la noción matemática (Reed, 1997). Esta tercera gran sección de genética clásica estará dedicada exclusivamente a la matemática de la genética clásica, la aplicación de principios sencillos del algebra a la resolución de los problemas clásicos de la genética y especialmente a la superación del cuadro de Punnett como estándar de trabajo de los ejercicios de lápiz y papel de la genética clásica más complejos. Tradicionalmente el modelo que empleamos es el cuadro de Punnett, sin embargo el cuadro de Punnett no es más que una herramienta matemática para no matemáticos que no saben ejecutar una factorización algebraica simple, llamada el binomio cuadrado perfecto (Baldor, 2008; Lial, Hornsby, & McGinnis, 2012).
Hasta ahora hemos trabajado el modelo matemático de los mendelianos empleando una convención bastante simple para representar el alelo dominante y el alelo recesivo, pero ¿Qué pasa cuando tenemos un sistema con más de dos alelos? El grupo de investigación de Morgan fue tal vez el primero en ponerle cara seriamente a este problema y desarrolló sistemas nuevos para denotar los alelos diferentes. En el sistema que ellos desarrollaron para la mosca de la fruta se concentraron en distinguir los caracteres silvestres de los caracteres mutantes. El sistema emplea la primera o primeras letras del carácter. Si el carácter es recesivo se emplea la letra minúscula mientras que si es dominante se emplea un superíndice positivo (+).
Tabla 22.1. Genotipo barra. El símbolo que sirve como base es el nombre del gen o de la mutación. En este caso e significa gen de ébano.
La barra diagonal entre los símbolos de los alelos indica que la designación representa dos alelos en un mismo locus, o en otras palabras un mismo gen. Este sistema posee algunas variaciones, por ejemplo, el genotipo silvestre se puede simbolizar como (+) sin emplear la letra. En caso de tener más de dos alelos se emplea la letra para el rasgo en mayúscula y se emplean designadores de caso alfanuméricos (números, letras o combinaciones) ya sea como superíndices, subíndices o un código.
Tabla 22.2. Notación de polimorfismo para tipos de sangre AB0. Dado que los sistemas polimórficos tienen más de dos alelos y más de dos fenotipos en cada locus, se deben emplear códigos tanto para fenotipos como genotipos.
22.1 Expansión polimórfica
La factorización de un sistema multialélico es inviable cuando hablamos de cruces entre individuos, pero no cuando hablamos de poblaciones y deseamos saber cuáles serán los posibles genotipos de la población en términos del conocimiento de las cantidades de cada uno de los alelos presentes. En tal caso podemos evolucionar del binomio monohibrido a tronomios, tetranomios y más dependiendo de la cantidad de alelos presentes. En este orden de ideas, aunque el procedimiento matemático es semejante, las definiciones son completamente diferentes. Por ejemplo, los términos ( A + a ) ya no significan gametos sino las cantidades respectivas de cada alelo en la población, mientras que ( A + a ) ( A + a ) nos dará las proporciones esperadas de cada uno de los genotipos en la población así como sus diversos tipos.
(Eq. 22.1) Probabilidad de cualquier genotipo homocigoto en términos de la frecuencia relativa del alelo A-ésimo.
(Eq. 22.2) Probabilidad de cualquier genotipo heterocigoto en términos de la frecuencia relativa del alelo A-ésimo y un alelo B-ésimo.
(Eq. 22.3) Probabilidad de cualquier genotipo homocigoto en términos de la frecuencia relativa del alelo A-ésimo en un cruce de dos parentales.
(Eq. 22.4) Probabilidad de cualquier genotipo heterocigoto en términos de la frecuencia relativa del alelo A-ésimo y un alelo B-ésimo en un cruce de dos parentales.
La principal diferencia que hay entre una expansión polinómica para una población, y su modificación para un ejercicio clásico radica en que en el cruce mendeliano la permutación/organización de los alelos que provienen de cada parental si importa, por lo que las expresiones de probabilidad de cada alelo dependerán no solo del tipo de alelo, sino también de la fuente, siendo un progenitor u otro (♀/♂), en caso de que el ejercicio no indique cual es el progenitor, simplemente se puede colocar en su orden parental 1 (1) y parental 2 (2).
22.2 Acervo genético
Para poder aplicar las ecuaciones anteriores es necesario plantear las probabilidades de cada alelo provenientes de cada parental, lo cual se sencillo, para homocigotos dominantes uno de los alelos tiene probabilidad 1 y el otro cero, y para heterocigotos las probabilidades de ambos alelos es de ½, a este paso lo denominaremos como determinación del acervo genético.
Un acervo genético se refiere a la combinación de todos los genes (incluidos los alelos) presentes en una población o especie en reproducción. Un gran acervo genético tiene una gran diversidad genómica y es más capaz de resistir los desafíos ambientales. La endogamia contribuye a un acervo genético más pequeño, lo que hace que las poblaciones o especies sean menos capaces de adaptarse y sobrevivir cuando se enfrentan a desafíos ambientales.
Aunque en teórica esta técnica debería ser más sencilla ya que genera un algoritmo rígido en invariante, cuando se lo compara con otras técnicas, se puede volver más demorado. Sin embargo, si tiene una ventaja con respecto al cuadro de Punnett y a la factorización, y es que al basarse en ecuaciones rígidas pero universales, posee lenguaje programable, por lo que nos permite programar una calculadora en Excel.
DEMOSTRACIÓN. Programar una calculadora del cruce monohíbrido en Excel empleando las ecuaciones de la expansión factorial.
A parte del cálculo de frecuencias, existen otros parámetros importantes a la hora de resolver monohíbridos polimórficos como son el número de genotipos teóricamente posibles y de ellos los que son homocigotos y heterocigotos; así como los fenotipos posibles. Miremos si es posible poder ofrecer fórmulas para estas preguntas que sea de algún modo demostrables, en lugar de tener que basarnos en fuentes externas.
(Eq. 22.5) Número de genotipos heterocigotos en términos del número de alelos.
(Eq. 22.6) Número de genotipos totales en términos del número de alelos.
(Eq. 22.7) Número de genotipos homocigotos en términos del número de alelos.
Un número triangular o número triangular cuenta objetos dispuestos en un triángulo equilátero. Los números triangulares son un tipo de número figurado, otros ejemplos son los números cuadrados y los números cúbicos. El n-ésimo número triangular es el número de puntos en el arreglo triangular con n puntos en cada lado, y es igual a la suma de los n números naturales de 1 a n. La secuencia de números triangulares, comenzando con el número triangular 0, es 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666. Los números triangulares en realidad se originan en los pitagóricos, quienes desarrollaron relaciones entre las formas geométricas y los números; de ahí el nacimiento de los números triangulares, los números cuadrados y los números pentagonales, etc.
(Eq. 22.8) El número de fenotipos en un sistema de dominancia completa en términos del número de alelos.
(Eq. 22.9) El número de fenotipos en un sistema de dominancia incompleta o codominancia.
22.3 Dihíbrido con distribución independiente
Para el caso del dihíbrido de distribución independiente simplemente es realizar una matriz para multiplicar las frecuencias correspondientes, lo mismo que en el trihíbrido.
DEMOSTRACIÓN. Programar una calculadora del cruce dihíbrido en Excel empleando las ecuaciones de la expansión factorial.
Al igual que con el monohíbrido nos interesa saber el número de genotipos teóricamente posibles, y el número de fenotipos, así como expandirlo más allá del dihíbrido.
(Eq. 22.10) Número de genotipos posibles en un sistema de 2 genes y n alelos para cada gen.
(Eq. 22.11) Número de genotipos posibles en un sistema de k genes y n alelos para cada gen.
Ejemplo. Cuantos genotipos posibles pueden generarse en un sistema de dos genes y dos alelos.
Ejemplo. Cuantos genotipos posibles pueden generarse en un sistema de tres genes y dos alelos.
(Eq. 22.12) Número de fenotipos en un sistema de dos genes y n alelos para cada gen
(Eq. 22.13) Número de fenotipos en un sistema de k genes y 2 alelos para cada gen.
(Eq. 22.14) Número de fenotipos en un sistema de k genes y n alelos para cada gen.
22.4 Dihíbrido con distribución dependiente
23. Dominancia incompleta
|| REGRESAR AL INDICE ||
La dominancia incompleta se define cuando un alelo dominante nen el heterocigoto no logra manifestar todo el fenotipo dominante, sino un fenotipo intermedio o mezclado con su respectivo recesivo. Aunque esto puede ser generado por mezclas polimórficas, el concepto se emplea más cuando es generado por pares mendelianos típicos de un gen y dos alelos.
23.1 Historia del concepto
A parte de construir el mito de Mendel, el botánico alemán Carl Correns (1864-1933) propuso el término "dominancia incompleta" para referirse a los rasgos que aparentan mezclarse y podían ser modelados mendelianamente. Carl Correns continuó investigando y realizó un experimento con flores de Don Diego de la Noche Mirabilis jalapa. Este experimento condujo al descubrimiento de una dominancia incompleta, una condición en la que un individuo heterocigoto no muestra un rasgo dominante, sino un rasgo intermedio de los fenotipos de los alelos dominante y recesivo (Shourie, 2021).
Figura 23.1. Tres fenotipos de Mirabilis jalapa, el puro dominante púrpura, el mixto híbrido lila, y el puro recesivo blanco.
El propio trabajo de Bateson sobre la herencia en las aves de corral mostró que los rasgos se "mezclan" en los híbridos, aunque los rasgos todavía se segregan claramente en la descendencia según el modelo de mendeliano 1:2:1. “El grado de mezcla en los heterocigotos”, declaró Bateson, “no tiene nada que ver con la pureza de los gametos” (p. 152). (De nuevo, las formas intermedias eran posibles, denotadas aquí por Bateson, erróneamente, como una forma de "herencia combinada"). El ejemplo de Bateson de las gallinas andaluzas azules Gallus gallus domesticus que son híbridos azul-grisáceos de padres blancos y negros que forman una proporción de 1: 2: 1 en la generación F2 pronto se convirtió en un caso clásico, citado en los libros de texto a lo largo del siglo XX (Allchin, 2002).
Figura 23.2. Cruce de P hasta F2 de las gallinas andaluzas generando tres fenotipos, el puro dominante negro, el puro recesivo blanco y el mixto híbrido azul.
23.2 Reevaluando el concepto de dominancia
Dado los fenómenos anteriores vale la pena preguntarnos, ¿qué significa el concepto de dominancia cuando nos encontramos ante un carácter que no expresa dominancia completa?
Tenga en cuenta que, en los 2 ejemplos biológicos anteriores, tanto el rasgo dominante como el rasgo de recesivo se definen arbitrariamente, porque a algún individuo le parece que blanco es recesivo. Sin embargo, alguien puede anotar desde un punto de vista diferente que blanco es dominante, y en ese caso no habría manera de contradecirlo porque el rasgo híbrido es una mezcla entre dos rasgos puros.
23.3 Modelo matemático
Lo anterior, aunque pueda parecer una discusión filosófica nos afecta en cómo vamos a interpretar el modelo matemático. de lo único que podremos estar seguros es que el nombre del fenotipo del híbrido (Aa) será mezcla y su símbolo algebraico será (M). El problema radica ahora en cómo describir a los dos o más fenotipos puros. Así pues, de aquí en adelante no emplearemos la pareja mayúscula o minúscula, sino códigos con sus índices.
Ley de la dominancia incompleta, se caracteriza porque los heterocigotos manifiestan un fenotipo propio y distinguible de los fenotipos de línea pura. Dado que ambos se manifiestan ya no existe concepto de dominante y recesivo, por lo que no usamos mayúsculas o minúsculas para diferenciar los alelos, a menos que estemos ante un alelo funcional y un alelo carente de función.
DEMOSTRACIÓN: Crear una calculadora de Excel para el cruce de dominancia incompleta.
24. Codominancia
|| REGRESAR AL INDICE ||
Un carácter codominante es aquel en el cual sus 2 rasgos se manifiestan simultáneamente y con la misma intensidad que tendrían cuando se encuentran puros y aislados. En otras palabras, los dos rasgos se manifiestan como un mosaico, o en parches de intensidad máxima pero simultáneos. aunque superficialmente se parece al concepto de dominancia incompleta, en la dominancia incompleta la mezcla tiene un fenotipo intermedio o disminuido, qué es homogéneo.
24.1 Historia del concepto
Al igual que sucede con el concepto de dominancia incompleta, el concepto de codominancia también fue acuñado y estudiado inicialmente por Carl Correns (Craig, 2003), y es por esto que en este curso de genética clásica insistimos mucho en el hecho de que Carl Correns fue el verdadero padre en las sombras de la genética clásica.
La vaca ruana que contiene tanto pelos rojos como blancos es un ejemplo de codominancia. El grupo sanguíneo AB también muestra codominancia en humanos.
Figura 24.1. Cruce de dos variedades puras de camelias, que en la F1 manifiestan un fenotipo codominante y de tipo mosaico.
Un cruce entre las flores de camelia homocigotas rojas y las flores de camelia homocigotas blancas produce una descendencia con manchas rojas y blancas dentro de la misma flor.
Así pues, la codominancia se puede visualizar como un mosaico o un conjunto de parches simultáneos. ese tipo de herencia es más fácil de visualizar a un nivel molecular como en los tipos de sangre humana.
24.2 Modelo matemático
Nuevamente tenemos un caso en el que los conceptos de dominante y recesivo se desdibujan completamente, y es por eso que la tabla o representación de la ley de dominancia que se desee emplear deberá implementar una serie de códigos arbitrarios únicos para describir el sistema de estudio,
Ley de codominancia, en este caso los rasgos no se mezclan en un punto intermedio, sino que se manifiestan con igual intensidad, pero simultáneamente, el código para el fenotipo simultáneo varía dependiendo del sistema de estudio.
24.3 El caso del sistema de sangre AB0
Para la enseñanza escolarizada el caso más común es el sistema de tipos de sangre AB0, el problema es que dicho sistema es un ejemplo de codominancia y de sistema polimórfico al mismo tiempo. El fenotipo (0) es recesivo frente a cualquier otro rasgo encontrado, ya sea el fenotipo (A), el fenotipo (B) o el fenotipo codominante (AB). Adicionalmente podemos decir que este es un sistema de herencia polimórfico pues tenemos tres alelos en lugar de los dos que trabajamos normalmente. Debido a esta complejidad, empleamos símbolos en código, los tres alelos serán IA, IB, I0 mientras que los fenotipos son A, B, AB y 0. Dado que tenemos un sistema de un gen con 3 alelos, la cantidad de genotipos teóricos posible debe ser de: 3 genotipos puros y 3 genotipos híbridos que deben cumplir la regla factorial de homocigotos como cuadrado de la frecuencia del alelo y heterocigotos como dos veces el producto de los dos alelos mezclados.
Leyes de dominancia variable que afectan al sistema de sangre AB0. Sin embargo, la cantidad de fenotipos es menor debido a que 2 genotipos híbridos manifiestan dominancia completa (IA I0)( IB I0).
24.4 Ejemplos
DEMOSTRACIÓN: Programar una calculadora en Excel para la codominancia en un monohíbrido de dos alelos.
DEMOSTRACIÓN: Programar una calculadora en Excel para el sistema de tipos de sangre AB0.
25. Letalidad genética
|| REGRESAR AL INDICE ||
La letalidad genética implica cualquier tipo de herencia que genera la muerte prematura del individuo o una disminución de su éxito reproductivo. La letalidad puede presentar varios tipos de herencia, desde patrones mendelianos hasta ligamientos al sexo.
Figura 25.1. Lucien Claude Marie Julien Cuénot (21 de octubre de 1866 - 7 de enero de 1951) fue un biólogo francés. En la primera mitad del siglo XX, el mendelismo no era un tema popular entre los biólogos franceses. Cuénot desafió la opinión popular y eludió las "pseudociencias" como las llamaba. Tras el redescubrimiento del trabajo de Mendel por Correns, De Vries y Tschermak, Cuénot demostró que el mendelismo se aplicaba tanto a los animales como a las plantas.
25.1 Historia del concepto
En 1905, Lucien Cuénot observó patrones inusuales cuando estudiaba la herencia de un gen de color de pelo en ratones. Después de aparearse dos ratones amarillos, observó que la descendencia nunca mostró una proporción fenotípica 3: 1 normal. En cambio, Cuénot siempre observó una relación de 2:1, con dos ratones amarillos por cada ratón no amarillo (Cuenot, 1905; Paigen, 2003). Cuénot determinó así que el color amarillo del pelaje era el rasgo fenotípico dominante, y al usar cruces de prueba, mostró que todos sus ratones amarillos eran heterocigotos. Sin embargo, de sus muchas cruces, Cuénot nunca produjo un solo ratón amarillo homocigoto. ¿Cómo podría ser esto posible a la luz del mendelismo?
Poco después, en 1910, W. E. Castle y C. C. Little confirmaron las inusuales proporciones de segregación de Cuénot. Además, demostraron que las cruces de Cuénot resultaron en lo que parecían relaciones no mendelianas porque había descubierto un gen letal. Castle y Little lo hicieron al mostrar que una cuarta parte de la descendencia de cruzas entre heterocigotos murió durante el desarrollo embrionario (Castle & Little, 1910; Paigen, 2003). ¡Por eso Cuénot nunca observó ratones homocigotos de color amarillo! Por lo tanto, al considerar la letalidad embrionaria, o la muerte, como una nueva clase fenotípica, la clásica relación Mendeliana 1: 2: 1 de genotipos podría restablecerse (Lobo, 2008b).
Como lo ilustran estos ejemplos, los genes letales causan la muerte de los organismos que los portan. A veces, la muerte no es inmediata; incluso puede llevar años, según el gen. En cualquier caso, si una mutación resulta en letalidad, entonces esto es indicativo de que el gen afectado tiene una función fundamental en el crecimiento, desarrollo y supervivencia de un organismo. Los genes letales pueden ser recesivos, como en los experimentos con ratones antes mencionados. Los genes letales también pueden ser dominantes, condicionales, semiletales o sintéticos, según el gen o los genes implicados. Las siguientes secciones exploran estas variaciones en detalle (Lobo, 2008b).
La letalidad puede deberse a un solo alelo dominante, a un solo alelo recesivo o a la interacción tóxica de dos alelos, lo cual cambiará la ley de dominancia a trabajar, por lo que se debe estar muy pendiente del contexto del problema, o las probabilidades serán inadecuadas al partir de axiomas falsos.
25.2 Letalidad del homocigoto dominante
En 1907, Edwin Baur comenzó su trabajo con la planta dragonaria Antirrhinum antirrhinum y caracterizó la condición aurea, en la que las plantas tenían hojas doradas en lugar de verdes (Castle & Little, 1910; Schwarz-Sommer, Davies, & Hudson, 2003; von Schwerin, n.d.). Cuando se cruzaron dos plantas de dragonaria dorada, Baur observó una relación de 2:1 de plántulas verdes a plántulas amarillas. Las plantas homocigóticas para la condición aurea carecían de desarrollo normal de clorofila y murieron durante la etapa embrionaria o cuando las plántulas de la planta tenían dos o tres días de edad. En otras palabras, como los ratones homocigotos de Cuénot, las plantas homocigóticas de aurea no podían desarrollarse completamente, por lo que murieron todos sus portadores (Castle & Little, 1910). En ambos casos, el gen es dominante para coloraciones, pero homocigoto para muerto. Los ejemplos de enfermedades humanas causadas por alelos letales recesivos incluyen fibrosis quística, anemia drepanocítica y acondroplasia. La acondroplasia es un trastorno óseo autosómico dominante que causa enanismo. Si bien la herencia de un alelo de acondroplasia puede causar la enfermedad, la herencia de dos alelos letales homocigotos es fatal (Lobo, 2008b).
25.3 Letalidad del dominante
Los genes letales dominantes se expresan tanto en homocigotos como en heterocigotos. Pero, ¿cómo pueden pasar alelos como este de una generación a otra si causan la muerte con una sola copia? Los genes letales dominantes rara vez se detectan debido a su rápida eliminación de las poblaciones. Un ejemplo de una enfermedad causada por un alelo letal dominante es la enfermedad de Huntington, un trastorno neurológico en los seres humanos, que reduce la esperanza de vida. Debido a que la aparición de la enfermedad de Huntington es lenta, las personas que portan el alelo pueden transmitirlo a su descendencia. Esto permite que el alelo se mantenga en la población. Los rasgos dominantes también se pueden mantener en la población a través de mutaciones recurrentes o si la penetrancia del gen es menor al 100% (Lobo, 2008b).
25.4 Genes de letalidad condicionada
El favismo es una afección hereditaria ligada al sexo que resulta de la deficiencia en una enzima llamada glucosa-6-fosfato deshidrogenasa. Es más común entre las personas de ascendencia judía mediterránea, africana, del sudeste asiático y sefardí (Allison, 1960). La enfermedad fue nombrada porque cuando los individuos afectados comen frijoles fava, desarrollan anemia hemolítica, una condición en la que los glóbulos rojos se separan y bloquean los vasos sanguíneos. El bloqueo puede causar insuficiencia renal y provocar la muerte (Bowman & Walker, 1961). Las personas afectadas también pueden desarrollar anemia cuando se les administran dosis terapéuticas de medicamentos antipalúdicos y otras drogas (Allison, 1960). Sin embargo, tenga en cuenta que el alelo defectuoso de glucosa-6-fosfato deshidrogenasa solo causa la muerte en ciertas condiciones, lo que lo convierte en un gen letal condicional. Pero ¿por qué este alelo sería tan común? Lo interesante de las personas con el alelo favismo es que son resistentes a la malaria, porque es más difícil que los parásitos de la malaria se multipliquen en las células con cantidades deficientes de glucosa-6-fosfato deshidrogenasa. Por lo tanto, llevar el alelo al favismo confiere una ventaja genética o adaptativa intrínseca al proteger a las personas contra la malaria (Lobo, 2008b).
Los genes letales condicionales también se pueden expresar debido a circunstancias específicas, como la temperatura. Por ejemplo, una proteína mutante puede modificarse genéticamente para que sea completamente funcional a 30 ° C y completamente inactiva a 37 ° C. Mientras tanto, la proteína de tipo salvaje es completamente funcional a ambas temperaturas. La condición en la que se expresa el fenotipo mutante se denomina no permisiva. Mientras tanto, la condición en la que se expresa el fenotipo salvaje se llama permisiva. Con el fin de estudiar un mutante letal condicional, el organismo debe mantenerse en condiciones permisivas y luego cambiar a la condición no permisiva durante el curso de un experimento específico. Al desarrollar una versión letal condicional de un gen letal dominante, los científicos pueden estudiar y mantener organismos portadores de alelos letales dominantes y estudiar el comportamiento de enzimas y genes concretos (Lobo, 2008b).
25.5 Genes semiletales y subletales
La hemofilia es una enfermedad hereditaria causada por deficiencias en los factores de coagulación, que da como resultado una coagulación sanguínea deficiente o nula. Debido a que el alelo responsable de la hemofilia se transmite ligado al cromosoma X, los individuos afectados son predominantemente varones y heredan el alelo de sus madres. Normalmente, los factores de coagulación ayudan a formar una costra temporal después de que un vaso sanguíneo se lesiona para prevenir el sangrado, pero los hemofílicos no pueden sanar adecuadamente después de las lesiones debido a sus bajos niveles de factores de coagulación sanguínea. Por lo tanto, las personas afectadas sangran durante un período de tiempo más prolongado hasta que ocurre la coagulación. Esto significa que normalmente las heridas menores pueden ser fatales en una persona con hemofilia. Los alelos responsables de la hemofilia se denominan así genes semiletales o subletales, porque causan la muerte de solo algunos de los individuos u organismos con el genotipo afectado (Lobo, 2008b).
25.6 Genes letales sintéticos o de combinación mortal
Los científicos que estudiaron la mosca de la fruta observaron que las combinaciones emparejadas de algunos alelos mutantes no eran viables, mientras que, por separado, los mismos alelos mutantes no causaban la muerte (Boone, Bussey, & Andrews, 2007). En otras palabras, algunas mutaciones solo son letales cuando se combinan con una segunda mutación. Estos genes se llaman genes letales sintéticos. Cuando las funciones de los dos genes afectados no se comprenden por completo, los científicos pueden crear y estudiar mutantes sintéticos letales y sus fenotipos para identificar la función de un gen, y mucho más importante, las interacciones entre dos genes diferentes. Los mecanismos también pueden ser hipotetizados a partir de las funciones conocidas de los pares de alelos mutados (Lobo, 2008b).
Por ejemplo, si ambas mutaciones ocurren en genes no esenciales, un científico podría hipotetizar que los dos genes funcionan en vías paralelas que comparten información entre sí. Cada una de las dos vías podría compensar un defecto en la otra, pero cuando ambas vías tienen una mutación, la combinación produce letalidad sintética o por combinación mortal. La letalidad sintética también puede indicar que dos genes afectados tienen el mismo papel y, por lo tanto, la letalidad solo se produce cuando ambas copias no son funcionales y un gen no puede sustituir al otro, proceso normalmente conocido como compensación de dosis. Además, ambos genes pueden funcionar en la misma ruta esencial, y la función de la ruta puede verse disminuida por cada mutación, pero solo hasta que las dos funciones se eliminan la viabilidad general se ve afectada (Lobo, 2008b).
Cuando un alelo causa letalidad, esto es evidencia de que el gen debe tener una función crítica en un organismo. Los descubrimientos de muchos alelos letales han proporcionado información sobre las funciones de los genes durante el desarrollo. Además, los científicos pueden usar alelos letales condicionales y sintéticos para estudiar las funciones fisiológicas y las relaciones de los genes en condiciones específicas (Lobo, 2008b).
25.7 Modelos matemáticos simples
Aunque no podemos pasar a lápiz y papel varios tipos de letalidad antes mencionados, si podemos expresar la letalidad del homocigoto dominante y la letalidad del dominante junto con otros dos posibles casos teóricos.
👉 En este caso solo el genotipo homocigoto dominante genera el fenotipo muerto o enfermo.
👉 Letalidad dominante. En este caso todos los portadores del alelo dominante serán afectados. Muerte espontánea, siempre sanos.
👉 Letalidad del heterocigoto. En este caso el efecto solo se observa cuando se combinan dos alelos que normalmente no son letales.
Los casos anteriores asumen letalidades completas o enfermedades demasiado incapacitantes como para permitir el conteo de fenotipo aparente generando un aborto, por lo que el fenotipo muerto no aparece en los conteos, alterando las proporciones como pasa en los conejos de Cuénot. Sin embargo, si trabajamos con letalidades menos marcadas, estas permitirán el conteo de los individuos, por lo que no necesitamos un modelo matemático especial, y podremos resolverlo empleando los algoritmos de los monohíbridos simples, donde el fenotipo enfermo puede contarse en comparación del fenotipo sano.
25.8 Problemas de lápiz y papel
Los problemas de lápiz y papel involucran que el estudiante pueda modificar las condiciones genéticas en la cabecera para dar una conclusión textual, aunque el cuerpo del problema generalmente se modela en términos de un monohíbrido.
26. Ligamiento al sexo
|| REGRESAR AL INDICE ||
En humanos y muchas otras especies de animales, el sexo está determinado por cromosomas específicos. Pero ¿cómo descubrieron los investigadores estos llamados cromosomas sexuales? Los cromosomas que llevan esos genes relacionados con las características sexuales tienen una larga e intrigante historia de exploración. Como sucede a menudo durante un curso tan largo de descubrimiento, los científicos notaron la aparición de estos cromosomas antes de saber exactamente qué eran estas estructuras.
26.1 Los cromosomas sexuales
El primer indicio de que los cromosomas sexuales eran diferentes de todos los demás cromosomas restantes provino de los experimentos realizados por el biólogo alemán Hermann Henking en 1891. En este momento, los científicos podrían ver fácilmente la división de células mitóticas mediante microscopía óptica. De hecho, mientras usaba este método para estudiar la formación de esperma en avispas, Henking observó que algunas células de esperma de avispa tenían 12 cromosomas, mientras que otras solo tenían 11. Además, mientras observaba las etapas de la meiosis que formaban estas células espermáticas, Henking notó que el cromosoma 12 extra se veía diferente de todos los demás. Así llamó a este cromosoma el "elemento X" para representar su naturaleza desconocida. Curiosamente, en estudios posteriores sobre la formación de huevos de saltamontes hembra, Henking no pudo detectar el elemento X (Brown, 2003; Pierce, 2005). Sobre la base de estas observaciones, Henking hipotetizó que este cromosoma adicional debía desempeñar un papel en la determinación del sexo en los insectos. Sin embargo, no pudo reunir ninguna evidencia directa que respaldara esta hipótesis.
Aproximadamente 10 años después de los estudios de Henking, el zoólogo estadounidense C. E. McClung comenzó una extensa investigación sobre la idea de que el elemento X debe tener algo que ver con la determinación del sexo. En primer lugar, McClung afirmó que este extraño cromosoma se denominaría "cromosoma accesorio" porque parecía tener un propósito diferente en comparación con los otros cromosomas. Luego, decidió emprender un amplio estudio comparativo de la espermatogénesis, no solo en insectos, sino en muchos organismos diferentes, incluidas las arañas y los ratones. Mientras observaba la generación de esperma en los saltamontes, McClung observó que el cromosoma accesorio no se comportaba como los otros cromosomas durante la primera división meiótica. Específicamente, este "duodécimo cromosoma" no se distribuyó por igual a las cuatro células espermáticas que surgieron de un espermatogonio de saltamontes; en cambio, estaba presente solo en la mitad de ellos. Este patrón constante de segregación en la espermatogénesis de muchos organismos diferentes hizo que McClung especule que debe haber alguna razón fundamental para la generación de dos tipos de células de esperma.
McClung pensó en las consecuencias de esta distribución 50/50 del cromosoma accesorio, consecuencias de las cuales Darwin ya había hablado a Wallace debían ser de tipo categórico a Wallace, y se preguntó cómo esta distribución probablemente resultó en dos tipos diferentes de cigotos. También observó que, en realidad, solo había una característica que variaba entre zigotos de muchas especies diferentes en proporciones de 50/50, y esa característica era el sexo. Por lo tanto, cuando reunió todas las pruebas, McClung propuso que el cromosoma accesorio debe influir en la determinación del sexo en un cigoto (Brown, 2003). McClung estaba tan ansioso por comunicar formalmente su hipótesis de que escribió una vista previa de esta idea (McClung, 1901) que se publicó como una breve carta aproximadamente un año antes de que su manuscrito completo apareciera en un diario (McClung, 1902).
26.2 La teoría cromosómica de la herencia
Figura 26.1. Cromosomas humanos sexuales. Los cromosomas X e Y están indicados por flechas.
Más o menos por la misma época, Walter Sutton, que fue uno de los antiguos alumnos de McClung, publicó un artículo independiente que examinaba completamente los cromosomas en el saltamontes y proporcionaba datos que apoyaban firmemente la hipótesis de McClung con respecto al cromosoma accesorio. En su estudio, Sutton siguió de cerca el camino de los cromosomas a lo largo de la meiosis en células espermáticas, y demostró con dibujos de etapas meióticas sucesivas que las células espermáticas contenían la mitad del número total de cromosomas presentes en cigotos de saltamontes. La cuidadosa consideración de Sutton de cómo el material cromático segregado en células espermáticas se convirtió en el punto de partida para la teoría cromosómica de la herencia. Para desarrollar esta teoría, Sutton contó cada cromosoma presente en células de esperma de saltamontes y midió su tamaño. Luego clasificó cada cromosoma según estas medidas de tamaño. La observación cuidadosa de Sutton del número de cromosomas y la segregación lo llevaron a concluir que los gametos llevan la mitad de la colección cromosómica total en un cigoto; también determinó que la fusión de dos gametos durante la fertilización debe ser el mecanismo por el cual los pares de cromosomas se reforman (Miko, 2008c). A lo largo de las numerosas observaciones que condujeron a esta conclusión, Sutton tomó nota cuidadosamente del camino del cromosoma accesorio. Con base en estas observaciones, afirmó que, aunque era diferente en su segregación en células de esperma, el cromosoma accesorio era de hecho un verdadero cromosoma (Sutton, 1902).
La idea de que el sexo podía ser determinado por los cromosomas era una idea nueva. Antes de los informes de Henking, McClung y Sutton, la determinación del sexo se atribuía a factores distintos de los gametos, como el entorno en el que existían las células de huevo, idea que venía desde tiempos de Aristóteles. Por lo tanto, el tema del cromosoma accesorio fue un animado tema de debate a principios del siglo XX. La controversia pronto comenzó a desvanecerse, sin embargo, ya que varios otros científicos informaron casos similares de cromosomas "no coincidentes" en otros organismos. Por ejemplo, al examinar las diferencias entre los escarabajos machos y hembras, la investigadora estadounidense Nettie Stevens reconoció patrones de cromosomas que diferían entre los dos sexos. En particular, encontró un par de cromosomas desequilibrados en las células masculinas, y llamó a estas estructuras "heterocromosomas" (Miko, 2008c).
De manera similar, el genetista estadounidense E. B. Wilson trabajó con varias especies de insectos diferentes y observó que, aunque había un número igual de cromosomas en las células masculinas y femeninas, un par en los machos era diferente en tamaño. Llamó a estos pares no coincidentes "idiocromosomas", tal vez porque eran idiosincrásicos (Wilson, 1905). Wilson se convenció de que el más grande de los dos era en realidad el "cromosoma accesorio" y que su cromosoma asociado más pequeño y arrugado no había sido detectado por Henking, McClung y Sutton. Por lo tanto, de acuerdo con Wilson, aunque el cromosoma accesorio sí tenía algo que ver con la determinación del sexo, no era un cromosoma solitario, no apareado; en la mayoría de los casos, tenía una pareja.
Después del descubrimiento de Wilson, surgió cierta confusión acerca de cómo llamar a estas aparentes diferencias en la clasificación cromosómica observada en cada sexo. Parte de esta confusión se relacionaba con el hecho de que numerosas especies estaban siendo examinadas, y estas especies variaban en términos de número cromosómico y disposición. Por lo tanto, persistieron los desafíos para el desarrollo de una teoría unificadora sobre cómo los cromosomas realmente determinan el sexo de un organismo (Miko, 2008c).
26.3 Diferentes seres vivos determinan su sexo de manera diferente
Una pregunta principal que enfrentaban los científicos de la época era si la masculinidad estaba asociada con la ausencia o la presencia del cromosoma deformado. Una vez más, E. B. Wilson se propuso encontrar la respuesta. Wilson se interesó profundamente en el trabajo de su colega Nettie Stevens, y se propuso combinar sus encuestas de especies de escarabajos múltiples con las suyas.
👉 Escarabajos: Stevens (1905) había observado que, en las especies de escarabajos de Tenebrio, había un par de cromosomas de apariencia inusual que se separaban para formar diferentes células espermáticas. Con base en las comparaciones de la apariencia cromosómica en otras células de Tenebrio masculino y femenino, ella propuso que estos cromosomas accesorios probablemente estaban relacionados con la herencia del sexo. Wilson observó independientemente patrones similares en una variedad de insectos. Reforzado por el trabajo de Stevens, Wilson propuso que, entre los dos "cromosomas sexuales" reconocibles, era posible que uno fuera un "determinante femenino" y el otro un "determinante masculino" (Wilson, 1905). Sin embargo, en algunos insectos, incluidas las avispas, la masculinidad se asoció con la ausencia de un cromosoma adicional. ¿Cómo, entonces, podrían conciliarse las observaciones en escarabajos con las de las avispas?
En un intento de resolver este dilema, Wilson intentó organizar los datos recientes de su laboratorio y de otros junto con las observaciones anteriores de Henking, y comenzó con los recuentos cromosómicos. Específicamente, Wilson comparó el número de cromosomas en las células somáticas regulares de cada especie con el número de cromosomas en las células germinales de estas especies. Con base en sus hallazgos, propuso que existían dos categorías de patrones de emparejamiento cromosómico, y denotó estas categorías tipo A y tipo B. Las células somáticas de los machos de tipo A tenían un cromosoma menos que las células somáticas de las hembras de la misma especie. En la especie de Tipo B, sin embargo, el número de cromosomas era el mismo en ambos sexos Tabla 26.1. Por lo tanto, el sexo no podría determinarse de forma universal por la cantidad de cromosomas en las células somáticas regulares de los organismos (Miko, 2008c).
Tabla 26.1. Cromosoma cuenta en las células somáticas de varias especies de tipo A y tipo B
Pero, ¿cómo se relacionan estos recuentos de cromosomas en las células somáticas con los recuentos en los gametos? Wilson argumentó que la cantidad de cromosomas en los gametos de un organismo dependía de si el organismo era de una especie Tipo A “heterogamética” o una especie Tipo B “homogamética”. Wilson luego definió los dos grupos basándose en cómo sus cromosomas sexuales se separaron en gametos. Sus descripciones fueron las siguientes (Miko, 2008c).
👉 Especie tipo A o heterogamética: En los organismos de estas especies, las células somáticas masculinas tienen un cromosoma no apareado, el accesorio. Entonces, mientras que las hembras tienen n cromosomas, los machos siempre tendrán cromosomas n-1. Además, los gametos femeninos (óvulos) siempre tendrán n / 2 cromosomas, mientras que los gametos de los machos (espermatozoides) tendrán una mitad (n-1)/2 y la otra mitad n/2, por lo que el cromosoma accesorio desapareado pasa solo a la mitad de las células espermáticas, por lo que la mitad tendrá este cromosoma, mientras que la otra mitad estará sin él. Dado que el hacho produce dos tipos de gametos con cantidades cromosomales diferentes se los denomina heterogaméticos (Miko, 2008c).
👉 Especies de tipo B u homogamética: En los organismos de estas especies, todos los pares de cromosomas son del mismo tamaño en las células somáticas femeninas, y cada cromosoma tiene una pareja, como las cantidades cromosomales son homogéneas, se los denomina homogaméticos. En las células somáticas masculinas, todos los pares de cromosomas son de igual tamaño excepto por un par: estos son los "idiocromosomas". De hecho, el miembro más pequeño y de aspecto más arrugado solo está presente en las células masculinas. Tanto los óvulos como los espermatozoides de estas especies contienen n / 2 cromosomas. Sin embargo, en los espermatozoides, los cromosomas de tamaños desiguales se separan en dos tipos diferentes de gametos masculinos, uno con el idiocromosoma X más grande y el otro con el idiocromosoma de aspecto más pequeño y arrugado (Miko, 2008c).
26.4 Otras formas de determinación del sexo
👉 Temperatura La determinación del sexo en los seres vivos es diversa, algunos dependen de factores físicos como la temperatura en muchas especies de reptiles, En las cuales los machos se generan cuando el huevo incuba a unos 25°C o menos, mientras que las hembras se generan cuando el huevo incuba entre 26-30°C (Georges & Holleley, 2018; Pezaro, Doody, & Thompson, 2017).
👉 Nivel de ploidía Otros lo realizan dependiendo de la cantidad de copias de todos los cromosomas “ploidía”, de esta forma en las abejas los machos son haploides (n) mientras que las hembras y la reina son diploides (2n). Este proceso es denominado poliandría (Bachtrog et al., 2014; Tarpy & Page, 2002).
👉 Sistema ZZ/ZW En las aves y otros insectos se presenta el sistema ZZ (macho)/ ZW (hembra), siendo un proceso inverso al que determina el sexo en los mamíferos. El ligamiento al sexo es importante ya que muchas enfermedades genéticas de importancia presentan un claro ligamiento a cromosomas sexuales (Miko, 2008c).
26.5 El tamaño del cromosoma sí importa
El cromosoma X especialmente, se estima que este posee cerca de 1100 genes en comparación de los aproximadamente 86 genes del cromosoma Y; de esos 1100 genes aproximadamente el 40% han sido asociados con variantes relacionadas con fenotipos patológicos. De esta manera vamos a tener dos patrones de ligamiento en los mamíferos como el ser humano, el (6)ligamiento al cromosoma X y el ligamiento al cromosoma Y (Klug et al., 2012).
👉 Recesivas Por lo general las enfermedades genéticas se provocan por perdidas funcionales de un gen, lo cual genera un alelo letal recesivo, de allí que los problemas de ligamiento al sexo se involucren principalmente con herencias recesivas, como es el caso de la hemofilia, que se hereda precisamente ligada al cromosoma X como un alelo recesivo. En las herencias recesivas letales debemos tener en cuenta el proceso de compensación de dosis, en los cuales el heterocigoto aun cuando porta el alelo letal, no manifiesta síntomas de la enfermedad, pero puede heredarla a sus descendientes, especialmente a los hemicigotos. Es por esto por lo que estos heterocigotos también se llamados portadores asintomáticos. En el siguiente cruce tenemos una madre sana pero portadora de la enfermedad y un padre sano (Miko, 2008c). La cantidad de mujeres con fenotipo sano es mayor que el de niños ya que las mujeres pueden tener el genotipo heterocigoto que es portador asintomático, mientras que los hombres son hemicigóticos.
Letalidad recesiva ligada al cromosoma X humano. Las hembras sanas portadoras se cuentan como sanas, pero también como portadoras dependiendo de la pregunta.
Miremos un ejemplo:
DEMOSTRACIÓN: Programar una calculadora en Excel para la herencia letal recesiva/dominante ligada al cromosoma X.
Todas las hembras se verán sanas (♀), aunque la mitad de ellas será portadora (XAXa). La mitad de los machos serán sanos (♂) y la otra mitad enfermos (♂E). Las mujeres tenderán a transmitir la enfermedad a sus hijos varones.
La selección en los machos contra los desórdenes del cromosoma X es severa, es decir, muchos de los niños afectados son incapaces de llegar a la edad reproductiva y reproducirse. Las niñas portadoras son quienes mantienen los alelos recesivos-letales en la población debido a que al manifestar fenotipos normales la selección natural nada puede hacer en su contra. Un ejemplo es la hemofilia, donde solo el 70% de los descendientes hemofílicos son capaces de llegar a la edad reproductiva, es decir la aptitud darwiniana de estos individuos es de w(♂)=0,7. Existen otras anormalidades tan severas que matan a los niños antes de llegar a la edad reproductiva casi con un 100% de certeza, y ese es el caso de la distrofia muscular de Duchenne. Las mutaciones de novo o espontáneas representan una fracción significativa de los casos aislados para enfermedades ligadas el cromosoma X. De estas aquellas con dominancia tienden a ser eliminadas de la población debido a que la selección natural puede eliminar a los individuos enfermos, pero las que son recesivas ingresarán a la población, y dependiendo de la deriva genética se quedarán o serán eliminadas.
👉 Dominantes La herencia dominante ligada al cromosoma X, es un modo de herencia genética por el cual un gen dominante se transmite en el cromosoma X. Como patrón de herencia, es menos común que el tipo recesivo vinculado a X. En medicina, la herencia dominante ligada a X indica que un gen responsable de un trastorno genético se encuentra en el cromosoma X, y solo una copia del alelo es suficiente para causar el trastorno cuando se hereda de un padre que tiene el trastorno. En este caso, alguien que exprese un alelo dominante ligado a X exhibirá el trastorno y se considerará afectado.
Los rasgos dominantes ligados al X no necesariamente afectan a los hombres más que a las mujeres (a diferencia de los rasgos recesivos ligados al X). El patrón exacto de herencia varía, dependiendo de si el padre o la madre tienen el rasgo
de interés. Todos los padres afectados por un trastorno dominante ligado a X habrán afectado a las hijas pero no a los hijos afectados. Sin embargo, si la madre también está afectada, los hijos tendrán la posibilidad de verse afectados, dependiendo de si se transmite un cromosoma X dominante o recesivo. Cuando el hijo se ve afectado, la madre siempre se verá afectada.
Algunos estudiosos han sugerido que se descontinúen los términos dominante y recesivo al referirse a la herencia ligada al X debido a los múltiples mecanismos que pueden resultar en la expresión de rasgos ligados al X en las hembras, que incluyen expresión celular autónoma, inactivación X sesgada, expansión clonal y mosaicismo somático. Sin embargo, como se mencionó anteriormente, para los problemas de lápiz y papel asumiremos condiciones ideales.
La Hipofosfatemia ligada al cromosoma X (XLH) en un ejemplo de este tipo de herencia, es una forma dominante de raquitismo (u osteomalacia) ligada al X que difiere de la mayoría de los casos de raquitismo en que la suplementación con vitamina D no la cura. Puede causar deformidad ósea, incluyendo estatura baja y genu varum (pierna pálida). Se asocia con una mutación en la secuencia del gen PHEX (Xp.22) y la inactividad subsiguiente de la proteína PHEX (Saito et al., 2009). La prevalencia de la enfermedad es 1: 20000 (Carpenter, 1997).
26.6 Herencia ligada al cromosoma Y
En este caso dado que nunca se encuentra en presencia de dos alelos, no hay concepto de dominante o recesivo, y lo que importa es determinar la presencia o transferencia del alelo marcado como importante y su correspondiente fenotipo, el cual nuevamente, se estudia para algunas enfermedades genéticas. Característicamente, si un padre posee un rasgo heredado por ligamiento a cromosoma y, todos sus hijos varones portaran el rasgo marcado. Algunos ejemplos son: ASMTY (acetilserotonina metiltransferasa); TSPY (proteína testicular), IL3RAY (receptor de interleuquina-3); SRY (región de determinación sexual); TDF (factor de determinación testicular); ZFY (proteína de dedo de Zn); RKY (quinasa de proteínas ligadas al cromosoma Y), AMGL (amelogenina), CSF2RY (granulocite-macrofago, factor de recepción de estimulación de colonización, subunidad alfa), ANT3Y (translocador 3 de adenina), SOX21 (calvicie); AZF2 (factor 2 de azoospermia); BPY2 (proteína básica del cromosoma Y); AZF1 (factor 1 de azoospermia), entre otros.
26.7 Silenciamiento del cromosoma X
Los casos que vimos anteriormente asumen que los dos cromosomas X presentan compensación de dosis, sin embargo, ese no es siempre el caso, al menos en los seres humanos. En los mamíferos como el ser humano uno de los cromosomas X se silencia, por lo que las probabilidades de expresar un fenotipo dado en las hembras heterocigotas no será 100% para el dominante, sino que será una probabilidad del 50% de expresar el dominante o el recesivo, y esto afecta los procesos de deducción matemática real. Raras veces se expresa el silenciamiento del cromosoma X en los ejercicios de lápiz y papel básicos.
Los alelos dominantes y recesivos pueden asociarse de manera preferente al cromosoma X que es activado o desactivado. La inactivación es el caso en el que el alelo funcional se ubica en el cromosoma que es inactivado de manera preferente, lo cual incrementa la penetrancia de alelo recesivo en los heterocigotos. Los efectos varían, por ejemplo, en el síndrome de Hunter la penetrancia es baja, pero en el síndrome del cromosoma X frágil la penetrancia es alta. El síndrome del cromosoma X frágil "genera autismo" afecta a todos los niños que portan el cromosoma afectado, pero en las niñas heterocigotas que deberían ser portadoras silenciosas existe un alto nivel de penetrancia debido a la inactivación preferente del cromosoma X que porta el alelo normal. La otra alternativa es que el alelo no funcional esté asociado de forma preferente al cromosoma que es inactivado, en estos casos tenemos una inactivación de la enfermedad, fenómeno que disminuye la penetrancia de la enfermedad. Algunos síndromes autoinmunes, la disqueratosis congénita siguen este patrón de herencia.
Los patrones dominante y recesivo en la herencia vinculada al cromosoma X se distinguen en base al fenotipo de las hembras heterocigotas. Si el gen que se está rastreando no es afectado por la inactivación del cromosoma X la herencia de las mujeres es de forma mendeliana clásica. El problema ocurre con los genes afectados por la inactivación, ya que las hembras heterocigotas enfrentan un efecto de aleatoriedad del 50% de presentar o no el fenotipo dominante aun cuando portan el alelo dominante. En términos de patologías o desordenes genéticos: Cerca del 40% se clasifican como recesivos debido a que presentan una penetrancia mínima con respecto al alelo dominante. El 30% se pueden considerar dominantes ya que su penetrancia es mayor al 85% que el alelo está presente. El otro 30% posee una penetrancia variable entre el 15-85% cuando se encuentran en estado heterocigoto.
26.8 Impronta genética
En contraste con la herencia ligada a los cromosomas sexuales, los patrones de expresividad genética pueden ser afectados por el sexo de un individuo incluso cuando los loci de estos genes son autosómicos. Múltiples ejemplos, en diferentes organismos muestran que el sexo de los individuos juega un rol semejante al de la epistasis (interferencia, sobrelapamiento o acoplamiento) lo cual provoca que los machos y las hembras presenten fenotipos diferenciados. Se pueden dar casos fuertes en los que existen fenotipos restringidos para cada sexo, o casos suaves en los que existe una frecuencia mayor de un fenotipo para un sexo, pero con presencia de individuos excepcionales.
Un solo gen controla la forma de las plumas de la cola en Gallus, existen 3 varianes, el homocigoto dominante HH, el heterocigoto Hh y el homocigoto hh. Todas las hembras sin importar el genotipo tienen colas cortas, pero los machos homocigotos recesivos tienen colas largas. En ambos casos los loci de los genes involucrados son autosómicos, es decir se encuentran localizados en posiciones que no tienen nada que ver con los cromosomas sexuales, pero su expresividad depende de la adecuada señalización celular gracias a las hormonas sexuales. Ejemplos de estos caracteres son la cola de los gallos, la calvicie en los hombres, la forma de los cuernos en algunos corderos.
Matemáticamente provoca la apariencia como si el cromosoma y tuviera genes en el cromosoma X homólogos, pero eso solo es una ilusión, lo que sucede es que el cromosoma y posee factores de transcripción que activan parejas de cromosomas somáticos que si tienen loci homólogos. Estos loci no se activan sin la presencia del cromosoma y, creando una restricción de fenotipo diferenciado para machos. La impronta constituye un ejemplo de un proceso más general llamado epistasis.
27. Epistasis
|| REGRESAR AL INDICE ||
Uno de los ejemplos más simples de interacción entre diferentes genes es la epistasis. El significado de la epistasis puede intuirse de algún modo por la etimología de la palabra, epistasis viene de dos raíces griegas “epi” que significa sobre y “stasis” que significa detención u obstrucción. En resumen, un gen epistático es aquel que está sobre otros genes enmascarándolos o que los obstruye de alguna forma. La razón por la cual es el primer ejemplo de interacción génica que es asumido es debido a que sus resultados son cualitativos y poco ambiguos, al igual que los cruces originales de Mendel. Pero al igual que en el caso de Mendel la epistasis es solo un ejemplo muy evidente en relación a otro tipo de interacción que puede ser más sutil. En la epistasis el efecto de un determinado gen enmascara, obstruye o modifica el efecto de otro gen. Algunas veces los genes involucrados afectan al mismo carácter de forma antagonista, lo cual conlleva a que se enmascaren de forma simultánea. En otros casos, los genes involucrados pueden cooperar.
Por ejemplo, en los problemas clásicos del cruce dihíbrido los dos genes analizados afectan dos caracteres diferentes. Pero, ¿qué sucede cuando dos loci diferentes afectan la misma característica? Por ejemplo, ¿qué pasaría si los dos loci en el experimento de Mendel afectaran el color de la semilla? Cuando dos genes están implicados en el resultado de una característica, la proporción fenotípica 9: 3: 3: 1 puede verse alterada radicalmente. Bajo estas circunstancias, hay más de dos productos genéticos que afectan el mismo fenotipo, y estos productos pueden tener relaciones jerárquicas complejas. Cada vez que dos genes diferentes contribuyen a un solo fenotipo y sus efectos no son meramente aditivos, se dice que esos genes son epistáticos (Miko, 2008a).
Aunque algunos investigadores han intentado categorizar todas las interacciones epistáticas digenas (dos genes) con nombres específicos, esos esquemas de clasificación rara vez se usan hoy en día. Una razón por la que han caído en desgracia es que los términos como "dominante" y "recesivo" se usan mejor para describir los efectos de los alelos de genes individuales. Además, la epitasis no está restringida a las interacciones de solo dos genes. Por el contrario, epistasis ocurre en todos los siguientes escenarios:
👉 Siempre que dos o más loci interactúen para crear nuevos fenotipos.
👉 Siempre que un alelo en un locus enmascara los efectos de los alelos en uno o más loci.
👉 Cuando un alelo en un locus modifica los efectos de los alelos en uno o más loci.
Epistasis es una interacción en el nivel de la organización de un fenotipo complejo. Los genes que están involucrados en una interacción epistática específica aún pueden mostrar una variedad independiente a nivel genotípico. En tales casos, sin embargo, las proporciones fenotípicas pueden parecer desviarse de las esperadas 9:3:3:1.
Como se mencionó anteriormente, los científicos han realizado numerosos estudios en un intento de comprender y clasificar mejor las relaciones epistáticas digenas, es decir, aquellas modelables por un sistema matemático de tipo dihíbrido. Algunos de los ejemplos más famosos de investigación en los que se encontró que la interacción entre dos genes produce un nuevo fenotipo se examinan en las siguientes secciones.
27.1 La cresta de los gallos y la epistasis simple por interacciones de dos genes
En la primera década del siglo XX, los genetistas británicos William Bateson y R. C. Punnett realizaron una investigación que muestra que la forma de la cresta en los gallos es causada por la interacción entre dos genes diferentes. Bateson y Punnett eran conscientes del hecho de que las diferentes variedades de gallos poseen crestas distintivas. Por ejemplo, los wyandottes tienen una cresta "en rosa", los brahmas tienen una cresta en "Arveja" y los leghorns tienen una cresta "única". Cuando Bateson y Punnett cruzaron un gallo wynadotte con una gallina Brahma, toda la progenie F1 tuvo un nuevo tipo de cresta llamada "nuez".
Figura 27.1. Existen distintos tipos de crestas entre los más comunes en los ejemplares mapuches en restauración son las anteriores, esas 4 crestas son las más presentes, (A) es simple (B) en rosa o wyandottes (C) es una cresta Arveja o Brahma (D) nuez.
En este caso, ni la cresta en rosa del wyandotte ni la cresta arveja del brahma parecían ser dominantes, porque los descendientes F1 tenían su propio fenotipo único. Además, cuando dos de estas progenies F1 se cruzaron entre sí, algunos de los miembros de la generación F2 resultante tenían crestas en nogal, algunos tenían crestas rosadas, algunos tenían crestas guisante y algunos tenían cresta única, como el que se ve en leghorns. Debido a que las cuatro formas de cresta aparecieron en una proporción de 9: 3: 3: 1 (es decir, nueve crestas nuez por cada tres crestas en rosa; por cada tres crestas en arveja; por cada cresta única), parecía que dos genes diferentes debían jugar un papel en forma de la cresta (Miko, 2008a).
Tabla 27.1. La ley de epistasis simple. Esta plantea la generación de cuatro fenotipos diferentes, por lo que cambiaremos el símbolo de fenotipo a fi donde el subíndice indica cada uno de los fenotipos generables.
Tabla 27.2. Fórmulas de probabilidad opcional de la epistasis simple en términos de dos cruces monohíbridos independientes.
Aunque Bateson y Punnett emplearon las letras R y P, lo más conveniente realmente es dejar el modelo lo más simple posible, empleando las letras A y B. A través de la investigación continua, Bateson y Punnett dedujeron que los pollos wyandotte (cresta rosa) deben tener el genotipo AAbb, mientras que los pollos brahma deben tener el genotipo aaBB. Un cruce entre un wyandotte y un brahma produciría descendientes que todos tenían el genotipo AaBb, que se manifestó como el fenotipo cresta en nuez. De hecho, cualquier pollo con al menos un alelo cresta en rosa rosa (A) y un alelo de cresta (B) tendría una cresta en nuez. Así, cuando se cruzaban dos pollos F1 de cresta en nuez, la generación F2 resultante produciría pollos de cresta en rosa (A_bb), pollos de cresta en arveja (aaB_) y pollos de cresta en nuez (A_B_), así como pollos con un nuevo cuarto fenotipo: el fenotipo de cresta único. Basado en el proceso de eliminación, se puede suponer que estos pollos de cresta única tenían el genotipo aabb (Bateson & Punnett, 1905; 1906; 1908).
Tenga en cuenta que, al seguir las proporciones de un cruce dihíbrido típico, el modelo matemático de este tipo de epistasis no difiere significativamente de los ejemplos para el dihíbrido, lo único que cambia será la determinación de los fenotipos.
27.2 El color de la flor en las arvejas, epistasis por duplicación recesiva
Bateson y Punnett luego realizaron una serie de experimentos en guisantes que también mostraron la interacción aparente de dos genes independientes. El dúo optó por usar guisantes porque es relativamente fácil realizar cruces híbridos con estas plantas, y eligieron enfocarse en la característica del color de la flor. Bateson y Punnett comenzaron cruzando dos variedades de arvejas, cada una de las cuales era de pura raza para flores blancas. Esta cruza produjo una generación F1 en la que toda la progenie tenía flores de color púrpura. A continuación, se cruzaron dos plantas F1 para crear la generación F2. En esta generación, Bateson y Punnett contaron un total de 382 plantas de flores de color púrpura y 269 de flores blancas. La proporción de flores de color púrpura a flores blancas fue de 9,4:6,6, o aproximadamente 9:7 (Miko, 2008a).
¿Qué podría explicar esta variación de las proporciones mendelianas? Bateson se dispuso a responder esta pregunta en un artículo de 1909, en el que primero propuso lo que llamó la capacidad de un "par alelomórfico" (par de alelos genéticos) para enmascarar los efectos de los alelos de otro gen. Para reformular esto en términos del experimento del guisante de Bateson y Punnett, parecía que dos alelos recesivos en un locus de una flor podrían enmascarar los efectos de los alelos en el otro locus de la flor. Vamos a designar el primer locus C de la Figura 27.2 con la pareja A/a, y el segundo locus P de la Figura 27.2 con la pareja B/b.
Figura 27.2. Producción de antocianina en dos pasos. Dos genes son responsables de la reacción química que produce el pigmento vegetal antocianina de una molécula precursora. El gen C controla el primer paso en la reacción para producir el producto del paso 1, y el gen P controla el segundo paso en la reacción para producir antocianina.
Si la teoría de Bateson fuera cierta, significaría que cualquier flor con el genotipo aa sería blanca, sin importar qué alelos estuvieran presentes en su locus B/b. De manera similar, cualquier flor con el genotipo bb también sería blanca, sin importar qué alelos estuvieran presentes en su locus A/a. Posteriormente Bateson usó la palabra "epistasis", que se traduce como "parado sobre/por encima de", para definir la acción enmascaradora de un gen por otro. Desde entonces, los científicos han llegado a comprender que los genes pueden interactuar en más formas que simplemente enmascaramiento (Miko, 2008a). Normalmente se espera que el fenotipo dominante sea púrpura en base a los cruces mendelianos clásicos, sin embargo, Bateson y Punnett escogieron variedades que no habían tenido el grado de purificación que tuvo Mendel, y por ende estas dos variedades en este experimento de epistasis tienen un comportamiento diferente del esperado.
Muchos años después de que Bateson describiera por primera vez esta proporción fenotípica de 9:7 en plantas de guisantes, los investigadores finalmente pudieron determinar los dos genes responsables (Dooner, Robbins, & Jorgensen, 1991). Estos genes controlan el color de las flores al controlar la bioquímica de las plantas de guisantes, en particular las relacionadas con los compuestos de pigmentos llamados antocianinas. En los guisantes, hay una reacción química en dos etapas que forma antocianinas; el gen C es responsable del primer paso, y el gen P es responsable del segundo (Figura 27.2). Si alguno de los pasos no es funcional, entonces no se produce pigmento morado, y la planta de guisante afectada solo tiene flores blancas. Los alelos dominantes C y P codifican los pasos funcionales en la producción de antocianinas, mientras que los alelos c y p recesivos codifican los pasos no funcionales. Por lo tanto, si se producen dos alelos recesivos para cualquiera de los genes, se obtendrán flores blancas.
¿Cómo con cuerda esto con los resultados mendelianos? Probablemente Mendel purificó sin saberlo individuos que tenían siempre un homocigoto dominante en uno de los dos genes, dejando variedades dominantes y recesivas para el segundo.
Tabla 27.3. Regla para la epistasis de dos genes en serie. Los dos genes deben tener alelos dominantes simultáneos para expresar el fenotipo dominante.
Tabla 27.4. Fórmulas de probabilidad opcional de la epistasis duplicación recesiva en términos de dos cruces monohíbridos independientes.
DEMOSTRACION: Programar una calculadora en Excel para la epistasis “de duplicación recesiva” en un cruce de dos dobles heterocigotos
En el ejemplo anterior podemos ver con claridad cómo se resuelve un problema de epistasis. El problema, aunque aparentemente complejo se puede resolver con modificaciones a la factorización que emergen de las condiciones mismas de la epistasis.
27.3 Color de los pétalos de la Primula, epistasis por obstrucción de un gen dominante
Más tarde, los investigadores descubrieron que el color del pétalo de la flor también puede ser controlado por las fuerzas epistáticas dominantes. Por ejemplo, en la planta de Primula, el pigmento malvidina crea flores de color azul. La síntesis de malvidina está controlada por el gen K que modelaremos como A/a, aunque la producción de este pigmento puede ser suprimida por el gen D que modelaremos como B/b, que se encuentra en un locus completamente diferente. En este caso, el alelo B/b es dominante-epistáticas para el alelo A/a, por lo que las plantas con el genotipo AaBb no producirán malvidina debido a la presencia del alelo B bloqueador. Por lo tanto, se trata de una epistasis por obstrucción. Por lo tanto, si dos plantas con genotipo AaBb se cruzan entre sí, ¿cuál es la relación entre la descendencia azul y la descendencia no azul?
Tabla 27.5. Regla para la epistasis de obstrucción dominante.
Tabla 27.6. Fórmulas de probabilidad opcional de la epistasis por obstrucción de un gen dominante en términos de dos cruces monohíbridos independientes.
Todos los genotipos no azules en el ejemplo anterior indican una ausencia de malvidina. En particular, los genotipos amarillos presentan al menos un alelo B, y la presencia del alelo B suprime la producción de malvidina. La relación fenotípica es por lo tanto 13:3. Este tipo de epistasis a veces se denomina supresión dominante, porque la desviación de 9: 3: 3: 1 es causada por un único alelo que produce un fenotipo dominante, y la acción de este alelo es suprimir la expresión de algún otro gen (Miko, 2008a).
27.4 Color del grano de trigo, epistasis por duplicación dominante
Sin embargo, los genes no siempre tienen que actuar en oposición entre sí para que una interacción sea epistática. A veces, dos genes que tienen el mismo papel en la producción de proteínas se pueden sustituir entre sí por compensación de dosis, esto sucede cuando un gen se ha duplicado recientemente por medio de un evento de retrotrasposición. Un evento de retrotrasposición sucede cuando un virus infecta una parte del genoma, pero se degenera a tal punto que solo logra copiar parte de sí mismo, junto con algún gen propio de su anfitrión cercano, pero n o logra generar una capcide, por lo que la copia nueva se inserta en otro lugar del mismo cromosoma. Los retrotrasposones se pueden considerar como retrovirus que tienen un ciclo infectivo al interior de los mismos cromosomas, lo cual da lugar a que generen cientos o miles de copias de genes propios del anfitrión (Naville et al., 2016).
Tabla 27.7. Expresión de la relación fenotipo genotipo en la epistasis por duplicación de un gen.
Tabla 27.8. Fórmulas de probabilidad opcional de la epistasis por duplicación de un gen dominante en términos de dos cruces monohíbridos independientes.
El mecanismo por el cual se determina el color del grano de trigo es un ejemplo de acción genética duplicada. En el trigo, el color del grano depende de una reacción bioquímica que convierte una sustancia precursora en un pigmento, y esta reacción se puede realizar con el producto del gen A o del gen B. Por lo tanto, tener un alelo A o un alelo B produce color en el núcleo, pero la falta de cualquiera de estos alelos producirá un núcleo blanco que carece de color, la solución para el cruce doble heterocigoto se puede obtener por medios analíticos simples. El único genotipo recesivo se genera por el genotipo doble homocigoto recesivo aabb, que en un cruce de dihíbridos AaBb x AaBb siempre tiene una probabilidad de 1/16, por lo que la probabilidad del dominante que suma a todos los demás es de 15/16, así las proporciones obtenidas serán 15:1.
27.5 Conclusiones
Hoy en día, los científicos saben que las predicciones de Mendel sobre la herencia dependían de los genes que él eligió para estudiar, y que purificó rigurosamente para que quedaran parejas de un gen un rasgo único con solo una variabilidad de dominante/recesivo. Específicamente, Mendel seleccionó cuidadosamente siete genes no vinculados que afectaban a siete rasgos diferentes. Sin embargo, a diferencia de los fenotipos que Mendel consideró, la mayoría de los fenotipos se ven afectados por más de un gen. De hecho, la mayoría de las características de los organismos son mucho más complejas que las características que Mendel estudió, y la epistasis es una fuente de esta complejidad. La epistasis puede ocurrir en una variedad de formas diferentes y dar lugar a una variedad de diferentes proporciones fenotípicas. Es más, las epistasis de la tabla anterior solo muestran la interacción de dos genes, pero en la realidad podemos tener decenas o cientos de genes en interacciones mendelianas o epistáticas con más de dos alelos. Más allá de la epistasis, las interacciones gen-ambiente aumentan aún más la variedad de fenotipos que vemos a nuestro alrededor cada día.
Tabla 27.9. Tipos de epistasis dígenas causadas por la interacción de dos genes en un mismo estado del carácter. Tenga en cuenta que esta tabla solo toma en cuenta dos genes por cada carácter, y en la naturaleza pueden ser más de dos.
|
Radio en el cruce doble heterocigoto (AaBB x AaBb) |
Descripción |
Nombre específico de la relación |
|
9:3:3:1 |
Dominancia completa en ambos pares de genes; nuevos fenotipos resultan de la interacción entre alelos dominantes, así como de la interacción entre ambos recesivos homocigotos |
No nombrada ya que aunque los genes interactúan, los fenotipos siguen la proporción de la segregación independiente. |
|
9:4:3 |
Dominancia completa en ambos pares de genes; sin embargo, cuando un gen es homocigoto recesivo, oculta el fenotipo del otro gen |
Epistasis recesiva |
|
9:7 |
Dominancia completa en ambos pares de genes; sin embargo, cuando cualquiera de los genes es homocigoto recesivo, oculta el efecto del otro gen |
Epistasis por duplicación recesiva |
|
12:3:1 |
Dominancia completa en ambos pares de genes; sin embargo, cuando un gen es dominante, oculta el fenotipo del otro gen |
Epistasis dominante |
|
15:1 |
Dominancia completa en ambos pares de genes; sin embargo, cuando cualquiera de los genes es dominante, oculta los efectos del otro gen |
Epistasis por duplicación dominante |
|
13:3 |
Dominancia completa en ambos pares de genes; sin embargo, cuando cualquiera de los genes es dominante, oculta los efectos del otro gen |
Epistasis dominante y recesiva |
|
9:6:1 |
Dominancia completa en ambos pares de genes; sin embargo, cuando cualquiera de los genes es dominante, oculta los efectos del otro gen |
Interacción duplicada |
|
7:6:3 |
Dominancia completa en un par de genes y dominio parcial en el otro; cuando es homocigoto recesivo, el primer gen es epistático del segundo gen |
Sin nombre |
|
3:6:3:4 |
Dominancia completa en un par de genes y dominio parcial en el otro; cuando es homocigoto recesivo, cualquiera de los genes oculta los efectos del otro gen; cuando ambos genes son homocigotos recesivos, el segundo gen oculta los efectos del primero |
Sin nombre |
|
11:5 |
Dominancia completa para ambos pares de genes solo si ambos tipos de alelos dominantes están presentes; de lo contrario, aparece el fenotipo recesivo |
Sin nombre |
28. Penetrancia y expresividad
|| REGRESAR AL INDICE ||
Las relaciones de dominancia entre alelos para un rasgo dado pueden afectar las proporciones fenotípicas, pero las interacciones entre diferentes genes también pueden afectar el fenotipo. Tales rasgos que resultan de la interacción entre múltiples genes y su entorno se llaman rasgos complejos. Entonces, dado un rasgo específico, ¿cómo podemos saber si es complejo? Una forma de reconocer un rasgo complejo es a través de patrones de herencia inconsistentes en generaciones sucesivas. Por ejemplo, un rasgo dominante podría omitir toda una generación y aun así expresarse en la siguiente generación. ¿Cómo es esto posible? La respuesta a esta pregunta radica en los conceptos de penetrancia y expresividad (Miko, 2008b).
28.1 Penetrancia
Al estudiar las relaciones entre genotipo y fenotipo, es importante examinar la ocurrencia estadística de fenotipos en un grupo de genotipos conocidos. En otras palabras, dado un grupo de genotipos conocidos para un rasgo, ¿cuántos genotipos idénticos muestran el fenotipo relacionado? Puede que se sorprenda al saber que, para algunos rasgos, el fenotipo puede no ocurrir tan a menudo como el genotipo que debería generarlo. Por ejemplo, supongamos que todos en la población W tienen las mismas combinaciones de alelos para un determinado rasgo, pero solo el 85% de la población muestra realmente el fenotipo esperado de esas combinaciones de alelos. La proporción de genotipos que realmente muestran fenotipos esperados se llama penetrancia. Por lo tanto, en el ejemplo anterior, la penetrancia es del 85%. Este valor se calcula al observar poblaciones cuyos genotipos conocemos (Miko, 2008b), y por lo tanto en los ejercicios de lápiz y papel es un dato que viene en el enunciado o que debe obtenerse al comparar las probabilidades esperadas y experimentales.
Figura 28.1. La función del ADN es almacenar las instrucciones para producir proteínas activas, pero en medio de eso hay una serie de pasos conocidos como: transcripción “ADN → ARNmi conocido como transcripto primario o mensajero inmaduro”; procesamiento o maduración “ARNmi → ARNm”; transporte del mensajero madurado al ribosoma; transcripción “ARNm → proteína inactiva”; y activación “proteína inactiva a forma activa”. En cada uno de los pasos el loci inicial puede ser bloqueado o alterado por proteínas encargadas de cada uno de los pasos, todos estos son los controles epigenéticos.
De hecho, se necesitan grandes estudios poblacionales para medir la penetrancia, y los estudios de penetrancia nos ayudan a predecir qué tan probable es que un rasgo sea evidente en aquellos que portan los alelos subyacentes. En general, cuando sabemos que el genotipo está presente pero el fenotipo no es observable, el rasgo muestra una penetrancia incompleta. Básicamente, cualquier cosa que muestre menos del 100% de penetrancia es un ejemplo de penetrancia incompleta. Por lo tanto, aunque la penetrancia de un rasgo es un valor estadísticamente calculado basado en la aparición de un fenotipo entre genotipos conocidos, la penetrancia incompleta es simplemente una descripción cualitativa de un grupo de genotipos conocidos (Miko, 2008b).
Un ejemplo específico de penetrancia incompleta es la osteogénesis imperfecta (OI) una enfermedad del desarrollo de los huesos humanos. La mayoría de las personas con esta enfermedad tienen una mutación dominante en uno de los dos genes que producen colágeno tipo 1, COL1A1 o COL1A2. El colágeno es un tejido que fortalece los huesos, los músculos y otros tejidos corporales múltiples. Las personas con OI tienen huesos débiles, color azulado en el blanco de los ojos y una variedad de afecciones que causan debilidad en sus articulaciones y dientes. Sin embargo, esta enfermedad no afecta a todos los que tienen mutaciones COLIA1 y COLIA2 de la misma manera. De hecho, algunas personas pueden portar la mutación, pero no tienen síntomas. Por lo tanto, las familias pueden, sin saberlo, transmitir la mutación de una generación a otra a través de alguien que porta la mutación, pero no expresa el fenotipo de OI (Miko, 2008b).
Tenga en cuenta que la expresión de otros genes, como los reguladores transcripcionales o translacionales, puede influir en el efecto final de un producto génico. Cualquier cosa que interfiera con la ruta de la transcripción a la activación de proteínas se conoce como un factor epigenético. De hecho, hay múltiples puntos en los que otro producto génico puede intervenir en las etapas previas a la producción de una proteína. La interferencia en estas etapas puede detener la producción por completo, crear una forma alterada de la proteína que podría no estar activa, o hacer cualquier cantidad de otras, si las cosas siempre conllevan al silenciamiento de la proteína implica una disminución de la penetrancia, pero si solo la denilita hablaremos de expresividad. Por lo tanto, la etapa final de una proteína activa refleja muchos procesos diferentes, que conducen a la secuencia de aminoácidos y a la forma definitiva de la proteína, todos los cuales pueden ser interferidos por otros genes, lo cual indica que hay que ir más allá del viejo aforismo “un gen, una proteína, un rasgo”. Además, algunos genes pueden regular hacia arriba o hacia abajo las tasas de transcripción, lo que cambia la cantidad total de proteína producida. Por lo tanto, los genes que afectan la forma final y la cantidad de expresión de otro gen pueden ser influyentes en la formación del fenotipo derivado del gen regulado.
Entonces, si existen tantos puntos de modificación posibles diferentes para un producto génico, ¿cómo podemos reducir la pregunta de qué causa la penetración incompleta? Curiosamente, algunos científicos han intentado hacer esto al observar cómo las mutaciones genéticas que causan la OI afectan a los ratones. Estos investigadores insertaron una forma mutada de COL1A1 en ratones y los criaron para que todos contengan esta mutación. Los ratones se vieron afectados de forma similar a aquellos con OI humana: muchos tenían debilidad ósea severa y múltiples fracturas óseas, incluso al nacer. De hecho, cuando los investigadores examinaron de cerca los huesos del ratón, descubrieron que el 70% de los ratones con el gen COL1A1 mutado mostraban evidencia de OI (fracturas óseas); sin embargo, el 30% restante parecía completamente normal. En estos ratones sin fenotipo OI, hubo la misma cantidad de expresión de COL1A1 que en aquellos ratones que mostraron el fenotipo. Además, los investigadores utilizaron una raza pura de ratones que tenían poca variabilidad en sus genomas, para empezar. Esto significa que el contexto genético en el que se expresó COL1A1 no varió entre los ratones estudiados. Sin embargo, a pesar del hecho de que todos los ratones tenían genomas extremadamente similares y todos expresaban la misma cantidad de COL1A1, el 30% de ellos no mostraba ningún fenotipo OI. Estos resultados continúan siendo desconcertantes. Por lo tanto, incluso las poderosas técnicas experimentales actualmente disponibles no pueden explicar la penetrancia. Las dos explicaciones más populares para la penetrancia incompleta, el fondo genético y los niveles de expresión variables, no explicaron la falta de fenotipo en el 30% de los ratones (Pereira, Halford, Sokolov, Khillan, & Prockop, 1994).
28.2 Expresividad
Individuos con el mismo genotipo también pueden mostrar diferentes grados “y cuando hablamos de grados, debemos hacer referencioa de manera inevitable a las ideas darwinistas” del mismo fenotipo. La expresividad es el grado en que la expresión del rasgo difiere entre los individuos. A diferencia de la penetrancia, la expresividad describe la variabilidad individual, no la variabilidad estadística entre una población de genotipos. Por ejemplo, las características del síndrome de Marfan varían ampliamente; algunas personas tienen solo síntomas leves, como ser altos y delgados con dedos largos y delgados, mientras que otros también experimentan complicaciones potencialmente mortales que afectan el corazón y los vasos sanguíneos. Aunque las características del síndrome de Marfan son muy variables, todas las personas con este trastorno tienen una mutación dominante en el gen que codifica la fibrilina 1, FBN1. Sin embargo, resulta que la posición de la mutación en el gen FBN1 se correlaciona con la severidad del fenotipo de Marfan. Los investigadores encontraron que una mutación en una posición de FBN1 es frecuente en familias con síntomas graves, mientras que una mutación en otra posición es frecuente en familias con síntomas menos graves. Estos hallazgos son una pista alentadora sobre cómo los defectos específicos en la proteína de la fibrilina 1 pueden explicar la expresividad variable en el síndrome de Marfan (Li et al., 2008).
Figura 28.2. El gato de Hemingway con polidactilia. Debido a que el gen de la polidactilia siempre causa dedos extra en los gatos, pero el número de dedos adicionales varía entre los individuos con el gen, la polidactilia se considera un ejemplo de "expresividad" variable.
Otro ejemplo de expresividad en el trabajo es la aparición de dedos extra, o polidactilia, en gatos. La presencia de dedos extra en la pata de un gato es un fenotipo que surge en grupos de gatos que se han cruzado por generaciones de manera endogámica. De hecho, hay varios grupos conocidos de estos gatos, como los de Key West Island (conocidos como "los gatos de Hemingway"), así como los que se encuentran en clusters de reproducción en el este de los EE. UU, y las costas de las Islas Británicas. El primero en informar sobre este fenómeno fue C. H. Danforth, quien estudió la herencia de la polidactilia en 55 generaciones de gatos. Observó que el fenotipo de polidactilia mostraba "buena penetrancia, pero expresión variable" porque el gen siempre causa dedos extra en la pata, pero el número de dedos adicionales varía ampliamente de un gato a otro (Li et al., 2008). A través de sus estudios de crianza, Danforth descubrió que, aunque un alelo dominante subyace a la causa de la polidactilia, el grado de polidactilia depende de la condición de los tejidos estratificados adyacentes en la extremidad en desarrollo; es decir, la expresión de los genes en los tejidos que rodean al tejido que se convertirá en el dedo del pie determina el grado de polidactilia (Li et al., 2008).
28.3 Modelo matemático
El modelo matemático en este caso se hace complejo pues debemos manejar muchas probabilidades, y dado que el símbolo de probabilidad se repite mucho, emplearemos la misma solución que se usa para la concentración molar en química, y usaremos un corchete para representar implícitamente que estamos trabajando probabilidades.
En este caso la probabilidad esperada del fenotipo dominante corregido con penetrancia [D]0,p dependerá de la probabilidad teórica de los genotipos corregida con la penetrancia [genotipo]0,p. A su vez, dicha probabilidad corregida será el producto de la probabilidad teórica tal como se obtiene de un cuadro de Punnett u otras técnicas factoriales [genotipo]0 por la probabilidad de la penetrancia [genotipo]p.
(Eq. 28.1) Probabilidad de un genotipo teórico corregido con la penetrancia. Esta expresión aplica para homocigotos dominantes y heterocigotos, pero no para los homocigotos recesivos. Tenga en cuenta que la probabilidad corregida con penetrancia también se conoce como la probabilidad de éxito de la penetrancia.
Si aplicamos lo anterior a un sistema monohíbrido de dos alelos A/a, obtendremos que:
(Eq. 28.2) Probabilidades teóricas corregidas con penetrancia de los fenotipos dominante (D) y recesivo (R), en un sistema monohíbrido de dos alelos.
28.4 Hacia una mirada evolutiva sintética
La relación entre genotipo y fenotipo no es simple. Algunas veces, los alelos dominantes pueden ser silenciados por otros genes que minimizan la apariencia del fenotipo. En otros casos, la expresión génica puede modificarse de manera sutil, pero puede tener un gran impacto en el fenotipo. Las causas exactas de la penetrancia y la expresividad aún no se conocen bien. Cuanto más aprendamos sobre los mecanismos moleculares que rigen la regulación genética, más podremos formular y probar hipótesis sobre cómo surge esta variabilidad. Sin embargo, en este punto ya nos acercamos al tipo de herencia gradual que le interesaba a Darwin y Wallace, la herencia continua o gradual.
29. Análisis de pedigrí
|| REGRESAR AL INDICE ||
Los pedigrís se empleaban mucho antes de los estudios de genética humana, eran y son empelados en su forma heráldica como arboles familiares, diagramas que representan los parentescos entre familias preocupadas por la manutención de un estatus social y la integridad de un patrimonio en común. De todas las familias las más preocupadas por esto eran la nobleza y la realeza, aunque muchos otros grupos sociales como los burgueses en su afán se ser semejantes a los nobles también emplearon los árboles genealógicos (Resta, 1993). La simbología de un pedigrí cambia dependiendo de su uso, los empleados para la heráldica son bastante artísticos En términos de genética, los árboles genealógicos o pedigrís son herramientas que permiten realizar inferencias mediante razonamiento hipotético-deductivo de rasgos que se manifiestan a través de varias generaciones en una familia (Resta, 1993).
Figura 29.1. Símbolos básicos de un Pedigrí.
Mediante esta herramienta es posible estudiar la genética humana sin recurrir a cálculos estadísticos que necesitarían cientos o miles de individuos. Los pedigrís empleados en ejercicios de lápiz y papel se construyen a partir de ejercicios mendelianos clásicos o muy semejantes en los que existen pocos rasgos y pocos caracteres, generalmente limitándose al sistema de un carácter dos rasgos “o en términos del modelo genético después de la década del 1900s” a un gen y dos alelos (Resta, 1993). Los pedigrís son útiles para todos los modelos biológicos que, como el ser humano, poseen bajos índices de reproducción como, por ejemplo: perros, caballos, ganado entre otros.(Griffiths, Wessler, Lewontin, & Carroll, 2007; Klug, Cummings, Spencer, & Palladino, 2005; Klug et al., 2009; Nussbaum, McInnes, Willard, & Hamosh, 2007; Pierce, 2005, 2012; Sadava et al., 2014; Sadava, Hillis, Heller, & Berenbaum, 2011; Solomon, Berg, & Martin, 2008; Stracham & Read, 2010)
29.1 Herencia dominante autosómica
Los rasgos que se estudian mediante un pedigrí son generalmente enfermedades raras que se generan por mutaciones en un gen importante, lo cual genera un patrón de herencia semejante al mendeliano. Decimos semejante debido a la probabilidad de existencia de fenómenos que la afectan como la penetrancia. En cualquier caso, realizaremos análisis asumiendo las condiciones de los ejercicios de lápiz y papel, es decir, la presunción que estos caracteres patológicos siguen una herencia mendeliana perfecta. De aquí en adelante, llamaremos a la persona que expresa el rasgo anormal como un individuo AFECTADO. La herencia dominante tiene en los pedigrís las siguientes características.
1- Cada hijo afectado tiene al menos un padre afectado.
2- Aproximadamente la mitad o más de los descendientes resultará afectado.
3- El rasgo anormal ocurre sin importar el sexo.
Figura 29.2. Pedigrí de herencia dominante autosómica.
29.2 Herencia recesiva autosómica
Las pistas para encontrarlo son:
1- Aparecen individuos afectados de padres no afectados. En este tipo de herencia se da el caso que comúnmente se denomina salto de una generación, un rasgo que estaba presente en algún abuelo, pero no en los padres y reaparece en el nieto. Básicamente cuando aparece un rasgo como de la nada, que afecta a los dos sexos sin importar estamos hablando de una herencia recesiva.
2- En familias afectadas, alrededor de ¼ de los hijos estarán afectados por el rasgo anormal. A los individuos se los clasifica como afectados “recesivos homocigóticos” o portadores “heterocigóticos”.
Figura 29.3. Pedigrí de herencia recesiva autosómica.
29.3 Ligamiento al cromosoma X dominante
1- Los hijos varones de un padre “varón” afectado no se ven afectados debido a que reciben el cromosoma Y.
2- Los Padres afectados tienen siempre hijas afectadas. Aunque sus síntomas son menos marcados.
3- El patrón de Pedigrí es semejante al de la herencia autosómica dominante.
4- La proporción de hijas afectadas es casi el doble del de varones, pero con síntomas menos marcados generalmente
Figura 29.4. Pedigrí de herencia ligada al cromosoma X dominante.
29.4 Ligamiento al cromosoma X recesivo
Para rastrear la herencia ligada al cromosoma X en estado recesivo hay que seguir las siguientes indicaciones.
1- El rasgo afecta preferentemente a los hombres.
2- Las mujeres heterocigotas no manifiestan síntomas
3- El alelo responsable se transmite de un hombre afectado a todas sus hijas, los hijos tienen el 50% de heredarlo.
4- Si la herencia desaparece en varias generaciones ha sido transportado asintomáticamente de forma matrilineal.
5- Una proporción significativa de casos se debe a mutaciones espontáneas.
Figura 29.5. Pedigrí de herencia ligada al cromosoma X recesiva.
En los ejercicios de lápiz y papel se asume compensación de dosis en las mujeres, por lo que no hay que molestarse con la inactivación de uno de los cromosomas X.
29.5 Herencia ligada al cromosoma y
1- Igual que un apellido patrilineal, se hereda exclusivamente de padres a hijos varones.
2- El padre siempre hereda la anomalía a sus hijos varones.
3- Ninguna mujer es afectada o es portadora.
Figura 29.6. Pedigrí de herencia hemicigota de cromosoma Y.
29.6 El caso de la familia real rusa
La familia real rusa representa uno de los casos más paradigmáticos de la herencia ligada al sexo, la cual desencadenó una serie de eventos a nivel histórico de gran relevancia (Rogaev et al., 2009). El Zar Nicolas II de Risia tuvo muchas hijas y solo un hijo varón el cual resultó ser hemofílico, este detalle sumado a su ineptitud como gobernante desencadenó la revolución de las mayorías (bolcheviques) lo cual provocó que abdicara al trono, posteriormente toda la familia murió fusilada bajo el nuevo régimen comunista.
Figura 29.7. Pedigrí de herencia ligada al cromosoma X recesivo de las familias reales europeas de finales del siglo XIX.
En la presente sección nos enfocaremos en el Pedigree para rastrear el linaje de gen que provocó que el hijo de Nicolás II resultara no apto para el trono. Aparentemente dentro de la familia de Nicolás no se encuentran registros de hemofílicos, pero si en la familia de su esposa, y a partir de ella se ha elaborado el árbol genealógico. Como se mencionó anteriormente el rastreo se ha realizado hacia la familia de la esposa de Nicolas II la Zarina Alejandra de Hesse, la cual es de ascendencia inglesa. Este caso normalmente también se lo conoce como el caso de los descendientes de la reina Victoria de Inglaterra “generación II”, donde la mutación que causa la hemofilia parece haberse presentado de forma espontánea, esto se debe a que los registros anteriores a ella no implican la presencia de hemofílicos.
Referencias bibliográficas
|| REGRESAR AL INDICE ||
Allchin, D. (2002). Dissolving dominance. In Mutating concepts, evolving disciplines: Genetics, medicine, and society (pp. 43–61). Springer.
Allen, G. E. (1968). Thomas Hunt Morgan and the problem of natural selection. Journal of the History of Biology, 1(1), 113–139.
Allen, G. E. (1975). The introduction of Drosophila into the study of heredity and evolution: 1900-1910. Isis, 66(3), 322–333.
Allen, G. E. (1985). Thomas Hunt Morgan: Materialism and experimentalism in the development of modern genetics. Trends in Genetics, 1, 186–190.
Allison, A. C. (1960). Glucose-6-phosphate dehydrogenase deficiency in red blood cells of East Africans. Nature, 186, 531–532.
Arriaga, H. O. (1987). La evolución del mejoramiento del maíz. In III Jornada Científica organizada por la Academia Nacional de Agronomía y Veterinaria y la Universidad Nacional del Litoral (30 de noviembre al 1 de diciembre de 1987, Santa Fe, Argentina).
Bachtrog, D., Mank, J. E., Peichel, C. L., Kirkpatrick, M., Otto, S. P., Ashman, T.-L., … Ming, R. (2014). Sex determination: why so many ways of doing it? PLoS Biology, 12(7), e1001899.
Baldor, A. (2008). Álgebra de Baldor. Madrid. Ediciones y Distribuciones CODICE.
Barnett, J. A., & Robinow, C. F. (2002). A history of research on yeasts 4: cytology part I, 1890–1950. Yeast, 19(2), 151–182.
Bateson, W., Saunders, E. R., & Punnett, R. C. (1904). Experimental studies in the physiology of heredity. Molecular and General Genetics MGG, 2(1), 17–19.
Benfey, O. T. (2007). The conceptual structure of the sciences. In Philosophy of Chemistry: Synthesis of a New Discipline, Boston Studies in the Philosophy and History of Science (pp. 95–117). Springer.
Benton, E. (1974). Vitalism in nineteenth-century scientific thought: A typology and reassessment. Studies in History and Philosophy of Science Part A, 5(1), 17–48.
Bernal, J. D. (1953). Science and industry in the nineteenth century. Taylor & Francis.
Boone, C., Bussey, H., & Andrews, B. J. (2007). Exploring genetic interactions and networks with yeast. Nature Reviews Genetics, 8(6), 437.
Bowman, J. E., & Walker, D. G. (1961). Action of Vicia faba on erythrocytes: possible relationship to favism. Nature, 189(4764), 555.
Brooks, D. R. (2011). The extended synthesis: something old, something new. Evolution: Education and Outreach, 4(1), 3–7.
Brown, S. J. (2003). Entomological contributions to genetics: Studies on insect germ cells linked genes to chromosomes and chromosomes to Mendelian inheritance. Archives of Insect Biochemistry and Physiology: Published in Collaboration with the Entomological Society of America, 53(3), 115–118.
Cahoone, L. (2013). Physicalism, the Natural Sciences, and Naturalism. Philo, 16(2), 130–144.
Carlile, M., Watkinson, S., & Gooday, G. (2001). The fungi (2nd ed.). San Diego: Academic Press.
Carpenter, T. O. (1997). New perspectives on the biology and treatment of X-linked hypophosphatemic rickets. Pediatric Clinics, 44(2), 443–466.
Carroll, S. B. (2008). Evo-devo and an expanding evolutionary synthesis: a genetic theory of morphological evolution. Cell, 134(1), 25–36.
Castillo Murillo, L. M. (2011). Sistema didáctico para el aprendizaje de la genética.
Castle, W. E., & Little, C. C. (1910). On a modified Mendelian ratio among yellow mice. Science, 32(833), 868–870.
Cherif, A. H., Roze, M., & Movahedzadeh, F. (n.d.). The Winding Road to Discovering the Link between Genetic Material and DNA.
Chevallard, Y. (1985). La transposition didactique. Grenoble: La pensée sauvage.
Chevallard, Y., & Perrenoud, P. (1998). La transposition didactique à partir de pratiques: des savoirs aux compétences. Revue Des Sciences de l’éducation, 24(3), 487–514.
Chippindale, A. K., & Rice, W. R. (2001). Y chromosome polymorphism is a strong determinant of male fitness in Drosophila melanogaster. Proceedings of the National Academy of Sciences, 98(10), 5677–5682.
Churchill, F. B. (1970). Hertwig, Weismann, and the meaning of reduction division circa 1890. Isis, 61(4), 429–457.
Churchill, F. B. (1974). William Johannsen and the genotype concept. Journal of the History of Biology, 7(1), 5–30.
Cleophas, T. J., & Zwinderman, A. H. (2017). Medical Statistics: A Discipline at the Interface of Biology and Mathematics. In Understanding Clinical Data Analysis (pp. 193–221). Springer.
Craig, R. (2003). Creating a more beautiful world: A century of progress in the breeding of floral and nursery plants. HortScience, 38(5), 928–936.
Cremer, T., & Cremer, C. (1988). Centennial of Wilhelm Waldeyer’s introduction of the term “chromosome” in 1888. Cytogenetic and Genome Research, 48(2), 66–67.
Crosland, M. (1977). History of science in a national context. The British Journal for the History of Science, 10(02), 95–113.
Crow, E. W., & Crow, J. F. (2002). 100 years ago: Walter Sutton and the chromosome theory of heredity. Genetics, 160(1), 1–4.
Cuenot, L. C. M. J. (1905). Les races pures et leurs combinaisons chez les Souris (Notes et Revue). Archives de Zoologie Experimentale, 3(7).
Darden, L. (1985). Hugo de Vries’s lecture plates and the discovery of segregation. Annals of Science, 42(3), 233–242.
Dobzhansky, T. (1959). Variation and evolution. Proceedings of the American Philosophical Society, 103(2), 252–263.
Doebley, J. F., Gaut, B. S., & Smith, B. D. (2006). The molecular genetics of crop domestication. Cell, 127(7), 1309–1321.
Donis-Keller, H., Green, P., Helms, C., Cartinhour, S., Weiffenbach, B., Stephens, K., … Lander, E. S. (1987). A genetic linkage map of the human genome. Cell, 51(2), 319–337.
Dooner, H. K., Robbins, T. P., & Jorgensen, R. A. (1991). Genetic and developmental control of anthocyanin biosynthesis. Annual Review of Genetics, 25(1), 173–199.
Edwards, A. W. F. (2008). GH Hardy (1908) and Hardy–Weinberg Equilibrium. Genetics, 179(3), 1143–1150.
Edwards, S. B. (1991). Crops with wild relatives found in Ethiopia. Plant Genetic Resources of Ethiopia, 42–47.
Einstein, A. (1905). The photoelectric effect. Ann. Phys, 17(132), 4.
Fairbanks, D. J., & Rytting, B. (2001). Mendelian controversies: a botanical and historical review. American Journal of Botany, 88(5), 737–752.
Falk, R. (2001). Mendel’s hypothesis. In Science, History and Social Activism (pp. 77–86). Springer.
Falk, R. (2006). Mendel’s impact. Science in Context, 19(02), 215–236.
Franklin, A. (2008). The mendel-fisher controversy. Ending the Mendel-Fisher Controversy, 1–77.
Franklin, A., Edwards, A. W. F., Fairbanks, D. J., & Hartl, D. L. (2008). Ending the mendel-fisher controversy. University of Pittsburgh Pre.
Georges, A., & Holleley, C. E. (2018). How does temperature determine sex? Science, 360(6389), 601–602.
Glass, B., & Kistler, J. C. (1953). Distal hyperextensibility of the thumbs. Human Heredity, 4(2–3), 192–206.
Goodman, A. H. (2000). Why genes don’t count (for racial differences in health). American Journal of Public Health, 90(11), 1699.
Gould, R. (2011). Variability: One statistician’s view. Department of Statistics, UCLA.
Gould, S. J. (1982). Darwinism and the expansion of evolutionary theory. Science, 216(4544), 380–387.
Griffiths, A., Wessler, S., Lewontin, R., & Carroll, S. B. (2007). Introduction to Genetic Analysis (9th ed.). USA: Freeman.
Hamilton, W. D., Axelrod, R., & Tanese, R. (1990). Sexual reproduction as an adaptation to resist parasites (a review). Proceedings of the National Academy of Sciences, 87(9), 3566–3573.
Hamoir, G. (2003). The discovery of meiosis by E. Van Beneden, a breakthrough in the morphological phase of heredity. International Journal of Developmental Biology, 36(1), 9–15.
Harris, H., & Joseph, J. (1949). Variation in extension of the metacarpo-phalangeal and interphalangeal joints of the thumb. Bone & Joint Journal, 31(4), 547–559.
Hartl, D. L. (1979). Biography of Thomas Hunt Morgan Thomas Hunt Morgan: The Man and His Science G. E. Allen. BioScience, 29(8). https://doi.org/10.2307/1307543
Harwood, J. (2000). The rediscovery of Mendelism in agricultural context: Erich von Tschermak as plant-breeder. Comptes Rendus de l’Académie Des Sciences-Series III-Sciences de La Vie, 323(12), 1061–1067.
Henig, R. M. (2001). The monk in the garden: the lost and found genius of Gregor Mendel, the father of genetics. Houghton Mifflin Harcourt.
Hopkins, B. C. (2021). Jacob Klein on François Viète and the birth of the modern symbolic concept of “number.” In The New Yearbook for Phenomenology and Phenomenological Philosophy (pp. 446–458). Routledge.
Inman, H. F. (1994). Karl Pearson and RA Fisher on statistical tests: a 1935 exchange from Nature. The American Statistician, 48(1), 2–11.
Johnston, T. D. (1995). The influence of Weismann’s germ‐plasm theory on the distinction between learned and innate behavior. Journal of the History of the Behavioral Sciences, 31(2), 115–128.
Jorgenson, J. W., & Lukacs, K. D. (2009). Electroforesis. Chem. Science, 130(222).
Karp, G. C. (2013). Cell and Molecular Biology, Concepts and Experiments (7th ed.). USA: Wiley Online Library.
Klug, W. S., Cummings, M. R., Spencer, C. A., & Palladino, M. A. (2005). Concepts of Genetics (8th ed.). USA: Pearson.
Klug, W. S., Cummings, M. R., Spencer, C. A., & Palladino, M. A. (2009). Concepts of Genetics (9th ed.). USA: Pearson.
Klug, W. S., Cummings, M. R., Spencer, C. A., & Palladino, M. A. (2012). Concepts of Genetics (10th ed.). USA: Pearson.
Kohler, R. E. (1994). Lords of the fly: Drosophila genetics and the experimental life. University of Chicago Press.
Kuhn, T. S. (1970). The structure of scientific revolutions, 2nd. Chicago: Univ. of Chicago Pr.
Kutschera, U., & Niklas, K. J. (2004). The modern theory of biological evolution: an expanded synthesis. Naturwissenschaften, 91(6), 255–276.
Leitze, A., & Kitt, N. A. (2000). Algebra for all: Using homemade algebra tiles to develop algebra and prealgebra concepts. The Mathematics Teacher, 93(6), 462–520.
Li, D., Yu, J., Gu, F., Pang, X., Ma, X., Li, R., … Ma, X. (2008). The roles of two novel FBN1 gene mutations in the genotype–phenotype correlations of Marfan syndrome and ectopia lentis patients with marfanoid habitus. Genetic Testing, 12(2), 325–330.
Lial, M. L., Hornsby, J., & McGinnis, T. (2012). Beginning algebra. Pearson Addison-Wesley,.
Lobo, I. (2008a). Discovery and Types of Genetic Linkage. Nature Education, 1(1), 139. Retrieved from https://www.nature.com/scitable/topicpage/discovery-and-types-of-genetic-linkage-500#
Lobo, I. (2008b). Mendelian Ratios and Lethal Genes. Nature Education, 1(1), 138. Retrieved from https://www.nature.com/scitable/topicpage/mendelian-ratios-and-lethal-genes-557
Lobo, I., & Shaw, K. (2008). Thomas Hunt Morgan, genetic recombination, and gene mapping. Nature Education, 1(1), 205.
Löwy, I. (1994). On hybridizations, networks and new disciplines: The Pasteur Institute and the development of microbiology in France. Studies in History and Philosophy of Science Part A, 25(5), 655–688.
Magnello, M. E. (1998). Karl Pearson’s mathematization of inheritance: from ancestral heredity to Mendelian genetics (1895–1909). Annals of Science, 55(1), 35–94.
Marinella, L. (2007). The nobility and excellence of women and the defects and vices of men. University of Chicago Press.
Mayr, E. (1982). The growth of biological thought: Diversity, evolution, and inheritance. Harvard University Press.
Mayr, E. (1985). Weismann and evolution. Journal of the History of Biology, 18(3), 295–329.
Mayr, E. (1986). Joseph Gottlieb Kolreuter’s contributions to biology. Osiris, 135–176.
McClung, Clarence E. (1902). The accessory chromosome—sex determinant? The Biological Bulletin, 3(1–2), 43–84.
McClung, Clarence Erwin. (1901). Notes on the accessory chromosome. Anatomischer Anzeiger, 20, 220–226.
McDonald, J. H. (2011). Myths of Human Genetics. Baltimore: Sparky House.
McKusick, V. A. (1960). Walter S. Sutton and the physical basis of Mendelism. Bulletin of the History of Medicine, 34, 487.
Meijer, O. G. (1985). Hugo de vries no mendelian? Annals of Science, 42(3), 189–232.
Mendel, G. (1866). Versuche über Pflanzenhybriden. Verhandlungen Des Naturforschenden Vereines in Brunn 4: 3, 44. Retrieved from https://academic.oup.com/genetics/article/204/2/407/6072056?login=true
Mendel, G. (1996). Experiments in plant hybridization (1865). Verhandlungen Des Naturforschenden Vereins Brünn.) Available Online: Www. Mendelweb. Org/Mendel. Html (Accessed on 1 January 2013).
Miko, I. (2008a). Epistasis: Gene Interaction and Phenotype Effects. Nature Education, 1(1), 197. Retrieved from https://www.nature.com/scitable/topicpage/epistasis-gene-interaction-and-phenotype-effects-460
Miko, I. (2008b). Phenotype Variability: Penetrance and Expressivity. Nature Education, 1(1), 137.
Miko, I. (2008c). Sex Chromosomes and Sex Determination. Nature Education, 1(1), 108.
Monaghan, F. V, & Corcos, A. F. (1987). Tschermak: a non-discoverer of Mendelism II. A critique. Journal of Heredity, 78(3), 208–210.
Monaghan, F. V, & Corcos, A. F. (1990). The real objective of Mendel’s paper. Biology and Philosophy, 5(3), 267–292.
Moore, R. (2001). The “rediscovery” of Mendel’s work. Bioscene, 27(2), 13–24.
Morgan, T H, Sturtevant, A. H., Muller, H. J., & Bridges, C. B. (1972). The Mechanism of Mendelian Heredity (1915). New York.
Morgan, Thomas Hunt. (1915). The mechanism of Mendelian heredity. Holt.
Morgan, Thomas Hunt. (1916). A Critique of the Theory of Evolution. Princeton University Press.
Morgan, Thomas Hunt. (1919a). The genetic and the operative evidence relating to secondary sexual characters. Carnegie Institution of Washington.
Morgan, Thomas Hunt. (1919b). The physical basis of heredity. JB Lippincott.
Morgan, Thomas Hunt, & Bridges, C. B. (1916). Sex-linked inheritance in Drosophila. Carnegie institution of Washington.
Müller-Wille, S. (2007). Hybrids, pure cultures, and pure lines: from nineteenth-century biology to twentieth-century genetics. Studies in History and Philosophy of Science Part C: Studies in History and Philosophy of Biological and Biomedical Sciences, 38(4), 796–806.
Naik, P. P., & Farrukh, S. N. (2022). Influence of ethnicities and skin color variations in different populations-A Review. Skin Pharmacology and Physiology, 1.
Naville, M., Warren, I. A., Haftek-Terreau, Z., Chalopin, D., Brunet, F., Levin, P., … Volff, J.-N. (2016). Not so bad after all: retroviruses and long terminal repeat retrotransposons as a source of new genes in vertebrates. Clinical Microbiology and Infection, 22(4), 312–323.
Niklas, K. J. (1997). The evolutionary biology of plants. University of Chicago Press.
Nussbaum, R. L., McInnes, R. R., Willard, H. F., & Hamosh, A. (2007). Thompson & Thompson, Genetics in Medicine (7th ed.). Saunders, Elsevier.
Olby, R. (1979). Mendel no mendelian? History of Science, 17(1), 53–72.
Olesko, K. M. (2006). The Century of Science. A Companion to Nineteenth-Century Europe, 1789-1914, 333–344.
Onaga, L. (2010). Toyama Kametaro and Vernon Kellogg: Silkworm Inheritance Experiments in Japan, Siam, and the United States, 1900–1912. Journal of the History of Biology, 43(2), 215–264.
Paigen, K. (2003). One hundred years of mouse genetics: an intellectual history. I. The classical period (1902-1980). Genetics, 163(1), 1–7.
Pereira, R., Halford, K., Sokolov, B. P., Khillan, J. S., & Prockop, D. J. (1994). Phenotypic variability and incomplete penetrance of spontaneous fractures in an inbred strain of transgenic mice expressing a mutated collagen gene (COL1A1). The Journal of Clinical Investigation, 93(4), 1765–1769.
Pezaro, N., Doody, J. S., & Thompson, M. B. (2017). The ecology and evolution of temperature‐dependent reaction norms for sex determination in reptiles: a mechanistic conceptual model. Biological Reviews, 92(3), 1348–1364.
Pflanze, O. (2014). Bismarck and the Development of Germany, Volume II: The Period of Consolidation, 1871-1880 (Vol. 2). Princeton University Press.
Pickstone, J. V. (1973). Globules and coagula: Concepts of tissue formation in the early nineteenth century. Journal of the History of Medicine and Allied Sciences, 28(4), 336–356.
Pierce, B. A. (2005). Genetics, a Conceptual Aproach (2nd ed.). USA: Freeman.
Pierce, B. A. (2008). Genetics, a Conceptual Aproach (3rd ed.). USA: Freeman.
Pierce, B. A. (2012). Genetics, a Conceptual Aproach (4th ed.). USA: Freeman.
Pigliucci, M. (2009). An extended synthesis for evolutionary biology. Annals of the New York Academy of Sciences, 1168(1), 218–228.
Pilgrim, I. (1986). A solution to the too-good-to-be-true paradox and Gregor Mendel. Journal of Heredity, 77(3), 218–220.
Pires, A. M., & Branco, J. A. (2010). A Statistical Model to Explain the Mendel—Fisher Controversy. Statistical Science, 545–565.
Plackett, R. L. (1983). Karl Pearson and the chi-squared test. International Statistical Review/Revue Internationale de Statistique, 59–72.
Preus, A. (1977). Galen’s criticism of Aristotle’s conception theory. Journal of the History of Biology, 10(1), 65–85.
Punnett, Reginald C. (1923). Linkage in the sweet pea (Lathyrus odoratus). Journal of Genetics, 13(1), 101–123.
Punnett, Reginald Crundall. (1905). Mendelism. London: Cosimo, Inc. Macmillan “original”.
Punnett, Reginald Crundall. (1927). Linkage groups and chromosome number in Lathyrus. Proc. R. Soc. Lond. B, 102(716), 236–238.
Reed, M. (1997). Algebraic structure of genetic inheritance. Bulletin of the American Mathematical Society, 34(2), 107–130.
Resta, R. G. (1993). The crane’s foot: the rise of the pedigree in human genetics. Journal of Genetic Counseling, 2(4), 235–260.
Rheinberger, Hans-Jorg. (1995). When did Carl Correns read Gregor Mendel’s paper? A research note. Isis, 86(4), 612–616.
Rheinberger, Hans-Jörg. (2000). Mendelian inheritance in Germany between 1900 and 1910. The case of Carl Correns (1864–1933). Comptes Rendus de l’Académie Des Sciences-Series III-Sciences de La Vie, 323(12), 1089–1096.
Rice, W R, & Chippindale, A. K. (2001). Intersexual ontogenetic conflict. Journal of Evolutionary Biology, 14(5), 685–693.
Rice, William R, & Chippindale, A. K. (2001). Sexual recombination and the power of natural selection. Science, 294(5542), 555–559.
Rivas Mosquera, J. (n.d.). Desarrollo de una unidad didáctica del tema cruces monohíbridos de las leyes de Mendel soportada por TIC para grado octavo: estudio de caso en la Institución Educativa Fe y Alegría Popular No1, de la ciudad de Medellín. Universidad Nacional de Colombia-Sede Medellín.
Rogaev, E. I., Grigorenko, A. P., Moliaka, Y. K., Faskhutdinova, G., Goltsov, A., Lahti, A., … Morozova, I. (2009). Genomic identification in the historical case of the Nicholas II royal family. Proceedings of the National Academy of Sciences, 106(13), 5258–5263.
Sadava, D., Berenbaum, M., & Hillis, D. (2014). Life the Science of Biology (10th ed.). Sinauer & MacMillian.
Sadava, D., Hillis, D., Heller, C., & Berenbaum, M. (2011). Life: The Science of Biology (9th ed.). USA: Sinauer & Freeman.
Saito, T., Nishii, Y., Yasuda, T., Ito, N., Suzuki, H., Igarashi, T., … Fujita, T. (2009). Familial hypophosphatemic rickets caused by a large deletion in PHEX gene. European Journal of Endocrinology, 161(4), 647–651.
Sarkar, S. (2004). Evolutionary theory in the 1920s: the nature of the “synthesis.” Philosophy of Science, 71(5), 1215–1226.
Schwarz-Sommer, Z., Davies, B., & Hudson, A. (2003). An everlasting pioneer: the story of Antirrhinum research. Nature Reviews Genetics, 4(8), 655.
Shourie, A. (2021). Unit-2 Extension & Modifications of Mendelian Genetic Analysis-I. Indira Gandhi National Open University, New Delhi.
Solomon, E. P., Berg, L. R., & Martin, D. W. (2008). Biology 8th edition. Thomsom Brooks/Cole, USA.
Stearns, F. W. (2010). One hundred years of pleiotropy: a retrospective. Genetics, 186(3), 767–773.
Stracham, T., & Read, A. (2010). Human Molecular Genetics (4th ed.). Garland Science.
Stubbe, H. (1972). History of genetics: from prehistoric times to the rediscovery of Mendel’s laws.
Sturtevant, A. H. (1965). AHistory of Genetics. Harper&Row, NewYork.
Sutton, W. S. (1902). On the morphology of the chromoso group in brachystola magna. The Biological Bulletin, 4(1), 24–39.
Sutton, W. S. (1903). The chromosomes in heredity. The Biological Bulletin, 4(5), 231–250.
Tarpy, D. R., & Page, R. E. (2002). Sex determination and the evolution of polyandry in honey bees (Apis mellifera). Behavioral Ecology and Sociobiology, 52(2), 143–150.
Teicher, A. (2014). Mendel’s use of mathematical modelling: ratios, predictions and the appeal to tradition. History and Philosophy of the Life Sciences, 36(2), 187–208.
Tubbs, R. S., Ditty, B., Bosmia, A. N., & Bosmia, A. N. (2015). Ischiopagus and Diprosopus in India: Two Pairs of Conjoined Twins Perceived as Incarnations of Hindu Deities. Journal of Religion and Health, 54(1), 87–92.
Van Melsen, A. G. (2004). From atomos to atom: The history of the concept atom. Courier Dover Publications.
von Schwerin, A. (n.d.). Seeing, Breeding and the Organisation of Variation: Erwin Baur and the Culture of Mutations in the 1920s. A Cultural History of Heredity IV: Heredity in the Century of the Gene, 259.
Whaley, L. A. (2003). Women’s history as scientists: a guide to the debates. ABC-CLIO.
Williams, N. (2003). Speaking volumes. Current Biology, 13(20), R789–R790.
Williams, N. (2005). Darwin on the web. Current Biology, 15(14), R530.
Wilson, E. B. (1905). The chromosomes in relation to the determination of sex in insects. Science, 22(564), 500–502.
Winther, R. G. (2001). August Weismann on germ-plasm variation. Journal of the History of Biology, 34(3), 517–555.
Zacharias, H. (2001). Key word: chromosome. Chromosome Research, 9(5), 345–355.
Ejercicios resueltos
|| REGRESAR AL INDICE ||
Demostraciones
DEMOSTRACIÓN. Factorizar todos los casos del cruce monohíbrido empleando el cuadro de Punnett.
DEMOSTRACIÓN. Factorizar todos los casos del cruce monohíbrido empleando técnicas de factorización.
DEMOSTRACIÓN. Programar una calculadora del cruce monohíbrido en Excel empleando las ecuaciones de la expansión factorial.
DEMOSTRACIÓN. Programar una calculadora del cruce dihíbrido en Excel empleando las ecuaciones de la expansión factorial.
DEMOSTRACIÓN: Crear una calculadora de Excel para el cruce de dominancia incompleta.
DEMOSTRACIÓN: Programar una calculadora en Excel para la codominancia en un monohíbrido de dos alelos.
DEMOSTRACIÓN: Programar una calculadora en Excel para el sistema de tipos de sangre AB0.
DEMOSTRACIÓN: Programar una calculadora en Excel para la herencia letal recesiva/dominante ligada al cromosoma X.
DEMOSTRACION: Programar una calculadora en Excel para la epistasis “de duplicación recesiva” en un cruce de dos dobles heterocigotos
Propios
Ejemplo. Cuente los siguientes objetos y exprese su valor como un parámetro matemático.
Ejemplo. Cuente los siguientes objetos y exprese su valor como un parámetro matemático.
Ejemplo. Cuente los siguientes objetos y exprese su valor como un parámetro matemático.
Ejemplo. Cuente los siguientes objetos y exprese su valor como un parámetro matemático.
Ejemplo. Determine la frecuencia o probabilidad experimental mediante la siguiente figura.
Ejemplo. Determine la frecuencia o probabilidad experimental mediante la siguiente figura.
Ejemplo. Determine la frecuencia o probabilidad experimental mediante la siguiente figura.
Ejemplo. Convierta los siguientes porcentajes a frecuencias: 75 % 25 % 33 % 50 %.
Ejemplo. Convierta la siguiente frecuencia relativa a porcentaje: 2/4, 2/8, 6/8, 4/6, 2/6, 4/16.
Ejemplo. ¿Cuál es la probabilidad de que al arrojar dos dados de 4 caras ideales me aparezca un doble III?
Ejemplo. ¿Cuál es la probabilidad de que al arrojar tres dados de 6 caras ideales me aparezca un triple VI?
Ejemplo. Si la probabilidad de un dado ideal para la cara II es de 1/4, y además lo lanzara unas 60 veces, ¿Cuál sería el número de veces que debería aparecer el número II?
Ejemplo. Resolver el cruce mendeliano AaBb por AaBb con el cuadro de Punnett.
Ejemplo. Resolver el cruce mendeliano AaBb por AaBb con la factorización algebraica.
Ejemplo. Cuales son todos los fenotipos posibles de un cruce dihíbrido con distribución independiente
Ejemplo. Cuantos genotipos posibles pueden generarse en un sistema de dos genes y dos alelos.
Ejemplo. Cuantos genotipos posibles pueden generarse en un sistema de tres genes y dos alelos.
Manual de problemas y casos prácticos de genética

















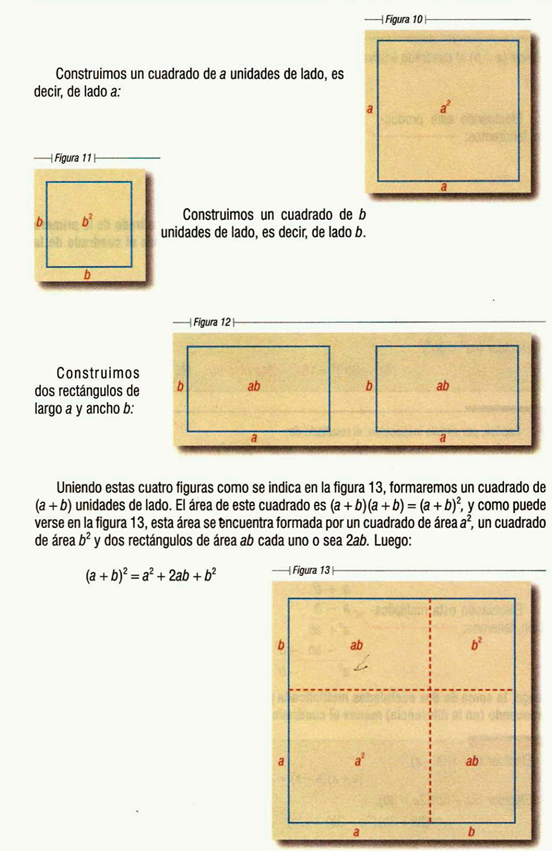





















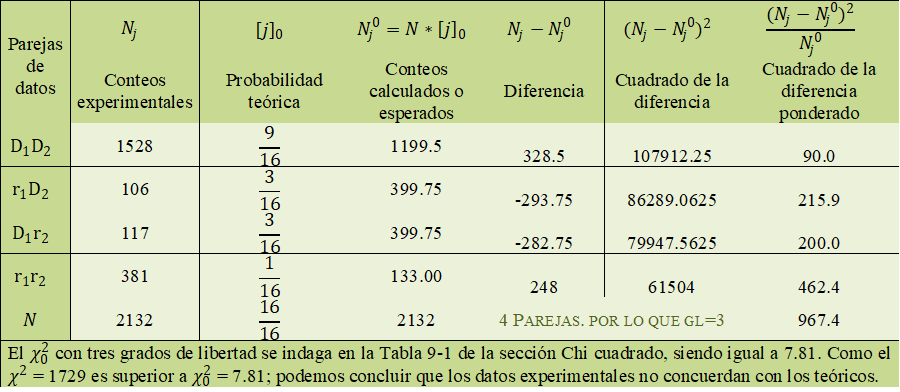









































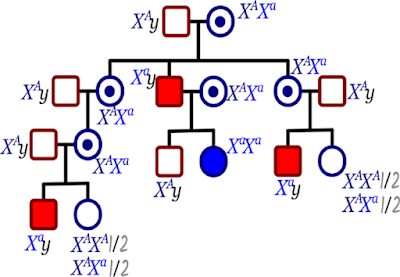


No hay comentarios:
Publicar un comentario