Teorema. Cambio de energía interna de una reacción de gases a presión constante

[Demostración] El teorema del cambio de energía interna, en el contexto de reacciones químicas, ofrece una perspectiva unificada para comprender cómo el calor y el trabajo influyen en la energía de un sistema. Este teorema postula que el cambio de energía interna (ΔU) de una reacción se puede expresar como una función de la cantidad de reacción (ξ), un parámetro que mide el progreso de la reacción, y de los parámetros de calor y trabajo asociados a esta. Dado que la cantidad de reacción (ξ) es inherentemente común tanto al calor de reacción (Q) como al trabajo de reacción (W), se convierte en un factor común en la ecuación que describe ΔU. En este contexto, la cantidad de reacción se define como el ratio entre la masa de la sustancia clave (generalmente el reactante limitante) y el producto de su número estequiométrico (considerado como una magnitud, es decir, sin signo en este cálculo inicial) y su masa molar. La formulación de este teorema busca simplificar y optimizar los cálculos termodinámicos, evitando las redundancias que a menudo se encuentran en aproximaciones más clásicas.

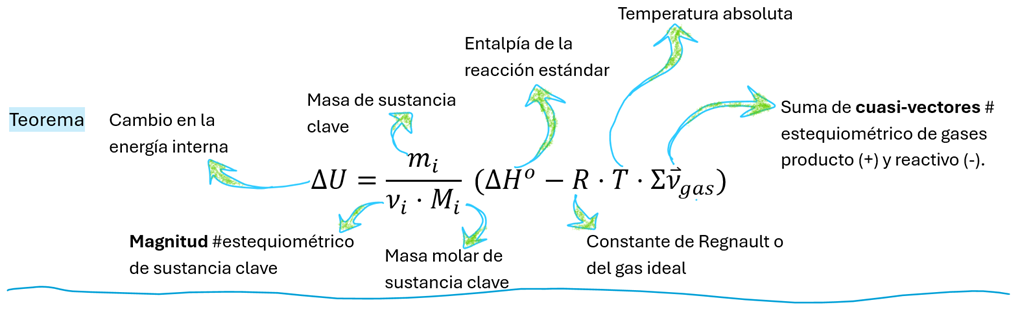
Dentro de la expresión matemática del teorema, los términos de calor y trabajo se ponderan por esta cantidad de reacción. De manera más específica, el teorema integra la entalpía de reacción estándar (ΔH°) y un término que considera la expansión o contracción de los gases durante la reacción, el cual se relaciona con RT (constante de los gases ideales por temperatura absoluta) y la suma de los números estequiométricos de los gases. Es en esta suma de números estequiométricos de gases donde se utiliza un lenguaje "cuasivectorial": los números estequiométricos de los gases producto se consideran positivos, indicando su formación, mientras que los de los gases reactivos se consideran negativos, señalando su consumo. Esta convención de signos es crucial para reflejar correctamente la dirección del cambio de volumen y, por ende, el trabajo asociado a la expansión o compresión de gases.

Este teorema representa una herramienta poderosa que resume varios pasos de cálculo complejos en una única expresión concisa. Al integrar de forma elegante la entalpía de reacción estándar, el trabajo de expansión/contracción de gases y la cantidad de reacción, se evitan los cálculos redundantes que surgen al aplicar aproximaciones más clásicas. Su formulación permite una comprensión más directa y una determinación más eficiente del cambio de energía interna en procesos químicos, facilitando la modelización y el análisis de sistemas reaccionantes con precisión termodinámica. En esencia, optimiza el proceso de cálculo al combinar información que de otro modo requeriría múltiples pasos y consideraciones separadas.

Contrariamente, el lenguaje del factor de conversión, si bien es una herramienta fundamental en los cálculos estequiométricos y dimensionales, impide crear una forma homóloga tan compacta y unificada para este teorema. Su naturaleza paso a paso, donde cada unidad debe ser transformada explícitamente y cada magnitud calculada de forma individual, resulta en una extensión operativa que no permite la condensación conceptual de una única ecuación. Por lo tanto, mientras el enfoque por teoremas ofrece una visión global y un cálculo directo, el método de los factores de conversión requiere que el problema se resuelva en pasos secuenciales y detallados.