Figura. Fracción molar y la probabilidad

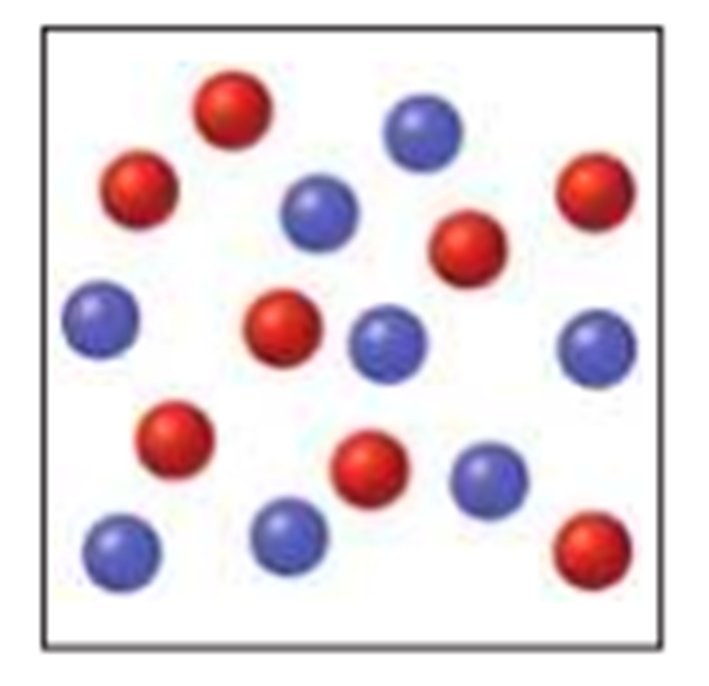
En este modelo de esferas, contamos con 8 entidades rojas y 8 entidades azules, lo que nos da un total de 16 entidades. Es importante recordar que el valor total se considera independiente de las identidades individuales, lo cual significa que lo relevante es el número total de entidades presentes, sin importar su color o naturaleza. Para calcular la fracción molar, simplemente se toma el cociente entre el número de entidades de un tipo y el número total. En este caso, la fracción molar de esferas rojas es 8 /16 = 0.5 y lo mismo ocurre con las azules.

Este mismo modelo se utiliza con frecuencia en la enseñanza de la probabilidad elemental, debido a que el razonamiento detrás de ambas nociones es análogo. Si consideramos que cada esfera representa una partícula indistinguible en términos de masa o volumen, pero distinguible por su "identidad" (como el color, el tipo de átomo, o el compuesto), entonces elegir una esfera al azar equivale a hacer un experimento probabilístico. Así, la probabilidad de extraer una esfera roja es simplemente la fracción de esferas rojas en el total, que coincide exactamente con su fracción molar.

La analogía permite construir un puente entre la química cuantitativa y el razonamiento estadístico, particularmente útil cuando se trabaja con modelos moleculares simplificados como los que se representan con esferas tipo Dalton. En este sentido, la fracción molar puede interpretarse como la probabilidad de seleccionar al azar una partícula de una sustancia dada, dentro de un conjunto definido. Este enfoque resulta poderoso tanto para la comprensión de mezclas ideales como para establecer conexiones intuitivas entre conceptos físicos y matemáticos que subyacen a la química.