Índice
||1|| Introducción ||2|| El concepto de fuerza ||3|| La fuerza de gravedad ||4|| Historia ||5|| Controversias ||6|| La fuerza ||7|| Diagrama de cuerpo libre ||8|| La primera ley ||9|| Masa ||10|| La segunda ley | ||11|| La fuerza peso ||12|| La tercera ley ||13|| La normal ||14|| La fuerza elástica ||15|| La fuerza tensión ||16|| Las fuerzas fricción ||17|| La fuerza de arrastre ||18|| La fuerza centrípeta ||R|| Referencias ||E|| Ejercicios resueltos |
Portada
1. Introducción
|| REGRESAR AL ÍNDICE ||
El movimiento llama nuestra atención. El movimiento en sí mismo puede ser hermoso, haciéndonos maravillarnos de las fuerzas necesarias para lograr un movimiento espectacular, como el de un delfín que salta fuera del agua, o un saltador de pértiga, o el vuelo de un pájaro, o la órbita de un satélite. El estudio del movimiento es la cinemática, pero la cinemática solo describe la forma en que se mueven los objetos: su velocidad, posición, desplazamiento, distancia y aceleración. La dinámica considera las fuerzas que afectan el movimiento de objetos y sistemas en movimiento. Las leyes del movimiento de Newton son la base de la dinámica. Estas leyes proporcionan un ejemplo de la amplitud y simplicidad de los principios bajo los cuales funciona la naturaleza. También son leyes universales en el sentido de que se aplican a situaciones similares tanto en la Tierra como en el espacio (OpenStax, 2017).
1.1 Isaac Newton (1642-1727)
Fue un físico, matemático y astrónomo inglés que es conocido por sus contribuciones fundamentales a la física y la astronomía, incluyendo sus tres leyes del movimiento.
👉 Sus aportes
En 1687, publicó su obra principal, Philosophiæ Naturalis Principia Mathematica (Principios Matemáticos de la Filosofía Natural), en la que formuló las tres leyes del movimiento.
(a) La primera ley, también conocida como la Ley de la Inercia, establece que un objeto en reposo permanecerá en reposo y un objeto en movimiento continuará moviéndose con velocidad constante en línea recta a menos que actúe sobre él una fuerza externa.
(b) La segunda ley, también conocida como la Ley de Fuerza y Aceleración, establece que la fuerza neta que actúa sobre un objeto es igual a su masa multiplicada por su aceleración. Esta ley establece la relación entre la fuerza aplicada sobre un objeto y su movimiento.
(c) Finalmente, la tercera ley, conocida como la Ley de Acción y Reacción, establece que por cada acción hay una reacción igual y opuesta. Esta ley establece que todas las fuerzas vienen en pares y que cuando un objeto ejerce una fuerza sobre otro objeto, el segundo objeto ejerce una fuerza igual y opuesta sobre el primero.
Estas leyes del movimiento de Newton son consideradas fundamentales para la física y han sido esenciales en el desarrollo de la tecnología moderna. Además, Newton también hizo importantes contribuciones en otros campos de la física, como la óptica y la ley de la gravitación universal, que explicaba la relación entre la masa de dos objetos y la fuerza gravitacional que actúa entre ellos.
👉 Su infancia
La infancia de Isaac Newton no fue fácil. Nació en 1642 en Inglaterra, en una época en la que la educación formal no era accesible para todos. Sus padres eran granjeros y no podían pagar una educación escolar para él, así que su madre le enseñó a leer y escribir en casa. Newton mostró habilidades matemáticas y mecánicas desde una edad temprana, y a los 14 años, fue enviado a la escuela King's School en Grantham, donde mostró ser un estudiante brillante. Después de graduarse, Newton ingresó en la Universidad de Cambridge para estudiar matemáticas y física. Sin embargo, la vida universitaria no fue fácil para Newton, ya que tuvo que trabajar duro para pagar sus estudios y también lidiar con la falta de apoyo emocional de su familia. A pesar de los obstáculos, Newton perseveró y comenzó a hacer importantes contribuciones a la ciencia, incluyendo sus leyes del movimiento.
👉 Sus amistades
Newton tuvo algunos amigos cercanos, aunque no se le consideraba una persona muy sociable. Uno de sus amigos más cercanos fue el filósofo y teólogo John Locke, con quien mantuvo correspondencia durante muchos años. También era amigo del matemático y astrónomo Edmond Halley, quien más tarde sería el que publicaría la obra más importante de Newton, los Principia Mathematica. Además, Newton también tenía una amistad con el matemático y filósofo Nicolas Fatio de Duillier, con quien trabajó en una teoría de la gravitación alternativa a la suya propia, aunque esta colaboración terminó en un conflicto. También mantuvo una relación amistosa con la matemática y filósofa Anne Conway, con quien discutió sobre temas filosóficos y religiosos. En general, aunque Newton no era conocido por ser un gran amigo o tener una vida social activa, sí tuvo algunas amistades cercanas y colaboradores importantes en su vida.
La relación de Newton con el astrónomo Edmond Halley fue muy importante para el desarrollo de las leyes del movimiento. Halley visitó a Newton en 1684 y le preguntó acerca de la forma en que los planetas se movían alrededor del Sol. Newton le explicó su teoría de la gravedad y le comentó que estaba trabajando en un libro que explicaría las leyes del movimiento. Halley quedó impresionado por las ideas de Newton y le instó a publicar su trabajo. En 1687, Newton publicó su libro "Philosophiæ Naturalis Principia Mathematica" (Principios Matemáticos de la Filosofía Natural), en el que explicaba las tres leyes del movimiento y la ley de la gravitación universal. Halley fue fundamental para la publicación del libro, ya que lo financió y promovió su distribución entre los científicos y filósofos de la época. La relación de Newton con Halley fue importante porque Halley no solo ayudó a Newton a publicar sus ideas, sino que también le apoyó y le inspiró a seguir trabajando en la física y la astronomía. Además, Halley fue uno de los primeros científicos que comprendió la importancia y el alcance de las ideas de Newton, y contribuyó a difundirlas y popularizarlas entre la comunidad científica y el público en general.
👉 Enemigos
Isaac Newton tuvo varios enemigos y rivales durante su vida, y las razones de estas enemistades pueden variar dependiendo de cada caso. A continuación, se mencionan algunos ejemplos:
(a) Robert Hooke: Hooke fue un científico y matemático que también hizo importantes contribuciones a la física y la óptica. Hooke y Newton tuvieron una relación tensa debido a una disputa sobre la autoría de algunas ideas sobre la ley de la gravitación. Hooke afirmó que había desarrollado la teoría antes que Newton y sugirió que Newton le había plagiado. Esto llevó a una disputa pública entre los dos científicos, y aunque Newton finalmente fue reconocido como el autor original de la teoría, la relación entre ambos quedó dañada.
(b) Gottfried Wilhelm Leibniz: Leibniz fue un filósofo y matemático que también desarrolló el cálculo diferencial e integral, al igual que Newton. Hubo una disputa sobre quién había desarrollado el cálculo primero, lo que llevó a una controversia conocida como la "querella del cálculo". Newton acusó a Leibniz de plagio y trató de desacreditarlo públicamente. La disputa fue larga y amarga, y aunque se llegó a un acuerdo para poner fin a ella, la enemistad entre Newton y Leibniz continuó durante años.
(c) John Flamsteed: Flamsteed fue un astrónomo real y uno de los principales astrónomos de la época de Newton. Newton estaba interesado en utilizar los datos de Flamsteed para sus propias investigaciones, pero Flamsteed se negó a compartir sus observaciones debido a una desconfianza hacia Newton. Esto llevó a una disputa entre ambos, y Newton finalmente recibió los datos de Flamsteed solo después de que este muriera.
En general, Newton tuvo varias enemistades y conflictos con otros científicos y filósofos de su época, debido a disputas sobre la autoría de ideas y teorías, desacuerdos sobre metodologías y enfoques científicos, y diferencias personales y profesionales.
👉 Caballero del rey
Newton fue nombrado caballero en 1705 por la reina Ana de Inglaterra, en reconocimiento a sus servicios como científico y funcionario público. El título de caballero no es un título de nobleza, sino un título honorífico que se otorga en el Reino Unido por distinción en diversos campos. Newton también fue miembro de la Royal Society y fue elegido presidente de la misma en 1703, lo que le otorgó un gran prestigio en el mundo científico de la época. Además, fue nombrado miembro del Parlamento británico en 1689 y sirvió como director de la Casa de la Moneda de Inglaterra durante 30 años, lo que lo convirtió en una figura influyente en la política y la economía de su país. Sin embargo, no recibió ningún otro título de nobleza aparte del de caballero.
👉 Legado
Isaac Newton es considerado uno de los científicos más influyentes de la historia. Su trabajo en la física y las matemáticas sentó las bases para muchas áreas de la ciencia moderna y su legado continúa siendo relevante en la actualidad. Algunos de los principales legados de Newton son los siguientes:
(a) Leyes del movimiento: Newton desarrolló tres leyes del movimiento que explican cómo los objetos se mueven y cómo se relacionan entre sí.
(b) Ley de gravitación universal: Newton descubrió que la fuerza de la gravedad actúa entre todos los objetos en el universo, y que esta fuerza es proporcional a la masa de los objetos y inversamente proporcional al cuadrado de la distancia entre ellos.
(c) Cálculo: Newton también es conocido por su trabajo en el cálculo, una rama de las matemáticas que se utiliza para calcular las tasas de cambio y las áreas bajo curvas.
(d) Óptica: Newton realizó importantes avances en el estudio de la luz y la óptica, incluyendo la descripción de la descomposición de la luz blanca en colores del espectro.
(e) Método científico: La metodología científica rigurosa que Newton empleó en sus investigaciones sentó las bases para el desarrollo de la ciencia moderna.
En resumen, el legado de Newton abarca muchos campos de la ciencia y las matemáticas, y su trabajo sigue siendo relevante en la actualidad.
Tomado de : (Gianopoulos, 2007).
2. El concepto de fuerza
|| REGRESAR AL ÍNDICE ||
Todo el mundo tiene una comprensión básica del concepto de fuerza a partir de la experiencia cotidiana. Cuando empujas tu plato vacío, ejerces una fuerza sobre él. De manera similar, ejerces una fuerza sobre una pelota cuando la lanzas o la pateas. En estos ejemplos, la palabra fuerza se refiere a una interacción con un objeto por medio de la actividad muscular y algún cambio en la velocidad del objeto. Sin embargo, las fuerzas no siempre causan movimiento. Por ejemplo, cuando estás sentado, una fuerza gravitatoria actúa sobre tu cuerpo y, sin embargo, permaneces estacionario. Como segundo ejemplo, puedes empujar (en otras palabras, ejercer una fuerza) sobre una roca grande y no poder moverla.
¿Qué fuerza (si la hay) hace que la Luna gire alrededor de la Tierra? Newton respondió a esta y otras preguntas relacionadas al afirmar que las fuerzas son las que causan cualquier cambio en la velocidad de un objeto.
(a) La velocidad de la Luna cambia de dirección a medida que se mueve en una órbita casi circular alrededor de la Tierra. Este cambio de velocidad es causado por la fuerza gravitatoria que ejerce la Tierra sobre la Luna. Cuando se tira de un resorte en espiral, como en la Figura. 2.1a, el resorte se estira.
(b) Cuando se tira de un carro estacionario, como en la figura Figura. 2.1b, el carro se mueve.
(c) Cuando se patea una pelota de fútbol, como en la figura Figura. 2.1c, se deforma y se pone en movimiento.
Figura. 2.1. Algunos ejemplos de fuerzas aplicadas. En cada caso, se ejerce una fuerza sobre el objeto dentro del área encuadrada. Algún agente en el entorno externo al área encuadrada ejerce una fuerza sobre el objeto.
2.1 Fuerzas de contacto
Todas estas situaciones son ejemplos de una clase de fuerzas llamadas fuerzas de contacto. Es decir, implican el contacto físico entre dos objetos. Otros ejemplos de fuerzas de contacto son la fuerza que ejercen las moléculas de gas sobre las paredes de un recipiente y la fuerza que ejercen los pies sobre el suelo.
2.2 Fuerzas de campo
Otra clase de fuerzas, conocidas como fuerzas de campo, no involucra contacto físico entre dos objetos. Estas fuerzas actúan a través del espacio vacío.
(a) La fuerza de atracción gravitatoria entre dos objetos con masa, ilustrada en la Figura. 2.1d, es un ejemplo de esta clase de fuerza. La fuerza gravitacional mantiene los objetos unidos a la Tierra y los planetas en órbita alrededor del Sol.
(b) Otra fuerza de campo común es la fuerza eléctrica que una carga eléctrica ejerce sobre otra (Figura. 2.1e), como la fuerza eléctrica de atracción entre un electrón y un protón que forman un átomo de hidrógeno.
(c) Un tercer ejemplo de fuerza de campo es la fuerza magnética que ejerce un imán de barra sobre una pieza de hierro (Figura. 2.1f).
2.3 Ambigüedades
La distinción entre las fuerzas de contacto y las fuerzas de campo no es tan clara como la discusión anterior le ha hecho creer. Cuando se examinan a nivel atómico, todas las fuerzas que clasificamos como fuerzas de contacto resultan ser causadas por fuerzas (de campo) eléctricas del tipo ilustrado en la figura Figura. 2.1e.
Sin embargo, al desarrollar modelos para fenómenos macroscópicos, es conveniente utilizar ambas clasificaciones de fuerzas.
2.4 Las fuerzas fundamentales del universo
Las únicas fuerzas fundamentales conocidas en la naturaleza son todas las fuerzas de campo:
(a) fuerzas gravitacionales entre objetos,
(b) fuerzas electromagnéticas entre cargas eléctricas,
(c) fuerzas fuertes entre partículas subatómicas y
(d) fuerzas débiles que surgen en ciertas desintegraciones radiactivas. procesos.
Estas fuerzas son llamadas fundamentales porque no se han encontrado evidencias de que sean el resultado de alguna otra fuerza más básica. Se cree que todas las interacciones físicas pueden ser explicadas por la acción de estas cuatro fuerzas, y que todas las demás fuerzas son una combinación o una manifestación de estas cuatro (Griffiths, 2020).
El estudio de estas fuerzas fundamentales es uno de los principales objetivos de la física teórica moderna y se espera que la comprensión más profunda de ellas pueda llevar a importantes avances en la comprensión del universo y la tecnología (Griffiths, 2020).
2.5 Posibilidades futuras
Una mayor comprensión de las cuatro fuerzas fundamentales de la naturaleza podría llevar a importantes avances en diversas áreas de la tecnología (Tegmark, 2015), incluyendo:
(a) Energía: La comprensión de las fuerzas fundamentales puede llevar al desarrollo de nuevas tecnologías de energía, como la fusión nuclear, que utiliza la fuerza nuclear fuerte para producir energía.
(b) Materiales: La comprensión de las fuerzas fundamentales puede permitir una revolución en la ciencia de la química con el desarrollo de nuevos materiales y técnicas de fabricación, utilizando la fuerza electromagnética y la fuerza nuclear para controlar y manipular la estructura de los materiales.
(c) Comunicaciones: La comprensión de las fuerzas fundamentales puede mejorar las comunicaciones, como la tecnología de comunicación cuántica, que utiliza las propiedades de la física cuántica para garantizar la seguridad en las transmisiones de datos gracias al principio de incertidumbre.
(d) Medicina: La comprensión de las fuerzas fundamentales puede mejorar la tecnología médica, como la terapia de protones, que utiliza la fuerza electromagnética para tratar el cáncer.
(e) Computación: La comprensión de las fuerzas fundamentales puede llevar a la computación cuántica, que utiliza las propiedades cuánticas de la materia y la fuerza electromagnética para procesar información de manera más rápida y eficiente.
En general, una mayor comprensión de las fuerzas fundamentales puede conducir a avances significativos en una amplia gama de campos tecnológicos y científicos, lo que podría mejorar significativamente la calidad de vida humana. Sin embargo, los novatos deberán conformarse de momento con lo que en la física clásica denominados gravitación.
3. La fuerza de gravedad
|| REGRESAR AL ÍNDICE ||
En física, la gravedad (del latín gravitas 'peso') es
la atracción mutua entre todas las masas del universo,
también conocida como atracción gravitatoria. La gravedad es la atracción gravitacional en la superficie de un planeta u otro cuerpo celeste. Matemáticamente los principales parámetros que afectan a la gravedad son la masa de dos objetos y la distancia que los separa y por ende esos parámetros se encuentran contenidos en su definición matemática, a parte de una constante de proporcionalidad.
3.1 Importancia nivel molecular
La gravedad es, con mucho, la más débil de las cuatro interacciones fundamentales, aproximadamente 1038 veces más débil que la interacción fuerte, 1036 veces más débil que la fuerza electromagnética y 1029 veces más débil que la interacción débil. Como resultado, no tiene una influencia significativa a nivel de partículas subatómicas (Krebs, 1999).
3.2 Importancia macroscópica
Sin embargo, la gravedad es la interacción más importante entre los objetos a escala macroscópica y determina el movimiento de los planetas, las estrellas, las galaxias e incluso la luz.
En la Tierra, la gravedad da peso a los objetos físicos, y la gravedad de la Luna es responsable de las mareas sublunares en los océanos (la marea antípoda correspondiente es causada por la inercia de la Tierra y la Luna orbitando entre sí).
Figura. 3.1. La atracción gravitatoria es bidireccional, sin embargo, un objeto pequeño como el cuerpo humano no posee suficiente masa como para atraer objetos gravitatoriamente. La luna por otro lado si tiene el suficiente empuje como para atraer la masa oceánica.
3.3 Efectos en los seres vivos
La gravedad también tiene muchas funciones biológicas importantes, ya que ayuda a guiar el crecimiento de las plantas a través del proceso de gravitropismo e influye en la circulación de fluidos en los organismos multicelulares (Sathasivam, Hosamani, & Swamy, 2021; Vandenbrink & Kiss, 2019). La investigación sobre los efectos de la ingravidez ha demostrado que la gravedad puede desempeñar un papel en la función del sistema inmunológico y la diferenciación celular dentro del cuerpo humano (Blaber et al., 2015; Green, Aylott, Williams, Ghaemmaghami, & Williams, 2021; Ruden et al., 2018; Zayzafoon, Meyers, & McDonald, 2005).
3.4 Importancia en la historia del universo
La atracción gravitacional entre la materia gaseosa original del universo permitió que se fusionara y formara estrellas que finalmente se condensaron en galaxias, por lo que la gravedad es responsable de muchas de las estructuras a gran escala del universo. La gravedad tiene un alcance infinito, aunque sus efectos se debilitan a medida que los objetos se alejan.
4. Historia
|| REGRESAR AL ÍNDICE ||
El concepto de gravedad o peso ha sido estudiado y discutido por filósofos, científicos y matemáticos a lo largo de la historia:
(a) Filósofos griegos: Los filósofos griegos como Aristóteles y Demócrito desarrollaron teorías sobre la naturaleza de la materia y la caída de los cuerpos en la Tierra. Según Aristóteles, los cuerpos más pesados caen más rápido que los cuerpos más ligeros, y esta velocidad de caída está relacionada con la proporción de los elementos en el cuerpo.
(b) Galileo Galilei: En el siglo XVI, Galileo realizó una serie de experimentos sobre la caída de los cuerpos, que contradecían la teoría aristotélica. Descubrió que la velocidad de caída de un objeto no depende de su peso, sino de la fuerza gravitacional que actúa sobre él. También desarrolló la idea de que todos los objetos en la Tierra están sujetos a la misma aceleración debido a la gravedad.
(c) Isaac Newton: En el siglo XVII, Newton desarrolló su teoría de la gravitación universal, que explicaba cómo los cuerpos se atraen entre sí debido a la fuerza gravitatoria. Su ley de la gravitación universal establece que la fuerza gravitatoria entre dos objetos es proporcional a sus masas e inversamente proporcional al cuadrado de la distancia entre ellos.
(d) Albert Einstein: En el siglo XX, Einstein propuso su teoría de la relatividad general, que describe cómo la fuerza de la gravedad se relaciona con la curvatura del espacio-tiempo causada por la presencia de materia y energía.
Figura. 4.1. Albert Einstein (1879-1955) fue un físico teórico alemán, considerado uno de los científicos más influyentes del siglo XX. Sus aportaciones a la física incluyen la teoría de la relatividad, la equivalencia masa-energía (plasmada en la famosa fórmula E=mc²) y la explicación del movimiento browniano. Además, recibió el Premio Nobel de Física en 1921 por su explicación del efecto fotoeléctrico. Einstein también tuvo una destacada participación en la defensa de los derechos civiles y la paz mundial.
A lo largo de la historia, el concepto de gravedad o peso se ha estudiado a través de experimentos, observaciones astronómicas y teorías matemáticas complejas. Estas investigaciones han llevado a un mejor entendimiento de la gravedad y su papel en el universo.
4.1 Imagen de los filósofos antiguos
La naturaleza y el mecanismo de la gravedad fueron explorados por una amplia gama de eruditos antiguos.
(a) En Grecia, Aristóteles creía que los objetos caían hacia la Tierra porque la Tierra era el centro del Universo y atraía hacia ella toda la masa del Universo. También pensó que la velocidad de un objeto que cae debería aumentar con su peso, una conclusión que luego se demostró que era falsa (Rovelli, 2015). Si bien el punto de vista de Aristóteles fue ampliamente aceptado en la Antigua Grecia, hubo otros pensadores como Plutarco que predijeron correctamente que la atracción de la gravedad no era exclusiva de la Tierra (Bakker & Palmerino, 2020).
(b) Aunque no entendió la gravedad como una fuerza, el antiguo filósofo griego Arquímedes descubrió el centro de gravedad de un triángulo (Netz & Noel, 2011). También postuló que si dos pesos iguales no tuvieran el mismo centro de gravedad, el centro de gravedad de los dos pesos juntos estaría en el medio de la línea que une sus centros de gravedad (Wolpert, 2002).
(c) Dos siglos más tarde, el ingeniero y arquitecto romano Vitruvio sostuvo en su De architectura que la gravedad no depende del peso de una sustancia sino de su "naturaleza" (Pollio, 1914).
(e) En el siglo VI d. C., el erudito bizantino alejandrino John Philoponus propuso la teoría del ímpetu, que modifica la teoría de Aristóteles de que "la continuación del movimiento depende de la acción continua de una fuerza" al incorporar una fuerza causal que disminuye con el tiempo.
Figura. 4.2. John Philoponus (c. 490 - c. 570) fue un filósofo, teólogo y científico bizantino que realizó importantes contribuciones en la física, la lógica y la teología. Es conocido por su trabajo en la crítica de la filosofía aristotélica y por sus estudios en la caída de los cuerpos en la gravedad terrestre. También se le atribuyen avances en la teoría de la inercia y en la explicación de la formación de las sombras. Philoponus fue un destacado defensor del cristianismo y se desempeñó como presbítero en Constantinopla.
(f) En la India, en el siglo VII EC, Brahmagupta propuso la idea de que la gravedad es una fuerza de atracción que atrae objetos a la Tierra y usó el término gurutvākarṣaṇ para describirla (Pickover, 2008; Sharp & Visual, n.d.).
(g) En el antiguo Medio Oriente, la gravedad era un tema de feroz debate. El intelectual persa Al-Biruni creía que la fuerza de la gravedad no era exclusiva de la Tierra, y asumió correctamente que otros cuerpos celestes también deberían ejercer una atracción gravitatoria (Starr & Buell, 2014).
(h) En contraste, Al-Khazini sostuvo la misma posición que Aristóteles de que toda la materia del Universo es atraída hacia el centro de la Tierra (Rashid, 1996).
4.2 Teoría del ímpetu
La teoría del impetu, también conocida como teoría de la inercia impetuosa, fue desarrollada por el filósofo y físico bizantino John Philoponus (c. 490-570). Esta teoría propone que los cuerpos en movimiento tienen una cierta cantidad de impulso o "impetu" que los mantiene en movimiento (Sarnowsky, 2008).
Según Philoponus, cuando un objeto se mueve, adquiere un impulso que es proporcional a su velocidad y su masa. Este impulso se almacena en el objeto y lo mantiene en movimiento incluso cuando se detiene la fuerza que lo impulsó inicialmente. Philoponus argumentó que este impulso era una propiedad inherente del objeto y no requería la acción continua de una fuerza para mantenerse en movimiento (Sarnowsky, 2008).
La teoría del impetu de Philoponus fue un precursor importante de la ley de inercia de Newton. Aunque la teoría de Philoponus no se basaba en las matemáticas y no era tan completa como la ley de Newton, sentó las bases para la comprensión moderna de la inercia y el movimiento de los cuerpos(Sarnowsky, 2008).
4.3 La revolución científica
A mediados del siglo XVI, varios científicos europeos refutaron experimentalmente la noción aristotélica de que los objetos más pesados caen a un ritmo más rápido
(a) En particular, el sacerdote dominico español Domingo de Soto escribió en 1551 que los cuerpos en caída libre aceleran uniformemente. De Soto puede haber sido influenciado por experimentos anteriores realizados por otros sacerdotes dominicos en Italia, incluidos los de Benedetto Varchi, Francesco Beato, Luca Ghini y Giovan Bellaso, que contradecían las enseñanzas de Aristóteles sobre la caída de los cuerpos (Wallace, 2018).
Figura. 4.3. Domingo de Soto (1494-1560) fue un filósofo y teólogo español del Renacimiento. Nació en Segovia y se formó en la Universidad de Salamanca, donde llegó a ser catedrático de Teología. Es conocido por sus contribuciones al estudio de la lógica y la ética, así como por su defensa de los derechos de los pueblos indígenas de América durante la colonización española. También fue uno de los principales promotores de la Escuela de Salamanca, un grupo de pensadores españoles del siglo XVI que desarrollaron la teoría económica y el derecho internacional modernos.
(b) El físico italiano de mediados del siglo XVI, Giambattista Benedetti, publicó artículos en los que afirmaba que, debido a la gravedad específica, los objetos hechos del mismo material pero con diferentes masas caerían a la misma velocidad (Drabkin, 1963).
(c) Con el experimento de la torre de Delft de 1586, el físico flamenco Simon Stevin observó que dos balas de cañón de diferentes tamaños y pesos caían a la misma velocidad cuando se dejaban caer desde una torre (Schilling, 2017).
(d) Finalmente, a finales del siglo XVI, las cuidadosas mediciones de bolas rodando por pendientes de Galileo Galilei le permitieron establecer firmemente que la aceleración gravitatoria es la misma para todos los objetos. Galileo postuló que la resistencia del aire es la razón por la que los objetos con baja densidad y gran área superficial caen más lentamente en la atmósfera. En 1604, Galileo planteó correctamente la hipótesis de que la distancia de un objeto que cae es proporcional al cuadrado del tiempo transcurrido (Gamow, 2002; Milsom, 2018).
(e) Esto fue confirmado más tarde por los científicos italianos jesuitas Grimaldi y Riccioli entre 1640 y 1650. También calcularon la magnitud de la gravedad de la Tierra midiendo las oscilaciones de un péndulo (Heilbron, 2022).
4.4 La física newtoniana
En 1684, Newton envió un manuscrito a Edmond Halley titulado De motu corporum in gyrum ('Sobre el movimiento de los cuerpos en una órbita'), que proporcionaba una justificación física para las leyes del movimiento planetario de Kepler (Hanich et al., 2014; Sagan, 1997).
Halley quedó impresionado por el manuscrito e instó a Newton a ampliarlo, y unos años más tarde, Newton publicó un libro innovador llamado Philosophiæ Naturalis Principia Mathematica (Principios matemáticos de la filosofía natural). En este libro, Newton describió la gravitación como una fuerza universal y afirmó que "las fuerzas que mantienen a los planetas en sus esferas deben [ser] recíprocamente como los cuadrados de sus distancias desde los centros alrededor de los cuales giran". Esta afirmación se condensó más tarde en Eq. 3.1.
Los Principia de Newton fueron bien recibidos por la comunidad científica, y su ley de la gravitación se extendió rápidamente por todo el mundo europeo (Fellmann, 1988), aunque no sin algunas controversias que analizaremos más adelante.
Figura. 4.4. En una entrevista con el portal de noticias Big Think, Neil deGrasse Tyson dijo que el libro "Principia" de Isaac Newton fue "quizás el libro más importante que se haya escrito en la historia de la ciencia". También elogió la forma en que Newton estableció los fundamentos de la física moderna y sentó las bases de la teoría de la gravitación universal. Sin embargo, también señaló que la obra es conocida por su complejidad matemática, lo que la hace difícil de entender para el público en general.
Más de un siglo después, en 1821, su teoría de la gravitación adquirió una importancia aún mayor cuando se utilizó para predecir la existencia de Neptuno. En ese año, el astrónomo francés Alexis Bouvard usó esta teoría para crear una tabla que modelaba la órbita de Urano, que se demostró que difería significativamente de la trayectoria real del planeta. Para explicar esta discrepancia, muchos astrónomos especularon que podría haber un objeto grande más allá de la órbita de Urano que estaba interrumpiendo su órbita. En 1846, los astrónomos John Couch Adams y Urbain Le Verrier utilizaron de forma independiente la ley de Newton para predecir la ubicación de Neptuno en el cielo nocturno, y el planeta fue descubierto allí en un día (Hanson, 1959; Sheehan, 2021).
4.5 Una crisis
Aunque el descubrimiento de Neptuno fue un gran triunfo para la teoría newtoniana de la gravedad, eventualmente se descubrieron casos en los cuales su modelo era incapaz de describir un fenómeno natural excelentemente medido, lo cual adicionado a otros fenómenos moleculares en los cuales la teoría newtoniana era inefectiva llevaron a una crisis científica que finalmente desembocó en el desarrollo de las dos grandes teorías de la física moderna:
(a) la teoría cuántica para los objetos muy pequeños, y
(b) la relatividad general para los objetos muy grandes.
Como mencionamos anteriormente, dado que la gravedad es importante para los objetos muy grandes su explicación moderna se encuentra contenida en la teoría general de la relatividad de Einstein.
Figura. 4.5. Las crisis científicas son importantes porque representan momentos en los que los paradigmas científicos existentes se ven desafiados y se cuestionan. Estas crisis pueden conducir a avances significativos en la comprensión científica y a la adopción de nuevos paradigmas que permiten una comprensión más profunda de la naturaleza. Además, estas crisis pueden fomentar la colaboración y el intercambio de ideas entre científicos de diferentes disciplinas y culturas, lo que a su vez puede dar lugar a nuevos enfoques y soluciones innovadoras a los problemas científicos. En resumen, las crisis científicas pueden ser vistas como oportunidades para el progreso y la innovación en la ciencia.
4.6 Una nueva teoría para la gravedad
Eventualmente, los astrónomos notaron una excentricidad en la órbita del planeta Mercurio que no podía ser explicada por la teoría de Newton: el perihelio de la órbita aumentaba alrededor de 42.98 segundos de arco por siglo, en palabras más simples, Mercurio no se movía como debería si la teoría newtoniana fuera cierta.
La explicación más obvia para esta discrepancia fue un cuerpo celeste aún no descubierto (como un planeta que orbita alrededor del Sol incluso más cerca que Mercurio), pero todos los esfuerzos por encontrar ese cuerpo resultaron infructuosos. Finalmente, en 1915, Albert Einstein desarrolló una teoría de la relatividad general que pudo modelar con precisión la órbita de Mercurio (Nobili & Will, 1986).
En relatividad general, los efectos de la gravitación se atribuyen a la curvatura del espacio-tiempo en lugar de a una fuerza. En consecuencia, los objetos en realidad siguen un movimiento uniformemente rectilíneo en el espacio, hoy eso es lo que el espacio es lo que se encuentra curvado. Al igual que en la primera ley del movimiento de Newton, Einstein creía que una fuerza aplicada a un objeto haría que se desviara de una geodésica. La descripción de la gravedad de Einstein fue aceptada rápidamente por la mayoría de los físicos, ya que podía explicar una amplia variedad de resultados experimentales que antes desconcertaban y se ignoraban a propósito para no dejar a la física sin una teoría que le diera sentido y propósito (Brush, 1999).
5. Controversias de la teoría newtoniana
|| REGRESAR AL ÍNDICE ||
La teoría Newtoniana ha sido objeto de diversas controversias y ataques a lo largo de la historia, y algunas de las principales son las siguientes:
5.1 Críticas religiosas:
Las controversias religiosas en torno a la teoría de la gravedad de Newton se centraron en gran medida en el tema de la explicación de la naturaleza y el movimiento de los cuerpos celestes, como los planetas y las estrellas, y cómo esto se relacionaba con la creencia religiosa de que Dios había creado un universo ordenado y perfecto (Westfall, 1977).
(a) Uno de los principales críticos de la teoría de Newton desde un punto de vista religioso fue el clérigo francés Pierre Louis Moreau de Maupertuis. En su obra "Discours sur les différentes figures des astres" ("Discurso sobre las diferentes formas de los astros"), publicada en 1744, Maupertuis argumentó que la teoría de Newton de la gravedad no podía ser cierta porque contradecía la idea de que Dios había creado un universo perfecto y armonioso. Según Maupertuis, si los cuerpos celestes se movían de acuerdo con una ley de la gravedad, entonces esto sugería que Dios había creado un universo imperfecto en el que los cuerpos celestes estaban "arrastrados" por una fuerza desconocida (Westfall, 1977).
(b) Los filósofos y críticos de Newton pensaban que el movimiento de los planetas debía ocurrir en círculos perfectos debido a las ideas de la época sobre la naturaleza y el orden del universo. Según la filosofía aristotélica y ptolemaica, que eran las principales corrientes filosóficas y científicas antes del advenimiento de la teoría de la gravedad de Newton, el universo era un sistema ordenado y armonioso que estaba gobernado por leyes matemáticas precisas. Debido a esta concepción del universo, se creía que los movimientos celestes debían ser circulares y perfectos, ya que los círculos eran considerados la forma más perfecta y armoniosa en la geometría. Además, el movimiento circular se consideraba divino y eterno, y por lo tanto, era más adecuado para describir los movimientos celestes que el movimiento lineal o cualquier otra forma de movimiento. Por lo tanto, cuando Newton propuso su teoría de la gravedad, que explicaba los movimientos planetarios en términos de órbitas elípticas, muchos filósofos y críticos de la época se mostraron escépticos y reacios a aceptarla. Sin embargo, con el tiempo, la teoría de Newton se convirtió en la explicación científica dominante para el movimiento planetario, y se demostró que las órbitas elípticas eran consistentes con las observaciones astronómicas (Westfall, 1977).
Figura. 5.1. A pesar de que Newton era muy religioso y escribió más sobre teología que sobre ciencia, sus teorías del movimiento y la gravitación fueron controversiales en algunos círculos religiosos en su época. La razón de esto es que algunas personas interpretaron sus teorías como una forma de negar la existencia de Dios como el motor principal del universo. En la época de Newton, se creía comúnmente que Dios era responsable de todos los movimientos en el universo y que cualquier movimiento continuo requería la intervención divina. La teoría de Newton desafió esta idea al proponer que los objetos en movimiento podrían continuar moviéndose por inercia sin la necesidad de una fuerza externa. Esta idea se interpretó por algunos como una negación de la existencia de Dios, ya que parecía que el universo podría funcionar sin su intervención constante. Sin embargo, en la actualidad, la mayoría de los científicos y teólogos han llegado a un consenso de que la ciencia y la religión son dos campos distintos y que la ciencia no puede probar o refutar la existencia de Dios.
5.2 Críticas al concepto de inercia
A parte de las nociones religiosas, uno de los principales desafíos de la teoría newtoniana se centró en la definición de inercia y su relación con la fuerza. Entre los autores que cuestionaron o criticaron la definición newtoniana de inercia y su relación con la fuerza se encuentran:
(a) George Berkeley: Filósofo y obispo irlandés que argumentó que la inercia es una propiedad que no necesita de ninguna fuerza para mantenerse. Berkeley también sugirió que la idea de la inercia podría explicarse por la creencia en la continuidad del ser.
(b) Ernst Mach: Físico austriaco que propuso una definición alternativa de la inercia que enfatizaba su relación con la distribución de materia en el universo. Mach argumentó que la inercia de un objeto está determinada por la distribución de masa en el universo y no por la masa del objeto en sí.
(c) Pierre Duhem: Físico y filósofo francés que cuestionó la definición de la inercia de Newton en su libro "La théorie physique: son objet, sa structure" (1906). Duhem argumentó que la inercia es una propiedad de los sistemas físicos en lugar de una propiedad de los objetos individuales.
(d) Henri Poincaré: Matemático y físico francés que también cuestionó la definición newtoniana de la inercia y su relación con la fuerza. Poincaré argumentó que la inercia es una propiedad emergente de los sistemas físicos y no puede explicarse simplemente por la masa de los objetos.
En general, estos autores y otros más plantearon objeciones y desafíos a la definición de inercia de Newton y su relación con la fuerza. Estos debates y críticas llevaron a una mayor comprensión y refinamiento del concepto de inercia en la física moderna.
5.3 Críticas sobre la naturaleza de la gravedad
La teoría de Newton también fue criticada por algunos filósofos que argumentaron que la idea de la gravedad actuando a distancia era una idea absurda y que contradecía las leyes de la física.
Los críticos de Newton no aceptaban fácilmente la idea de la gravedad como una fuerza que actúa a distancia, sin necesidad de contacto mecánico, porque esta idea parecía desafiar el concepto tradicional de fuerza en la filosofía natural de la época. Según las teorías filosóficas y científicas predominantes antes de Newton, se creía que la única forma en que un objeto podía mover a otro era a través de un contacto físico directo, mediante la transmisión de alguna forma de movimiento o impulso (Cohen, 1980).
Sin embargo, la teoría de la gravedad de Newton proponía que la atracción entre los cuerpos celestes se debía a una fuerza que se propagaba a través del espacio vacío, sin necesidad de un medio material de transmisión. Esta idea parecía ir en contra de la comprensión tradicional de la naturaleza de las fuerzas (Cohen, 1980).
Además, algunos críticos argumentaban que la idea de una fuerza de atracción a distancia no podía explicar por qué la Luna, por ejemplo, no caía directamente hacia la Tierra, sino que describía una órbita alrededor de ella. Esta objeción se basaba en la idea de que una fuerza de atracción a distancia debería hacer que la Luna se acelerara continuamente hacia la Tierra, en lugar de mantener una órbita estable (Cohen, 1980).
A pesar de estas objeciones, la teoría de la gravedad de Newton demostró ser muy exitosa en la explicación y predicción de los movimientos planetarios y otros fenómenos gravitatorios. Con el tiempo, la idea de una fuerza gravitatoria a distancia se convirtió en una de las ideas más fundamentales y aceptadas en la física y la astronomía modernas (Cohen, 1980).
Entre los principales críticos de Newton que no aceptaban fácilmente la idea de la gravedad como una fuerza que actúa a distancia (Westfall, 1977), sin necesidad de contacto mecánico, se encuentran:
(a) Gottfried Wilhelm Leibniz: Filósofo y matemático alemán que fue uno de los principales adversarios intelectuales de Newton. Leibniz criticó la idea de la gravedad como una fuerza a distancia en sus escritos y argumentó a favor de la teoría del éter, la cual sostenía que el universo debía estar lleno de un éter sutil que transmitía la fuerza de la gravedad.
(b) John Flamsteed: Astrónomo inglés que trabajó con Newton en la elaboración del Principia Mathematica. Flamsteed fue un crítico temprano de la teoría de la gravedad de Newton y argumentó que la luna no podía estar en una órbita estable alrededor de la Tierra si solo se debía a una fuerza de atracción a distancia.
(c) George Berkeley: Filósofo y obispo irlandés que también fue crítico de la teoría de la gravedad de Newton. Berkeley argumentó que la idea de una fuerza de atracción a distancia era incoherente y que solo podía haber movimiento si se producía un contacto físico directo entre los cuerpos.
(d) Robert Hooke: Físico inglés que trabajó en la Royal Society y que había tenido desacuerdos con Newton en el pasado. Hooke argumentó que la idea de la gravedad como una fuerza a distancia no podía explicar por qué los planetas seguían órbitas elípticas en lugar de circulares perfectas.
Estos críticos y otros más plantearon objeciones y desafíos a la teoría de la gravedad de Newton, pero con el tiempo, la idea de una fuerza gravitatoria a distancia se convirtió en una de las ideas más fundamentales y aceptadas en la física y la astronomía modernas.
5.4 Controversias en la astronomía y la llegada de la relatividad
La teoría de Newton también enfrentó críticas en el campo de la astronomía. Por ejemplo, la existencia de ciertos fenómenos, como las perturbaciones en las órbitas de los planetas exteriores, no podían explicarse completamente con la teoría de Newton y llevaron a algunos a proponer la existencia de un planeta desconocido, lo que finalmente se resolvió con el descubrimiento de Neptuno, sin embargo, esto no pudo lograrse con Mercurio, pues su movimiento solo pudo predecirse de forma precisa empleando la relatividad de Einstein.
5.5 La controversia sobre la luz y la llegada de la mecánica cuántica
La teoría de Newton sobre la luz también fue objeto de controversia. La idea de que la luz estaba compuesta por partículas o corpúsculos no encajaba con la teoría ondulatoria de la luz propuesta por Huygens, lo que llevó a una larga disputa entre partidarios de ambas teorías.
A la larga, el problema de la naturaleza de la luz sería la principal estocada en la teoría newtoniana, y aunque reacios, los físicos debieron descartarla, y en esta crisis científica emergió una nueva teoría, la mecánica cuántica, que no solo explicaba y predecía bien el comportamiento de la luz, también afecto la comprensión del concepto de átomo y su estructura (Pais, 1986).
5.6 Cartesianos vs Newtonianos sobre las matemáticas avanzadas
Con la publicación de Principa, hubo una clara división en la comunidad científica de la época, separándose en dos bandos, los cartesianos y los newtonianos (Gingras, 2001; Greenberg, 1986).
(a) Los partidarios de la física cartesiana, como Pierre-Sylvain Régis, sostenían que la física debía ser expresada en términos simples y geométricos, sin recurrir a las matemáticas avanzadas como el cálculo. Según ellos, el uso de estas herramientas matemáticas era innecesario y podía conducir a resultados falsos o especulativos.
(b) Por otro lado, los partidarios de la física newtoniana, como John Wallis y John Collins, sostenían que las matemáticas avanzadas eran fundamentales para el desarrollo de la física moderna y la comprensión de la naturaleza. Para ellos, el cálculo y otras herramientas matemáticas permitían una mayor precisión y rigor en la descripción de los fenómenos físicos.
Esta controversia se centró en gran medida en la naturaleza de la fuerza y el movimiento, y en la forma en que estas cantidades debían ser representadas y calculadas matemáticamente.
En resumen, la controversia sobre el uso de matemáticas avanzadas en la física newtoniana enfrentó a los partidarios de la física cartesiana, que preferían una expresión geométrica y simplificada de la física, y los partidarios de la física newtoniana, que defendían el uso de herramientas matemáticas avanzadas como el cálculo para una mayor precisión y rigor en la descripción de los fenómenos físicos. Entre los principales proponentes de ambas posturas se encontraban Pierre-Sylvain Régis, John Wallis y John Collins.
5.7 Físicos contra ingenieros
En general, no se puede decir que existió una gran controversia o animadversión entre los ingenieros o físicos experimentales que trabajaban con máquinas reales y las teorías matemáticas de Isaac Newton. De hecho, muchas de las teorías de Newton fueron desarrolladas específicamente para describir y explicar el movimiento de las máquinas y otros sistemas físicos (Gingras, 2001).
Figura. 5.2. En la cultura popular, como en series de televisión como "The Big Bang Theory", a menudo se presenta un conflicto entre ingenieros y físicos teóricos debido a la forma en que se representan estos personajes y sus áreas de especialización. Por ejemplo, los ingenieros son retratados como más prácticos y tendientes a hacer sacrificios matemáticos enfocados en la aplicación de la ciencia para resolver problemas reales que no necesitan una precisión total, mientras que los físicos teóricos se representan como más abstractos y enfocados en la investigación fundamental. Sin embargo, en la vida real, la relación entre ingenieros y físicos teóricos es mucho más colaborativa y complementaria. Los ingenieros a menudo aplican los principios y teorías desarrollados por los físicos teóricos para crear tecnología y solucionar problemas prácticos, mientras que los físicos teóricos a menudo colaboran con los ingenieros para aplicar y adaptar sus teorías a situaciones del mundo real. Ambas disciplinas son importantes y tienen un papel crucial en el avance de la ciencia y la tecnología.
(a) Sin embargo, hubo algunos desacuerdos y diferencias de opinión entre los ingenieros y físicos experimentales sobre la aplicación de las teorías de Newton en situaciones prácticas. Por ejemplo, algunos ingenieros argumentaban que las teorías matemáticas de Newton eran demasiado abstractas y no se podían aplicar directamente en la práctica, mientras que otros físicos experimentales sostenían que las teorías de Newton eran insuficientes para describir todos los aspectos del movimiento de las máquinas y otros sistemas físicos.
(b) Uno de los principales oponentes de la aplicación de las teorías de Newton en situaciones prácticas fue el físico y matemático francés Jean Le Rond d'Alembert. D'Alembert argumentó que las teorías de Newton no eran adecuadas para describir el movimiento de las máquinas y otros sistemas físicos debido a que no tenían en cuenta las fuerzas de fricción y otros factores que afectan el movimiento en el mundo real.
5.8 Su importancia en la instrucción escolar
Como discutimos anteriormente, la física newtoniana es una teoría histórica, que ha sido superada por las dos ramas de la física moderna: la relatividad general y la mecánica cuántica. De lo anterior surge la pregunta
(a) ¿Por qué debemos estudiar la física newtoniana en la escuela si ya existen teorías mejores? La física newtoniana es la base de la física moderna, y es una teoría fundamental que sigue siendo relevante hoy en día. Aunque las teorías de la relatividad general y la mecánica cuántica proporcionan una descripción más precisa del mundo físico a escalas extremadamente grandes y pequeñas, respectivamente, la física newtoniana sigue siendo aplicable a una amplia gama de situaciones cotidianas (Brown, 1989; Galili & Tseitlin, 2003).
Además, el estudio de la física newtoniana es fundamental para comprender cómo se desarrolló la física moderna y cómo se llegó a las teorías actuales. La física newtoniana también es importante en la educación científica, ya que enseña habilidades matemáticas y de razonamiento analítico que son fundamentales para muchas otras disciplinas (Brown, 1989; Galili & Tseitlin, 2003).
El razonamiento analítico es la capacidad de describir una situación cotidiana en sus principales componentes físicos, aislando los más importantes y suprimiendo los menos relevantes, de forma tal que el modelo resultante permite predecir el comportamiento cualitativa o cuantitativamente de manera precisa (Brown, 1989; Galili & Tseitlin, 2003).
Otra razón importante para estudiar la física newtoniana es que muchas de sus leyes y principios se aplican a campos más allá de la física, como la ingeniería, la química y la biología. Por lo tanto, una comprensión sólida de la física newtoniana puede ser valiosa en una amplia gama de carreras y campos de estudio.
(b) Se podría argumentar que esto solo aplica a aquellos que van a estudiar alguna ciencia, o ingeniería, así que la segunda pregunta que debemos hacernos es ¿Cuál es la importancia de que un ciudadano promedio, no científico, conozca sobre la física de Newton?
Conocer sobre la física newtoniana es importante para cualquier ciudadano promedio porque las leyes y principios que Newton formuló son aplicables a muchas situaciones cotidianas (Arons & Redish, 1997; Bloomfield, 2015; Olmos, Roncancio, & Velazco, 2023; Weinberg, 1987). A continuación, presento algunas razones por las cuales es importante que los ciudadanos conozcan sobre la física de Newton:
(c) Seguridad vial: Las leyes del movimiento de Newton se aplican a la conducción de vehículos y son esenciales para garantizar la seguridad en las carreteras. Comprender la relación entre velocidad, distancia y tiempo es fundamental para evitar accidentes y conducir de manera segura.
(d) Deportes: Las leyes de la física newtoniana se aplican a muchos deportes, como el fútbol, el baloncesto y el golf. Comprender el movimiento de los objetos y las fuerzas involucradas en un juego ayuda a los jugadores a mejorar su desempeño.
(e) Tecnología: Mucha de la tecnología que utilizamos en nuestra vida cotidiana, como los teléfonos móviles, los aviones y los satélites, se basa en la física newtoniana. Comprender las leyes del movimiento y la gravedad es esencial para el diseño y la construcción de estos dispositivos.
(f) Toma de decisiones: La comprensión de la física newtoniana también puede ser útil para tomar decisiones informadas en situaciones cotidianas. Por ejemplo, al determinar la velocidad necesaria para alcanzar una meta, o para calcular la cantidad de energía que se necesita para realizar una tarea.
6. La fuerza
|| REGRESAR AL ÍNDICE ||
En el lenguaje cotidiano, una fuerza es un empujón o un tirón. Una mejor definición es que una fuerza es una interacción entre dos cuerpos o entre un cuerpo y su entorno (Fig. 4.1). Por eso siempre nos referimos a la fuerza que un cuerpo ejerce sobre un segundo cuerpo. Cuando empujas un automóvil que está atascado en la nieve, ejerces una fuerza sobre el automóvil; un cable de acero ejerce una fuerza sobre la viga que está izando en una obra de construcción; etcétera. Como muestra la figura 4.1, la fuerza es una cantidad vectorial; puedes empujar o jalar un cuerpo en diferentes direcciones. En física, una fuerza es
una influencia/interacción que hace que el movimiento de un objeto con masa cambie su velocidad
por ejemplo, iniciando un movimiento desde el reposo hasta alcanzar cierta velocidad v en un tiempo t determinado.
6.1 Midiendo fuerzas
Un instrumento común para medir magnitudes de fuerza es la balanza de resorte o dinamómetro. Consiste en un resorte helicoidal encerrado en una caja con un puntero unido a un extremo. Cuando se aplican fuerzas a los extremos del resorte, se estira en una cantidad que depende de la fuerza. Podemos hacer una escala para el puntero utilizando varios cuerpos idénticos con pesos de exactamente 1 N cada uno. Cuando uno, dos o más de estos están suspendidos simultáneamente de la balanza, la fuerza total que estira el resorte es 1 N, 2 N, etc., y podemos etiquetar las posiciones correspondientes del puntero 1 N, 2 N y así sucesivamente. Entonces podemos usar este instrumento para medir la magnitud de una fuerza desconocida. También podemos hacer un instrumento similar que mida los empujones en lugar de los tirones, empleando una medida de cuanto se compacta un resorte.
Figura. 6.1. Dinamómetro analógico de resorte. Recuerde que un instrumento análogo es aquel que tiene una escala de medición análoga a una regla, y su incertidumbre sistemática es la mitad de su medida mas pequeña.
6.2 Unidades de medida
Dado que las fuerzas se perciben como empujones o tirones, esto puede proporcionar una comprensión intuitiva para describir las fuerzas. Al igual que con otros conceptos físicos (por ejemplo, la temperatura), la comprensión intuitiva de las fuerzas se cuantifica utilizando definiciones operativas precisas que son consistentes con las observaciones directas y se comparan con una escala de medición estándar corporizada en instrumentos de medida.
Al igual que sucede con muchos otros parámetros físico-químicos como la temperatura o la presión, la fuerza ha sido medida en diferentes escalas estandarizadas por los diferentes imperios que han ido y venido a lo largo de la historia desde la Revolución Científica. Eso nos ha dejado con la infelicidad histórica de varias escalas de medición para la fuerza que son aceptables, y por lo tanto deberemos ser muy conscientes que en muchos escenarios deberemos aplicar conversiones de unidades de fuerza.
(a) El newton y el kg⋅m/s2: (símbolo: N) es la unidad de fuerza en el Sistema Internacional de Unidades (SI). Se define como 1 kg⋅m/s2, es decir es la fuerza necesaria para mover una masa de 1 kg con una aceleración de 1 m/s2. Tenga en cuenta que, debido a la ley conmutativa de la multiplicación, esta definición también puede interpretarse como la fuerza necesaria para acelerar un objeto de 1 g a 1 km/s2. Lleva el nombre de Isaac Newton en reconocimiento a su trabajo sobre la mecánica clásica, específicamente la segunda ley del movimiento de Newton.
(b) La dina: (símbolo: dyn; del griego antiguo δύναμις (dúnamis) 'poder, fuerza') es una unidad de fuerza derivada especificada en el sistema de unidades centímetro-gramo-segundo (CGS), un predecesor del SI moderno. El nombre dina fue propuesto por primera vez como unidad de fuerza CGS en 1873 por un Comité de la Asociación Británica para el Avance de la Ciencia. La dina se define como "la fuerza requerida para acelerar una masa de 1 g a 1 cm/s2".
(c) El kilogramo-fuerza: (kgf o kgF), o kilopondio (kp, del latín: pondus, lit. 'peso'), es una unidad de fuerza métrica gravitatoria no estándar. No cumple con el Sistema Internacional de Unidades (SI) y está obsoleto para la mayoría de los usos modernos. El kilogramo-fuerza es igual a la magnitud de la fuerza ejercida sobre un kilogramo de masa en un campo gravitatorio de 9.80665 m/s2 (gravedad estándar terrestre, un valor convencional que se aproxima a la magnitud media de la gravedad en la Tierra). Es decir, es el peso de un kilogramo bajo gravedad estándar. Por lo tanto, un kilogramo-fuerza es por definición igual a 9.80665 N. El kilogramo-fuerza es una unidad no estándar y está clasificada en el Sistema Internacional de Unidades (SI) como una unidad que no se acepta para usar con el SI.
(d) La libra-fuerza: (símbolo: lbf) es una unidad de fuerza utilizada en algunos sistemas de medida, incluidas las unidades de ingeniería inglesas y el sistema pie-libra-segundo. La libra-fuerza no debe confundirse con la libra-masa (lb), a menudo llamada simplemente libra, que es una unidad de masa, ni tampoco debe confundirse con la libra-pie (ft⋅lbf), una unidad de energía, o la libra-pie (lbf⋅ft), una unidad de torsión. La libra-fuerza es igual a la fuerza gravitacional ejercida sobre una masa de una libra avoirdupois en la superficie de la Tierra. Desde el siglo XVIII, la unidad se ha utilizado en mediciones de baja precisión, para las cuales los pequeños cambios en la gravedad de la Tierra (que varía de ecuador a polo hasta en medio por ciento) pueden despreciarse con seguridad. El siglo XX, sin embargo, trajo la necesidad de una definición más precisa, requiriendo un valor estandarizado para la aceleración debida a la gravedad.
(e) El libral o poundal: (símbolo: pdl) es una unidad de fuerza, introducida en 1877, que forma parte del sistema de unidades del inglés absoluto, que a su vez es un subsistema coherente del sistema pie-libra-segundo. El poundal se define como la fuerza necesaria para acelerar 1 lb a 1 ft/s2.
Figura. 6.2. Dinamómetro digital. Recuerde que su incertidumbre será igual a la medida más pequeña, a menos que las instrucciones del fabricante indiquen otra cosa.
Física de Sears
Ejemplo. Convierta 5.0 libras-fuerza a newtons.
Ejemplo. Convierta 40.0 newtons a dinas
6.3 Naturaleza vectorial de la fuerza
Puede ser un empujón o un tirón, siempre con magnitud y dirección, por lo que la fuerza es una cantidad vectorial. Se mide en la unidad SI de newton (N = kg m/s2) y se representa con el símbolo F, cuando tenemos en cuenta su magnitud (F) y su sentido (θF) simultáneamente.
De lo anterior se desprende que los vectores fuerza estarán ligados a la trigonometría de descomposición y recomposición de las componentes en los ejes de coordenadas, igual que otros vectores que ya hemos visto.
Sir Isaac Newton describió el movimiento de todos los objetos usando los conceptos de inercia y fuerza, y al hacerlo descubrió que obedecen ciertas leyes de conservación. En 1687, Newton publicó su tesis Philosophiæ Naturalis Principia Mathematica (Newton, 2013). En este trabajo, Newton estableció tres leyes de movimiento que hasta el día de hoy son la forma en que se describen las fuerzas en la física. Los principales parámetros con los que vamos a vincular al vector fuerza son la aceleración y la masa.
6.4 Naturaleza aditiva de la fuerza
Si dos o más fuerzas individuales actúan simultáneamente sobre un objeto, el resultado es como si una sola fuerza, igual a la suma vectorial de las fuerzas individuales, actuara en lugar de las fuerzas individuales.
El vector fuerza total o fuerza resultante “algunas veces simplemente La Resultante” F, es igual a la suma de las fuerzas individuales Fj que se ejercen sobre el objeto.
La suma vectorial de las fuerzas individuales sobre un objeto se denomina fuerza neta F. Una sola fuerza que tenga la misma magnitud y dirección que la fuerza neta calculada F tendría entonces el mismo efecto que todas las fuerzas individuales ∑Fj.
Este hecho, llamado principio de superposición de fuerzas, hace que las fuerzas cotidianas sean razonables y predecibles. De hecho, el mundo sería extraño e impredecible si, por ejemplo, tú y un amigo tiraran cada uno del cuerpo estándar con una fuerza de 1 N y, de alguna manera, el tirón neto fuera de 14 N y la aceleración resultante fuera de 14 m/s2. En este libro, las fuerzas se representan con mayor frecuencia con un símbolo vectorial como Fj y una fuerza neta se representa con el símbolo vectorial F.
Al igual que con otros vectores, una fuerza o una fuerza neta pueden tener componentes a lo largo de ejes de coordenadas. Cuando las fuerzas actúan solo a lo largo de un solo eje, son fuerzas de un solo componente Fj,n, donde n representa el eje de coordenadas dado.
7. Diagrama de cuerpo libre
|| REGRESAR AL ÍNDICE ||
En física e ingeniería, un diagrama de cuerpo libre es una ilustración gráfica o modelo que se utiliza para visualizar las fuerzas aplicadas, los momentos y las reacciones resultantes en un cuerpo en una condición dada. Representa un cuerpo o cuerpos conectados con todas las fuerzas y momentos aplicados, y reacciones, que actúan sobre el(los) cuerpo(s). El cuerpo puede constar de varios elementos internos (como una armadura) o ser un cuerpo compacto (como una viga). Puede ser necesaria una serie de cuerpos libres y otros diagramas para resolver problemas complejos.
Estos diagramas se utilizan con frecuencia tanto para determinar la carga de componentes estructurales individuales como para calcular fuerzas internas dentro de una estructura. Son utilizados por la mayoría de las disciplinas de ingeniería, desde la biomecánica hasta la ingeniería estructural. En el entorno educativo, un diagrama de cuerpo libre es un paso importante en la comprensión de ciertos temas, como la estática, la dinámica y otras formas de mecánica clásica.
Los diagramas de cuerpo libre adicionalmente facilitan resolver escenarios de física de manera abstracta o analítica. Optar por soluciones analíticas en la resolución de problemas físicos antes de reemplazar valores concretos desde el principio tiene múltiples ventajas:
(a) Claridad Conceptual: Al trabajar con símbolos en lugar de valores numéricos desde el principio, se enfatizan los conceptos y las relaciones fundamentales antes de introducir números específicos, lo que facilita una comprensión profunda.
(b) Flexibilidad: Las soluciones analíticas permiten adaptar las fórmulas y relaciones a diferentes situaciones sin necesidad de recalcular cada vez, lo que ahorra tiempo y esfuerzo.
(c) Generalización: Al utilizar símbolos en lugar de valores concretos, se pueden analizar patrones y tendencias más amplias, lo que facilita la identificación de comportamientos generales en distintos contextos.
(d) Evitar Errores Numéricos Tempranos: Las operaciones numéricas tempranas pueden llevar a errores de redondeo y cálculos incorrectos que se propagan a lo largo de los pasos posteriores. Retrasar los cálculos numéricos minimiza este riesgo.
(e) Simplificación de Ecuaciones: Las soluciones analíticas permiten simplificar ecuaciones y expresiones algebraicas antes de enfrentar cálculos numéricos complejos.
(f) Unidades Constantes: Al trabajar con símbolos, las unidades permanecen constantes en todos los pasos, lo que previene confusiones y errores relacionados con las unidades.
(g) Mayor Enfoque en Conceptos: Al eliminar la necesidad de manipular constantes numéricas, los estudiantes pueden centrarse en comprender los conceptos detrás de las fórmulas y relaciones.
(h) Habilidades Transferibles: La capacidad de trabajar con soluciones analíticas desarrolla habilidades algebraicas y analíticas que son valiosas en una variedad de campos además de la física.
(k) Análisis implícito de la dimensionalidad: Trabajar con soluciones analíticas permite un análisis implícito de las unidades y dimensiones involucradas en un problema. Al mantener símbolos en lugar de valores numéricos, es posible identificar inconsistencias en unidades y dimensiones sin necesidad de ubicar unidades en los cálculos. Esto conduce a una mayor coherencia y precisión en los resultados finales, evitando errores relacionados con unidades desde el inicio.
(l) Metodología de los Físicos: Los físicos utilizan el enfoque analítico y deductivo al formular y demostrar teoremas basados en axiomas y relaciones fundamentales. Luego, ponen a prueba estas teorías en entornos de laboratorio para confirmar su validez y alcance. Buscan la generalidad y la universalidad en sus teorías, aspirando a desarrollar teorías unificadas que expliquen fenómenos diversos bajo un marco coherente. Este proceso iterativo de formulación, contrastación y expansión de teorías es una característica distintiva de la metodología científica en la física moderna.
7.1 Modelo o abstracción
Un diagrama de cuerpo libre no es un dibujo a escala, es un diagrama o modelo idealizado/abstraído. Recuerde que la abstracción o idealización es una técnica de análisis que consiste:
∘ en suprimir las características poco relevantes de un sistema para enfocarnos en aquellas características que van a aportar mayor información, o
∘ que van a aportar una mayor influencia al fenómeno que se está estudiando,
por lo que la podemos categorizar también como una técnica científica reduccionista. Los símbolos utilizados en un diagrama de cuerpo libre dependen de cómo se modele el cuerpo, aunque los mas comunes son:
∘ Una versión simplificada del cuerpo (a menudo un punto o un cuadro)
∘ Las fuerzas se muestran como flechas rectas que apuntan en la dirección en que actúan sobre el cuerpo.
∘ Los momentos se muestran como curvas con una punta de flecha o un vector con dos puntas de flecha que apuntan en la dirección en que actúan sobre el cuerpo.
∘ Uno o más sistemas de coordenadas de referencia
∘ Por convención, las reacciones a las fuerzas aplicadas se muestran con marcas a lo largo del tallo del vector
El número de fuerzas y momentos mostrados depende del problema específico y de las suposiciones hechas. Las suposiciones comunes son
∘ despreciar la resistencia del aire y
∘ la fricción y
∘ suponer una acción de cuerpo rígido.
En estática todas las fuerzas y momentos deben equilibrarse a cero; la interpretación física es que, si no lo hacen, el cuerpo está acelerando y los principios de la estática no se aplican. En dinámica, las fuerzas y los momentos resultantes pueden ser distintos de cero. Los diagramas de cuerpo libre pueden no representar un cuerpo físico completo. Se pueden seleccionar partes de un cuerpo para su análisis. Esta técnica permite el cálculo de fuerzas internas, haciéndolas parecer externas, permitiendo su análisis. Esto se puede usar varias veces para calcular fuerzas internas en diferentes lugares dentro de un cuerpo físico, como la pierna de un corredor, el brazo de un levantador de pesas, la viga de soporte principal en un puente entre otros.
Figura 7.1. Una cruz de hierro es una destreza gimnástica sobre los anillos en la que el cuerpo está suspendido en posición vertical mientras los brazos se extienden lateralmente, formando la forma de la cruz cristiana. Es un movimiento que requiere una fuerza significativa en los tendones de los hombros y los bíceps. El código de puntos de la Federación Internacional de Gimnasia enumera la cruz de hierro (o cruz en L) como una habilidad de valor "B".
Por ejemplo, una gimnasta que realiza la cruz de hierro: modelar las cuerdas y la persona permite calcular las fuerzas globales (peso corporal, despreciando el peso de la cuerda, brisas, flotabilidad, electrostática, relatividad, rotación de la tierra, etc.). Luego retire a la persona y muestre solo una cuerda; obtienes la dirección de la fuerza. Entonces, solo mirando a la persona, se pueden calcular las fuerzas en la mano. Ahora solo mire el brazo para calcular las fuerzas y los momentos en los hombros, y así sucesivamente hasta que se pueda calcular el componente que necesita analizar.
7.2 Código para el diagrama de cuerpo libre
Dado que un diagrama de cuerpo libre normalmente no solo involucra los vectores de fuerza, sino que en él se pueden dibujar vectores de otras naturalezas, es importante emplear un código de colores para poder distinguirlas con claridad
Los códigos de colores van a ser entidades completamente arbitrarias definidas por seres humanos que gocen de algún nivel de prestigio o autoridad sobre el tema. por ejemplo, el libro de texto con el cual yo estudié física clásica fue la física de Serway, y por ende voy a utilizar dicho código de colores con algunas modificaciones.
(a) Gris sólido para el vector posición (r) y gris segmentado para sus componentes.
(b) Negro sólido para el vector desplazamiento (d), Y negro segmentado para sus componentes.
(c) Rojo sólido para el vectores velocidad (v o ω), y rojo segmentado para sus componentes
(d) Azul sólido para el vector fuerza (F), y azul segmentado para sus componentes.
(e) Púrpura sólido para el vector aceleración (a), y púrpura segmentada para sus componentes.
(f) Verde sólido para el vector momento cinético (p o L), y verde segmentado para sus componentes.
(g) Amarillo sólido para el vector torque (τ), y amarillo segmentado para sus componentes.
Sin embargo, estas convenciones de colores no son universales ni están estandarizadas internacionalmente, y su uso puede variar entre diferentes disciplinas y campos de estudio. En general, es importante que cualquier diagrama vectorial incluya una leyenda que explique claramente el significado de cada elemento representado, para evitar confusiones o malinterpretaciones.
Para resolver problemas con la segunda ley de Newton, a menudo dibujamos un diagrama de cuerpo libre en el que el único cuerpo que se muestra es aquel para el que estamos sumando fuerzas. Algunos profesores prefieren un boceto del propio cuerpo, pero, para ahorrar espacio en estos capítulos, normalmente representaremos el cuerpo con un punto, aunque los cuadros o rectángulos que representan cajas son muy populares. Además, cada fuerza sobre el cuerpo se dibuja como una flecha vectorial con su cola anclada en el cuerpo. El punto desde donde emergen, o hacia donde tienden en el cuerpo será su centro de masas a menos que se especifique otra cosa.
Por lo general, se incluye un sistema de coordenadas y, a veces, la aceleración del cuerpo se muestra con una flecha vectorial (etiquetada como aceleración). Todo este procedimiento está diseñado para centrar nuestra atención en el cuerpo de interés.
Física de Sears
Ejemplo 4.1. Tres luchadores profesionales luchan por el cinturón de un campeón. El luchador numero 1 ejerce 250 N en dirección noroeste a 53º del eje negativo. El luchador 2 ejerce 50 N alineado con el eje x positivo. El luchador 3 ejerce 120 N en dirección sur. Encuentre las componentes x e y de la fuerza neta sobre la correa, y encuentre su magnitud y dirección.
8. La primera ley
|| REGRESAR AL ÍNDICE ||
Existen 2 definiciones cualitativas para el principio de inercia dependiendo de si el objeto se estaba moviendo o se encontraba estático con respecto a nuestro marco de referencia:
∘ todo objeto que se encuentre en reposo continuará en el reposo a menos que una fuerza resultante lo afecte.
∘ todo objeto que se encuentre en movimiento rectilíneo uniforme mantendrá su movimiento rectilíneo uniforme a menos que una fuerza resultante lo afecte.
el efecto en ambos casos es una aceleración es decir un cambio en la rapidez y/o un cambio en la dirección.
matemáticamente podemos definirla de una manera un poco más sencilla, pues simplemente diremos que se genera inercia
cuando la suma de todas las fuerzas es igual a cero o cuando la resultante es igual a cero.
El vector fuerza total o fuerza resultante “algunas veces simplemente La Resultante” F, es igual a la suma de las fuerzas individuales Fj que se ejercen sobre el objeto.
8.1 La hipótesis de Aristóteles
Aunque el principio de inercia aparece evidente en su propia simplicidad, el hecho es que cuando lo razonamos con respecto a nuestro diario vivir no tiene mucho sentido. En el diario vivir, sabemos que para mover un automóvil debemos aplicar una fuerza todo el tiempo de lo contrario es se regresa a un punto de equilibrio estático, de allí podríamos llegar a pensar que se necesita una fuerza constante para mantener el movimiento y que la naturaleza del movimiento es estar quieto, a esto lo denominaremos la hipótesis de Aristóteles.
Figura 8.1. Los motores LA son una familia de motores de gasolina con configuración en V de 90° de bloque pequeño OHV de varilla de empuje fabricados por Chrysler Corporation. Resulta intuitivo que, se necesita que el motor esté andando y transmitiendo impulso al automóvil, solo para que este permanezca en una rapidez constante en una pista recta.
Es decir, la primera ley empírica de Newton contradice la creencia intuitiva aristotélica de que se requiere una fuerza neta para mantener un objeto en movimiento con velocidad constante. En otras palabras, lo intuitivo es pensar que se requiere de una fuerza constante para mantener el movimiento, y en el momento en que se deja de empujar, el movimiento se detiene al estado de naturaleza estático.
8.2¿Cuál es el problema del modelo de Aristóteles?
Aunque el argumento de Aristóteles es lo cotidiano, este se debe a que no toma en cuenta el efecto de dos fuerzas que se oponen al empuje, siendo estas la resistencia del aire (u otros medios que rodean al móvil como el agua o la tierra), y el rozamiento del suelo contra las ruedas o rieles. Estas fuerzas que se oponen al movimiento poco a poco aceleran el móvil en contra del sentido del movimiento.
8.3 El problema del marco de referencia
Dado que la primera ley tiene dos definiciones coloquiales posibles el reposo se hace físicamente indistinguible de la velocidad constante distinta de cero. Esto se debe a que el movimiento o el reposo son conceptos relativos que dependen de como los sistemas definen su marco de referencia, si el marco de referencia se mueve con respecto al objeto, ¿cómo podemos estar seguros de que el objeto no es en verdad quien está quieto y el marco de referencia el que se mueve a su alrededor? La respuesta es que no lo estamos, por lo tanto deberemos tener en cuenta la existencia de dos tipos de ejercicios,
(a) aquellos que toman en cuenta que todo está en movimiento, y
(b) aquellos en los que se define arbitrariamente un marco de referencia estático.
8.4 Efectos de un marco de referencia móvil
Por ejemplo, mientras viaja en un vehículo en movimiento a una velocidad constante, las leyes de la física no cambian como resultado de su movimiento.
(a) Si una persona que viaja dentro del vehículo lanza una pelota hacia arriba, esa persona observará que sube verticalmente y cae verticalmente y no tendrá que aplicar una fuerza en la dirección en que se mueve el vehículo.
(b) Otra persona, al observar pasar el vehículo en movimiento, observaría que la pelota sigue una trayectoria parabólica curva en la misma dirección que el movimiento del vehículo.
Es la inercia de la pelota asociada con su velocidad constante en la dirección del movimiento del vehículo lo que asegura que la pelota continúe moviéndose hacia adelante incluso cuando es lanzada hacia arriba y vuelve a caer. Desde la perspectiva de la persona en el automóvil, el vehículo y todo lo que hay dentro de él está en reposo: es el mundo exterior que se mueve con una velocidad constante en la dirección opuesta al vehículo. Dado que no existe ningún experimento que pueda distinguir si es el vehículo el que está en reposo o el mundo exterior el que está en reposo, las dos situaciones se consideran físicamente indistinguibles. Por lo tanto, la inercia se aplica igualmente bien al movimiento de velocidad constante como al reposo.
8.5 Abstracción contra experimentación
De lo anterior se deduce que la única manera de llegar al principio de inercia sin la tecnología necesaria para crear un vacío verdadero es mediante la abstracción, es decir la primera ley no era más que una idea un experimento mental que no se podía poner a prueba. Sin embargo, en la actualidad tenemos la tecnología para generar vacíos extrayendo el aire de una columna, dentro de la cual podemos someter a los objetos a diversos tipos de movimientos y percatarnos de que pueden ser descritos mediante las ecuaciones newtonianas que asumen el principio de inercia como verdadero.
9. Masa
|| REGRESAR AL ÍNDICE ||
Podríamos saltar directamente a la segunda ley de newton asumiendo intuitivamente que es cuando la fuerza resultante es diferente de cero, pero en tales casos los sistemas empiezan a hacerse un poco más complejos pues deberemos tener en cuenta un nuevo parámetro, la masa m.
Hasta ahora el modelo mental que hemos empleado era el de una partícula que se mueve en el vacío, sin estructura interna y sin masa, o con una masa despreciable.
9.1 Importancia del modelo de la partícula simple
El modelo mental de una partícula que se mueve en el vacío, sin estructura interna y sin masa, o con una masa despreciable, es muy importante en la física teórica porque permite simplificar y analizar muchos problemas físicos complejos. Al considerar una partícula como una entidad sin estructura interna, se puede analizar su movimiento y su interacción con otras partículas de manera más sencilla.
El primer físico en utilizar este modelo mental fue Isaac Newton, quien en su obra "Philosophiæ Naturalis Principia Mathematica" (Principios matemáticos de la filosofía natural) publicada en 1687, formuló las leyes del movimiento que establecen la dinámica de una partícula. Newton propuso que una partícula sin estructura interna y con una masa despreciable se movería en línea recta a una velocidad constante si no hay fuerzas externas actuando sobre ella, y que la fuerza aplicada a la partícula es igual a la masa de la partícula multiplicada por su aceleración.
Este modelo mental de partícula ha sido muy útil en la física teórica, permitiendo a los científicos desarrollar modelos matemáticos para describir y predecir el comportamiento de partículas subatómicas, átomos, planetas y otros sistemas físicos complejos.
9.2 La partícula con masa
En resumen, el modelo mental de una partícula sin estructura interna y con una masa despreciable es útil en muchos problemas físicos, pero hay situaciones en las que es necesario incorporar el concepto de masa al modelo para lograr una descripción más precisa y completa del sistema físico que se está estudiando:
(a) Cuando se quiere estudiar la colisión de partículas: En la colisión de partículas, la masa es un factor crucial en la conservación del momento y la energía. La masa de las partículas involucradas en la colisión determina la cantidad de energía transferida y la dirección del momento después de la colisión.
(b) Cuando se quiere estudiar el movimiento de objetos a velocidades cercanas a la velocidad de la luz: A velocidades cercanas a la velocidad de la luz, el modelo de partícula sin masa ya no es adecuado. La masa de la partícula se convierte en un factor importante en la descripción del movimiento, y la teoría de la relatividad de Einstein se utiliza para describir el movimiento de la partícula.
(c) Cuando se quiere estudiar sistemas que involucren fuerzas gravitatorias: La masa es el factor que determina la fuerza gravitatoria entre dos partículas. Si se quiere estudiar el movimiento de una partícula en un sistema gravitatorio, es necesario considerar la masa de la partícula y la fuerza gravitatoria que actúa sobre ella.
(d) La que más nos interesa, cuando se quiere estudiar la aceleración de un objeto ejercida por una fuerza. En este caso, la fuerza aplicada a la partícula es igual a la masa de la partícula multiplicada por su aceleración, lo que se conoce como la segunda ley de Newton.
9.3 Que es la masa
Por lo tanto, al estudiar la aceleración de un objeto bajo la influencia de una fuerza, es necesario conocer su masa para determinar cómo la fuerza afectará su movimiento. Si la masa del objeto es grande, será más difícil de acelerar con una fuerza dada, mientras que si la masa es pequeña, será más fácil de acelerar.
Sin embargo, la fuerza es un parámetro vinculado a la masa. Es evidente que un cuerpo más masivo, con más materia, es más difícil de acelerar que uno menos masivo, aun cuando apliques la misma fuerza. Observe que hemos empleado el concepto de masivo y no el de pesado, por una razón importante, en física, son parámetros que miden cosas diferentes.
La masa es una propiedad intrínseca de un cuerpo. Tradicionalmente se creía que estaba relacionado con la cantidad de materia en un cuerpo físico, hasta el descubrimiento de la física del átomo y las partículas. Se encontró que diferentes átomos y diferentes partículas elementales, teóricamente con la misma cantidad de materia, tienen sin embargo masas diferentes. La masa en la física moderna tiene múltiples definiciones que son conceptualmente distintas, pero físicamente equivalentes. La masa puede definirse experimentalmente como una medida de la inercia del cuerpo, es decir,
masa es la resistencia a la aceleración (cambio de velocidad) cuando se aplica una fuerza neta.
9.4¿En que casos la masa no está vinculada a la cantidad de sustancia?
La masa es una propiedad física fundamental que se relaciona con la cantidad de materia presente en un objeto (Eq. 9.1.).
Ley de la conservación de la masa de una sustancia pura, la masa total de una sustancia pura j-qualquiera mj es igual a la masa de una partícula pura de dicha sustancia mpj por el número de partículas agrupadas en el sistema Nj.
En la mayoría de los casos, la masa está directamente relacionada con la cantidad de sustancia presente en un objeto (Eq. 9.1.), especialmente cuando se trata de sustancias puras. Sin embargo, hay situaciones en las que la masa no está vinculada directamente a la cantidad de sustancia presente en un objeto. Algunos ejemplos son:
(a) La masa inercial: La masa inercial es una propiedad fundamental de la materia que se relaciona con la resistencia de un objeto al cambio en su movimiento. La masa inercial de un objeto no depende de la cantidad de sustancia presente en el objeto, sino de la forma en que los átomos y moléculas de la materia están dispuestos y de la interacción de estas partículas entre sí.
(b) La masa gravitatoria: La masa gravitatoria es una propiedad fundamental de la materia que se relaciona con la fuerza gravitatoria que actúa sobre un objeto en un campo gravitatorio. La masa gravitatoria de un objeto no depende de la cantidad de sustancia presente en el objeto, sino de la cantidad de materia que contiene y de cómo está distribuida.
(c) La masa equivalente de energía: Según la teoría de la relatividad de Einstein, la energía y la masa están relacionadas a través de la famosa ecuación E = m c². Esto significa que la energía puede ser convertida en masa y viceversa, y que la masa equivalente de energía no depende necesariamente de la cantidad de sustancia presente en un objeto.
En resumen, aunque la masa está generalmente vinculada a la cantidad de sustancia presente en un objeto, hay situaciones en las que la masa no está directamente relacionada con la cantidad de sustancia, como en el caso de la masa inercial, la masa gravitatoria y la masa equivalente de energía. Para la siguiente discusión en física asumiremos la definición de masa inercial.
9.5 Midiendo la masa
Existen diferentes métodos para medir la masa de un cuerpo, algunos de los más sencillos se describen a continuación:
(a) Balanza de brazos: Este es uno de los métodos más comunes para medir la masa de un objeto. Consiste en comparar la masa del objeto desconocido con la de uno o varios objetos conocidos de masa conocida, utilizando una balanza de brazos. El objeto desconocido se coloca en un brazo de la balanza y se ajusta la posición del otro brazo hasta que se equilibran. La masa del objeto desconocido se determina entonces a partir de la masa de los objetos conocidos y su posición en la balanza.
(b) Balanza electrónica: Las balanzas electrónicas utilizan sensores que detectan la deformación producida por el peso del objeto sobre una superficie. La masa del objeto se calcula a partir de la fuerza ejercida por su peso sobre la superficie y la aceleración debida a la gravedad en ese lugar.
(c) Métodos volumétricos: En algunos casos, se puede determinar la masa de un objeto midiendo su volumen y densidad. Por ejemplo, en el caso de un líquido, se puede medir su volumen y su densidad y, a partir de ahí, calcular su masa.
(d) Método de oscilación: En este método, se cuelga el objeto desconocido de un resorte y se mide la frecuencia de oscilación del resorte. A partir de la frecuencia de oscilación y la constante elástica del resorte, se puede determinar la masa del objeto. En general la masa nunca se mide directamente,
los instrumentos utilizados para medir la masa de un objeto lo hacen a través de la fuerza que se ejerce sobre el objeto.
La mayoría de los métodos de medición de la masa utilizan una relación entre la fuerza aplicada y la masa del objeto, empleando diversas leyes físicas:
(a) ley de la fuerza gravitatoria de Newton: para las balanzas electrónicas o de platos se utiliza la fuerza gravitatoria que actúa sobre el objeto de masa desconocida para medir su masa. La balanza mide la fuerza gravitatoria que actúa sobre el objeto y la compara con la fuerza gravitatoria que actúa sobre una masa de referencia de masa conocida, que se encuentra en el otro plato de la balanza. La diferencia entre estas dos fuerzas es utilizada para calcular la masa del objeto desconocido, utilizando la ley de la fuerza gravitatoria de Newton.
(b) ley de Hooke: para las balanzas de compresión, esta ley mide cuanta fuerza de compresión genera una masa patrón, y luego se compara el patrón con respecto a otras masas.
9.6 Unidades de masa
Existen varias unidades de masa que se utilizan en diferentes sistemas de unidades de medida. Algunas de las principales unidades de masa son:
(a) Kilogramo (kg): es la unidad de masa básica del Sistema Internacional de Unidades (SI). Se define como la masa igual a la del prototipo internacional del kilogramo, que es un cilindro de platino e iridio almacenado en la Oficina Internacional de Pesas y Medidas en Francia.
(b) Gramo (g): es una unidad de masa del sistema métrico, que equivale a una milésima parte del kilogramo. Es la unidad de masa más comúnmente utilizada en la vida diaria.
(c) Libra imperial (lb): es una unidad de masa que se utiliza en el sistema inglés de unidades. Una libra equivale a aproximadamente 0.4536 kg. No confundir con la libra métrica 0.500 kg, aunque parece una diferencia sutil es bastante importante, especialmente si usted es un comerciante y está comprando o vendiendo bienes medidos en masa.
(d) Onza (oz): es una unidad de masa que también se utiliza en el sistema inglés de unidades. Una onza equivale a aproximadamente 28.35 g.
(e) Tonelada imperial (t): es una unidad de masa que equivale a 1016 kg. No confundir con la tonelada métrica 1000 kg.
(f) Quintal: es una unidad de masa que equivale a 100 kg.
(g) Arroba: es una unidad de masa que se utiliza en algunos países de habla hispana, como España y algunos países de América Latina. Una arroba equivale a 11.34 kg.
Cabe destacar que el uso de estas unidades puede variar dependiendo del país o región geográfica. Sin embargo, en la ciencia y la ingeniería, la unidad de masa más utilizada es el kilogramo (kg) del Sistema Internacional de Unidades (SI).
9.7¿Por qué el patrón de masa es el kilogramo y no el gramo?
Cuando comparas los nombres de las unidades básicas de diferentes cantidades físicas como la fuerza (newton), presión (pascal), hola temperatura (kelvin), te das cuenta que la unidad para la masa en el sistema internacional tiene una pequeña peculiaridad, y es que su unidad fundamental no es el gramo. ¿por qué se debe esto?
(a) Una respuesta superficial: La unidad básica de masa del Sistema Internacional de Unidades (SI) es el kilogramo, y no el gramo, debido a que se considera que el kilogramo es una unidad más conveniente para la mayoría de las aplicaciones prácticas. El kilogramo es una unidad de masa que es lo suficientemente grande para medir objetos comunes, pero no tan grande como para ser incómoda de manejar o medir.
Además, el kilogramo se define en términos de una masa física real, el prototipo internacional del kilogramo, que es un cilindro de platino e iridio IPK almacenado en la Oficina Internacional de Pesas y Medidas en Francia. La definición del kilogramo como una masa física se eligió porque se consideró que era la forma más precisa y reproducible de establecer una unidad de masa básica.
Por otro lado, el gramo es una unidad de masa que es útil en algunos contextos, como en la medición de pequeñas cantidades de sustancias químicas en un laboratorio. Sin embargo, para la mayoría de las aplicaciones prácticas, el kilogramo es la unidad de masa más conveniente y se utiliza como la unidad básica en el Sistema Internacional de Unidades.
Hola queríamos llegar a considerar que la respuesta anterior es superficial en el sentido de que lo único que se necesitaría es definir el nombre gramo como el equivalente al kilogramo patrón o el kilogramo estándar que se use en la actualidad que ya no es el IPK (Schlamminger, 2018).
(b) La grava y la revolución francesa: resulta que cuando se estaban definiendo las unidades fundamentales para el sistema decimal francés que es el primer antecesor del sistema internacional de unidades, sí hubo una unidad con nombre sencillo para la masa y fue la grava. Sin embargo, la palabra grava en francés era muy semejante a un título de nobleza equivalente al de Conde. Normalmente eso no acarrearía mayores problemas sin embargo al mismo tiempo se estaba llevando la Revolución francesa. Durante la Revolución francesa los entes revolucionarios abolieron todo lo que pudieron que pudiera recordar a la influencia de la nobleza y su importancia, en consecuencia, el nombre de la unidad de masa no podía tener una semejanza a un título nobiliario, de allí qué se recurrió al siguiente nombre que era gramo para definir a la unidad de masa patrón. Sin embargo, el gramo era 1000 veces más pequeño que la masa patrón, por lo tanto, la masa patrón quedó para siempre vinculada a kilogramo (BIPM, 2016).
9.8 Naturaleza escalar de la masa
Decimos que la masa es de naturaleza escalar porque es una magnitud física que se describe únicamente con un valor numérico y una unidad de medida, sin necesidad de especificar una dirección o un sentido. Lo que implica que:
El parámetro masa no tiene ángulos asociados.
Es decir, la masa es una cantidad física que solo tiene magnitud y no tiene dirección ni sentido, a diferencia de las magnitudes vectoriales como la velocidad o la fuerza.
Además, cuando se suman o restan masas, simplemente se suman o restan los valores numéricos, sin necesidad de considerar su orientación o dirección. Por ejemplo, si tenemos dos objetos con masas de 2 kg y 3 kg, la masa total de los dos objetos es simplemente 5 kg.
En resumen, la masa se considera una magnitud escalar porque se puede representar solo con un valor numérico y una unidad de medida, sin necesidad de una dirección o un sentido.
10. La segunda ley, relación masa, fuerza y aceleración
|| REGRESAR AL ÍNDICE ||
Si realizáramos una gráfica de un experimento en el cual vinculemos masa aceleración y fuerza, en el cual varía la masa y la aceleración a una fuerza constante nos daremos cuenta rápidamente de que la gráfica adquiere la misma forma de la ley de Boyle.
Figura 10.1. Gráfica de un experimento en el cual se mide la aceleración con masas variables a una fuerza constante. hoy dado que adquiere la forma de una inversa a la recta (y =k 1/x), la ecuación por lo tanto al transliterar se a los parámetros físicos sigue la estructura (a = k 1/m)
De lo anterior se desprenden dos conclusiones importantes:
(a) la aceleración y la masa son inversamente proporcionales.
(b) la constante de proporcionalidad que vincula a ambas no es otra que la fuerza que aplicamos de manera constante.
la fuerza en ese experimento fue una única resultante, sin embargo, en una situación un poco más realista esta resultante deberá ser igual a la suma vectorial de todas las fuerzas que se apliquen sobre el objeto, de allí que la forma general es la siguiente:
La suma de un número indeterminado j de fuerzas que se aplican sobre un objeto i (Fi) es igual al producto entre la masa de dicho objeto (mi) y por su aceleración (ai).
ecuación que definiremos de aquí en adelante como la segunda ley de newton:
La fuerza neta sobre un cuerpo es igual al producto de la masa del cuerpo por su aceleración.
Física de Tipler
10.1 Importancia de la identidad del cuerpo
Aunque al principio de este curso de física se les dijo que la identidad de una sustancia o cuerpo es relativamente poco importante en el contexto físico, con la masa y los diagramas de cuerpo libre esto deja de ser cierto.
(a) Si no se conoce la identidad del cuerpo, no se puede determinar su masa, y por lo tanto, no se puede aplicar la segunda ley de Newton para predecir su movimiento o su respuesta a una fuerza externa. Por lo tanto, determinar la identidad del cuerpo es un paso crítico en la aplicación de la segunda ley de Newton.
(b) Adicionalmente si no podemos identificar la identidad del cuerpo sobre el cual están ejerciendo su efecto las fuerzas, no podremos dibujar un diagrama de cuerpo libre en el cual podamos identificar un marco de referencia inercial o absoluto, y por consecuencia no podremos identificar los ángulos, lo que haría imposible la resolución de un ejercicio de segunda ley de newton.
De lo anterior si un objeto:
(a) no tiene un nombre propio o
(b) no le podemos asignar uno evidentemente o
(c) nos da flojera porque el nombre es muy largo
vamos a emplear el subíndice i, como la masa de el objeto i (mi), o la fuerza total resultante para dicho objeto (Fi).
Esta ecuación simple es la idea clave para casi todos los problemas de tarea de este capítulo, pero debemos usarla con cautela. Primero, debemos estar seguros de a qué cuerpo lo estamos aplicando. Solo las fuerzas que actúan sobre ese cuerpo deben incluirse en la suma vectorial (y en el diagrama de cuerpo libre), no las fuerzas que actúan sobre otros cuerpos que podrían estar involucrados en la situación dada.
Figura 10.2. Por ejemplo, si estás en una melee (pogo) de metaleros, la fuerza neta sobre ti es la suma vectorial de todos los empujones y tirones de tu cuerpo. No incluye ningún empujón o tirón de otro metalero por parte tuyo o de cualquier otra persona.
Cada vez que resuelve un problema de fuerza, su primer paso es establecer claramente el cuerpo al que está aplicando la ley de Newton.
10.2 Importancia de la identidad de la fuerza
Para determinar la fuerza neta, es necesario conocer la magnitud y dirección de cada una de las fuerzas individuales que actúan sobre el objeto. Si se desconocen las identidades de las fuerzas, no se puede determinar su magnitud ni su dirección, y por lo tanto, no se puede calcular la fuerza neta y la aceleración resultante del objeto.
Además, cada una de las fuerzas que actúa sobre el objeto puede tener un efecto diferente en su movimiento. Por ejemplo, si un objeto se mueve en una superficie horizontal y se aplica una fuerza de fricción y una fuerza hacia adelante, la fuerza de fricción actúa en la dirección opuesta al movimiento y puede disminuir la velocidad del objeto, mientras que la fuerza hacia adelante puede aumentar la velocidad. Si no se conocen las identidades de estas fuerzas por separado, no se puede determinar cómo afectan el movimiento del objeto.
Un sistema consta de uno o más cuerpos, y cualquier fuerza ejercida sobre los cuerpos dentro del sistema por parte de cuerpos fuera del sistema se denomina fuerza externa. Si los cuerpos que componen un sistema están rígidamente conectados entre sí, podemos tratar el sistema como un cuerpo compuesto, y la fuerza neta sobre él es la suma vectorial de todas las fuerzas externas. No incluimos las fuerzas internas, es decir, las fuerzas entre dos cuerpos dentro del sistema.
Las fuerzas internas no pueden acelerar el sistema.
Por ejemplo, una locomotora de ferrocarril y un vagón conectados forman un sistema. Si, por ejemplo, una cuerda de remolque tira de la parte delantera del motor, la fuerza debida a la cuerda de remolque actúa sobre todo el sistema motor-automóvil. Al igual que para un solo cuerpo, podemos relacionar la fuerza externa neta sobre un sistema con su aceleración con la segunda ley de Newton, donde m es la masa total del sistema. Sin embargo, una persona que empuja una de las paredes internas del vagón de pasajeros de la locomotora no generará ningún efecto en el movimiento del sistema locomotora y vagón.
10.3 Descomposición vectorial
Dado que las fuerzas son vectores, normalmente empleamos la estrategia de descomposición vectorial para hacer sumas restas y otras operaciones con ellos. hoy cuando realizamos la descomposición del vector dejamos de representarlo con la letra sólida (y la flecha vectorial en caso de que su procesador de texto lo permita), y pasaremos a operarlo con el símbolo de cualquier magnitud física no vectorial es decir en letra cursiva.
El eje de coordenadas de la magnitud de este vector puede indicarse de tres formas posibles.
(a) empleando subíndice donde se represente el eje de coordenadas,
(a) encerrando la fórmula completa, y colocándole exterior como un enorme factor común con el símbolo para el vector unitario.
(c) la tercera es indicar de otras maneras que una ecuación dada está fijada para un eje de coordenadas como por ejemplo un subtítulo en la parte superior.
10.4 Ejercicios
Física de Serway 9
Física de Tipler
Física de Sears
11. La fuerza peso
|| REGRESAR AL ÍNDICE ||
Estamos familiarizados con la frase cotidiana, el "peso de un objeto". El peso, sin embargo, no es una propiedad inherente de un objeto; más bien, es una medida de la fuerza gravitacional entre el objeto y la Tierra (u otro planeta). Por tanto, el peso es una propiedad de un sistema de elementos: el objeto y la Tierra, mediado por la segunda ley de Newton.
11.1 Representación y unidades
A pesar de las declaraciones populares de pesos expresados en kilogramos, el kilogramo no es una unidad de peso, es una unidad de masa. Dado que el peso es una fuerza simbolizada como Fp entonces sus unidades serán las mismas de la fuerza es decir newtons y sus derivados.
Representamos a la fuerza peso sin una naturaleza vectorial por una razón bastante sencilla, hoy tiene un solo componente, y es el vector unitario que apunta hacia el centro de masas del objeto con mayor masa, que para nuestros intereses mundanos y diarios es el centro del planeta Tierra. el símbolo para la aceleración gravitacional g también carece de una naturaleza vectorial por la misma razón.
Dado que la aceleración es relativamente constante dentro de la superficie de la Tierra que nos interesa entonces va a carecer de una identidad. Eq. 11.1 cuantifica la fuerza gravitacional sobre el objeto, pero observe que esta ecuación no requiere que el objeto se mueva. Incluso para un objeto estacionario o para un objeto sobre el que actúan varias fuerzas, Eq. 11.1 se puede utilizar para calcular la magnitud de la fuerza gravitacional. El resultado es un cambio sutil en la interpretación de m en la ecuación. La masa m en Eq. 14.1 determina la fuerza de la atracción gravitatoria entre el objeto y la Tierra. Esta función es completamente diferente a la descrita anteriormente para la masa, la de medir la resistencia a los cambios de movimiento en respuesta a una fuerza externa.
En ese papel, la masa también se llama masa inercial. Llamamos a m en Eq. 11.1 la masa gravitatoria. Aunque esta cantidad tiene un comportamiento diferente al de la masa inercial, una de las conclusiones experimentales de la dinámica newtoniana es que la masa gravitatoria y la masa inercial tienen el mismo valor. Aunque esta discusión se ha centrado en la fuerza gravitatoria sobre un objeto debido a la Tierra, el concepto es generalmente válido en cualquier planeta. El valor de g variará de un planeta a otro, pero la magnitud de la fuerza gravitacional siempre estará dada por el valor de m g.
A pesar de las sutilezas mencionadas anteriormente, es fundamental comprender que el parámetro "m" de masa debe interpretarse como la masa total del sistema en cuestión. Estamos considerando la masa total del sistema, la cual está sujeta a la ley de conservación de la masa en el contexto de sistemas mecánicos no cuánticos. Esta ley nos indica que la masa total de un sistema se mantiene constante a lo largo de cualquier proceso mecánico, en la escala macroscópica que experimentamos en nuestra vida cotidiana. Por lo tanto, podemos utilizar la siguiente expresión para representar la masa total de un sistema:
En esta expresión, sumamos las masas individuales de todas las partes o componentes del sistema. Esto nos permite considerar la masa total del sistema en nuestros cálculos y análisis. Es importante destacar que esta perspectiva es aplicable en el ámbito de la mecánica clásica, donde los objetos macroscópicos se rigen por leyes físicas deterministas y no cuánticas.
11.2 Variación de la aceleración gravitacional en el sistema Solar
Los valores en m/s² de diferentes cuerpos del sistema solar son: Mercurio 3.7; Venus 8.9; La Luna terrestre 1.6; Marte 3.7; Júpiter 24.8; Saturno 10.4 m/s²; Urano: 8.9 m/s²; Neptuno: 11.2 m/s²; Plutón: 0.62 m/s². La aceleración gravitatoria en la superficie del Sol es de aproximadamente 274 m/s². Sin embargo, debido a que el Sol es una estrella y no un cuerpo sólido, no tiene una superficie definida como los planetas y otros cuerpos del sistema solar. En lugar de eso, el Sol tiene una "fotosfera" que es la capa visible y externa de la atmósfera solar. La aceleración gravitatoria en la "superficie" de la fotosfera del Sol es ligeramente menor, alrededor de 274 m/s². Es importante tener en cuenta que la aceleración gravitatoria varía con la distancia desde el centro del Sol. En la fotosfera, la gravedad es de alrededor de 274 m/s², pero en la corona solar, la capa más externa de la atmósfera solar, la gravedad es mucho más débil debido a la mayor distancia al centro del Sol.
14.3 Variación de la aceleración gravitacional en el planeta Tierra
La aceleración gravitacional, denotada por "g", varía con la distancia desde el centro de la Tierra y con la altitud sobre el nivel del mar. En general, la aceleración gravitacional disminuye a medida que se aleja del centro de la Tierra y también disminuye a medida que se eleva sobre el nivel del mar.
La aceleración gravitatoria a nivel del mar ha sido medida con una precisión muy alta, y el valor aceptado actualmente es de 9.80665 m/s². Este valor se ha definido como la aceleración gravitatoria estándar a nivel del mar y se utiliza como referencia para muchas mediciones relacionadas con la gravedad y la física en general. Tiene una incertidumbre en la octava cifra decimal debido a la variación local en la gravedad y la deformación de la Tierra, pero se considera una constante universal bien establecida.
En la ciudad de Bogotá, que se encuentra a una altitud de aproximadamente 2 640 metros sobre el nivel del mar, la aceleración gravitacional es ligeramente menor que en la superficie de la Tierra, con un valor de alrededor de 9.78 m/s2. Esto se debe a que la ciudad se encuentra a una altitud más alta y más lejos del centro de la Tierra que la superficie del mar.
En el Monte Everest, que tiene una altura de 8 848 metros sobre el nivel del mar, la aceleración gravitacional es ligeramente menor que en la superficie de la Tierra, con un valor de alrededor de 9.78 m/s2. Esto se debe a que la altitud del Monte Everest está más lejos del centro de la Tierra que la superficie del mar.
Aunque se podría pensar que el monte Everest es el punto de la Tierra donde se puede caminar con menos peso en el planeta la verdad es un poco más complicada. El Chimborazo es una montaña ubicada en Ecuador que tiene una altitud de 6 268 metros sobre el nivel del mar y a pesar de ello, el valor de la aceleración gravitacional en el Chimborazo es aproximadamente de 9.76 m/s2, lo que es ligeramente menor que en el monte Everest.
La aceleración gravitacional depende de la distancia desde el centro de la Tierra, por lo que cuanto más lejos se encuentre un objeto del centro de la Tierra, menor será la aceleración gravitacional que experimente. A pesar de que el Everest es más alto, Chimborazo está ubicado cerca del ecuador. Aunque esta diferencia parece irrelevante, el problema radica en que la Tierra no es una esfera perfecta, el ecuador está abultado, es como si a parte de ser redonda, la Tierra sufriera de sobrepeso, así que todo en el ecuador está mas lejos del centro de la tierra que cualquier cosa que esté mas cercana a los polos.
En las minas más profundas, la aceleración gravitacional aumenta ligeramente debido a la masa adicional de la Tierra por encima de la mina. Sin embargo, la variación de la aceleración gravitacional en las minas más profundas es pequeña y difícil de medir con precisión.
11.4 La ausencia de gravedad
Se considera que una aceleración gravitacional es baja cuando está en el rango de 0.100 a 1.000; Se considera que una aceleración gravitacional es microgravedad cuando está en el rango de 0.001 a 0.100. Se considera que una aceleración gravitacional es nula cuando es igual a 0. La microgravedad, o la ausencia de gravedad, tiene varios efectos en el cuerpo humano, tanto a corto, mediano y largo plazo. Algunos de ellos son:
(a) A corto plazo: Los astronautas pueden experimentar náuseas, mareos y desorientación durante los primeros días en el espacio. Esto se debe a que el sistema vestibular del oído interno, que es responsable del equilibrio, no está acostumbrado a la falta de gravedad.
(b) A mediano plazo: Los astronautas pueden experimentar pérdida de masa ósea y muscular debido a la falta de gravedad, lo que puede afectar su capacidad para caminar y realizar tareas físicas cuando regresan a la Tierra.
(c) A largo plazo: La exposición prolongada a la microgravedad puede tener efectos más graves en la salud de los astronautas, como cambios en el sistema cardiovascular, disminución de la capacidad pulmonar y debilidad en el sistema inmunológico.
Figura 11.1. La Estación Espacial Internacional (ISS) se encuentra en una órbita terrestre baja, aproximadamente a una altitud de 408 km sobre la superficie de la Tierra. A esa altitud, la aceleración gravitacional es aproximadamente del 90% de lo que se experimenta en la superficie de la Tierra. Sin embargo, la ISS está en constante caída libre alrededor de la Tierra, lo que significa que los astronautas están en un estado de ingravidez o "microgravedad". Esto significa que, aunque la aceleración gravitacional no es cero, los efectos de la gravedad se cancelan con la velocidad orbital de la ISS, lo que permite que los astronautas experimenten una sensación de flotación.
Además, la microgravedad también puede afectar otros aspectos de la vida en el espacio, como la calidad del sueño, la digestión, la eliminación de desechos y la capacidad para realizar tareas cotidianas. Por esta razón, es importante que los astronautas se sometan a un entrenamiento y monitoreo rigurosos antes, durante y después de las misiones espaciales para minimizar los efectos negativos de la microgravedad en su salud.
Física de Serway 9
12. La tercera ley
|| REGRESAR AL ÍNDICE ||
Una fuerza que actúa sobre un cuerpo siempre es el resultado de su interacción con otro cuerpo, por lo que las fuerzas siempre vienen en pares. No puedes jalar el picaporte de una puerta sin que el picaporte tire hacia atrás de ti. Cuando pateas una pelota de fútbol, la fuerza hacia adelante que tu pie ejerce sobre la pelota la lanza en su trayectoria, pero también sientes la fuerza que la pelota ejerce sobre tu pie. Debido a que la masa de la pelota no es muy grande y tu pie está protegido no eres demasiado consciente de ello, pero tal vez has tenido una situación especial en la cual dos personas patean el balón al mismo tiempo, en ese caso sí habrá sentido la fuerza que rebota desde el balón hacia tu pie.
En cada uno de estos casos, la fuerza que ejerces sobre el otro cuerpo es en dirección opuesta a la fuerza que ese cuerpo ejerce sobre ti. Los experimentos muestran que cada vez que dos cuerpos interactúan, las dos fuerzas que ejercen entre sí son siempre iguales en magnitud y opuestas en dirección. Este hecho se llama la tercera ley del movimiento de Newton:
Si el cuerpo A ejerce una fuerza sobre el cuerpo B (una "acción"), entonces el cuerpo B ejerce una fuerza sobre el cuerpo A (una "reacción"). Estas dos fuerzas tienen la misma magnitud, pero son de dirección opuesta. Estas dos fuerzas actúan sobre cuerpos diferentes.
Las paráfrasis sobre simplificada de la tercera ley, como "acción es igual a reacción", podrían haber causado confusión entre generaciones de estudiantes: la "acción" y la "reacción" se aplican a diferentes cuerpos. Pero qué pasa cuando en nuestro sistema de análisis nos enfocamos en un solo cuerpo que se encuentra estático.
12.1 Importancia de la tercera ley
Esta ley es de gran importancia en la física y en muchas otras áreas de la ciencia y la tecnología. A continuación, se explican algunos de los aspectos más relevantes de la tercera ley de Newton:
(a) Conservación del momento: La tercera ley de Newton es esencial para la conservación del momento en un sistema físico cerrado. El momento es la cantidad física que describe la cantidad de movimiento de un objeto, y se define como el producto de la masa y la velocidad de un objeto. Cuando dos objetos interactúan entre sí, sus momentos deben sumar cero antes y después de la interacción. En otras palabras, la tercera ley de Newton asegura que la cantidad total de momento en un sistema cerrado se mantiene constante.
(b) Diseño de cohetes y motores de reacción: La tercera ley de Newton es fundamental para el diseño de cohetes y motores de reacción. Estos dispositivos funcionan expulsando gases a gran velocidad en una dirección opuesta a la dirección de movimiento deseada, lo que genera una fuerza de acción. La tercera ley de Newton asegura que, como resultado, se produce una fuerza de reacción igual y opuesta en la dirección opuesta, lo que empuja al cohete o al motor en la dirección deseada.
(c) Fuerzas de fricción: La tercera ley de Newton también es relevante para comprender las fuerzas de fricción. Cuando un objeto se mueve a través de un fluido, como el aire o el agua, la resistencia que experimenta se debe a la acción y reacción de las fuerzas ejercidas por el objeto y el fluido. La tercera ley de Newton asegura que la fuerza de fricción que actúa sobre el objeto es igual y opuesta a la fuerza que el objeto ejerce sobre el fluido.
(d) Deformaciones elásticas: La tercera ley de Newton también es importante para comprender las deformaciones elásticas de los materiales. Cuando un objeto ejerce una fuerza sobre otro objeto, se produce una deformación en el segundo objeto. La tercera ley de Newton asegura que el segundo objeto ejercerá una fuerza igual y opuesta sobre el primer objeto, lo que puede resultar en una deformación elástica.
Figura 12.1. La tercera ley de Newton tiene importantes implicaciones para comprender el comportamiento de las fuerzas en la interacción entre herramientas y materiales. Los carpinteros y metalúrgicos deben tener en cuenta esta ley para asegurarse de que su trabajo se realice de manera segura y eficiente.
(d) En carpintería y metalistería, la tercera ley de Newton tiene importantes aplicaciones prácticas. Algunos ejemplos son: Clavado y atornillado: Al clavar o atornillar una pieza de madera o metal, la fuerza ejercida por el martillo o el destornillador sobre el clavo o tornillo genera una fuerza de acción. La tercera ley de Newton asegura que se produce una fuerza de reacción igual y opuesta sobre el martillo o destornillador, lo que puede resultar en un rebote o en una torsión. Los carpinteros y metalúrgicos deben tener en cuenta esta ley para evitar lesiones y asegurarse de que su trabajo se realice de manera eficiente. Soldadura: En la soldadura, la tercera ley de Newton es relevante para comprender la fuerza necesaria para unir dos piezas de metal. Cuando se aplica calor y se agrega metal de soldadura a una junta, se genera una fuerza de acción. La tercera ley de Newton asegura que se produce una fuerza de reacción igual y opuesta en la dirección opuesta, lo que puede afectar la calidad de la soldadura. Corte y mecanizado: En el corte y mecanizado de madera y metal, la tercera ley de Newton es relevante para comprender la fuerza necesaria para cortar o dar forma a un material. La fuerza aplicada sobre la herramienta de corte genera una fuerza de acción. La tercera ley de Newton asegura que se produce una fuerza de reacción igual y opuesta en la dirección opuesta, lo que puede afectar la calidad del corte o mecanizado.
12.2 Algunos tipos de fuerza y situaciones especiales
Es importante analizar situaciones especiales como cuerdas, poleas, resortes, rozamiento e interacción entre objetos porque estas situaciones son comunes en la vida real y en muchos sistemas físicos. Además, estas situaciones especiales a menudo implican conceptos físicos que van más allá de las simples ecuaciones de movimiento y pueden ser más desafiantes de entender y resolver.
Por ejemplo, las cuerdas y poleas son comunes en muchos sistemas mecánicos y se utilizan para transmitir fuerzas y movimiento a través de distancias. Comprender cómo funcionan las cuerdas y poleas implica conceptos como la tensión, la fricción y la energía, que son importantes para muchos campos de la ingeniería y la física.
Los resortes también son comunes en muchos sistemas físicos y se utilizan para almacenar y liberar energía elástica. La comprensión de cómo funcionan los resortes implica conceptos como la ley de Hooke y la energía potencial elástica, que son importantes en la física y la ingeniería mecánica.
El rozamiento también es un fenómeno común en la vida real y puede tener un gran impacto en el movimiento de los objetos. La comprensión del rozamiento implica conceptos como la fuerza de rozamiento y el coeficiente de rozamiento, que son importantes para muchos sistemas físicos y tienen aplicaciones en la ingeniería.
La interacción entre objetos también es importante de entender porque muchos sistemas físicos involucran múltiples objetos que interactúan entre sí. La comprensión de cómo interactúan los objetos implica conceptos como la ley de acción y reacción de Newton y la conservación del momento y la energía, que son importantes en muchos campos de la física y la ingeniería.
13. La fuerza normal o de contacto
|| REGRESAR AL ÍNDICE ||
Considere por ejemplo un libro que se encuentra inmóvil sobre una superficie. dado que se encuentra inmóvil sabemos que la fuerza resultante es igual a cero, pero aparentemente solo estaría siendo afectado por la fuerza gravitatoria que empuja hacia abajo. En consecuencia, la superficie sobre la cual se encuentra en reposo debe estar ejerciendo una fuerza de igual magnitud que la gravitatoria pero en sentido opuesto.
A las fuerzas que ejercen las superficies en oposición al movimiento las denominaremos como fuerza normal.
La fuerza normal es la fuerza que actúa sobre un objeto en reposo o en equilibrio sobre una superficie, perpendicular a dicha superficie.
Esta fuerza es igual y opuesta a la fuerza que el objeto ejerce sobre la superficie, de acuerdo con la tercera ley de Newton, también conocida como ley de acción y reacción. La propuesta de la fuerza normal es atribuida a Isaac Newton, quien estableció las leyes fundamentales del movimiento y la dinámica en su obra "Principia Mathematica", publicada en 1687. La fuerza normal es un concepto importante en la física, ya que permite entender cómo los objetos interactúan con las superficies que los sostienen y cómo se mantiene el equilibrio en situaciones estáticas.
13.1¿Por qué el nombre de normal?
La fuerza normal recibe su nombre por el hecho de que es una fuerza perpendicular a la superficie de contacto entre dos objetos, y actúa en dirección opuesta a la fuerza que el objeto ejerce sobre la superficie. Esta fuerza se conoce como "normal" porque es perpendicular a la superficie, es decir, se encuentra en dirección perpendicular ("normal") a la superficie de contacto.
En cuanto a por qué se le llama "fuerza normal" y no "fuerza reactiva" o "fuerza de oposición", esto puede deberse a que el término "fuerza normal" ha sido ampliamente utilizado y aceptado en el campo de la física desde hace mucho tiempo, y ha sido adoptado como un término estándar para describir esta fuerza. Además, el término "fuerza reactiva" puede ser confuso, ya que también se utiliza para describir otras fuerzas que actúan en reacción a una fuerza aplicada, mientras que la fuerza normal se refiere específicamente a la fuerza perpendicular a una superficie de contacto.
13.2 Límite crítico de la normal
Existe un límite crítico para la fuerza normal en una superficie, más específicamente, en la fuerza normal máxima que puede soportar una superficie sin romperse o deformarse permanentemente. Este límite se conoce como límite elástico o límite de fluencia de la superficie, y depende de la resistencia y propiedades físicas del material que compone la superficie.
El límite elástico es una medida de la capacidad del material para resistir la deformación y fractura bajo cargas aplicadas. Si la fuerza normal ejercida sobre la superficie supera el límite elástico, la superficie se deformará de forma permanente, se romperá o se desplazará de su posición de equilibrio, lo que puede tener consecuencias peligrosas o dañinas.
Por tanto, el límite elástico depende de la resistencia y propiedades físicas del material que compone la superficie, tales como la resistencia a la tracción, la dureza, la densidad y la elasticidad. Además, el límite elástico también puede variar en función de la forma y tamaño de la superficie, la temperatura, la humedad y otros factores ambientales.
13.3 Otras fuerzas de contacto
La fuerza normal es solo una forma especial o ejemplo de la aplicación de la tercera ley de Newton, que establece que las fuerzas siempre vienen en pares iguales y opuestos. La fuerza normal no podría existir sin la presencia de una fuerza opuesta ejercida por el objeto sobre la superficie. Por lo tanto, la fuerza normal y la tercera ley de Newton están estrechamente relacionadas y son conceptos fundamentales en la física clásica.
En algunos casos existen sistemas hechos por múltiples componentes, los cuales pueden modelarse como entidades totales, sin embargo en su interior también se generan fuerzas internas llamadas fuerzas de contacto. La fuerza de contacto es una interacción física que ocurre entre dos objetos en contacto directo. Es la fuerza que se ejerce mutuamente entre las superficies de dos objetos cuando están en contacto y se presionan uno contra el otro. Esta fuerza surge debido a la interacción entre las moléculas de las superficies de los objetos y puede manifestarse en diferentes formas, como la compresión, la tensión o la fricción.
La fuerza de contacto puede ser tanto normal como tangencial. La fuerza normal de contacto actúa perpendicularmente a la superficie de contacto (es decir, es una oposición de la superficie contra una fuerza de la incide) y es responsable de sostener o soportar el peso de los objetos en contacto. Por otro lado, la fuerza de contacto tangencial, como la fricción, actúa paralelamente a la superficie de contacto y se opone al deslizamiento relativo de los objetos.
En un sistema donde hay múltiples objetos en contacto, la suma de las fuerzas de contacto debe ser igual a cero. Esto se basa en la tercera ley de Newton, también conocida como el principio de acción y reacción, que establece que por cada acción hay una reacción de igual magnitud pero en dirección opuesta y dado que las fuerzas de contacto son de igual magnitud y opuesta disposición, como en el peso y la normal, no generarán movimiento.
Cuando aplicas una fuerza neta sobre un sistema, deberás asumir que la fuerza incidente cuenta únicamente para el objeto con el que está en contacto directo, mientras que el segundo objeto solo estará afectado por la fuerza de contacto y la aceleración del sistema como un todo.
Física de Serway
Donde Fs es la fuerza incidente y Fc la magnitud de ambas fuerzas de contacto en newtons, y m2 es la masa del objeto que NO está en contacto con la fuerza incidente Fs. Observe que a medida que la m2 aumenta, la fracción de masas (m2/m) se acerca a 1, por lo que si una m2 es infinitamente mayor a la m1, entonces la magnitud de Fc será infinitamente semejante a Fs, creando una normal.
En un sistema en el que una fuerza incidente Fs actúa sobre un objeto m1, y a su vez m2 ejerce una fuerza sobre otro objeto m2, es importante comprender la diferencia entre las fuerzas de contacto y las fuerzas resultantes. Las fuerzas de contacto son las fuerzas que se transmiten directamente entre los objetos en contacto. En este caso, la fuerza ejercida por m1 sobre m2 es una fuerza de contacto, ya que se produce debido a la interacción física entre los dos objetos a razón de la fracción de masa (m2/m) del objeto 2.
Por otro lado, las fuerzas resultantes FR son las fuerzas parciales que actúan sobre cada objeto individualmente. Estas fuerzas resultantes son el resultado de la dispersión de la fuerza incidente en cada una de las partículas que componen al sistema, de forma tal que se asegure la misma aceleración de todas las partículas. De lo anterior se sigue que la suma de fuerzas de contacto es cero, pero la suma de fuerzas resultantes es la fuerza incidente.
13.4 Fuerza de contacto con dos fuerzas incidentes opuestas la fuerza de compresión
En los ejercicios anteriores, nos hemos enfocado en situaciones donde solo había una fuerza incidente actuando sobre un cuerpo. Sin embargo, ¿qué ocurre cuando hay dos fuerzas incidentes que actúan en direcciones opuestas? Aunque el diagrama de cuerpo libre en este caso puede volverse más complejo, podemos hacer un argumento general sobre la fuerza de contacto.
Independientemente de la dirección de las fuerzas incidentes, podemos afirmar que la fuerza de contacto se ejerce de manera dependiente en cada cuerpo en contacto con su fuerza incidente. Esto nos permite generalizar la ecuación 12.4, estableciendo que la fuerza de contacto neta es la suma de todas las fuerzas de contacto involucradas.
Demostración. Demuestre una fórmula para calcular la fuerza de contacto resultante al comprimir dos cajas con fuerzas opuestas.
Donde Fc es la magnitud de la fuerza de contacto resultante o fuerza de compresión. Una fuerza de compresión es una fuerza que actúa para comprimir o comprimir un objeto o material. Cuando se aplica una fuerza de compresión a un objeto, este tiende a reducir su tamaño en la dirección de la fuerza aplicada. La fuerza de compresión es una fuerza de contacto, lo que significa que se transmite a través del contacto directo entre dos objetos. Ejemplos comunes de fuerzas de compresión incluyen empujar un resorte, apretar un tornillo o comprimir un cojín. Es importante destacar que una fuerza de compresión puede deformar o cambiar la forma del objeto o material sobre el cual actúa. En algunos casos, si se aplica una fuerza de compresión demasiado grande, el objeto puede llegar a romperse o aplastarse.
La generalización 13.5 nos proporciona un atajo valioso, evitándonos la necesidad de plantear ecuaciones desde cero en casos más complejos. Podemos reciclar fórmulas y aplicar procedimientos aritméticos más sencillos para resolver estos escenarios de manera más eficiente.
El resultado final es una resolución más estandarizada y algorítmica, lo cual facilita el cálculo de situaciones más triviales. En el siguiente video, exploraremos ejemplos concretos para comprender mejor esta idea y mejorar nuestra habilidad para resolver problemas de física.
13.5 El plano inclinado sin rozamiento
En física general, el plano inclinado es un escenario especial que se utiliza para estudiar el movimiento de objetos bajo la influencia de fuerzas inclinadas en relación con la dirección horizontal. Consiste en una superficie plana que forma un ángulo con la horizontal, lo que proporciona un cambio en la dirección y magnitud de las fuerzas que actúan sobre un objeto.
El plano inclinado permite analizar el efecto de la gravedad y otras fuerzas en el movimiento de un objeto a lo largo de la superficie inclinada. Al inclinar el plano, se crea una componente de la fuerza gravitatoria en la dirección del plano, lo que resulta en una aceleración a lo largo del mismo. Esto permite estudiar cómo la masa del objeto, el ángulo de inclinación y las fuerzas aplicadas afectan su movimiento.
En el plano inclinado, es común considerar diferentes situaciones, como la presencia o ausencia de fricción entre el objeto y la superficie. Esto permite explorar las variaciones en la aceleración, la fuerza normal y otras magnitudes dependiendo de las condiciones específicas.
El estudio teórico del plano inclinado es fundamental para comprender conceptos clave en física, como las leyes de Newton, el equilibrio de fuerzas y la resolución de problemas de movimiento en dos dimensiones.
14. La fuerza elástica
|| REGRESAR AL ÍNDICE ||
En física, la ley de Hooke es una ley empírica que establece que la fuerza necesaria para extender o comprimir un resorte una cierta distancia depende de una constante de proporcionalidad que depende del material del que está hecho el resorte. Dado que un resorte es una entidad unidimensional podemos representar su modelo matemático en términos componentes en una dimensión.
Dónde d es el desplazamiento que sufre el resorte k es la constante de proporcionalidad que depende del material del que está hecho el resorte y de su estilo de fabricación.
Un valor negativo de d significa que el resorte ha sido comprimido a una distancia de su longitud sin tensión. El signo negativo en Eq. 13.1 significa que
cuando el resorte se estira (o comprime) en una dirección, la fuerza que ejerce es en la dirección opuesta.
Esta relación, conocida como ley de Hooke, resulta ser bastante importante. Un objeto en reposo bajo la influencia de fuerzas que equilibran se dice que está en equilibrio estático. Si un pequeño desplazamiento da como resultado una fuerza restauradora neta hacia la posición de equilibrio, el equilibrio se denomina equilibrio estable. Para pequeños desplazamientos, casi todas las fuerzas restauradoras obedecen la ley de Hooke.
13.1 Historia
La ley lleva el nombre del físico británico del siglo XVII Robert Hooke. Primero declaró la ley en 1676 como un anagrama latino. Publicó la solución de su anagrama en 1678 como: ut tensio, sic vis ("como la extensión, así la fuerza" o "la extensión es proporcional a la fuerza"). Hooke afirma en el trabajo de 1678 que conocía la ley desde 1660.
La ecuación de Hooke se cumple (hasta cierto punto) en muchas otras situaciones en las que se deforma un cuerpo elástico, como el viento que sopla sobre un edificio alto y un músico que toca la cuerda de una guitarra. Un cuerpo o material elástico para el cual se puede asumir esta ecuación se dice que es lineal-elástico o de Hooke.
Figura 14.1. Robert Hooke (1635-1703) fue un científico inglés conocido por sus contribuciones a la física, la biología y la arquitectura. Estudió en la Universidad de Oxford y trabajó como asistente de Robert Boyle en la Royal Society. Es famoso por su ley de elasticidad, conocida como Ley de Hooke, que establece que la fuerza necesaria para estirar o comprimir un objeto es proporcional a su deformación. Hooke también realizó importantes avances en el campo de la microscopía y descubrió las células en los seres vivos. Además, fue un arquitecto reconocido y diseñó varios edificios importantes en Londres. Hooke tuvo conflictos con Isaac Newton, particularmente en lo que respecta a la teoría de la gravedad. Hooke sugirió que la ley de la gravedad podría ser una relación inversa al cuadrado de la distancia, pero Newton fue quien finalmente formuló la ley y recibió el crédito por su descubrimiento. Esto llevó a una disputa entre los dos científicos, aunque Hooke también hizo importantes contribuciones a la teoría de la gravedad. Hooke tenía un retrato pintado de sí mismo que colgaba en la Royal Society, pero después de su muerte, el retrato desapareció y nunca se ha recuperado. Algunos han sugerido que Newton, que era presidente de la Royal Society en ese momento y no tenía una buena relación con Hooke, podría haber destruido el retrato.
14.2 Límite crítico
La ley de Hooke es solo una aproximación lineal de primer orden a la respuesta real de los resortes y otros cuerpos elásticos a las fuerzas aplicadas. Eventualmente debe fallar una vez que las fuerzas superan algún límite, ya que ningún material puede comprimirse más allá de un cierto tamaño mínimo, o estirarse más allá de un tamaño máximo, sin alguna deformación permanente o cambio de estado. Muchos materiales se desviarán notablemente de la ley de Hooke mucho antes de que se alcancen esos límites elásticos.
Por otro lado, la ley de Hooke es una aproximación precisa para la mayoría de los cuerpos sólidos, siempre que las fuerzas y las deformaciones sean lo suficientemente pequeñas. Por esta razón, la ley de Hooke se usa ampliamente en todas las ramas de la ciencia y la ingeniería, y es la base de muchas disciplinas como la sismología, la mecánica molecular y la acústica. También es el principio fundamental detrás de la escala de resorte, el manómetro, el galvanómetro y el volante del reloj mecánico.
14.3 Calculo de la constante elástica
La constante elástica, también conocida como constante de resorte o constante de elasticidad, es una medida de la rigidez de un resorte. Representa la relación entre la fuerza aplicada a un resorte y la deformación resultante que experimenta el resorte.
En sistemas ideales, la constante elástica es una propiedad intrínseca del resorte y no depende de las condiciones externas. Se considera constante independientemente de la magnitud de la fuerza aplicada o de la deformación del resorte. Sin embargo, en sistemas reales, la constante elástica puede variar ligeramente debido a factores como la calidad del material, las imperfecciones de fabricación y el desgaste.
La importancia de la constante elástica radica en que determina la respuesta del resorte ante una fuerza aplicada. Un resorte con una constante elástica alta es más rígido y requiere una mayor fuerza para deformarse, mientras que un resorte con una constante elástica baja es más suave y se deforma más fácilmente.
La constante elástica está influenciada por varios factores relacionados con la construcción y los materiales del resorte. Algunos de estos factores incluyen el grosor del alambre utilizado para fabricar el resorte, la longitud total del resorte y el tipo de material utilizado (como acero, bronce, etc.). En general, un resorte con un alambre más grueso y una longitud más corta tendrá una constante elástica mayor, lo que significa que será más rígido. Por otro lado, un alambre más delgado y una longitud mayor resultarán en una constante elástica menor, lo que implica una mayor flexibilidad del resorte.
Demostración. Determine la constante de un resorte, cuando a este le cuelga una masa y se deforma al estirarse
Donde la dilatación del resorte dy deberá reemplazarse como un valor positivo.
15. La fuerza tensión
|| REGRESAR AL ÍNDICE ||
Las cuerdas se usan para jalar cosas. Podemos pensar en una cuerda como un resorte con una constante de fuerza tan grande que la extensión de la cuerda es despreciable. Sin embargo, las cuerdas son flexibles, por lo que, a diferencia de los resortes, no pueden empujar cosas. En cambio, se flexionan o doblan bruscamente. La magnitud de la fuerza que un segmento de una cuerda ejerce sobre un segmento adyacente se denomina tensión. De ello se deduce que si una cuerda tira de un objeto, la magnitud de la fuerza sobre el objeto es igual a la tensión, pero no igual a sus unidades.
15.1 La tensión
La tensión no es propiamente una fuerza, sino más bien una propiedad que se asocia con la existencia de fuerzas. La tensión se refiere a la fuerza interna que se desarrolla dentro de un objeto o material cuando se somete a una carga externa, como la tracción, la compresión o la flexión. En otras palabras, la tensión es la medida de la resistencia que un objeto tiene al ser estirado o deformado por la aplicación de una fuerza (Gere & Timoshenko, 1997).
Por ejemplo, cuando tiras de una cuerda, la tensión es la fuerza interna que se desarrolla dentro de la cuerda como resultado de la fuerza aplicada en los extremos de la cuerda. Sin embargo, la tensión no es la fuerza que se aplica en sí misma, sino más bien una propiedad que surge en respuesta a la fuerza aplicada, de forma semejante a como la normal surge como efecto de la tercera ley de Newton (Gere & Timoshenko, 1997).
Las unidades de tensión son las mismas que las unidades de presión: en el Sistema Internacional de Unidades (SI), la unidad de tensión se mide en pascales (Pa), que se define como la fuerza en newtons (N) por unidad de área en metros cuadrados (m²). Además del pascal, existen otras unidades de medida comunes para la tensión, como el bar (1 bar = 100.000 Pa) y el kilopascal (1 kPa = 1000 Pa). También se utilizan unidades de medida no SI, como la libra por pulgada cuadrada (psi) y el kilogramo-fuerza por centímetro cuadrado (kgf/cm² o kg/cm²) (Gere & Timoshenko, 1997).
El símbolo de la tensión es una letra griega sigma mayúscula (Σ), que se utiliza comúnmente para representar la tensión normal o la tensión perpendicular a una superficie, mientras que la letra tau mayúscula (Τ) se utiliza para representar la tensión tangencial o la tensión paralela a una superficie. Tenga en cuenta que la letra griega sigma mayúscula (Σ) también se utiliza comúnmente para denotar una sumatoria matemática. Sin embargo, cuando se usa en el contexto de la tensión, la letra sigma se escribe en negrita o en cursiva (Σ) para indicar que se está utilizando como símbolo para la tensión, y no para una sumatoria (Σ).
Figura 15.1. La cuerda más resistente que se puede hacer actualmente es la hecha de nanotubos de carbono, que son materiales extremadamente fuertes y ligeros. La resistencia de estas cuerdas se debe a la alta resistencia a la tracción de los nanotubos de carbono individuales, que se agrupan en hilos para formar la cuerda. La resistencia de estas cuerdas puede variar dependiendo de su composición y método de producción, pero en general se estima que pueden ser hasta 100 veces más resistentes que el acero de la misma masa.
Además, es importante tener en cuenta que, en el contexto de la mecánica de materiales, la tensión se refiere a una propiedad física que puede ser medida experimentalmente, mientras que la suma es una operación matemática abstracta. En general, los símbolos utilizados en la física y en otras disciplinas científicas se escogen cuidadosamente para evitar confusiones innecesarias y para asegurar que los conceptos sean claramente comunicados. Por lo tanto, aunque el símbolo sigma se utiliza tanto para la tensión como para las sumatorias, el contexto en el que se utiliza debería ser suficiente para evitar confusiones y para entender claramente a qué se refiere el símbolo. Algo semejante pasaría con tau y T para tensión y temperatura.
15.2 Problemática dimensional con la tensión
En muchas fuentes nos encontraremos la igualdad de que la tensión es igual a la fuerza (F = T), sin embargo, tal expresión aunque es cierta en términos de valores numéricos no es correcta en términos de un análisis dimensional exhaustivo, esto se debe a que la atención posee unidades de presión, mientras que la fuerza posee unidades de fuerza o sea newtons u otras unidades derivadas. Por lo anterior para expresar una fórmula adecuada de la atención es necesario expresar una constante de proporcionalidad. Dado que 1 Pa = 1 N/m2, eso implica que la constante de tensión μT tendrá unidades 1 m-2. La constante de tensión sólo vale uno para una cuerda ideal (Gere & Timoshenko, 1997). De lo anterior se desprende que la fuerza aplicada será igual a la fuerza tensión.
Y a su vez, la tensión será expresar el valor de la fuerza sobre unidades de m2, siempre y cuando estemos analizando una cuerda ideal.
15.3 Efectos de la variación en la constante de tensión de una cuerda
La diferencia principal entre una cuerda ideal y una real con respecto a la constante de proporcionalidad fuerza-tensión μT es que una cuerda real tiene una cierta resistencia mecánica, debido a su material, diámetro, longitud, técnica de trenzado y otros factores. En consecuencia, la tensión en la cuerda no será exactamente igual en magnitud y dirección a la fuerza aplicada en cualquier punto de la cuerda, sino que estará relacionada por una constante de proporcionalidad diferente a 1 (Gere & Timoshenko, 1997).
Esto se debe a que la cuerda real experimenta deformación elástica y/o plasticidad, lo que significa que parte de la energía de la fuerza aplicada se disipa en forma de calor y deformación permanente, en lugar de ser transferida directamente como tensión (Gere & Timoshenko, 1997).
En la práctica, la resistencia mecánica de una cuerda real puede ser muy importante en la fabricación de cuerdas industriales, ya que determina su capacidad de carga y su durabilidad. Por lo tanto, los fabricantes de cuerdas deben tener en cuenta la constante de proporcionalidad fuerza-tensión μT al diseñar y fabricar cuerdas para aplicaciones específicas, como la elevación de cargas pesadas, la tracción de vehículos, el anclaje de estructuras, y otros usos (Gere & Timoshenko, 1997).
Figura 15.2. Los humanos comenzaron a fabricar cuerdas hace aproximadamente 40000 años. La evidencia más temprana de cuerdas se encuentra en Europa y se remonta al Paleolítico Superior. Se han encontrado cuerdas hechas de fibras vegetales en cuevas donde los humanos prehistóricos vivían. Se cree que los humanos comenzaron a hacer cuerdas porque necesitaban herramientas más avanzadas para sobrevivir. Las cuerdas eran útiles para la caza, la pesca y la construcción de refugios. También se utilizaron en la fabricación de ropa y en la elaboración de herramientas.
Los factores que afectan la constante de proporcionalidad fuerza-tensión μT incluyen el material de la cuerda (por ejemplo, acero, nylon, poliéster), el diámetro y la longitud de la cuerda, la tensión previa o pre-carga aplicada a la cuerda antes de su uso, y otros factores como la temperatura, la humedad y la exposición a la luz solar y a los agentes químicos. Por lo tanto, los fabricantes de cuerdas deben llevar a cabo pruebas y análisis rigurosos para determinar la constante de proporcionalidad adecuada para cada tipo de cuerda y aplicación (Gere & Timoshenko, 1997).
15.4 Sistemas de cuerdas en tensión estática
Un problema común en la física general es el estudio de un sistema de cuerdas tensionadas que actúan sobre una masa estática. Este tipo de problema se encuentra dentro del campo de la estática, que se enfoca en el equilibrio de objetos y sistemas en reposo.
Imaginemos un sistema en el cual una o varias cuerdas se encuentran sujetas a una masa fija o estática, es decir, un objeto que no se mueve. Estas cuerdas están sometidas a una tensión generada por fuerzas que actúan sobre ellas. El objetivo del problema es determinar las características y magnitudes de estas fuerzas y cuerdas, así como las propiedades del objeto estático.
Para resolver este tipo de problema, se deben tener en cuenta algunas consideraciones fundamentales. En primer lugar, se debe aplicar el principio de equilibrio estático, que establece que la suma de todas las fuerzas que actúan sobre el sistema debe ser igual a cero. Esto implica que las fuerzas en juego deben estar equilibradas, de manera que la masa estática permanezca en reposo sin moverse.
Además, es necesario considerar las propiedades de las cuerdas, como su longitud, masa y la tensión que pueden soportar. Estas características determinarán cómo se distribuye la tensión entre las cuerdas y cómo se relaciona con la masa estática.
La resolución del problema puede involucrar el uso de leyes fundamentales de la física, como la ley de Newton o las leyes del movimiento de los cuerpos. También es posible aplicar conceptos de la estática, como la suma de momentos o la descomposición de fuerzas en componentes vectoriales.
En el análisis algebraico de un problema de cuerdas tensionadas, se deben generar un número igual de ecuaciones que cuerdas involucradas en el sistema. Cada ecuación representa el equilibrio de fuerzas en una dirección específica, ya sea horizontal o vertical. Estas ecuaciones permiten resolver el sistema algebraicamente utilizando técnicas como la sustitución o el uso de matrices.
En el caso de un sistema con n cuerdas tensionadas, se necesitarán n ecuaciones para determinar todas las tensiones y características del sistema. Sin embargo, es importante destacar que en escenarios escolarizados es poco común encontrar problemas con más de tres cuerdas. Esto se debe a la complejidad adicional que representa el análisis algebraico y la dificultad para visualizar y resolver sistemas de ecuaciones más grandes.
En muchos problemas de cuerdas tensionadas, se asume que una de las cuerdas es vertical y su tensión es conocida. Esta cuerda vertical se utiliza a menudo para soportar el peso de un objeto estático. La magnitud de esta tensión vertical será igual al peso del objeto colgante, ya que en equilibrio estático la fuerza hacia arriba ejercida por la cuerda vertical debe ser igual y opuesta al peso hacia abajo.
Esta consideración simplifica el análisis del sistema, ya que proporciona una ecuación adicional que relaciona directamente la tensión conocida con el peso del objeto estático. En consecuencia, el número de incógnitas se reduce y, por lo tanto, se facilita la resolución algebraica del problema.
En relación a los ángulos en un sistema de cuerdas tensionadas, es importante tener en cuenta cómo se miden y qué valores se consideran positivos o negativos. Esta consideración es relevante para evitar confusiones en el análisis trigonométrico del sistema.
En el contexto descrito, se menciona que los ángulos se miden con respecto al techo, y se considera que los ángulos a la derecha del eje de unión de las cuerdas atadas son positivos. Esto implica que, en el plano de referencia, se toma como ángulo inicial el eje positivo de x y se incrementa en sentido contrario a las manecillas del reloj.
Sin embargo, se menciona que los ángulos a la izquierda del eje de unión deben considerarse como negativos. Esto se debe a que, en este contexto, se está utilizando una convención en la cual los ángulos a la izquierda del eje positivo de x se representan como valores negativos.
Para evitar confusiones trigonométricas, se aconseja corregir estos ángulos negativos al ángulo verdadero con respecto al eje positivo de x. Esto se logra sumando 180° al valor negativo. Esta corrección asegura que los ángulos se midan en sentido antihorario a partir del eje positivo de x, sin importar si están a la derecha o a la izquierda del eje de unión de las cuerdas.
Por otro lado, se menciona que el ángulo de la tensión vertical es 270°. Esta medida indica que el ángulo se encuentra en el cuarto cuadrante del plano de referencia, donde la componente y es negativa y la componente x es cero. Esta definición es consistente con la posición vertical de la cuerda y su dirección hacia abajo.
Donde ϕiz es el ángulo de la cuerda de la izquierda contra el techo, θde es el ángulo de la cuerda de la derecha contra el techo, Tg es la tensión de la cuerda vertical y también la fuerza peso; y x Tde, Tiz son las tensiones de las cuerdas derecha e izquierda.
Ejemplo. Calcule las tensiones entre las cuerdas A y B si se sabe que sostienen un cuerpo de 200 N.
Ejemplo. Calcule las tensiones entre las cuerdas A a 50° y B a 0° si se sabe que sostienen un cuerpo de 800 N.
Serway
15.5 Sistemas de cuerdas en tensión dinámica
Antes de continuar a las poleas, resulta importante analizar un caso que es aparentemente mas sencillo que el que trabajamos previamente, y es el de determinar la tensión total que hay entre una cuerda tensada por dos fuerzas opuestas que a demás están en movimiento. Cuando analizamos una cuerda tensada por dos fuerzas opuestas en movimiento, es fundamental considerar varios aspectos. En primer lugar, debemos tener en cuenta la masa de la cuerda misma, ya que contribuye a la tensión total experimentada por la cuerda.
Además, es necesario examinar las características de las fuerzas opuestas y cómo interactúan entre sí. Dependiendo de la dirección y la magnitud de estas fuerzas, la tensión total en la cuerda puede variar. Es esencial determinar la tensión en cada punto de la cuerda y comprender cómo se distribuye a lo largo de su longitud. Un enfoque clave para resolver este tipo de problemas es aplicar las leyes del movimiento y las ecuaciones de la dinámica, como la segunda ley de Newton. Estas herramientas nos permiten relacionar las fuerzas, la masa y la aceleración del sistema, lo que a su vez nos ayudará a calcular la tensión total en la cuerda.
La clave para abordar el análisis de la tensión en sistemas de cuerdas en tensión dinámica radica en considerar la tensión como fuerzas de contacto. Esto implica aplicar el modelo matemático que ya hemos examinado en la tercera ley de Newton. De acuerdo con la tercera ley de Newton, por cada acción hay una reacción de igual magnitud pero en sentido opuesto. En el caso de una cuerda tensada, cuando aplicamos una fuerza en un extremo de la cuerda, la cuerda responde ejerciendo una fuerza de reacción en dirección opuesta, pero cuya magnitud se ve afectada por la aceleración del sistema como un todo.
Al considerar este principio, podemos analizar el sistema de cuerdas como un conjunto de fuerzas de contacto que se transmiten entre los objetos conectados por la cuerda. Estas fuerzas se transmiten a lo largo de la cuerda y son responsables de la tensión experimentada en diferentes puntos.
Aunque la dirección del movimiento también se puede calcular con la aceleración, si solo deseamos determinar la dirección, solo debemos sacar la diferencia de fuerzas incidentes.
15.6 La tensión y la fuerza peso en un plano inclinado
Nuevamente, antes de adentrarnos en el tema de las poleas, es esencial reconocer que muchos de sus escenarios triviales involucran uno o dos planos inclinados. Por lo tanto, resulta fundamental comprender cómo calcular el vector fuerza en un plano inclinado en función del peso y el ángulo de inclinación.
Si bien podríamos omitir este análisis y hacerlo explícitamente en cada demostración o escenario trivial por separado, reconocer las peculiaridades del plano inclinado nos permitirá acelerar los análisis y cálculos posteriores, evitando enredarnos en el tedioso análisis de ángulos, los cuales pueden resultar frustrantes.
¡Prepárate para dominar los conceptos fundamentales y agilizar tus análisis en escenarios con planos inclinados! Únete a nosotros en Ciencias de Joseleg mientras exploramos cómo calcular el vector fuerza en un plano inclinado, allanando el camino para un estudio más profundo sobre las poleas y sus aplicaciones. ¡No te pierdas este enriquecedor video!
Lo anterior implica que la fuerza resultante en un plano inclinado, por ejemplo hacia la derecha Fd es el producto de la fuerza peso de una masa en un plano proyectado hacia la derecha Fgd por el seno del ángulo del plano inclinado proyectado hacia la derecha.
Ahora debemos hacer una demostración análoga pero para la solución dinámica.
Lo anterior implica que la fuerza resultante en un plano inclinado, por ejemplo hacia la derecha Fd es el producto de la fuerza peso de una masa en un plano proyectado hacia la derecha Fgd por el seno del ángulo del plano inclinado proyectado hacia la derecha.
15.7 Poleas
En física clásica, una polea es un dispositivo mecánico que consta de un disco circular con un borde cóncavo y un eje en su centro, que se utiliza para cambiar la dirección de la fuerza aplicada en una cuerda o cable y así facilitar el levantamiento o movimiento de objetos pesados. La cuerda o cable se enrolla alrededor de la polea, y la tensión de la cuerda en un lado de la polea se transmite a la tensión en el otro lado de la polea, lo que permite aplicar una fuerza en una dirección diferente.
La función principal de la polea es reducir la fuerza necesaria para levantar un objeto pesado. Al cambiar la dirección de la fuerza, la polea permite que una fuerza menor pueda mover un objeto más pesado. Por lo tanto, se utiliza ampliamente en una variedad de aplicaciones, desde la maquinaria industrial hasta la mecánica del cuerpo humano.
Existen varios tipos de poleas, incluyendo poleas fijas, poleas móviles y poleas compuestas. En una polea fija, la polea se fija en su posición, mientras que, en una polea móvil, la polea se mueve con la carga. Las poleas compuestas combinan una polea fija y una polea móvil para proporcionar una ventaja mecánica adicional. Además, las poleas también se clasifican según el número de ranuras en el borde de la polea.
Figura 15.3. Los antiguos griegos son conocidos por el uso de poleas debido a que inventaron y desarrollaron una de las primeras máquinas simples conocidas como "polipastos". Los polipastos son máquinas que utilizan una o más poleas móviles para multiplicar la fuerza necesaria para levantar un objeto pesado. Los antiguos griegos utilizaron polipastos para construir grandes estructuras como templos y teatros, así como para mover objetos pesados en la industria y en la agricultura. También se utilizaron en la construcción de armas y maquinaria militar. El uso de poleas y polipastos permitió a los griegos realizar trabajos que de otra manera serían imposibles de realizar manualmente, lo que les permitió construir estructuras más grandes y complejas y realizar tareas que requerían una gran cantidad de fuerza. Por lo tanto, los griegos son famosos por su habilidad en la creación y uso de estas herramientas simples, que han sido fundamentales para el desarrollo de la tecnología y la ingeniería en todo el mundo.
La presencia de una polea puede afectar las ecuaciones del movimiento al cambiar la dirección de la fuerza aplicada. Si la polea es fija, la magnitud de la fuerza se mantiene constante a través de la polea, pero la dirección de la fuerza puede cambiar. Si la polea es móvil, la magnitud de la fuerza en la cuerda que soporta la carga es menor que la fuerza aplicada en la cuerda opuesta debido a la presencia de la polea. Además, la polea también puede afectar la aceleración del objeto en movimiento debido a la fricción entre la cuerda y la polea. Por lo tanto, al utilizar una polea en una aplicación, se debe tener en cuenta su efecto en las ecuaciones del movimiento y tomar medidas para minimizar cualquier pérdida de energía debida a la fricción.
Escenarios de poleas fijas estáticas
Las formas estáticas son ecuaciones mas sencillas que las dinámicas, sin embargo, el escenario base estático no lo demostramos en la sección de tensiones estáticas, donde nos enfocamos en el sistema de tres cuerdas. De allí que primero realizaremos la solución para una tensión sin polea lineal de dos cajas jaladas por dos fuerzas estáticas.
Demostración. Demuestre un sistema de ecuaciones que permita calcular la tensión y la masa/ángulo de una de las dos cajas en un sistema de dos cajas unidos por una cuerda jalados por fuerzas opuestas estáticos Versión 1.0. Versión 2.0
Escenarios de poleas fijas dinámicas
En los escenarios escolares más comunes donde se analizan las poleas fijas ideales, se exploran diferentes situaciones relacionadas con el levantamiento y movimiento de objetos. Estas poleas son dispositivos mecánicos que permiten cambiar la dirección de una fuerza aplicada a través de una cuerda o cable.
Uno de los escenarios más básicos es el levantamiento de objetos verticales utilizando una fuerza vertical. En este caso, la polea fija cambia la dirección de la fuerza en 180 grados, lo que facilita el levantamiento del objeto en sentido contrario al que se aplica la fuerza.
Figura 15.4. Modelo de un sistema de fuerza vertical en una polea simple.
En otro escenario común, se estudia el levantamiento de objetos verticales utilizando una fuerza horizontal. En este caso, la polea fija cambia la dirección de la fuerza en 90 grados, lo que significa que la fuerza aplicada horizontalmente se convierte en una fuerza vertical que permite levantar el objeto.
Figura 15.5. Modelo de un sistema de fuerza vertical/vertical en una polea simple.
Cuando se trata de levantar objetos verticales con una fuerza inclinada, la polea fija cambia la dirección de la fuerza de acuerdo con la inclinación del plano. Esto implica que la fuerza aplicada en un ángulo con respecto al plano se convierte en una fuerza vertical que permite el levantamiento del objeto.
Figura 15.6. Modelo de un sistema de fuerza diagonal/vertical en una polea simple.
Figura 15.7. Modelo de un sistema de fuerza diagonal/diagonal en una polea simple.
16. Las fuerzas fricción
|| REGRESAR AL ÍNDICE ||
Si empujas un libro que está sobre un escritorio, es probable que el libro se deslice por el escritorio. Si el escritorio es lo suficientemente largo, el libro eventualmente patinará hasta detenerse. Esto sucede porque el escritorio ejerce una fuerza de fricción sobre el libro en una dirección opuesta a la velocidad del libro. Esta fuerza, que actúa sobre la superficie del libro en contacto con el escritorio, se conoce como fuerza de fricción.
La fuerza de fricción es la fuerza que actúa sobre un objeto en contacto con una superficie y se opone al movimiento relativo entre el objeto y la superficie. La fricción es causada por la interacción de las moléculas de la superficie del objeto y las moléculas de la superficie con la que está en contacto.
Las fuerzas de fricción son una parte necesaria de nuestras vidas. Sin fricción, nuestro sistema de transporte terrestre, desde caminar hasta automóviles, no podría funcionar. La fricción le permite comenzar a caminar, y una vez que ya se está moviendo, la fricción le permite cambiar su velocidad o dirección. La fricción le permite arrancar, conducir y detener un automóvil. La fricción mantiene una tuerca en un tornillo, un clavo en la madera y un nudo en un trozo de cuerda. Sin embargo, por importante que sea la fricción, a menudo no es deseable. La fricción provoca desgaste cuando las piezas móviles de la maquinaria están en contacto, y se gastan grandes cantidades de tiempo y dinero tratando de reducir tales efectos.
La fricción es un fenómeno complejo que no se comprende del todo y que surge de la atracción entre las moléculas de una superficie y las moléculas de una segunda superficie en estrecho contacto. La naturaleza de esta atracción es electromagnética, lo mismo que el enlace molecular que mantiene unido un objeto. Esta fuerza de atracción de corto alcance se vuelve insignificante a distancias de solo unos pocos diámetros atómicos.
16.1 Interpretación de la fuerza fricción a nivel molecular
Como se muestra en la Figura 14.1, los objetos ordinarios que se ven suaves y se sienten suaves son ásperos y desiguales a escala microscópica (atómica). Este es el caso incluso si las superficies están muy pulidas. Cuando las superficies entran en contacto, solo se tocan en las prominencias, llamadas asperezas, que se muestran en la Figura 16.1 y en la Figura 16.2.
Figura 16.1. El área microscópica de contacto entre la caja y el piso es solo una pequeña fracción del área macroscópica de la superficie inferior de la caja. El área microscópica de contacto es proporcional a la fuerza normal ejercida entre las superficies. Si la caja descansa de lado, el área macroscópica aumenta, pero la fuerza por unidad de área disminuye, por lo que el área microscópica de contacto no cambia. Ya sea que la caja esté en posición vertical o de costado, se requiere la misma fuerza horizontal aplicada F para mantenerla deslizándose con rapidez constante.
La fuerza normal ejercida por una superficie se ejerce en las puntas de estas asperezas donde la fuerza normal por unidad de área es muy grande, lo suficientemente grande como para aplanar las puntas de las asperezas. Si las dos superficies se presionan juntas con más fuerza, la fuerza normal aumenta y también lo hace este aplanamiento, lo que da como resultado un área de contacto microscópica más grande. Bajo una amplia gama de condiciones, el área microscópica de contacto es proporcional a la fuerza normal. La fuerza de fricción es proporcional al área de contacto microscópica; entonces, como el área de contacto microscópica, es proporcional a la fuerza normal.
Figura 16.2. Sección ampliada de una superficie de acero pulido que muestra las irregularidades de la superficie. Las irregularidades son altas, una altura que corresponde a varios miles de diámetros atómicos. (Tomado de F. P. Bowden y D. Tabor, Lubrication of Solids, Oxford University Press, 2000.).
16.2 La fricción estática
Existen cuatro tipos principales de fricción, la fricción estática fs, la fricción dinámica fk la fricción de rodamiento fr, y la fricción de arrastre fa.
La fricción estática fs es la fuerza de fricción que actúa sobre un objeto en reposo y que impide que comience a moverse. Se produce cuando la fuerza externa aplicada al objeto no es suficiente para superar la fuerza de fricción entre las superficies en contacto. La fricción estática se puede superar aplicando una fuerza externa mayor que la fuerza de fricción estática, lo que permite que el objeto comience a moverse.
Dado que la fricción se desprende de las fuerzas normales a nivel microscópico en muchas direcciones, esta posee las propiedades de la fuerza normal, en el sentido de que el objeto no entrará en movimiento a menos que la fuerza aplicada supere el límite crítico de la fuerza de fricción estática. Eso se debe porque la fuerza de fricción estática aumentará en el sentido opuesto al movimiento manteniendo el objeto en equilibrio estático. De allí que lo que en verdad nos interesa en los ejercicios de lápiz y papel es el valor crítico de la fricción estática o fuerza de fricción estática máxima fs,max.
La fricción estática tiene muchas aplicaciones prácticas en la vida cotidiana y en la industria, algunas de las cuales se describen a continuación:
(a) La fricción estática es esencial para el funcionamiento seguro de muchos objetos cotidianos, como zapatos con suelas antideslizantes, frenos de automóviles y bicicletas, y herramientas de agarre como alicates y llaves inglesas. En todos estos casos, la fricción estática es necesaria para que los objetos se mantengan en su lugar o se detengan cuando se aplica una fuerza.
(b) En la industria, la fricción estática se utiliza para mantener los objetos en su lugar durante la fabricación y el transporte. Por ejemplo, los objetos pesados en un almacén pueden ser sujetados con bandas de fricción para evitar que se deslicen y se caigan. De manera similar, las cargas en un camión o en un barco pueden ser aseguradas con bandas de fricción para evitar que se muevan durante el transporte.
(c) La fricción estática también se utiliza en la fabricación de materiales resistentes al deslizamiento, como el asfalto rugoso utilizado en las carreteras y las baldosas con textura para el suelo. Estos materiales tienen una superficie áspera que aumenta la fricción estática, lo que reduce el riesgo de resbalones y caídas.
(d) En el ámbito deportivo, la fricción estática es esencial para deportes como el escalado, donde los escaladores utilizan la fricción estática entre sus zapatos y la pared de roca para mantenerse en su lugar.
En el modelo matemático, dado sus derivaciones de la normal, diremos que esta fuerza es menor o igual a su valor crítico, después de lo cual, el objeto debería iniciar su movimiento en la dirección de la fuerza aplicada, siendo esta fuerza aplicada, la normal con respecto a la superficie de rozamiento n. \[f_{smax}\leq \mu \cdot n\]Eq 16.1. Desigualdad de Fuerza de Fricción Máxima (Vista imagen).
Serway 9na edición
Ejemplo 5.11. Demuestre una fórmula para calcular la fuerza de contacto resultante al comprimir dos cajas con fuerzas opuestas.
16.3 La fricción dinámica o cinética
Por otro lado, la fricción dinámica fc o fk es la fuerza de fricción que actúa sobre un objeto en movimiento en relación con una superficie y que se opone al movimiento del objeto. Es la fuerza que se opone al movimiento de un objeto y hace que se desacelere. La magnitud de la fricción dinámica depende del coeficiente de fricción entre las superficies en contacto, la normal o fuerza de reacción de la superficie y la velocidad del objeto. Históricamente podemos considerar a la fuerza de fricción dinámica como la causa por la cual Aristóteles se equivocó, hoy dado que él no concebía mentalmente la existencia de la fricción dinámica que se opone al movimiento, el opinaba que se necesitaba siempre una fuerza aplicada para que el objeto se mantuviera en movimiento.
Sin embargo, en nuestra perspectiva la fricción dinámica va a oponerse a la fuerza aplicada y eso es lo que explica por qué los objetos en la vida cotidiana aparentan no cumplir el principio de inercia, sin embargo, si un objeto se mueve en un sistema que no ofrezca resistencia dinámica por fricción, este cumplirá completamente la ley de inercia.
La fricción dinámica también tiene varias aplicaciones prácticas en la vida cotidiana y en la industria. A continuación, se presentan algunas de ellas:
(a) La fricción dinámica es esencial para el funcionamiento de los sistemas de frenos de automóviles y bicicletas. En estos sistemas, las pastillas de freno ejercen una fuerza de fricción sobre los discos o las ruedas, lo que reduce la velocidad del vehículo. Sin la fricción dinámica, los frenos no funcionarían correctamente y podrían producirse accidentes.
(b) Los sistemas de transmisión de energía, como las cadenas de bicicletas, también dependen de la fricción dinámica para funcionar correctamente. En este caso, la fuerza de fricción entre la cadena y los dientes de los piñones permite que la energía se transfiera eficientemente de los pedales a las ruedas.
(c) La fricción dinámica también se utiliza en la fabricación de herramientas abrasivas, como lijas y discos de corte. Estas herramientas tienen partículas abrasivas incrustadas en una matriz dura que se frotan contra la superficie de trabajo para pulirla o cortarla. La fricción dinámica entre las partículas abrasivas y la superficie es lo que produce el efecto de lijado o corte.
(d) En la industria de la maquinaria pesada, la fricción dinámica se utiliza en los sistemas de frenado y embrague para controlar la velocidad y la potencia de las máquinas. Por ejemplo, en una grúa o una excavadora, la fricción dinámica entre las pastillas de freno y los discos permite controlar la velocidad de la carga que se levanta o mueve.
Algunos ejercicios sencillos que implican fricción cinética abordan parámetros de movimiento acelerado, típicamente enfocados en la modelación de situaciones de frenado. Estos problemas de física exploran cómo los objetos en movimiento interactúan con la fuerza de fricción que se opone a su dirección. Durante estas situaciones, es crucial comprender cómo la fricción cinética influye en la aceleración de un objeto y cómo afecta su velocidad en función del tiempo.
En estos ejercicios, se consideran factores como el coeficiente de fricción entre las superficies en contacto y la masa del objeto en movimiento. Estos parámetros influyen en la magnitud de la fuerza de fricción y, por lo tanto, en la aceleración resultante. Resolver estos problemas implica aplicar principios fundamentales de la física, como la segunda ley de Newton, para determinar cómo cambia la velocidad de un objeto a medida que experimenta un frenado gradual debido a la fricción cinética. Esto nos permite comprender mejor cómo se comportan los objetos en movimiento en situaciones del mundo real.
El modelo matemático en este caso es mas simple, aunque vuelve a ser lineal y mediado por una constante de proporcionalidad llamada coeficiente de fricción.
Figura 16.3. Gráfica de la fuerza de fricción ejercida sobre la caja por el piso como función de la fuerza aplicada. La fuerza de fricción equilibra la fuerza aplicada hasta que la caja comienza a deslizarse, lo que ocurre cuando la fuerza aplicada excede por una cantidad infinitesimal a la fuerza máxima de rozamiento estático. Posterior a esto, la fuerza de oposición cae pasando a ser modelada por el rozamiento dinámico, lo cual implica que se necesita ejercer mas fuerza para iniciar el movimiento que para mantenerlo
Por lo general, al analizar las fuerzas de rozamiento, solemos caer en la trampa de aplicar signos positivos o negativos, lo que puede llevar a confusiones, especialmente en situaciones que involucran planos inclinados. Es por eso que proponemos abordar el estudio del rozamiento desde la perspectiva del ángulo en lugar de depender únicamente de los signos. Esto nos permitirá tener un enfoque más claro y preciso en nuestro análisis.\[f = \mu \cdot n\]Eq 16.2. Definición de la fuerza de fricción cinética en términos del coeficiente de fricción cinético \(\mu\) y la normal \(n\) (Vista imagen).
Una de las características fundamentales de la fricción cinética es su resistencia al movimiento, una cualidad que a menudo pasa desapercibida. Por lo tanto, al definir la ecuación relacionada con esta fuerza, la abordaremos considerando el ángulo del vector de desplazamiento.
Demostración: Exprese la normal en términos de la fuerza peso y el ángulo de desplazamiento.\[f = -\mu \cdot F_g \cdot \Theta_d\]Eq 16.3. Definición de la fuerza de fricción cinética en términos del coeficiente de fricción cinético \(\mu\) y la fuerza peso \(n\) y el ángulo del desplazamiento \(\theta_d\) (Vista imagen).
Si consideramos una o más fuerzas incidentes además de la fricción en un plano horizontal, podemos desarrollar una fórmula que simplifique la resolución de este escenario, evitándonos la necesidad de realizar un análisis detallado de fuerzas en cada ocasión. Esta fórmula proporcionará una manera eficiente de calcular la resultante de todas las fuerzas involucradas en el movimiento de un objeto sobre la superficie horizontal, teniendo en cuenta tanto las fuerzas aplicadas como la resistencia debida a la fricción. Esta herramienta matemática nos permitirá abordar de manera más ágil y precisa situaciones en las que múltiples fuerzas actúan simultáneamente en un plano horizontal, lo que simplificará el proceso de resolución de problemas y nos ayudará a comprender mejor el comportamiento de los objetos en movimiento en estas condiciones específicas.
Demostración: Obtenga una fórmula que permita calcular la aceleración en términos de una o mas fuerzas incidentes y la fricción cinética.\[a_x = \frac{F_i \cdot \cos(\theta_i) - \mu \cdot F_g \cdot \cos(\theta_d)}{m} \]Eq 16.4a. \[\mu = \frac{F_i \cdot \cos(\theta_i) - m \cdot a_x}{F_g \cdot \cos(\theta_d)} \]Eq 16.4b. Cálculos de la aceleración o el coeficiente de fricción en un plano horizontal simple (Vista imagen).
La ecuación 16.4(a y b) presenta una limitación crítica: solo es aplicable cuando la fuerza incidente se encuentra a un ángulo de 0° o 180°. En caso de que cambie a cualquier otro ángulo, la fuerza normal se verá influenciada y, como resultado, la fricción experimentará modificaciones. Esta restricción nos impulsa a buscar una alternativa más robusta y versátil que nos permita abordar situaciones en las que la fuerza actúa en ángulos distintos, brindando una solución más precisa y completa.
Demostración. Demuestre una fórmula para calcular la aceleración en términos de una fuerza incidente en cualquier ángulo de rotación teniendo en cuenta la fricción cinética.\[a_x = \frac{\mu \cos(\theta_d) (F_i \sin(\theta_i) - F_g) + F_i \cos(\theta_i)}{m} \]Eq 16.5a. \[\mu = \frac{m \cdot a_x - F_i \cos(\theta_i)}{\cos(\theta_d) (F_i \sin(\theta_i) - F_g)}\]Eq 16.4b.
Cálculos de la aceleración \(a_x\) o el coeficiente de fricción \(\mu\) en un plano horizontal simple en términos de una fuerza incidente \(F_i\) en cualquier dirección \(\theta_i\). (Imagen)
Hipertexto 1 Ejemplo página 112. Sobre una caja de masa 8.0 kg se aplica una fuerza de 80.0 N que forma con la horizontal un ángulo de 30° (300°) y este se desliza sobre una superficie plana. El coeficiente de rozamiento cinético entre el bloque y la superficie es de 0.20. Determinar la aceleración con la cual se mueve el objeto.
16.5 Fricción y planos inclinados
En el ámbito de la mecánica, la fricción es un fenómeno omnipresente que juega un papel crucial en una amplia gama de situaciones. Una de las configuraciones más interesantes donde la fricción se manifiesta de manera notable es en el contexto de los planos inclinados y las máquinas de Atwood con poleas simples. Estas situaciones desafiantes implican la interacción entre la gravedad, la fricción y la tensión en las cuerdas, creando un entorno ideal para estudiar cómo estas fuerzas interactúan y afectan el comportamiento de los sistemas mecánicos.
En esta subsección, exploraremos detalladamente los conceptos relacionados con la fricción en el plano inclinado y cómo esta fuerza influye en el movimiento de objetos a lo largo de una superficie inclinada. Investigaremos las fuerzas que actúan sobre un cuerpo colocado en un plano inclinado y cómo la fricción contrarresta el movimiento. Analizaremos tanto el caso de la fricción estática, donde el objeto permanece en reposo, como el caso de la fricción cinética, cuando el objeto se desplaza a lo largo del plano.
Además, nos sumergiremos en el intrigante mundo de las máquinas de Atwood con poleas simples, una configuración mecánica que involucra dos masas conectadas por una cuerda que pasa por una polea. Estudiaremos cómo la fricción en la polea y en las superficies de contacto afecta el equilibrio de las masas y cómo se traduce en los movimientos observados. A través de análisis detallados y cálculos precisos, exploraremos cómo las fuerzas de fricción pueden tanto limitar como habilitar el movimiento en estas máquinas ingeniosas. Iniciaremos nuestro análisis con el plano inclinado sin poleas, que consta de tres casos especiales a saber:
(a) Dirección de la fuerza indidente: Aunque en planos inclinados es común que la fuerza incidente se alinee con el desplazamiento, esta no es siempre la situación. Por lo tanto, es fundamental abordar el escenario general en el que la fuerza incidente, que puede ser una fuerza neta, está actuando en cualquier ángulo. Esto es aplicable tanto en un plano inclinado como en un plano horizontal.
En algunos casos, la fuerza aplicada puede actuar en una dirección diferente al movimiento principal del objeto, lo que complica el análisis. Es importante considerar este escenario más general y aplicar principios fundamentales de la física, como la segunda ley de Newton y las componentes de fuerza, para comprender cómo la fuerza incidente afecta la aceleración y el movimiento en diferentes direcciones. Esta comprensión nos permite resolver problemas de manera más completa y precisa, independientemente del ángulo en el que actúe la fuerza.
(b) Dirección del desplazamiento: En un plano inclinado, el vector de desplazamiento estará alineado con el plano inclinado en una sola dirección, que consideraremos como positiva en el sentido ascendente y negativa en el sentido descendente. Para abordar este comportamiento de manera más clara y consistente, optamos por realizar análisis basados en ángulos. Esto implica definir el ángulo del desplazamiento de manera que sea igual al ángulo del plano inclinado en un caso y en el otro, sumarle 180°.
De manera similar, cuando horizontalizamos el plano inclinado, cambiamos la relación entre el desplazamiento y el plano. En este caso, establecemos que el ángulo es de 0° para el desplazamiento positivo y 180° para el desplazamiento negativo.
Por convención, asumimos que la dirección positiva en cualquier plano inclinado es aquella que va en contra de la fuerza peso, lo que nos permite mantener una referencia coherente en nuestros cálculos y análisis, independientemente de la dirección del movimiento.
Demostración: Demuestre una fórmula para calcular una aceleración en términos de una fuerza incidente que apunta en cualquier dirección, teniendo en cuenta la fricción cinética en un plano inclinado. Aunque aún no hemos proporcionado una ecuación final para la aceleración, es importante destacar que con las expresiones de las fuerzas involucradas, podemos simplificar el cálculo de la aceleración a una suma directa de fuerzas y luego aplicar la segunda ley de Newton
\[F_{gx} = -F_g \sin\phi \]Eq 16.6. Componente en el plano inclinado de la fuerza peso.
\[F_{ix} = F_i \cos\theta_i \]Eq 16.7. Componente en el plano inclinado de la fuerza incidente.
\[f_x =\pm \mu (F_i \sin\theta_d - F_g \cos\phi) \]Eq 16.8. Fuerza de rozamiento \(f_x\) en términos de la fuerza peso \(F_g\), la fuerza incidente \(F_i\) de dirección cualquiera \(\theta_i\) y la dirección del desplazamiento \(\theta_d\).
Ten en cuenta que el ángulo de la fuerza incidente puede expresarse en relación al plano inclinado o al plano horizontal, por lo que es esencial leer cuidadosamente para evitar cálculos innecesarios. En caso de que el enunciado proporcione el ángulo de incidencia real, puedes aplicar la siguiente fórmula, donde \(\theta_{i} = \phi_i - \phi \), donde \(\phi_i\) es el ángulo incidente verdadero y \(\phi\) es el ángulo del plano inclinado: Esta fórmula te permite relacionar el ángulo de incidencia real con el ángulo del plano inclinado. Utilizarla te ayudará a interpretar correctamente el problema y aplicar los conceptos adecuados sin realizar cálculos innecesarios.
Es esencial tener precaución con enunciados que mencionan "aceleración cero", ya que, a menos que sean explícitos, suelen conllevar dos posibles soluciones. Estas abarcan tanto el movimiento ascendente como el descendente. La ausencia de aceleración no siempre indica inmovilidad, por lo que en tales contextos, debemos presentar ambas soluciones para abarcar todas las posibilidades.
Antes de calcular la fricción, debes tener en cuenta dos detalles. En primer lugar, si el enunciado indica una dirección de movimiento, entonces la fricción actuará en sentido contrario a esa dirección. Por otro lado, si no se especifica la dirección, debes sumar la fuerza incidente y la fuerza peso. El signo del resultado será opuesto al de la fricción.
16.6 Máquinas de Atwood
Una máquina de Atwood es un dispositivo mecánico que se utiliza para analizar sistemas en los cuales dos objetos con masas diferentes están conectados a través de una cuerda que pasa por una polea. La máquina de Atwood se usa comúnmente en problemas de física para estudiar la aceleración y la tensión en la cuerda cuando los dos objetos están sometidos a la gravedad. Existen varios tipos de máquinas de Atwood, que varían según la configuración y las fuerzas involucradas:
(a) Máquina de Atwood Simple: En este tipo básico, dos masas diferentes están suspendidas a ambos lados de una polea, y la cuerda pasa sobre la polea sin fricción. La diferencia de masa entre los objetos crea una aceleración.
(b) Máquina de Atwood Compuesta: En esta versión, se agregan más masas conectadas por cuerdas adicionales a la configuración básica. Esto puede hacer que el problema sea más complejo al considerar múltiples fuerzas y aceleraciones.
(c) Plano Inclinado con rozamiento con dos cuerpos: Este es uno de los tipos más complejos de máquinas de Atwood. Aquí, uno o ambos objetos pueden estar en un plano inclinado con rozamiento, lo que agrega la complicación de las fuerzas de fricción al análisis. Esta configuración se utiliza para problemas más realistas que incluyen superficies rugosas y pendientes.
Sin embargo, trabajar con un algoritmo que involucra 8 ecuaciones puede resultar tedioso, a pesar de que reduce a la mitad el tiempo de resolución en comparación con la técnica clásica que mis colegas enseñan. Por esta razón, basándonos únicamente en la intuición, buscaremos un algoritmo que requiera menos ecuaciones y cálculos, pero que aún nos permita responder a 4 preguntas esenciales: la dirección de movimiento en ausencia de fricción, la masa efectiva de la fricción, la aceleración y la tensión en el sistema.
Demostración: Optimice el sistema de ecuaciones del plano inclinado doble.
\[\Delta m_{\text{ef}} = m_{\text{de}} \cdot \sin\phi_{\text{de}} - m_{\text{iz}} \cdot \sin\phi_{\text{iz}}\]Eq 16.9. Diferencia de masas efectivas que aportan a la dirección de la aceleración, el signo de esta operación será el signo inverso de la fricción.
\[\Sigma m_{\text{fr}} = \mu_{\text{de}} \cdot m_{\text{de}} \cdot \cos\phi_{\text{de}} + \mu_{\text{iz}} \cdot m_{\text{iz}} \cdot \cos\phi_{\text{iz}}\]Eq 16.10. Suma de masas efectivas que aportan a la fricción.
\[a = g \left(\frac{\Delta m_{\text{ef}} \pm \Sigma m_{\text{fr}}}{m}\right)\]Eq 16.11. Aceleración del sistema de masas conectadas \(a\) en términos de la diferencia de masas efectiva \(\Delta m_{\text{ef}}\) y la suma de masas que aportan al rozamiento \(\Sigma m_{\text{fr}}\).
\[T = m_{\text{iz}} \left(a - g(-\sin\phi_{\text{iz}} \pm \mu_{\text{iz}} \cos\phi_{\text{iz}})\right)\]Eq 16.12. Tensión de la cuerda.
(d) Plano Inclinado con rozamiento con tres cuerpos: Este es uno de los tipos más complejos de máquinas de Atwood. Aquí, tenemos tres cuerpos, dos poleas y dos tensiones.
16.7 La fricción de rodamiento
Es un tipo de fricción que se produce cuando un objeto rueda sobre una superficie en lugar de deslizarse sobre ella. La fricción de rodamiento es diferente de la fricción estática y dinámica, ya que depende de otros factores además del coeficiente de fricción, como el tamaño y la forma de los objetos en contacto y la elasticidad de los materiales. La fricción de rodamiento se produce cuando un objeto rueda sobre una superficie y la fricción actúa en la zona de contacto entre el objeto y la superficie.
Donde el coeficiente de fricción depende de la naturaleza de las superficies en contacto y la composición de la rueda y la carretera. Los valores típicos de son de 0.01 a 0.02 para llantas de caucho sobre concreto y de 0.001 a 0.002 para ruedas de acero sobre rieles de acero. Los coeficientes de fricción de rodadura suelen ser menores que los coeficientes de fricción cinética en uno o dos órdenes de magnitud. La fricción de rodadura se considera insignificante en este libro, excepto donde se indique específicamente que es significativa.
La fricción de rodamiento se presenta en situaciones en las que un objeto rueda sobre una superficie. Algunas aplicaciones de la fricción de rodamiento en la vida cotidiana y la industria son:
(a) Vehículos: La fricción de rodamiento se presenta en los neumáticos de los automóviles y otros vehículos. El coeficiente de fricción de los neumáticos en la carretera es un factor importante en la eficiencia del combustible y la estabilidad del vehículo.
(b) Rodillos transportadores: En la industria, se utilizan transportadores con rodillos que permiten mover materiales de un lugar a otro. La fricción de rodamiento es esencial para el funcionamiento de estos transportadores.
(c) Maquinaria pesada: En la construcción y la minería, se utilizan maquinarias pesadas que tienen ruedas o cadenas que permiten el movimiento de la máquina. La fricción de rodamiento es importante para el rendimiento y la eficiencia de estas máquinas.
(d) Juguetería: Muchos juguetes, como los carritos, tienen ruedas que requieren fricción de rodamiento para moverse.
(e) Equipo deportivo: Muchos deportes, como el patinaje sobre ruedas y el skateboarding, involucran la fricción de rodamiento para el movimiento.
(f) Industria alimentaria: En la industria alimentaria, las cintas transportadoras y otros equipos también requieren fricción de rodamiento para el movimiento de los productos.
16.6 Fricción de arrastre
Se produce cuando un objeto se mueve a través de un medio poco denso como el aire, el agua o incluso la tierra, se llama fricción por arrastre o fricción por fluidos. Este tipo de fricción se debe a la interacción entre el objeto en movimiento y las moléculas del fluido que lo rodea.
La fricción de arrastre, también conocida como fricción viscosa o fricción de fluidos, se presenta en situaciones en las que un objeto se mueve a través de un fluido como aire o agua. Algunas aplicaciones de la fricción de arrastre en la vida cotidiana y la industria son:
(a) Aviación: La fricción de arrastre es importante en la aviación, ya que se debe superar para que un avión pueda volar. Las formas aerodinámicas de los aviones y la elección de materiales tienen en cuenta la fricción de arrastre para reducir la resistencia al aire y mejorar la eficiencia del combustible.
(b) Automóviles: En los automóviles, la fricción de arrastre es un factor importante en la resistencia del aire que afecta la velocidad y la eficiencia del combustible. La aerodinámica del vehículo y la elección de materiales también tienen en cuenta la fricción de arrastre.
(c) Barcos: La fricción de arrastre es un factor importante en la velocidad y la eficiencia del combustible de los barcos. La forma del casco y la elección de materiales tienen en cuenta la fricción de arrastre para mejorar la eficiencia.
(d) Industria química: En la industria química, la fricción de arrastre es importante en el diseño y la operación de tuberías y otros equipos que transportan fluidos.
(e) Deportes acuáticos: Los deportes acuáticos, como el remo y el kayak, implican el movimiento a través del agua y, por lo tanto, la fricción de arrastre es un factor importante en la velocidad.
(f) Aeronáutica: En la aeronáutica, la fricción de arrastre es un factor importante en la resistencia del aire que afecta la velocidad y la eficiencia del combustible. La aerodinámica del avión y la elección de materiales tienen en cuenta la fricción de arrastre.
Figura 16.5. Los lubricantes son una sustancia clave en el mantenimiento de la maquinaria y los equipos mecánicos, ya que tienen como objetivo principal reducir la fricción y el desgaste entre las superficies que entran en contacto. Al hacerlo, protegen las piezas móviles de la maquinaria contra el desgaste y la corrosión, alargando así su vida útil y reduciendo los costos de mantenimiento y reparación. Además, los lubricantes también tienen otras funciones importantes, como la reducción de la temperatura y el ruido en las piezas móviles, el sellado de las juntas y la prevención de la oxidación y la contaminación del sistema. En resumen, los lubricantes son esenciales para garantizar el correcto funcionamiento y la durabilidad de la maquinaria y los equipos mecánicos en una amplia gama de industrias, desde la fabricación y la construcción hasta la automotriz y la aeroespacial.
16.7 Determinación del coeficiente de rozamiento
Los coeficientes de rozamiento se determinan experimentalmente a través de pruebas de fricción. Para ello, se utiliza un aparato llamado "máquina de ensayo de fricción", que puede variar según la aplicación específica. Sin embargo, el principio básico es el mismo: se aplica una fuerza conocida a un cuerpo y se mide la fuerza de fricción que se opone al movimiento.
Para determinar el coeficiente de rozamiento estático, se aplica gradualmente una fuerza horizontal a un objeto en reposo sobre una superficie y se mide la fuerza necesaria para hacer que el objeto comience a moverse. El coeficiente de rozamiento estático se define como la razón entre la fuerza necesaria para mover el objeto y la fuerza perpendicular a la superficie de contacto.
Para determinar el coeficiente de rozamiento dinámico, se aplica una fuerza horizontal constante a un objeto en movimiento sobre una superficie y se mide la fuerza de fricción que se opone al movimiento. El coeficiente de rozamiento dinámico se define como la razón entre la fuerza de fricción y la fuerza perpendicular a la superficie de contacto.
Es importante tener en cuenta que los coeficientes de rozamiento dependen de muchos factores, como el tipo de materiales que entran en contacto, la rugosidad de las superficies y la temperatura. Por lo tanto, es importante realizar las pruebas de fricción en condiciones controladas y reproducibles para obtener resultados precisos y confiables.
Tabla 16.2. Coeficientes aproximados de fricción cinética y estática según la Tipler sexta edición.
tenga en cuenta que los coeficientes de fricción son aproximaciones que pueden variar de un libro de texto a otro por lo tanto para poder resolver un ejercicio de fricciones es conveniente que revise en el libro de texto cuáles son los valores que se han empleado allí.
A diferencia de la tensión, la fricción si se consideraba una fuerza por lo tanto en su fórmula lineal en la que se relaciona la fuerza aplicada con la fuerza de fricción el coeficiente de fricción va a ser adimensional.
16.8 Frenos de antibloqueo
El bloqueo de los frenos ocurre cuando la fuerza de fricción estática es superada y la rueda se detiene de manera brusca. En este caso, la fricción cinética entre la superficie de la rueda y la del suelo se reduce significativamente, lo que hace que la rueda pueda deslizarse o patinar. El bloqueo de los frenos puede ocurrir cuando se aplican los frenos de manera brusca y la fuerza de fricción estática entre las ruedas y el suelo se excede.
Para evitar el bloqueo de los frenos, se han desarrollado sistemas de frenos antibloqueo (ABS). Los sistemas ABS utilizan sensores para detectar si una rueda se está bloqueando y ajustan la fuerza de frenado para evitar el bloqueo. Esto se logra mediante la reducción temporal de la fuerza de frenado, lo que aumenta la fricción cinética y reduce la posibilidad de que la rueda se bloquee.
En términos de las leyes del movimiento, el bloqueo de los frenos y el uso del sistema de frenos ABS se pueden explicar mediante la segunda ley de Newton. Esta ley establece que la fuerza neta sobre un objeto es igual a la masa del objeto multiplicada por su aceleración. En el caso de los frenos, la fuerza neta sobre el vehículo se debe principalmente a la fuerza de fricción entre las ruedas y la superficie del suelo. Si la fuerza de frenado es mayor que la fuerza de fricción máxima, la rueda se bloquea y la fuerza de fricción se reduce significativamente, lo que hace que el vehículo pierda tracción y se deslice sin control en su tangente rectilínea.
Por lo tanto, para mantener un frenado eficiente y evitar el bloqueo de los frenos, es necesario conocer los coeficientes de fricción estática y cinética entre las ruedas y la superficie del suelo, y utilizar los sistemas de frenos adecuados para evitar la pérdida de tracción, o ¡no frenar como un animal!
17. La fuerza de arrastre
|| REGRESAR AL ÍNDICE ||
Sacar la mano por la ventana de un automóvil que se mueve rápidamente te convencerá de la existencia de la resistencia de los fluidos, la fuerza que un fluido (gas o líquido) ejerce sobre un cuerpo que se mueve a través de él en contra de su avance. La dirección de la fuerza de resistencia del fluido que actúa sobre un cuerpo siempre es opuesta a la dirección de la velocidad del cuerpo con respecto al fluido, lo cual no debe sorprender, pues aunque un fluido no pueda ejercer una normal poderosa que detenga inmediatamente, si es lo suficientemente grande como para disminuir la velocidad de movimiento.
La magnitud de la fuerza de resistencia del fluido generalmente aumenta con la velocidad del cuerpo a través del fluido, y disminuye con el área de contacto, de allí que los móviles con forma de flecha se muevan mejor que los que tienen una cara de ladrillo.
Figura 17.1. Cuando el paracaídas se despliega, las fibras del tejido crean una gran superficie que se encuentra con el aire que se mueve a alta velocidad. Esta colisión entre el aire y el tejido del paracaídas crea una fuerza de fricción de arrastre que actúa en sentido contrario al movimiento de la persona. A medida que la velocidad del paracaidista disminuye, la fuerza de fricción de arrastre se reduce, permitiendo al paracaídas descender de manera segura. Es importante que el paracaídas esté diseñado y fabricado de manera que la fricción de arrastre sea suficiente para reducir la velocidad del paracaidista de manera controlada, pero no tanto que lo frene bruscamente, lo que podría causar lesiones o dañar el equipo. Por lo tanto, los diseñadores de paracaídas deben considerar cuidadosamente la forma, el tamaño y los materiales utilizados en su construcción para garantizar un descenso seguro y controlado del paracaidista.
17.1 Modelos matemáticos
El modelo matemático de la fricción de arrastre es muy diferente de otras fuerzas de fricción entre dos superficies en contacto, que normalmente podemos considerar como independiente de la velocidad. Para objetos pequeños que se mueven a velocidades muy bajas:
donde μd es una constante de proporcionalidad que depende de la forma y tamaño del cuerpo y de las propiedades del fluido. Eq. 17.1 es apropiada para partículas de polvo que caen en el aire o un cojinete de bolas que cae en aceite. Para objetos más grandes que se mueven a través del aire a la velocidad de una pelota de tenis lanzada al aire o más rápido, la fuerza de resistencia es aproximadamente proporcional a v2 en lugar de a v. Entonces se llama arrastre del aire o simplemente arrastre. Los aviones, las gotas de lluvia que caen y los ciclistas experimentan la resistencia del aire. En este caso reemplazamos Eq. 17.1 por
Debido a la dependencia de v2, la resistencia aerodinámica aumenta rápidamente al aumentar la velocidad. La resistencia del aire en un automóvil típico es insignificante a bajas velocidades, pero comparable o mayor que la resistencia a la rodadura a velocidades de autopista. El valor de μD depende de la forma y tamaño del cuerpo y de la densidad del aire.
17.2 Nuevas ecuaciones de movimiento
Debido a los efectos de la resistencia de los fluidos, un objeto que cae en un fluido no tiene una aceleración constante. Para describir su movimiento, no podemos usar las relaciones de aceleración constante; en cambio, tenemos que empezar de nuevo con la segunda ley de Newton.
DEMOSTRACION. Determinar la fórmula para la velocidad terminal.
Esta expresión para la velocidad terminal explica por qué los objetos pesados en el aire tienden a caer más rápido que los objetos ligeros. Dos objetos que tienen el mismo tamaño físico pero diferente masa (digamos, una pelota de tenis de mesa y una pelota de plomo con el mismo radio) tienen el mismo valor de μD pero diferentes valores de m. El objeto más masivo tiene una velocidad terminal más alta y cae más rápido. La misma idea explica por qué una hoja de papel cae más rápido si primero la arrugas en una bola; la masa m es la misma, pero el tamaño más compacto hace que μD sea más pequeña (menos arrastre del aire para una velocidad dada) y vt más grande. Los paracaidistas usan el mismo principio para controlar su descenso.
Figura 17.2. Cuando un nadador se desplaza a través del agua, su cuerpo crea una gran resistencia debido a la fricción de arrastre, ya que el agua es un fluido mucho más denso que el aire. Esto puede ralentizar al nadador y hacer que se fatigue más rápido, reduciendo su eficiencia y su rendimiento. Para reducir la fricción de arrastre en un nadador, se toman varias medidas. Una de ellas es la utilización de trajes de baño de materiales especiales que reducen la fricción al aumentar la hidrodinámica del nadador, permitiendo que el agua fluya más suavemente alrededor del cuerpo. Los trajes de baño también pueden ser ajustados para adaptarse a la forma del cuerpo del nadador y reducir el espacio entre la piel y la tela. Además, la técnica de natación también puede reducir la fricción de arrastre. Los nadadores olímpicos suelen utilizar movimientos suaves y fluidos en el agua, evitando movimientos bruscos o de alta resistencia que puedan aumentar la fricción. También pueden utilizar técnicas de respiración adecuadas para reducir la resistencia del agua en la cabeza y el cuello.
18. La fuerza centrípeta
|| REGRESAR AL ÍNDICE ||
Cuando escribimos el modelo matemático de la partícula en movimiento circular uniforme asumimos que se trataba de una partícula sin masa. Sin embargo, si la partícula tiene una masa m determinada, y adicionalmente tenemos una aceleración centrípeta determinada, resultó evidente que podremos calcular una fuerza centripeta empleando el producto de estos dos valores.
La fuerza centrípeta es la fuerza que mantiene a un objeto en movimiento circular. Esta fuerza siempre apunta hacia el centro de la trayectoria circular y su magnitud depende de la masa del objeto, la velocidad a la que se mueve y el radio de la trayectoria circular.
La importancia de la fuerza centrípeta en la historia de la ciencia radica en que fue uno de los conceptos clave que permitieron a los científicos entender y explicar el movimiento de los planetas alrededor del Sol. En particular, la ley de gravitación universal de Newton, combinada con la fuerza centrípeta, permitió a los científicos explicar por qué los planetas se mueven en órbitas elípticas alrededor del Sol.
En la vida cotidiana, la fuerza centrípeta es importante en muchas situaciones en las que se produce movimiento circular, como en las curvas de las carreteras, los giros en los parques de atracciones o las vueltas en una lavadora. En estas situaciones, la fuerza centrípeta es necesaria para mantener a las personas o los objetos en movimiento circular y evitar que salgan despedidos hacia afuera de la trayectoria.
En la industria, la fuerza centrípeta también es importante en muchas aplicaciones, como en las centrífugas utilizadas para separar líquidos de sólidos o para medir la densidad de una muestra. En estas aplicaciones, la fuerza centrípeta se utiliza para separar los componentes de una mezcla en función de su densidad, ya que los componentes más densos se desplazan hacia el exterior de la trayectoria circular con mayor rapidez que los menos densos.
R. Referencias
|| REGRESAR AL ÍNDICE ||
Arons, A. B., & Redish, E. F. (1997). Teaching introductory physics (Vol. 22). Wiley New York.
Bakker, F., & Palmerino, C. R. (2020). Motion to the Center or Motion to the Whole? Plutarch’s Views on Gravity and Their Influence on Galileo. Isis, 111(2), 217–238.
BIPM. (2016). The name “kilogram”: a historical quirk. Retrieved December 24, 2016, from http://www.bipm.org/en/measurement-units/history-si/name-kg.html
Blaber, E. A., Finkelstein, H., Dvorochkin, N., Sato, K. Y., Yousuf, R., Burns, B. P., … Almeida, E. A. C. (2015). Microgravity reduces the differentiation and regenerative potential of embryonic stem cells. Stem Cells and Development, 24(22), 2605–2621.
Bloomfield, L. A. (2015). How things work: the physics of everyday life. John Wiley & Sons.
Brown, D. E. (1989). Students’ concept of force: the importance of understanding Newton’s third law. Physics Education, 24(6), 353.
Brush, S. G. (1999). Why was relativity accepted? Physics in Perspective, 1, 184–214.
Cohen, I. B. (1980). The newtonian revolution. Cambridge University Press.
Drabkin, I. E. (1963). Two Versions of GB Benedetti’s Demonstratio Proportionum Motuum Localium. Isis, 54(2), 259–262.
Fellmann, E. A. (1988). The Principia and continental mathematicians. Notes and Records of the Royal Society of London, 42(1), 13–34.
Galili, I., & Tseitlin, M. (2003). Newton’s first law: Text, translations, interpretations and physics education. Science & Education, 12(1), 45–73.
Gamow, G. (2002). Gravity. Courier Corporation.
Gere, J. M., & Timoshenko, S. P. (1997). Mechanics of Materials. ed. Boston, MA: PWS.
Gianopoulos, A. (2007). Isaac Newton and the laws of motion. Capstone.
Gingras, Y. (2001). What did mathematics do to physics? History of Science, 39(4), 383–416.
Green, M. J., Aylott, J. W., Williams, P., Ghaemmaghami, A. M., & Williams, P. M. (2021). Immunity in space: prokaryote adaptations and immune response in microgravity. Life, 11(2), 112.
Greenberg, J. L. (1986). Mathematical physics in eighteenth-century France. Isis, 77(1), 59–78.
Griffiths, D. (2020). Introduction to elementary particles. John Wiley & Sons.
Halliday, D., Resnick, R., & Walker, J. (2014). Fundamentals of Physics (10th ed.). John Wiley & Sons.
Hanich, L., Holtzman, S., Druyan, A., Soter, S., Braga, B., Tyson, N. G., … Sagan, C. (2014). Cosmos: A Spacetime Odyssey: When Knowledge Conquered Fear. Usa: Twentieth Century Fox Home Entertainment Ltd.
Hanson, N. R. (1959). On the symmetry between explanation and prediction. The Philosophical Review, 68(3), 349–358.
Heilbron, J. L. (2022). Electricity in the 17th and 18th centuries: A study of early modern physics. Univ of California Press.
Krebs, R. E. (1999). Scientific development and misconceptions through the ages: a reference guide. Greenwood Publishing Group.
Milsom, J. (2018). The hunt for earth gravity: A history of gravity measurement from Galileo to the 21st Century. Springer.
Netz, R., & Noel, W. (2011). The Archimedes codex: revealing the secrets of the world’s greatest palimpsest. Hachette UK.
Newton, I. (2013). Philosophie naturalis principia Mathematica.
Nobili, A. M., & Will, C. M. (1986). The real value of Mercury’s perihelion advance. Nature, 320(6057), 39–41.
Olmos, C. Y. M., Roncancio, J. D. R., & Velazco, E. H. B. (2023). Gamification In Physics Class For Athletes: Concerns And Attitudes For A Positive Sporting Life. Journal of Positive School Psychology, 28–48.
OpenStax. (2017). College Physics. Retrieved from https://openstax.org/details/college-physics
Pais, A. (1986). Inward bound: of matter and forces in the physical world.
Pickover, C. (2008). Archimedes to Hawking: laws of science and the great minds behind them. Oxford University Press.
Pollio, V. (1914). Vitruvius, the ten books on architecture. Harvard University Press.
Rashid, R. (1996). Encyclopedia of the History of Arabic Science: Astronomy-Theoretical and Applied. Routledge.
Rovelli, C. (2015). Aristotle’s Physics: A Physicist’s look. Journal of the American Philosophical Association, 1(1), 23–40.
Ruden, D. M., Bolnick, A., Awonuga, A., Abdulhasan, M., Perez, G., Puscheck, E. E., & Rappolee, D. A. (2018). Effects of gravity, microgravity or microgravity simulation on early mammalian development. Stem Cells and Development, 27(18), 1230–1236.
Sagan, C. (1997). Comet. Ballantine Books.
Sarnowsky, J. (2008). Concepts of Impetus and the History of Mechanics. Springer.
Sathasivam, M., Hosamani, R., & Swamy, B. K. (2021). Plant responses to real and simulated microgravity. Life Sciences in Space Research, 28, 74–86.
Schilling, G. (2017). Ripples in spacetime: Einstein, gravitational waves, and the future of astronomy. Harvard university press.
Schlamminger, S. (2018). Redefining the Kilogram and Other SI Units.
Sears, F. W., Zemansky, M. W., Young, H. D., & Freedman, R. A. (2017). University physics with modern physics. (Addison Wesley, Ed.) (14th ed.).
Serway, R. A., & Jewett, J. W. J. (2014). Physics for Scientists and Engineers with Modern Physics, Ninth Edition (9th ed.). Boston: Brooks/Cole.
Sharp, J., & Visual, J. (n.d.). List of Indian inventions and discoveries.
Sheehan, W. (2021). Preliminaries to the Neptune Discovery: Newtonian Gravitational Theory. In Neptune: From Grand Discovery to a World Revealed: Essays on the 200th Anniversary of the Birth of John Couch Adams (pp. 1–40). Springer.
Starr, S. F., & Buell, P. D. (2014). Lost Enlightenment: Central Asia’s Golden Age from the Arab Conquest to Tamerlane. Aestimatio: Sources and Studies in the History of Science, 11, 232–235.
Tegmark, M. (2015). Our mathematical universe: My quest for the ultimate nature of reality. Vintage.
Tipler, P. A., & Mosca, G. (2008). Physics for scientists and engineers, with modern physics (6th ed.). New York: W. H. Freeman and Company.
Vandenbrink, J. P., & Kiss, J. Z. (2019). Plant responses to gravity. In Seminars in Cell & Developmental Biology (Vol. 92, pp. 122–125). Elsevier.
Wallace, W. A. (2018). Domingo de Soto and the early Galileo: essays on intellectual history. Routledge.
Weinberg, S. (1987). Newtonianism and today’s physics. Three Hundred Years of Gravitation, 5–16.
Westfall, R. S. (1977). The construction of modern science: Mechanisms and mechanics. Cambridge University Press.
Wolpert, L. (2002). Science and mathematics in ancient Greek culture. Oxford University Press on Demand.
Zayzafoon, M., Meyers, V. E., & McDonald, J. M. (2005). Microgravity: the immune response and bone. Immunological Reviews, 208(1), 267–280.




































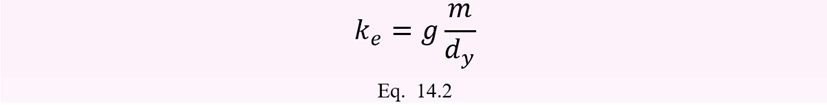







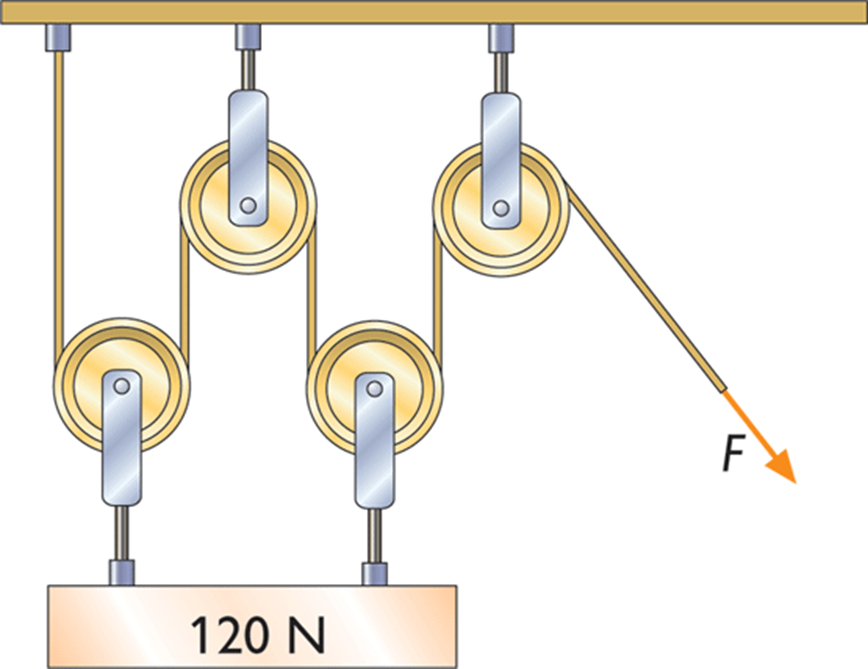



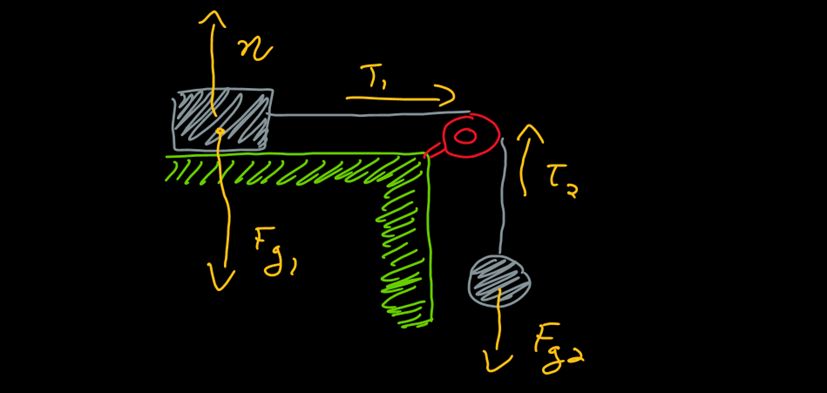



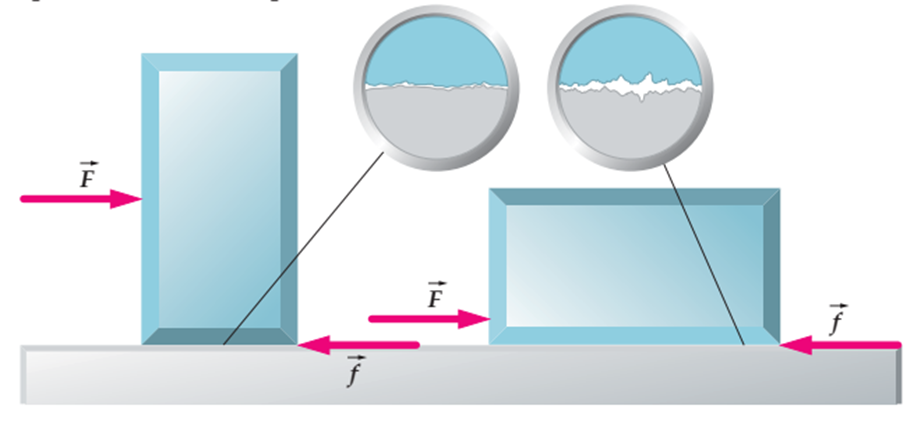











No hay comentarios:
Publicar un comentario