Índice
Índice
||1|| Introducción ||2|| Historia ||3|| La actividad química ||4|| Cantidad de reacción ||5|| La velocidad de una reacción ||6|| Factores que afectan la velocidad de la reacción ||7|| Estequiometría de la cinética de la reacción ||8|| Masa total y cantidad de sustancia total ||9|| La velocidad instantánea | ||10|| Ley de la velocidad de reacción ||11|| Reacciones de primer orden ||12|| Reacciones de segundo orden ||13|| Reacciones de orden cero ||14|| Vida media de un reactivo y la medida de tiempo ||15|| Energía de activación ||16|| Usando la ecuación de Arrhenius ||17|| Mecanismos de reacción ||18|| Catalizadores |
1. Introducción
1. Introducción
La cinética química, también conocida como cinética de reacción, es la rama de la química física que se ocupa de comprender las velocidades de las reacciones químicas. Debe contrastarse con la termodinámica, que se ocupa de la dirección en la que ocurre un proceso, pero en sí misma no dice nada sobre su velocidad. La cinética química incluye investigaciones de cómo las condiciones experimentales influyen en la velocidad de una reacción química y producen información sobre el mecanismo de la reacción y los estados de transición, así como la construcción de modelos matemáticos que también pueden describir las características de una reacción química.
(1.1) Peter Waage
Peter Waage fue un químico noruego que, junto con Cato Guldberg, desarrolló la ley de acción de masa en 1864. Esta ley establece que la velocidad de una reacción química es proporcional al producto de las concentraciones de los reactivos elevados a la potencia de sus coeficientes estequiométricos. La ley de acción de masa es una de las leyes fundamentales de la química y ha tenido un impacto significativo en el desarrollo de la ciencia.
Contexto social
Peter Waage nació en el pequeño pueblo de Laurvig, Noruega, en 1833. En ese momento, Noruega era un país independiente, pero estaba bajo la influencia de Dinamarca. La economía de Noruega estaba basada en la agricultura y la pesca. La sociedad noruega era conservadora y tradicional. La religión predominante era el luteranismo. La cultura noruega estaba influenciada por las tradiciones escandinavas.
Waage recibió su educación en la Universidad de Christiania (Oslo), donde estudió química. Después de graduarse, se convirtió en profesor de química en la Universidad de Oslo.
El contexto político, económico, social, religioso y cultural de Peter Waage tuvo un impacto significativo en su vida y su trabajo. La influencia de Dinamarca en Noruega limitó el desarrollo de la ciencia en el país. La economía basada en la agricultura y la pesca dificultaba el acceso a la educación y a la investigación científica. La sociedad conservadora y tradicional no favorecía la innovación. El luteranismo era la religión dominante, pero Waage era un hombre abierto de mente y estaba interesado en diferentes culturas. La cultura noruega, con sus tradiciones escandinavas, influyó en el trabajo de Waage, que se centró en el estudio de los procesos químicos naturales.
A pesar de las limitaciones de su contexto, Waage logró desarrollar una teoría fundamental de la química que sigue siendo relevante en la actualidad
Infancia
Peter Waage nació el 29 de junio de 1833 en la isla de Hidra, Noruega. Era el segundo de ocho hijos de un capitán de barco y un propietario de barcos. El padre de Waage estaba a menudo en el mar, por lo que fue criado principalmente por su madre. La infancia de Waage transcurrió en la isla de Hidra, que se encuentra en una zona remota de Noruega. La isla está rodeada de montañas y mar, y el paisaje es muy bello. Waage adoraba pasar tiempo al aire libre, y desarrolló un fuerte interés por la naturaleza.
Waage era un niño inteligente y curioso, y siempre estaba ansioso por aprender. Asistió a la Escuela Catedralicia de Bergen, donde sobresalió en sus estudios. Se interesó especialmente por la ciencia y las matemáticas. Después de graduarse de la escuela secundaria, Waage estudió química y mineralogía en la Universidad de Christiania (actualmente Oslo). Se graduó en 1859 con una licenciatura en química.
La infancia de Waage fue una experiencia formativa que moldeó sus intereses y valores. Su amor por la naturaleza y su curiosidad por el mundo lo llevaron a una carrera en la ciencia. Fue un científico brillante que hizo contribuciones significativas al campo de la química.
Las experiencias de la infancia de Waage lo ayudaron a convertirse en el científico que fue. Fue un pensador brillante e innovador que hizo contribuciones significativas al campo de la química. Su trabajo sobre la ley de acción de masas sigue siendo relevante hoy en día y se utiliza para comprender y predecir las velocidades de las reacciones químicas.
En particular, Waage pasó gran parte de su infancia en la naturaleza, lo que le dio una apreciación temprana por la belleza y la complejidad del mundo natural. Esta apreciación influyó en su interés por la ciencia y lo llevó a centrarse en el estudio de los procesos químicos naturales.
Waage también fue un niño inteligente y curioso, lo que le facilitó el aprendizaje y la comprensión de conceptos científicos complejos. Estas habilidades lo ayudaron a lograr grandes avances en el campo de la química.
Logros
Estudió química y mineralogía en la Universidad de Christiania (Oslo), donde se graduó en 1859. Después de graduarse, Waage se convirtió en profesor de química en la Universidad de Oslo. En 1864, Waage publicó un artículo con su colega Cato Guldberg, en el que describían la ley de acción de masas. Esta ley establece que la velocidad de una reacción química es proporcional al producto de las concentraciones de los reactivos elevados a la potencia de sus coeficientes estequiométricos.
La ley de acción de masas es una de las leyes fundamentales de la química y ha tenido un impacto significativo en el desarrollo de la ciencia. Ha permitido a los científicos comprender mejor cómo funcionan las reacciones químicas y predecir cómo se producirán.
Otros logros científicos de Waage incluyen:
(a) El desarrollo de un método para determinar la composición de los gases.
(b) El estudio de las propiedades del agua.
(c) El estudio de las reacciones químicas que tienen lugar en el cuerpo humano.
Waage fue un científico brillante e innovador que hizo contribuciones significativas al campo de la química. En 1861, Waage fue nombrado profesor asociado y en 1866 fue nombrado profesor de química en la Universidad de Kristiania. Continuó siendo profesor en la Universidad durante más de 30 años. También fue presidente de la Sociedad Politécnica Noruega de 1868 a 1869, y el primer presidente de la rama noruega de la YMCA cuando se estableció en 1880.
Comunidad científica
La comunidad científica de Peter Waage estaba compuesta por químicos y científicos que trabajaban en el campo de la química física y la termodinámica química en el siglo XIX. Aunque hubo opositores iniciales, con el tiempo, la Ley de Acción de Masas se estableció como un principio fundamental en la química y recibió un amplio respaldo en la comunidad científica.
Los principales colaboradores fueron:
(a) Cato Maximilian Guldberg: Guldberg fue el colaborador más cercano de Waage y juntos formaron un equipo altamente influyente en la química física. La Ley de Acción de Masas, propuesta por ambos, sigue siendo un pilar en la química.
(b) Svante Arrhenius: Aunque Arrhenius no trabajó directamente con Waage, sus contribuciones a la teoría de las soluciones y la teoría de ácidos y bases fortalecieron las ideas de Waage y Guldberg. Arrhenius también propuso la idea de los iones y el concepto de disociación iónica.
(c) Wilhelm Ostwald: Ostwald fue un químico alemán que respaldó y difundió la Ley de Acción de Masas de Waage y Guldberg. Fue fundamental en la promoción de sus ideas en la comunidad científica.
(d) Jacobus Henricus van 't Hoff: Aunque no estuvo directamente relacionado con Waage, van 't Hoff desarrolló de manera independiente ideas similares en termodinámica química, lo que contribuyó a la consolidación de estos conceptos en la comunidad científica.
Y sus principales opositores:
(a) Friedrich Beilstein: Beilstein fue un químico ruso que criticó inicialmente la Ley de Acción de Masas. Sin embargo, con el tiempo, reconoció su validez y comenzó a trabajar en áreas relacionadas.
(b) Marcellin Berthelot: Berthelot, un influyente químico francés, también se mostró escéptico al principio respecto a la Ley de Acción de Masas. Sin embargo, más tarde aceptó la teoría y realizó investigaciones para respaldarla.
Reconocimientos
Peter Waage, el químico noruego conocido por su trabajo en termodinámica y la Ley de Acción de Masas, recibió varios reconocimientos tanto en vida como póstumos. Aunque no se le otorgaron títulos nobiliarios, sus contribuciones a la química le valieron reconocimiento en la comunidad científica y la sociedad en general:
Reconocimientos en Vida:
(a) Miembro de la Real Academia Noruega de Ciencias y Letras: En 1878, Peter Waage fue elegido como miembro de esta prestigiosa institución académica en Noruega, reconociendo su destacada contribución a la ciencia.
(b) Medalla Guldberg-Waage: En honor a su colaboración con Cato Maximilian Guldberg en la formulación de la Ley de Acción de Masas, se estableció la Medalla Guldberg-Waage, que se otorga a científicos destacados en el campo de la química.
(c) En 1858, recibió la medalla de oro del Príncipe Heredero (Kronprinsens gullmedalje) por su trabajo en el desarrollo de la Teoría de los radicales ácidos. Se convirtió en un cand.real. en 1859.
Reconocimientos Póstumos:
(a) Continuación del Legado Científico: La Ley de Acción de Masas de Waage y Guldberg se ha convertido en un pilar fundamental de la química y la termodinámica química, y su legado científico perdura hasta la actualidad.
(b) Conferencias y Simposios en su Honor: En ocasiones, se han organizado conferencias y simposios en honor a Peter Waage y su contribución a la química. Estos eventos reúnen a científicos y académicos para discutir los avances en el campo.
(c) Calles y Edificios Nominados en su Honor: En Noruega y otros lugares, se han nombrado calles, edificios y laboratorios en honor a Peter Waage como una forma de reconocer su importancia en la historia de la ciencia.
¿Como nos afecta su trabajo?
(a) Industria Química: La Ley de Acción de Masas es fundamental en la industria química. Ayuda a los químicos e ingenieros a comprender cómo se comportan las reacciones químicas en diferentes condiciones, lo que es esencial para la producción de una amplia variedad de productos químicos y materiales que utilizamos a diario, como plásticos, medicamentos, productos de limpieza y alimentos procesados.
(b) Farmacología: En la fabricación de medicamentos y productos farmacéuticos, la comprensión de la cinética y equilibrio químico basada en la Ley de Acción de Masas es esencial para garantizar la eficacia y seguridad de los medicamentos que consumimos para tratar diversas enfermedades y afecciones.
(c) Diseño de Baterías y Energía: En la investigación y desarrollo de baterías y tecnologías de almacenamiento de energía, se aplican principios termodinámicos relacionados con el equilibrio químico para mejorar la eficiencia y la duración de las baterías utilizadas en dispositivos electrónicos, vehículos eléctricos y energía renovable.
(d) Procesos Industriales: En la fabricación y producción de productos químicos, petróleo y gas, así como en la generación de energía, se utilizan principios de termodinámica y cinética química para optimizar los procesos, reducir costos y minimizar el impacto ambiental.
(e) Control de la Contaminación: La comprensión de las reacciones químicas y los equilibrios químicos también es esencial en la gestión y el control de la contaminación del aire y el agua, lo que tiene un impacto directo en la calidad de vida y la salud de las comunidades.
(f) Productos de Consumo: La formulación de productos de consumo como alimentos, bebidas, productos de limpieza y cosméticos se basa en la química y la termodinámica química para garantizar la calidad, la estabilidad y la seguridad de estos productos.
¿Qué debemos aprender de él?
La vida y el trabajo de Peter Waage ofrecen varias lecciones valiosas que pueden inspirarnos en diferentes aspectos de nuestras vidas. Aquí hay algunas formas en las que podemos inspirarnos en su vida, limitaciones, obstáculos, logros y su impacto:
A lo largo de su vida, Peter Waage enfrentó obstáculos y desafíos, como la falta de recursos y el escepticismo inicial hacia su trabajo. Sin embargo, perseveró en su búsqueda del conocimiento y continuó trabajando en su investigación hasta alcanzar logros significativos. Su persistencia nos enseña que no debemos rendirnos fácilmente ante las dificultades, sino seguir adelante con determinación.
Waage colaboró estrechamente con Cato Maximilian Guldberg para desarrollar la Ley de Acción de Masas. Esta colaboración demuestra cómo el trabajo en equipo y la cooperación pueden llevar a avances científicos significativos. Nos inspira a valorar las contribuciones de los demás y buscar asociaciones productivas en nuestras vidas y carreras.
A pesar de las limitaciones y obstáculos que enfrentó en su época, el legado de Peter Waage perdura en la ciencia y la química hasta el día de hoy. Esto nos recuerda que nuestras acciones y contribuciones pueden tener un impacto duradero en el mundo, incluso cuando no vemos resultados inmediatos.
Waage fue un pensador creativo que desarrolló una teoría innovadora en un campo científico complejo. Su enfoque en la investigación científica y su capacidad para desafiar las ideas convencionales nos inspiran a adoptar un enfoque crítico y creativo hacia nuestros propios desafíos y problemas. Recuerda que la creatividad no se limita al mundo de las artes plásticas, como la cultura popular moderna nos lo ha hecho creer. La creatividad es algo más amplio, es una habilidad que puede aplicarse en cualquier campo, desde la ciencia y la tecnología hasta los negocios y la resolución de problemas cotidianos. Peter Waage, a través de su trabajo innovador en química, nos muestra que la creatividad científica es igual de valiosa y que pensar de manera original y buscar soluciones novedosas a los desafíos es esencial para impulsar el avance y la innovación en todas las disciplinas.
A través de su trabajo y su colaboración con otros científicos, Peter Waage contribuyó al avance del conocimiento en su campo. Su dedicación a la investigación y su disposición para compartir sus hallazgos nos recuerdan la importancia de la educación y la difusión del conocimiento para el progreso de la sociedad.
2. Historia
2. Historia
Las reacciones químicas tardan tiempo en ocurrir. Algunas reacciones, como la oxidación del hierro o el cambio de color en las hojas, ocurren de manera lenta desde nuestra perspectiva humana y requieren días, meses o años para completarse. Otros, como la reacción de combustión que genera el empuje de un cohete, suceden mucho más rápidamente.
Las reacciones químicas que rigen el metabolismo de los alimentos, el transporte de nutrientes esenciales y la capacidad de su cuerpo para adaptarse a los cambios de temperatura requieren que ocurran reacciones con la velocidad adecuada. De hecho, las consideraciones sobre la velocidad de las reacciones se encuentran entre los aspectos más importantes del diseño de nuevos procesos químicos. El área de la química relacionada con las velocidades de las reacciones es la cinética química.
Como químicos, debemos preocuparnos por la velocidad con la que ocurren las reacciones químicas, así como por los productos de las reacciones, lo implica invocar una variable del lenguaje de la física, el tiempo t. En capítulos anteriores solo hemos tenido en cuenta al tiempo relativo es decir como estado inicial y estado final, pero sin tener en cuenta cuanto tiempo ocurre entre esos dos estados, pero en cinética química, ese período de tiempo se hace importante, por lo que debemos tener en cuenta al tiempo como una cantidad física continua que debe ser modelada matemáticamente por medio del cálculo de derivadas e integrales.
¿Cómo puede un experimento confirmar que una reacción está ocurriendo de una manera particular? ¿Cuál es el mecanismo de la reacción? ¿Qué intermedios están ocurriendo y en qué orden tienen lugar los pasos de creación y ruptura de bonos?
Hay muchos experimentos diseñados para ilustrar cómo ocurren las reacciones. Uno de los métodos utilizados es la cinética química, en la que se mide la velocidad de una reacción. Al hacer cambios en las condiciones de reacción y medir el efecto de los cambios en la velocidad de reacción, podemos inferir lo que está sucediendo a nivel molecular. La cinética química es la medida de la rapidez con que ocurren las reacciones.
Si los cambios en las condiciones afectan la velocidad de reacción, podemos aprender algo sobre cómo ocurre la reacción. Los estudios cinéticos son importantes para comprender las reacciones, y también tienen implicaciones prácticas. Por ejemplo, en la industria, las reacciones se llevan a cabo en reactores en los que los compuestos se mezclan, posiblemente se calientan y se agitan durante un tiempo, y luego se mueven a la siguiente fase del proceso. Es importante saber cuánto tiempo dura la reacción en una etapa antes de continuar, para asegurarse de que la reacción haya terminado antes de comenzar la siguiente.
Al comprender cómo se produce una reacción, se pueden mejorar muchos procesos. Por ejemplo, si se sabe que un intermedio particular está involucrado en una reacción, se puede evitar el uso de condiciones (como ciertos solventes) que sean incompatibles con ese intermedio. Además, se podrían agregar reactivos que harían que ciertos pasos en la reacción sucedan más fácilmente. Los estudios cinéticos no solo son importantes en la industria, sino que también se utilizan para comprender los procesos biológicos, especialmente las reacciones catalizadas por enzimas.
También juegan un papel en la química ambiental y atmosférica, como parte de un esfuerzo por comprender una variedad de cuestiones que van desde el destino de los medicamentos recetados en las aguas residuales hasta la cascada de reacciones involucradas en el ciclo del ozono.
Hasta ahora, nos hemos centrado en el principio y el final de las reacciones químicas: comenzamos con ciertos reactivos y vemos qué productos producen. Este punto de vista es útil, pero no nos dice qué sucede en el medio, es decir, qué enlaces químicos se rompen, cuáles se forman y en qué orden ocurren estos eventos. La velocidad a la que ocurre una reacción química se llama velocidad de reacción o tasa de reacción, simbolizada como (r) dado que ya empleamos la uve para el coeficiente estequiométrico.
Las tasas de reacción pueden ocurrir en escalas de tiempo muy diferentes. Para investigar cómo ocurren las reacciones, debemos examinar las tasas de reacción y los factores que influyen en ellas. La información experimental sobre la velocidad de una reacción dada proporciona evidencia importante que nos ayuda a formular un mecanismo de reacción, que es una vista paso a paso a nivel molecular de la ruta de los reactivos a los productos.
Nuestro objetivo en este capítulo es comprender cómo determinar las velocidades de reacción y considerar los factores que controlan estas velocidades. ¿Qué factores determinan qué tan rápido se estropea la comida, por ejemplo? ¿Cómo se diseña un airbag automotriz que se llena extremadamente rápido después de un accidente automovilístico? ¿Qué determina la velocidad a la que se oxida el acero? ¿Cómo podemos eliminar los contaminantes peligrosos en el escape del automóvil antes de que el escape salga del tubo de escape? Aunque no abordaremos estas preguntas específicas, veremos que las tasas de todas las reacciones químicas están sujetas a los mismos principios.
(Brady & Humiston, 1986; Brown, LeMay, Bursten, Murphy, & Woodward, 2009; Brown et al., 2015; Chang, 2006, 2010; Chang & Overby, 2011; Ebbing & Gammon, 2008; Gilbert, Kirss, Foster, & Davies, 2012; Gorzynski, 2010; Jespersen, Brady, & Hyslop, 2012; Matamála & Gonzalez, 1976; Petrucci, Harwood, & Herring, 2003; Petrucci, Herring, Madura, & Bissonnette, 2010; Raymond, 2014; Silberberg, 2009; Timberlake, 2015; Whitten, Davis, Peck, & Stanley, 2010; Zumdahl & Zumdahl, 2007; Zumdahl, Zumdahl, & DeCoste, 2018).
Como estudiantes de química debemos reconocer el hecho problemático de que mucha de la simbología a la cual estamos acostumbrados como algo casi natural, no fue estandarizada sino hasta la mitad de la década de los años 70 del siglo XX. Lo anterior provoca que sea muy difícil de entender las notaciones empleadas históricamente por los químicos que desarrollaron originalmente conceptos relacionados con la cinética química y la termodinámica. Dado lo anterior, en lo que sigue de esta breve descripción histórica de la cinética química trataremos de omitir lo más posible las notaciones químicas, y si se hacen muy indispensables emplearemos lenguaje moderno.
(2.1) Ludwig Ferdinand Wilhelmy y William Esson (Ptáček, Opravil, & Šoukal, 2018).
El primer estudio cuantitativo en cinética química lo realizó el científico alemán Ludwig Ferdinand Wilhelmy (1812-1864) en 1850, quien utilizó la polarimetría para investigar la conversión catalizada por ácido de la sacarosa. En este primer estudio, Wilhelmy reconoció que la velocidad de reacción era proporcional a la concentración de sacarosa y ácido según una ecuación diferencial que no podríamos entender actualmente dado que no emplea el conjunto de símbolos modernos. Lo importante de la ecuación de Wilhelmy radica en que es una ecuación diferencial que involucra a la variable tiempo.
Sin embargo, se considera que el químico inglés Augustus George Vernon Harcourt (1934-1919) es el primer científico que hizo una contribución significativa en el campo de la cinética química. Fue uno de los primeros en planificar los experimentos para seguir el curso de un cambio químico, aunque su progreso en el área no fue tan bueno debido a sus limitaciones en formación matemática. La primera reacción que fue investigada por Harcourt en cooperación con el matemático británico William Esson fue:
Figura 2.1.
Esta reacción, que ocurre en una solución acuosa muy diluida, avanza a una velocidad conveniente a temperatura ambiente (constante) y podría iniciarse en un instante dado y detenerse abruptamente mediante la adición de yoduro de hidrógeno, que libera yodo. A continuación, se pudo determinar el avance de la reacción valorando la cantidad de yodo con una solución de tiosulfato. Harcourt también se dio cuenta de que la reacción se acelera cuando se forma sulfato manganoso, es decir, ocurre en más de un paso, y propuso la siguiente secuencia de reacción:
Figura 2.2.
Luego, Esson trató de encontrar ecuaciones matemáticas que interpretarían los resultados, basándose en la hipótesis de que: "... la cantidad total de cambio que ocurre en cualquier momento será proporcional a la cantidad de sustancia que queda en ese momento". Debido a la complejidad de las reacciones, Harcourt y Esson solo tuvieron un éxito limitado en la interpretación de sus resultados. Por otro lado, sus trabajos son importantes por contener un tratamiento matemático claro de las reacciones de primer y segundo orden, y de ciertos tipos de reacciones consecutivas. Los procedimientos matemáticos de Esson son los que se utilizan en la actualidad. Estableció ecuaciones diferenciales apropiadas que expresan la relación entre la derivada del tiempo de la concentración de la sustancia reaccionante y la concentración restante y luego obtuvo las soluciones por integración. En 1865, Harcourt y Esson habían comenzado a trabajar en la reacción cinéticamente más simple entre el peróxido de hidrógeno y el yoduro de hidrógeno:
Figura 2.3.
Cuando las soluciones de yoduro de potasio y peróxido de sodio se introducen en presencia de un bicarbonato ácido o medio alcalino, se produce un desarrollo gradual de yodo. Si se agrega hiposulfito sódico (tiosulfato de sodio, Na2S2O3) a la solución, este reconvierte (reduce) el yodo, tan pronto como se forma, en yoduro, pero no parece afectar de otra manera el curso de la reacción. En consecuencia, si el peróxido está presente en exceso sobre el hiposulfito, todo este último se transforma por la acción del yodo naciente en tetrationato. Después de esta conversión, aparece yodo libre en la solución, y su liberación se puede observar con la ayuda de un poco de almidón (indicador, formación de clatrato de yodo-almidón) previamente añadido al líquido.
Esson encontró una ecuación satisfactoria, que describía los resultados de los experimentos de Harcourt. Su primer artículo sobre esto apareció en 1866, y aunque continuaron su trabajo sobre esta reacción durante otros 30 años, no publicaron ningún dato sobre esto hasta 1895 cuando Harcourt y Esson escribieron conjuntamente la Bakerian Lecture pronunciada en el Royal Society.
Anteriormente, en 1884, Jacobus Henricus van’t Hoff (1852-1911) había propuesto varias ecuaciones alternativas para la dependencia de la temperatura, y una de ellas fue adoptada en 1889 por Svante A. Arrhenius. Dicha ecuación proporcionaba una idea del mecanismo de la reacción, por ejemplo, que la energía de activación es la energía mínima requerida para que prosiga la reacción.
Por otro lado, un aspecto interesante del trabajo de Harcourt y Esson es que predijeron un "cero absoluto cinético", en el que cesarían todas las reacciones. Su valor fue -272.6 °C, que está en notable acuerdo con el valor recientemenete descubierto en su época de -273.15 C para el cero absoluto. También hay que señalar que Harcourt, junto con su trabajo cinético, fue tratado de manera muy exhaustiva por M. C. King y J. Shorter.
(2.2) Peter Waage y Cato Guldberg (Ferner & Aronson, 2016)
En 1864, Peter Waage y Cato Guldberg fueron pioneros en el desarrollo de la cinética química al formular la ley de la acción de masas, que establece que la velocidad de una reacción química es proporcional a la cantidad de sustancias que reaccionan.
Figura 2.4. Peter Waage (27 de junio de 1833, Flekkefjord – 13 de enero de 1900, Oslo) fue un químico noruego y profesor de la Universidad de Oslo. Junto a su amigo, el también químico y matemático Cato Guldberg, Waage descubrió y desarrolló la ley de acción de masas entre los años 1864 y 1879.
Hace poco más de 150 años, el 15 de marzo de 1864, Peter Waage y Cato Guldberg publicaron un artículo en el que proponían lo que ha llegado a conocerse como la Ley de la Acción de Masas. La Ley de Acción de Masas es el fundamento sobre el que se basa la interpretación de la relación entre dosis y respuesta en farmacología.
Figura 2.5. Cato Maximilian Guldberg (11 de agosto de 1836 - 14 de enero de 1902) fue un matemático y químico noruego. Guldberg es mejor conocido como pionero en química física.
El concepto de 'afinidad' como la fuerza química que mantiene unidas sustancias diferentes se le atribuye a Herman Boerhaave (1668-1738), el influyente médico de Leiden y autor de Elementa chemiae. Como escribió: “... las partículas disueltas y disueltas [ …] Se unen, por la afinidad de su propia naturaleza, en cuerpos homogéneos ”.
El químico francés Claude Louis Berthollet (1748-1822) consideró entonces la fuerza impulsora detrás de las reacciones químicas y estableció la relación entre la masa de una sustancia y la velocidad a la que sufre una reacción química. Estableció esta idea en su tratado de 1801 Recherches sur les lois de l'affinité, en el que describía "las leyes de la afinidad por las que los cuerpos tienden a unirse o combinarse". La relevancia de la afinidad química para la terapéutica fue rápidamente reconocida. Por ejemplo, Jonathan Pereira en The Elements of Materia Medica escribió que 'La acción de un medicamento sobre un órgano y no sobre otro se explica en la hipótesis química, asumiendo la existencia de afinidades desiguales del agente medicinal por diferentes tejidos'.
Sin embargo, no fue hasta 1864 que el matemático noruego Cato Guldberg (1836-1902) y el químico Peter Waage (1833-1900), cuñado de Guldberg, propusieron claramente la Ley de la acción de masas. Aunque inicialmente su artículo fue rechazado, lo cual era quizás previsible, ya que estaba escrito en noruego. La población de Noruega era en ese momento de alrededor de 1.7 millones y pocos fuera del país habrían hablado el idioma en el que se escribió el documento. Por lo tanto, Guldberg y Waage ampliaron el alcance de su contribución, publicando otro artículo en francés en 1867, titulado Etudes sur les affinités chimiques.
Su teoría fue posteriormente apoyada por el trabajo del químico danés Julius Thomsen, utilizando técnicas termoquímicas, pero la idea todavía se pasó por alto en gran medida hasta que fue redescubierta en 1877 por el químico holandés Jacobus van 't Hoff (1852-1911), quien clasificó las reacciones químicas y definió sus órdenes y mostró cómo la Ley de Acción de Masas se podía deducir directamente a partir de principios termodinámicos. Basado en el trabajo de van ’t Hoff, el químico sueco Svante August Arrhenius (1859-1927) dedujo una fórmula para el efecto de la temperatura sobre la constante de velocidad de una reacción.
El problema que había ocupado a Guldberg y Waage era cómo dar una descripción matemática de las afinidades que impulsan las reacciones químicas. Esto involucró tanto las velocidades de las reacciones, que describieron como dinámica química, como, para las reacciones reversibles, el equilibrio final entre la reacción hacia adelante y la reacción hacia atrás, que denominaron estática química.
Tomando primero la cuestión de la velocidad de reacción, los noruegos propusieron que para una reacción reversible que tiene lugar en una fase (sus datos se derivaron de reacciones en solución), la velocidad era proporcional a la 'masa activa' de los reactivos ('La force est porportionelle au produit des masses actives des deux corps A et B'), donde 'masa activa' es la masa por unidad de volumen, es decir, la concentración.
Por lo tanto, la velocidad está relacionada con el número de especies involucradas en la reacción y, por lo tanto, depende de la ruta de reacción precisa. Esto significa que si hay una serie de reacciones intermedias cuya forma se desconoce, es posible que no sea posible calcular la velocidad de reacción, incluso cuando se conoce la reacción general. Como Guggenheim señaló más tarde, "El punto ... de que el comportamiento cinético de una reacción particular debe determinarse experimentalmente y no puede predecirse a partir de la fórmula estequiométrica fue mejor apreciado por ... van 't Hoff que por muchos escritores posteriores, especialmente los escritores de libros de texto".
Las ideas fundamentales detrás de la ley de acción de masas de Guldberg y Waage, a saber, que en una reacción elemental
(a) la velocidad de la reacción depende de las concentraciones de reactivos y la estequiometría de la reacción y que…
(b) en el equilibrio los productos y reactivos están en una proporción fija,…
… han influido profundamente en la farmacología. Ehrlich y otros propusieron que las interacciones entre las drogas y el cuerpo tenían lugar en sitios receptores específicos y eso, a su vez, permitió a Langley y Hill aplicar la teoría química a los procesos biológicos. La teoría sigue siendo la base de nuestra comprensión cuantitativa de las interacciones fármaco-receptor.
(2.3) Jacobus Henricus van’t Hoff (Ptáček et al., 2018)
Van’t Hoff también señaló que las reacciones de primer y segundo orden son relativamente comunes, mientras que las reacciones de tercer orden son raras. Proporcionó un ejemplo basado en la reacción 3.4, que experimentalmente se comporta como la reacción de segundo orden, a pesar de que hay tres moléculas de reactivo. Lo más probable es que la reacción proceda en dos pasos mediante la formación de un intermedio de reacción de corta duración (HOI) de la siguiente manera:
Figura 2.6.
Aunque el científico holandés J.H. van’t Hoff logró el reconocimiento a través de la química orgánica, por sus trabajos pioneros en el campo de la estereoquímica, a finales de la década de 1870, ya no estaba interesado principalmente en estudiar estructuras moleculares orgánicas. Su enfoque se centró en las transformaciones moleculares, una investigación de por qué las reacciones químicas se desarrollan a velocidades muy diferentes. Para comprender el equilibrio químico y la afinidad química, inició una investigación de una década en termodinámica, equilibrio químico y cinética, es decir, dinámica química. En palabras de van’t Hoff: “La dinámica se dedica a las acciones mutuas de varias sustancias, es decir, al cambio químico, la afinidad, la velocidad de reacción y el equilibrio químico.”
Figura 2.7. Jacobus Henricus van 't Hoff (Róterdam, 30 de agosto de 1852 - Berlín, 1 de marzo de 1911) fue un químico holandés ganador del Premio Nobel de Química del año 1901 por establecer los principios de la estereoquímica y de la cinética química.
En la actualidad, la expresión “cinética química” se refiere al estudio de las velocidades de las reacciones químicas y no a las propiedades de los sistemas químicos en equilibrio. Entre otras, las aportaciones más significativas de J.H. van’t Hoff incluyen:
(a) Deducción de un modelo matemático para explicar las tasas de reacciones químicas basadas en la variación en la concentración de reactivos con el tiempo.
(b) Derivación de la ecuación que dio la relación entre el calor de reacción y la constante de equilibrio, que se conoce ampliamente como la ecuación de van’t Hoff.
(c) La sugerencia de un nuevo método para determinar el orden (molecularidad) de una reacción química que implica la medición de la velocidad (r) a varias concentraciones (c) del reactivo.
(d) La explicación del efecto de la temperatura sobre el equilibrio de la reacción de Henry Louis Le Chatelier mostrando la aplicabilidad de esta relación, y esto ahora se conoce como principio de van't Hoff - Le Châtelier. La ley proporciona una discusión cualitativa importante de la forma en que la constante de equilibrio químico se ve afectada por la temperatura, cuestión que abordaremos en el capítulo de equilibrio químico.
(e) La definición de afinidad química en términos de trabajo externo máximo realizado en una reacción química a temperatura y presión constantes como fuerza impulsora de la reacción. Las conclusiones de van't Hoff, J. Thomsen y M. Berthold fueron posteriomente utilizadas por físicos como Josiah Willard Gibbs y Hermann Ludwig Ferdinand von Helmholtz para extender los principios termodinámicos a los sistemas químicos.
Van’t Hoff también señaló que la cinética química era diferente de la termodinámica química y el físico alemán Hermann von Helmholtz había propuesto una teoría similar en 1882.
3. La actividad química
3. La actividad química
En termodinámica química, la actividad (símbolo \(a\)) es una medida de la “concentración efectiva” de una especie en una mezcla, en el sentido de que el potencial químico de la especie depende de la actividad de una solución real del mismo modo que dependería sobre la concentración para una solución ideal. Por convención, la actividad se trata como una cantidad adimensional, aunque su valor depende de las elecciones habituales del estado estándar de la especie. La actividad de las sustancias puras en fases condensadas (sólidas o líquidas) normalmente se toma como unidad (el número 1). La actividad depende de la temperatura, la presión y la composición de la mezcla, entre otras cosas. Para los gases, la actividad es la presión parcial efectiva y generalmente se denomina fugacidad.
La diferencia entre la actividad y otras medidas de composición surge porque las moléculas en gases o soluciones no ideales interactúan entre sí, ya sea para atraerse o repelerse. La actividad de un ion está particularmente influenciada por su entorno. El uso de actividades permite a los químicos explicar varias discrepancias entre soluciones ideales y soluciones reales. La descripción matemática de una solución ideal debe modificarse para describir una solución real, al igual que la ley de los gases ideales \(P V = n R T\) debe modificarse para describir los gases reales.
De manera similar, la diferencia entre las concentraciones de soluto calculadas en una solución ideal y en una solución real puede dar lugar a amplias variaciones en los resultados experimentales. Los siguientes tres ejemplos comparan los resultados obtenidos cuando se utilizan concentraciones formales (suponiendo idealidad) y cuando se utilizan actividades (suponiendo no idealidad). Al igual que los gases, las "soluciones ideales" tienen ciertas propiedades físicas predecibles (por ejemplo, propiedades coligativas) de las que a menudo se desvían las soluciones reales. Al igual que con la ecuación de van der Waal para gases reales, esta desviación se origina en las interacciones soluto-solvente, solvente-solvente y soluto-soluto. La magnitud de esta no idealidad es naturalmente mayor cuanto mayor es la concentración de soluto y mayor la interacción intermolecular (p. ej., iones frente a especies sin carga). Lewis introdujo la idea de 'concentración efectiva' o 'actividad' para tratar este problema al permitir una descripción de "solución ideal" para soluciones no ideales.
La actividad de una sustancia (simbolizada \(a\) según el libro de Oro de la IUPAC) describe la concentración efectiva de esa sustancia en la mezcla de reacción. La actividad tiene en cuenta la no idealidad de la mezcla de reacción, incluidas las interacciones disolvente-disolvente, disolvente-soluto y soluto-soluto. Por lo tanto, la actividad proporciona una descripción más precisa de cómo actúan todas las partículas en solución. Para soluciones muy diluidas, las actividades de las sustancias en la solución se acercan mucho a la concentración formal (la concentración calculada debe basarse en la cantidad de sustancia que se midió). A medida que las soluciones se vuelven más concentradas, las actividades de todas las especies tienden a ser menor que la concentración formal. La disminución de la actividad a medida que aumenta la concentración es mucho más pronunciada para los iones que para los solutos neutros.
Las actividades son en realidad proporciones adimencionales que comparan una presión efectiva o una concentración efectiva con una presión o concentración de estado estándar (el término correcto para la presión efectiva es fugacidad). Hay varias formas de definir estados estándar para los diferentes componentes de una solución, pero un sistema común es:
(a) el estado estándar para la presión del gas, \(P^o\), es 1 bar (a menudo se aproxima a 1 atm)
(b) el estado estándar para la concentración de soluto, \(C^o\), es 1 molal (moles de soluto/kg de solvente) para soluciones diluidas. A menudo, la molalidad se aproxima con la molaridad (moles de soluto/Litro de solución).
(c) el estado estándar de un líquido es el líquido puro
(d) el estado estándar de un sólido es el sólido puro
Para la mayoría de las situaciones experimentales, se supone que las soluciones están diluidas con respecto al solvente. Esta suposición implica que el solvente se puede aproximar con líquido puro y podamos usar todo tipo de aproximaciones ideales.
4. Cantidad de reacción
4. Cantidad de reacción
Cuando analizamos la estequiometría básica en un estado no equilibrado, establecimos que la relación entre la cantidad de sustancia y el número estequiométrico era constante para todas las sustancias involucradas en una reacción química.
\[\frac{n_i}{v_i} = \frac{n_j}{v_j}\] Eq 4.1.
A esta expresión la conocemos como la ecuación fundamental de la estequiometría. No obstante, surge una pregunta importante: ¿Cuál es la razón fundamental que respalda su validez? ¿Cuál es su fundamento filosófico?
(4.1) Evento de reacción
Contrario a lo que podríamos anticipar, la respuesta es bastante sencilla. La propia reacción química actúa como un motor de ciclos, descomponiendo ciertas piezas para ensamblar otras. Esto ocurre de manera discreta, lo que significa que un ciclo no puede tener lugar sin la destrucción de cantidades específicas de reactivos para producir cantidades precisas de productos. Cada ciclo individual lo llamamos "evento de reacción".
En la electrólisis del agua, se descompone el agua (H2O) en sus componentes, hidrógeno (H2) y oxígeno (O2), mediante la aplicación de una corriente eléctrica a través de una solución acuosa de agua que contiene un electrólito, como el ácido sulfúrico (H2SO4).
A nivel molecular, un solo ciclo de electrólisis comienza con la participación de 4 electrones externos que descomponen 2 moléculas de agua, generando una molécula de oxígeno y dos de hidrógeno. La molécula que limita este ciclo es el oxígeno, ya que no es posible reducir el número moléculas de oxígeno a menos de uno. Por lo tanto, el número estequiométrico del oxígeno será igual al número de eventos de reacción completos.
\[\textrm{H}_{2}\textrm{O} + 4e^{-} \rightarrow 2 \textrm{H}_{2} + \textrm{O}_{2}\] Eq 4.2.
(4.2) Avance de la reacción
sin embargo, debido a que estos eventos ocurren en gran cantidad, necesitamos utilizar múltiplos para manejar estas cifras. En este contexto, el único múltiplo adecuado para lidiar con números en química es el número de Avogadro.
El avance de la reacción o cantidad de reacción, representado por \(\xi\), se define como la cantidad de veces que se produce una reacción química completa en paquetes de Avogadro. En este contexto, el número de Avogadro no se refiere a partículas individuales, sino más bien a la cantidad de veces que se repite un proceso químico. Por ejemplo, si el avance de la reacción es de 1 mol, esto implica que la reacción se ha repetido \(6.022\times 10^{23}\) veces. Esta perspectiva nos permite comprender el concepto de avance de la reacción en un nivel más profundo, relacionándolo con la repetición de procesos químicos a una escala molecular que va más allá de la mera cantidad de partículas (García-García, 2021; Garst, 1974).
En consecuencia, las unidades de avance de reacción serán idénticas a las de la cantidad de sustancia expresada en moles. Sin embargo, es crucial recordar que estos moles de reacción no representan partículas individuales, sino más bien repeticiones de un proceso químico. Cada mol de avance de reacción simboliza la ocurrencia de ese proceso químico específico una cantidad inmensa de veces, lo que subraya la importancia de comprender la naturaleza repetitiva y profunda de la química a nivel molecular.
Si seguimos empleando el ejemplo de la electrólisis del agua, sabemos que el número de eventos de reacción debe ser igual a el número de moléculas de una sustancia con número estequiométrico 1, y por ende, si lo unimos a la ecuación 4.1, podemos definir tentativamente que
\[\xi_{fd} = \frac{n_i}{v_i}\] Eq 4.3.
Donde \(\xi_{fd}\) representa el avance de la reacción directa o en el setido (→) de una reacción elemental de reversibilidad des prteciable. También podemos definir la forma molecular de la ecuación como:
\[\Xi_{fd} = \frac{N_i}{v_i}\] Eq 4.4.
En la ecuación 4.4, podemos ver la constancia de las relaciones empleando la electrólisis del agua, si reemplazamos para agua, electrones, hidrógeno y oxígeno suficientes para completar dos eventos de reacción:
Propios.
Ejemplo. ¿Cuántos eventos de reacción ocurren en la electrólisis del agua si se necesitaron 8 electrones para electrolizar 2 moléculas de agua? Nota, usar ecuación 4.4.
Ejemplo. ¿Cuántas moles de electrones se necesitan para la electrólisis de 7 moles de agua? Nota, usar ecuación 4.3.
(4.3) Actividad de la reacción
Como hemos mencionado anteriormente, una de las aproximaciones más comunes para estudiar la actividad química es mediante la concentración molar. De manera similar, al igual que existe una concentración molar para sustancias químicas, también podemos aplicar este concepto a las reacciones químicas. En este caso, la cantidad de la reacción se mide en moles (aunque es importante destacar que estos moles no representan partículas individuales, sino eventos discretos).
Estos eventos de reacción ocurren en un espacio específico y definido. Por lo tanto, si tomamos la relación entre el avance de la reacción y el volumen en litros, podemos establecer un nuevo parámetro que denominamos "concentración molar de reacción". Esta concentración nos proporciona información sobre la actividad de la reacción en relación con la cantidad de sustancia por unidad de volumen.
\[c=\frac{\xi}{V}\] Eq 4.5.
5. La velocidad de una reacción
5. La velocidad de una reacción
La velocidad de una reacción es un concepto complejo que surgió antes de que se estableciera el concepto de cantidad de reacción \(\xi\). Se definió inicialmente en función de las concentraciones molares de las sustancias involucradas en la reacción, en lugar de considerar la reacción en su conjunto. Para alinear nuestra propuesta con los estándares definidos, vamos a definir la velocidad de la reacción como el cambio infinitesimal en la concentración de la reacción en función del cambio infinitesimal en el tiempo.
\[r=\frac{\delta c}{\delta t}\] Eq 5.1.
(5.1) Símbolos y unidades
Del mismo modo, la velocidad o rapidez de una reacción química es el cambio en la concentración de reactivos o productos por unidad de tiempo. Las unidades para la velocidad de reacción son generalmente la molaridad por segundo (M/s), es decir, el cambio en la concentración medido en la molaridad del producto dividido por un intervalo de tiempo medido en segundos.
Según el libro de oro de la IUPAC el símbolo para la velocidad o rapidez de reacción debe ser \(v\) (IUPAC, 2020) (Enlace), el cual es demasiado semejante al símbolo que empleamos para el número estequiométrico \(\nu\), lo cual nos puede traer confusiones debido a que son muy semejantes y ambos parámetros aparecen comúnmente en este capítulo de manera simultánea en muchas ecuaciones clave. De hecho, en algunos libros de texto sí que hacen esa salvajada (Atkins, De Paula, & Keeler, 2018), mientras que la mayoría de los libros de texto de química general ni siquiera se preocupan por acuñar un parámetro algebraico para la rapidez de reacción y simplemente emplean la expresión tasa (rate) como parámetro de rapidez de reacción
Figura 5.1. Ejemplo del uso simultáneo del parámetro de velocidad de reacción y número estequiométrico en (Atkins et al., 2018).
… lo cual puede hacer que leer una ecuación se haga un poco difícil. Afortunadamente el mismo libro de oro plantea el símbolo \(r\) como alternativa común para representar la rapidez de reacción, y que es mucho más acertado ya que en realidad estamos midiendo la rapidez de la reacción, que, a diferencia de una velocidad, la rapidez no es un vector y por ende, no debemos preocuparnos por cálculos vectoriales.
A pesar de lo complejo de la simbología introducida por (Atkins et al., 2018), si estamos de acuerdo en que la rapidez de una reacción no puede definirse empleando las tasas de aparición y desaparición de reactivos y productos como lo hacen los libros de texto de química general y el propio Libro de Oro de la IUPAC.
Nuestra principal razón para rechazar la definición común es que para una sola ecuación química tendríamos tantas definiciones algebraicas (ecuaciones) como sustancias, ya sean reactivos o productos, que se involucran apareciendo o desapareciendo. De allí que la fórmula para calcular la rapidez de la reacción generalmente se expresa con un ejemplo para la reacción química general como aA+bB→pP+qQ+... ocurriendo bajo condiciones de volumen constante, sin una acumulación apreciable de intermedios de reacción, la velocidad de reacción r se define como
(5.2) Tiempo y el problema de los infinitos
La velocidad de un evento se define como el cambio que ocurre en un intervalo de tiempo \(t\) dado, lo que significa que siempre que hablamos de velocidad, necesariamente traemos la noción de tiempo. Por ejemplo, la velocidad de un automóvil se expresa como el cambio en la posición del automóvil durante un cierto intervalo de tiempo. En Colombia, la velocidad de los automóviles generalmente se mide en unidades de kilómetros por hora, es decir, la cantidad que está cambiando (posición medida en kilómetros) dividida por un intervalo de tiempo (medido en horas).
Cuando hablamos de velocidad en cinética química, entramos en un terreno donde debemos considerar las diferencias y los cambios promedio. Comencemos nuestra discusión centrándonos en las velocidades promedio.
En cinética química, las velocidades promedio se utilizan para describir el proceso empleando restas simples entre dos estados del sistema, sin que nos importe su comportamiento en medio, es el mismo problema de la velocidad promedio y la velocidad instantánea en cinemática.
\[r_{avg}=\frac{\Delta c}{\Delta t}\] Eq 5.2.
Es importante destacar que las velocidades promedio pueden variar en diferentes intervalos de tiempo a medida que la reacción progresa y las concentraciones cambian, es decir, no son lineales necesariamente, por lo que pueden existir diferencias con las versiones instantáneas.
La elegancia de la ecuación anterior esconde un problema, durante el capítulo de estequiometría nos tuvo sin cuidado la distinción entre estado inicial y final para los reactantes, pero aquí, esa cuestión se hace problemática.
(5.3) Avance de la reacción en términos de las sustancias
En nuestra previa discusión sobre estequiometría, establecimos que, en una reacción química, la relación entre la cantidad de sustancia y el número estequiométrico es constante y proporcional entre todos los participantes de la reacción. Esta constante se conoce como el avance de la reacción. Sin embargo, en ese contexto, no era relevante distinguir entre sustancias que actuaban como reactivos o productos.
En el ámbito de la cinética química, esta distinción adquiere una importancia crucial. Aquí, debemos considerar si una sustancia es un reactivo (que se consume) o un producto (que se forma) en la reacción. Si un reactante se consume entonces la cantidad final es menor que la inicial y al ejecutar la resta (\(\Delta n=n-n_{o})) obtendremos un valor negativo, lo que sería incongruente con una velocidad de reacción siempre positiva. Por esta razón, a partir de aquí asumiremos que:
El signo del número estequiométrico asociado a los reactantes es negativo por definición
Esto mantendrá las ecuaciones siempre en una forma positiva, y al hacerlo así, solo necesitaremos manejar una serie única de ecuaciones.
(5.4) Símbolos especiales
Dado que el símbolo de concentración molar "\(c\)" comienza a repetirse de manera constante, optaremos por el uso de corchetes "[ ]" en su lugar, ya que ambos simbolizan lo mismo: la relación entre la cantidad de sustancia y el volumen, es decir, la concentración molar. De esta manera, podemos presentar de forma más clara y concisa las definiciones de la velocidad de la reacción, así como la velocidad de aparición y desaparición, casi de la misma manera en que se encuentran en los libros de texto:
(5.5) Definición general de la rapidez de la reacción y la rapidez de aparición y desaparición
De esta forma podemos definir el avance de la reacción directa (A + B → c + D) como:
Demostración 4.1: Demuestre la ecuación de calculo de rapidez de reacción iniciando con la definición fundamental, para poder calcularla con las concentraciones de las sustancias.
Velocidad de la reacción promedio
\[r_{avg}=\frac{1}{\nu_{i}}\ \frac{\Delta \left [ i \right ]}{\Delta t}\] Eq 5.3.
Velocidad de aparición/desaparición promedio
\[r_{avg,i}= \frac{\Delta \left [ i \right ]}{\Delta t}\] Eq 5.4.
En ocasiones resulta más práctico en ecuaciones de producción o de absorción de gases medir parámetros como la presión o el volumen, con los cuales podemos llegar a la cantidad de sustancia, por lo que la definición de rapidez de reacción puede expresarse para parámetros diferentes de masa, cantidad de sustancia y concentración líquida.
|
\[ r_{avg,i} = \frac{1}{R \cdot T} \cdot \frac{\Delta P_i}{\Delta t_i}\] Eq 5.5. |
\[r_{1} = \frac{1}{R \cdot T} \cdot \frac{\delta P_i}{\delta t_i}\] Eq 5.6. |
Recuerde que al reemplazar números estequiométricos de la ecuación balanceada, los reactantes van negativo por definición, lo cual implica que la rapidez de desaparición es por definición un valor negativo, a menos que se la multiplique por -1 o se asuma solo su valor absoluto.
La ecuación \(r_{avg}=\frac{1}{\nu_{i}}\ \frac{\Delta \left [ i \right ]}{\Delta t}\) recibe el nombre de expresión de tasa promedio (avarage rate expression) aunque puede traducirse como expresión de rapidez promedio o expresión de velocidad de reacción promedio, la cual cambia para cada sustancia en cada ecuación específica, y evidentemente la ecuación química debe encontrarse balanceada para poder emplear los números estequiométricos correctos. Tenga en cuenta que debido a la ausencia de notación vectorial usaremos las palabras rapidez y velocidad como sinónimos en este contexto.
Química de Chang 10
✔️ (Ejemplo 13.1b): Escriba las expresiones de velocidad para la siguiente reacción en términos de la desaparición de los reactivos y la aparición de los productos 4NH3(g) + 5O2(g) → 4NO(g) + 6H2O(g)
✔️ (Práctica 13.1): Escriba las expresiones de velocidad para la siguiente reacción en términos de la desaparición de los reactivos y la aparición de los productos CH4(g) + 2O2(g) → CO2(g) + 2H2O(g)
✔️ (Problema 13.5a): Escriba las expresiones de velocidad para la siguiente reacción en términos de la desaparición de los reactivos y la aparición de los productos H2(g) + I2(g) → 2HI(g)
✔️ (Problema 13.6a): Escriba las expresiones de velocidad para la siguiente reacción en términos de la desaparición de los reactivos y la aparición de los productos 2H2(g) + O2(g) → 2H2O(g)
✔️ (Problema 13.6b): es el mismo que el ejemplo 13.1 b.
Química la ciencia central 13
✔️ (Problema 14.23a) Indique cómo se relaciona la velocidad de desaparición de cada reactivo con la velocidad de aparición de cada producto en H2O2(g) → H2(g) + O2(g)
✔️ (Problema 14.23b) Indique cómo se relaciona la velocidad de desaparición de cada reactivo con la velocidad de aparición de cada producto en 2 N2O(g) → 2 N2(g) + O2(g)
✔️ (Problema 14.23c) Indique cómo se relaciona la velocidad de desaparición de cada reactivo con la velocidad de aparición de cada producto en N2(g) + 3 H2(g) → 2 NH3(g)
✔️ (Problema 14.23d) Indique cómo se relaciona la velocidad de desaparición de cada reactivo con la velocidad de aparición de cada producto en C2H5NH2(g) → C2H4(g) + NH3(g)
✔️ (Problema 14.24a) Indique cómo se relaciona la velocidad de desaparición de cada reactivo con la velocidad de aparición de cada producto en 2 H2O(g) → 2 H2(g) + O2(g)
✔️ (Problema 14.24b) Indique cómo se relaciona la velocidad de desaparición de cada reactivo con la velocidad de aparición de cada producto en 2 SO2(g) + O2(g) → 2 SO3(g)
✔️ (Problema 14.24c) Indique cómo se relaciona la velocidad de desaparición de cada reactivo con la velocidad de aparición de cada producto en 2 NO(g) + 2 H2(g) → N2(g) + 2 H2O(g)
✔️ (Problema 14.24d) Indique cómo se relaciona la velocidad de desaparición de cada reactivo con la velocidad de aparición de cada producto en N2(g) + 2 H2(g) → N2H4(g)
(5.6) Variación en la velocidad de la reacción
Las velocidades de reacción pueden variar drásticamente. Por ejemplo, la oxidación lenta del hierro bajo la atmósfera terrestre es una reacción que puede llevar muchos años, pero la combustión de la celulosa en un incendio es una reacción que ocurre en fracciones de segundo. En la mayoría de las reacciones, la velocidad disminuye a medida que la reacción avanza.
La cinética química es la parte de la química física que se ocupa de cómo se miden y predicen las velocidades de las reacciones químicas, y de cómo los datos de velocidad de reacción se pueden utilizar para deducir probables mecanismos de reacción. Los conceptos de la cinética química se aplican en muchas disciplinas, como la ingeniería química, la enzimología y la ingeniería ambiental.
6. Factores que afectan la velocidad de la reacción
6. Factores que afectan la velocidad de la reacción
Cuatro factores afectan la velocidad a la que ocurre cualquier reacción particular:
(6.1) Naturaleza de los reactivos
La velocidad de reacción varía según las sustancias que reaccionen. Las reacciones ácido / base, la formación de sales y el intercambio iónico suelen ser reacciones rápidas. Cuando tiene lugar la formación de enlaces covalentes entre las moléculas y cuando se forman moléculas grandes, las reacciones tienden a ser más lentas. La naturaleza y la fuerza de los enlaces en las moléculas reactivas influyen en gran medida en la velocidad de su transformación en productos.
(6.2) Estado de la materia de los reactivos
Los reactivos deben unirse para reaccionar. Cuanto más fácilmente reaccionan las moléculas reactivas, más rápidamente reaccionan. Las reacciones pueden clasificarse en general como homogéneas, involucrando todos los gases o todos los líquidos, o como heterogéneas, en las cuales los reactivos están en diferentes fases. En condiciones heterogéneas, una reacción está limitada por el área de contacto de los reactivos. Por lo tanto, las reacciones heterogéneas que involucran sólidos tienden a proceder más rápidamente si se aumenta el área superficial del sólido. Por ejemplo, un medicamento en forma de polvo fino se disuelve en el estómago y entra en la sangre más rápidamente que el mismo medicamento en forma de tableta.
(6.3) Área de la superficie del estado sólido
En un sólido, solo las partículas que se encuentran en la superficie pueden participar en una reacción. Triturar un sólido en partes más pequeñas significa que hay más partículas presentes en la superficie y la frecuencia de colisiones entre estas y las partículas reactivas aumenta, por lo que la reacción ocurre más rápidamente.
(a) Por ejemplo, el sorbete (polvo) es una mezcla de un polvo muy fino de ácido málico (un ácido orgánico débil) e hidrogenocarbonato de sodio. Al entrar en contacto con la saliva en la boca, estos productos químicos se disuelven y reaccionan rápidamente, liberando dióxido de carbono y proporcionando la sensación de efervescencia.
(b) Los fabricantes de fuegos artificiales modifican el área de superficie de los reactivos sólidos para controlar la velocidad a la que se oxidan los combustibles de los fuegos artificiales, y lo utilizan para crear diversos efectos. Por ejemplo, el aluminio finamente dividido confinado en un caparazón explota violentamente. Si se utilizan piezas más grandes de aluminio, la reacción es más lenta y se ven chispas a medida que se expulsan piezas de metal en llamas.
(6.4) Concentraciones de reactivos
La mayoría de las reacciones químicas se producen más rápidamente si aumenta la concentración de uno o más reactivos. Por ejemplo, la lana de acero se quema solo lentamente en el aire, que contiene 20% de O2, pero estalla en llamas en oxígeno puro. A medida que aumenta la concentración de reactivo, aumenta la frecuencia con la que chocan las moléculas de reactivo, lo que aumenta las tasas de reacción.
(6.5) Temperatura de reacción
Las velocidades de reacción generalmente aumentan a medida que aumenta la temperatura. Las reacciones bacterianas que estropean la leche, por ejemplo, proceden más rápidamente a temperatura ambiente que a la temperatura más baja de un refrigerador. El aumento de la temperatura aumenta las energías cinéticas de las moléculas. A medida que las moléculas se mueven más rápidamente, colisionan con más frecuencia y con mayor energía, lo que lleva a una mayor velocidad de reacción.
(6.6) La presencia de un catalizador
Un catalizador es una sustancia que altera la velocidad de una reacción química, pero permanece químicamente sin cambios después. El catalizador aumenta la velocidad de la reacción al proporcionar un nuevo mecanismo de reacción para que ocurra con una energía de activación más baja. En la autocatálisis, un producto de reacción es en sí mismo un catalizador para esa reacción que conduce a una retroalimentación positiva. Las proteínas que actúan como catalizadores en reacciones bioquímicas se denominan enzimas. La cinética de Michaelis-Menten describe la velocidad de las reacciones mediadas por enzimas. Un catalizador no afecta la posición del equilibrio, ya que el catalizador acelera las reacciones hacia atrás y hacia adelante por igual. En ciertas moléculas orgánicas, los sustituyentes específicos pueden influir en la velocidad de reacción en la participación del grupo vecino.
(6.7) Presión
El aumento de la presión en una reacción gaseosa aumentará el número de colisiones entre los reactivos, aumentando la velocidad de reacción. Esto se debe a que la actividad de un gas es directamente proporcional a la presión parcial del gas. Esto es similar al efecto de aumentar la concentración de una solución. Lo cual se puede observar al despejar la presión en términos de la concentración molar de un gas en la ley de los gases ideales (Procedimiento), pues a temperatura constante, la presión y la concentración molar son directamente proporcionales.
\[ P=c_i \cdot R \cdot T_i\] Eq 6.1.
Además de este sencillo efecto de acción de masas, los propios coeficientes de velocidad pueden cambiar debido a la presión. Los coeficientes de velocidad y los productos de muchas reacciones en fase gaseosa a alta temperatura cambian si se agrega un gas inerte a la mezcla; las variaciones de este efecto se denominan caída y activación química. Estos fenómenos se deben a reacciones exotérmicas o endotérmicas que ocurren más rápido que la transferencia de calor, lo que hace que las moléculas que reaccionan tengan distribuciones de energía no térmica (distribución no-Boltzmann). El aumento de la presión aumenta la tasa de transferencia de calor entre las moléculas que reaccionan y el resto del sistema, reduciendo este efecto.
Los coeficientes de velocidad de fase condensada también pueden verse afectados por la presión, aunque se requieren presiones bastante altas para un efecto medible porque los iones y moléculas no son muy comprimibles. Este efecto se estudia a menudo utilizando yunques de diamantes.
La cinética de una reacción también se puede estudiar con un enfoque de salto de presión. Esto implica realizar cambios rápidos de presión y observar el tiempo de relajación del retorno al equilibrio.
(6.8) Absorción de luz
La energía de activación para una reacción química se puede proporcionar cuando una molécula de reactivo absorbe luz de longitud de onda adecuada y se promueve a un estado excitado. El estudio de las reacciones iniciadas por la luz es la fotoquímica, siendo un ejemplo destacado la fotosíntesis.
(6.9) La interpretación molecular
A nivel molecular, las velocidades de reacción dependen de la frecuencia de colisiones entre moléculas. Cuanto mayor es la frecuencia de las colisiones, mayor es la velocidad de reacción. Sin embargo, para que una colisión provoque una reacción, debe ocurrir con suficiente energía para romper los enlaces y con una orientación adecuada para que se formen nuevos enlaces en los lugares adecuados. Consideraremos estos factores a medida que avancemos en este capítulo.
7. Estequiometría de la cinética de la reacción
7. Estequiometría de la cinética de la reacción
Sí se ha percatado hasta este punto sólo hemos logrado dar instrumentos para calcular las velocidades de aparición y desaparición, pero no una técnica para calcular la velocidad de la reacción como un todo, o calcular la velocidad de aparición o desaparición de una sustancia difícil de medir, en términos de la velocidad de aparición o desaparición de otra sustancia que sí es fácil de medir, en otras palabras aparte de esta discusión teórica aún nos falta completar un algoritmo matemático más robusto.
A continuación por lo tanto desarrollaremos un modelo matemático para resolver 2 situaciones comunes:
(a) calcular la rapidez de la reacción como un todo en términos de la rapidez de aparición o desaparición de alguna sustancia fácil de medir .
(b) calcular la rapidez de aparición o desaparición de una sustancia difícil de medir “que llamaremos incógnita o sustancia i”, en términos de la rapidez de aparición o desaparición de una sustancia fácil de medir “ que llamaremos el dato o sustancia ii”.
En ocasiones es posible que necesitemos calcular la velocidad de una sustancia en términos de la velocidad de reacción de otra sustancia.
Y evidentemente la ecuación anterior se puede extender para las relaciones instantáneas.
\[\frac{r_{\text{avg},i}}{r_{\text{avg},d}} = \frac{\nu_i}{\nu_d}\] Eq 7.1.
Con lo cual vuelve a aparecer un cociente que hemos venido estudiando desde el capítulo de estequiometría y es el radio estequiométrico \(\frac{\nu_i}{\nu_d}\), el cual a su vez requiere que la ecuación química que modela la situación esté balanceada para masa y carga.
Química de Chang 10
Química la ciencia central13
✔️ (Problema 14.20) Un matraz se carga con 0.100 mol de A y se deja reaccionar para formar B de acuerdo con la reacción hipotética en fase gaseosa A(g)→ B(g). Se recogen los siguientes datos: (a) Calcule el número de moles de B en cada momento de la tabla, suponiendo que A se convierte limpiamente en B sin intermediarios. (b) Calcule la tasa promedio de desaparición de A para cada intervalo de 40 s en unidades de mol/s. (c) ¿Cuál de los siguientes sería necesario para calcular la velocidad en unidades de concentración por tiempo: (i) la presión del gas en cada momento, (ii) el volumen del matraz de reacción, (iii) la temperatura, o (iv) el peso molecular de A?
8. Masa total y cantidad de sustancia total
8. Masa total y cantidad de sustancia total
En la cinética de la masa de reacción, asumimos que, independientemente de los procesos cinéticos que ocurran en el reactor, la masa del sistema \(m\) no cambiará a menos que entren reactantes o salgan productos. En consecuencia, la masa de reacción se mantiene constante.
Tal declaración se puede escribir como:
\[\frac{\delta m}{\delta t} = 0\] Eq 8.1.
Un valor de 0 en el lado derecho de la ecuación indica que no hay cambio en la masa con respecto al tiempo, es decir, la masa total dentro del reactor no está aumentando ni disminuyendo. En otras palabras, si el reactor está completamente aislado para flujos de materia, significa que no se permite la entrada ni la salida de materiales en el sistema. En este escenario, la cantidad total de masa \(m\) en el reactor se mantiene constante con el tiempo. No se produce ningún cambio neto en la masa, lo que implica que la masa dentro del reactor es conservada y no hay intercambio de sustancias con su entorno.
Otra interpretación de esto es que la masa de reacción total \(m\) es igual a la suma de masas de cada componente del sistema.
\[m = \sum_{i} m_i\] Eq 8.2.
Sin embargo, aquí surge una cuestión importante: aunque la masa de reacción se mantiene constante, el número de entidades y sus paquetes, es decir, los moles, pueden cambiar. Esto significa que, a pesar de que la masa de reacción permanece invariable, la cantidad de partículas en la reacción puede variar.
\[\Delta m = 0, \quad \Delta n \neq 0\] Eq 8.3.
Para poder evaluar cual es el efecto de la conservación de la masa en el número de partículas, lo que haremos es tomar una tabla de cinética de concentración contra tiempo de varias sustancias, vinculadas por una reacción química cuyos números estequiométricos sean diferentes de uno, como esta:
Tabla 8.1. Cambios de concentraciones de reactivos y productos en la reacción química 2NO+O2→2NO2. Si siente que los intervalos de tiempo son un poco arbitrarios, es porque la razón de estos es que son intervalos en los cuales las diferencias de concentraciones son iguales.
Ahora analíticamente lo que haremos es:
Con lo cual obtenemos la forma general:
\[\Delta n = \frac{\Delta n_d}{v_d} \sum_{i} \nu_i\] Eq 8.4.
Diferencia de cantidad de sustancia total, en términos de la diferencia de la cantidad de la sustancia dato y los números estequiométricos de las demás sustancias en una ecuación química balanceada.
Tenga en cuenta que, para calcular la cantidad instantánea en lugar de la diferencia de cantidades totales, el intervalo de tiempo entre la diferencia total y la diferencia de la sustancia dato debe ser el mismo.
Propio
9. La velocidad instantánea
9. La velocidad instantánea
En la ecuación 5.4 definimos la velocidad de aparición/desaparición \(r_{avg,i}=\frac{\delta c_{i}}{\delta t}\); como la tasa de cambio que ocurre entre la concentración de una sustancia sobre tiempo. Esta es quizá la definición más primitiva de velocidad de reacción, ya que es lo que experimentalmente se mide en un laboratorio.
Es importante recordar que, con el fin de evitar una excesiva cantidad de ecuaciones por definición, los números estequiométricos de los reactantes deben ser representados como negativos. Esto garantiza que la velocidad de un reactante sea negativa. En consecuencia, una pendiente negativa en un gráfico de concentración respecto al tiempo refleja la disminución de la concentración, lo cual es congruente con el hecho de que los reactantes disminuyen durante la reacción.
Incluso en la ecuación 5.4, que no incluye el término del número estequiométrico, el signo negativo se manifiesta en la diferencia entre la concentración inicial y final. Esto se debe a que cuando la concentración del reactante disminuye, la simple resta nos proporcionará un valor negativo. Por lo tanto, por definición, una tasa de desaparición es equivalente a una tasa negativa.
(9.1) Rectas y curvas
A pesar de los nombres pomposos que podamos darle a la ecuación \(r_{avg,i}=\frac{\delta c_{i}}{\delta t}\) en su aplicación en el contexto de la cinética química, desde la perspectiva matemática es una pendiente de recta, el problema es que experimentalmente, la rapidez de la reacción no es constante y no manifiesta rectas, cómo lo expondremos en los siguientes ejemplos:
En soluciones acuosas, el bromo molecular reacciona con el ácido fórmico (HCOOH) de la siguiente manera: Br2(aq) + HCOOH(aq) → 2Br-(aq) + 2H+(aq) + CO2(g). El bromo molecular Br2 es de color marrón rojizo. Todas las demás especies en la reacción son incoloras. A medida que avanza la reacción, la concentración de Br2 disminuye constantemente y su color se desvanece.
Figura 9.1. De izquierda a derecha: La disminución de la concentración de bromo a medida que transcurre el tiempo se manifiesta como una pérdida de color (de izquierda a derecha).
Esta pérdida de color y, por lo tanto, de concentración se puede monitorear fácilmente con un espectrómetro, que registra la cantidad de luz visible absorbida por el bromo. Ahora ya dependiendo de qué tan tecnológico o sea tu espectrómetro, podrás tomar medidas discretas (sólo algunas medidas a lo largo del tiempo de reacción), o medidas más continuas (una mayor cantidad de datos a lo largo del tiempo de reacción).
Química la ciencia central 13
Estos cálculos demuestran que la velocidad promedio de la reacción depende del intervalo de tiempo que elijamos en otras palabras, la rapidez de la reacción no es constante. Para recalcar este punto ahora consideremos la reacción entre el cloruro de butilo C4H9Cl y el agua para formar alcohol butílico C4H9OH y ácido clorhídrico:
\[\textrm{C}_{4}\textrm{H}_{9}\textrm{Cl(aq)} + \textrm{H}_{2}\textrm{O(l)} \rightarrow \textrm{C}_{4}\textrm{H}_{9}\textrm{OH(aq)} + \textrm{HCl(aq)}\] Eq 9.1
Supongamos que preparamos una solución acuosa de C4H9Cl 0.1000 M y luego medimos la concentración de C4H9Cl en varios momentos después del tiempo cero (que es el instante en que se mezclan los reactivos, iniciando así la reacción). Podemos usar los datos resultantes, que se muestran en las dos primeras columnas de la tabla 6.1, para calcular la tasa promedio de desaparición de C4H9Cl durante varios intervalos de tiempo; Estas tasas se dan en la tercera columna.
Tabla 9.1. Datos de velocidad para la reacción de C4H9Cl con agua
Observe que la tasa promedio disminuye durante cada intervalo de 50 s para las primeras mediciones y continúa disminuyendo en intervalos aún mayores a través de las mediciones restantes. Es típico que las velocidades disminuyan a medida que avanza la reacción porque disminuye la concentración de reactivos.
(9.2) Visualizando la rapidez de aparición y desaparición
El hecho de que las tasas de aparición de producto y desaparición de reactivo no sean constantes, implica necesariamente que cuando grafiquemos en el plano cartesiano concentración contra tiempo, obtendremos curvas en lugar de rectas. Consideremos la reacción hipotética A→B, representada en la siguiente figura.
Figura 9.2. Progreso de una reacción hipotética A→B. El volumen del matraz es 1.0 L.
Cada esfera roja representa 0.01 mol de A, cada esfera azul representa 0.01 mol de B, y el recipiente tiene un volumen de 1.00 L. Al comienzo de la reacción, hay 1.00 mol A, entonces la concentración es 1.00 mol/L = 1.00 M. Después de 20 s, la concentración de A ha caído a 0.54 M y la concentración de B ha aumentado a 0.46 M. La suma de las concentraciones todavía es 1.00 M porque se produce 1 mol de B por cada mol de A que reacciona. Después de 40 s, la concentración de A es de 0.30 M y la de B es de 0.70 M.
Figura 9.3. Gráfica de las velocidades de aparición y desaparición de productos y reactivos. Tenga en cuenta que las únicas medidas reales son los puntos, por lo que estamos trabajando con cálculos de estado o promedios, en lugar de cálculos infinitesimales o instantáneos.
Empleando las herramientas que hemos aprendido en el curso de cálculo nos podemos dar cuenta que, a medida que el tiempo tiende a infinito, la rapidez de aparición de producto y desaparición de reactivo tenderá a cero. Ese análisis matemático le podemos dar un sentido químico en el hecho de que, a medida que el tiempo tiene infinito, la cantidad de partículas de reactivos se hacen más escasas y por lo tanto más improbable que se encuentren para reaccionar y producir las respectivas partículas de producto, de allí que la cantidad de eventos de reacción por unidad de tiempo va disminuyendo paulatinamente.
(9.3) Rapidez de aparición y desaparición instantánea
Otro aspecto del cálculo que debemos notar de la Figura 9.3, es el hecho de que los puntos realmente medidos se encuentran separados por una cantidad de tiempo sensible, de allí que esta medición sólo nos permite aproximarnos a una velocidad de reacción promedio. A medida que tomemos más medidas en una menor cantidad de tiempo podremos obtener una gráfica más continua, y por ende aproximarnos a la velocidad de reacción instantánea.
Figura 9.4. Tasa de cambio instantánea de masa de oxígeno contra tiempo en un contenedor de 1 L para la reacción 2C2H5(g) → 4 NO2(g) + O2(g). La pendiente instantánea de esta curva se define como la tasa de formación de O2 con respecto al tiempo, dado que es una curva, debemos emplear técnicas del cálculo infinitesimal para determinar la tasa de cambio instantánea.
La tasa de cambio instantánea es el valor para la tasa de cambio en un intervalo de tiempo muy pequeño e idealmente infinitesimal.
\[r_i = \frac{\delta c_i}{\delta t_i}\] Eq 9.2
Tasa de cambio instantánea o velocidad de la reacción instantánea.
El problema con la gráfica de concentración por unidad de tiempo es que ¡tenemos una curva! ¿Cuál es el problema con que sea curva? El problema con una gráfica curva es que los valores para la tasa de cambio instantánea son diferentes de la obtenida para la tasa de cambio promedio, en otras palabras, no podemos usar pendientes de líneas rectas para determinar la tasa de cambio instantánea, ya que esta formación es una curva.
(9.4) Midiendo la velocidad de reacción para varios puntos
Hasta este punto, hemos utilizado la velocidad de aparición/desaparición promedio, lo cual ha sido suficiente para considerar la rapidez de una reacción como una función de estado en la que solo los estados inicial y final son relevantes. Sin embargo, ahora debemos explorar lo que sucede en el transcurso entre estos dos estados, y esta información solo puede obtenerse experimentalmente, ya que cada reacción química puede tener un comportamiento único.
Para aproximarse experimentalmente una tasa de reacción instantánea hay que tener en cuenta las limitaciones experimentales y que tipo de tasa de reacción. Con limitaciones experimentales nos referimos a que la cantidad de medidas de concentración que podemos realizar por unidad de tiempo con nuestro instrumento de laboratorio, en otras palabras, si contamos con instrumentos experimentales más sofisticados es probable que logremos obtener una mayor cantidad de medición en una menor cantidad de tiempo.
Con respecto al tipo de reacción hacemos referencia a que algunas reacciones son lo suficientemente lentas como para permitir una toma de datos relativamente continua con instrumentos no muy sofisticados.
Los métodos químicos para determinar la cantidad de sustancia producida y consumida por lo general permiten evaluar una cantidad limitada de puntos, lo cual genera una serie de tasas de reacción promedio que unen los puntos determinados. Los métodos físicos por el contrario permiten la determinación continua de las cantidades de sustancia producida o consumida durante el intervalo de tiempo analizado. Debido a que las cantidades de producto y reactivo están relacionadas de manera estequiométrica, cualquier especie química dentro de la reacción puede ser empleada para expresar la tasa de cambio de la reacción y de las demás sustancias como veremos más adelante.
Figura 9.5. Tasas de reacción en una determinación discontinua.
(9.5) La velocidad instantánea aproximada
En general, en los textos de química general, a menudo se asume que se necesitan aproximaciones gráficas para calcular las velocidades instantáneas \(\frac{\delta c_i}{\delta t_i}\). Estos ejercicios pueden resultar un poco desafiantes ya que implican que, con la ayuda de una regla y la vista, te aproximes a lo que percibió la persona que creó una gráfica similar a la siguiente. Es importante destacar que esta aproximación manual nunca será completamente precisa, ya que se trata de una estimación.
Figura 9.6. Concentración de cloruro de butilo C4H9Cl en función del tiempo.
La gráfica anterior implica que los libros de texto nos piden hallar velocidades instantáneas con la fórmula de la velocidad promedio, y descaradamente así lo indican. relieve hecho los libros de texto de química general solo introducen técnicas sofisticadas de cálculo cuando introducimos los conceptos de orden de reacción. Dado lo anterior, en ejercicios de lápiz y papel donde nos piden hallar la rapidez de reacción instantánea, en realidad nos estarán pidiendo calcular la rapidez de la reacción promedio para un punto determinado.
Química la ciencia central 13
(9.6) La velocidad verdadera
Una vez que se han registrado los puntos que representan la concentración como una función que depende de tiempo \(c_{i}= f_{t}\) es necesario encontrar una ecuación que modele estos puntos, es decir, que genere atomáticamente a \(f_{t}\). Este proceso puede llevarse a cabo utilizando técnicas de regresión polinómica o exponencial, las cuales pueden realizarse automáticamente en programas como Excel u otros paquetes matemáticos.
Una vez que hemos obtenido una ecuación \(f(t)\) que describe adecuadamente los puntos \(c_{i}\) para una variedad de puntos de tiempo \(t\), el siguiente paso es derivar esta ecuación \(f(t)\). Ahora, si usted, al igual que yo, no recuerda con claridad cómo realizar esta derivación, puede utilizar una calculadora de derivadas, como la que se encuentra disponible en el siguiente enlace: Calculadora de Derivadas.
https://es.symbolab.com/solver/derivative-calculator
Al utilizar esta calculadora, obtendrá la función derivada \(f{}'(t)\), la cual le permitirá calcular la rapidez instantánea en cualquier punto deseado. Es importante destacar que, si bien el cálculo integral tiene una relevancia especial en la cinética química y se abordará en secciones posteriores, en esta etapa nos estamos centrando en la derivación como una herramienta fundamental para comprender la rapidez de una reacción en un momento específico.
10. Ley de la velocidad de reacción
10. Ley de la velocidad de reacción
Una forma de estudiar el efecto de la concentración en la velocidad de reacción es determinar la forma en que la velocidad inicial de una reacción depende de las concentraciones iniciales. Por ejemplo, podríamos estudiar la velocidad de la reacción con la información de la tabla
Tabla 10.1. Velocidad de reacción inicial para diferentes concentraciones iniciales en la reacción: NH4++NO2-→N2+2H2 O, a 25°C
Al estudiar una reacción química, es importante tener en cuenta no solo las propiedades químicas de los reactivos, sino también las condiciones bajo las cuales se produce la reacción, el mecanismo por el cual tiene lugar, la velocidad a la que ocurre y el equilibrio hacia el cual Se procede.
La relación entre la velocidad de una reacción y las concentraciones de reactivos se expresa mediante una ley de velocidad, la cual debe ser medida experimentalmente, y se define de la siguiente forma.
\[r_{\text{avg}} = k \prod_r (c_r^ {a_r}) = k \prod_r [r_e]^{a_r}\] Eq 10.1
Velocidad promedio de la reacción en términos de las concentraciones de los reactivos y el orden de reacción.
Tenga en cuenta que solo las concentraciones molares de los reactivos \(c_{re}\) aparecen en la ley de velocidad, normalmente. La constante \(k\) se llama constante de velocidad. La magnitud de \(k\) cambia con la temperatura y, por lo tanto, determina cómo la temperatura afecta la velocidad. Los exponentes \(a_{re}\) se denominan ordenes parciales de reacción son típicamente números enteros pequeños pero no siempre, que se determinan experimentalmente, no puede determinarse solo a partir de una ecuación química balanceada, y los denominaremos orden de reacción. Como veremos en breve, si conocemos \(a\) para una reacción, podemos obtener una gran comprensión de los pasos individuales que ocurren.
Química la ciencia central 13
(10.1) Ordenes de reacción
Debe tener en cuenta que ni el orden de reacción general, ni los órdenes parciales de reacción, tienen un símbolo estandarizado en el libro de oro de la IUPAC así que emplearemos a para el orden general y \(a_{re}\) para el orden parcial que depende de cada reactivo.
\[a = \sum_{r} a_{r}\] Eq 10.2
Orden general de reacción \(a\) en términos del orden de reacción parcial de cada reactivo \(a_{re}\).
Puesta en palabras, el orden general de reacción es la suma de los órdenes de reacción de cada reactivo individual.
Química de Chang 10
Química la ciencia central 13
✔️ (Muestra 14.5a) Calcular los órdenes de reacción totales para las siguientes expresiones de rapidez de reacción promedio r = k[N2O5]; r = k[CHCl3] [Cl2]1/2
(10.2) Magnitudes y unidades de \(k\)
Si los químicos quieren comparar reacciones para evaluar cuáles son relativamente rápidas y cuáles son relativamente lentas, la cantidad de interés es \(k\). Una buena regla general es que un valor grande de \(k\) (∼109 o superior) significa una reacción rápida y un valor pequeño de \(k\) (10 o inferior) significa una reacción lenta.
Las unidades de la constante de velocidad dependen del orden de reacción general de la ley de velocidad. En una reacción de segundo orden general, por ejemplo, las unidades de la constante de velocidad deben satisfacer la ecuación:
\[k = \frac{{r_{avg}}}{c_{r1}(c_{r2})^2} \Rightarrow \frac{\text M}{\text s\cdot \text M\cdot \text M^2}=\frac{1}{\text s \cdot \text M}\]
Química de Chang 10
Química la ciencia central 13
✔️ (Muestra 14.5b) Deducir las unidades de la constante k en r = k[N2O5].
✔️ (Práctica 14.5.1) Deducir las unidades de la constante k en r = k[CHCl3] [Cl2]1/2.
✔️ (Práctica 14.5.2) Calcular el orden de reacción del hidrógeno elemental y las unidades de la constante k en r = k[H2][I2]
(10.3) Como calcular los órdenes de reacción
Hemos visto que la ley de velocidad para la mayoría de las reacciones tiene la forma general \(a = \sum_{r} a_{r}\). Por lo tanto, la tarea de determinar la ley de velocidad se convierte en determinar los órdenes de reacción parciales \(a_{re}\). En la mayoría de las reacciones, los órdenes de reacción son 0, 1 o 2, pero no necesariamente serán enteros. Calcular los órdenes de reacción parciales involucra a los siguientes pasos generales:
(a) crear series de datos en los cuales tengamos una sustancia variable y las demás constantes: con eso podremos identificar cuál es el efecto de la concentración de cada sustancia por separado.
(b) identificar el efecto de una concentración variable: si al variar la concentración no cambia la velocidad de reacción promedio, podremos concluir que el orden de reacción es cero. por el contrario, sí con la variación de la concentración cambia la velocidad de la reacción entonces sí tendremos un efecto, bueno que deberemos despejar algebraicamente.
(c) Cuantificar el efecto de la concentración variable: para ello vamos a utilizar el mismo truco que empleamos para analizar las leyes de los gases, es decir todos los términos constantes se fusionan en una nueva constante, de forma tal que la constante general absorber a las concentraciones que mantenemos constantes convirtiéndose en una segunda constante k2 que no nos interesará de momento, pues la podremos cancelar al ejecutar un ratio o regla de tres analítica, luego es sólo cuestión de despejar el orden de reacción parcial de la sustancia que sí es variable usando las leyes de los logaritmos naturales.
(nota, usaremos la barra promedio en lugar del subíndice avg desde este punto)
\[a_i = \ln\left(\frac{\bar{r}_o}{\bar{r}}\right) \left(\ln\frac{c_{oi}}{c_i}\right)^{-1}\] Eq 10.3
Orden general de reacción parcial de un reactivo único \(a_{i}\) en términos las velocidades de reacción promedio para estados inicial \(\overline {r}_{o}\) y final \(\overline {r}\) del sistema, así como las concentraciones molares iniciales \(c_{oi}\). Recuerde que es común reemplazar \(c_{i}\) por \(\left \lfloor i \right \rfloor\), lo cual faciliuta la lectura de la ecuación en un formulario, pero complica el álgebra en las demostraciones, por eso se intercambian entre una y otra forma constantemente en este capítulo.
Aunque hay que saberse las leyes de los algoritmos el álgebra para deducir la ecuación \(a_i = \ln\left(\frac{\bar{r}_o}{\bar{r}}\right) \left(\ln\frac{c_{oi}}{c_i}\right)^{-1}\) no es particularmente exigente, lo cual es sorprendente porque los libros de texto en los cuales se hallan este tipo de ejercicios no emplean esta ecuación, y en su lugar emplean un análisis cualitativo que nos puede llevar más tiempo que simplemente reemplazar y calcular.
En algunos ejercicios no es necesario calcular la constante de velocidad, sino simplemente expresar la ley de rapidez para una forma dinámica, es decir, dividiendo los parámetros de estado final entre sus iguales pero de estado inicial y cancelando la constante.
Química de Chang 10
✔️ (Problema 13.14): Use los datos de la tabla 13.2 para calcular la velocidad de la reacción en el momento en que [F2] = 0.010 M y [ClO2] = 0.020 M.
✔️ (Problema 13.15): Considere la reacción A + B → productos. A partir de los siguientes datos obtenidos a cierta temperatura, determine el orden de la reacción y calcule la constante de velocidad.
Química la ciencia central 13
✔️ (Muestra 14.6) Se midió la velocidad inicial de una reacción A + B → C para varias concentraciones iniciales diferentes de A y B, y los resultados son los que se muestran en la tabla: Usando estos datos, determine (a) la ley de velocidad para la reacción, (b) la velocidad constante, (c) la velocidad de la reacción cuando [A] = 0.050M y [A] = 0.100 M. (Enlace a la tabla).
✔️ (Práctica 14.6.2) Se midieron los siguientes datos para la reacción de óxido nítrico con hidrógeno: 2 NO(g) + 2 H2(g) → N2(g) + 2 H2O(g). (a) Determine la ley de velocidad para esta reacción. (b) Calcule la constante de velocidad. (c) Calcule la tasa cuando [NO] = 0.050 M y [H2] = 0.150 M. Enlace a la tabla.
11. Reacciones de primer orden
11. Reacciones de primer orden
Las leyes de velocidad que hemos examinado hasta ahora nos permiten calcular la velocidad de una reacción a partir de la velocidad constante y las concentraciones de reactivo. En esta sección, mostraremos que las leyes de velocidad también se pueden convertir en ecuaciones que muestran la relación entre las concentraciones de reactivos o productos y el tiempo. La matemática requerida para lograr esta conversión implica cálculo y ecuaciones diferenciales. No esperamos que pueda realizar las operaciones de cálculo, pero debería poder usar las ecuaciones resultantes. Aplicaremos esta conversión a tres de las leyes de tasas más simples: las de primer orden general, las de segundo orden general y las de cero orden general.
Una reacción de primer orden es aquella cuya velocidad depende de la concentración de un solo reactivo elevado a la primera potencia. Si una reacción de los productos tipo re → pe es de primer orden, podemos igualar dos ecuaciones para la velocidad promedio:
\[\frac{\Delta c_{re}}{\Delta t} = -k \cdot c_{re}\] Eq 11.1
Velocidad de desaparición de un reactivo A en una ecuación química r → p
Esta forma de ley de velocidad de reacción, que expresa cómo la tasa depende de la concentración, se llama ley de velocidad diferencial. Usando la operación de cálculo llamada integración, esta relación puede transformarse en una ecuación conocida como la ley de tasa integrada para una reacción de primer orden que relaciona la concentración inicial de A, con su concentración en cualquier otro momento.
(11.1) Formas integradas
La respuesta puede expresarse en una forma logarítmica o en una forma euleriana:
| \[c_i = c_{oi} \cdot e^{-k \cdot t}\] Eq 11.2 |
\[\ln(c_i) = -k \cdot t + \ln(c_{oi})\] Eq 11.3 |
Donde \(c_{i}\) es la concentración final, \(c_{oi}\) la concentración inicial, \(k\) la constante, \(t\) el tiempo y \(e\) el número de Euler.
|
\[P_i = P_{oi} \cdot e^{-k \cdot t}\] Eq 11.4 |
\[\ln(P_i) = -k \cdot t + \ln(P_{oi})\] Eq 11.5 |
En este caso las concentraciones molares se reemplazan por las presiones parciales inicial \(P_{oi}\) y final \(P_{i}\) .
La ventaja de la forma euleriana radica en que al hacer análisis de regresión empleando Excel, obtendremos precisamente una ecuación con una estructura que contiene el número de Euler, lo cual será indicador que se trata de una ecuación de primer orden. La forma linealizada es útil cuando no tienes un sistema de graficación automático como Excel, pues la forma euleriana es una curva, mientras que la forma logarítmica es una recta. Tenga en cuenta que el parámetro t toma como referencia el momento inicial o cero (\(t_{o}=0\)), por lo que toda comparación de tiempo deberá tener en cuenta el tiempo absoluto desde el inicio de la medición, lo que trae como consecuencia que todas las concentraciones iniciales \(c_{oi}\) sean las concentraciones a (\(t_{o}=0\)).
Para una reacción de primer orden, las ecuaciones \(\ln(c_i) = -k \cdot t + \ln(c_{oi})\) y \(\ln(P_i) = -k \cdot t + \ln(P_{oi})\) puede despejarse para hallar:
(a) la constante, e indican que las unidades de la constante en una reacción de primer orden son unidades de frecuencia o se tiempo inverso como s-1 o min-1.
| \[k = -\frac{1}{t} \ln\left(\frac{c_i}{c_{oi}}\right)\] Eq 11.6 |
\[k = -\frac{1}{t} \ln\left(\frac{P_i}{P_{oi}}\right)\] Eq 11.7 |
(b) la concentración de un reactivo restante en cualquier momento después de que la reacción haya comenzado,
(c) el intervalo de tiempo requerido para que una fracción dada de una muestra reaccione, o
(d) el tiempo intervalo requerido para que una concentración de reactivo caiga a cierto nivel.
(11.2) Vida media
En cuanto a la concentración de un reactivo restante en cualquier momento después de que la reacción haya comenzado podemos tener una variación, normalmente esperamos que nos pidan la concentración en valores absolutos a partir de la concentración en valores absolutos. Sin embargo, podemos tener una solicitud de calcular un valor relativo es decir un porcentaje de consumo. Normalmente el porcentaje de consumo que más nos interesa es el 50% para calcular la vida media de una sustancia, pero nos pueden pedir cualquier porcentaje del reactivo.
\[t = -\frac{\ln\left(f_r\right)}{k} = -\frac{\ln\left(1 - f_c\right)}{k}\] Eq 11.8
Tiempo con respecto a una fracción, en ese caso la fracción \(f_{re}\) corresponde a la fracción de la concentración final que queda sin reaccionar del reactivo clave. Adicionalmente recuerde que la ecuación funciona para fracciones sino para porcentajes así que dividir entre 100 y que existe otro parámetro semejante pero opuesto que es la fracción consumida \(f_{c}=0\) .
Ejemplo. Hallar el tiempo requerido para consumir el 50% del reactivo clave para cualquier valor de k.
\[t_{\text{med}} = \frac{0.693}{k}\] Eq 11.9
Vida media de una reacción de primer orden.
Tenga en cuenta que la vida media también puede estimarse gráficamente como el tiempo requerido para que cualquier concentración disminuya a la mitad.
Química de Chang10
✔️ Práctica 13.6. Calcular la vida media de la descomposición de N2O5 si la constante de velocidad es 5.7 x 10-4 s-1.
Química la ciencia central 13
La ecuación (11.3) \(\ln(c_i) = -k \cdot t + \ln(c_{oi})\) se puede usar para verificar si una reacción es de primer orden y para determinar su velocidad constante. Esta ecuación tiene la forma de la ecuación general para una línea recta, \(y = m \cdot x + b\), en la que \(m\) es la pendiente y \(b\) es la intersección en \(y\) de la línea. Por lo tanto, para una reacción de primer orden, una gráfica de \(m\) versus tiempo da una línea recta con una pendiente de \(-k\) y una intersección en \(y\) de \(\ln(c_{oA})\). Una ecuación de primer orden siempre tiene su forma de logaritmo natural como una línea recta.
La anterior es una prueba importante porque algunos procesos relevantes para otras áreas del conocimiento se fundamentan en este tipo de matemáticas, estamos hablando específicamente de los métodos de datación radiométricos, los cuales deben estandarizarse inicialmente en laboratorios antes de poderse aplicar a muestras geológicas, y uno de los pasos de estandarización es precisamente la corroboración de que estos obedecen a una cinética de primer orden a varias concentraciones iniciales y finales, lo cual permite construir una curva de interpolación.
En el laboratorio sería imposible determinar todos los puntos de una curva debido a que muchas cinéticas de reacción son muy demoradas, pero se pueden hacer mediciones en varios puntos diferentes, y determinar que la tendencia general es la de la curva predicha por la de la ecuación de Euler. Sin embargo, la cinética de primer orden no sólo modela a los métodos de datación radiométricos sino a muchos otros tipos de procesos químicos como por ejemplo la conversión del metil isonitrilo CH3NC en su isómero acetonitrilo. Como los experimentos muestran que la reacción es de primer orden, podemos escribir la ecuación de velocidad:
\[ \ln[A] = -k \cdot t + \ln[A]_o \] Eq 11.10
Ecuación de cinética de reacción de primer orden empleando la notación corchete para un reactivo A que en este caso será el metil isonitrilo.
Llevamos a cabo la reacción a una temperatura a la que el isonitrilo de metilo es un gas de (199 °C) y en la Figura 11.1a se muestra cómo la presión de este gas varía con el tiempo. Podemos usar la presión como una unidad de concentración para un gas porque sabemos por la ley del gas ideal que la presión es directamente proporcional al número de moles por unidad de volumen. La figura Figura 11.1b se muestra que una gráfica del logaritmo natural de la presión frente al tiempo es una línea recta. La pendiente de esta línea es -5.1 × 10-5 s-1. (Debe verificar esto usted mismo, recordando que su resultado puede variar ligeramente del nuestro debido a imprecisiones asociadas con la lectura del gráfico). Debido a que la pendiente de la línea es igual a \(-k\), la constante de velocidad para esta reacción es igual a 5.1 × 10-5 s-1.
Figura 11.1. Datos cinéticos para la conversión de metil isonitrilo en acetonitrilo.
12. Reacciones de segundo orden
12. Reacciones de segundo orden
Una reacción de segundo orden es aquella en la que la velocidad depende de una concentración de reactivo elevada a la segunda potencia o de las concentraciones de dos reactivos cada una elevada a la primera potencia. Para simplificar, consideremos las reacciones de los productos tipo “A → productos” o “A + B → productos” que son de segundo orden en un solo reactivo, A:
\[\frac{1}{{c_i}} = k \cdot t + \frac{1}{{c_{oi}}}\] Eq 12.1
(12.1) Distinguiendo órdenes de reacción
La ecuación \(\frac{1}{{c_i}} = k \cdot t + \frac{1}{{c_{oi}}}\), como la ecuación \(\ln(c_i) = -k \cdot t + \ln(c_{oi})\), tiene cuatro términos y cualquiera de estas puede calcularse conociendo las otras tres. La ecuación 12.1 también tiene la forma de una línea recta \(y = m \cdot x + b\). Si la reacción es de segundo orden, una gráfica de \(\frac{1}{c_{oA}}\) versus \(t\) produce una línea recta con pendiente \(k\) (positiva) e intersección en \(\frac{1}{c_{oA}}\). Una forma de distinguir entre las leyes de tasa de primer y segundo orden es hacer sus respectivas gráficas y la que arroje una forma recta será el modelo al que pertenece realmente la ecuación química.
Sin embargo, a veces es más fácil decirlo que hacerlo, debido a los errores experimentales intrínsecos de la realidad del laboratorio, puede que tengamos una serie de datos en la cual resulta un poco difícil distinguir si es una línea recta o una curva. En tales casos emplearemos la función de Excel denominada valor Rcuadrado.
Un modelo lineal y en general cualquier modelo de regresión se ajusta más a los datos medidos si su valor de R cuadrado es 1 o cercano a 1, y entre más diferente es el Rcuadrado de 1, significa que los datos se diferencian de manera cada vez más significativa del modelo empleado.
Por ende, en la práctica lo que vamos a hacer es generar los valores de Rcuadrado de los modelos que deseamos comparar, ya sean exponenciales o lineales, Excel hace ambas regresiones automáticamente, aunque lo más congruente es linealizar para comparar siempre modelos lineales. Aquella regresión (mediante agregar línea de tendencia) que tiene un R cuadrado más cercano a 1, será aquella que tiene sus datos de manera más congruente con el modelo matemático que estamos empleando.
(12.2) Vida media
Al igual que con las reacciones de primer orden un parámetro importante es el tiempo requerido para consumir cierto porcentaje de un reactivo clave.
\[t_f = \frac{1}{{c_{oi} \cdot k}} \left(\frac{1}{{f_r}} - 1\right) = \frac{1}{{c_{oi} \cdot k}} \left(\frac{1}{{1 - f_c}} - 1\right)\] Eq 12.2
Tiempo con respecto a una fracción, en ese caso la fracción \(f_{re}\) corresponde a la fracción de la concentración final que queda sin reaccionar del reactivo clave. Adicionalmente recuerde que la ecuación funciona para fracciones sino para porcentajes así que dividir entre 100 y que existe otro parámetro semejante pero opuesto que es la fracción consumida \(f_{c}=0\).
\[t_{\text{med}} = \frac{1}{{c_{oi} \cdot k}}\] Eq 12.3
Vida media de una reacción de segundo orden.
Química de Chang10
✔️ Práctica 13.7a. La reacción 2A → B es de segundo orden con una constante de velocidad de 51/M-min a 24°C. (a) Comenzando con [A]0 = 0.0092 M, ¿cuánto tardará [A]t = 3.7 x 10-3 M?
✔️ Práctica 13.7a. La reacción 2A → B es de segundo orden con una constante de velocidad de 51/M-min a 24°C. (b) Calcule la vida media de la reacción si la concentración inicial es de A es 0.0092 M.
Química la ciencia central 13
13. Reacciones de orden cero
13. Reacciones de orden cero
Hemos visto que, en una reacción de primer orden, la concentración de un reactivo A disminuye de forma no lineal, como lo muestra la curva roja en la Figura 13.1. A medida que [A] disminuye, la tasa a la que desaparece disminuye en proporción. Una reacción de orden cero es aquella en la que la tasa de desaparición de A es independiente de [A].
Figura 13.1. Comparación de las reacciones de primer orden y de orden cero para la desaparición del reactivo A con el tiempo.
La ley de velocidad para una reacción de orden cero es:
\[c_i = -k \cdot t + c_{oi}\] Eq 13.1
Esta es la ecuación para una línea recta con intersección vertical \(c_{oA}\) y pendiente \(-k \cdot t\), como se muestra en la curva azul de la Figura 13.1. El tipo más común de reacción de orden cero ocurre cuando un gas sufre descomposición en la superficie de un sólido. Si la superficie está completamente cubierta por moléculas en descomposición, la velocidad de reacción es constante porque el número de moléculas de superficie en reacción es constante, siempre que quede algo de sustancia en fase gaseosa.
Al igual que con las reacciones de primer orden un parámetro importante re es el tiempo requerido para consumir cierto porcentaje de un reactivo clave.
\[t = \frac{c_{oi} \cdot (1 - f_r)}{k} = \frac{c_{oi} \cdot f_c}{k}\] Eq 13.2
Tiempo con respecto a una fracción, en ese caso la fracción \(f_{re}\) corresponde a la fracción de la concentración final que queda sin reaccionar del reactivo clave. Adicionalmente recuerde que la ecuación funciona para fracciones sino para porcentajes así que dividir entre 100 y que existe otro parámetro semejante pero opuesto que es la fracción consumida \(f_{c}=0\).
\[t_{\text{med}} = \frac{0.5 \cdot c_{oi}}{k}\] Eq 13.3
Vida media de una reacción de cero orden.
14. Vida media de un reactivo y la medida de tiempo
14. Vida media de un reactivo y la medida de tiempo
La vida media de una reacción, es el tiempo requerido para que la concentración de un reactivo alcance la mitad de su valor inicial. La vida media es una forma conveniente de describir qué tan rápido ocurre una reacción, especialmente si se trata de un proceso de primer orden. Una reacción rápida tiene una vida media corta. Las vidas medias para las reacciones de cero, primer y segundo orden fueron determinadas en las secciones anteriores y corresponden a:
|
\[t_{\text{med}} = \frac{0.693}{k}\] Primer orden |
\[t_{\text{med}} = \frac{1}{{c_{oi} \cdot k}}\] Segundo orden |
\[t_{\text{med}} = \frac{0.5 \cdot c_{oi}}{k}\] Cero orden |
De lo anterior, vemos que el tiempo de vida media para una ley de tasa de primer orden no depende de la concentración inicial de ningún reactivo, mientras que para las otras dos ordenes de reacción sí. En consecuencia, la vida media permanece constante durante toda la reacción de primer orden. Si, por ejemplo, la concentración de un reactivo es 0.120 M en algún momento de la reacción, será 0.060 M después de una vida media. Después de que pase una vida media más, la concentración caerá a 0.030 M, y así sucesivamente. La ecuación vida media de una reacción de primer orden también indica que podemos calcular \(t_{med}\) si sabemos \(k\) y calcular \(k\) si sabemos \(t_{med}\). Adicionalmente podemos saber que \(k\) es constante si calculamos diferentes segmentos de la curva con diferentes valores de concentración
Figura 14.1. Los datos cinéticos para la reordenación de metil isonitrilo a acetonitrilo a 199 °C, que muestran la vida media de la reacción. Observe que no se tomaron datos durante toda la descomposición, sino solo algunos segmentos de la curva, pero que como se predice analíticamente, será irrelevante dado que la constante permanece constante sin importar la concentración inicial.
El cambio en la concentración a lo largo del tiempo para el reordenamiento de primer orden del metil isonitrilo gaseoso a 199 ° C se representa gráficamente en la Figura 14.1. Debido a que la concentración de este gas es directamente proporcional a su presión durante la reacción, hemos elegido graficar la presión en lugar de la concentración en este gráfico. La primera vida media ocurre a 13600 s (3.78 h). En un momento 13600 s más tarde, la presión de metil isonitrilo (y, por lo tanto, la concentración) ha disminuido a la mitad de la mitad, o un cuarto, del valor inicial. En una reacción de primer orden, la concentración del reactivo disminuye a la mitad en cada una de una serie de intervalos de tiempo regularmente espaciados, cada intervalo igual a \(t_{med}\).
(14.1) Etilbromuro en la atmósfera
Los compuestos conocidos como clorofluorocarbonos (CFC) son agentes bien conocidos responsables de la destrucción de la capa protectora de ozono de la Tierra. Otra molécula simple que tiene el potencial de destruir la capa de ozono estratosférico es el bromuro de metilo, CH3Br (Figura 14.2). Debido a que esta sustancia tiene una amplia gama de usos, incluido el tratamiento antimicótico de semillas de plantas, se ha producido en grandes cantidades en el pasado (alrededor de 150 millones de libras por año en todo el mundo en 1997, en el apogeo de su producción). En la estratosfera, el enlace C - Br se rompe a través de la absorción de radiación de longitud de onda corta. Los átomos de Br resultantes catalizan la descomposición de O3.
Figura 14.2. Distribución y destino del metilbromuro en la atmósfera de la Tierra.
El bromuro de metilo se elimina de la atmósfera inferior mediante una variedad de mecanismos, incluida una reacción lenta con el agua del océano: CH3Br(g)+H2O(l)→CH3OH(aq)+HBr(aq).
Para determinar la importancia potencial del CH3Br en la destrucción de la capa de ozono, es importante saber qué tan rápido la reacción elimina el CH3Br de la atmósfera inferior antes de que pueda difundirse en la estratosfera.
La vida útil promedio de CH3Br en la atmósfera inferior de la Tierra es difícil de medir porque las condiciones que existen en la atmósfera son demasiado complejas para ser simuladas en el laboratorio. En cambio, los científicos analizaron casi 4000 muestras atmosféricas recolectadas sobre el Océano Pacífico en busca de varias sustancias orgánicas traza, incluido el bromuro de metilo. A partir de estas mediciones, fue posible estimar el tiempo de residencia atmosférica para CH3Br.
El tiempo de residencia atmosférica está relacionado con la vida media de CH3Br en la atmósfera inferior, suponiendo que el CH3Br se descompone mediante un proceso de primer orden. A partir de los datos experimentales, se estima que la vida media del bromuro de metilo en la atmósfera inferior es de 0.8-0.1 años. Es decir, una colección de moléculas de CH3Br presentes en cualquier momento dado, en promedio, se descompondrá al 50% después de 0.8 años, el 75% se descompondrá después de 1,6 años, y así sucesivamente. Una vida media de 0.8 años, aunque relativamente corta, es lo suficientemente larga como para que CH3Br contribuya significativamente a la destrucción de la capa de ozono.
En 1997 se llegó a un acuerdo internacional para eliminar el uso de bromuro de metilo en los países desarrollados en 2005. Sin embargo, en los últimos años se han solicitado y otorgado exenciones para usos agrícolas críticos. Sin embargo, la producción mundial autorizada se redujo a 26 millones de libras en 2012, tres cuartos de los cuales se utilizan en los Estados Unidos.
(14.2) Datación radiológica y antigüedad de la Tierra
Puede consultar este enlace: https://cienciasdejoseleg.blogspot.com/2023/05/geologia.html#6., para obtener información más detallada, sin embargo, el punto de es que el decaimiento radiactivo sigue una cinética de reacción de primer orden, en consecuencia, la concentración inicial del reactivo clave, es irrelevante. De hecho, en el enlace podrá ver que el argumento que se emplea para llegar a la ecuación de cinética de primer orden es diferente de que hemos empleado en esta sección, por lo que no es un copia y pega exacto, pero aun así se llega a la misma conclusión la vida media de una reacción de primer orden.
En consecuencia, es posible calcular la vida media de la reacción con sólo un segmento o pocos segmentos de la curva, lo cual trae a su vez la consecuencia de que es innecesario medir la descomposición radioactiva durante miles de millones de años, siempre y cuando tengamos un equipo lo suficientemente sensible como para medir la descomposición radioactiva durante unas pocas horas, días, meses, o años de una reacción de transmutación muy lenta. Con el equipo adecuado será posible tomar datos de varios momentos de una curva, y corroborar que la constante de decaimiento es independiente de la concentración inicial, y en consecuencia será argumento suficiente para poder medir la antigüedad de una muestra siempre y cuando no tengamos contaminantes, o pérdidas de sustancia clave.
15. Energía de activación
15. Energía de activación
Las velocidades de reacción de la mayoría de las reacciones químicas aumentan a medida que aumenta la temperatura. Por ejemplo, la masa aumenta más rápido a temperatura ambiente que cuando está refrigerada, y las plantas crecen más rápidamente en clima cálido que en frío. Podemos ver el efecto de la temperatura sobre la velocidad de reacción al observar una reacción de quimioluminiscencia (una que produce luz), como la de las barras de luz Cyalume® (Figura 15.1.).
Figura 15.1. La temperatura afecta la velocidad de la reacción de quimioluminiscencia en barras de luz: la reacción de quimioluminiscencia ocurre más rápidamente en agua caliente y se produce más luz.
¿Cómo se refleja este efecto de temperatura observado experimentalmente en la ley de velocidad de reacción? La velocidad más rápida a una temperatura más alta se debe a un aumento en la velocidad constante al aumentar la temperatura. Por ejemplo, reconsideremos la reacción de primer orden que vimos en la Figura 14.1, a saber, CH3NC →CH3CN.
Figura 15.2. Dependencia de la temperatura de la constante de velocidad para la conversión de metilisonitrilo en acetonitrilo.
La Figura 15.2 muestra la constante de velocidad para esta reacción en función de la temperatura. La velocidad constante y, por lo tanto, la velocidad de la reacción aumenta rápidamente con la temperatura, aproximadamente el doble por cada aumento de 10 °C.
(15.1) Modelo de colisiones
Las velocidades de reacción se ven afectadas tanto por las concentraciones de reactivos como por la temperatura. El modelo de colisión, basado en la teoría cinético-molecular (química de gases), explica ambos efectos a nivel molecular. La idea central del modelo de colisión es que las moléculas deben colisionar para reaccionar. Cuanto mayor es el número de colisiones por segundo, mayor es la velocidad de reacción. A medida que aumenta la concentración de reactivo, por lo tanto, aumenta el número de colisiones, lo que conduce a un aumento en la velocidad de reacción. De acuerdo con la teoría cinética molecular de los gases, el aumento de la temperatura aumenta las velocidades moleculares. A medida que las moléculas se mueven más rápido, chocan con más fuerza (con más energía) y con mayor frecuencia, aumentando las velocidades de reacción.
Para que ocurra una reacción, sin embargo, se requiere más que simplemente una colisión: debe ser el tipo correcto de colisión. Para la mayoría de las reacciones, de hecho, solo una pequeña fracción de colisiones conduce a una reacción. Por ejemplo, en una mezcla de H2 e I2 a temperaturas y presiones normales, cada molécula sufre aproximadamente 1010 colisiones por segundo. Si cada colisión entre H2 e I2 resultara en la formación de HI, la reacción terminaría en mucho menos de un segundo. En cambio, a temperatura ambiente, la reacción avanza muy lentamente porque solo una de cada 1013 colisiones produce una reacción. ¿Qué impide que la reacción ocurra más rápidamente?
(15.2) Orientación de la molécula
En la mayoría de las reacciones, las colisiones entre moléculas provocan una reacción química solo si las moléculas están orientadas de cierta manera cuando colisionan.
Figura 15.3. Las colisiones moleculares pueden o no conducir a una reacción química entre Cl y NOCl.
Las orientaciones relativas de las moléculas durante la colisión determinan si los átomos están posicionados adecuadamente para formar nuevos enlaces. Por ejemplo, considere la reacción Cl + NOCl→ NO + Cl2., que tiene lugar si la colisión une a los átomos de Cl para formar Cl2, como se muestra en el panel superior de la Figura 15.3. En contraste, en la colisión que se muestra en el panel inferior, los dos átomos de Cl no chocan directamente entre sí, y no se forman productos.
(15.3) Energía de activación
La orientación molecular no es el único factor que influye en si una colisión molecular producirá una reacción. En 1888, el químico sueco Svante Arrhenius sugirió que las moléculas deben poseer una cierta cantidad mínima de energía para reaccionar. Según el modelo de colisión, esta energía proviene de las energías cinéticas de las moléculas en colisión. Tras la colisión, la energía cinética de las moléculas se puede utilizar para estirar, doblar y finalmente romper enlaces, lo que lleva a reacciones químicas. Es decir, la energía cinética se usa para cambiar la energía potencial de la molécula. Si las moléculas se mueven muy lentamente, en otras palabras, con muy poca energía cinética, simplemente rebotan entre sí sin cambiar. La energía mínima requerida para iniciar una reacción química se llama energía de activación, \(E_a\) y su valor varía de una reacción a otra.
Figura 15.4. Se necesita energía para superar una barrera entre los estados inicial y final.
La situación durante las reacciones es análoga a la que se muestra en la Figura 15.4. El golfista golpea la pelota para que se mueva sobre la colina en dirección a la copa. La colina es una barrera entre la pelota y la copa. Para alcanzar la copa, el jugador debe impartir suficiente energía cinética con el putter para mover la pelota hacia la parte superior de la barrera. Si no imparte suficiente energía, la pelota rodará hasta la mitad de la colina y luego regresará hacia él. Del mismo modo, las moléculas requieren una cierta energía mínima para romper los enlaces existentes durante una reacción química. Podemos pensar en esta energía mínima como una barrera energética. En el reordenamiento de metil isonitrilo a acetonitrilo, por ejemplo, podríamos imaginar la reacción pasando a través de un estado intermedio en el que la porción N C de la molécula de metil isonitrilo está de lado.
La Figura 15.5 muestra que se debe suministrar energía para estirar el enlace entre el grupo H3C y el grupo N ‚C para permitir que el grupo N C gire. Después de que el grupo N C se ha torcido lo suficiente, el enlace C C comienza a formarse y la energía de la molécula cae.
Figura 15.5. Perfil energético para la conversión de metil isonitrilo H3CNC en su isómero acetonitrilo H3CCN.
Por lo tanto, la barrera para la formación de acetonitrilo representa la energía necesaria para forzar a la molécula a pasar por un estado intermedio relativamente inestable, análogo a forzar la bola en la Figura 15.4 sobre la colina. La diferencia entre la energía de la molécula inicial y la energía más alta a lo largo de la vía de reacción es la energía de activación, \(E_{a}\). La molécula que tiene la disposición de los átomos que se muestra en la parte superior de la barrera se denomina complejo activado o estado de transición.
La conversión de H3C N≡C a H3C C≡N es exotérmica. Por lo tanto, la Figura 15.5 muestra que el producto tiene una energía menor que el reactivo. Sin embargo, el cambio de energía para la reacción, \(\Delta E\), no tiene efecto sobre la velocidad de reacción. La tasa depende de la magnitud de \(E_{a}\); en general:
cuanto menor es el valor de \(E_{a}\), más rápida es la reacción.
Tenga en cuenta que la reacción inversa es endotérmica. La energía de activación para la reacción inversa es igual a la energía que debe superarse si se acerca a la barrera desde la derecha: \(\Delta E + E_{a}\). Por lo tanto, alcanzar el complejo activado para la reacción inversa requiere más energía que para la reacción directa; para esta reacción, hay una barrera más grande que vencer de derecha a izquierda que de izquierda a derecha.
Brown13 química la ciencia central
Muestra 14.10. Ordenar las reacciones modeladas con los siguientes perfiles de energía de activación, desde la mas lenta a la mas rápida.
Cualquier molécula particular de metil isonitrilo adquiere energía suficiente para superar la barrera de energía a través de colisiones con otras moléculas. Recordemos de la teoría cinética-molecular de los gases que, en cualquier instante, las moléculas de gas se distribuyen en energía en un amplio rango. La Figura 15.6 muestra la distribución de energías cinéticas para dos temperaturas, comparándolas con la energía mínima necesaria para la reacción, \(E_{a}\). A la temperatura más alta, una fracción mucho mayor de las moléculas tiene una energía cinética mayor que \(E_{a}\), lo que conduce a una mayor velocidad de reacción.
Figura 15.6. El efecto de la temperatura sobre la distribución de las energías cinéticas de las moléculas en una muestra.
Para una colección de moléculas en la fase gaseosa, la fracción de moléculas que tienen energía cinética igual o mayor que \(E_{a}\) tiene dada por la expresión:
\[f = e^{-\frac{E_a}{R \cdot T}}\] Eq 15.1.
En esta ecuación, \(R\) es la constante de los gases ideales (8.14 J/mol-K) y \(T\) es la temperatura absoluta. Para tener una idea de la magnitud de \(f\), supongamos que \(E_{a}\) es 100 kJ/mol, un valor típico de muchas reacciones, y que \(T\) es 300 K. El valor calculado de \(f\) es 3.9×10-18, un número extremadamente pequeño. A 320 K, \(f\) = 4.7×10-17. Por lo tanto, solo un aumento de 20° en la temperatura produce un aumento de más de diez veces en la fracción de moléculas que poseen al menos 100 kJ/mol de energía.
(15.4) La ecuación de Arrhenius
Arrhenius señaló que, para la mayoría de las reacciones, el aumento de la velocidad con el aumento de la temperatura no es lineal (Figura 15.2). Encontró que la mayoría de los datos de velocidad de reacción obedecían a una ecuación basada en:
(a) la fracción de moléculas que poseen energía \(E_{a}\) o mayor,
(b) el número de colisiones por segundo, y
(c) la fracción de colisiones que tienen la orientación apropiada. Estos tres factores se incorporan a la ecuación de Arrhenius:
\[k = A \cdot e^{-\frac{E_a}{R \cdot T}}\] Eq 15.2
El factor de frecuencia, \(A\), es constante, o casi, a medida que varía la temperatura. Este factor está relacionado con la frecuencia de las colisiones y la probabilidad de que las colisiones estén orientadas favorablemente para la reacción, debido a que la frecuencia de colisión aumenta con la temperatura, \(A\) también tiene cierta dependencia de la temperatura, pero esta dependencia es mucho menor que el término exponencial. Por lo tanto, \(A\) se considera aproximadamente constante. A medida que aumenta la magnitud de \(E_{a,k}\) disminuye porque la fracción de moléculas que poseen la energía requerida es menor. Por lo tanto, a valores fijos de \(T\) y \(A\), las velocidades de reacción disminuyen a medida que \(E_{a}\) aumenta.
16. Usando la ecuación de Arrhenius
16. Usando la ecuación de Arrhenius
La cinética química es una rama fundamental de la química que se encarga de estudiar las velocidades de las reacciones químicas y los factores que las afectan. Una de las herramientas más poderosas para comprender y modelar estas velocidades es la Ecuación de Arrhenius. Propuesta por el químico sueco Svante Arrhenius a finales del siglo XIX, esta ecuación establece una relación entre la velocidad de una reacción química y la temperatura, proporcionando una base sólida para el diseño y optimización de procesos químicos.
\[k = A \cdot e^{-\frac{E_a}{R \cdot T}}\] Eq 15.2
Sin embargo, trabajar con la Ecuación de Arrhenius puede parecer desafiante en un principio, ya que involucra términos exponenciales y cálculos que pueden resultar complicados. En este artículo, exploraremos algunos atajos algebraicos y técnicas de representación gráfica que facilitarán significativamente la aplicación de esta poderosa ecuación. Veremos cómo podemos simplificar el análisis cinético y obtener información valiosa sobre las reacciones químicas de una manera más eficiente.
A través de ejemplos concretos y explicaciones paso a paso, desglosaremos los conceptos clave detrás de la Ecuación de Arrhenius y cómo podemos utilizarla para comprender y predecir las tasas de reacción. Estas técnicas simplificarán los cálculos y nos permitirán obtener información importante sobre las energías de activación, las constantes de velocidad y otros parámetros cinéticos.
Así que, prepárense para explorar el emocionante mundo de la cinética química a través de la lente de la Ecuación de Arrhenius y descubrir cómo los atajos algebraicos y las representaciones gráficas pueden hacer que este campo sea más accesible y fascinante que nunca. ¡Comencemos nuestro viaje hacia una comprensión más profunda de las reacciones químicas y sus velocidades!
|
\[ \ln k = -\frac{E_a}{R} \cdot \frac{1}{T} + \ln A \] |
Eq 16.1 Forma linealizada de la ecuación de Arrhenius. |
|
\[E_a = -R \ln\left(\frac{k}{k_0}\right)\left(\frac{1}{T_0} - \frac{1}{T}\right)^{-1}\] |
Eq 16.2 Primera forma dinámica de la ecuación de Arrhenius para calcular la energía de activación. |
|
\[k = k_o \cdot e^{-\frac{E_a}{R}\left(\frac{1}{T_o} - \frac{1}{T}\right)}\] |
Eq 16.3 Segunda forma dinámica de la ecuación de Arrhenius para calcular la constante de velocidad final en términos de la constante de velocidad inicial, la energía de activación y dos temperaturas. |
(16.1) Opción gráfica
La ecuación \(k = k_o \cdot e^{-\frac{E_a}{R}\left(\frac{1}{T_o} - \frac{1}{T}\right)}\) muestra una opción gráfica para calcular la energía de activación. Una gráfica de \(\ln k\) versus \(1/T\) es una línea con una pendiente igual a \(-\frac{E_a}{R}\) y una intersección en (y) igual a \(\ln A\). Por lo tanto, la energía de activación se puede determinar midiendo k en una serie de temperaturas, graficando \(\ln k\) versus \(1/T\), y calculando \(E_a\) a partir de la pendiente de la línea resultante. Adicionalmente, en la opción gráfica vamos a tener dos subopciones para resolver esto:
(a) Opción manual: deberemos elegir: de la línea recta de manera arbitraria y calcular la pendiente manualmente. esta opción tiene el problema de que, si los datos no apoyan una línea recta perfecta, podremos calcular una energía de activación errónea, si elegimos precisamente aquellos puntos que más se desvían de la línea recta. De allí que para esta estrategia usted debe analizar la gráfica y escoger los puntos que más se aproximen a la recta.
(b) Opción automática: básicamente se trata de usar Excel, mediante los comandos insertar → Gráficos → Dispersión → Dispersión con líneas suavizadas y marcadores → seleccionar la recta en la gráfica → clic derecho → insertar línea de tendencia → lineal y activar los comandos de ecuación del gráfico y valor de Rcuadrado. Al graficar en Excel tenga cuidado de colocar primero la columna para el eje (x), y luego la columna para el eje (y) en la tabla de datos antes que insertar una gráfica de dispersión.
(16.2) Opción analítica
La ecuación 13.4 nos muestra una opción analítica para calcular la energía de activación. Debido a que podemos usar una variedad de parejas de datos, lo aconsejable es calcular para las parejas adyacentes presentes y luego calcular el promedio aritmético.
(16.3) El valor de la constante de los gases ideales
Recuerde que la constante de gases ideales deberá expresarse en unidades de energía: 8.314 J /mol-K. Si lo que desea es expresar directo en kilojulios debe usar 8.314 x 10-3 kJ /mol-K.
(16.4) Cual opción es más conveniente
Aunque la teoría nos dice que la gráfica \(\ln k\) vs \(1/T\) debe ser una línea recta, en la práctica los datos pueden no tener una relación de línea recta simplemente debido a errores de muestreo, errores experimentales entre otros, por lo que el método gráfico establecido por el libro de texto como la química de Chang presenta un problema, elegir arbitrariamente las coordenadas para dibujar la línea recta nos puede llevar a generar valores de energía de activación diferentes aún dentro de la misma serie de datos, incluso los valores que obtengamos como resultado de una regresión lineal o del promedio de las energías de activación para cada pareja posible en la serie de datos puede llevarnos a resultados que no son exactamente iguales. La pregunta es ¿cuándo esperar que los valores por las dos rutas sean diferentes? y la respuesta radica en el valor \(R^2\) de la regresión lineal que nos da Excel:
👉 para un valor de \(R^2\) igual a 1 significa que la regresión lineal se ajusta perfectamente a un modelo de línea recta, y en consecuencia es de esperarse que la energía de activación calculada gráficamente y analíticamente sean iguales.
👉 si el valor de \(R^2\) de la regresión lineal en Excel es menor que uno, deberemos esperar que las energías de activación calculadas por la ruta gráfica y por la ruta analítica tengan sus diferencias. las diferencias aumentarán a medida que el valor de \(R^2\) se haga más diferente de 1.
Química de Chang10
Brown13 química la ciencia central
17. Mecanismos de reacción
17. Mecanismos de reacción
Una ecuación equilibrada para una reacción química indica las sustancias presentes al comienzo de la reacción y las presentes al final de la reacción. Sin embargo, no proporciona información sobre los pasos detallados que ocurren a nivel molecular a medida que los reactivos se convierten en productos. Los pasos por los cuales ocurre una reacción se llama mecanismo de reacción “e involucran fórmulas extrañas que normalmente no deberían ser correctas, de allí que son transitorias e inestables”. En el nivel más sofisticado, un mecanismo de reacción describe el orden en que los enlaces se rompen y forman y los cambios en las posiciones relativas de los átomos en el curso de la reacción.
En química, un mecanismo de reacción es la secuencia paso a paso de reacciones elementales por las cuales ocurre un cambio químico general. Un mecanismo químico es una conjetura teórica que trata de describir en detalle lo que ocurre en cada etapa de una reacción química general. Los pasos detallados de una reacción no son observables en la mayoría de los casos. El mecanismo conjeturado se elige porque es termodinámicamente factible y tiene soporte experimental en intermedios aislados u otras características cuantitativas y cualitativas de la reacción. También describe cada intermedio reactivo, complejo activado y estado de transición, y qué enlaces se rompen (y en qué orden), y qué enlaces se forman (y en qué orden). Un mecanismo completo también debe explicar la razón de los reactivos y catalizadores utilizados, la estereoquímica observada en los reactivos y productos, todos los productos formados y la cantidad de cada uno.
(17.1) Reacciones elementales
Hemos visto que las reacciones tienen lugar debido a colisiones entre las moléculas que reaccionan. Por ejemplo, las colisiones entre moléculas de metil isonitrilo CH3NC pueden proporcionar la energía para permitir que el CH3NC se reorganice en acetonitrilo:
Figura 17.1. Mecanismo de reacción de la síntesis de acetonitrilo.
De manera similar, la reacción de NO y O3 para formar NO2 y O2 parece ocurrir como resultado de una sola colisión que involucra moléculas de NO y O3 adecuadamente orientadas y suficientemente energéticas: NO(g)+O3(g)→NO2(g)+O2(g), ambas reacciones ocurren en un solo evento o paso y se llaman reacciones elementales. El número de moléculas que participan como reactivos en una reacción elemental define la molecularidad de la reacción. Si está involucrada una sola molécula, la reacción es unimolecular. La reorganización del metil isonitrilo es un proceso unimolecular. Las reacciones elementales que implican la colisión de dos moléculas reactivas son bimoleculares. La reacción entre NO y O3 es bimolecular. Las reacciones elementales que implican la colisión simultánea de tres moléculas son termoleculares. Las reacciones termoleculares son mucho menos probables que los procesos unimoleculares o bimoleculares y son extremadamente raras. La posibilidad de que cuatro o más moléculas choquen simultáneamente con cualquier regularidad es aún más remota; en consecuencia, tales colisiones nunca se proponen como parte de un mecanismo de reacción. Por lo tanto, casi todos los mecanismos de reacción contienen solo reacciones elementales unimoleculares y bimoleculares.
(17.2) Mecanismos multi-paso
El cambio neto representado por una ecuación química equilibrada a menudo ocurre por un mecanismo de varios pasos que consiste en una secuencia de reacciones elementales. Por ejemplo, por debajo de 225 ° C, la reacción: NO2(g)+CO(g)→NO(g)+CO2(g)., Parece proceder en dos reacciones elementales (o dos pasos elementales), cada uno de los cuales es bimolecular. Primero, dos moléculas de NO2 chocan y un átomo de oxígeno se transfiere de una a la otra. El NO3 resultante luego colisiona con una molécula de CO y le transfiere un átomo de oxígeno. Como el NO3 no es un reactivo ni un producto de la reacción, se forma en una reacción elemental y se consume en la siguiente, se llama intermedio. Los mecanismos de múltiples pasos involucran uno o más intermedios. Los intermedios no son lo mismo que los estados de transición. Los intermedios pueden ser estables y, por lo tanto, a veces pueden identificarse e incluso aislarse.
Figura 17.2. Suma de ecuaciones químicas, recuerde que si la misma sustancia está en lados opuestos, se cancela.
Los estados de transición, por otro lado, siempre son inherentemente inestables y, como tales, nunca pueden aislarse. Sin embargo, el uso de técnicas avanzadas "ultrarrápidas" a veces nos permite caracterizarlas.
Figura 17.3. El perfil energético de una reacción, que muestra estados de transición y un intermedio.
(17.3) Ley de velocidad de reacción para reacciones elementales
En secciones anteriores, enfatizamos que las leyes de velocidad de reacción deben determinarse experimentalmente; no pueden predecirse a partir de los coeficientes de ecuaciones químicas equilibradas. Ahora estamos en condiciones de entender por qué esto es así. Cada reacción se compone de una serie de uno o más pasos elementales, y las leyes de velocidad y las velocidades relativas de estos pasos dictan la ley de velocidad general para la reacción. De hecho, la ley de velocidad para una reacción se puede determinar a partir de su mecanismo, como veremos en breve, y se puede comparar con la ley de velocidad experimental. Por lo tanto, nuestro próximo desafío en cinética es llegar a mecanismos de reacción que conduzcan a leyes de velocidad consistentes con las observadas experimentalmente. Comenzamos examinando las leyes de velocidad de las reacciones elementales. Las reacciones elementales son significativas de una manera muy importante: si una reacción es elemental, su ley de velocidad se basa directamente en su molecularidad. Por ejemplo, considere la reacción unimolecular (A → B).
A medida que aumenta el número de moléculas A, el número que reacciona en un intervalo de tiempo dado aumenta proporcionalmente. Por lo tanto, la tasa de un proceso unimolecular es de primer orden:
\[\bar{r} = k[A]\] Eq 17.1
Para los pasos elementales bimoleculares ( A + B → C + D), la ley de velocidad es de segundo orden, como en la reacción.
\[\bar{r} = k[A] [B]\] Eq 17.2
La ley de tasa de segundo orden se deriva directamente de la teoría de colisión. Si duplicamos la concentración de A, el número de colisiones entre las moléculas de A y B se duplica; asimismo, si duplicamos [B], el número de colisiones entre A y B se duplica. Por lo tanto, la ley de tasas es de primer orden tanto en [A] como [B] y en segundo orden en general. Las leyes de velocidad para todas las reacciones elementales factibles se dan en la tabla:
Tabla 17.1. Reacciones elementales y sus leyes de velocidad de reacción.
Observe cómo cada ley de velocidad se sigue directamente de la molecularidad de la reacción, en otras palabras, aunque la ley de velocidad general no usa los números estequiométricos las leyes de velocidad para los mecanismos si lo hacen. Es importante recordar, sin embargo, que no podemos decir simplemente observando una ecuación química global equilibrada si la reacción involucra uno o varios pasos elementales. De lo anterior se sigue que:
(a) En una reacción de mecanismo a un paso, los órdenes de reacción son iguales a los números estequiométricos;
(b) si lo anterior no se cumple, significa que el mecanismo de reacción involucrados o más pasos elementales.
El problema ahora radica en que cada paso elemental al poseer su propia cinética va a generar efectos distintivos en la ley de cinética general. A continuación, analizaremos dos casos para reacciones cuyo mecanismo involucra dos pasos. Adicionalmente es conveniente recordar que:
(c) los mecanismos termoleculares son raros comparados con los monomoleculares y bimoleculares.
(17.4) El paso determinante de la velocidad para un mecanismo de varios pasos
La mayoría de las reacciones ocurren por mecanismos que involucran dos o más reacciones elementales. Cada paso del mecanismo tiene su propia constante de velocidad y energía de activación.
Primer paso más lento
A menudo, un paso es mucho más lento que los demás y la velocidad general de una reacción no puede exceder la velocidad del paso elemental más lento. Debido a que el paso lento limita la velocidad de reacción general, se le llama paso determinante de la velocidad.
En algunas reacciones químicas la diferencia de velocidad de reacción entre los pasos puede llegar a ser de varios órdenes de magnitud diferentes, por lo que la velocidad de reacción de la más lenta va a ser casi igual a la velocidad de reacción general, asumiendo que las velocidades de reacción de los siguientes pasos son insignificantes.
Química de Chang 10
Brown13 química la ciencia central
✔ Muestra 14.13. Si la siguiente reacción ocurre en una sola reacción elemental, prediga su ley de velocidad: H2(g) + Br2(g) → 2 HBr(g)
Segundo paso más lento
En este caso la rapidez promedio general parece no concordar, o no estar expresada en términos del paso determinante, esto se debe a que el paso determinante está expresado en términos de intermediarios, pero aun así sigue siendo un embudo de paso. Lo que debe hacerse es expresar la sustancia intermedia en términos de las concentraciones de la reacción rápida asumiendo que se ha alcanzado un equilibrio. De esta manera para el mecanismo A ⇌ B, B → C para la forma general A → C tendríamos que:
(a) Plantear la rapidez promedio para las reacciones reversa y directa del paso 1.
(b) Despejar la concentración de la o las sustancias intermediarias.
(c) Igualar en la rapidez promedio del paso 2.
(d) Cancelar términos.
Brown13 química la ciencia central
✔ Práctica 14.15.2. El primer paso de un mecanismo que implica la reacción del bromo es Br2(g) ⇌ 2 Br(g) (rápido), ¿Cuál es la expresión que relaciona la concentración de Br(g) con la de Br2(g)?
18. Catalizadores
18. Catalizadores
Un catalizador es una sustancia que cambia la velocidad de una reacción química sin sufrir un cambio químico permanente. La mayoría de las reacciones en el cuerpo, la atmósfera y los océanos ocurren con la ayuda de catalizadores. Gran parte de la investigación química industrial es dedicada a la búsqueda de catalizadores más efectivos para reacciones de importancia comercial. También se dedican grandes esfuerzos de investigación a encontrar medios para inhibir o eliminar ciertos catalizadores que promueven reacciones indeseables, como las que corroen metales, envejecen nuestros cuerpos y causan caries.
(18.1) Catálisis homogénea
Un catalizador que está presente en la misma fase que los reactivos en una mezcla de reacción se llama catalizador homogéneo. Los ejemplos abundan tanto en solución como en fase gaseosa. Considere, por ejemplo, la descomposición de peróxido de hidrógeno acuoso, en agua y oxígeno: 2 H2O2(aq)→2H2O(l)+O2(g). En ausencia de un catalizador, esta reacción ocurre de forma extremadamente lenta. Sin embargo, muchas sustancias son capaces de catalizar la reacción, incluido el ion bromuro, que reacciona con el peróxido de hidrógeno en solución ácida, formando bromo acuoso y agua: H2O2(aq)+2Br-(aq)+2H+(aq)→2H2O(l)+Br2(aq).
Figura 18.1. Catálisis homogénea. Efecto del catalizador sobre la velocidad de descomposición del peróxido de hidrógeno en agua y oxígeno gaseoso.
Si esta fuera la reacción completa, el ion bromuro no sería un catalizador porque experimenta un cambio químico durante la reacción. Sin embargo, el peróxido de hidrógeno también reacciona con el Br—(aq): H2O2(aq)+Br2(aq)→2Br-(aq)+2H+(aq)+O2(g)
Figura 18.2. Suma de ecuaciones químicas.
Cuando el H2O2 se ha descompuesto por completo, nos queda una solución incolora de Br— (aq), lo que significa que este ion es de hecho un catalizador de la reacción porque acelera la reacción sin sufrir ningún cambio neto. En contraste, Br2 (aq) es un intermedio porque primero se forma y luego se consume. Ni el catalizador ni el intermedio aparecen en la ecuación para la reacción global. Tenga en cuenta, sin embargo, que el catalizador está allí al comienzo de la reacción, mientras que el intermedio se forma durante el curso de la reacción.
¿Cómo funciona un catalizador? Si pensamos en la forma general de las leyes de velocidad de reacción:
\[\overline{r} = k \prod_{a=1}^n c_r^a\] Eq 18.1
Debemos concluir que el catalizador debe afectar el valor numérico de \(k\), la constante de tasa. Sobre la base de la ecuación de Arrhenius
\[k = A \cdot e^{-\frac{E_a}{RT}}\] Eq 18.2
Donde \(k\) está determinado por la energía de activación \(E_a\) y el factor de frecuencia \(A\). Un catalizador puede afectar la velocidad de reacción al alterar el valor de \(E_{oa}\). Podemos imaginar que esto suceda de dos maneras: el catalizador podría proporcionar un nuevo mecanismo para la reacción que tenga un valor de \(E_a\) menor que el valor de \(E_a\) para el reacción no catalizada, o el catalizador podría ayudar en la orientación de los reactivos y así aumentar \(A\). Los efectos catalíticos más dramáticos provienen de la disminución de \(E_a\). Como regla general, un catalizador reduce la energía de activación general para una reacción química.
Figura 18.3. Perfiles de energía para la descomposición no catalizada y catalizada por bromuro de H2O2.
Un catalizador puede reducir la energía de activación para una reacción al proporcionar un mecanismo diferente para la reacción. En la descomposición del peróxido de hidrógeno, por ejemplo, tienen lugar dos reacciones sucesivas de H2O2, primero con bromuro y luego con bromo. Debido a que estas dos reacciones juntas sirven como una vía catalítica para la descomposición del peróxido de hidrógeno, ambas deben tener energías de activación significativamente más bajas que la descomposición no catalizada.
(18.2) Catálisis heterogénea
Un catalizador heterogéneo es uno que existe en una fase diferente de la fase de las moléculas reactivas, generalmente como un sólido en contacto con reactivos gaseosos o reactivos en una solución líquida. Muchas reacciones de importancia industrial son catalizadas por las superficies de los sólidos. Por ejemplo, el petróleo crudo se transforma en moléculas de hidrocarburos más pequeñas mediante el uso de los llamados catalizadores de "craqueo". Los catalizadores heterogéneos a menudo están compuestos de metales u óxidos metálicos.
El paso inicial en la catálisis heterogénea suele ser la adsorción de reactivos. La adsorción se refiere a la unión de moléculas a una superficie, mientras que la absorción se refiere a la absorción de moléculas en el interior de una sustancia. La adsorción ocurre porque los átomos o iones en la superficie de un sólido son extremadamente reactivos. Debido a que la reacción catalizada ocurre en la superficie, a menudo se usan métodos especiales para preparar catalizadores para que tengan áreas de superficie muy grandes. A diferencia de sus contrapartes en el interior de la sustancia, los átomos e iones superficiales tienen una capacidad de unión no utilizada que puede usarse para unir moléculas desde la fase gaseosa o de solución a la superficie del sólido.
Figura 18.4. Catálisis heterogénea. Mecanismo de reacción de etileno con hidrógeno en una superficie catalítica.
La reacción del gas hidrógeno con el gas etileno para formar gas etano proporciona un ejemplo de catálisis heterogénea: C2H4(g)+H2(g)→C2H6(g) con un \(\Delta H^{o}\) = -137 kJ/mol. Aunque esta reacción es exotérmica, ocurre muy lentamente en ausencia de un catalizador. Sin embargo, en presencia de un metal finamente pulverizado, como el níquel, el paladio o el platino, la reacción se produce fácilmente a temperatura ambiente a través del mecanismo diagramado en la Figura 18.4. Tanto el etileno como el hidrógeno se adsorben en la superficie del metal. Tras la adsorción, el enlace H-H del H2 se rompe, dejando inicialmente dos átomos de H unidos a la superficie del metal pero relativamente libres para moverse. Cuando un hidrógeno encuentra una molécula de etileno adsorbida, puede formar un enlace con uno de los átomos de carbono, destruyendo efectivamente el enlace C-C π y dejando un grupo etilo C2H5 unido a la superficie a través de un enlace metal-carbono . Este enlace es relativamente débil, por lo que cuando el otro átomo de carbono también encuentra un átomo de hidrógeno, se forma fácilmente un sexto enlace C-H , y se libera una molécula de etano C2H6 de la superficie del metal.
(18.3) Enzimas
El cuerpo humano se caracteriza por un sistema extremadamente complejo de reacciones químicas interrelacionadas, todo lo cual debe ocurrir a ritmos cuidadosamente controlados para mantener la vida. Una gran cantidad de catalizadores biológicos maravillosamente eficientes conocidos como enzimas son necesarios para que muchas de estas reacciones ocurran a velocidades adecuadas. La mayoría de las enzimas son moléculas de proteínas grandes con pesos moleculares que varían de aproximadamente 10 000 a aproximadamente 1 millón de u. Son muy selectivos en las reacciones que catalizan (aunque pueden catalizar varias reacciones semejantes con sustratos parecidos), y algunos son absolutamente específicos, que operan para una sola sustancia en una sola reacción. La descomposición del peróxido de hidrógeno, por ejemplo, es un proceso biológico importante. Debido a que el peróxido de hidrógeno se oxida fuertemente, puede ser fisiológicamente dañino. Por esta razón, la sangre y el hígado de los mamíferos contienen una enzima, la catalasa, que cataliza la descomposición del peróxido de hidrógeno en agua y oxígeno.
Figura 18.5. Las enzimas aceleran las reacciones. El hígado macerado libera muchas enzimas, entre ellas la catalasa, que agregada al agua oxigenada, libera oxígeno.
La Figura 18.5 muestra la aceleración dramática de esta reacción química por la catalasa en el hígado de res. La reacción que cataliza cualquier enzima dada tiene lugar en una ubicación específica en la enzima llamada sitio activo. Las sustancias que reaccionan en este sitio se llaman sustratos. El modelo de cerradura y llave proporciona una explicación simple de la especificidad de una enzima.
Figura 18.6. Modelo de cerradura y llave para la acción enzimática.
La combinación de enzima y sustrato se llama complejo enzima-sustrato. Aunque la Figura 18.6 muestra que tanto el sitio activo como su sustrato tienen una forma fija, el sitio activo a menudo es bastante flexible y, por lo tanto, puede cambiar de forma a medida que se une al sustrato. La unión entre el sustrato y el sitio activo implica atracciones dipolo-dipolo, enlaces de hidrógeno y fuerzas de dispersión. A medida que las moléculas de sustrato ingresan al sitio activo, se activan de alguna manera para que puedan reaccionar rápidamente. Este proceso de activación puede ocurrir, por ejemplo, por el retiro o la donación de densidad electrónica de un enlace particular o grupo de átomos en el sitio activo de la enzima. Además, el sustrato puede distorsionarse en el proceso de adaptación al sitio activo y hacerse más reactivo. Una vez que se produce la reacción, los productos salen del sitio activo, permitiendo que entre otra molécula de sustrato.
El sustrato se muestra como que encaja perfectamente en el sitio activo, al igual que una llave encaja en una cerradura. La lisozima es una enzima que es importante para el funcionamiento de nuestro sistema inmunitario porque acelera las reacciones que dañan (o "lisan") las paredes celulares bacterianas. La Figura 18.7 muestra un modelo de la enzima lisozima sin y con una molécula de sustrato unida.
Figura 18.7. La lisozima fue una de las primeras enzimas para las cuales se describió una relación estructura-función. Este modelo muestra cómo el sustrato (amarillo) "encaja" en el sitio activo de la enzima.
Las enzimas son enormemente más eficientes que los catalizadores no bioquímicos. El número de eventos de reacción catalizados individuales que ocurren en un sitio activo particular, llamado número de rotación, generalmente está en el rango de 103 a 107 por segundo. Tales números de rotación grandes corresponden a energías de activación muy bajas. En comparación con un catalizador químico simple, las enzimas pueden aumentar la velocidad constante para una reacción dada en un millón de veces o más.
R. Referencias bibliográficas
R. Referencias bibliográficas
Atkins, P. W., De Paula, J., & Keeler, J. (2018). Atkins’ physical chemistry. Oxford university press.
Baeza-Baeza, J. J., & García-Alvarez-Coque, M. C. (2014). Extent of Reaction Balances: A Convenient Tool to Study Chemical Equilibria. World J. Chem. Educ, 2, 54–58. Retrieved from https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1015.5804&rep=rep1&type=pdf
Brady, J. E., & Humiston, G. E. (1986). General Chemistry: Principles and Structure. Wiley & Sons.
Brown, T. L., LeMay, H. E. J., Bursten, B. E., Murphy, C. J., & Woodward, P. (2009). Chemistry the central science (11th ed.). Pearson; Prentice Hall.
Brown, T. L., LeMay, H. E. J., Bursten, B. E., Murphy, C. J., Woodward, P., & Stoltzfus, M. W. (2015). Chemistry the Central Science.
Chang, R. (2006). Chang’s “General Chemistry - Essential Concepts” (4th ed.). McGraw-Hill New York.
Chang, R. (2010). Chemistry (10th ed.). McGraw-Hill New York.
Chang, R., & Overby, J. (2011). General Chemistry,Th e Essential Concepts (11th ed.). McGraw-Hill New York.
Ebbing, D. D., & Gammon, S. D. (2008). General chemistry. (Houghton Mifflin Company, Ed.) (9th ed.). Bonston.
Ferner, R. E., & Aronson, J. K. (2016). Cato Guldberg and Peter Waage, the history of the Law of Mass Action, and its relevance to clinical pharmacology. British Journal of Clinical Pharmacology, 81(1), 52–55.
García-García, J. L. (2021). Hacia un equilibrio químico verdaderamente analítico. Educación Química, 32(1), 133–146. Retrieved from http://revistas.unam.mx/index.php/req/article/view/75075
Garst, J. F. (1974). The extent of reaction as a unifying basis for stoichiometry in elementary chemistry. Journal of Chemical Education, 51(3), 194. Retrieved from https://files.eric.ed.gov/fulltext/EJ1179603.pdf
Gilbert, T. R., Kirss, R. V, Foster, N., & Davies, G. (2012). Chemistry, the science in context (3rd ed.). W. W. Norton & Company, Inc.
Gorzynski, J. (2010). General, organic, and biological chemistry (1st ed.). McGraw-Hill Education.
Hanyak Jr, M. E. (2014). Extent of Reaction or Events of Reaction?
IUPAC. (2020). Compendium of chemical terminology. (International Union of Pure and Applied Chemistry, Ed.) (Version 3.). Blackwell Science Oxford. Retrieved from https://goldbook.iupac.org/
IUPAC, McNaught, A. D., & Wilkinson, A. (2019). extent of reaction, ξ. In Compendium of Chemical Terminology, 2nd ed. (the “Gold Book”) (2nd ed.). Blackwell Scientific Publications, Oxford. Retrieved from https://goldbook.iupac.org/terms/view/E02283
Jespersen, N. D., Brady, J. E., & Hyslop, A. (2012). Chemistry The Molecular Nature of Matter (6th ed.). USA: Wiley.
Matamála, M., & Gonzalez, P. (1976). Química General. Cultural.
Moretti, G. (2015). The “extent of reaction”: a powerful concept to study chemical transformations at the first-year general chemistry courses. Foundations of Chemistry, 17(2), 107–115.
Petrucci, R. H., Harwood, W. S., & Herring, F. G. (2003). Química General (8th ed.). Prentice Hall.
Petrucci, R. H., Herring, F. G., Madura, J. D., & Bissonnette, C. (2010). General Chemistry Principles and Modern Applications (10th ed.). Pearson.
Ptáček, P., Opravil, T., & Šoukal, F. (2018). A Brief Introduction to the History of Chemical Kinetics. Introducing the Effective Mass of Activated Complex and the Discussion on the Wave Function of This Instanton.
Raymond, K. W. (2014). General, Organic, and Biological Chemistry, an Integrated Aproach (4th ed.). Wiley.
Silberberg, M. S. (2009). Chemistry, The Molecular Nature of Matter and Change (5th ed.). McGraw-Hill Education.
Timberlake, K. C. (2015). Chemistry An Introduction to General, Organic, and Biological Chemistry (15th ed.). USA: Pearson.
Whitten, K. W., Davis, R. E., Peck, M. L., & Stanley, G. G. (2010). Chemistry (9th ed.). Brooks/Cole.
Zumdahl, S. S., & Zumdahl, S. A. (2007). Chemistry (7th ed.). Boston: Houghton Mifflin Company.
Zumdahl, S. S., Zumdahl, S. A., & DeCoste, D. J. (2018). Chemistry (10th ed.). Cengage Learning.




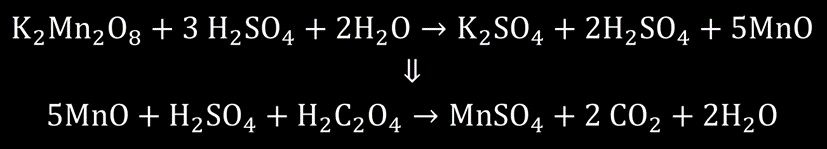





































No hay comentarios:
Publicar un comentario